Emergence of social cohesion in a model society of greedy, mobile individuals

Abstract

Human wellbeing in modern societies relies on social cohesion, which can be characterized by high levels of cooperation and a large number of social ties. Both features, however, are frequently challenged by individual self-interest. In fact, the stability of social and economic systems can suddenly break down as the recent financial crisis and outbreaks of civil wars illustrate. To understand the conditions for the emergence and robustness of social cohesion, we simulate the creation of public goods among mobile agents, assuming that behavioral changes are determined by individual satisfaction. Specifically, we study a generalized win-stay-lose-shift learning model, which is only based on previous experience and rules out greenbeard effects that would allow individuals to guess future gains. The most noteworthy aspect of this model is that it promotes cooperation in social dilemma situations despite very low information requirements and without assuming imitation, a shadow of the future, reputation effects, signaling, or punishment. We find that moderate greediness favors social cohesionby a coevolution between cooperation and spatial organization, additionally showing that those cooperation-enforcing levels of greediness can be evolutionarily selected. However, a maladaptive trend of increasing greediness, although enhancing individuals’ returns in the beginning, eventually causes cooperation and social relationships to fall apart. Our model is, therefore, expected to shed light on the long-standing problem of the emergence and stability of cooperative behavior.

Contemporary societies are complex systems that are permanently challenged by the selfishness of their members. For example, the recent financial crisis and subsequent turmoil illustrate the vulnerability of modern socioeconomical systems. However, the problem is not new. The history of civilizations displays a recurrent pattern of development and collapse of both medium-sized cultures and large empires. Different theories have been proposed to explain why such systemic failures occur again and again, despite experience gained in the past. Such theories are based, for example, on the growing complexity of societies during their evolution (1) or an overexploitation of the environment (2).

Here, we will explore possible psychosocial reasons that may underlie these processes of rise and fall, which are in close relationship with the emergence and stability of social cohesion. Although cooperation and agglomeration provide the fabric that allows civilizations to emerge and thrive (3), they are also subject to strong destabilizing forces. We investigate a twofold operational definition of social cohesion, comprising cooperation (4, 5) and agglomeration (6). By cooperation, we mean contributions of work or goods to achieve a common end (7, 8), and by agglomeration, we mean the establishment of relationships between peers. Destabilizing forces are modeled by means of social dilemma situations, particularly public goods games (9, 10) (PGGs), which exemplify the joint but discretionary contribution to a common good.

In our stylized formalization of societal enterprises, the wellbeing of participants improves if they contribute to the public good, but there is a free-rider problem: why contribute if one can enjoy the benefits without bearing the costs, and why cooperate if one may obtain a greater personal benefit by cheating? Hence, game theory predicts for the Homo economicus (a strictly optimizing egoist) a socially deficient outcome called the tragedy of the commons, where nobody contributes. This paradigm of selfishness, however, seems to be challenged by a large number of experiments (11). To explain this discrepancy, a number of additional mechanisms have been proposed, such as a shadow of the future or reputation effects. In particular, the punishment of free riders by cooperators is able to sustain and enhance initial levels of cooperation, which is observed in experimental iterated PGGs (12, 13).

Another cooperation-supporting mechanism is spatial agglomeration (14), particularly if strategy choices can coevolve with spatial configurations as in migratory games (15). To account for agglomeration as an emergent phenomenon in our model, some freedom is needed in the choice of interaction partners for the PGGs (16, 17). To this end, we embed our population in a spatial network, allowing individuals to be mobile (15). As we will see, agglomeration offers higher potential benefits to individuals, because it allows them to participate in a larger number of PGGs. However, for our specification of PGGs, more populated groups endanger the stability of cooperation. Although increasing levels of cooperation and agglomeration provide the largest benefits to society, they also make it more vulnerable to exploitation. This problem establishes a dual social dilemma in our model society.

The particular relevance of our model resides in studying a fully experience-based, self-referential satisfying rule for the decision making of individuals. This rule extends, among other models, the learning model proposed by Macy and Flache (18) and the win-stay-lose-shift rule of Nowak and Sigmund (19). To this end, we posit a very low-information setting, which particularly avoids greenbeard effects and the related capability to determine or guess others’ payoffs and strategies. Such assumptions are typically made by models based on imitation rules, which have been questioned by recent experimental results for spatial games (20, 21). Therefore, the exploration of mechanisms that can promote cooperation seems to be more pressing than ever. Our results show that the decision model that we propose is able to solve the dual dilemma posed by social cohesion, sustaining both cooperation and social agglomeration in an evolutionarily consistent and robust manner.

Model

A population of individuals is distributed over a spatial network (14, 20, 22) like, for instance, a 2D square lattice with degree k = 8 (i.e., the number of neighbors of each node is eight). Because the population density is lower than one, individuals can move around and occupy any empty site within a certain range R.

Every player i is the center of a neighborhood with N_i interaction partners, where N_i depends on the number of occupied sites around the player (0 ≤ N_i ≤ k). A PGG is held in each neighborhood, and therefore, each individual i participates in N_i + 1 PGGs, one in which she is the center of the neighborhood and N_i others centered in her neighbors. SI Appendix, Fig. S1 provides an illustration of such spatially distributed PGGs.

In a PGG, contributing to the public good is voluntary. Hence, we can distinguish two strategies, which are called cooperate (C) if the player contributes or defect (D) otherwise. The quantity contributed by each cooperator to each PGG is assumed to be one. The total amount contributed by cooperators in the neighborhood is then multiplied by a synergy factor r > 1, which reflects the benefits reached by cooperation. Finally, the resulting amount is shared among all players, regardless of their contribution. Therefore, if there are n cooperators among the N participants (including the focal player), the payoffs per PGG of a C player and a D player are, respectively (Eqs. 1 and 2),

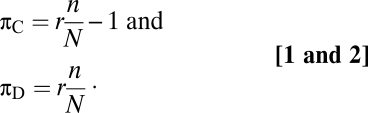It is clear that, for any positive value of the synergy factor r and any number of cooperators in the neighborhood, defectors obtain larger benefits than cooperators. For this reason, D is the strictly dominant strategy of the game, and hence, the only evolutionarily stable strategy (23). This finding implies that the expected outcome of the game is no contribution by anybody. If r > 1, a social dilemma arises, because then, full cooperation is more profitable for everyone than full defection (everyone would receive large benefits instead of no benefits); however, individual self-interest seems to prevent this desirable outcome.

Given the dependence on the group size N in our definition of PGGs (Eqs. 1 and 2), not only cooperation but also agglomeration constitute a dilemma in our model. For any given PGG, the benefit obtained per contribution decreases if the group size increases, which makes cooperation benefits in larger groups more dependent on others’ contributions and in consequence, riskier (24). However, having more neighbors implies getting involved in more PGGs, which enables larger potential benefits. From the viewpoint of achievable payoffs, it is most promising to be involved in the largest possible number of PGGs. In a lattice of degree k, this finding means being surrounded by k neighbors and thus, participating in k + 1 PGGs. The best-performing society is, therefore, the one formed by individuals who behave cooperatively and are densely connected through social interactions. However, as stated before, it also increases the number of people participating in the different PGGs, which raises the risk of exploitation by free riders. In summary, a dual dilemma of both cooperation and agglomeration exists in our model.

Concerning the behavioral update, individuals in our model society are expected to maintain or change their strategy (C or D) and/or their social relationships (position) depending on the payoffs obtained in the PGGs. A standard kind of decision rule is constituted by the learning rules (18, 25–27), according to which subjects have a tendency to repeat actions that maintain or improve their current wellbeing and avoid those that reduce it (19). In our model, individuals tend to change their strategy or social neighborhood when they are dissatisfied with their current payoffs. Hence, they follow a satisfying dynamic (28). Each player i has an individual aspiration level a_i, which determines her satisfaction s_i, defined as (Eq. 3)

π_i is the payoff in the current round of PGGs (which is accumulated in all of the neighborhoods to which the player belongs), whereas η_i represents a Gaussian noise with zero mean. If s_i > 0, the player is satisfied and maintains strategy and position, whereas if s_i ≤ 0, the player is dissatisfied and changes strategy and/or location in a random and statistically independent way. The probability of change is proportional to the amount of dissatisfaction |s_i| (s_i < 0). The amplitude of the noise η_i in Eq. 3 is chosen to create a trembling hand effect (29), especially when the subject is uncertain about the situation (i.e., when |s_i| ∼ 0).

In the low-information setting assumed in this study, individuals are not aware of other subjects’ payoffs, and they do not know the range of payoffs theoretically attainable from the PGGs, which is in stark contrast to the quite extensive information requirements of previously investigated migratory games (15). Players neither know how many neighbors they have nor realize others’ strategies. Greenbeard effects (30, 31), which would allow players to identify cooperative neighbors by a distinctive trait, are excluded. As a result, individuals cannot imitate successful strategies of others or strictly optimize their own strategy. Instead, subjects attempt to be satisfied, which seems to make sense particularly for new environments and complex societies.

According to Eq. 3, the satisfaction of an individual is very much influenced by her aspiration level a_i. In our model, this aspiration level depends on the subject's greediness α_i, as given by (Eq. 4)

π_i,min(t) and π_i,max(t) denote the time-dependent minimum and maximum payoff, respectively, as remembered by the subject, who has a certain memory decay rate. The greediness of each individual has a range of 0 ≤ α_i ≤ 1, which allows the aspiration level to vary between π_i,min and π_i,max. These extreme payoff values correspond to the minimum and maximum payoffs that the individual experiences in the successive rounds of PGGs, and they are subject to a habituation effect. As a result, subjects adjust their aspiration level according to their personal payoff history and their individual greediness. Materials and Methods has full details of the learning rule.

Results and Discussion

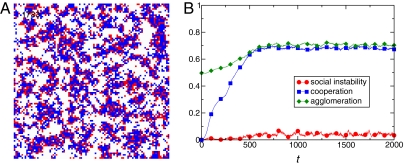
Fig. 1 presents the typical behavior of our model when individuals are moderately greedy (α_i = 0.3). Fig. 1A displays a snapshot of the stationary state, and Fig. 1B shows the time evolution of the following three population variables: (i) social instability (i.e., the fraction of individuals who have changed strategy and/or social neighborhood in the last time step), (ii) cooperation (the fraction of cooperative individuals in the population), and (iii) agglomeration [the average value of the actual number of neighbors of an individual divided by the maximum possible value (the degree k of the underlying network)]. All three measures are bounded by the range between zero and one. The evolution displayed in Fig. 1B starts with a population of defectors only, randomly distributed in the network (here, a regular square lattice). Interestingly, after some time, cooperation and agglomeration emerge, reaching a stationary state where clearly more than one-half of the population is cooperative and individuals tend to agglomerate and form cooperative clusters. Note that the initial appearance of cooperation is possible only because of the presence of noise in the decision rule. Later on, cooperation and agglomeration are rapidly promoted by the spatiotemporal dynamics in the population as individuals experience the possibility of higher payoffs and try to realize them. It is also worth mentioning that the average number of behavioral changes is very low in the stationary state, which implies that a large majority of subjects are satisfied with their payoffs.

Fig. 1.

Evolution of social cohesion in a model society with moderately greedy individuals. (A) Snapshot of the stationary state (cooperators are in blue and defectors are in red). (B) Time evolution of three population variables (details in the text). The time dependence of the levels of cooperation and agglomeration shows that the emergence of cooperation is based on a coevolution of prosocial behavior and spatial organization. The low level of social instability indicates that changes of strategy and/or location are rare, which corresponds to a majority of satisfied individuals. All subjects are assumed to have the same greediness of α = 0.3. The synergy factor of the PGGs was set to r = 5, and the underlying network was a half-occupied square lattice of size 10⁴ with eight neighbors. The initial population consisted only of defectors, who were randomly distributed over the lattice.

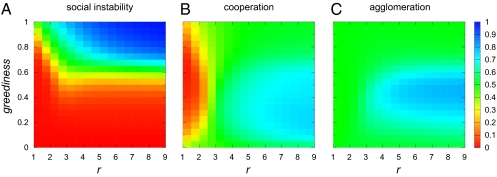
In stark contrast, high levels of greediness destabilize this well-performing society. Fig. 2 explores the parameter dependence of the stationary behavior of the model averaged over many realizations. The parameter space presented here is spanned by the synergy factor r and the greediness α, which are the most relevant control parameters of the model (additional parameter dependencies are discussed in SI Appendix). Our results reveal that, when levels of greediness increase beyond a certain threshold, society becomes unstable, with most individuals dissatisfied and prone to change their strategy and social neighborhood.

Fig. 2.

Stationary state of a model society composed of greedy, mobile individuals. The panels display the asymptotic value of three variables describing the stationary state of the population as a function of the synergy factor r and the greediness level α: (A) social instability, (B) cooperation, and (C) agglomeration. All other model parameters are the same as those parameters used in Fig. 1. Note that high values of greediness imply social instability (i.e., frequent strategy and location changes because of dissatisfaction). A coevolution of social cooperation and spatial agglomeration results from moderate levels of greediness (0.2 ≲ α ≲ 0.55) and sufficiently high synergy factors. Note that cooperation for a PGG in the corresponding well-mixed case (i.e., with nonstructured interactions) would be expected only for r > k + 1 = 9.

In comparison, a model society of individuals with low levels of greediness is unable to realize social benefits. It lacks the drive to develop effective cooperation and agglomeration, because nongreedy individuals become easily satisfied with whatever payoffs they obtain and thus, maintain their strategy and position. In consequence, neither cooperation nor agglomeration emerges in such a society. On the contrary, moderate greediness causes individuals’ dissatisfaction, making them explore other strategies and/or positions and experience the benefits of being cooperative in a cooperative neighborhood. As long as those benefits are sufficient to satisfy individuals’ aspirations, cooperation and agglomeration coevolve and create a stable population with a high level of cohesion. At high levels of greediness, finally, individuals are so difficult to satisfy that they keep exploring other locations and strategies, thereby destroying cooperative clusters.

Another interesting insight resulting from Fig. 2 is that challenging PGGs with very low synergy factors (r ∼ 1) create a stable society, but one that is locked in noncooperative behavior. Defection is, in this case, the only behavior that is compatible with the aspirations of individuals, regardless of their level of greediness.

The most salient feature of our model is the emergence and stability of a society with widespread cooperation and agglomeration despite the low information requirements. It is important to point out that this behavior is robust against changes of many model details provided that some crucial properties are preserved, namely a sufficient amount of habituation in the learning rule and some amount of mobility. Habituation implies that improvements or deteriorations in achieved payoffs are eventually forgotten, which is equivalent in our learning model to individuals adapting their expectations to the range of payoffs that they have experienced recently. Materials and Methods and SI Appendix have full implementation details and additional examples.

Our results, therefore, suggest that, as long as social dilemma situations are not too severe, a main determinant of social stability and wellbeing is the greediness of individuals. Moderate greediness promotes cooperation and the stability of dense social relationships, whereas high levels of greediness destabilize the social fabric, undermining cooperation and social agglomeration.

It is crucial to ask the following questions. What determines the greediness of individuals? Is it a matter of genetic inheritance? Or is it driven by cultural forces (32, 33)? From our perspective, prevalent levels of greediness in a population should be those levels that provide subjects with an evolutionary advantage in the long run. To explore this idea, we introduced the following extension to our model. Instead of specifying a fixed value of greediness, as we did in the simulations underlying Figs. 1 and 2, we started with a certain initial distribution of individual greediness levels. We then made these greediness parameters α_i evolve according to an endogenous evolutionary process. More specifically, we implemented a selection of the greediness parameters α_i using a Moran process (34, 35). After every individual had the opportunity to update her strategy and her location, one of them was selected proportionally to her payoff (her fitness in evolutionary terms), and her greediness was copied by one randomly chosen individual. This birth–death process was repeated a number of times before another round of PGGs and behavioral updates (strategy and position) took place. It is worth noting that, in a given round, the behavioral updates are performed for every individual in the population, whereas the Moran updates only affect a few individuals per round.

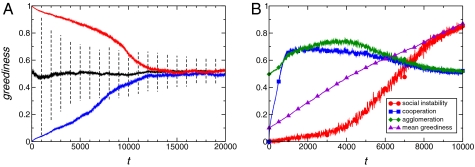
Simulating cultural imitation, be it success-biased or not, would require information about others’ behavior and eventually, performance, which would make it incompatible with the fundamental low-information assumptions of our model. In consequence, we treat the Moran updates of greediness as evolution of a genetic trait under natural selection. For this reason, we have chosen a number of Moran updates between PGGs rounds, which allows the evolution of greediness to take place on a significantly slower time scale than that of behavioral changes (36). Fig. 3A displays three examples of the evolution of greediness. One of them starts from a uniform initial distribution of greediness over the full range of possible values, whereas the other two begin with extreme values and evolve with the addition of a small mutation term. Remarkably, the stationary distribution of greediness converges to similar values in all three cases, falling into the range that corresponds to the cooperative and aggregated state of society (Fig. 2). This finding has a very clear and interesting implication: levels of greediness that promote a society with widespread cooperation and agglomeration can be evolutionarily selected.

Fig. 3.

Evolution of greediness (A) with selection performed by a Moran process and (B) in the case of maladaptation effects. (A) Evolutionary selection of greediness when a Moran process is applied to the individual greediness parameters α_i. The time scale of greediness evolution is 100 times slower than the time scale of behavioral evolution (strategy and position changes). The remaining model parameters are the same those parameters used in Fig. 1. The continuous lines show the population average of greediness 〈α_i〉, and the dashed bars (black curve) display the 2σ range every 1,000 steps. The black curve corresponds to a population initialized with randomly assigned values of α_i in the interval of zero to one in a uniform distribution. The blue and red curves represent the evolution of a population where all individuals start with α_i = 0 and α_i = 1, respectively, and there is random mutation implemented with the addition of a term that follows a normal distribution with SD σ = 0.02. In all three cases, the average value of greediness ends up in a similar stationary state, with a value that corresponds to a stable and cooperative society (Fig. 2). (B) Evolution of several population variables when a maladaptive trend biases the evolution of greediness to higher values. At the beginning, all individuals are assigned low greediness, with a random uniform distribution in the interval of 0 to 0.2. All other model features and parameters are the same as in A, with the exception of the positive bias to rising values of greediness. The drift term follows a half-normal distribution with SD = 0.01. Slowly increasing greediness is beneficial at the beginning of evolution, because it promotes social cohesion; however, it eventually destabilizes the model society, damaging cooperation and agglomeration.

Finally, Fig. 3B illustrates the effect of maladaptations in the evolution of subjects’ greediness. They can arise when past payoff increases are associated with growing levels of greediness and are projected into the future. To model this finding, let us assume that a small positive drift biases the evolution of greediness, and therefore, we add a small random positive term when the greediness of successful individuals is inherited by their offspring. At the early stage of evolution, increasing greediness supports cooperation and agglomeration. At some tipping point, however, the trend reverses, and social cohesion breaks down, although no structural change has taken place. From the viewpoint of the members of this society, this turn of events comes completely unexpected; the same growth of greediness that accelerated social development at the beginning causes a disastrous effect on society later.

In summary, we have studied a minimalist model of society with very low-information assumptions. Subjects simply aim to satisfy their aspirations according to a trait that we call greediness. We have shown that, even in the presence of social dilemma situations, cooperation and agglomeration can flourish if individuals are moderately greedy. It is remarkable that, in our model, subjects’ behavior is solely based on individual experience. There are no greenbeard effects, which would allow individuals to distinguish favorable neighborhoods from unfavorable ones in advance. Additionally, there are no additional mechanisms known to support cooperation, such as a shadow of the future, reputation, or punishment. Additionally, we have shown that a moderate level of greediness provides individuals with a clear evolutionary advantage given that it can be evolutionarily selected. We have also seen that this beneficial influence might lead to maladaptations, because the projection of current growing payoffs into the future would result in an increase of greediness to levels at which social cohesion ultimately breaks down. Our results strongly suggest that learning rules, particularly self-referential factors in decision making, can be a key component in the explanation of the emergence and stability of cooperation and agglomeration in human societies.

Materials and Methods

Model Definition.

In this section, we present additional details that complete the definition of the model.

In each round of PGGs, each subject is assigned a probability of changing behavior and/or location. To ensure an adequate range and scaling, this probability is calculated as (Eq. 5)

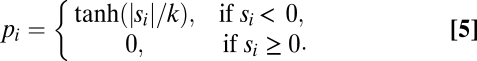The term |s_i| is the amount of dissatisfaction of subject i, whereas k normalizes it by the degree of the underlying network.

Concerning the maximum and minimum perceived payoffs π_i,max and π_i,min, we assume that individuals are able to remember important improvements or deteriorations in their experienced payoffs and that they also adjust their expectations to recent payoffs (habituation), which altogether can be interpreted as a memory effect. Therefore, we define π_i,max in this way: at the starting time (t = 0), π_i,max is initialized with the first payoff that the player obtains, and then, it is updated according to (Eq. 6)

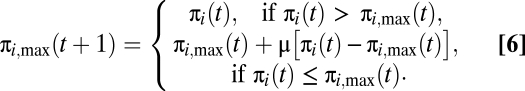In this manner, an outcome that exceeds the current maximum enters future expectations immediately. Otherwise, the last maximum payoff is eventually forgotten and becomes more similar to recent payoffs. The parameter μ, with 0 < μ < 1, determines the time scale of this exponential memory loss or habituation effect. π_i,min is analogously defined as (Eq. 7)

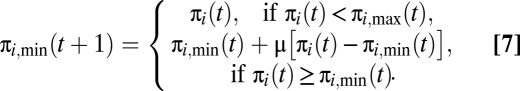On one hand, if μ were zero, there would be no forgetting, and π_i,max (π_i,min) would monotonously increase (decrease) to the maximum (minimum) achievable value. In practical terms, this limiting case converges to the one with a fixed aspiration level (similar to the rule studied in ref. 18). Infinite memory (or lack of habituation), however, does not support social cohesion in our model. It turns out that a finite memory (or some habituation) is required for the satisfaction of individuals. On the other hand, if μ were one, previous maxima and minima would be immediately forgotten, and the aspiration level would become equal to the last obtained payoff, which has a strong destabilizing effect in the model. Therefore, to implement a realistic habituation or memory effect, small nonzero values have to be chosen (0 < μ << 1), such as μ = 0.01.

A round of PGGs and the subsequent updating are performed in the following way. Every player participates in and collects payoffs from all of the PGGs played in the neighborhoods to which she belongs. The aspiration levels of each player are updated, and their satisfactions are evaluated. Those players who are dissatisfied are assigned a probability of changing strategy and/or neighborhood. They do so according to two independent random trials, one for the strategy and another for the location. The update order among subjects is randomly assigned for each round. After these updates have been performed for all of the individuals in the population, a new round begins.

Model Parameters.

Game theoretical evolutionary models may be quite sensitive to implementation details (37). For this reason, we have thoroughly checked the robustness of our results against changes in many different aspects of the model. Specifically, we have considered different values or options for (i) system size, (ii) population density, (iii) initial fraction of cooperators, (iv) migration range, (v) network topology, (vi) definition of the PGGs, (vii) aspiration noise, (viii) noise in the behavioral rule, (ix) imitative perturbations of the behavioral rule, (x) ratio between the time scales of migration and strategy change, and (xi) ratio between the time scales of evolution of behavior and greediness when the latter evolves endogenously. In all cases, the behavior of the model was qualitatively the same, and therefore, our main findings remain unchanged within reasonable parameter variations and perturbations of the model (full details in SI Appendix).

Here, we give the values of the model parameters used for the simulations reported here. The network was a 2D square regular lattice with degree k = 8 (Moore neighborhood). The network size was 10⁴ nodes. The population size was 5 × 10³ individuals, which implied a density of 0.5. Players were randomly located at initial time, all of them being defectors. The SD of the aspiration noise was η = 0.1. The maximum range of migration was R = 10. The memory parameter was μ = 0.01. Each cooperator contributed the same quantity one to each PGG in which she participated. To evaluate the stationary state (Fig. 2), we simulated the model for 5 × 10³ time steps, calculated the mean value over the last 500 steps, and averaged the results of 20 independent realizations. Test runs were made for much longer time periods, but this change did not affect the stationary state.