Measurement of c-axis angular orientation in calcite (CaCO₃) nanocrystals using X-ray absorption spectroscopy

Abstract

We demonstrate that the ability to manipulate the polarization of synchrotron radiation can be exploited to enhance the capabilities of X-ray absorption near-edge structure (XANES) spectroscopy, to include linear dichroism effects. By acquiring spectra at the same photon energies but different polarizations, and using a photoelectron emission spectromicroscope (PEEM), one can quantitatively determine the angular orientation of micro- and nanocrystals with a spatial resolution down to 10 nm. XANES-PEEM instruments are already present at most synchrotrons, hence these methods are readily available. The methods are demonstrated here on geologic calcite (CaCO₃) and used to investigate the prismatic layer of a mollusk shell, Pinctada fucata. These XANES-PEEM data reveal multiply oriented nanocrystals within calcite prisms, previously thought to be monocrystalline. The subdivision into multiply oriented nanocrystals, spread by more than 50°, may explain the excellent mechanical properties of the prismatic layer, known for decades but never explained.

X-ray linear dichroism (1) has been studied extensively theoretically (1, 2) and used experimentally to characterize man-made systems such as magnetic materials (3–7), organic molecules (8), molecular monolayers (1, 9), and liquid crystals (10). Recently, Metzler et al. showed that there is a strong X-ray linear dichroism effect in natural calcium carbonate minerals and biominerals (11, 12). Based on this effect, polarization-dependent imaging contrast (PIC) mapping done using X-ray photoelectron emission spectromicroscopy (X-PEEM) revealed the gradual ordering mechanisms in mollusk shell nacre (13), the existence of mineral blocks alternating in orientation in sea urchin teeth (14), and the mechanism of coorientation via secondary nucleation also in sea urchin teeth (15).

Here, we demonstrate that by exploiting the properties of elliptically polarizing undulators (EPUs) (16), PIC mapping can quantitatively determine orientations of individual nanocrystals with a spatial resolution of 10 nm. We note that EPUs are available at most synchrotrons around the world (17–21), and that they also produce linearly polarized X-ray beams, in which the electric field vector (hereafter referred to as linear polarization vector) can be rotated at will, in the plane perpendicular to the X-ray propagation direction. The methods presented here have similarities to those that have been used to determine the magnetization direction in magnetic materials and can be applied to any crystal with uniaxial symmetry in which dipole transitions are dominant (6, 22), including calcite and aragonite, two materials that are common in marine biominerals. The effectiveness of the technique is demonstrated here by determining the orientations of calcite nanocrystals embedded in a single crystal of geologic calcite, and then used to demonstrate that calcite prisms in the shell of the mollusk Pinctada fucata comprise multiply oriented nanocrystals, and are not single crystals, as previously believed (23–26). Analogous observations have been reported in other biominerals such as sea urchin teeth (14) and the mechanism of coorientation via secondary nucleation also in sea urchin teeth (15). The subdivision into nanocrystals may be a general strategy in biomineralization and provide the animals with improved robustness (27). The misorientation of nanocrystals described here may provide another advantage for the biomineral and thus for the host organism: Crystals that are not cooriented do not share low-energy cleavage planes, thus they eliminate the main cleaving disadvantage of all crystalline materials, while retaining the hardness of crystals.

Results and Discussion

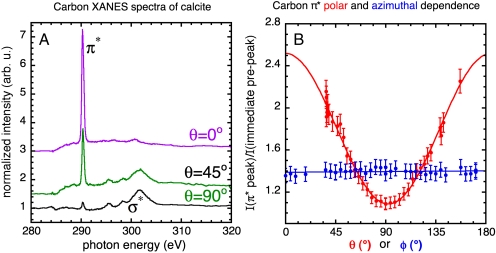
Fig. 1 shows X-ray linear dichroism as exhibited in the dependence of X-ray absorption near-edge structure (XANES) spectra from a single crystal of calcite (CaCO₃), on the polar angle θ and azimuthal angle ϕ, defined in the caption of Fig. 1. The intensity of the π^∗ peak in XANES spectra has a cos²θ dependence (11, 12) and does not depend on ϕ. A single PIC map thus can be used to show that two crystallites have different orientations, but does not yield information about absolute orientation.

Fig. 1.

(A) XANES spectra of the carbon K edge obtained from a single crystal of calcite, at three linear polarization vector angles. We define the polar angle θ to be the angle between the calcite c axis and the linear polarization vector. Fig. S1 gives a complete description of the calcite crystal and its c-axis direction. The π^∗ and σ^∗ peak intensities are anticorrelated: At large polar angles (θ = 90°) the π^∗ and σ^∗ peaks have minimum and maximum intensity, respectively. The π^∗ peak is most intense at low polar angles (θ = 0°). This effect, known as X-ray linear dichroism, is the basis for PIC mapping. (B) Polar dependence (red data points) is obtained by plotting the intensity of the π^∗ peak at 290.3 eV as a function of the polar angle θ. In this case, the linear polarization vector was fixed while the calcite crystal was rotated. As expected and predicted by theory (9), the peak intensities vary as cos²θ (the red curve is a fit of the π^∗ peak intensity to the form A + B cos²θ). The azimuthal angle ϕ is the rotation angle of the ab plane of the crystal about the c axis. The azimuthal dependence (blue data points) was obtained by varying ϕ, while keeping θ constant at 64°. No variation in the π^∗ peak intensity is observed as a function of ϕ, at this or any other angle.

Now we show that utilizing the capability to rotate the linear polarization vector enables one to determine the actual orientation of the c axis of the crystal. The method requires the elimination of artifacts arising from differences in beam intensity, sample preparation, and mounting. This elimination can be achieved either in the conventional fashion, by taking the ratio of the intensities of two anticorrelated peaks (in carbonates, this is the ratio of π^∗- over σ^∗-images; refs. 11, 12), or by taking the ratio of intensities from different polarizations at a single photon energy, determined by the position of the most polarization-sensitive peak, which in carbonates is the π^∗ peak energy.

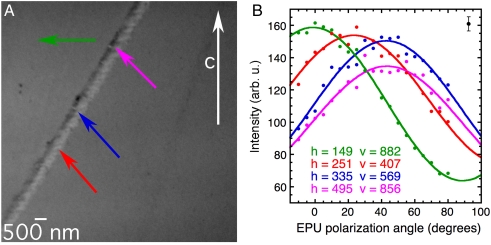
Fig. 2 demonstrates how changing the linear polarization angle enables the measurement of the c-axis orientations in crystals and nanocrystals using X-PEEM. The X-PEEM image shown (Fig. 2, Left) is of a geologic calcite crystal with a defect containing calcite nanocrystals with different orientations. The right panel shows the dependence of the unnormalized peak height at 290.3 eV on the direction of the linear polarization vector, varying from vertical to horizontal (EPU polarization angle, EPU°, varying from 0° to 90°). Each nanocrystal exhibits a cos² dependence on EPU polarization angle. The different amplitudes and phases yield the additional information that enables extraction of the c-axis orientation itself.

Fig. 2.

Stack of X-PEEM images of a geologic calcite crystal with a line of calcite defects, acquired while varying the angle of the linear polarization vector with respect to the vertical in the EPU (here referred to as EPU polarization angle or EPU°). The main crystal imaged here is illuminated by X-rays from the right-hand side of this image, as shown in the schematic of Fig. 3, and has its c axis oriented vertically, and in the plane of the sample surface. Each image in the stack is composed of 10⁶ pixels, and the field of view is 10 μm. The stack of images of the same field of view was acquired at 19 polarization angles, varying from horizontal (EPU° = 90°) to vertical (EPU° = 0°) every 5°. An animated version of this stack is shown in Movie S1. (A) Average of all 19 images. The vertical white arrow indicates the direction of the c axis of the main geologic calcite crystal, as determined using X-ray diffraction. The lighter gray level line across the field of view is a defect that contains randomly oriented nanocrystals of calcite. The colored arrows indicate the positions of the single pixels from which the polar spectra in B were acquired. (B) Intensity of the π^∗ peak at a photon energy of 290.3 eV versus EPU polarization angle. These spectra were extracted from the 10-nm pixels indicated in A and correspondingly colored and labeled with horizontal (h) and vertical (v) coordinates, on the main calcite crystal and various nanocrystals along the calcite defect. The solid curves are best fits of the experimental data, according to the function A + B cos² (EPU°-γ), where A, B, and γ are fit parameters. Notice that for the main crystal (green, pixel coordinates h = 149, v = 882), for which the orientation was known to be with the c axis vertical and in plane (in other words, along the x axis), the maximum of the polar intensity is at EPU° = θ = γ = 0°, as expected for an intensity that varies as cos²θ, with θ the angle between the electric field vector and the c axis. For the nanocrystals along the calcite defect, the unknown θ can be measured from these spectra. Notice that the magenta (h = 495, v = 856) and blue (h = 335, v = 569) curves have maxima at the same angle (45°) but with different intensities, indicating that the c axis of the magenta pixel is farther out of the xy plane than the blue pixel. The error bars were estimated from repeated acquisitions as well as from the value of γ extracted from the measurements on the main crystal, and they are consistent with the distances of the data points from the solid lines of the fits, as indicated by the error bar at the top-right corner of the plot.

To obtain the orientations of the c axes of the different nanocrystals from the data in Fig. 2, we choose the z direction to be along the propagation direction of the radiation, perpendicular to all the linear polarization vectors, the x direction as the direction of the linear polarization vector when the EPU° = 0°, and the y direction as the direction of the linear polarization vector when the EPU° = 90°.

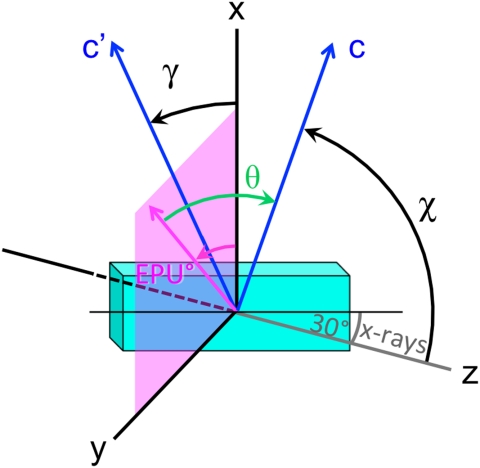
We define the angles χ and γ for each nanocrystal as in Fig. 3, so that the unit vector describing the direction of the c axis is (sin χ cos γ, sin χ sin γ, cos χ). Our analysis assumes that the measured image pixel intensity varies as A_o + B_o cos²θ with A_o and B_o both positive and known from the acquisition of a stack of images such as those in Fig. 2, which is appropriate for uniaxial crystals in which the electrical dipole contribution to the X-ray absorption is dominant (2, 28). For the data shown in Fig. 2, we determined A_o and B_o by mounting the sample with the c axis of the main crystal in plane and parallel to the x axis, so that the angle θ between the linear polarization vector and the c axis is equal to -EPU°, hence χ = 90° and cos²θ = cos² (EPU°-γ). The signal intensity from the main crystal [e.g., the green pixel at coordinates (h = 149, v = 882)] is therefore A_o + B_o cos² (EPU°-γ), and A_o and B_o can be determined by fitting the data from this pixel to this form. Once A_o and B_o are determined, one can find γ and χ for a pixel with arbitrary crystal orientation: One fits the π^∗ intensity to the form A + B cos² (EPU°-γ); the fit thus directly yields A, B, and γ, then one can calculate χ from sin²χ = B/B_o. The data from the other pixels in Fig. 2 yield the results for c-axis orientations in Table 1.

Fig. 3.

Geometry of the experiment yielding the data shown in Fig. 2. The radiation propagates along the z direction, and the linear polarization vector (magenta) is rotated between the x direction and the y direction (x is in plane on the sample surface) in the magenta-shaded xy plane. The vector c^′ is the projection of the c axis c onto the xy plane. The orientation of the c axis is specified by the angles χ and γ, where χ is the angle between the z direction and c, and γ is the angle between the x direction and c^′.

Table 1.

Results for angles characterizing the orientation in space of the c axis for the data shown in Fig. 2

Location and color of pixel	Ao	Bo	γ	χ
h = 149, v = 882 green	64	95	1°	90°
	A	B	γ	χ
h = 251, v = 407 red	74	80	23°	67°
h = 335, v = 569 blue	67	84	43°	70°
h = 495, v = 856 magenta	65	70	43°	59°

A, B, and γ result directly as the best-fit parameters obtained from fitting the experimental data to A + B cos² (EPU°-γ). Simple geometry implies that B = B_o sin²χ. The known orientation yields the value for B_o (first row of this table) thus χ can be calculated, assuming that A has a constant value and specifically that A_o = A, which is reasonable within the experimental errors. The errors (estimated by comparing the results for unconstrained fits and fits in which the parameter A is constrained to be the same for all the curves) are approximately 3° for γ and approximately 10° for χ.

We now show that measuring at three different polarizations yields sufficient information to determine cos²χ and cos²γ. This analysis is useful because (i) it provides closed-form expressions for the orientation angles χ and γ in terms of measured quantities, and (ii) it demonstrates how to obtain these angles using a minimum number of measurements, which promises to be useful for samples prone to radiation damage, such as organic molecules, in which aberration correction in X-PEEM will greatly improve the signal-to-noise ratio. We again use the geometry of Fig. 3 and consider the three EPU polarization angles (which we could denote as 0°, 90°, and 45°) 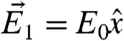, , 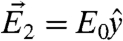, 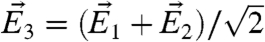where 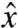and 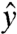are unit vectors. The unit vector 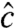describing the orientation of the c axis is 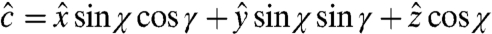, and the signal intensities for three linear polarization angles are 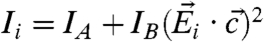. Straightforward algebraic manipulations yield that

and

so that

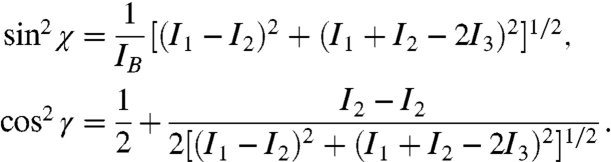[1]

Eq. 1 holds for both positive and negative I_B, though I_B happens to be positive for calcite and aragonite, making this case most relevant to biominerals.

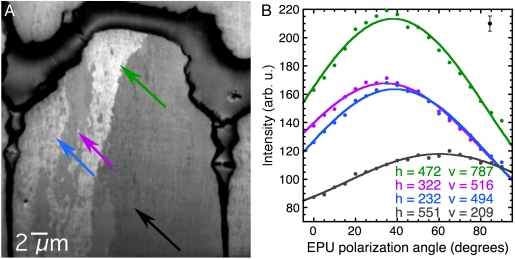
We now use this method to determine the orientation of calcite nanocrystals in a natural biomineral. The data in Fig. 4 were obtained from a calcite prism, one of the many parallel structures composing the prismatic layer of the mollusk shell Pinctada fucata, the Japanese pearl oyster. The prismatic structure of many mollusk shells is an array of parallel calcite prisms, polygonal in cross-section, straight, and elongated along the direction perpendicular to the shell’s outer surface. First described by Bowerbank (29) and Bøggild (30), the prismatic layer has been the subject of intense structural studies (24, 31–33). In some mollusk shells, the prisms are aragonitic (34), but for Pinctada fucata, studied here, the prisms are calcitic. In previous studies, the calcite prisms were consistently described as monocrystals, each with the fast-growing c axis parallel to the prism axis (24–26, 35). Fig. 4 shows that higher spatial resolution reveals that each prism is not a single crystal but instead comprises many nanocrystals, with several orientations.

Fig. 4.

The nanocrystalline structure of the prismatic layer in Pinctada fucata. The image and spectra data were acquired as described in Fig. 2. An animated version of this stack is shown in Movie S2. (A) Average image showing one prism near the prismatic-nacre boundary of the shell. The boundary itself is the darker, thick organic layer at the top, and two vertical interprismatic organic layers separate the central prism from the adjacent ones on the left- and the right-hand sides. The central prism extends for 100–300 μm and is only partially displayed in this 30-μm field-of-view image. (B) Spectra extracted from the 30-nm pixels indicated in A and correspondingly colored, selected within the central prism. The spectra clearly show three different crystal orientations. Table 2 shows the values for the angles obtained from these data.

Using the unit vector describing the direction of the c axis for each pixel in Table 2 (sin χ cos γ, sin χ sin γ, cos χ), we now compare pairs (for instance 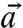and 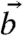) of c-axis orientations in the prism of Fig. 4, and find the angle α between and 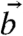, according to the formula :

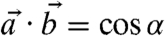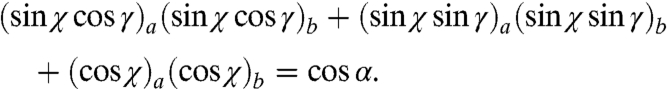The α angles for each pair of pixels in Table 2 are 5°, 22°, 26°, 31°, 34°, 56°, where 5° is the angle spread between the purple and the blue pixels, and 56° that between the green and the gray pixels. Hence the c axes of the various nanocrystals in this prism are spread by more than 50°.

Table 2.

Results for angles characterizing the orientation in space of the c axis for the data shown in Fig. 4

Location and color of pixel	Ao	Bo	γ	χ
h = 472, v = 787 green	85	128	38°	90°
	A	B	γ	χ
h = 322, v = 516 purple	79	89	35°	56°
h = 232, v = 494 blue	70	93	39°	59°
h = 551, v = 209 gray	78	40	32°	34°

To obtain the values of χ, we assumed that the green pixel with the greatest intensity at EPU° = 0° had its c axis vertical and in plane.

A previous indirect observation of multiple orientations within one prism was reported by Dauphin (36), based on the crystal appearance after dissolution of the organic phase, partial etching, and morphological imaging with scanning electron microscopy. Here we analyze an undisrupted portion of the mollusk shell, the observation is direct, quantitative, and has unprecedented spatial resolution. Another direct method, electron backscatter diffraction (EBSD), could in principle observe similar results (35, 37), and in fact would be more complete because it can also measure the orientations of the a- and b-axes, and is not limited to the c-axes as ours. EBSD, however, has a resolution of 500 nm at best, whereas the polarization method used here provides data on the scale of a few tens of nanometers.

Excellent articles preceding the present work stated explicitly that calcite prisms are monocrystalline (24–26, 35). The observation of Fig. 4, therefore, was at first puzzling. We thus verified and corroborated it with a more conventional imaging method: visible light microscopy (VLM), with crossed-polarizers. VLM images could be acquired on a much larger scale, and thus included many more prisms in the mollusk shell, as shown in Fig. 5. The results of Fig. 5 demonstrate that all or almost all prisms in the prismatic layer of P. fucata indeed do not behave as single crystals but are subdivided into intraprism domains of cooriented crystals extending 10–100 μm.

Fig. 5.

Low-magnification micrograph of a Pinctada fucata shell embedded in epoxy (E), and polished to reveal the cross-section in reflected light. The prismatic (P) and nacre (N) layers are visible, as are the prismatic lamellae (L) on the outer surface of the shell. This image was acquired in reflected visible light, with crossed polarizers, thus calcite crystals with different orientations appear with different gray levels. Notice that some of the prisms (arrows) do not exhibit homogeneous orientation, but are subdivided into domains of different orientations, consistent with the X-PEEM data in Fig. 4. At different angles between polarizers, all the prisms exhibit contrasting intraprism domains.

A comparison of the high- and low-resolution (30 and 300 nm, respectively, in Figs. 4 and 5) images of P. fucata prisms reveals that calcite nanoparticles are locally cooriented within an intraprism domain, at the submicron scale, but at the long-range scale the orientation may extend for 10–100 μm, or it may change abruptly across domain boundaries.

The local coorientation revealed by X-PEEM is only sensitive to variations of 2° or more, hence, if between adjacent nanoparticles within a domain, the orientation changed by 0.05°, as observed by diffraction in the prisms of Atrina rigida (24), we would not detect it. However, the 300-nm coherence length measure by Berman et al. (24) is consistent with the submicron coorientation observed here.

The observation that calcite prisms are not monocrystalline but contain calcite nanocrystals with multiple orientations is relevant to the materials properties of the prismatic layer in Pinctada fucata and other mollusk shells. In general, a polycrystalline material is more resistant to fracture than a monocrystalline one. Specifically, in a prism with multiply oriented calcite nanoparticles, the easy-cleavage calcite {104} planes remain confined to the nanoscale, thus preventing longer-range cleavage, which is a clear evolutionary advantage for the shell. Both the subdivision into nanoparticles observed here and their orientation inhomogeneity may explain the origin of the excellent mechanical performances of the prismatic layer in compression and impact tests, as well as hardness and resistance to fracture (38), which have long fascinated scientists but have never been explained.

Conclusions

In summary, we have exploited the ability to change the polarization of synchrotron radiation to use X-PEEM to measure the orientation in space of the c axis of nanocrystals in geologic calcite and in calcite prisms of the mollusk shell Pinctada fucata. Because of the intrinsic capabilities of X-PEEM, spatial resolution on the order of 10 nm is achievable. We anticipate that this experimental capability will be particularly useful for elucidating the highly controlled nanoscale organization of many biominerals.

We revealed that the prisms in P. fucata are not monocrystalline, but exhibit intraprism domains of cooriented nanoparticles, which may elucidate the origin of the calcite prisms’ materials properties.

Materials and Methods

Shells.

Pinctada fucata were purchased from Hai de Ming Pearl Co., Ltd. They were washed in ethanol and air dried. One square centimeter portions of the shells were cut with a chisel and embedded in epoxy (EpoThin resin and hardener, Buehler). Once cured, the blocks were polished with decreasing size alumina grit down to 0.05 μm (Masterprep, Buehler) so that their growth direction was in plane, on the polished sample surface. Finally, sample surfaces were coated using a sputter coater (208HR, Cressington) with 40 nm of platinum, while the region to be analyzed by PEEM was masked off, then the mask was removed, and a final coating of 1-nm platinum was applied to the entire surface (39, 40).

Calcite.

Polished calcite single-crystalline wafers, with the c axis in plane, were purchased from MTI Corporation. Their surfaces were coated using a sputter coater (208HR, Cressington) with 40 nm of platinum, then 1-nm platium, as described above.

X-PEEM Analysis.

X-ray photoelectron emission spectromicroscopy was performed using the PEEM-3 microscope, on the 11.0.1 beamline at the Advanced Light Source in Berkeley, CA, which is described at length in ref. 13. The EPU at this beamline was calibrated to provide precise linear X-ray polarization and reproducible intensities at polarization angles between 0°–90° with a 5° step size.

Stacks of X-PEEM Images.

Nineteen separate X-PEEM images were obtained from each region of calcite crystals or P. fucata shells. Images were either 10 × 10 μm in size with 10-nm pixels, or 30 × 30 μm in size, with 30-nm pixels. Stacks of 19 images were composed in which each image was acquired with different EPU polarization, varying from 0°–90°, in 5° steps. For all the images the photon energy was kept constant, at 290.3 eV, the carbon K-edge π^∗ peak, which is the peak most sensitive to the linear polarization position as shown in Fig. 1. The spectra extracted from single pixels in Figs. 2 and 4 were all normalized to the beamline Izero, acquired simultaneously on a gold mesh.

XANES Spectroscopy.

The XANES spectra in Fig. 1A were also acquired using PEEM-3 at the Berkeley–Adanced Light Source, on beamline 11.0.1. For this experiment, we first identified the accurate crystal orientation on the microdiffraction beamline 12.3.2, we then mounted the crystal with the c axis in plane and vertical in the PEEM-3 sample holder. Three XANES spectra at the carbon K edge were acquired scanning the monochromator and EPU gap between 280 and 320 eV, with 0.5 eV steps in the featureless 280–284 and 305–320 eV regions, and 0.1 eV steps in the 284–305 eV regions, where all peaks are localized. The beamline Izero background was acquired independently, on a freshly coated, thick Pt region, showing only the carbon dips. All spectra were divided by this Izero, and then rescaled so the pre-edge is at 0 intensity and the postedge is at intensity 1. The three spectra were then displaced vertically for clarity.

The polar and azimuthal dependence curves in Fig. 1B were acquired using the Advanced X-Ray Inelastic Scattering Science (AXIS) chamber on the Advanced Light Source beamline 7.0.1.1 and also from a macroscopic single crystal of calcite, with a macroscopic beam, as described in ref. 12. The source for this beamline is an undulator with fixed, horizontal linear polarization. The manipulator on the AXIS chamber enables the vertically mounted sample to rotate around the normal to the surface, hence rotating a crystal with the c axis in plane provides a complete set of polar angles θ. At each angle θ, we acquired a complete XANES spectrum at the carbon K edge, then measured the normalized intensity of the π^∗ peak. Each red data point in Fig. 1B, therefore, is obtained from a separate spectrum. Repeated experiments at the same angle θ provide a measurement of the experimental error, and this error was applied to all data points. The polar dependence curve was then fit by a A + B cos²θ function, as plotted in Fig. 1B by the solid red curve.

The azimuthal dependence curve in Fig. 1B was obtained using a different crystal, with the c axis normal to the sample surface. Rotating the sample position around the normal provides a complete set of azimuthal angles ϕ, and from each corresponding XANES spectrum, we extracted the normalized π^∗ peak intensity. Normal incidence of the X-ray beam in this case would be ideal, but it is not available in the AXIS chamber. We therefore chose a value of θ = 64° and kept it constant for all spectra at various ϕ angles. As expected there was no variation in the intensity of the π^∗ peak as a function of azimuthal angle ϕ, as clearly shown by the blue data points in Fig. 1B.

Visible Light Microscopy.

VLM micrographs of embedded and polished P. fucata shells were acquired using a Zeiss Axio Imager.A1m in the Gilbert Lab at University of Wisconsin, Madison. This reflected-light microscope is equipped with two polarizers: one in the illumination channel and another rotatable one in the analysis channel (Lukas Microscope Services).

Image Manipulation.

Image manipulation was kept to a minimum. For all X-PEEM and VLM images, only the contrast was adjusted, using Adobe Photoshop® for Macintosh, and this was done to the entire image.