Coordinated Conditional Simulation with SLINK and SUP of Many Markers Linked or Associated to a Trait in Large Pedigrees

Abstract

Simulation of genotypes in pedigrees is an important tool to evaluate the power of a linkage or an association study and to assess the empirical significance of results. SLINK is a widely-used package for pedigree simulations, but its implementation has not previously been described in a published paper. SLINK was initially derived from the LINKAGE programs. Over the 20 years since its release, SLINK has been modified to incorporate faster algorithms, notably from the linkage analysis package FASTLINK, also derived from LINKAGE. While SLINK can simulate genotypes on pedigrees of high complexity, one limitation of SLINK, as with most methods based on peeling algorithms to evaluate pedigree likelihoods, is the small number of linked markers that can be generated. The software package SUP includes an elegant wrapper for SLINK that circumvents the limitation on number of markers by using descent markers generated by SLINK to simulate a much larger number of markers on the same chromosome, linked and possibly associated with a trait locus. We have released new coordinated versions of SLINK (3.0; available from http://watson.hgen.pitt.edu) and SUP (v090804; available from http://mlemire.freeshell.org/software or http://watson.hgen.pitt.edu) that integrate the two software packages. Thereby, we have removed some of the previous limitations on the joint functionality of the programs, such as the number of founders in a pedigree. We review the history of SLINK and describe how SLINK and SUP are now coordinated to permit the simulation of large numbers of markers linked and possibly associated with a trait in large pedigrees.

Introduction

Computer simulation of genotype data on pedigrees has been used for more than two decades for power and significance evaluations of genetic linkage studies. For example, MacCluer et al. [1] describe a software implementation of the gene-dropping method (see ‘Implementation of SLINK and SUP’) and its application to studies of large animal pedigrees. One commonly-used pedigree simulation package is SLINK, which was initially derived from the LINKAGE [2] package in 1989–1990. Instead of focusing on gene dropping, SLINK supports simulation conditional on observed trait (and/or marker) phenotypes. Conditional simulation is valuable because, for example, it permits estimates of whether linkage studies are likely to be successful based on partially collected data. To evaluate the level of SLINK usage, we checked the Science Citation Index, which shows that the abstract [3], which SLINK users are asked to cite, has been cited over 350 times, at a steady rate of 15–20 citations per year. The theory of SLINK was formally described by Ott [4], but the initial implementation was announced only by a conference abstract [3]. Here, we describe subsequent improvements that make SLINK much faster and more capable, especially when its usage is coordinated with another software package, SUP [5].

Typical usages of SLINK may be loosely classified into three types: (1) to evaluate power; (2) to evaluate significance, and (3) to evaluate new methods in linkage and/or association analysis.

The typical usage of SLINK to evaluate power happens prospectively, before any genotype data are collected for a possible linkage or family-based association study. One or more pedigree structures are collected, phenotypes are collected, and either DNA samples are collected or some speculation is made about which DNA samples will be available. Then r replicates of the pedigree structures have simulated genotypes filled in by the principal program slink of the SLINK package. Then, taking linkage studies as an illustration, linkage statistics, such as LOD scores, are computed on the r replicates by other programs, which may be part of the simulation package or not. SLINK includes the programs msim, lsim, and isim to compute summary statistics; msim, lsim, isim are respectively analogs of the LINKAGE programs mlink (especially suited for one-marker analysis), linkmap (multipoint analysis with a fixed marker map of recombination fractions), and ilink (numerically optimized recombination fractions) that compute LOD scores in the different practical situations summarized in parentheses. Finally one computes the probability that a significant outcome will arise from the linkage study. A typical assessment would be: what is the probability, conditional on the pedigree structures and observed trait phenotypes, that the LOD score will be >3.0? If this probability is high enough, typically 0.8 (80% of the replicates), then the investigator is encouraged to proceed with the study.

In the typical usage for significance testing, the real data are collected first and analyzed using genetic linkage analysis methods such as LINKAGE/FASTLINK [2,6]. These methods produce a test statistic, such as a LOD score or NPL score. Then the researchers must decide whether the observed score is large enough to conclude that the evidence for linkage is statistically significant. Although various significance thresholds have been established based on theory and experience [7], some cases are borderline. For example, LOD scores slightly over 3.0 for an autosomal study are usually considered of questionable significance [[7], chapter 4]. General thresholds for declaring significance can be derived by asymptotic theory. However, the asymptotic theory depends on having a large number of families, and is not tailored to the details of a particular data set [7]. A more accurate measure of significance may be obtained by estimating an empirical p value [7]. To compute an empirical p value, one would generate r replicates in which the markers are unlinked to the trait and again calculate a score for each replicate. The empirical p value is then the percentage of times a simulated score is larger than the observed score. Because one does not have to condition on a trait locus, simulation of unlinked markers is usually much faster than simulation of linked markers, and more specialized software such as SIMULATE [8] may be better suited for simulation of unlinked markers for significance testing. Empirical p values are particularly useful when one has a single family, where asymptotic arguments about appropriate significance thresholds do not apply. Zuppan et al. [9] used this approach to determine that their observed LOD score of 1.85 for linkage between breast cancer and the estrogen receptor in a single extended family was expected to occur only once in 2,000 trials by chance.

In any simulation experiment, both the simulation step and analysis step include parameters such as the number of markers, the allele frequencies, the recombination fractions between the loci, the mode of inheritance, and penetrances. Because the simulation and analysis steps are separate, the parameters may be set differently, and simulation can be used to predict how well linkage methods will do in a variety of situations. For example, one can test if false linkages are likely when parameters are mis-specified [e.g. [10]] or test whether a generic set of parameters has good power to detect linkage when the true values of the parameters cannot be easily estimated [e.g. [11]]. SLINK can generate linked replicates, unlinked replicates, or a mixture in a user-specified proportion.

The third category of SLINK usage, evaluation of new methods, takes advantage of the simulation step and the analysis step being separate in SLINK. (This is also one of the differences between SLINK and SIMLINK [12], as SIMLINK uses the same model for both simulation and analysis.) Any analysis method that can take as input LINKAGE-formatted files can be used instead of msim, lsim, or isim to evaluate the replicates. For other methods, minimal reformatting of the LINKAGE-formatted files is generally sufficient. Recent examples of using SLINK to test new methods include: a method to detect parent-of-origin effects in large pedigrees [13]; a test of the deleterious effects of incorrect phenotypes on the power of a common linkage study design [14]; a method to identify influential observations in quantitative-trait linkage analysis [15]; and a method to evaluate whether an association result and a linkage result at the same locus have the same underlying cause [16]. These four examples collectively make use of some important features of SLINK: (1) that simulation can be conditional on any part of the data being observed, leaving the rest to be simulated; (2) that linkage disequilibrium (LD) is supported, even with the trait locus, by specifying haplotype frequencies rather than allele frequencies for each marker, and (3) that traits for simulation can be quantitative, not just dichotomous.

After the initial release, development of SLINK continued in various spurts during 1990–1994. The software was stable during 1994–2006 – continually used, but not improved. SLINK improvements resumed in 2006 when Lemire [5] made a technological breakthrough, described further below, that allowed the simulation of many more linked markers in one run. This was implemented as a separate package called SUP that functions as a set of wrapper programs around SLINK, some data formatting scripts, and a program run after receiving output from SLINK. In 2007–2010, we re-engineered SLINK and SUP so that they are easier to use together and limitations that existed in 2006 have been removed. Documentation and release of the new versions of SLINK (3.0; available from http://watson.hgen.pitt.edu) and SUP (v090804; available from http://mlemire.freeshell.org/software or http://watson.hgen.pitt.edu) have been coordinated. These new software releases motivate us to formally describe the engineering of SLINK and recent developments coordinating SLINK and SUP.

Implementation of SLINK and SUP

High-Level Summary of a Typical Usage

The primary intended usage of SLINK and SUP is to generate genotype data for markers linked and possibly associated with a trait locus. As explained above, power estimation is the most common situation in which simulated markers linked to a trait locus are used. Therefore, we summarize and compare how power estimation can be done with SLINK alone and with SLINK+SUP.

SLINK alone:

(0)Prepare LINKAGE-formatted files, adding availability codes which indicate which individuals are available and should have genotypes simulated.

(1)Simulate r replicates of m markers together with the trait.

(2)Compute test statistics and summary distributions.

The usage of SLINK alone is generally limited to 5 or fewer markers because the computation time grows exponentially with the number of markers. For what follows below, we emphasize that in step 1, all m + 1 loci are simulated together, so any genotypes computed internally are multi-locus phase-known genotypes.

SLINK + SUP:

(0)Prepare LINKAGE-formatted files, adding availability codes, as above. Additionally, assign unique alleles to founders at one marker locus, hereafter referred to as the descent marker.

(1)Use SLINK to simulate r replicates of one descent marker together with the trait.

(2)Use SUP to extend the inheritance process via gene dropping from one descent marker to m markers.

(3)Compute test statistics and summary distributions.

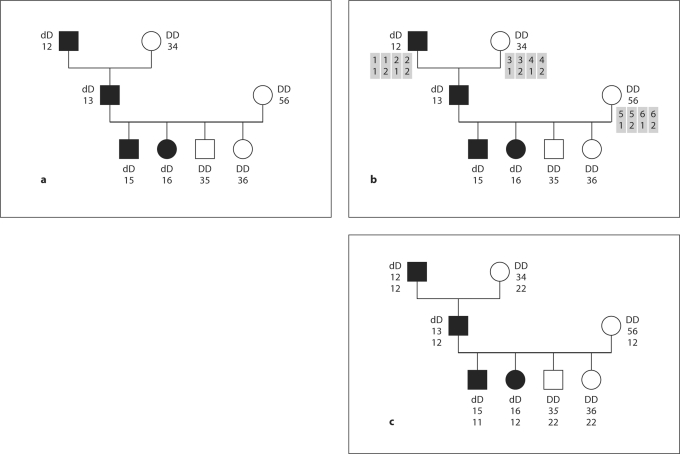
This SLINK+SUP approach can handle many more markers than SLINK alone can, because step 1 uses only two loci, and the time for step 2 (SUP) grows linearly with the number of markers. The need for extra alleles (steps 0 and 1) can slow the computation if there are a lot of founders, but the time grows quadratically with the number of founders and alleles, not exponentially. Figure 1a illustrates step 1. Figure 1b illustrates identifying possible haplotypes to transmit to founders. Figure 1c illustrates selecting and dropping the haplotypes down to non-founders. The stages of panels 1b and 1c are done together in a single run of SUP and hence are considered as a single computational step above.

Fig. 1.

Three stages of sampling markers linked to a trait with SLINK and SUP. a The descent marker alleles (1, 2, 3, 4, 5, 6) are specified at the founders and the affection status may be specified in all individuals, if known. All alleles at the trait locus and the alleles of the non-founders at the descent marker locus are sampled by SLINK. b To begin filling in data at a SNP marker, SUP identifies possible haplotypes, which are shaded, combining the descent marker and a new SNP marker in the founders. In general if m − 1 markers are to be added, there would be 2^m possible haplotypes. However, if some of the newly sampled markers are in LD with each other, then the probabilities of some haplotypes may be 0. c To complete the sampling, SUP does haplotype dropping from founders to non-founders, while modeling the recombination process. In this example, there is a single recombination between the descent marker and the new SNP marker, occurring in the maternal meiosis to the unaffected grandson, and those alleles are shown in italics.

Converting a Method to Compute Pedigree Likelihoods into a Method to Simulate Genotypes

SLINK implements the simulation algorithm proposed by Ott [4]. In this algorithm, we wish to sample a genotype vector g for the entire pedigree, given a vector of phenotype information x, i.e. we wish to sample according to the conditional probability P(g ∣ x). Ott's brilliant insight was that this can be broken down into a series of incremental sampling choices according to this equation [equ. 1 from ref. [4]]:

P(g ∣ x) = P(g₁ ∣ x)P(g₂ ∣ g₁, x)P(g₃ ∣ g₂, g₁, x)P(g₄ ∣ g₃, g₂, g₁, x) …

To implement this, we select a genotype at random for person 1 from the probability distribution P(g₁ ∣ x) of person 1's possible genotypes given the phenotypes. Once a genotype for person 1 has been selected, then we select a genotype at random for person 2 from the probability distribution P(g₂ ∣ g₁, x). In essence, this is a series of risk calculations, one for each person in the pedigree, each time conditioning on the phenotypes and all selected simulated genotypes assigned so far. Thus, the newly selected genotype for the current proband is guaranteed to be consistent with the previously selected genotypes for this replicate.

SLINK was derived from LINKAGE [2], which implements a generalized peeling algorithm for likelihood computations in pedigrees, generalizing the Elston-Stewart algorithm [17]. LINKAGE's algorithm is a generalization for several reasons including that complex and looped pedigrees can be accepted, and there is increased flexibility in the order of traversal (peeling) of the pedigree; the latter change is important in SLINK. Using LINKAGE, it is possible to carry out a risk computation for one individual P, the ‘proband’; this meaning is different from the clinical meaning of ‘first patient recruited in a family’. To do this risk computation, the pedigree likelihood is computed by iteratively traversing the pedigree, from nuclear family to nuclear family, ultimately ‘collapsing’ all the information in the pedigree down onto the chosen proband P. To implement Ott's simulation algorithm, SLINK does one traversal of the pedigree for each individual whose genotype is to be simulated, choosing that individual as P.

In practice, the computations during the traversal of the pedigree are done one nuclear family at a time, rather than one individual at a time. A main loop of LINKAGE implicitly chooses how to number the nuclear families and individuals. In SLINK, this main loop is wrapped inside a new outer loop over all individuals.

For each available individual, let that individual be the proband P for one traversal.

For each nuclear family, renumber so that the nuclear family containing the proband P is last.

Update conditional probabilities.

Select a genotype for P by sampling from the appropriate conditional probability distribution.

If there are n individuals in the pedigree, then after n iterations of the new outer loop, every individual will have a genotype assigned. The SLINK code has never enforced that the order of individuals in the outer loop have any mathematical relationship with the order in which the nuclear families are updated in the inner loop.

For readers who may wish to modify the code, perhaps following the ideas suggested in the Discussion, it is useful to know where the two principal loops are implemented. The inner loop and the genotype selection are implemented by a small change to the LINKAGE procedure ‘likelihood’. The outer loop is added to the LINKAGE procedure ‘iterpeds’, which in LINKAGE iterates over pedigrees and recombination fraction values. Other than the genotype selection, all other procedure calls from within ‘likelihood’ in the original version of SLINK were essentially unchanged from LINKAGE.

After all available individuals have genotypes filled in, the replicate can be output. SLINK has substantial new code to keep track of the replicates and choose for each replicate whether the trait locus should be linked or unlinked to the marker loci. In all versions except the current one, the output format of each replicate looked exactly like a post-makeped LINKAGE-formatted pedigree file, except that the input availability code was printed back out in an extra column on the right. Of particular relevance to the recent changes, only genotypes at the marker loci were printed; the value of the phenotype locus (for a discrete trait) was printed as one of 0 (unknown status), 1 (unaffected), or 2 (affected), even though SLINK would have also chosen underlying genotypes for the trait locus as part of the simulated multi-locus genotype.

Improvements to SLINK

LINKAGE was implemented in PASCAL, since that language was popular in the 1980s. The first version of SLINK was also in PASCAL, as it was originally derived from LINKAGE 4.9. When LINKAGE was substantially upgraded to version 5.1 in the early 1990s, most of those changes were ported to SLINK as well. During 1989–1992 various bugs were fixed, and the ability to simulate under heterogeneity was added, allowing the user to specify the proportion p of the replicates in which the markers are linked to the trait.

In 1992, version 1.0 of FASTLINK [6] was released as an improvement to LINKAGE and further improvements were done in 1992–1997. The most important improvements in the early versions of FASTLINK were to the procedures for computing the conditional genotype probabilities. Since these methods were identical in LINKAGE and SLINK, it was not difficult to port the improved methods for probability calculations to SLINK.

However, FASTLINK was implemented in C, rather than PASCAL, by starting from a machine translation by p2c of the LINKAGE 5.1 code. By the early 1990s, C was far more popular than PASCAL, and the language translation yielded an immediate speed improvement because C compilers have better code optimization than PASCAL compilers. Therefore, as a first step towards combining FASTLINK and SLINK, the simulation program was also translated to C. Then the procedures called (indirectly) from within ‘likelihood’ in FASTLINK could be reused identically in SLINK. Other improvements in the initial FASTLINK/SLINK combination included: some modularization of the code, compilation with make, and some dynamic allocation of memory that was previously allocated at compilation time. Except for one bug fix, and a few syntactic changes to improve portability, SLINK was unchanged during 1994–2007.

The new SLINK code release includes three important sets of improvements implemented in 2007–2009. First, some additional algorithmic improvements implemented in FASTLINK during 1994–1996 were ported to SLINK. These include making allocation of almost all important arrays dynamic at run time. Consequently, some important ‘constants’ that determine array sizes no longer need to be set by the user and the subsequent code recompilation is avoided. When the ‘constants’ in version 2 were higher than they needed to be, arrays occupied unnecessary memory, and the new code (version 3) runs faster. For example, using the complex pedigree in [18] that has 55 individuals and 15 founders, and a Linux computer and the gcc compiler, to generate 1,000 replicates with the disease plus one five-allele marker takes 11 s with the new version as compared with 22 s with the previous version. To generate 100 replicates with the disease plus two five-allele markers takes 437 s with the new version and 572 s with the previous version. When the constants in version 2 were set too low for some input data, the user would get error messages and needed to change the code; now this problem is eliminated.

Second, the old code had an inherent limit of 32 alleles at a marker. This arose because LINKAGE implemented the alleles that an individual has as a bit array, meaning that if an individual has alleles 3 and 7, then positions 3 and 7 in the array are set to 1, while all other positions are set to 0. There were two reasons to do this when LINKAGE was originally implemented, but both reasons have become unimportant 20 years later. First, memory was much more precious, and a single integer-size bit array takes less space than two integers. Second, some labs were using markers (such as the ABO blood group) where the genotype at a marker is determined by a set of binary tests, not numbered alleles. The bit array representation could compactly store the results of b binary tests, provided b is at most the number of bits in a computer integer. The limitation of alleles at a marker in SLINK had the unfortunate consequence of creating a limitation of at most 16 founders in a pedigree when SLINK and SUP were used together, as explained below. In the current version (3.0), each marker allele is stored as an integer, so there is no meaningful limit to the number of alleles or founders that SUP can handle.

Third, SLINK can now print the internally selected alleles at the trait locus to a second, new output pedigree file. Previously, these alleles could only be obtained by simulating a marker locus in perfect LD with the trait locus. Since SUP needs the trait locus alleles in order to simulate LD between them and any marker loci, this simplifies the workflow, as described below.

Improvements to SUP

SUP is a package, developed by Lemire, that interacts with SLINK to permit the generation of many markers linked to the trait, overcoming the limitation that the time and memory usage of the methods in SLINK grow exponentially with the number of markers. The primary programs of SUP are implemented in C++; some auxiliary programs are implemented in Perl. The ideas and methods underlying SUP were originally discussed in [8], but not implemented.

SUP combines three techniques used previously in disparate genetic linkage analysis applications. To describe these methods, we assume there is a single pedigree, but they can be applied to each pedigree in sequence. In the descriptions below, we assume autosomal inheritance, but the latest version of SUP also supports X chromosome inheritance.

The first technique is called ‘gene dropping’ or ‘allele dropping’. To generate simulated data for a single marker, first select alleles at random (sampling from the allele frequency distribution specified in the input locus file) and assign them to the founders. Then the alleles are ‘dropped’ (equivalent to ‘transmitted’ or ‘inherited’) down from the founders to the most recent generation, following the rules of Mendelian inheritance. More specifically, suppose N is a non-founder such that the alleles of the parents of N have been selected. For N, we select at random one of the two alleles from the father and one of the two alleles from the mother. By traversing the pedigree from top to bottom, all non-founders eventually get their alleles selected (fig. 1b, c). If in the observed pedigree, some individual is unavailable for sampling, then the genotype selected for that individual can be printed as unknown (usually 0 0) in the output replicate. To combine this technique with the next technique, it is important that within the gene-dropping procedure the genotypes have known phases (meaning that we distinguish the paternal and maternal alleles), even though LINKAGE-formatted pedigree files are usually treated as phase-unknown.

The second technique is to model the recombination process along the chromosome, from one marker to the next. Suppose one has generated genotypes for the entire pedigree on m − 1 markers, and the recombination fraction between the last marker generated and the m-th marker is specified in the input as θ. The phase-known alleles for the m-thmarker in the founders are chosen at random from the population distribution, just as for the first marker. The pedigree is traversed from top to bottom, one meiosis at a time. For each meiosis, the parental allele on the same haplotype the child has at marker m − 1 is inherited with probability 1 – θ, and the allele on the other haplotype is inherited with probability θ(fig. 1c). Because each meiosis is sampled separately, this method can be used if the male and female recombination fractions differ. Because the genotypes are phase-known, no markers preceding the (m − 1)-th marker enter into the sampling for the m-th marker, and hence the time and space needed grows only linearly with the number of markers.

The techniques of gene dropping and sampling the recombination process can be used to generate a long series of markers along a hypothetical chromosome, and this was implemented, for example, in the software packages SIMULATE [8], SimPed [19] and SimM [20]. However, to extend the capability to include a linked trait locus requires a third technique called a ‘descent marker’. Following the notation of [5], users of LINKAGE/FASTLINK usually model a discrete trait locus as having two alleles D (lower risk) and d (disease or higher risk). One might be tempted to consider D and d as numbered alleles 1 and 2 at a typical marker, and then simulate the data at the trait locus by gene dropping. Doing so would be incorrect for two reasons. First, the usage of gene dropping as explained above does not take into account the observed phenotypes and the penetrance function (relating phenotype to genotype) at the trait locus. Second and more importantly, using only two alleles creates ambiguities in phase, when individuals are homozygous, for example. When all the loci are simulated together within SLINK, the phase is disambiguated because the internal representation of genotypesdistinguishes each possible phase-known multi-locus genotype. When the simulation of the descent marker in SLINK is separated from the generation of the additional conditional markers in SUP, then SUP needs to receive or infer more information about the phase than previous versions of SLINK would print. Therefore, SLINK had to be modified to output additional information needed by SUP to keep track of the phase of inheritance of the descent marker alleles.

SUP uses the insight that as long as mutations cannot occur within the meioses of the pedigree, all distinct alleles represented by D and d get introduced in the founders (fig. 1a). If there are F distinct founders, then 2F distinct alleles may be needed; this explains why the limitation on the number of alleles in earlier versions of SLINK was a serious limitation when SLINK was used with SUP. To formalize this idea that the founders introduce all the trait locus alleles, SUP uses a descent marker with alleles 1, …s, 2F assigned to the founders by the auxiliary program DistinctAlleleToFounders. The descent marker is a regular numbered allele marker perfectly linked (θ = 0) to the trait locus; it describes both the descent path and the phase of the trait locus alleles along the pedigree lines.

Because each founder gets alleles distinct from all other founders, the phase of the descent marker alleles at each meiosis is unambiguous. With only two loci, one trait and one descent marker, SLINK can be used to simulate replicates for these two loci, conditional on the input phenotypes (fig. 1a). The founders keep the input genotypes rather than having their genotypes selected at random. Since all founder alleles are specified to be distinct, the allele frequencies at the descent marker (which would be part of the input) are irrelevant to the computations in SLINK.

Given the replicate data for the trait and descent marker, the main program of SUP uses the techniques of gene dropping and of simulating the recombination process on both sides of the trait locus/descent marker, conditional on the observed descent marker alleles, to generate as many more markers as desired (fig. 1b, c). Both SLINK and SUP support LD, and when SUP fills in markers by gene dropping, it can sample from the set of possible haplotypes (fig. 1b). To simplify this implementation and to allow for LD between the markers and the trait locus, it helps to have the phase-known genotypes from the two loci simulated by SLINK (the descent marker and the trait locus). So, as explained above, SLINK was adjusted to output the alleles at the trait locus, in addition to the usual affection status. The marker genotypes selected by SUP are output in a LINKAGE-formatted pedigree file that can then be used to compute test statistics, as explained in the Introduction.

SUP is very fast. Using the same 55-individual, 15-founder pedigree [18] used above, SLINK takes 109 s to simulate the descent marker for 1,000 pedigrees. SUP takes less than 3 s to fill in marker data for anywhere from two to ten SNPs; the time increase as more SNPs are added is miniscule. The time for the SLINK phase is different from that reported above because, for this experiment, we are using a 30-allele descent marker (twice the number of founders) and filling in the alleles for the founders. Above, we used a five-allele marker but did not fill in any alleles prior to the computation.

Discussion

We described the integration of the software packages SLINK, FASTLINK, and SUP to make it possible to generate simulated pedigree replicates for large pedigrees, with many markers, linked to the trait locus and possibly associated with it. SLINK and SUP support LD among the markers and among the markers and the trait locus, and can be used to generate two interacting trait loci, as explained in [5]. The limitations on early versions of SUP have been removed and usage is simpler. Other simulation packages include SIMLINK [12], SIMULATE [8], SimPed [19], SIMLA [21], and ALLEGRO [22]. These five packages are all compared to the initial version of SUP in [5], and to our knowledge have not changed much since 2006.

The most important strength of SLINK is that it can simulate data linked and possibly associated with a trait locus and more generally conditional on other observed data, such as the phenotypes and/or genotypes of some individuals. In contrast, SIMULATE, SimPed, and SIMLA have either no or very limited capability to generate markers linked to a trait. SIMLINK can generate data linked to a trait, but has the same severe limitation on number of markers that SLINK had before SUP was introduced. The principal limitation on ALLEGRO is that the pedigrees have to be small, while SLINK can simulate replicates for pedigrees of hundreds of individuals.

Within the SLINK package, the focus of improvements has been on the program slink itself that generates the replicates, rather than the analysis programs msim, isim, and lsim. For these, we have translated the three programs to C via p2c and resolved some portability problems. Reasons to focus effort on the generation of replicates include:

(1) The generation of a replicate takes much more time than its analysis, because the generation requires one pedigree traversal per individual, while the analysis requires only one traversal.

(2) The replicate generation usually starts with no genotypes filled in, while the analysis works on a pedigree with genotypes filled in.

(3) Newer, fast linkage analysis packages such a Merlin [23] and Superlink [24] can be used to analyze the replicates, but either have no simulation capability or simulation capability limited to unconditional gene dropping.

The 1993–1994 improvements of SLINK focused on speed. Recent improvements focused on software engineering for both better speed and integration with SUP. Conversely, recent improvements to SUP included adding support for X chromosome markers and taking advantage of the increased capabilities of SLINK to simplify usage. Without SUP, SLINK is severely limited in terms of the number of markers that can be simulated. When SLINK is used with SUP, however, the SLINK step uses only the trait and one marker. As a consequence, the running time for the SLINK/SUP combination can be seconds or minutes for pedigrees with many individuals.

For the one trait, one marker case, further speed improvements in SLINK may be possible by:

(1) Incorporating methods developed for linkage analysis during the past 15–20 years, such as gene flow trees [23] or Bayesian networks [24], although these methods may not be applicable to simulation in an obvious way.

(2) Implementing methods to choose the order in which the individuals are selected to fill in genotypes.

(3) Assigning alleles to more than one individual during a pedigree traversal by more sophisticated use of conditional probabilities. For example, if alleles have been assigned to a father and mother whose children are at the youngest generation, then alleles could be assigned to all their children in one traversal.

(4) Caching the results of partial pedigree traversals like an opening book in computer chess.

Versions of SLINK have been in active use for 20 years and SUP has been used for 4 years. We hope the recent improvements will increase their effective lifetimes.