Abstract
The high-throughput gas chromatography-mass spectrometry (GC-MS) technology offers a powerful means of analyzing a large number of chemical and biological samples. One of the important analyses of GC-MS data is compound identification. In this work, novel spectral similarity measures based on the discrete wavelet and Fourier transforms were proposed. The proposed methods are composite similarities that are composed of weighted intensities and wavelet/Fourier coefficients using cosine correlation. The performance of the proposed approaches along with the existing similarity measures was evaluated using the NIST Chemistry WebBook mass database maintained by the National Institute of Standards and Technology (NIST) as a library of reference spectra and repetitive mass spectral data as query spectra. The analysis results showed that the identification accuracies of the wavelet/Fourier transform-based methods were improved by 2.02% and 1.95%, respectively, comparing the weighted dot product (cosine correlation) and by 3.01% and 3.08%, respectively, comparing to the composite similarity measure. The improved identification accuracy demonstrates that the proposed approaches outperformed the existing similarity measures in the literature.
Keywords: mass spectral similarity, wavelet/Fourier transform, compound identification, NIST mass data
1. Introduction
High-throughput gas chromatography-mass spectrometry (GC-MS) is currently a workhorse technique for analyzing a large number of chemical or biological samples in petroleum industry, food sciences, biomedical sciences, etc.1, 2 One of the most important procedures for the analyses of GC-MS data is chemical compound identification by assigning an experimental mass spectrum to a compound recorded in a reference spectral library using a spectrum matching algorithm.
Many methods have been proposed for the spectrum matching-based compound identification including composite similarity 3, probability-based matching system 4, cosine correlation 5–8, Hertz similarity index 9, normalized Euclidean distance (L2-norm) 3, 10, 11, absolute value distance (L1-norm) 3, 11, etc. Stein and Scott 3 and Hisayuki et al. 12 examined the performance of composite measure with other measures using the National Institute of Standards and Technology (NIST) mass database and MassBank database, respectively, and demonstrated that the composite measure performed better than other methods.
Even though various spectrum similarity measures have been developed for compound identification, the existing compound identification methods still generate a high rate of false-positive and false-negative identifications13, resulted from the significant enrichment of the reference spectral library and the increased sample complexity. A large spectral library increases the chance that the mass spectrum of the true compound is included in the library. However, it also increases the chance that more spectra originated from different compounds are similar, which requires high sensitivity and accuracy of the spectrum matching algorithms to pick the spectrum of the true compound from the similar spectra of a large number of compounds. With the remarkable updates of the GC-MS mass spectral database during the last few years, prospective trials are therefore required to confirm the results made in previous studies with the updated database as well as to develop novel algorithms to overcome the issues on the existing compound identification methods.
The objective of this work was to develop novel similarity measures of mass spectra based on wavelet and Fourier transforms. The discrete Fourier transform (DFT) converts the discrete time domain signal into a series of frequency coefficients. The discrete wavelet transform (DWT) shares the same properties as the discrete Fourier transform except that the output of its transform contains both time and frequency information14–16. We further examined the performance of the proposed approaches using two types of measures: simple and composite similarities. Cosine correlation, cosine correlation with weighted intensities (weighted cosine correlation), ratio of an intensity pair, and cosine correlation with wavelet/Fourier transformed intensities (wavelet/Fourier cosine correlation) are defined as the simple similarity measures. The composite similarity is a mixture of two simple similarities. All the simulations were rendered using the NIST Chemistry WebBook mass database as a library of reference spectra and the repetitive mass data as query spectra.
2. Materials and Methods
NIST mass spectrometry and repetitive database
The NIST Chemistry WebBook service (http://webbook.nist.gov/chemistry/) provides users with chemical and physical information for chemical compounds including mass spectra generated by electron ionization mass spectrometry 17. The mass spectra of 21,310 compounds were extracted from this NIST Chemistry Webbook database out of 72,618 chemical compounds since the mass spectra of other compounds were not available. The fragment ion m/z values were ranged from 1 to 1036 with a bin size of 1.
The repetitive library contains 28,307 mass spectra generated by 18,569 compounds. The same chemical compounds are identified and grouped by Chemical Abstracts Service (CAS) registry number. Interestingly, although it was constructed by repetitive experiments for the same compound, we found that 61% of the compounds recorded in the repetitive library have only one mass spectrum. Table S-1 (Supporting Information) shows the detailed distribution of the mass spectra in the repetitive library.
In the simulation studies, we considered the mass spectra extracted from the NIST Chemistry WebBook (NIST library) as a reference library and the repetitive library as query data. In addition, since we assume that the NIST library has the mass spectrum information for all the query compounds, all the compounds that were not present in the NIST library were removed from the repetitive library. After the removal, there were 12,025 compounds with 20,441 mass spectra left in the repetitive library. The distribution of the filtered mass spectra in the repetitive library is shown in parentheses in Table S-1. The most reduction of the number of compounds was occurred for the cases that the number of repetitive mass spectra of a compound is 1 and 2 as can be seen in Table S-1.
Peak intensity weighting
Stein and Scott 3 evaluated the importance of m/z values and peak intensities with different weights. The peaks with large m/z values usually have small peak intensities, but carry the most important characteristics for compound identification. Therefore, weighting the peak intensity based on its m/z value can increase the relative significance of smaller peaks as well as their contribution to compound identification, resulting in improving the performance of compound identification. Weighted peak intensity was represented as
| (1) |
where a and b represent the contribution of the m/z value and the peak intensity, respectively. Stein and Scott 3 suggested that the cosine correlation with an optimal intensity scaling of 0.5 (i.e., b = 0.5) and mass weighting of 3 (i.e., a = 3). These two values for the weighing factors, a and b, were employed in this study as well.
Performance evaluation
In order to evaluate the performance of compound identification of each similarity measure, we calculated the accuracy, precision, recall, and F1 score. The accuracy is the proportion of the spectra identified correctly in query data. In other words, if a pair of unknown and reference spectra has the same CAS index, we consider this pair as the correct match and, otherwise, the incorrect match. Then, by counting all the correct matches, the accuracy of identification can be calculated by
| (2) |
The precision is also called the true positive rate and the recall the predictive positive rate. The F1 score is the harmonic mean between the precision and recall. The precision, recall, and F1 score in this study are calculated as follows:
| (3) |
| (4) |
| (5) |
where TP is the number of true-positives that is the number of spectrum pairs having the same compound CAS information, FP is the number of false-positive that is the spectrum pairs having the different compound CAS information, TN is the number of true-negatives, and FN is the number of false-negatives. All the simulation studies and analyses were performed using wavelet, parallel computing, and statistical toolboxes in Matlab R2011a software.
3. Theoretical Basis
Let us consider the two signals, X= (x1, x2,…, xn) and Y= (y1, y2,…, yn), which are the unknown and reference mass spectra, respectively. In order to calculate the spectrum similarity of these two mass spectra, we considered both the cosine correlation and the composite measure using weighting and DFT/DWT transforms of the mass spectra.
Cosine correlation
Cosine correlation, which is also known as the dot product 3, is a measure of correlation between two signals using the cosine value of the angle and is defined as follows:
| (6) |
where X Y= Σxkyk and . Then its value ranges from −1 to 1 theoretically, but it is always greater than or equal to zero since all the intensities are non-negative.
Stein and Scott’s composite similarity
Stein and Scott 3 proposed a composite similarity measure of cosine correlation with weighted intensities, Sw, and peak ratios, Sr. Cosine correlation with weighted intensities, Sw, can be calculated by
| (7) |
In Equation (7), and are the weighted intensities based on the expression (1) and
| (8) |
where zi is the m/z value of k th intensity, k=1,2,…, n, and a =3 and b =0.5 are the weight factors that were optimized by Stein and Scott 3. We call the cosine correlation with weighted intensities the weighted cosine correlation. The ratio of peak pairs Sr is defined by
| (9) |
where n = 1 or −1 if the term in parentheses is less than or greater than unity, respectively, and NX^Y is the number of peaks with non-zero peak intensity in both the reference and the unknown query spectra. Using Sw and Sr in Equations (8) and (9), their composite similarity was then defined as
| (10) |
where NX and NX^Y are the number of non-zero peak intensities existing in the unknown query and in both the reference and the unknown query spectra, respectively.
Discrete Fourier transform
The discrete Fourier transform (DFT) 18, 19 is a special case of Fourier transform, which is an operator mapping the original time signal function into a series of frequencies. Fourier transform decomposes time domain functions into periodic functions. Its series of frequencies are called the frequency domain representation of the original signal function, which is often a function in the time domain. But the DFT requires a discrete input function whose non-zero values have a limited (finite) duration.
In general, a signal X= (x1, x2,…, xn) is transformed into by the DFT according to the following formula:
| (11) |
where i is the imaginary unit and is a primitive N th root of unity. Since , the equation (11) becomes , k=1,…, n.
Therefore, the real, imaginary, and absolute DFTs of a signal X can be calculated by the following equations:
| (12) |
| (13) |
| (14) |
Discrete wavelet transform
The discrete wavelet transform (DWT) 20, 21 is a wavelet transform that converts a discrete time domain signal into a time-frequency domain. As with other wavelet transforms, a key advantage of DWT is temporal resolution, i.e., it captures both frequency and location information in time. The DWT of a signal X= (x1, x2,…, xn) is calculated by passing it through a low-pass filter g and a high-pass filter h, resulting in two subsets of signals: approximations and details. The approximations are the high-scale and low-frequency components of the signal X after passing the high-pass filter. The details are the low-scale and high-frequency components after passing the low-pass filter. The coefficients of approximations and details are defined by the following expressions:
| (15) |
| (16) |
where g and h are low-pass and high-pass filters, respectively. Then the approximation and detail DWTs of a signal X are as follows, respectively:
In the simulation studies, we used one of the Daubechies wavelets 20 whose scaling function has order of 4.
Simple and composite similarities
We considered two types of similarity measures: simple and composite similarities. The simple similarity calculates the similarity scores of two mass spectra using cosine correlation. The composite similarity calculates the similarity scores between two mass spectra based on Stein and Scott 3’s approach in the equation (10). As for the simple similarity, we employed DFT/DWT transforms and then added five types of mass spectra transformed along with the weighted intensities and the ratio of peak pairs. The five types are real, imaginary, absolute DFT transformed intensities and approximations and details DWT transformed intensities as described in the equations (12)–(16). In addition, we replaced the ratio of peak pairs with five DFT/DWT transformed intensities in the composite similarity of the equation (10) and then developed five composite similarities. The simple similarities and their abbreviations between two signals, X and Y, are as follows:
CC: Cosine correlation, Sc (X,Y), with unweighted intensities based on Equation (6)
WC: Weighted cosine correlation, Sw (X,Y)= Sc (Xw,Yw), that is cosine correlation with weighted intensities based on Equation (7)
RstC: Stein and Scott’s ratio of peak pairs, Sr(X,Y), with unweighted intensities based on Equation (9)
DFT.R: Cosine correlation using the real part of DFT, Sc(Xfr,Yfr), with unweighted intensities based on Equation (12)
DFT.I: Cosine correlation using the imaginary part of DFT, Sc(Xfi,Yfi), with unweighted intensities based on Equation (13)
DFT.A: Cosine correlation using the absolute part of DFT, Sc(Xfa,Yfa), with unweighted intensities based on Equation (14)
DWT.A: Cosine correlation using the approximation part of DWT, Sc(Xva,Yva), with unweighted intensities based on Equation (15)
DWT.D: Cosine correlation using the detail part of DWT, Sc(Xvd,Yvd), with unweighted intensities based on Equation (16)
The composite similarities and their abbreviations of two signals, X and Y, are described in the following list:
W+RstC: the composite of WC and RstC based on Equation (10)
W+DFT.R: the composite of WC and DFT.R by replacing with Sc(Xfr,Yfr).
W+DFT.I: the composite of WC and DFT.I by replacing with Sc(Xfi,Yfi).
W+DFT.A: the composite of WC and DFT.A by replacing with Sc(Xfa,Yfa).
W+DWT.A: the composite of WC and DWT.A by replacing with Sc(Xva,Yva).
W+DWT.D: the composite of WC and DWT.D by replacing with Sc(Xvd,Yvd).
In detail, the main difference among these composite similarities is the second part in Equation (10). For instance, W+DFT.R and W+DWT.D are constructed by replacing the second part, RstC, of Equation (10) with DFT.R and DWT.D, respectively, and so defined by
| (17) |
and
| (18) |
respectively, where Zfr(Zvd) are the real part of its DFT (the detail part of its DWT) of a signal Z.
4. Results
The simple and composite similarities including the novel DFT/DWT based similarity measures were implemented using the NIST mass database as a reference library and the repetitive library as query data, to evaluate the performance of each approach for the compound identification. The performance was compared based on the accuracy, precision, recall, and F1 value as described in Section 2.
The accuracies of all the similarity measures were investigated by counting the number of spectra identified correctly as depicted in Table 1. Since the compound identification was done using all data present in the reference library and the repetitive library described in Section 2, no standard error of the accuracies was calculated in Table 1. Therefore, in order to take account of the variation in accuracy, we considered the accuracy of compound identification according to the three levels of rank, similar to Stein and Scott’s work 3. Note that the library compound having the highest similarity score has rank 1. In case of the simple approach, WC outperformed other simple similarities. In particular, DFT/DWT-based simple similarities had the lower accuracies than WC. This may be because WC used the weighted intensities, while DFT/DWT-based methods employed the intensities without weighting. For this reason, we calculated the accuracies of CC without weighting the intensities to see the effect of weighted intensities and obtained the accuracies which are in Table 1. In this case, DFT.R showed larger accuracy than others excluding WC. However, although DFT.R has a better performance than CC, CC will be more attractive than DFT.R since DFT.R requires one more process before.
Table 1. Accuracy (%) of compound identification for simple and composite similarities.
Based on the number of spectra correctly identified in the repetitive library, the accuracy (%) of compound identification is calculated.
| Rank Threshold
|
||||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| Simple | WC | 80.68 | 90.54 | 94.17 |
| CC | 72.93 | 84.04 | 88.81 | |
| RstC | 3.31 | 8.19 | 13.46 | |
| DFT.I | 72.93 | 84.05 | 88.78 | |
| DFT.R | 72.95 | 84.04 | 88.79 | |
| DFT.A | 69.08 | 79.80 | 84.23 | |
| DWT.A | 69.74 | 81.19 | 86.39 | |
| DWT.D | 71.48 | 82.52 | 87.27 | |
|
| ||||
| Composite | W+RstC | 79.62 | 90.56 | 94.45 |
| W+DFT.I | 82.60 | 92.28 | 95.67 | |
| W+DFT.R | 82.63 | 92.31 | 95.67 | |
| W+DFT.A | 82.53 | 91.90 | 95.26 | |
| W+DWT.A | 81.68 | 91.74 | 95.28 | |
| W+DWT.D | 82.70 | 92.20 | 95.59 | |
To construct the composite similarities, we considered CC with weighted intensities, i.e., WC, since it performed the best. Using the weighted cosine correlation, WC, we examined the performance of the compound identification of six composite similarities as shown in Table 1. The DFT/DWT-based composite similarities outperformed W+RstC, resulting that W+DFT.R and W+DWT.D performed the best. These two transformation methods improved the identification accuracy of W+RstC by 3.01% and 3.08% when Rank 1 was considered. In order to examine the variation of the compound identification that may caused by the size of the query spectra, we further evaluated the performance of the proposed methods 100 times by randomly selecting a half size of the query spectra. In this case, we used the five similarity measures, CC, WC, W+RstC, W+DFT.R, and W+DWT.D. Then we calculated the average, standard deviation (SD), and 95% confidence interval (CI) of the accuracy of compound identification as shown in Table S-4 in the supporting information. We observed the same conclusion as listed in Table 1. In addition, the proposed methods were significantly different from the existing methods in terms of 95% CI.
A threshold of the spectrum similarity is usually used to determine whether an identification result is acceptable, meaning that the similarities larger than the threshold are considered as acceptable identifications while the similarities less than the threshold are discarded. In other words, a mass spectrum pair is classified as positive if their spectral similarity is higher than the threshold and, otherwise, it is classified as negative. We examined this practical calculation by employing different thresholds to the mass spectral similarity. Since we already observed that W+DFT.R and W+DWT.D have the better accuracies than others in Table 1, we employed only these two proposed similarity measures including WC and W+RstC for this examination.
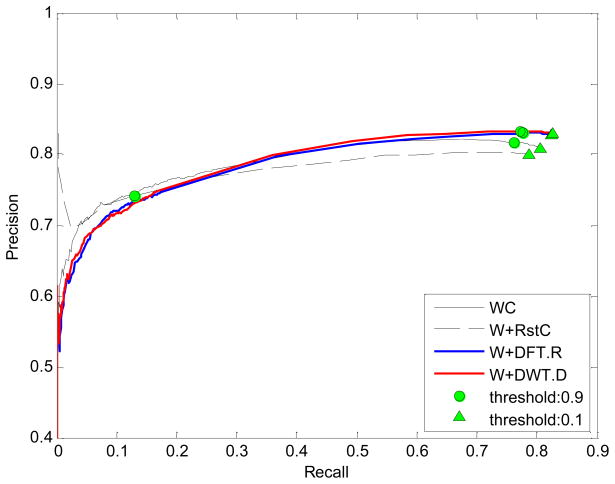
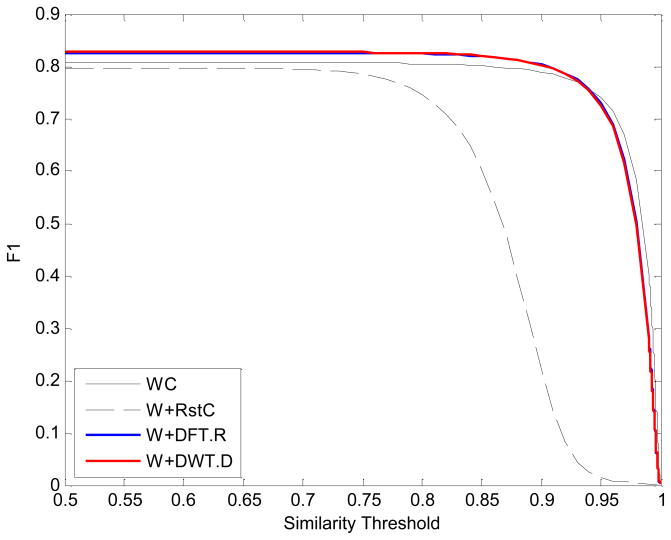
The precision-recall plot is depicted according to the different thresholds of the spectrum similarity between 0 and 1 as shown in Fig. 1. In general, the larger the precision and recall are, the better is the method in the precision-recall plot. It can be seen that the DFT/DWT-based similarities performed better than WC when the threshold is near zero. The green circle and triangle represent the threshold of 0.9 and 0.1, respectively. In particular, WC, W+DFT.R, and W+DWT.D have the small distance between two thresholds 0.9 and 0.1, while W+RstC has much longer distance between 0.9 and 0.1. It suggests that the W+RstC is sensitive to the threshold of mass spectra similarity. Fig. 2 is the F1 score plot with different thresholds. It is clear that W+DFT.R and W+DWT.D performed better than WC and W+RstC for almost all thresholds. Interestingly, the accuracy of W+RstC is suddenly decreased after the threshold of 0.8, while WC has the similar trend as W+DFT.R and W+DWT.D although its accuracy generally is not better. Moreover, W+RstC has the F1 score near zero when the threshold is equal to 0.95. This explains that it has much longer distance between two thresholds 0.9 and 0.1 observed in Fig. 1.
Figure 1.
The precision-recall plot. The four similarity measures, WC, W+RstC, W+DFT.R, and W+DWT.D, are used to construct the precision-recall plot according to the different similarity thresholds ranged from 0 to 1.
Figure 2.
The F1 scores curve. According to the different similarity thresholds between 0 and 1, the F1 scores for WC, W+RstC, W+DFT.R, and W+DWT.D are plotted.
Some compounds have spectrum information more than or equal to two repetitive, while some compounds have only one mass spectrum in the repetitive spectral library. The accuracies in Table 1 were calculated based on the total number of spectra identified correctly. Therefore, the accuracies in Table 1 could be biased to some specific compounds. In order to investigate this bias, we calculated the number of compounds identified correctly for WC, W+RstC, W+DFT.R, and W+DWT.D in Table S-2 (Supporting Information). In this case, we considered a compound as identified correctly if at least one of the repetitive spectra had the same CAS number with a compound in the reference library. It can be seen that W+DFT.R and W+DWT.D identified more compounds than WC and W+RstC in Table S-2. We further removed the compounds that have more than or equal to two repetitive and then calculated the number of compounds correctly identified based on compounds that have only one spectrum replication. Even in this case, W+DFT.R and W+DWT.D still have the largest number of compounds among others as shown in Table S-2, which suggests that the preference of a compound with multiple mass spectra in the query library does not affect the identification accuracy.
The cases having the maximum F1 score are reported in Table S-3 (Supporting Information). In this table, W+DWT.D shows the highest F1 score and the lowest F1 score occurred when W+RstC was employed. The threshold when the maximum F1 scores were observed ranges between 0.51 and 0.58, except for the threshold of W+DWT.D which is 0.69. It should be noted that the accuracies of WC, W+RstC, and W+DFT.R in Table 1 are the same as the F1 scores of these similarities in Table S-3, because the precision and the recall have very similar scores to each other and the maximum of the harmonic mean is occurred when two values are same.
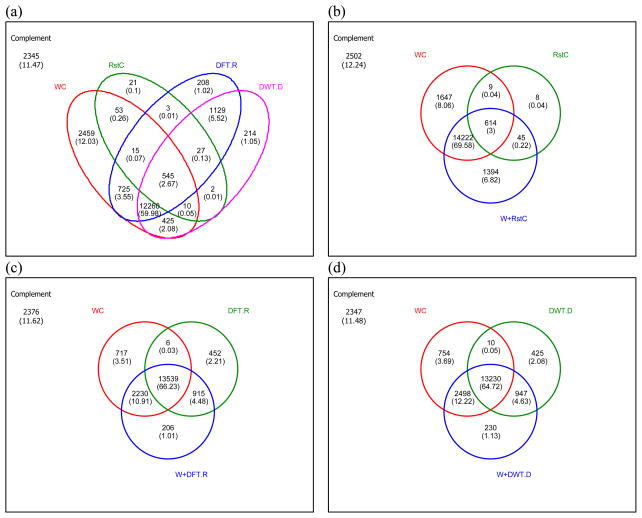
The Venn diagram analysis was performed to examine the contribution of similarity measures on compound identification as shown in Fig. 3. Note that the number in each cell is the number of spectra (compounds) correctly identified and its percentage is in parenthesis. The Venn diagram of four simple similarities is depicted in Fig. 3(a). Clearly, we can see that the contribution of RstC on compound identification is much smaller than DFT/DWT-based methods (0.1% vs. 7.59% (= 1.02% + 5.52% +1.05%)). On the other hand, DFT/DWT-based methods identified much larger number of spectra commonly with WC than RstC (65.62% (= 3.55% + 59.98% + 2.08%) vs. 0.26%). Moreover, the contribution of the composite similarities on compound identification was investigated as shown in Fig. 3(b)–3(d). Surprisingly, W+RstC contributed more to compound identification than DFT- and DWT-based methods (6.82% vs. 1.01% and 1.03%). Nevertheless, the amount that was not identified by the simple and the composite similarities on WC is two times larger for RstC than for DFT- and DWT-based methods (8.06% vs. 3.51% and 3.69%).
Figure 3.
The Venn diagram analysis of the simple similarities for compound identification. The values inside the Venn diagram are the number of spectra identified correctly and the values in parentheses the percentages (%) of the number of spectra identified correctly out of 20,441 spectra. (a) The Venn diagram for the four simple similarities, WC, RstC, DFT.R, and DWT.D. (b) The Venn diagram for WC, RstC, and W+RstC. (c) The Venn diagram for WC, DFT.R, and W+DFT.R. (d) The Venn diagram for WC, DFT.D, and W+DFT.D.
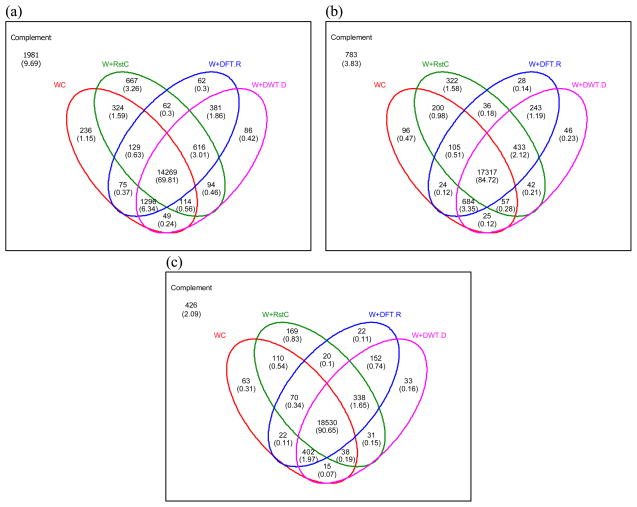
According to Ranks 1, 2, and 3, the Venn diagram was also considered for WC and three composite similarities, W+RstC, W+DFT.R, and W+DWT.D, in Fig. 4. Although W+RstC is the worst composite measure when Rank 1 was considered in Table 1, it has the larger number of spectra that can be correctly identified only by itself than that of DFT/DWT-based methods (3.26% vs. 2.58% (= 0.3% + 1.86% + 0.42%)) as shown in Fig. 4(a). However, W+DFT.R and W+DWT.D identified larger amounts of spectra which were identified by WC than that of W+RstC, resulting in the highest accuracy in compound identification. The Venn diagrams were further drawn for Ranks 2 and 3 in Fig. 4(b) and 4(c). As shown in Fig. 4, as Rank goes to three, the number of spectra that are identified only by DFT-and DWT-based methods increases and becomes bigger than that of RstC (0.85% (= 0.11% + 0.74%) and 0.90% (= 0.74% + 0.16%) vs. 0.83%, in Fig. 4(c)).
Figure 4.
The Venn diagram analysis of the composite similarities for compound identification. The Venn diagrams are drown for WC and three composite similarities (W+RstC, W+DFT.R, and W+DWT.D) according to Rank 1, 2, and 3. The values inside the Venn diagram are the number of spectra identified correctly and the values in parentheses the percentages (%) of the number of spectra identified correctly out of 20,441 spectra. (a) The Venn diagram when Rank 1 was considered. (b) The Venn diagram when Rank 2 was considered. (c) The Venn diagram when Rank 3 was considered.
5. Discussion and Conclusions
Novel simple and composite mass similarity measures were introduced using DFT/DWT based methods and their performances of compound identification were compared using the mass spectra extracted from NIST Chemistry WebBook as a library of reference and the repetitive data as a set of query spectra.
The cosine correlations for both WC and W+RstC were calculated with weighted intensities using the optimal factors reported by Stein and Scott 3. When the weighted intensities were used along with cosine correlation, the performance of CC in compound identification was significantly improved. W+RstC was decreased slightly, however, as can be seen in Table 1. Namely, W+RstC shows a worse performance than WC, which conflicts with Stein and Scott’s work 3 where W+RstC always performed better than WC (see, for details, Tables 2 and 3 in Stein and Scott 3). Therefore, this discrepancy may suggest that the optimal factors vary according to the mass spectrum library and experimental conditions.
On the other hand, W+DFT.R and W+DWT.D performed better than WC, which is consistent with Stein and Scott’s work in the sense that the composite measure improves the performance of compound identification. Moreover, it was observed that the DFT/DWT-based simple similarities, DFT.R and DWT.D, share a lot of spectra identified correctly with WC, while RstC shares a few spectra identified correctly with WC in Fig. 3(a). It implies that DFT/DWT transforms can reduce the sensitivity of WC to the optimal factors by maintaining the innate properties of intensities before weighting.
The simulation studies shows that DFT/DWT-based composite approaches can correctly identify ~3% more spectra than Stein and Scott’s composite approach (i.e., W+RstC) when the NIST mass spectrum and repetitive libraries were applied. This is because DFT/DWT-based composite approaches recover 4% more information of WC than W+RstC as can be seen in Fig. 4(a). It clearly demonstrates that DWT/DFT transforms can recover the different information from RstC.
Fig. S-1 shows the results of identification for the compound 1-Nonamine using WC, W+RstC, CC, and W+DFT.R/DWT.D (W+DFT.R and W+DWT.D). In this case, only DFT/DWT-based composite approaches could identify 1-Nonamine correctly. The original spectra of matched compounds by WC and W+RstC are much different from that of the query compound, while CC identifies a compound with similar structure to the query compound although it is not correct, as shown in Fig. S-1(a). On the other hand, WC, W+RstC, and W+DFT.R/DWT.D match the query spectrum to the similar compounds in terms of the weighted intensities as depicted in Fig. S-2 (b) and (c). This may be resulted from the weighting factor of mass (m/z) in the expression (1). That is, the intensities with higher m/z values have more weight than those with smaller m/z values. For this reason, if the peaks with large intensities are located in the range of small m/z value, WC may assign a wrong compound to the query compound. Interestingly, CC identifies a wrong compound although the compound 1-Nonamine has the larger intensities with the smaller m/z values. This means that both the unweighted and weighted intensities play an important role in identifying the compounds so that the composite measure is indispensible for the compound identification to take account of both characteristics of the unweighted and weighted intensities. However, in Stein and Scott’s composite measure, RstC has an issue that its similarity can decrease as the number of pairs of nonzero intensities increases since it is a product of the values less than one, so that it tends to match the spectrum having less number of nonzero intensities. For these reasons, the proposed composite approaches may be able to identify more compounds correctly than other approaches.
Moreover, the proposed composite methods are more efficient than the literature reported composite measure in terms of computation time. WC, W+RstC, W+DFT.R, and W+DWT.D require 8.9, 13113.1, 38.4, and 47.8 seconds for compound identification using the NIST library and the repetitive library. All experiments are performed on an Intel Core i7 X990 running at 3.47 GHz with a 12 GB main memory.
The point of interest here is that although W+RstC has the less identification accuracy than DFT/DWT-based composite approaches, it has the larger amount of spectra that identified only by itself than those of W+DFT.R and W+DWT.D in Fig 4(a) (Rank 1). Meanwhile, when Rank 3 was considered, W+DFT.R and W+DWT.D obtained the more number of spectra that identified only by themselves than that of W+RstC in Fig. 4(c), resulting in 95.67% and 95.59% identification accuracies, respectively, which are 1.22% and 1.14% more than that of W+RstC as observed in Table 1. This suggests that DFT/DWT-based transforms have more potential to reduce the false-positive rate than literature reported composite measure.
Supplementary Material
Acknowledgments
This work was supported by grant 1RO1GM087735 through the National Institute of General Medical Sciences (NIGMS) within the National Institute of Health (NIH), DE-EM0000197 through the Department of Energy (DOE).
Footnotes
Supporting Information Available
Additional tables and figure (Table S-1, Table S-2, Table S-3, Table S-4, and Figure S-1) as noted in text. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Fiehn O. Plant Molecular Biology. 2002;48:155–171. [PubMed] [Google Scholar]
- 2.Denkert C, Budczies J, Kind T, Weichert W, Tablack P, Sehouli J, Niesporek S, Konsgen D, Dietel M, Fiehn O. Cancer Research. 2006;66:10795–10804. doi: 10.1158/0008-5472.CAN-06-0755. [DOI] [PubMed] [Google Scholar]
- 3.Stein S, Scott D. Journal of the American Society for Mass Spectrometry. 1994;5:859–866. doi: 10.1016/1044-0305(94)87009-8. [DOI] [PubMed] [Google Scholar]
- 4.Atwater B, Stauffer D, McLafferty F, Peterson D. Analytical Chemistry. 1985;57:899–903. [Google Scholar]
- 5.Tabb D, MacCoss M, Wu C, Anderson S, Yates J., III Anal Chem. 2003;75:2470–2477. doi: 10.1021/ac026424o. [DOI] [PubMed] [Google Scholar]
- 6.Beer I, Barnea E, Ziv T, Admon A. Proteomics. 2004;4:950–960. doi: 10.1002/pmic.200300652. [DOI] [PubMed] [Google Scholar]
- 7.Craig R, Cortens J, Fenyo D, Beavis R. J Proteome Res. 2006;5:1843–1849. doi: 10.1021/pr0602085. [DOI] [PubMed] [Google Scholar]
- 8.Frewen B, Merrihew G, Wu C, Noble W, MacCoss M. Anal Chem. 2006;78:5678–5684. doi: 10.1021/ac060279n. [DOI] [PubMed] [Google Scholar]
- 9.Hertz H, Hites R, Biemann K. Analytical Chemistry. 1971;43:681–691. [Google Scholar]
- 10.Julian RK, Higgs RE, Gygi JD, Hilton MD. Analytical Chemistry. 1998;70:3249–3254. doi: 10.1021/ac971055v. [DOI] [PubMed] [Google Scholar]
- 11.Rasmussen GT, Isenhour TL. Journal of Chemical Information and Computer Sciences. 1979;19:179–186. [Google Scholar]
- 12.Horai H, Arita M, Nishioka T. IEEE. 2008. pp. 853–857. [Google Scholar]
- 13.Denkert C, Koch I, von Keyserlingk N, Noske A, Niesporek S, Dietel M, Weichert W. Modern Pathology. 2006;19:1261–1269. doi: 10.1038/modpathol.3800645. [DOI] [PubMed] [Google Scholar]
- 14.Unser M, Blu T. Image Processing, IEEE Transactions on. 2003;12:1080–1090. doi: 10.1109/TIP.2003.812329. [DOI] [PubMed] [Google Scholar]
- 15.Donoho D, JOHNSTONE J. Biometrika. 1994;81:425. [Google Scholar]
- 16.Antonini M, Barlaud M, Mathieu P, Daubechies I. Image Processing, IEEE Transactions on. 2002;1:205–220. doi: 10.1109/83.136597. [DOI] [PubMed] [Google Scholar]
- 17.Afeefy H, Liebman J, Stein S. NIST Chemistry WebBook, NIST Standard Reference Database. 2000;69 [Google Scholar]
- 18.Frigo M, Johnson S. IEEE. 2002:1381–1384. [Google Scholar]
- 19.Brigham E, Morrow R. Spectrum, IEEE. 2009;4:63–70. [Google Scholar]
- 20.Daubechies I. Ten lectures on wavelets. Society for Industrial Mathematics; 1992. [Google Scholar]
- 21.Mallat S. A wavelet tour of signal processing. Academic Pr; 1999. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.