Abstract
Due to thermal motion and molecular polarizability, electrical interactions in biological systems have a dynamic character. Zwitterions are dipolar molecules that typically are highly polarizable and exhibit both a positive and a negative charge depending on the pH of the solution. We use multilamellar structures of common lipids to identify and quantify the effects of zwitterionic buffers that go beyond the control of pH. We use the fact that the repeat spacing of multilamellar lipid bilayers is a sensitive and accurate indicator of the force balance between membranes. We show that common buffers can in fact charge up neutral membranes. However, this electrostatic effect is not immediately recognized because of the concomitant modification of dispersion (van der Waals) forces. We show that although surface charging can be weak, electrostatic forces are significant even at large distances because of reduced ionic screening and reduced van der Waals attraction. The zwitterionic interactions that we identify are expected to be relevant for interfacial biological processes involving lipid bilayers, and for a wide range of biomaterials, including amino acids, detergents, and pharmaceutical drugs. An appreciation of zwitterionic electrodynamic character can lead to a better understanding of molecular interactions in biological systems and in soft materials in general.
Introduction
Electrodynamic interactions in biomaterials and in soft materials in general are difficult to estimate and measure (1–4), and continue to pose challenging questions in fundamental research (5,6). However, a correct assessment of these interactions is required for a proper description of molecular processes in biological systems. Additional complications arise in the case of zwitterions due to the more-complicated nature of their electronic polarizabilities, which lead to a pH dependence of their charge state and dipole moments. Zwitterionic interactions are common in nature. Examples of common zwitterions include amino acids (the building blocks of proteins), phospholipid molecules present in biological membranes, certain classes of detergents used to solubilize hydrophobic materials, various pharmaceutical drugs, and a number of pH buffers used in biomolecular research.
By regulating the charged state of macromolecules, buffers serve an indispensable role in biochemical reactions and structural stability. Natural and synthetic buffers are responsible for preventing toxic levels of free hydrogen ions that accumulate during normal biological processes such as phosphorylation and cell metabolism (7–9). Examples of naturally occurring buffers include the carbonic acid-bicarbonate buffer that maintains human blood at pH 7.4, and the phosphate buffer that maintains the pH of intracellular fluid.
Laboratory research often involves the use of synthetic buffers that do not naturally occur in biological cells. However, selecting an inappropriate buffer for a particular biological assay can lead to erroneous or misleading experimental results. Good and colleagues (10) synthesized a number of buffers tailored to the specific needs of biological assays. These buffers fit a number of important criteria. They provide maximum buffering capabilities in the pH range of biological reactions (roughly between pH 6 and 8), form negligible amounts of metal-ion complexes, have high water solubility, and minimally affect the ionic composition of the solution being buffered (9–11). Good's buffers are zwitterionic.
Here we investigate a series of three zwitterionic buffers: 2-(N-morpholino)ethanesulfonic acid (MES), 3-(N-morpholino)propanesulfonic acid (MOPS), and 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES; see Materials and Methods). MES and HEPES are among the original list of Good's buffers. Although buffers have the ability to prevent hydrogen ion buildup (9), they can become toxic to biological matter at high concentrations. For example, MES was found to be markedly toxic at 20–40 mM in growth of mammalian cell lines (7), and HEPES was shown to affect neuronal and glial cells (12). HEPES buffers were also shown to increase toxic oxygen metabolites in endothelial cells (13), to decrease ciliary movement and induce epithelial injury in an in vivo hamster trachea model (14), and to increase endothelial permeability (15). More-recent studies in isolated rat endothelial cells revealed that high concentrations of MOPS buffer caused a decrease in the endothelial surface layer, a critical determinant of endothelial barrier function, leading to a loss of endothelial barrier (16). However, the physical mechanisms responsible for these biological observations remain unclear.
To investigate how zwitterionic buffers affect molecular interactions other than through changes in pH, we used model lipid membranes. We took advantage of the fact that most common phospholipids spontaneously form multilamellar vesicles (MLVs) composed of many stacked bilayers (17–19). The equilibrium spacing between neighboring membranes, which can be measured by x-ray scattering, is a sensitive and accurate indicator of the balance of attractive and repulsive forces between membranes (18–20). The attractive interaction, called van der Waals (vdW), occurs because of spontaneous polarization of matter (21). The repulsive interactions are due mainly to the tendency of molecules to reach a certain level of disorder (entropy) (18,19,22). If membranes acquire charges from solution, an electrostatic repulsion will be present as well (1,23,24). If any of these interactions are modified, the equilibrium repeat distance (D-spacing) between membranes changes. We therefore monitored changes in D-spacing to determine how zwitterionic buffers affect the forces between neighboring membranes. Focusing on MOPS, we then used three independent methods to show that at pH 7, MOPS charges zwitterionic membranes positively, and we quantified these interactions by measurements using monovalent salts.
Materials and Methods
Lipid samples
For each sample, ∼5–10 mg of highly purified (>99%) lipid powder (1,2-dilauroyl-sn-glycero-3-phosphocholine (DLPC); Avanti Polar Lipids, Alabaster, AL) were hydrated in 1 mL buffer solutions in plastic vials with o-ring caps. Buffer and salt solutions were prepared with the use of deionized water and HEPES, MOPS, MES, potassium bromide (KBr), and potassium chloride (KCl; Sigma Aldrich, St. Louis, MO). Multiple samples were prepared for the majority of solute compositions to verify proper equilibration under different thermal histories (25). Variations in sample equilibration included freeze-thawing cycles and different incubation times at 4°C, room temperature, and 30°C. On the day of the measurements, samples were removed from the refrigerator and reequilibrated for 30 min to 5 h at the temperature of the measurement. All samples were titrated to pH 7. Buffer solutions were titrated with saturated sodium hydroxide, and salt solutions were titrated with 10 mM MOPS pH 7.
X-ray measurements
X-ray scattering measurements were performed on a fixed-anode Bruker Nanostar U system operating at a power of 1.2 kW (40 kV × 30 mA). The instrument is equipped with a controlled-atmosphere sample chamber, computer-controlled sample positioning, and a real-time 2D detector with pixel size of 100 μm. Multiple measurements were performed at sample-to-detector distances of 255.5 mm and 615.5 mm, calibrated using silver behenate with a lattice spacing of 58.4 Å. Scan times varied between 10 min and 3 h. An in-house-built temperature controller was used to maintain a constant sample temperature within ±0.2°C or better. Interlamellar lattice spacings were calculated from scattering rings that appear at angles satisfying the Bragg law, 2Dsin(θ) = nλ, where D is the lattice spacing, λ is the x-ray wavelength (1.54 Å for the Cu Kα line), and n is an integer index. The program fit2D was used to integrate the 2D scattering data over the radial (χ) angle, and interlamellar D-spacings were calculated from the integrated profiles.
Refractive index measurements
Refractive indices for salt (KCl and KBr) and buffer (MES, MOPS, and HEPES) solutions were measured with an Abbe refractometer (model C10; VEE GEE Scientific, Kirkland, WA). Measurements were performed for both untitrated solutions and solutions titrated to pH 7.
ζ-Potential measurements
The initial lipid sample preparation for ζ-potential measurements followed the same protocol as described for the x-ray measurements. On the day of the measurements, samples were reequilibrated for at least 30 min at 30°C and sonicated for 2 min at 30-s intervals. ζ-Potential measurements were performed with a Nano ZS90 Zetasizer (Malvern, Worcestershire, UK).
Electric drift measurements
The setup for electric drift measurements consisted of a standard sample chamber (Warner Instruments, Hamden, CT) that contained two wells partitioned by a plastic cup. The cup had a small (100 μm) hole to allow the exchange of solution between the two wells. We added 500 μL of lipid suspension in buffer to one well, and 500 μL of buffer solution to the other well. A DC power supply (Hewlett Packard E3617A) was used to apply a constant voltage between the two wells. After waiting times that varied between 8 and 10 h, the solutions from each well were collected and transferred into a light-scattering instrument (model 370; Nicomp Particle Sizing Systems, Santa Barbara, CA) for detection of MLVs.
Ionization calculations
For calculations of amino group dissociated fractions, we used the relationship between the second dissociation constant pKa2 of the buffers considered and the solution pH:
| (1) |
where and represent the unprotonated and protonated solute fractions, respectively.
Force analysis
Within multilamellar vesicles, each membrane is subjected to an attractive vdW force (FvdW) from its neighbors (21). For neutral membranes, this force is balanced by a net repulsive force that is described as a sum of two terms: a hydration repulsion (Fhyd) (18,19,26) and a bending-fluctuation repulsion (Ffl) (19,27–29):
| (2) |
| (3) |
| (4) |
At equilibrium, and in the absence of external pressure, the sum of these three forces must be zero (19,25):
| (5) |
The physical parameters in Eq. 2 are the cross-sectional area per lipid AL, the Hamaker parameter H, the water spacing between neighboring membranes a, and the membrane thickness b. For the hydration force (Eq. 3), the parameters are the amplitude Ph and the decay length λh. The fluctuation repulsion (Eq. 4) is parameterized using the bending rigidity KC, the bending-fluctuation amplitude Afl, and decay length λfl. Equation 4 also contains the Boltzmann constant kB and the absolute temperature T. For DLPC at 30°C, the values for these parameters are as follows: AL = 63.2 Å2, H = 9.2 × 10−21 J, a = 20 Å, b = 38.9 Å, Ph = 160 × 10−24 J/Å3, λh = 2.1Å, KC = 58 × 10−21 J, Afl = 1.06 Å2, and λfl = 6.0 Å (25,30). When membranes become charged, an electrostatic repulsion must be added to Eq. 5. We calculate the electrostatic force using a charge-regulation procedure that involves solving the Poisson-Boltzmann equation including an ion-binding term (1,31).
Results
X-ray measurements of the interlamellar spacings of the zwitterionic lipid DLPC in buffer solutions at pH 7 are shown in Fig. 1. The figure also shows measurements in KCl and KBr solutions (also at pH 7) that provide reference curves for possible swelling mechanisms (1). As shown previously (1), both KCl and KBr reduce vdW attraction equally for concentrations up to 1 M. However, MLVs swell more in the presence of KBr because Br ions bind to lipid membranes (binding energy on the order of 2 kBT), generating an additional electrostatic repulsion (1). For the three buffers considered (see Fig. 2 for chemical structures), the D-spacings increase with increasing concentrations, indicating that the buffer molecules enter the interlamellar water space. The measured swelling curves resemble the KBr curve more than the KCl curve. Although the MES curve follows the KBr curve all the way up to 1 M concentrations, the swelling in the presence of MOPS and HEPES exceeds that observed with KBr at high concentrations.
Figure 1.
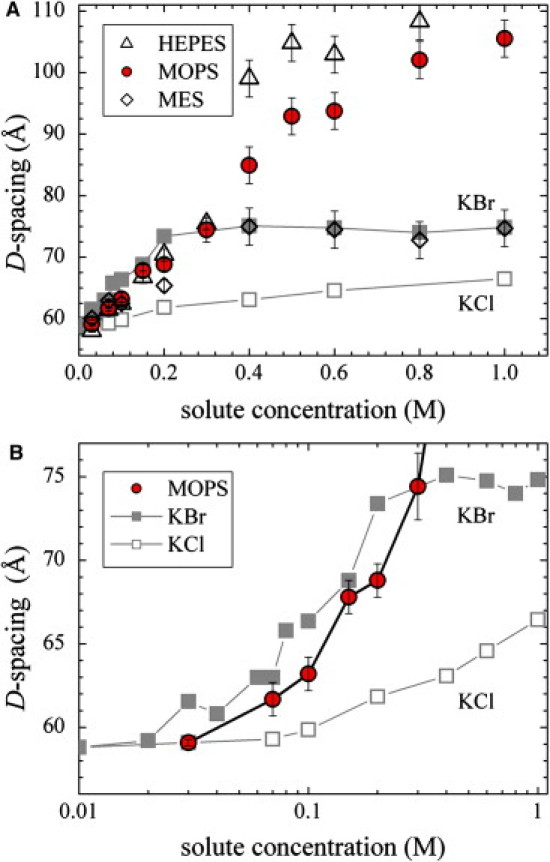
Swelling of DLPC multilayers at 30°C as a function of solute concentration, shown on a full (A) and reduced (B) scale of measured D-spacings. All samples were titrated to pH 7.
Figure 2.
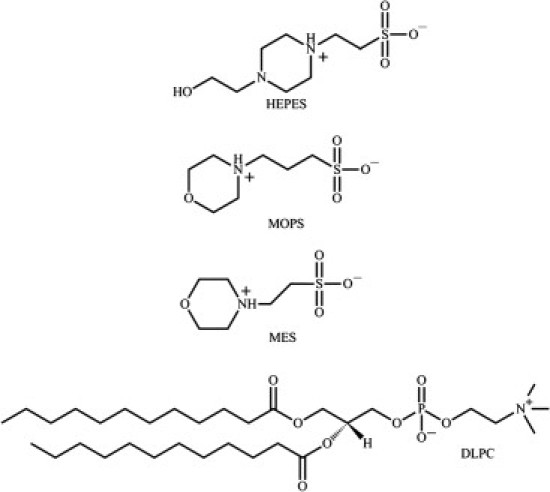
Zwitterionic structures of HEPES, MOPS, and MES buffers, and DLPC lipid.
One possible explanation for the observed swelling in the presence of buffers is a reduction in vdW attraction between membranes (1,25). Because the vdW interaction depends on the index of refraction of the solution, we measured the indices of refraction versus buffer concentration as shown in Fig. 3. The buffer's indices of refraction increase linearly with concentration just as observed with KCl and KBr, but have significantly larger values. Of the three buffers, MES has the lowest index of refraction and HEPES has the largest. This is consistent with the fact that MES swells MLVs less than MOPS and HEPES.
Figure 3.
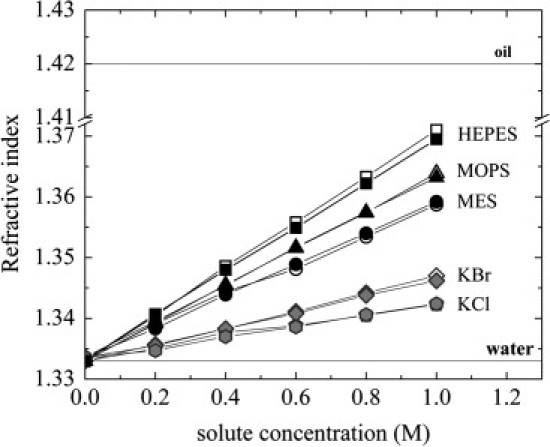
Optical index of refraction versus solute concentration. Measurements of titrated samples at pH 7 (solid symbols) and untitrated samples (open symbols) yield similar values.
Because the effect of buffers on D-spacing is similar to that of KBr, we investigated the possibility that lipid membranes become charged in the presence of buffers. For this part of the study, we chose to use MOPS, which shows an intermediate behavior between those of MES and HEPES. To determine the charge state of multilamellar lipid vesicles, we designed a new (to our knowledge) type of experiment in which we measured the drift of lipid vesicles under applied electric fields. The experimental setup consisted of a sample chamber (see Materials and Methods) that contained two wells separated by a partitioning with a 100 μm diameter hole to allow the drift of lipid vesicles from one cell to the other. One electrode was placed into the well containing the MLV/buffer solution, and the other electrode was placed into the well containing only buffer solution. Positive, negative, and zero voltage was applied to the system, and after time (∼8 h), the presence of lipid in each well was detected by light scattering. By taking the ratio between the scattering intensity before and after application of electric fields, we were able to determine the direction of the MLV drifts and consequently the sign of their electric charge. The results shown in Fig. 4 indicate that DLPC vesicles in the MOPS solutions moved in the direction of the applied field, whereas the negatively charged DOPS vesicles (32) used as controls moved against the field, as expected.
Figure 4.
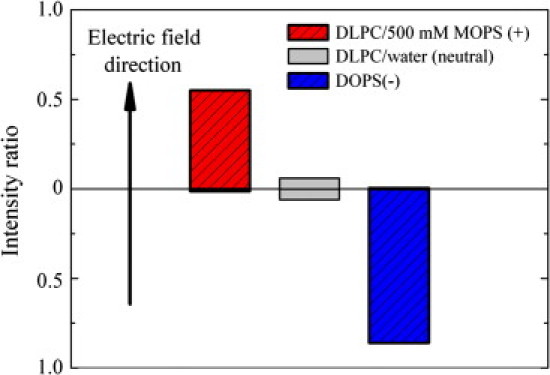
Measurements of MLV drift in a constant electric field. DLPC vesicles in MOPS solutions move in the direction of the field, whereas the negatively charged DOPS vesicles in water move against the field. The neutral DLPC vesicles in water move mainly due to thermal motion.
Electrophoretic measurements that detect the ζ-potential of macromolecules in solution (1,33) confirm the opposite charging effect of Br and MOPS on lipid vesicles. Results for KBr/MOPS mixtures at a total concentration of 150 mM are shown in Fig. 5. The measured potentials are within the typical range for zwitterionic lipid bilayers in monovalent salt solutions (1,33). In MOPS alone, DLPC vesicles were positively charged, whereas a sample of one part KBr to nine parts MOPS indicated a negative ζ-potential. In this particular sample, the concentrations of ions were 135 mM MOPS to 15 mM KBr for a total concentration of 150 mM. Note that the error bars for these measurements are quite large. This is because to make the measurement work, we had to sonicate the samples to break the large MLVs into smaller units. The broad distribution of vesicle sizes and the instability of broken MLVs lead to large variations in the measured ζ-potential. Despite these limitations, the ζ-potential measurements show that DLPC bilayers in MOPS solutions are positively charged, consistent with the MLV drift in Fig. 4.
Figure 5.
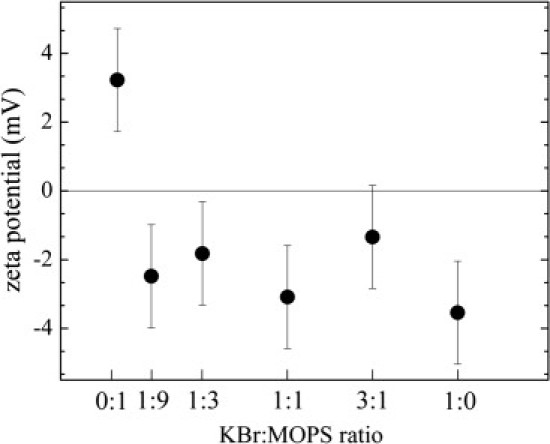
Measurements of ζ-potentials of DLPC membranes at 30°C in KBr/MOPS mixtures at a total concentration of 150 mM.
Because both ζ-potential and drift measurements depend mainly on the charge state of outer layers, we need a different approach to gain information on the charged state of lipid bilayers inside the MLVs. In fact, membrane charging can be most easily detected by x-ray scattering in mixed solutions. Because all of the solutions considered here reduce the vdW attraction (see index or refraction data in Fig. 3), adding more solutes to any given sample is expected to further increase the swelling, if vdW reduction is the sole mechanism responsible for the swelling. We tested this situation by comparing D-spacings in pure 100 mM solutions of KCl, KBr, and MOPS with 1:1 binary mixtures at total concentrations of 200 mM. These results are shown in Fig. 6, which reveals that addition of KCl to either KBr or MOPS solutions causes a decrease in D-spacings, indicating that KCl diminishes the effects of KBr and MOPS on membrane interactions by screening electrostatic repulsion.
Figure 6.
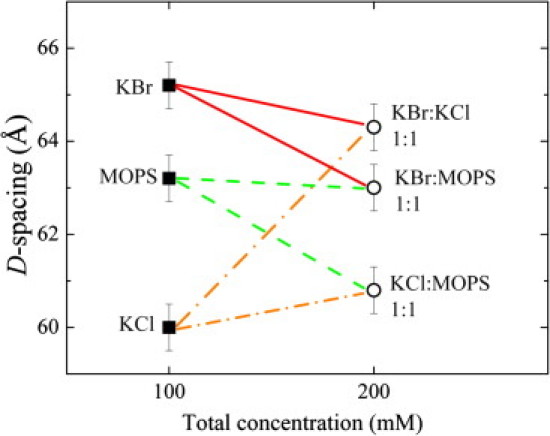
Comparison of interlamellar spacings for pure 100 mM solutions (squares) and 1:1 mixtures at 200 mM total concentration (circles).
Lastly, competition measurements obtained at a fixed total concentration reveal the strength and the relative sign of electrostatic charging. Measurements acquired at 200 mM total concentrations are shown in Fig. 7. Panel A shows how D-spacings decrease as either KBr or MOPS is gradually replaced by KCl. These curves are highly nonlinear, showing that replacement with Cl does more than just reduce the membrane charge, it also interferes with the charges that are still present. Cl is not an inert replacement, because it screens the electrostatic repulsion between membranes. The data also indicate that the charging effect of MOPS is weaker than that of Br. A direct competition between MOPS and Br should then give us the relative charging strength of MOPS and Br. This measurement is shown in panel B of Fig. 7. As KBr is gradually replaced by MOPS, the D-spacing decreases, reaches a minimum, and increases again. This competition measurement shows that the charging effect of MOPS is weaker than that of Br but not at all negligible. A shallow minimum is observed between 70% and 90% MOPS content, with D-spacing values similar to that observed in the presence of KCl at the same concentration for which membrane charging was shown to be negligible (1). This indicates that the electrostatic contributions of KBr and MOPS at the minimum D-spacing cancel each other. Just as with KCl, the residual swelling (compared with pure water) is due to the reduction of the vdW attraction.
Figure 7.
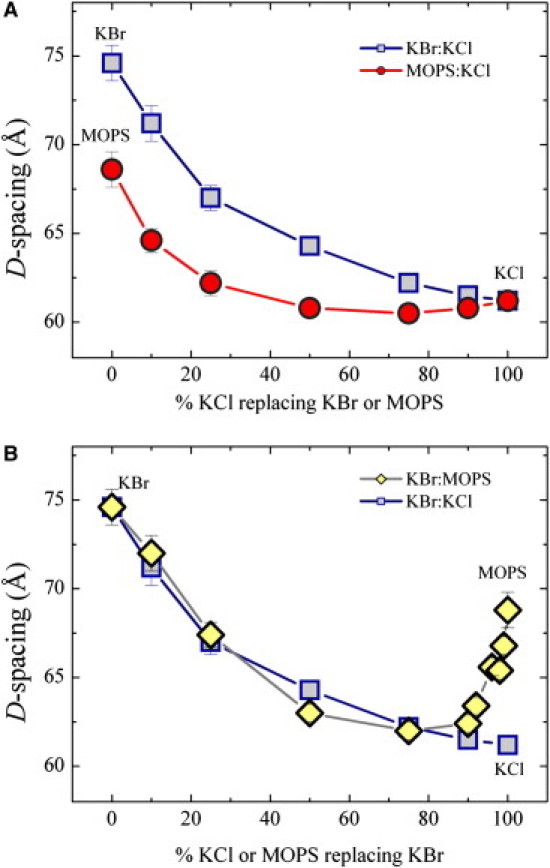
Measurements of interlamellar spacings for mixtures of KBr, KCl, and MOPS at 200 mM total concentration. Panel A shows the effect of KCl in substituting KBr and MOPS plotted versus mol % KCl. Labels to symbols indicate samples in pure salt solutions: KBr (square), MOPS (circle), and KCl (square and circle). Panel B compares the effects of KCl and MOPS in substituting KBr. Labels to symbols indicate samples in pure salt solutions: KBr (square and diamond), MOPS (diamond), and KCl (square).
Discussion
Addition of hydrophilic solutes to a suspension of lipid MLVs often leads to changes in interlamellar D-spacings. The exact way in which D-spacings change tells us how solutes and membranes interact. For neutral membranes, a reduction in D-spacing indicates that solutes stay outside of the MLVs and act osmotically (34). In contrast, an increase in D-spacing indicates that solutes enter the interlamellar space and modify interbilayer interactions (1,25,35). For MES, MOPS, and HEPES buffers, we observe the latter effect. This means that buffers enter the interlamellar space, modify interbilayer interactions, and possibly bind to lipid bilayers.
Generally, MLV swelling can be explained by a weakening of the attractive vdW force or by an increase of repulsive terms (hydration, fluctuation, and possibly electrostatics) (1,25). The index of refraction measurements (Fig. 3) indicates that the vdW interaction decreases with added buffer. This is because the strength of the vdW attraction is determined by differences in dielectric permittivities between solutions and lipid bilayers: the larger the difference, the stronger the vdW attraction. At optical frequencies, the dielectric permittivity is equal to the square of the index of refraction, which means that as the index of refraction of the interlamellar solution approaches that of the lipid bilayer, the difference in the dielectric permittivities decreases, leading to a weaker vdW attraction. Since MES, MOPS, and HEPES refractive indices are higher than those of KCl and KBr (Fig. 3), it shows that these buffers are more polarizable than Br ions and hence the enhanced swelling of MOPS and HEPES (Fig. 2) compared to MES, KBr, and KCl. Fig. 3 shows that the refractive indices of titrated and untitrated samples are practically the same; therefore, the effect of the additional solutes needed to titrate the samples was negligible.
In addition to weakening the vdW attraction (at least in the case of MOPS), an electrostatic repulsion is created by the charging effect of MOPS zwitterions on lipid membranes. Three independent measurements (x-ray of KBr/MOPS competition, drift in constant electric field, and ζ-potential measurements) show that DLPC bilayers in the presence of MOPS are positively charged. It is also possible that zwitterionic buffers can soften lipid bilayers, as suggested previously (36), which would add to the effect on the vdW and electrostatic forces examined here. The fact that MOPS and HEPES curves in Fig. 1 exceed the KBr curve at high concentrations would indeed support the softening hypothesis, but this remains to be determined by measurements of bending rigidities. The softening effect is expected to increase with the hydrophobicity of the buffers as seen here for MOPS and HEPES (37,38) and in a previous study (36) for the more-hydrophobic buffer PIPES.
To explain how electrostatic forces arise, we need to consider the zwitterionic nature of the buffers. Generally, MOPS, MES, and HEPES carry a positive charge on the protonated amino group and a negative charge on the deprotonated sulfonic acid group (10,39,40), as shown in Fig. 2. In aqueous solutions, deprotonation of the amino group (called the second dissociation in this case) occurs as a function of pH, generating molecules with a net negative charge. The pKa2 values for the amino group are 6.15 for MES (10,39), 7.2 for MOPS (39), and 7.55 for HEPES (10,39). When the pH of the solution equals the pKa2 of the solute, half of the solutes are zwitterionic and the other half carry a net negative charge. At pH 7, ∼61% of MOPS molecules are zwitterionic, compared with 12% for MES. Our measurements indicate that DLPC lipid bilayers become positively charged in the presence of MOPS at pH 7. This means that the negatively charged fraction of MOPS does not bind to lipid bilayers, and that the observed charging effect is due to a particular orientation of bound MOPS zwitterions. One possible scenario is as follows: The negative charge on the sulfonyl moiety's oxygen associates with the positive charge on the lipid choline. Then the positive charged morpholine or piperazine moieties on opposing bilayers repel each other. This molecular arrangement may be favored because the morpholine moieties (or piperazine in the case of HEPES) are bulky and may orient away from the lipid headgroup region instead of being embedded into it. In addition, because electric dipoles orient in electric fields, bound zwitterions will orient according to the local electric field at the lipid-water interface generated by lipid headgroups and anisotropic water (32).
This situation raises a number of interesting questions. First, is the pKa of buffer molecules at the lipid-water interface the same as in the bulk? If not, then either the dipolar or the charged fraction of buffer molecules will appear excluded from the interlamellar water. Second, how does the unbound fraction of buffer molecules (within the interlamellar water) affect the electrostatic forces between membranes? As shown recently (6), the presence of polarizable charged species in between weakly charged surfaces create forces that are unaccounted for by standard electrostatic models. Third, the fact that DLPC vesicles move in an electric field in the presence of MOPS buffer means that the MOPS molecules bind strongly enough to the lipid bilayer to cause whole MLVs to move. These questions could be addressed more quantitatively by a study of buffer partitioning in the interlamellar water as a function of pH.
We conclude with a brief discussion of interbilayer forces. At concentrations of 200 mM of monovalent charges, the Debye screening in the bulk approaches the Bjerrum length, which is the distance at which electrostatic interactions between two unit charges are equal to the thermal energy kBT. In pure water, this distance is 7 Å at 300 K. In the presence of membranes (or any other extended macromolecular surface), we distinguish between an ion-surface interaction regime at low concentration and an ion-pair correlation regime at high concentrations (41). The presence of ion (Bjerrum) pairs can reduce the screening of electrostatic forces (42) and the zero-frequency part of vdW forces (1) between neighboring membranes. This effect is reflected in an accelerated change in equilibrium spacings between 100 mM and 200 mM concentrations (Fig. 1). A similar situation could occur for zwitterionic solutes. As the concentration of solutes increases, the formation of dipole pairs becomes likely. The formation of such dipole pairs supports the hypothesis that zwitterionic buffers can soften lipid bilayers. Although the incorporation of charged species into the lipid headgroup region generally does not lead to softening of membranes (e.g., as in the case of Br ions (25)), softening is more likely to occur when solutes can penetrate into the hydrocarbon region of the lipid bilayers and disrupt the chain packing. The formation of dipole pairs that can occur at high solute concentrations can facilitate this process, leading to the enhanced swelling seen for MOPS and HEPES at concentrations above 300 mM.
As shown previously for the case of monovalent salt solutions, the calculation of membrane interaction parameters is far from a trivial task (1,25,41). This is because a number of independent measurements are needed to obtain the interaction parameters in Eqs. 2–4 above. In particular, a measurement of the actual solute concentration in the interlamellar space is needed as described previously (41). Here, we use a direct comparison between the effects of buffers and monovalent salt to illustrate the extent to which interlamellar forces are affected by solutes. The aqueous space between neighboring DLPC membranes increases from 20 Å in pure water to ∼30 Å in 200 mM concentrations of salt or zwitterionic buffers. Using the interaction parameters from Petrache et al. (25) (see Materials and Methods), the vdW force between membranes in pure water is 0.03 pN per lipid, and it is exactly balanced by a net repulsive force with opposite sign. Screened by the presence of solutes to 70% of its initial value (1), the vdW force is reduced to 0.02 pN per lipid, and at 20 Å separation, it is overcome by repulsive forces. The residual repulsion pushes membranes apart to a new equilibrium spacing. In the absence of electrostatic forces, the new equilibrium spacing would be at 26 Å, which is less than what is measured. The extra swelling to the observed distance of 30 Å is explained by an added electrostatic repulsion as calculated using a charge regulation model (1). At the new equilibrium point, the forces are FvdW ∼ 0.006 pN, Fhyd + Ffl ∼ 0.005 pN, and Felec ∼ 0.001 pN per lipid. Although each of these forces might appear weak, it is their relative strength that matters in deciding the equilibrium state of the system. When attractive forces are weak, electrostatic repulsions even at separations of ≥30 Å cannot be neglected.
In conclusion, we have shown that zwitterionic solutes can modify lipid interactions through a mechanism in which both dispersion forces (vdW) and electrostatic forces are modified. This modification of forces could play a role in the observed effects of buffers on cellular activity mentioned in the Introduction. In addition, the measurements reported here could stimulate and guide theoretical and computational studies that account for molecular polarizabilities and the dynamic nature of electrostatic forces in biological systems.
Acknowledgments
We thank Mangilal Agarwal for assistance with ζ-potential measurements, and Matthew J. Justice for help with the x-ray instrument.
This research was supported in part by a Purdue Research Foundation grant (to H.I.P.). The Integrated Nanosystems Development Institute at Indiana University Purdue University Indianapolis provided support and facilities for this research.
References
- 1.Petrache H.I., Zemb T., Parsegian V.A. Salt screening and specific ion adsorption determine neutral-lipid membrane interactions. Proc. Natl. Acad. Sci. USA. 2006;103:7982–7987. doi: 10.1073/pnas.0509967103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ben-Yaakov D., Andelman D., Podgornik R. Beyond standard Poisson-Boltzmann theory: ion-specific interactions in aqueous solutions. J. Phys. Condens. Matter. 2009;21:424106. doi: 10.1088/0953-8984/21/42/424106. [DOI] [PubMed] [Google Scholar]
- 3.Boström M., Williams D.R.M., Ninham B.W. Specific ion effects: why DLVO theory fails for biology and colloid systems. Phys. Rev. Lett. 2001;87:168103. doi: 10.1103/PhysRevLett.87.168103. [DOI] [PubMed] [Google Scholar]
- 4.Kjellander R. Intricate coupling between ion-ion and ion-surface correlations in double layers as illustrated by charge inversion-combined effects of strong Coulomb correlations and excluded volume. J. Phys. Condens. Matter. 2009;21:424101. doi: 10.1088/0953-8984/21/42/424101. [DOI] [PubMed] [Google Scholar]
- 5.French R.H., Parsegian V.A., Zemb T. Long range interactions in nanoscale science. Rev. Mod. Phys. 2010;82:1887–1944. [Google Scholar]
- 6.Ben-Yaakov D., Andelman D., Podgornik R. Dielectric decrement as a source of ion-specific effects. J. Chem. Phys. 2011;134:074705. doi: 10.1063/1.3549915. [DOI] [PubMed] [Google Scholar]
- 7.Eagle H. Buffer combinations for mammalian cell culture. Science. 1971;174:500–503. doi: 10.1126/science.174.4008.500. [DOI] [PubMed] [Google Scholar]
- 8.Croce C.M., Koprowski H., Eagle H. Effect of environmental pH on the efficiency of cellular hybridization. Proc. Natl. Acad. Sci. USA. 1972;69:1953–1956. doi: 10.1073/pnas.69.7.1953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ferguson W.J., Braunschweiger K.I., Good N.E. Hydrogen ion buffers for biological research. Anal. Biochem. 1980;104:300–310. doi: 10.1016/0003-2697(80)90079-2. [DOI] [PubMed] [Google Scholar]
- 10.Good N.E., Winget G.D., Singh R.M. Hydrogen ion buffers for biological research. Biochemistry. 1966;5:467–477. doi: 10.1021/bi00866a011. [DOI] [PubMed] [Google Scholar]
- 11.Zhao G., Chasteen N.D. Oxidation of Good's buffers by hydrogen peroxide. Anal. Biochem. 2006;349:262–267. doi: 10.1016/j.ab.2005.10.005. [DOI] [PubMed] [Google Scholar]
- 12.Cowan A.I., Martin R.L. Ionic basis of the membrane potential responses of rat dorsal vagal motoneurones to HEPES buffer. Brain Res. 1996;717:69–75. doi: 10.1016/0006-8993(96)00052-2. [DOI] [PubMed] [Google Scholar]
- 13.Bowman C.M., Berger E.M., Repine J.E. HEPES may stimulate cultured endothelial cells to make growth-retarding oxygen metabolites. In Vitro Cell. Dev. Biol. 1985;21:140–142. doi: 10.1007/BF02621350. [DOI] [PubMed] [Google Scholar]
- 14.Daniel P.F., Wolf G. Incorporation of labeled glucosamine into glycoproteins by organ cultures of hamster trachea: adverse effects of HEPES buffer. In Vitro. 1975;11:347–353. doi: 10.1007/BF02616370. [DOI] [PubMed] [Google Scholar]
- 15.Douglas G.C., Swanson J.A., Kern D.F. HEPES buffer perfusate alters rabbit lung endothelial permeability. J. Appl. Physiol. 1993;75:1423–1425. doi: 10.1152/jappl.1993.75.3.1423. [DOI] [PubMed] [Google Scholar]
- 16.van Haaren P.M., VanBavel E., Spaan J.A. Charge modification of the endothelial surface layer modulates the permeability barrier of isolated rat mesenteric small arteries. Am. J. Physiol. Heart Circ. Physiol. 2005;289:H2503–H2507. doi: 10.1152/ajpheart.00587.2005. [DOI] [PubMed] [Google Scholar]
- 17.Luzzati V., Gulik-Krzywicki T., Rand R.P. X-ray study of model systems: structure of the lipid-water phases in correlation with the chemical composition of the lipids. J. Gen. Physiol. 1968;51(5, Suppl):37S. [PubMed] [Google Scholar]
- 18.Rand R.P., Parsegian V.A. Hydration forces between phospholipid-bilayers. Biochim. Biophys. Acta. 1989;988:351–376. [Google Scholar]
- 19.Petrache H.I., Gouliaev N., Nagle J.F. Interbilayer interactions from high-resolution x-ray scattering. Phys. Rev. E. 1998;57:7014–7024. [Google Scholar]
- 20.Simon S.A., Mcintosh T.J., Magid A.D. Magnitude and range of the hydration pressure between lecithin bilayers as a function of headgroup density. J. Colloid Interface Sci. 1988;126:74–83. [Google Scholar]
- 21.Parsegian V.A. Cambridge University Press; New York: 2006. Van der Waals Forces: A Handbook for Biologists, Chemists, Engineers, and Physicists. [Google Scholar]
- 22.Mcintosh T.J., Magid A.D., Simon S.A. Repulsive interactions between uncharged bilayers. Hydration and fluctuation pressures for monoglycerides. Biophys. J. 1989;55:897–904. doi: 10.1016/S0006-3495(89)82888-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Leontidis E., Aroti A., Zemb T. Effects of monovalent anions of the hofmeister series on DPPC lipid bilayers. Part II: modeling the perpendicular and lateral equation-of-state. Biophys. J. 2007;93:1591–1607. doi: 10.1529/biophysj.107.109264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Elsayed M.M., Vierl U., Cevc G. Accurate potentiometric determination of lipid membrane-water partition coefficients and apparent dissociation constants of ionizable drugs: electrostatic corrections. Pharm. Res. 2009;26:1332–1343. doi: 10.1007/s11095-009-9842-1. [DOI] [PubMed] [Google Scholar]
- 25.Petrache H.I., Tristram-Nagle S., Parsegian V.A. Swelling of phospholipids by monovalent salt. J. Lipid Res. 2006;47:302–309. doi: 10.1194/jlr.M500401-JLR200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Simon S.A., McIntosh T.J. Magnitude of the solvation pressure depends on dipole potential. Proc. Natl. Acad. Sci. USA. 1989;86:9263–9267. doi: 10.1073/pnas.86.23.9263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 28.Simon S.A., Advani S., McIntosh T.J. Temperature dependence of the repulsive pressure between phosphatidylcholine bilayers. Biophys. J. 1995;69:1473–1483. doi: 10.1016/S0006-3495(95)80017-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Evans E.A., Parsegian V.A. Thermal-mechanical fluctuations enhance repulsion between bimolecular layers. Proc. Natl. Acad. Sci. USA. 1986;83:7132–7136. doi: 10.1073/pnas.83.19.7132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kucerka N., Liu Y.F., Nagle J.F. Structure of fully hydrated fluid phase DMPC and DLPC lipid bilayers using X-ray scattering from oriented multilamellar arrays and from unilamellar vesicles. Biophys. J. 2005;88:2626–2637. doi: 10.1529/biophysj.104.056606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ninham B.W., Parsegian V.A. Electrostatic potential between surfaces bearing ionizable groups in ionic equilibrium with physiologic saline solution. J. Theor. Biol. 1971;31:405–428. doi: 10.1016/0022-5193(71)90019-1. [DOI] [PubMed] [Google Scholar]
- 32.Petrache H.I., Tristram-Nagle S., Nagle J.F. Structure and fluctuations of charged phosphatidylserine bilayers in the absence of salt. Biophys. J. 2004;86:1574–1586. doi: 10.1016/S0006-3495(04)74225-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tatulian S.A. Effect of lipid phase transition on the binding of anions to dimyristoylphosphatidylcholine liposomes. Biochim. Biophys. Acta. 1983;736:189–195. doi: 10.1016/0005-2736(83)90283-3. [DOI] [PubMed] [Google Scholar]
- 34.Parsegian V.A., Rand R.P., Rau D.C. Osmotic stress, crowding, preferential hydration, and binding: a comparison of perspectives. Proc. Natl. Acad. Sci. USA. 2000;97:3987–3992. doi: 10.1073/pnas.97.8.3987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Demé B., Dubois M., Zemb T. Swelling of a lecithin lamellar phase induced by small carbohydrate solutes. Biophys. J. 2002;82:215–225. doi: 10.1016/S0006-3495(02)75388-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Peiró-Salvador T., Ces O., Seddon A.M. Buffers may adversely affect model lipid membranes: a cautionary tale. Biochemistry. 2009;48:11149–11151. doi: 10.1021/bi901662b. [DOI] [PubMed] [Google Scholar]
- 37.Koerner M.M., Mossa-Basha A., Petrache H.I. Interaction of buffers with lipid membranes. Biophys. J. 2009;96:459a. [Google Scholar]
- 38.Koerner M.M., Justice M.J., Petrache H.I. Buffer properties revealed with model lipid membranes. Biophys. J. 2010;98:273a–274a. [Google Scholar]
- 39.Vega C.A., Bates R.G. Buffers for the physiological pH range: thermodynamic constants of four substituted aminoethanesulfonic acids from 5 to 50° C. Anal. Chem. 1976;48:1293–1296. doi: 10.1021/ac50003a010. [DOI] [PubMed] [Google Scholar]
- 40.Feng D., Koch W.F., Wu Y.C. Second dissociation constant and pH of N-(2-hydroxyethyl)piperazine-N'-2-ethanesulfonic acid from 0 to 50° C. Anal. Chem. 1989;61:1400–1405. [Google Scholar]
- 41.Petrache H.I., Kimchi I., Parsegian V.A. Measured depletion of ions at the biomembrane interface. J. Am. Chem. Soc. 2005;127:11546–11547. doi: 10.1021/ja052549+. [DOI] [PubMed] [Google Scholar]
- 42.Zwanikken J., van Roij R. Inflation of the screening length induced by Bjerrum pairs. J. Phys. Condens. Matter. 2009;21:424102. doi: 10.1088/0953-8984/21/42/424102. [DOI] [PubMed] [Google Scholar]


