Abstract
Subcellular cargos are often transported by teams of processive molecular motors, which raises questions regarding the role of motor cooperation in intracellular transport. Although our ability to characterize the transport behaviors of multiple-motor systems has improved substantially, many aspects of multiple-motor dynamics are poorly understood. This work describes a transition rate model that predicts the load-dependent transport behaviors of multiple-motor complexes from detailed measurements of a single motor's elastic and mechanochemical properties. Transition rates are parameterized via analyses of single-motor stepping behaviors, load-rate-dependent motor-filament detachment kinetics, and strain-induced stiffening of motor-cargo linkages. The model reproduces key signatures found in optical trapping studies of structurally defined complexes composed of two kinesin motors, and predicts that multiple kinesins generally have difficulties in cooperating together. Although such behavior is influenced by the spatiotemporal dependence of the applied load, it appears to be directly linked to the efficiency of kinesin's stepping mechanism, and other types of less efficient and weaker processive motors are predicted to cooperate more productively. Thus, the mechanochemical efficiencies of different motor types may determine how effectively they cooperate together, and hence how motor copy number contributes to the regulation of cargo motion.
Introduction
Cytoskeletal motors are molecular machines that consume ATP as fuel to produce the forces necessary to move vesicular and protein cargos directionally within the viscous and crowded environments of eukaryotic cells (1). These proteins are therefore central to mechanisms that control the spatiotemporal distributions of subcellular commodities in the cytoplasm. Various microtubule motors are highly processive and can transport cargos against piconewton-sized forces and over micron-sized distances before disassociating from their filament, which suggests that they can function efficiently when acting independently as single-motor molecules (2,3). Nevertheless, processive motors often operate in groups in vivo (4–6), which raises questions regarding the extent to which collective motor dynamics influences intracellular transport processes. Cells may rely on the combined action of motors to surmount transport challenges that require high-force production or long-distance transport (7), and there is evidence that some transport defects associated with motor mutations can be more pronounced when cargo transport is driven by large numbers of motors (8). Collective motor dynamics may also help to regulate cargo motion (9,10). Many cargos move bidirectionally because they are transported by multiple, oppositely directed kinesin and dynein motors. Cells may tune the number/ratio of kinesins and dyneins such that one motor team has a net advantage over the other in controlling the direction in which these cargos are transported (10,11).
The role played by multiple-motor dynamics in intracellular transport naturally depends on the extent to which grouping motors together enhances their transport properties (i.e., increased force production, velocity, or cargo-filament affinity compared with single-motor molecules). Until recently, it has been challenging to characterize these dependencies because it is often difficult to determine the number of motors that are bound to moving cargos. However, several groups have developed experimental methods to facilitate more-detailed studies of the impact of motor number and various biochemical and mechanical factors on cargo transport (12–15). In two of these studies, our laboratory examined the collective dynamics of structurally defined motor complexes composed of two kinesin-1 molecules (14,15). This work showed that two interacting kinesins generally do not transport cargos over the distances or produce the forces that would be expected of a cooperative team. Instead, despite kinesin's efficiency and high processivity, kinesin complexes tend to transport their cargos while primarily using only one motor at a time (i.e., the motors seem to cooperate negatively).
Although the weak dependence of cargo transport on kinesin copy number can be attributed to geometric effects that reduce the ability of multiple motors to share their applied loads (15,16), it is unclear why such effects are so pronounced for multiple kinesins. When transporting a cargo, motors can bind to a range of different filament lattice sites, many of which are positioned far apart from one another (tens of motor step-size units). Yet, load sharing only occurs if motors occupy closely spaced microtubule lattice site positions. To cooperate productively, trailing kinesins therefore face the challenge of catching up to their continually advancing leading partners before either motor releases from the microtubule. Naturally, a motor's microtubule-bound lifetime will influence this process (16). However, both the mechanical (elastic) and mechanochemical properties of motors are known to vary nonlinearly with force, and the evolution of a motor complex's microtubule-bound geometry should also depend on interdependent relationships between these properties. Furthermore, the applied loads imposed on cargos in cells may either be relatively static or highly dynamic, as is the case when antagonistic motors compete and stretch their cargos (11,17). In the latter circumstance, the role of loading rates must also be considered. Thus, understanding the cooperative dynamics of multiple kinesins, as well as other processive motor types, will ultimately require detailed and accurate parameterization of transport models to account for competing factors that influence their dynamics.
Herein, we present a model of multiple motor dynamics that predicts a cargo's load-dependent transport properties from detailed measurements of single-motor velocities, detachment rates, and elasticities. Using these data, one can account for single-motor stepping behaviors, load-rate-dependent kinetics describing motor-filament detachment, and strain-induced stiffening of motors and their resultant nonlinear, force-dependent elasticities. As a test case, we examined the transport properties of our structurally defined two-kinesin complexes (15). Our model reproduces key signatures found in optical trapping experiments, in particular the observation that multiple-kinesin transport is driven primarily by a single, unassisted motor molecule. Although this behavior arises from generic kinetic and geometric constraints that affect multiple-kinesin dynamics in a variety of transport scenarios, the model also predicts that this behavior is influenced by spatiotemporal properties of the applied load in a static trap. In contrast, processive motors whose stepping mechanism is less efficient than kinesin's are found to cooperate more productively regardless of whether they experience variable or constant loads, and even though the geometric constraints that cause multiple kinesins to cooperate negatively still apply. Therefore, the sensitivity of cargo transport to motor copy number appears to depend inversely on the efficiency of a motor's mechanochemistry.
Discrete-Microstate Model
General modeling procedure
In the model presented here, we examine the progression of cargos against applied loads by computationally solving a system of master equations that describe the time-dependent transitions of multiple-motor complexes between different microtubule-bound configurations, or microstates (Fig. 1). The forces in each microstate are expected to be balanced because all of the linkages are assumed to reach their mechanical equilibrium rapidly relative to the time between the stepping (15,18,19), binding, and detachment events that drive the system from one microstate to the next. The rate at which a motor complex transitions between microstates depends on the difference in the stored mechanical energy of the final and initial configurations of the system (ΔEconfig), which we calculate using our previously described mechanical modeling/energy minimization procedure (15). Below, we describe how these energies and transition rates are calculated from fits to single-kinesin optical trapping data. A complete description of the modeling procedure is provided in the Supporting Material.
Figure 1.
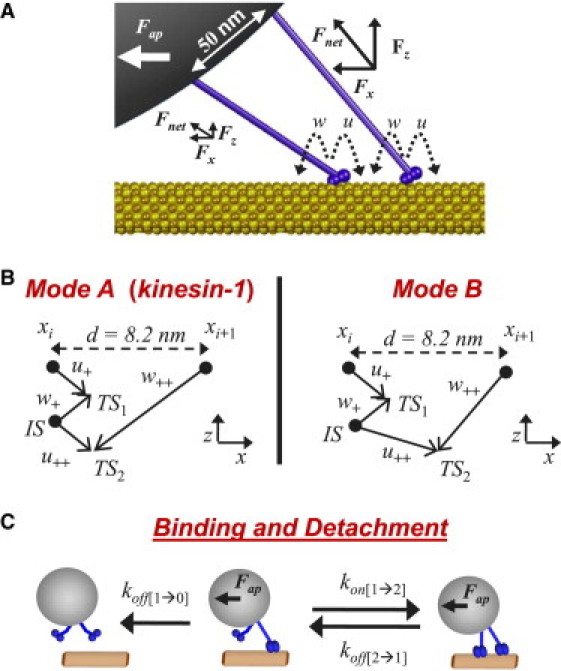
Stepping, binding, and detachment transitions enumerated in the discrete-microstate model. (A) Illustration depicting a two-kinesin complex in a specific bound configuration; on-microtubule spacing = 32.8 nm, on-bead spacing = 50 nm, Fap = 5 pN. (B) Reaction coordinates used to calculate two-state motor stepping rates. Substeps involve displacements both along and perpendicular to the microtubule axis. For stepping mode A, the positions of transition states (TSn) for each substep and the intermediate state (IS) correspond directly to those reported by Fisher and Kim (23). For stepping mode B, the position of the second transition state (TS2) was moved toward the final microtubule lattice site position (xi+1). This alteration caused the forward stepping rate to decrease more rapidly with increasing load. (C) Illustration of microstate transitions involving motor binding and detachment.
Defining the microstate energies of multiple-motor systems using single-kinesin stiffness data
In our previous study (15), we determined the force-dependent elasticity (stiffness) of a kinesin motor from power spectral analyses of bead positional fluctuations along the microtubule axis (x axis). These data are not a direct measurement of the motor's stiffness; rather, they serve as a projection of the motor's axial stiffness along the microtubule axis (if stretched from head to tail), and hence the measured stiffnesses are influenced by the angle between the motor's stalk and the microtubule. We therefore fit the data to a function κM(lax) describing the stiffness of a single kinesin via a regression routine that uses the mechanical model to determine the vectorial component of κM(lax) along the microtubule axis (i.e., the projection κM,x(lax)) over a range of applied loads. The unstretched head-to-tail length of the motor (lo) is assumed to be 50 nm. We find that κM(lax) can be approximated by a sigmoid function, which may reflect the fact that the kinesins are anchored to the beads via multiple mechanical elements.
The fitted function κM(lax) allows the effects from strain-induced stiffening of motor linkages (Fig. 2 A) (15,20) to be accounted for in our calculation of Econfig. The configurational energy of a microstate is the sum of the potential energy of the bead in the trap and the work required to stretch each motor from its unstrained length (lo) to the extended length (lax) found in the force-balanced microstate configuration:
| (1) |
where κT is the spring constant of the trap, (xT – xb) is the displacement of the bead from the trap center, is the force pointing along the stalk of that motor from its attachment site on the bead to its microtubule-binding site, and Δlax is the magnitude of a motor's extension from its unstretched length (l0).
Figure 2.
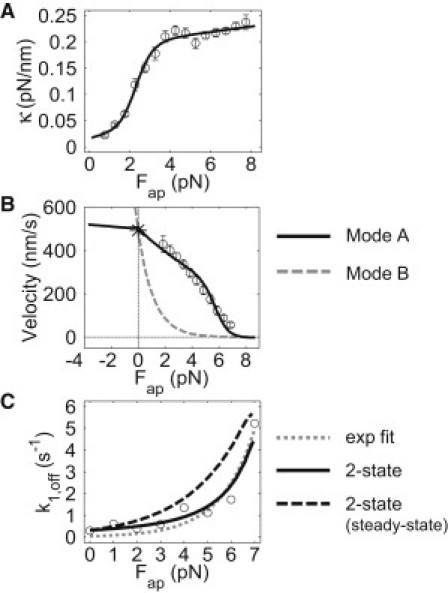
Parameterization of motor elasticity, stepping, and detachment kinetics. (A) Experimental measurements and a best fit describing the force-dependent elasticity κM,x(lax) of the single-kinesin construct that is incorporated into the multiple-motor systems (15). (B) Single-motor F-V curves determined via a best fit of the kinesin-1 optical trapping data using stepping mode A (solid line) and the corresponding curve calculated for motors that advance via stepping mode B (dashed line). (C) Single-kinesin detachment rates measured in an optical trap. Best fits are shown using a two-state detachment model describing load-rate-dependent motor unbinding (solid line), the corresponding steady-state detachment behavior (dashed line), and Kramer's theory (dotted line).
Modeling configuration-dependent motor stepping rates
Even if the loads experienced by a motor are the same, the angle between its stalk and the microtubule can differ greatly when cargo transport is driven by a single motor and multiple motors. Because stalk angles affect motor velocity (21,22), one should calculate the motor stepping rates using a model that accounts for the work done against vectorial loads. The model developed by Fisher and Kim (23) assumes that kinesin's forward and backward stepping motions consist of two separate biochemical transitions (substeps) corresponding to displacements of the molecule in two dimensions (x and z). Because the substeps involve motions of the molecule perpendicular to the axis of the microtubule (Fig. 1 B), loads in this direction influence the stepping rates. The position of the transition state in each substep determines the splitting of the work done along the reaction coordinate between the forward and reverse transitions. For each transition, conservation of energy allows the work to be calculated from the difference in Econfig from the beginning to the end of the motor stepping path via the following equations:
| (2) |
| (3) |
In these equations, u and w refer to forward and backward substep transition rates, respectively, as defined in Fig. 1 B. The notation i → TS1,i indicates a partial step of the motor from position i to the transition state at TS1,i, so that ΔEconfig(i → TS1,i) = Econfig(TS1,i) − Econfig(i). From these rates, effective full-step transition rates and average motor velocities can be calculated:
| (4) |
| (5) |
| (6) |
where d is the total step size of the motor molecule (d = 8.2 nm for kinesin).
Assuming that motors step asynchronously, we calculate their load-dependent stepping rates using the predetermined ΔEconfig values that describe transitions of motor complexes between different microtubule-bound configurations as each motor proceeds through all of its substep transitions, without any movement of the other motors. Thus, the only difference between this treatment and that of single-motor molecules is that some of the change in configuration energy is stored in the motor's partner(s) according to the definition of Econfig.
Specifying distinct motor stepping behaviors
To specify kinesin's stepping rates, we assume that the positions of kinesin's stepping intermediate (IS) and transition (TS1 and TS2) states correspond to the values previously reported by Fisher and Kim (23) (stepping mode A in Fig. 1 B). The forward and backward stepping rates were determined from fits to measured single-kinesin optical trapping data (Fig. 2 B). Here, we used our mechanical modeling procedure to calculate force-dependent ΔEconfig values for a single motor moving along its stepping path through each IS and TS position. We then approximated the single-kinesin data using a generic fitting algorithm, with the unloaded transition rate prefactors in Eqs. 2 and 3 used as fit parameters. This is likely the most appropriate adaptation of the motor stepping model for the analyses presented here. Our truncated kinesin-1 constructs should possess the same basic stepping mechanism as wild-type kinesins, but their zero-load, substep transition rates describe all other biochemical aspects of the reaction, which could be affected by other experimental factors.
The single-kinesin F-V fit presented in Fig. 2 B shows reasonable agreement with the measured trend and yields unloaded motor transition rates that reflect kinesin's strong directional bias: . To evaluate how the curvature of a motor's F-V relationship influences multiple-motor behaviors, we also generate an F-V curve for motors that possess a slightly modified stepping reaction coordinate (Fig. 1 B, stepping mode B), such that the position of the second transition state TS2 in the original coordinate is moved toward the final lattice site of the step (i + 1) by a distance of 3.0 nm. This alteration increases the amount of work performed during the second forward substep, and primarily increases the sensitivity with which the composite forward stepping rate decreases with increasing load (24). Using the unloaded stepping rates obtained via single-kinesin fits, such behavior produces the concave upward F-V curve plotted in Fig. 2 B.
Microstate transitions via motor detachment and binding
Average motor-microtubule detachment rates are commonly assumed to follow a load dependence described by Kramer's theory: , where Δsd is the distance a motor must move to release from the microtubule. However, this function does not reproduce our measurements of single-kinesin detachment rates (Fig. 2 C, dotted line, and Fig. S1 A). This disagreement likely stems from the time dependence of the applied load in the static trapping experiments (bond affinities between biomacromolecules typically increase with increasing loading rate) (25). Furthermore, we find much weaker agreement between our theoretical and experimental data when motor detachment is parameterized using this fit (Fig. S2 B). To address this, we treat motor-microtubule detachment as a two-state process that occurs along a reaction coordinate possessing two different energetic barriers (Fig. S1). We determine the barrier heights and positions of the coordinate's intermediate and transition states by fitting single-kinesin detachment data using a procedure that solves a system of rate equations that describe the time-dependent probability that a motor will occupy each of these states.
Because the above treatment allows a reaction coordinate describing motor detachment to be approximated, we can calculate detachment rates for various transport scenarios in which motors may experience different loading rates. For example, if the loading rate is negligible, the model predicts that motors will detach much more rapidly than the rates measured in the trapping assays (Fig. 2 C, dashed line).
Capturing the load-rate dependence of detachment transitions for multiple-motor systems ultimately requires detailed and cumbersome simulations to calculate the probability that a motor will occupy the different intermediate states along its unbinding reaction coordinate. These probabilities depend on the time-dependent progression of the loads motors experience as they bind and step along the filament, and hence the different trajectories taken by motors within a multiple-motor system. Nevertheless, one can approximate the influence of load rate by considering the generic constraints that dictate load-sharing behaviors. For example, the loading rate experienced by a motor will depend not only on how fast the bead moves and the trap's spring constant, but also on how load distributions within the complex shift in time. In general, the load assumed by a trailing motor will increase slowly because this motor has to catch up to the leading motor in the complex to take on the applied load. Analogously, the associated shift in the transport burden from the leading to the trailing motor can decrease the loading rate experienced by the leading motor; loads can even decrease on this motor. At low applied load, detachment rates for both motors will therefore tend toward the load-rate-independent detachment curve in Fig. 2 C instead of the fitted (load-rate-dependent) function. Yet, at high loads, we expect shifts in load distributions to affect multiple-motor dynamics to a lesser degree; in this regime, cargo transport necessitates load sharing. These considerations are important for approximating the observed detachment force and rate dependencies (see Section S5), and they allow the development of a much simpler model of multiple-motor dynamics that incorporates load-rate-dependent effects.
Unloaded motor-microtubule binding rates were assigned their previously reported values (kon[1→2](Fap=0) = 4.7 s−1). However, as in our earlier discrete state transition-rate model (26), these rates depend on the difference in the configuration energies of a motor complex before and after individual motors bind the microtubule filament. These energy differences are calculated via the same procedure used to determine ΔEconfig for motor stepping and detachment. Of note, motor binding rates are now also influenced by forward bead displacements that arise from shifts of load distributions between the microtubule-bound motors within a complex, and are reduced by the work required to produce these displacements.
Results and Discussion
Comparisons between theory and experiment
When our model is parameterized by the fits to our single-kinesin-1 data, it reproduces several key results found in our previous optical trapping studies of two kinesins (15). First, two-kinesin complexes most commonly detach at forces near the 7 pN stalling force of a single-kinesin motor (Fig. 3 A). These distributions are qualitatively similar to our measured detachment force distributions. However, one should be cautious when making comparisons between the measured and predicted detachment behaviors of multiple-motor complexes because they can detach partially during a single run before full detachment occurs, and the experimenter's choice of which events are counted can influence the resultant detachment force distributions and interpretations. Therefore, in Fig. 3 A we break down these detachment events into those caused by the release of a leading (gold), trailing (blue), or singly bound motor (red) within a complex, and also show them as the sum of all events (gray). This distribution shows that both partial and full complex detachments are most prevalent at or near the stalling force of a single kinesin.
Figure 3.
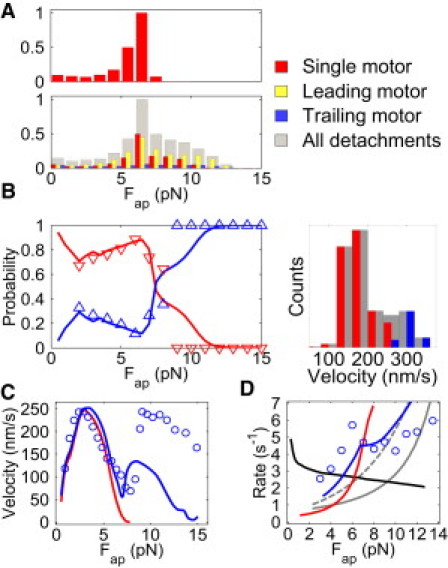
Predicting two-kinesin behaviors in an optical trap. (A) Histograms describing the force-dependent detachment distributions for the two-kinesin complex. Bin amplitudes are normalized by the peak bin in the cumulative histogram (gray). (B) The probabilities that a two-kinesin complex will adopt load-bearing microstates (red line) and nonload-bearing microstates (blue line) as a function of applied load. Optical trapping data are presented as triangles. The load-bearing probabilities are calculated as the fraction of beads at a given force that are driven by two microtubule-bound motors, each bearing at least 35% of the applied load. The nonload-bearing population fraction consists of both single- and two-motor-bound populations that do not meet this load-sharing criterion. A velocity distribution Fap = 5 pN is also provided; the color code is identical in each plot. (C) Average bead velocities for single kinesins (red line) and a two-kinesin complex (blue line). (D) Calculated average motor binding (kon[1→2]) and detachment (koff[2→1]) transition rates. Experimentally measured two-kinesin velocities and detachment rates are indicated by the blue circles in C and D.
In a characterization of how effectively motors cooperate, the central issue is the amount of time in which cargo transport is driven by one motor within a complex compared with the time in which two (or more) load-bearing motors drive transport. Our previous velocity analyses allowed us to measure these times and the associated microstate probabilities. Predictions from the model presented here approximate our observed trends when it is assumed that, to exhibit load-sharing behavior, both motors must bear at least 35% of the applied load (Fig. 3 B). Here, the force dependence of microstate probabilities appears to reflect the progression of a motor complex in the optical trap. In our calculations, bead transport starts with the binding of a single-motor molecule. As the simulation progresses, the second motor binds and the probability that the system will adopt microstates with a single load-bearing motor decreases until the applied load reaches 2 pN. Our experimental analyses cannot be performed in this force regime. However, as found experimentally, the probability that the system will adopt a single-load-bearing motor microstate increases between applied loads of 2 and 7 pN. This indicates that two-kinesin complexes do not adapt well to increasing loads in this regime, and do not cooperate by occupying load-sharing microstates in which motors are bound close together on the microtubule.
Similar agreement between experiment and theory is found in analyses of average bead velocities and two-motor detachment rates at low applied loads, providing additional verification that the model captures the extent of load sharing in this region (Fig. 3 C). Average cargo velocities follow the single-kinesin F-V relationship closely up to 7 pN, after which there is a dramatic increase in bead velocity.
As in our static trapping experiments, the transition rate describing the partial detachment of a complex, koff[2→1](Fap), is nonmonotonic and has a peak near the peak detachment force of the two-motor complex (Fig. 3 D). Although this feature persists regardless of our treatment of how loading rates affect motor detachment, the best agreement with the data is found when the influences of load-rate-dependent effects are distinguished based on the status of the motor as described in the Materials and Methods section (Fig. S2 and Fig. S3). This result further justifies our motor detachment fitting approach, but also illustrates that two-kinesin transport against the increasing load of the static trap is much more complicated than that of a single-motor molecule. In this case, one must consider the interrelationships among loading rates, load distributions, cargo velocities, and motor detachment to correctly describe cargo detachment behaviors.
In the vicinity of the koff[2→1](Fap) peak, measured detachment rates are significantly higher than those predicted if it is assumed that motors share their load equally (i.e., koff[2→1](Fap) = 2∗koff[1→0](Fap/2)) and that motor detachment is parameterized using the highest possible (load-rate-independent) curve in Fig. 3 D (the gray dashed curve). Such rates therefore provide strong evidence against load sharing, and further support the notion that when the static trap's load is smaller than kinesin's stalling force, cargo transport by a two-kinesin complex is primarily driven by one motor at a time.
Despite their agreement at low applied loads, there are still some significant differences between our experimental measurements and current model predictions. Measured two-kinesin velocities are appreciably higher than their calculated values above 7 pN (Fig. 3 C). Previous analyses of bead displacement sizes indicated that the motors may coordinate/synchronize their stepping mechanics at large applied loads (15), and this behavior is not incorporated into the model presented here. One would expect such positive (synergistic) cooperation to depend on the separation distance between motors on the microtubule (e.g., if this behavior stems from specific local intermotor interactions). Our model predicts that motors within the two-kinesin complexes will bind to closely spaced microtubule lattice sites at forces beyond the stall force of a single kinesin (Fig. 4 A). Such behavior is necessary to support the type of cooperation that may be occurring in our experiments, and thus the model's framework could be used to explore these effects.
Figure 4.
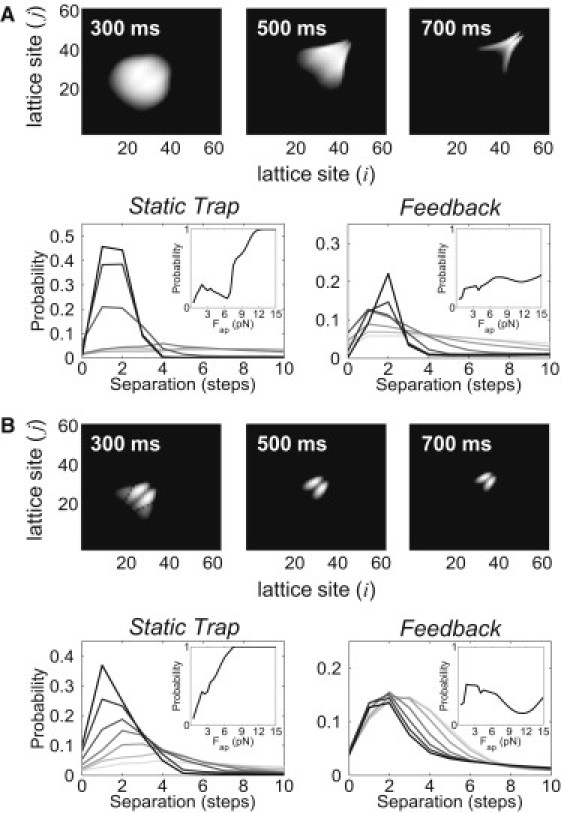
Microstate distributions and their dependence on stepping mode. (A) 2D plots showing the probability that a two-kinesin complex will adopt specific two-motor-bound configurations (top) at various time points when transporting cargos against the increasing load of an optical trap. Microstates are designated by the microtubule-bound positions of each motor; i and j are the lattice site positions of motors 1 and 2, respectively. Intensities along the diagonal represent microstates in which motors occupy the same lattice site. Bottom: Two-kinesin microstate probabilities plotted as a function of motor-microtubule binding site separation distance assuming that loads increase in time (left) or remain constant (right). Line colors indicate applied loads ranging from 1 to 13 (light to dark) in increments of 2 pN. The lines in the bottom panels are plotted for loads of 1–7 pN in increments of 1 pN. The inset in each plot displays the probability that a complex will adopt a load-sharing microstate (better than 35/65 splitting the applied load). (B) The equivalent plots for complexes composed of mode B motors.
We also examined how multiple-kinesin dynamics is influenced by the positions of the motors on the cargo (bead) and the presence of a third motor molecule (Fig. S4 and Fig. S5). In both cases, the detachment force distributions and cargo velocities follow the same trends predicted for the two-kinesin complexes. This implies that the deviations between predicted and measured two-kinesin velocities at high forces cannot be explained simply by variability in the structure of our complexes or the presence of a third motor. Of interest, the calculated three-kinesin velocities are only slightly higher than those produced in two-kinesin simulations between 7 and 12 pN, and, as with the two-motor systems, three-kinesin velocities exhibit a load dependence that suggests these complexes will not employ all of their motors until the applied load exceeds twice the stalling force of a single kinesin. Given this result, we do not anticipate that effects from the coordination between locally grouped motors described above would yield significant differences between two- and three-kinesin velocities at high loads (7–14 pN). This is because, to contribute to cargo motion, the third kinesin would face an even more formidable challenge of chasing down two synergistically coupled motor partners.
Evolution of microstate densities and their load-rate dependencies
The apparent inability of two kinesin motors to cooperate effectively is surprising, particularly considering the extent of the behavior and the resultant dependencies of the cargo velocities and detachment rates on the applied load. The unstrained binding rate of the second motor in the system (<kon[1→2](Fap = 0) > 4.7 s−1) greatly exceeds its detachment rate (0.31 s−1), suggesting that, from a thermodynamic point of view, two-motor-bound configurations of the system should be more prevalent than single-motor-bound configurations. However, the extent to which multiple-kinesin dynamics is also influenced by the spatiotemporal dependence of the applied load in the static trap must also be addressed. To explore this issue, we examined the dynamics of two-kinesin complexes while they transported cargos against a constant load (mimicking trapping assays employing force-feedback).
Comparisons of cargo transport by two kinesins against increasing (static trap) and constant (force-feedback) loads revealed both significant similarities and differences between these two transport scenarios. In both cases, the average microtubule binding rates <kon[1→2](Fap)> decrease with increasing load (Fig. 3 D; Fig. S5 B). Thus, the energetic costs (ΔEconfig) associated with binding transitions influence transport significantly in both circumstances. Overall, this constraint creates a strong preference for unbound motors to bind microtubule sites positioned far behind the leading motor. Such behavior is reflected in microstate probability distributions describing how often a two-motor complex will occupy different two-motor-bound configurations (Fig. 4 A). For both the increasing- and constant-load cases, intermotor separation distances are relatively large and broadly distributed below kinesin's stall force. Given the widths and similarities of these distributions, it is not surprising that much of the negative cooperative behavior observed in the static trapping experiments is also found in the constant-load simulations, implying that kinesins will not necessarily cooperate more productively when loading rates are negligible.
Despite the similarly weak response of bead transport to kinesin number in both cases, there are still several important differences between the static trap and constant-load simulations. Most strikingly, neither the rapid changes in bead velocities at kinesin's stall force nor the nonmonotonic dependence of koff[2→1] in the static trap are reproduced in the constant-load simulations (Fig. S5). Accordingly, there are significant differences in how the probabilities of two-motor-bound and load-sharing microstates change with the applied load for each simulation (Fig. 4 A and Fig. S6 A). The rapid increase in load-sharing microstate probabilities at kinesin's stalling force observed in the static trap is not found when applied loads are held constant. Furthermore, load-sharing microstates are more probable in constant-load simulations at low applied loads, but much less probable at high applied loads. Note that in addition to this behavior, the probability that both motors will be filament-bound decreases gradually with increasing load. Overall, these differences indicate that the two-kinesin complexes cooperate more effectively when cargo transport occurs against constant applied loads that are small. However, this behavior changes at high applied loads, and more-productive cooperation via load sharing is actually predicted for the static trap.
The above comparison between static-trap and constant-load simulations highlights significant mechanistic differences between cargo transport by single kinesins and multiple-kinesin complexes. As indicated by our detachment rate fits (Fig. 2 C), motor-filament affinities are typically enhanced when single motors transport cargos against variable (time and spatially dependent) applied loads because they cannot relax (i.e., advance along their unbinding reaction coordinate) fast enough to keep up with the changing load. However, several new pathological factors determine how the multiple-motor dynamics is influenced by the spatiotemporal dependence of an applied load. For example, the partial detachment of a multiple-motor complex is accompanied by a backward displacement of the cargo to a new, lower force in the static trap. This process therefore raises the average number of bound motors at high forces and lowers it at low forces, and in turn contributes significantly to the discontinuities/nonmonotonic behavior (of <v> and koff[2→1]) observed in the static trap. Furthermore, the measured detachment force distribution and koff[2→1] trend cannot be reproduced when motor detachment rates are parameterized by the single-motor (load-rate-dependent) fit. Here, our analyses indicate that time-dependent changes in load distributions tend to lower the loading rates experienced by the motors when the applied load is small, and hence the affinity enhancements found in single-motor assays will not influence multiple-motor dynamics. Together, these effects can actually result in decreased cargo-filament affinities relative to constant-load behaviors despite the presence of a nonzero loading rate. Finally, the energetic costs associated with motor binding appear to accentuate these effects by creating a tendency for motors to attach to lattice sites positioned well behind their bound partners. Thus, the rate at which separation distances between motors evolve in time will be critical for determining how multiple motors respond to variable applied loads.
Motor mechanochemistry tunes collective motor function
To assess how the stepping behaviors of processive molecular motors influence their collective dynamics, we also performed the above analyses for complexes composed of less-efficient motors that advance via stepping mode B (Figs. 1 B and 2 B). Here, the mode B motor's elastic properties and zero-load stepping rates correspond to those determined from our single-kinesin assays. However, because the motors now move much more slowly against the applied load of the trap, motor detachment is assumed to follow the load-rate-independent curve in Fig. 2 C.
Despite the assumption of increased motor-microtubule detachment rates, the alteration to kinesin's stepping mechanism introduced in mode B results in more effective multiple-motor cooperation than is observed with kinesins (Fig. 4 B, Fig. S6 B, and Fig. S7). The microstate probabilities are much more narrowly distributed, and configurations that should support load sharing are much more prevalent, even at early time points. Similar behavior is produced in constant-load simulations. Motor-microtubule binding rates still decrease with increasing force in both cases. However, the curve describing the average motor-filament detachment rates (<koff[2→1](Fap)>) does not contain a peak, and simply increases monotonically while following the equal-load-sharing trend much more closely (Fig. S5 B). In turn, such behavior results in a stronger dependence of cargo detachment forces and average velocities on motor number (Fig. S7).
The enhanced load-sharing ability of mode B motors indicates that although the high sensitivity of forward stepping rates to increasing load generally reduces the efficiency of individual motors under load, it actually assists in multiple-motor cooperation. This effect largely stems from the greater differential (proportionally) in motor velocities between leading (primary-load-bearing) and trailing (non- or weakly participating) motors, meaning that the rate at which the distance between the motors closes is greater with respect to the rate at which the cargo advances against the increasing load. To explore this issue, we tracked the temporal evolution of average cargo velocities under constant load after microstate distributions were allowed to reach their steady state at one force and then were subjected to an instantaneous increase of 1 pN in the applied load. After this jump, cargo velocities relaxed to their steady-state levels at the increased load in an approximately exponential manner that could be fit to yield an exponential time constant (Supporting Material). Although the absolute relaxation time constants (Fig. 5 A, left) are larger (longer) for stepping mode B than for mode A, they are shorter when normalized by the average time that it takes the cargo to advance forward a distance of 8.2 nm (Fig. 5 A, right). This means that when teams of motors with mode B stepping mechanics work against variable loads, they will be more capable of optimizing their intermotor separation distances before the load changes, and therefore defines a new optimum configuration. Moreover, the normalized relaxation time constants decrease monotonically for mode B motors, whereas mode A motors display a peak at 8 pN, which is close to the force where the largest discrepancy between the steady-state and static-trap distributions is found. This result strongly suggests that motors that advance via mode A (kinesin-1) are frustrated kinetically from assuming microtubule-bound configurations in which they share their applied load, and that such behavior significantly hampers the function of the two-motor complex.
Figure 5.
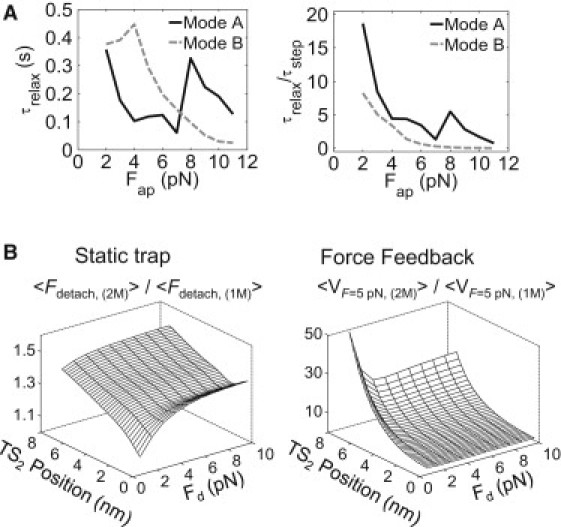
Two-motor transport performance depends on both the motor stepping efficiency and microtubule affinity. (A) Relaxation time constant of a two-motor system in stepping modes A and B (left), and the same values normalized by the stepping time constant (right). (B) Average detachment force of a two-motor system in a static trap, normalized by that of a single motor (left). A value of 2 indicates maximally (additive) cooperative behavior. (Right) Velocity of a two-motor system at constant load (Fap = 5 pN), normalized by single-motor velocities.
To further survey how multiple-motor cooperativity depends on the properties of a processive motor's stepping and detachment reaction coordinate, we examined how average two-motor detachment forces and cargo velocities depend on both the position of TS2 along a motor's stepping coordinate (which tunes motor stepping efficiency against an applied load) and its critical detachment force (Fd), which, as defined in the single-state Kramer's model, tunes a motor's microtubule-bound lifetime (Fig. 5 B). Although such analyses rigorously require more-exact treatments of motor detachment kinetics, we chose to use the single-state model because it simplifies the calculations. Furthermore, to facilitate comparison between motor types, we normalized the two-motor detachment forces and cargo velocities (at a constant load of 5 pN) by the average detachment forces/velocities of their single-motor counterparts. Plots of these values show that the weakest cooperative behavior (Fpeak(2)/Fpeak(1) = 1; ν 2/ν1 = 1.0) occurs when the stepping and detachment reaction coordinates approximate those expected for kinesin-1 (the corner of the plot near the origin). As suggested by our mode B motor simulations, there is a persistent increase in detachment/velocity enhancements over single motors as they become less efficient (as the location of TS2 moves away from the initial motor position on the stepping coordinate). Also, not surprisingly, motors that remain attached to the microtubule more tenaciously (large Fd) also cooperate more effectively. Thus, both characteristics should allow motor teams to share the applied load more equitably, because to accomplish this, a trailing motor must catch its leading partner before either detaches. However, what is striking is that a motor's stepping mechanism is equally as important as (and potentially even more important than) its detachment behavior in determining collective motor function.
Conclusions
We developed a theoretical framework that allows one to parameterize the collective dynamics of multiple-motor complexes using fits to single-motor optical trapping data nearly exclusively. All floating parameters are determined from single-kinesin fits, except for the unloaded motor-filament binding rate. With this treatment, differences between configuration-dependent strain energies of the complexes can be calculated and used to specify transition rates that determine how rapidly a complex's filament-bound geometry evolves in the presence of an applied load.
Although the deviations from measured multiple-kinesin velocities at loads exceeding kinesin's stall force suggest that motor coordination must be considered to describe multiple-kinesin dynamics at high loads, most model predictions support the idea that geometric and kinetic constraints largely limit how effectively a group of kinesins can cooperate as a team. Overall, it is difficult for multiple-kinesin complexes to adopt microtubule-bound configurations that support load sharing, both when loads increase in time and when they remain constant. However, these difficulties are exacerbated at low applied loads (Fap < 7 pN) by dynamic effects associated with the spatial and temporal dependence of the loads that multiple-kinesin complexes experience. Such effects could not be delineated in our previous experimental analyses, and were overlooked because motor-filament affinities are normally expected to increase when loading rates are appreciable. However, the results presented here show that unique load-rate dependencies can be produced when cargos are transported by teams of processive motors, and that the time it takes for a motor complex's microtubule-bound geometry to evolve in response to a load plays a critical role in determining the forces and velocities produced by the system.
One might expect a group of fast and efficient motors like kinesin to be able to cooperate effectively when transporting cargos because they should be able to adjust their bound geometry rapidly via motor stepping. However, we find that less-efficient processive motors whose velocities drop more rapidly with increasing load are actually more capable of cooperating productively. Even though the absolute relaxation time of such motor systems is longer than those calculated for multiple kinesins given the same elastic load (the trap's spring), the applied load on the cargo does not increase as rapidly in this case. Consequently, less-efficient motors not only possess microstate distributions at steady state that lead to better load-sharing behaviors, they also have more time to adjust their bound geometry, and hence can develop load-sharing configurations more readily.
The differences between the collective motor behaviors described above may have important implications for mechanisms that regulate cargo motion. First, they suggest that motor stepping efficiency can distinguish how sensitively cargo transport depends on the number of processive motors grouped together on a cargo. Furthermore, motor stepping efficiencies may play a role in bidirectional transport, where oppositely directed teams of kinesin and dynein compete antagonistically to drive cargo motion. In this case, the direction and magnitude of the applied load will change in time as the number of motors competing against each other changes, and because the cargo itself will be deformed (stretched) during this process (11,17). Furthermore, there is evidence that dynein stalls at significantly lower forces than kinesin (11). This inefficiency is consistent with observations that dynein's stepping patterns are much more irregular than kinesin's (backward stepping influences dynein's average F-V) (27). Thus, although more dyneins will be required to produce the forces of a single kinesin, a team of inefficient dyneins should still be able to compete with a stronger kinesin team because of the former's greater ability to cooperate effectively. With this behavior, the number of dyneins, but not kinesins (beyond binary responses), would serve as a regulator of bidirectional transport. To date, dynein's mechanochemistry has not been characterized in detail, and hence confirming such ideas requires further investigation. Nevertheless, the experimental and theoretical advances described here should provide a framework for investigating such behavior.
Acknowledgments
This work was supported by grants from the National Science Foundation (MCB-0643832), the National Institutes of Health (1R01GM094489-01), and the Welch Foundation (C-1559 to A.B.K. and C-1625 to M.R.D.).
Supporting Material
References
- 1.Howard J. Sinauer Associates; Sunderland, MA: 2001. Mechanics of Motor Proteins and the Cytoskeleton. [Google Scholar]
- 2.Carter N.J., Cross R.A. Mechanics of the kinesin step. Nature. 2005;435:308–312. doi: 10.1038/nature03528. [DOI] [PubMed] [Google Scholar]
- 3.Hancock W.O., Howard J. Processivity of the motor protein kinesin requires two heads. J. Cell Biol. 1998;140:1395–1405. doi: 10.1083/jcb.140.6.1395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ally S., Larson A.G., Gelfand V.I. Opposite-polarity motors activate one another to trigger cargo transport in live cells. J. Cell Biol. 2009;187:1071–1082. doi: 10.1083/jcb.200908075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kulic I.M., Brown A.E.X., Gelfand V.I. The role of microtubule movement in bidirectional organelle transport. Proc. Natl. Acad. Sci. USA. 2008;105:10011–10016. doi: 10.1073/pnas.0800031105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Holzbaur E.L., Goldman Y.E. Coordination of molecular motors: from in vitro assays to intracellular dynamics. Curr. Opin. Cell Biol. 2010;22:4–13. doi: 10.1016/j.ceb.2009.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Klumpp S., Lipowsky R. Cooperative cargo transport by several molecular motors. Proc. Natl. Acad. Sci. USA. 2005;102:17284–17289. doi: 10.1073/pnas.0507363102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ori-McKenney K.M., Xu J., Vallee R.B. A cytoplasmic dynein tail mutation impairs motor processivity. Nat. Cell Biol. 2010;12:1228–1234. doi: 10.1038/ncb2127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Levi V., Serpinskaya A.S., Gelfand V. Organelle transport along microtubules in Xenopus melanophores: evidence for cooperation between multiple motors. Biophys. J. 2006;90:318–327. doi: 10.1529/biophysj.105.067843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hendricks A.G., Perlson E., Holzbaur E.L. Motor coordination via a tug-of-war mechanism drives bidirectional vesicle transport. Curr. Biol. 2010;20:697–702. doi: 10.1016/j.cub.2010.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Soppina V., Rai A.K., Mallik R. Tug-of-war between dissimilar teams of microtubule motors regulates transport and fission of endosomes. Proc. Natl. Acad. Sci. USA. 2009;106:19381–19386. doi: 10.1073/pnas.0906524106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shubeita G.T., Tran S.L., Gross S.P. Consequences of motor copy number on the intracellular transport of kinesin-1-driven lipid droplets. Cell. 2008;135:1098–1107. doi: 10.1016/j.cell.2008.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ali M.Y., Lu H., Trybus K.M. Myosin V and kinesin act as tethers to enhance each others' processivity. Proc. Natl. Acad. Sci. USA. 2008;105:4691–4696. doi: 10.1073/pnas.0711531105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rogers A.R., Driver J.W., Diehl M.R. Negative interference dominates collective transport of kinesin motors in the absence of load. Phys. Chem. Chem. Phys. 2009;11:4882–4889. doi: 10.1039/b900964g. [DOI] [PubMed] [Google Scholar]
- 15.Jamison D.K., Driver J.W., Diehl M.R. Two kinesins transport cargo primarily via the action of one motor: implications for intracellular transport. Biophys. J. 2010;99:2967–2977. doi: 10.1016/j.bpj.2010.08.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Korn C.B., Klumpp S., Schwarz U.S. Stochastic simulations of cargo transport by processive molecular motors. J. Chem. Phys. 2009;131:245107–245116. doi: 10.1063/1.3279305. [DOI] [PubMed] [Google Scholar]
- 17.Gennerich A., Schild D. Finite-particle tracking reveals submicroscopic-size changes of mitochondria during transport in mitral cell dendrites. Phys. Biol. 2006;3:45–53. doi: 10.1088/1478-3975/3/1/005. [DOI] [PubMed] [Google Scholar]
- 18.Astumian D.R. The unreasonable effectiveness of equilibrium theory for interpreting nonequilibrium experiments. Am. J. Phys. 2006;74:683–688. [Google Scholar]
- 19.Leduc C., Ruhnow F., Diez S. Detection of fractional steps in cargo movement by the collective operation of kinesin-1 motors. Proc. Natl. Acad. Sci. USA. 2007;104:10847–10852. doi: 10.1073/pnas.0701864104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jeney S., Stelzer E.H.K., Florin E.L. Mechanical properties of single motor molecules studied by three-dimensional thermal force probing in optical tweezers. ChemPhysChem. 2004;5:1150–1158. doi: 10.1002/cphc.200301027. [DOI] [PubMed] [Google Scholar]
- 21.Fehr A.N., Gutiérrez-Medina B., Block S.M. On the origin of kinesin limping. Biophys. J. 2009;97:1663–1670. doi: 10.1016/j.bpj.2009.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gittes F., Meyhöfer E., Howard J. Directional loading of the kinesin motor molecule as it buckles a microtubule. Biophys. J. 1996;70:418–429. doi: 10.1016/S0006-3495(96)79585-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fisher M.E., Kim Y.C. Kinesin crouches to sprint but resists pushing. Proc. Natl. Acad. Sci. USA. 2005;102:16209–16214. doi: 10.1073/pnas.0507802102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Khalil A.S., Appleyard D.C., Lang M.J. Kinesin's cover-neck bundle folds forward to generate force. Proc. Natl. Acad. Sci. USA. 2008;105:19247–19252. doi: 10.1073/pnas.0805147105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Evans E. Probing the relation between force—lifetime—and chemistry in single molecular bonds. Annu. Rev. Biophys. Biomol. Struct. 2001;30:105–128. doi: 10.1146/annurev.biophys.30.1.105. [DOI] [PubMed] [Google Scholar]
- 26.Driver J.W., Rogers A.R., Diehl M.R. Coupling between motor proteins determines dynamic behaviors of motor protein assemblies. Phys. Chem. Chem. Phys. 2010;12:10398–10405. doi: 10.1039/c0cp00117a. [DOI] [PubMed] [Google Scholar]
- 27.Gennerich A., Carter A.P., Vale R.D. Force-induced bidirectional stepping of cytoplasmic dynein. Cell. 2007;131:952–965. doi: 10.1016/j.cell.2007.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


