Simulated Surface-Induced Thrombin Generation in a Flow Field

Abstract

A computational model of blood coagulation is presented with particular emphasis on the regulatory effects of blood flow, spatial distribution of tissue factor (TF), and the importance of the thrombomodulin-activated protein C inhibitory pathway. We define an effective prothrombotic zone that extends well beyond the dimensions of injury. The size of this zone is dependent on the concentrations of all reactive species, the dimensions of TF expression, the densities of surface molecules, and the characteristics of the flow field. In the case of tandem sites of TF, the relationship between the magnitude of the effective prothrombotic zone and the interval distance between TF sites dictate the net response of the system. Multiple TF sites, which individually failed to activate the coagulation pathway, are shown to interact in an additive manner to yield a prothrombotic system. Furthermore, activation of the thrombomodulin-activated protein C pathway in the regions between sites of TF downregulate the thrombin response at subsequent TF sites. The implications of prothrombotic effects, which extend downstream beyond the discrete site of injury to interact with subsequent lesions are critical given the systemic nature of atherosclerotic disease.

Introduction

Blood coagulation is a highly dynamic, nonlinear reaction network that is characterized by the activation and amplification of circulating zymogens, several surface-associated enzyme complexes, and positive and negative feedback loops. Exposure of subendothelial tissue factor (TF) to the bloodstream and subsequent formation of the TF/VIIa complex leads to activation of factors (F) IX and X. Generation of FXa by either intrinsic (IXa/VIIIa) or extrinsic (TF/VIIa) tenase leads to assembly of prothrombinase (Xa/Va), which cleaves prothrombin (FII) to thrombin (FIIa). Amplification of the cascade is achieved through positive feedback of thrombin to activate FV and FVIII (1,2). Regulators of thrombin generation include the thrombin- and thrombomodulin (TM)-dependent protein C pathway, FXa-dependent TF pathway inhibitor (TFPI), and the multisubstrate serine protease inhibitor, antithrombin III (ATIII) (1–4). In addition, blood flow serves as a critical regulator of thrombosis by removing activated enzymes from the site of reactivity (5). The temporal and spatial dynamics of coagulation under flow are complex, and mathematical modeling provides a means for the systematic study of individual components and their roles in promoting or regulating clot formation.

Rationale for the model approach

Mathematical models of blood coagulation vary widely and range from well-mixed solution-phase models to those which incorporate elements such as diffusion of solutes and vascular surface reactivity. In general, fluid-phase models of the kinetics of coagulation are computationally and experimentally less complex and, as such, are able to incorporate a number of species and reactions. Empirical data are often available for regression analysis and model validation. However, the essential role of blood flow in promoting the delivery of substrates to the vessel wall and in regulating the thrombin response by removing activated clotting factors is well recognized. The major limitation of the existing pseudo-one-compartment models of coagulation under flow (6,7), in which the vascular space is divided into a bulk and a boundary volume, is the assumption of spatially homogenous, or well-mixed, plasma compartments. This assumption breaks down as the dimensions of the boundary volume increase, as would occur, for example, at low shear rates and for large reaction areas, due to the potential for substrate depletion and product accumulation at the surface or at upstream sites. In contrast, although models incorporating spatial effects have recently been reported (8–10), most describe only reaction and diffusion and do not include convective effects. Recently, Leiderman and Fogelson (11) reported a spatiotemporal model of coagulation and platelet deposition over a short segment of exposed subendothelium under flow. The authors explored the hypothesis set forth by their previous works, which proposed that platelet deposition over an injury site physically inhibited further TF-mediated activation of coagulation. Furthermore, they suggest that for small injuries (∼10 μm in length), physical factors, i.e., fluid flow and platelet deposition, and not biochemical anticoagulants, may be the dominant regulators of thrombin generation. However, their model did not include endothelial reactions, including those of the TM-protein C pathway. Of note, models that have incorporated the TM-protein C pathway include a multiscale model by Xu et al. (12), in which the role of factor VII in venous thrombogenesis was examined, and earlier work by Fogelson et al. (13).

The finite-element method (FEM) does not require the assumption of spatial homogeneity and permits the definition of a flow model that accounts for distinct sites of TF and TM surface expression. Uniquely, spatial parameters quantifying the localization or propagation of thrombin formation, in both vertical and longitudinal directions, may be defined.

Methods

Model description

Here, we describe a spatially heterogeneous FEM model of thrombin generation under defined flow conditions that describes the events that occur after TF exposure at a discrete upstream site, as well as related mechanisms that regulate thrombin generation, including those mediated by an intact endothelium, represented as a TM-containing surface (Fig. 1 A). The primary analysis was performed assuming a 10-mm inert entrance region, 2-mm TF region, and a 34-mm TM region. The length of the TF region is similar in dimension to that of a ruptured coronary plaque or the interface between a vascular graft and host vessel at an anastomotic site (14). The nondimensionalized model is independent of absolute chamber height.

Figure 1.

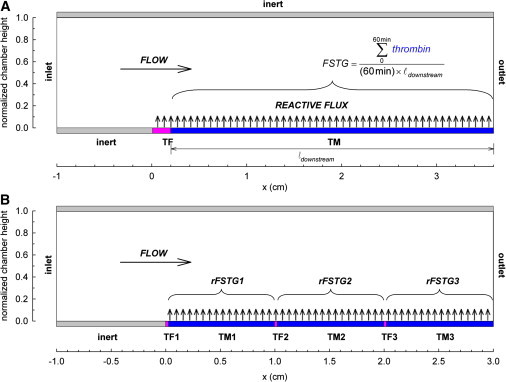
Formulation of a spatially heterogeneous model of surface-induced thrombin generation in a flow field. Soluble species enter the flow field at constant inlet concentrations. Diffusion transports coagulation factors to the lower reactive surface, where reaction kinetics define flux boundary conditions. The upper boundary is inert. Convective flux removes soluble species at the outlet. (A) Initial geometric conditions include a 10-mm entrance region, a 2-mm TF region, and a 34-mm TM region. FSTG is defined as the integral of the downstream thrombin surface concentration over the 60-min simulation time, normalized by time and length. (B) In the tandem model, overall chamber length is fixed at 3 cm. Three TF regions of length 200 μm each are spaced at fixed intervals (10 mm in this illustration) with intervening TM regions. rFSTG is defined as the integral of the thrombin surface concentration over the intervening TM surface over the 60-min simulation time, normalized by time and length.

In contrast to previous models of surface-induced coagulation, mass transfer approximations are not used to describe transport of reactants to the surface. Transport of soluble species is described by two-dimensional, unsteady, convection-diffusion-reaction equations. Surface-bound species are defined by time derivatives. All concentrations are initially set to zero, and surface TF and TM are both initially free of bound cofactors. Soluble species enter the flow field at mean physiologic values (Table S1 in the Supporting Material). Inlet FVIIa is assumed to be 1% of inlet FVII (15). Hemophilias A and B were defined at 5% of the normal plasma concentration of FVIII and FIX, respectively. The lower reactive boundary is divided into localized upstream TF and downstream TM regions. The upper boundary is inert. Reaction kinetics define flux boundary conditions on the upper and lower surfaces. Convective flux removes soluble species at the outlet.

The model incorporates fluid phase and surface-associated reactions of the extrinsic, intrinsic, and common pathways, as well as three inhibitory pathways—ATIII, TFPI, and the protein C (PC) pathway. A description and schematic can be found in Fig. S1. Table S2 summarizes all model reactions and kinetic parameters and distinguishes between surface-bound reactions and those that occur both in the fluid phase and at the blood-vessel-wall interface.

Model assumptions

Reactive surface

The model defines discrete regions of TF or TM expression, but otherwise does not discriminate between subendothelium, resting endothelium, activated endothelium, or platelet membrane surfaces. Total TF and TM surface expression is assumed constant over all time points. TF only binds FVIIa and not FVII. Activation of FVII is assumed to occur in the fluid phase only. The model assumes that phospholipid conditions promote surface-associated enzyme complex assembly, i.e., membrane-binding sites are in excess. All complexes not involving TF or TM are allowed to assemble along the entire length of the reactive surface. Surface complexes, such as prothrombinase, are assumed to be generated through a bimolecular reaction between two solution-phase species spatially localized at y = 0. The assembly of these complexes is assumed to occur in one step. Lateral diffusion along or within the membrane surface is considered negligible.

Kinetic parameters

Serine protease activation involves one or more cleavage events and is thus irreversible. All reactions are assumed to follow Michaelis-Menten kinetics. The capacity of enzymes in the absence of respective cofactors to convert primary substrates is considered negligible. For example, conversion of prothrombin to thrombin by Xa/Va is 10⁵-fold faster than by FXa alone (16). Only the former reaction is considered. Kinetic parameters were obtained from the experimental literature of isolated reaction systems (Table S2 and Table S3), with preference given to studies deemed most relevant with respect to concentrations within the physiologic range, presence of applicable cofactors, and method of measurement. In cases where only equilibrium binding constants, K_d, were reported, k_d was calculated (k_d = K_d × k_a) with k_a set to the diffusional limit, 10⁸ M⁻¹ s⁻¹. Association reactions are reversible except where noted.

Inhibitory reactions

Thrombin activates PC when bound to TM, and the thrombin-TM complex is considered the only source for PC activation. FXa-mediated activation of PC has not been confirmed and therefore is not considered (17,18). Thrombin's ability to participate in procoagulant reactions is eliminated once bound to TM. Inactivation of FVa and FVIIIa by activated protein C (APC) is irreversible. The cofactor activity of protein S (PS) was indirectly accounted for through the choice of kinetic parameters for APC-mediated inactivation of FVa and FVIIIa, which were measured in the presence of physiologic concentrations of PS (19). Inactivation of FVa and inactivation of FVIIIa are assumed to occur at equal rates (20). FIXa and FXa protect their respective cofactors FVIIIa and FVa from inactivation by APC when bound (19,21). ATIII irreversibly removes FIXa, FXa, and thrombin by a bimolecular binding reaction. Acceleration of ATIII activity by surface glycosaminoglycans is not included. TFPI acts in a two-step process by binding reversibly to FXa in the fluid phase, followed by reversible TFPI/Xa association with surface bound TF/VIIa (4). Only plasma TFPI is considered. Inducible TFPI from platelets and endothelial cells is not included.

Flow regime

Simulations were conducted assuming steady, nonpulsatile, fully developed parabolic flow. In select instances, analyses were performed for a range of shear rates between 100 and 1500 s⁻¹. However, in most cases, comparisons were conducted at simulated arterial (500 s⁻¹) and venous (50 s⁻¹) flow regimes.

Model implementation

Governing equations

Model reactions and corresponding rate constants are summarized in Table S2. The full set of partial differential equations and boundary conditions can also be found in the Supporting Material. Equations, bulk parameters, and initial values were nondimensionalized and geometrically scaled to moderate the range of parameter values and reduce mesh size. All fluid-phase species are defined by a conservation equation containing a rate of accumulation, a convective term, a diffusive term, and a fluid-phase reaction rate. Concentration is a function of time and two-dimensional space. Surface-phase reaction rates appear as flux conditions in the boundary conditions.

Computer implementation

The FEM model was implemented in COMSOL Multiphysics 3.4 (COMSOL, Burlington, MA) on a 64-bit Windows workstation. The automatically generated mesh contained ∼2100 triangular elements, with finer resolution over the reactive boundaries and intersection points. Increasing mesh resolution to 3500 and 7200 triangular elements yielded results within 99% of the presented results. Soluble species were defined by a convection-diffusion application mode. Surface-bound enzymatic complex formation was specified by a weak form (boundary) application mode. Time-dependent simulations were solved using a direct parallel solver. Simulations were run for 60 min. Postprocessing was performed in both COMSOL and MATLAB (The MathWorks, Natick, MA).

System parameters describing surface-induced thrombin generation over spatially discrete regions of TF and TM

Simulations provide transient concentration profiles in two dimensions for each of the 21 computationally defined species (16 fluid-phase and 5 surface-bound). System parameters were defined to describe the behavior of the initiating TF region and to quantify the effectiveness of the TM-expressing downstream region in modulating the thrombin response. Peak thrombin concentration and flow-simulated thrombin generation (FSTG) were chosen to evaluate the thresholdlike response of the model system. Peak thrombin concentration was defined as the maximum level of thrombin attained at any point in the computational space. FSTG is defined as the integral of downstream thrombin surface concentration over the 60-min simulation time, normalized by time and length, or, in other words, the average downstream surface thrombin concentration. FSTG acts as a global variable incorporating both spatial and temporal information. The downstream average was chosen as an indication of the effectiveness of downstream TM in limiting thrombin generation near to the upstream TF region. One hour was chosen as the default simulation time to ensure that all phases of coagulation, e.g., initiation and propagation, were included in the analysis for all runs. In other words, the simulation time exceeded the time course of the least thrombogenic simulation conditions. Finally, unique to our spatial model, an effective prothrombotic zone (EPZ) defined the extent to which thrombin propagated away from the site of surface-bound TF, in both axial and radial directions, by delineating a region wherein at any point within the space the thrombin concentration was within 95% of the peak level at steady state. The choice of a relative concentration represents a penetration distance that is the geometric area affected by the perturbation caused by the exposed TF segment regardless of the absolute magnitude of the effect. Thus, the parameter is an indicator of the decay in the rate of thrombin generation. The dimensions of this EPZ, the effective prothrombotic length (EPL) and the effective prothrombotic height (EPH), were determined as the x-intercept and maximum y-coordinate of the delineating contour line, respectively. It should be noted that the EPL includes the entire length of the site of expressed TF.

Modeling tandem lesions

We explored the behavior of systems containing multiple spatially distinct sites of surface-bound TF. The reactive boundary is divided into three sites of TF with intervening regions that present TM (Fig. 1 B). TF length and density were 200 μm and 9 fmol/cm², respectively. These conditions were previously found to be just below the activation threshold when adjacent to transport-limited levels of TM (1000 fmol/cm²). TF lengths shorter than the previous section were chosen to achieve a wider range of effective prothrombotic lengths that would fit within a manageable total chamber length. The total length of the system of interest was 3 cm unless otherwise noted. The TF interval was defined as the distance between the upstream ends of two adjacent sites of TF. Regional FSTG (rFSTG) was derived from a consideration of the total thrombin generated over the downstream interval regions during the course of a 60-min simulation. An rFSTG value >10 nM was similarly defined as a criterion for characterizing a segment as exceeding an activation-threshold limit. Model equations governing flow and reaction kinetics remained unchanged. Similar mesh and solver algorithms were employed.

Results

The system exhibits threshold responses to TF, TM, and wall shear rate

Characteristically, low levels of thrombin are produced during the initiation phase of coagulation. During this phase, inhibitors may dampen the thrombin response and prevent amplification and full activation of the coagulation cascade; this is considered a subthreshold thrombin response. When the capacity of these inhibitors is overwhelmed by the magnitude of the thrombogenic stimulus, thrombin levels cross an activation threshold and rapid amplification of thrombin generation occurs. This threshold effect may be defined with respect to a number of variables (e.g., blood flow, fluid- and surface-phase levels of procoagulant factors and inhibitors, and kinetic variables), and thus, an infinite set of threshold-defining permutations exist beyond which thrombin is produced in an almost instantaneous manner. Using our computational model, we conducted parametric studies that would not have been experimentally efficient. Peak thrombin concentration reflected the all-or-none behavior of thrombin generation and easily differentiated between subthreshold and fully activated systems. Likewise, by setting a cutoff of 10 nM for FSTG, notably the concentration reported to induce platelet activation (22), systems were reliably categorized as lying either below or above an activation threshold.

We examined the relationship between the length of the TF region and thrombin production while maintaining TF and TM surface densities at or near transport-limited levels of 1 and 1000 fmol/cm², respectively. At a shear rate of 500 s⁻¹, peak thrombin concentration and FSTG fell below the activation threshold of 10 nM if the TF site was <1.6 mm in length (Fig. 2, A and B). With further lengthening of the TF region, peak thrombin concentration and FSTG increased sharply and peak thrombin approached 1200 nM, consistent with full activation of the coagulation cascade.

Figure 2.

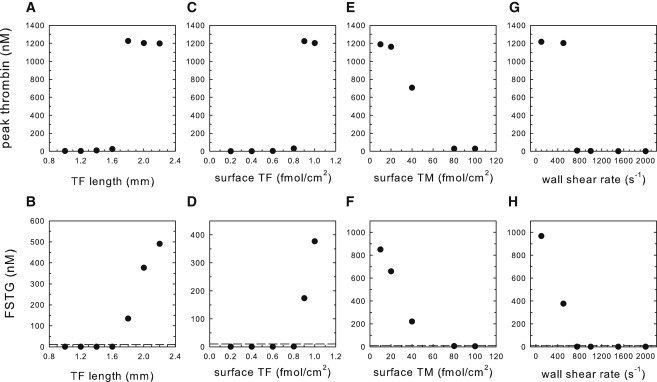
Threshold response of thrombin to TF site length, TF surface density, and TM surface density under simulated arterial flow (500 s⁻¹). (A and B) Peak thrombin concentration and FSTG as functions of TF length at a wall shear rate of 500 s⁻¹. [TF] and [TM] were 1 and 1000 fmol/cm², respectively. (C and D) Peak thrombin concentration and FSTG as functions of TF surface density. TF and TM lengths were 2 and 34 mm, respectively. [TM] was fixed at 1000 fmol/cm². (E and F) Peak thrombin concentration and FSTG as functions of TM surface density. [TF] was fixed at 0.8 fmol/cm². (G and H) Peak thrombin concentration and FSTG as functions of wall shear rate. TF and TM lengths were 2 and 34 mm, respectively. [TF] and [TM] were 1 and 1000 fmol/cm², respectively. Simulations were run to 60 min. Activation of clotting is defined at FSTG of 10 nM (dotted line).

A similar threshold effect was observed in relation to TF surface concentration. At venous (50 s⁻¹) and arterial (500 s⁻¹) shear rates, TM (1000 fmol/cm²) inhibited thrombin production at TF concentrations below 0.03 and 0.8 fmol/cm², respectively (Fig. 2, C and D; venous data not shown). The TF surface concentration threshold is attenuated under conditions of hemophilia A and B. Specifically, the concentration of surface-bound TF required to surpass the threshold for thrombin production was approximately two-fold higher for the simulated hemophilias than for normal hemostatic conditions (0.07 and 1.4 fmol/cm² for venous and arterial conditions, respectively). Furthermore, the hemophilias were associated with a decrease in the rate of thrombin generation and a lower FSTG (Fig. S3).

Threshold-type behavior was also observed in relation to TM surface concentration (Fig. 2, E and F). The minimum [TM]s required to limit thrombin propagation were 1.4 and 60 fmol/cm² for [TF]s of 0.03 and 0.8 fmol/cm² under venous and arterial shear rates, respectively. As would be anticipated, the magnitude of flow had a pronounced effect on the threshold for thrombin production. Assuming a TF site of 2 mm in length and [TF] and [TM] of 1 and 1000 fmol/cm², respectively, threshold activation was suppressed at shear rates >750 s⁻¹ (Fig. 2, G and H).

APC attenuates thrombin production and spatial propagation over the downstream TM surface

Surface factor concentrations were plotted for the 60-min simulation time. At the interface between TF and TM expression (x = 0.2 cm), under conditions in which an activation threshold was exceeded ([TF] of 0.9 fmol/cm², [TM] of 1000 fmol/cm², shear rate of 500 s⁻¹), modulation of Va and thrombin production by APC occurred within the first 3–5 min, but after an initiation period of 37 min, thrombin concentration rose rapidly and plateaued (Fig. S4 A). At points downstream (Fig. 3 A), procoagulant enzyme complexes continue to assemble and thrombin production propagates rapidly in a characteristic sigmoidal time course, however dampened by the inhibitory TM pathway.

Figure 3.

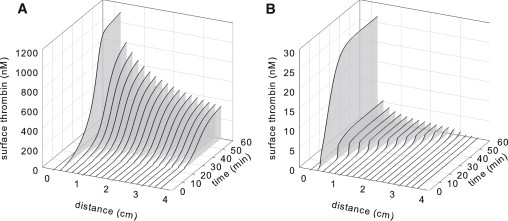
Thrombin concentration at various points along the surface as a function of time for systems that lie (A) above, with [TF] of 0.9 fmol/cm² and [TM] of 1000 fmol/cm², or (B) below, with [TF] of 0.8 fmol/cm² and [TM] of 1000 fmol/cm², a prothrombotic activation threshold at 500 s⁻¹. Note the different scales.

In contrast, below an activation threshold ([TF] of 0.8 fmol/cm², [TM] of 1000 fmol/cm², shear rate of 500 s⁻¹), Va decreased in response to increases in APC, restricting thrombin to very low levels. Va concentrations approached steady state by ∼20 min for the subthreshold case (Fig. S4 B). Downstream over the TM surface, both the time to maximum rate of thrombin production and the magnitude of thrombin generation are attenuated (Fig. 3 B).

TF, TM, and shear rate dictate the dimensions of an effective prothrombotic zone that extends beyond the initiating site of thrombin generation

These studies emphasize the existence of a spatially defined zone of thrombin that may extend well beyond the site of TF expression. This phenomenon holds true whether or not a system exceeds an activation threshold. EPZ is a convenient measure of the capacity of TM to confine thrombin generation to the vicinity of the injury site. As shown in Fig. 4 A, the relationship between a spatially discrete site of TF expression and EPL is a concave-up nonlinear function. The influence of the flow regime on the dimensions of the EPZ was investigated at shear rates ranging from 750 to 2000 s⁻¹. It might be anticipated that higher flow rates would promote downstream propagation of thrombin. However, increasing shear rate decreased the EPZ due to enhanced removal of activated clotting factors and greater APC generation attributed to increased transport of thrombin and PC to TM. Propagation of the EPZ parallel and perpendicular to the direction of flow was reduced at higher shear rates (Fig. 4 B). In particular, at the chamber outlet (x = 3.6 cm), EPH decreased linearly from 15.3% to 11.3% of the total chamber height, and EPL decreased nonlinearly from 0.95 to 0.49 cm when the shear rate increased from 750 to 2000 s⁻¹. Increasing TF and TM surface concentration led to a respective increase or decrease in the dimensions of the EPZ. Specifically, EPL increased significantly with TF density (Fig. 4 C), whereas it decreased in response to TM (Fig. 4 D). EPL was linearly related to peak APC concentration, R² = 0.998 (Fig. S5).

Figure 4.

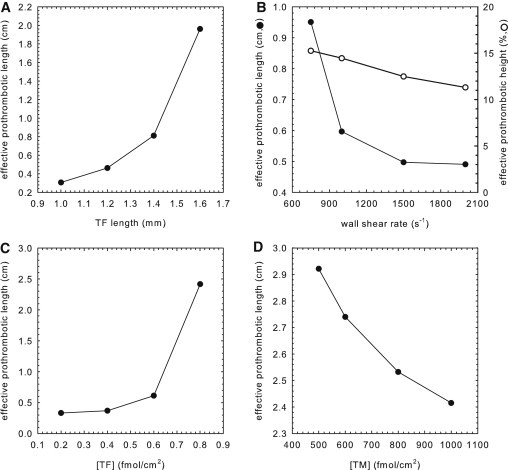
Factors influencing EPZ. (A–D) Relationship of EPL to TF length, wall shear rate, TF density, and TM density, respectively. For A–C, TF_length is 2 mm, wall shear rate is 500 s⁻¹, [TF] is 1 fmol/cm², and [TM] is 1000 fmol/cm² when fixed. In B, EPH is shown as a percentage of total chamber height. In D, [TF] is 0.8 fmol/cm², TF_length is 2 mm, and wall shear rate is 500 s⁻¹.

It is noteworthy that similar EPZ dimensions may arise from a wide variety of sizes of TF expression sites, [TF] and [TM], and shear rate. EPZ contours for decreasing concentrations of surface TM are shown in Fig. 5. Under conditions that did not exceed the activation threshold, EPZ remained near the site of TF expression. For conditions in which an activation threshold was exceeded, the EPZ encompassed and extended beyond the entire downstream region.

Figure 5.

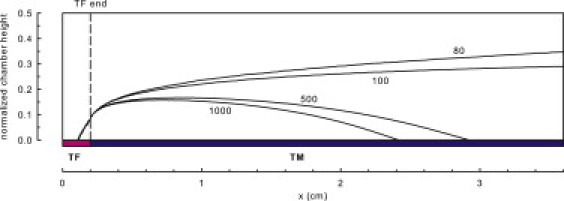
EPZ and its dependence on TM surface concentration (1000, 500, 100, and 80 fmol/cm²), for a wall shear rate of 500 s⁻¹, TF_length of 2 mm, and [TF] of 0.8 fmol/cm². Simulations were run to 60 min. The EPZ is delineated by a contour line, wherein at any point within the space, the thrombin concentration was within 95% of the peak level.

TM expression within the intervening regions dictates the suppressive interactions that occur between sequential TF sites

Multiple TF sites acted cooperatively to promote or suppress thrombin generation, dependent in part on the concentration of surface-bound TM within intervening regions. In Fig. 6, rFSTGs in three regions located between sequential sites of TF were compared as a function of TM surface density ranging from 40 to 1000 fmol/cm². TF length and concentration were fixed at 200 μm and 9 fmol/cm², respectively. The TF interval was 1 cm. At low levels of TM, thrombin generated from the first TF region enhanced thrombin production at downstream TF sites by driving positive feedback loops of the coagulation cascade. At intermediate levels of TM expression, thrombin generated by the upstream site additionally served to activate PC, thus counteracting thrombin propagation to some degree. At high densities of TM, the extent of thrombin-mediated APC generation was great enough to suppress thrombin production by downstream sites of TF. The degree of suppression between TF sites was proportional to TM concentration and was more pronounced between the first and second regions than between the second and third TF sites (56% and 8% decreases in rFSTG, respectively, for [TM] of 500 fmol/cm², and 83% and 28% decreases, respectively for [TM] of 1000 fmol/cm²). Because thrombin regulates its own generation through the production of APC, the dampened suppressive effects between the second and third TF sites can be accounted for by the reduced levels of thrombin generated by the second TF site. Representative surface plots of thrombin concentration for additive, intermediate, and suppressive interactions are shown in Fig. 6. The extent to which sequential regions of TF and TM acted to inhibit or promote thrombin generation was dictated by the degree to which tandem EPZs overlapped.

Figure 6.

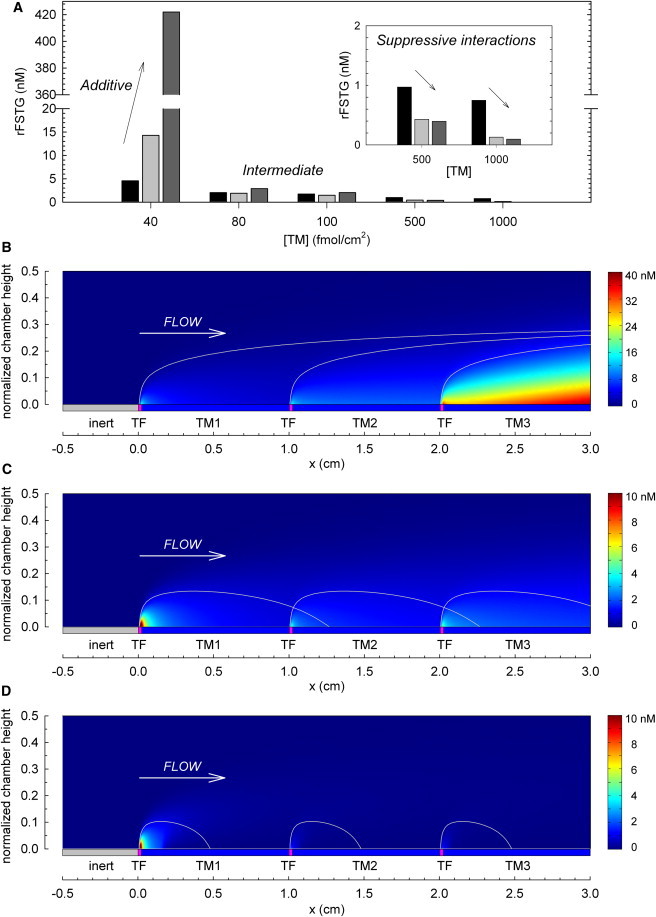
Additive, intermediate, and suppressive interactions between tandem prothrombotic sites. (A) rFSTG as a function of intervening TM surface density (40–1000 fmol/cm²) under simulated arterial conditions (500 s⁻¹) over three sequential sites of TF (TF_length = 200 μm, [TF] = 9 fmol/cm²). From left to right, each bar represents rFSTG for the regions downstream of each site of surface-bound TF. (B–D) The EPZ, previously calculated from a simulation of a single site of TF, is overlaid on the surface plot to illustrate the overlap of EPZ between sequential TF sites. Included are representations of additive effects at low surface densities of TM (40 fmol/cm²) (B), the net effect of both additive and suppressive interactions between TF sites at intermediate surface concentrations of TM (100 fmol/cm²) (C), and suppressive interactions between TF sites at high surface concentrations of TM (1000 fmol/cm²) (D). Simulations were run to 60 min. However, thrombin concentration profiles shown here are at t = 18 min to avoid scaling artifacts. Note the different scale bars.

The relationship between EPZ and TF interval is further illustrated in Fig. S6. The intensity of additive prothrombotic effects increased as the TF interval decreased, and conversely, the intensity of suppressive antithrombotic effects increased as TF interval and TM length increased.

Discussion

Computational modeling of blood coagulation

Mathematical models of blood coagulation have been developed with varying degrees of complexity and for applications including the study of coagulation phenomena, pharmacologic and biomaterial development, and simulation of clinical diagnostic values. A review and discussion of the literature, focusing on those studies that incorporate spatial effects, may be found in the Supporting Material. We have characterized a computational model of coagulation, which integrates the effects of reaction kinetics, a simple, yet computationally expandable, flow regime, and uniquely heterogeneous surface expression. Our model simulated threshold effects with respect to the length of the TF site, TF and TM surface densities, and wall shear rate, and reproduced the classic time course characterized by initiation and amplification of thrombin generation. Furthermore, our TF length threshold was consistent with experimental work by Shen and colleagues, who measured a TF threshold size of ∼400 μm in a capillary perfusion system under low shear rates (40 s⁻¹) in the absence of TM regulation (23). It is interesting to note that the threshold TF length in that study at transport-limited levels of TF and TM was found to be within the length range of ruptured plaques associated with acute thrombotic occlusion (14). With respect to TF density, we computed thresholds of 0.03 and 0.8 fmol/cm² for wall shear rates of 50 and 500 s⁻¹, respectively. Using patterned microarrays, Okorie et al. determined critical TF concentrations of 0.6, 1.4, and 1.7 fmol/cm² for wall shear rates of 100, 500, and 1000 s⁻¹, respectively (24). In a computational study, Kuharsky and Fogelson predicted a TF density threshold of ∼3 fmol/cm² at 500 s⁻¹ (7). It has been estimated using ex vivo carotid plaque scraping that the average phospholipid membrane-associated TF underlying atherosclerotic plaques is 33 pg TF/cm² or 1 fmol/cm² (25). The principle of a TF threshold is significant, since it is unlikely that the vasculature is completely without defect. An understanding of the regulation of blood coagulation requires consideration not only of antithrombotic biochemical pathways but also of coagulation thresholds. As we have demonstrated, these variables may not be studied in isolation; for example, wall shear rate has a profound effect on the TF density threshold.

In addition to generating transient concentration profiles, we have defined a global parameter, FSTG, that reflects three key qualities of the thrombin response: 1), intensity of the response; 2), relative onset of amplification; and 3), localization of the thrombin foci near to the upstream injury area. Subthreshold systems are characterized by FSTG <10 nM, whereas those systems that cause full activation of the coagulation cascade fall along a continuous scale where FSTG is >10 nM. The choice of a consistent 1-h simulation time ensured inclusion of early and late phases of coagulation. Although there is some postprocessing loss of information due to averaging, it is notable that the results of spatially homogeneous models are intrinsically averaged.

Perhaps the most intriguing result of this study was the identification of an EPZ that may be significantly larger than the dimensions of the spatially discrete site of TF expression in both radial (EPH) and axial (EPL) directions, with implications for clot growth leading to arterial or venous thrombosis, as well as systemic procoagulant effects leading to further hypercoagulability. The geometric parameters EPL and EPH are therefore measures of the vital function of hemostasis to confine thrombus formation to an injury site. Shen et al. reported that spatial propagation of thrombin was limited to a 100-μm distance from a discrete patch of TF under conditions that did not lead to exceeding a threshold for thrombin propagation (23). A remarkable increase in the EPZ may occur under conditions that lead to a reduction in the surface concentration of TM. This effect is further enhanced in a low-flow regime. These results are consistent with those reported by Ataullakhanov et al. for experimental and computational studies in a diffusion-limited system, in which thrombin generation and clot formation were inhibited by solution-phase TM, with final clot lengths of 0.2–2 mm under diffusive conditions (8,9).

Atherosclerosis and the importance of interactions between multiple lesions

Despite advances in prevention, patient education, and pharmaceutical therapies, atherosclerosis remains a significant source of morbidity and is estimated to be responsible for nearly 75% of all cardiovascular-related mortality (26). Atherosclerosis is a diffuse disease affecting all vessels, and long-range communication between sites cannot be excluded, particularly in the presence of flow. Furthermore, tandem lesions, consisting of more than one ulcerated plaque or stenosis in series within a single coronary or peripheral artery, are common occurrences and pose unique hemodynamic challenges (27,28). It may be concluded from these computational observations that neither measurement of lesion morphology alone nor identification of the isolated rupture risk of a single plaque is sufficient to determine the likelihood of acute coronary syndromes or sudden cardiac death. Indeed, it has been suggested that smaller, nonobstructive plaques could be most dangerous simply because they by far outnumber the larger, obstructive plaques (29). Accurate assessment of plaque vulnerability and subsequent management of high-risk plaques or systems of plaques through pharmaceutical or interventional therapies could greatly diminish morbidity associated with ischemic cardiac injury and decrease the incidence of sudden cardiac death.

Exposure of large amounts of TF to the bloodstream from within the necrotic core of plaque lesions is thought to be responsible for the hyperthrombotic state of atherosclerotic vessels (30). Campo et al. measured FVII and TF antigen levels for 256 patients admitted for acute myocardial infarction and correlated these levels with increased incidence of death and reinfarction within a median follow-up period of 397 days (hazard ratio of 2.1 for FVII and 4.1 for TF) (31). The investigators of the AtheroGene study, which included 1669 patients with coronary artery disease with a median follow-up of 2.3 years, reported a hazard ratio of 2.06 for soluble plasma TF levels and cardiovascular death in individuals with acute coronary syndrome (32). In a similar way, a 30-year review of the Northwick Park Heart Study (NPHS-1) observed a significant association of FVII with fatal coronary heart disease (relative risk 1.58 in men, 1.78 in women); no correlation was found with nonfatal heart disease (33). Amiodarone is known to decrease mortality in patients with coronary artery disease and decreased ejection fraction. Although it is recognized as an antiarrhythmic agent, amiodarone may mediate this effect by inhibiting tumor-necrosis-factor-α- and thrombin-induced TF expression, as observed in cultured human vascular cells, as well as in a mouse photochemical carotid injury model (34).

It is interesting that upstream TF regions promote TM and thrombin-mediated generation of the anticoagulant APC, which acts to dampen the thrombin response at distal sites. In a study of 335 patients admitted with ST-elevation myocardial infarction, decreased APC levels were found to be a prognostic parameter for high risk of death, with an adjusted odds ratio of 9.4 for an APC cutoff at 65% (35). In a retrospective study comparing patients with severe atherosclerosis and ischemic cardiomyopathy to matched controls, Laszik et al. (36) determined a 2.4-fold decrease in TM staining of endothelial cells of the coronary arteries. In concordance with our findings, it may be inferred that management strategies that support TM expression and upregulation should be pursued for patients found to have more than a few coronary plaques, despite the apparent subclinical size of individual lesions. The effects of TM surface concentration may also have implications for early autologous vein-graft failure due to thrombosis. Immunohistochemical staining and Western blot analysis revealed a transient reduction in TM expression of >95% during the first 2 weeks after implantation of autologous vein grafts in a rabbit model (37).

We have predicted that the additive interactions of more than one subclinical atherosclerotic lesion may result in a clinically relevant thrombotic response due in part to the existence of an EPZ that extends beyond the anatomical dimensions of an injury site. EPZ is governed by the dimension and concentration of the TF-expressing site, the integrity of the surrounding TM-APC system, and blood flow. Furthermore, a major determinant of a system's overall behavior is the relationship between EPL and the interval distance between lesions. It is important to note that suppressive interactions were also observed and were found to be governed by the surface density of TM within the intervening regions.

Limitations and extensions

The computational model presented here is capable of simulating features of the coagulation cascade, namely the rapid all-or-none response of thrombin activation, characteristic initiation and amplification phases, and quantitative values within an appropriate range of concentrations. Although it may be suggested that any phenomena may be mathematically reproduced given 16 diffusion coefficients, 10 inlet concentrations, and 36 kinetic parameters, it bears emphasis that the reaction pathways and related kinetic parameters are largely well defined for the coagulation cascade, and that no parameter fitting was performed in this model system. Given a different set of physiologically relevant parameters, the observed qualitative trends would likely have remained unchanged.

A number of assumptions were made for reasons of computational simplicity and feasibility. First, steady, one-dimensional laminar flow in a two-dimensional rectangular flow field was assumed. This algebraically defined flow profile enabled the effect of wall shear rate to be directly studied but did not reflect the pulsatile flow of the arterial system or turbulent flow patterns often observed at bifurcation, or branching, points. It should be noted that the FEM approach allows for the possibility of incorporating more complex flow geometries and nonsteady flows by the addition of the Navier-Stokes equation to solve for x- and y-components of flow velocity, or by coupling to other existing computational fluid dynamics models. Future work may model atherosclerotic lesions, which not only represent areas of increased TF, but are often areas of stenosis and consequently locally increased wall shear rates. Although our initial modeling studies would suggest a protective effect, the decreased shear immediately downstream of the plaque may decrease the ability of unaffected vasculature to abrogate the thrombin load.

TF surface presentation was assumed constant over the 60-min simulation period. In other words, the TF stimulus responsible for initiating the reaction cascade is never turned off, and its catalytic activity is inhibited only by TFPI. As suggested by Fogelson et al. (7,11), physical inhibition of surface-bound TF by fibrin and platelet deposition is an important regulatory mechanism to incorporate into future works. Related to this, platelet deposition contributes additional activated phospholipid surfaces not currently described by our model.

Summary

With the advances in computational methods, theoretical models of coagulation may consider many phenomenological aspects efficiently and more completely. We have presented a FEM of coagulation under flow, with particular attention to spatial regulation. By eliminating the assumption of spatial homogeneity and describing discrete sites of TF and TM surface reactivity, localization of thrombin formation by downstream TM was not only demonstrated but quantified by the definition of an EPZ in two dimensions. Although extension of thrombin generation away from the wall toward the center of the vascular space may contribute to vessel occlusion and stasis of flow, prothrombotic effects, which extend downstream beyond the discrete site of injury to interact with subsequent lesions, are critical given the systemic and generalized nature of atherosclerotic disease. The TM-APC pathway is a key determinant of the local thrombin response, particularly in the setting of regional systems of multiple TF-laden lesions.