The Role of Photon Scattering in Voltage-Calcium Fluorescent Recordings of Ventricular Fibrillation

Abstract

Recent optical mapping studies of cardiac tissue suggest that membrane voltage (V_m) and intracellular calcium concentrations (Ca) become dissociated during ventricular fibrillation (VF), generating a proarrhythmic substrate. However, experimental methods used in these studies may accentuate measured dissociation due to differences in fluorescent emission wavelengths of optical voltage/calcium (V_opt/Ca_opt) signals. Here, we simulate dual voltage-calcium optical mapping experiments using a monodomain-Luo-Rudy ventricular-tissue model coupled to a photon-diffusion model. Dissociation of both electrical, V_m/Ca, and optical, V_opt/Ca_opt, signals is quantified by calculating mutual information (MI) for VF and rapid pacing protocols. We find that photon scattering decreases MI of V_opt/Ca_opt signals by 23% compared to unscattered V_m/Ca signals during VF. Scattering effects are amplified by increasing wavelength separation between fluorescent voltage/calcium signals and respective measurement-location misalignment. In contrast, photon scattering does not affect MI during rapid pacing, but high calcium dye affinity can decrease MI by attenuating alternans in Ca_opt but not in V_opt. We conclude that some dissociation exists between voltage and calcium at the cellular level during VF, but MI differences are amplified by current optical mapping methods.

Introduction

Ventricular fibrillation (VF) is a lethal cardiac arrhythmia characterized by highly complex spatiotemporal patterns of electrical excitation throughout the myocardium. Such arrhythmias are often initiated and sustained through the fragmentation of wavefronts of depolarization, in a process called wavebreak, which perpetuates these chaotic sequences of activation. Although many potential mechanisms of wavebreak exist (1), attention has turned recently to the specific interplay between intracellular calcium and transmembrane voltage and how the relative association between these quantities at the cellular level may influence wavebreak in intact cardiac tissue, suggesting a mechanism of VF (2–5).

Specifically, a recent study by Omichi et al. showed that optically recorded voltage and calcium signals from swine right ventricle became entirely dissociated from one-another during VF, and that this dissociation was widespread across the entire mapped region; however, voltage and calcium signals were seen to remain closely related during both ventricular tachycardia and pacing (3). Simulations in the same study showed that allowing calcium to exhibit independent nonvoltage-gated dynamics in the model both increased the incidence of wavebreak and significantly lowered the statistical association between the action potential and calcium transients, suggesting that the nonvoltage-gated calcium release could be promoting the wavebreak seen in VF. A follow-up study by Wu et al. later showed that such an observation was not simply due to the rapid pacing rates associated with VF, demonstrating that the optical voltage and calcium signals remain closely associated during pacing of ≈12 Hz (4). However, a later study by Warren et al. observed a much closer association between fluorescent voltage and calcium signals during VF (5) across the mapped area, although the authors did note regions of higher dissociation confined to the specific sites of wavebreak, suggesting that voltage-calcium dissociation was a consequence, rather than a cause, of wavebreak in VF.

It is important to note that all of the above dual voltage-calcium studies were performed using the optical mapping technique, which is known to introduce significant distortions into the recorded fluorescent signals as a result of scattering of photons from tissue depth (6–9). The optical signal recorded from an isolated epicardial site thus represents a weighted-average of contributions from a scattering volume (or interrogation region), extending both laterally and in depth from the recording site (10,11), resulting in a characteristic prolongation of the optical action potential upstroke and spatial blurring of the activation wavefront (6–8). More recently, computer simulations of synthesized optical signals have been used to help explain a more intriguing effect of photon scattering in fluorescent measurements (9,12), the occurrence of so-called dual-humped action potentials, frequently witnessed during experimental recordings of arrhythmias (9,13,14). These studies showed that information regarding the passage of a reentrant wavefront within the scattering volume associated with a recording site (but which does not pass directly through the epicardial recording site itself) is transduced by scattered photons within the tissue to produce additional inflections in the optically recorded signal from the epicardial surface. Furthermore, the amplitude of these additional inflections (or humps) in the traces was seen to be closely related to the optical absorption and scattering properties of the tissue, which in turn govern the dimensions of the scattering volume (9).

It is widely known that the optical properties of light within cardiac tissue are highly wavelength-dependent, with longer wavelengths penetrating more deeply into the tissue than short wavelengths, causing greater distortions in the recorded fluorescent signals as contributions from larger scattering volumes are recorded (9,10,15). However, during dual voltage-calcium recordings, the voltage- and calcium-sensitive fluorescent dyes emit light at different wavelengths (usually ∼585 nm for the calcium dye Rhod-2 and >700 nm for the voltage dye RH-237, the most commonly used two-dye combination). At these wavelengths, the optical penetration depths in cardiac tissue have been recently measured at ≈1.65 mm (∼600 nm) and ≈3.31 mm (at 715 nm) (15), giving the calcium signal an overall scattering volume ∼70% that of the voltage signal (15). The resulting difference in scattering-volume dimensions for the respective voltage and calcium signals, combined with the high degree of wavefront complexity during VF, means that the fluorescent voltage signal from a particular epicardial recording site could contain contributions from a wider variety of wavefront events compared to the calcium signal. For example, individual fractionated wavefronts passing close to the recording site during VF could pass within the voltage-scattering volume, but not the calcium-scattering volume, leaving a signature in one optical trace but not in the other. It is therefore our hypothesis that the effects of fluorescent photon scattering in optical dual voltage-calcium recordings of VF distort the voltage and calcium signals, but to different degrees, due to differences in scattering-volume dimensions associated with the different emission wavelengths of the two dyes. We postulate that these factors will act to increase the measured dissociation between the voltage and calcium signals during VF (but not during pacing, due to the increased coherence of the wavefront patterns), which could affect experimental conclusions about the relative association of voltage and calcium signals during VF (2–5).

To investigate this hypothesis, we use a computational model of cardiac ventricular tissue to simulate the spatiotemporal dynamics of transmembrane voltage (V_m) and intracellular calcium (Ca) distributions during both VF and rapid pacing. Simulated signals are then combined with a photon-diffusion model, which accounts for the processes of illumination and fluorescent emission, to synthesize dual voltage-calcium optical mapping signals (V_opt/Ca_opt) from the epicardial surface. Through comparison between the respective electrical (V_m/Ca) and optical (V_opt/Ca_opt) traces, we aim to dissect the role of optical distortion due to fluorescent photon scattering in the measurement of voltage/calcium dissociation during VF and rapid pacing. The mutual information (MI) statistic is used throughout to directly relate our results to those of previous experimental studies (3–5), and allow quantitative assessment of statistical differences in signal association. To demonstrate the dependence of this effect upon differences in wavelength, optical penetration depths used in our fluorescent scattering model are varied. Furthermore, we also use the model to investigate the contributions of alignment error (which has been investigated experimentally (3)) and the role of calcium dye affinity (16) in MI. Finally, we look at how the parameters associated with the MI statistic may influence the results obtained in this and previous studies.

Materials and Methods

Geometrical tissue model

To represent a slab of ventricular myocardium, we generated a regular tetrahedral finite-element model of dimensions 40 mm × 40 mm × 8 mm in the x-, y-, and z-directions, respectively (Fig. 1), where z represents the transmural direction. Finite element node discretization was 200 μm. Physiologically-realistic anisotropic conduction within the model was represented through the assignment of a transmurally-rotating fiber orientation varying by 120 degrees between epi- and endocardium.

Figure 1.

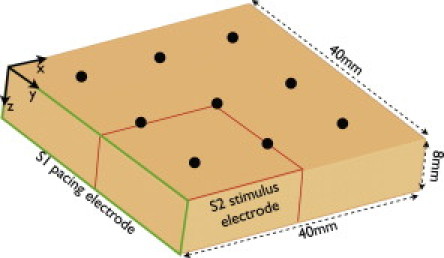
Model setup. (Left) Ventricular slab geometry measuring 40 × 40 × 8 mm in the x-, y-, and z-directions, respectively, showing the location of the S1 pacing electrode (green) and the S2 shock electrode for reentry induction (red). Nine regularly spaced black dots represent electrical and optical recording sites from the epicardial tissue surface. Please see online version for color descriptions.

Simulating electrical activation

Electrical activation within the ventricular model was simulated using a monodomain representation,

$$C_m\frac{\partial V_m}{\partial t}+I_{ion}=\nabla \times \left({\mathbf{\sigma }}_m\nabla V_m\right),$$ (1)

where V_m is the transmembrane potential, C_m the membrane capacitance per unit area, and I_ion the membrane ionic current density. σ_m is the harmonic mean conductivity tensor used to provide a match with effective bidomain conduction velocities within a monodomain framework (17). Experimentally-derived conductivities were assigned along the fiber and cross-fiber directions within the intracellular and extracellular domains (18). Cell-membrane dynamics within the myocardial tissue were represented by the Luo-Rudy mammalian ventricular cell model (19), slightly modified to induce sustained spiral-wave break-up through adjustment of the slow-inward current conductance ($G_{si}=0.09\to 0.06$).

Equation 1 was solved with the Cardiac Arrhythmia Research Package (CARP) (20), the specifics of the numerical regimes of which have been described extensively elsewhere (20). Using CARP, electrical V_m and Ca variables were output at every finite-element node at a temporal output granularity of 4 ms, in accordance with previous experimental studies (3).

Simulating optical mapping signals

Fluorescent voltage (V_opt) and calcium (Ca_opt) optical mapping signals were simulated computationally directly from the electrical V_m and Ca variables, using a previously published method (8). Briefly, photon density throughout the tissue during the processes of excitation illumination (Φ_illum) and voltage-/calcium-sensitive fluorescent emission (Φ_em) was calculated using the steady-state photon-diffusion equation

$$D{\nabla }^2\Phi \left(\mathbf{r}\right)-{\mathit{\mu }}_a\Phi \left(\mathbf{r}\right)=-w\left(\mathbf{r}\right),$$ (2)

where Φ is the photon density at any point r within the tissue, w the photon source, and D and μ_a the optical diffusivity and absorptivity, respectively, at the given wavelength. Equation 2 is solved with the finite-element method and partial-current boundary conditions imposed at tissue interfaces to faithfully represent the tissue-saline interface (8).

Uniform epicardial illumination was simulated using Eq. 2, assuming w = 0 within the tissue and imposing a uniform epicardial boundary condition of Φ_illum = Φ₀ along the surface, z = 0. The optical penetration depth, ($\delta =\sqrt{D/{\mathit{\mu }}_a}$), during illumination was taken at the typical excitation wavelength used in dual voltage-calcium optical mapping studies (532 nm) (3), having a value of δ_illum = 0.48 mm (16). Note that Eq. 2 fully represents photon scattering within a 3D volume and includes the effect of lateral scattering.

Fluorescent emission, for simulation of both voltage and calcium optical signals, was calculated at each time step in the electrical simulations by separately solving Eq. 2 with w = V_mΦ_illum for voltage-dependent emission and w = Ca_DΦ_illum for calcium-dependent emission, where Ca_D represents the intracellular bound calcium-dye concentration. As in Walton et al. (16), a simple chemical equilibrium relationship was used to relate Ca_D to the total intracellular calcium concentration, Ca:

$$C{a}_D=\frac{Ca\times D_T}{Ca+K_d},$$ (3)

where D_T is the total dye concentration and K_T is the dye's dissociation constant. Default values of K_T = 0.57 μM and D_T = 10 μM were used to simulate the high-affinity (HA) calcium dye Rhod-2 (3). Fick's Law was used to relate the fluorescent photon density throughout the tissue to the photon flux recorded by the detector (7). Optical penetration depths corresponding to the emission wavelengths of the voltage-sensitive dye RH-237 (715 nm) and the calcium-sensitive dye Rhod-2 (600 nm) were taken to have values of ${\delta }_{em}^{vm}$ = 3.31 mm and ${\delta }_{em}^{Ca}$= 1.65 mm, respectively (16).

The above optical mapping model was used to simulate optical fluorescent voltage (V_opt) and calcium (Ca_opt) signals on the epicardial tissue surface at the same output granularity as the electrical simulations (4 ms), facilitating a direct comparison between electrical and optical signals.

Simulation protocol

Two separate protocols of rapid pacing and VF induction were applied to the ventricular slab model. Before each protocol, the model was paced with a transmembrane current pulse of magnitude 0.005 μA/cm³ over 1-ms duration along the S1 pacing electrode (Fig. 1, green) (x = 0 face) for 20 paced beats at a constant basic cycle length (BCL) of 270 ms to achieve steady state. It is important to note that although the geometry of the S1 stimulus used here differs from point sources used in most experimental studies, the resulting diffrences in wavefront curvature are not expected to affect the activation rate of tissue within a given scattering volume. For rapid pacing, the model was then continually paced at the same BCL for a further 5 s. For VF induction, an S1-S2 protocol involving an initial pacing stimulus followed by an S2 stimulus applied to the lower quadrant of the slab (Fig. 1, red) was used to induce a rotating spiral wave. The induced spiral-wave subsequently broke up into sustained VF, which was then simulated for a further 5 s (5).

Measurement of dissociation: mutual information

MI is a robust signal-processing technique that provides a nonlinear measure of the statistical dependence between two variables, quantifying how much knowledge of one reduces our uncertainty in predicting the value of the other. MI can thus be applied to give a numerical measure of dissociation between two time-varying signals, such as voltage and calcium recordings. We use the method described in Section 1 of the Supporting Material to calculate MI for the respective pairs of voltage/calcium signals throughout this study.

Data analysis

All signals were normalized with respect to the maximum/minimum values during pacing, as in experimental optical mapping studies (9). Individual electrical (V_m and Ca) and optical (V_opt and Ca_opt) voltage and calcium traces were obtained from the nine evenly spaced epicardial recording sites shown in Fig. 1, similar to experimental studies (4). To ensure statistically independent points, the signals were decimated by resampling at an interval slightly greater than the autocorrelation time (time taken for the autocorrelation function to fall to zero), as in Omichi et al. (3). MI scores were then calculated to compare the level of dissociation between the electrical (V_m versus Ca) signals and the optical (V_opt versus Ca_opt) signals. Due to the inherent physiological time lag between voltage and calcium signals, and as a time lag between signals can affect MI scores, MI was calculated over a range of time lags (τ) from 0 to 200 ms, and the maximum, minimum, and mean MI over τ (3) were recorded. Reported values of minimum/mean/maximum corresponded to average values taken from all nine epicardial measurement sites in Fig. 1, with corresponding standard deviations. However, we note here that in accordance with the study of Warren et al., the majority of our analysis focuses on the variation in the maximum MI obtained over τ, as discussed in the Results.

Results

Qualitative distortion in voltage and calcium recordings during VF and rapid pacing

The upper traces of Fig. 2 show the spatial distributions of both the simulated electrical (V_m/Ca) and corresponding simulated optical (V_opt/Ca_opt) signals during the episode of rapid pacing. The lower traces of Fig. 2 give sample temporal V_m/Ca (blue/red) and V_opt/Ca_opt (orange/green) traces obtained from the central recording site in Fig. 1. The characteristic prolongation of the optical action potential and calcium transient upstrokes, as well as a smoothing of the action-potential notch as reported in (6,11,16), is evident in these recordings. Furthermore, we note that the V_opt/Ca_opt traces consistently track both each other and the corresponding V_m/Ca traces from which they are produced. However, it is important to note here that the slight appearance of alternans in the calcium transient amplitude (present in the Ca traces), due to the rapid nature of the pacing, appears smoothed out in the fluorescent Ca_opt traces.

Figure 2.

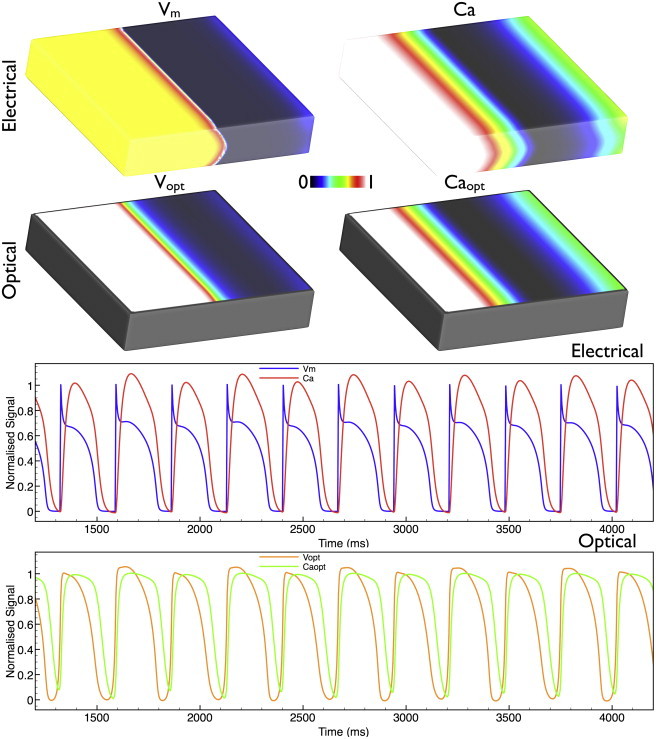
Rapid pacing dynamics. (Upper) Distributions of V_m, V_opt, Ca, and Ca_opt at the same instance in time (1044 ms) into an episode of rapid pacing. (Lower) Comparison of V_m/Ca traces (blue/red) and V_opt/Ca_opt traces (orange/green) taken from the central recording site in Fig. 1. Please see online version for color descriptions.

Fig. 3 shows information similar to that in Fig. 2 for the case of VF. Immediately evident from the images of Fig. 3 is the complexity of the VF episode, along with the distortion seen in spatial wavefront morphology in both the V_opt and Ca_opt images. The temporal traces of Fig. 3 show that the electrical V_m/Ca traces track each other fairly consistently throughout the entire episode of VF. However, upon examination of the optical V_opt/Ca_opt traces, a number of interesting phenomena are evident.

Figure 3.

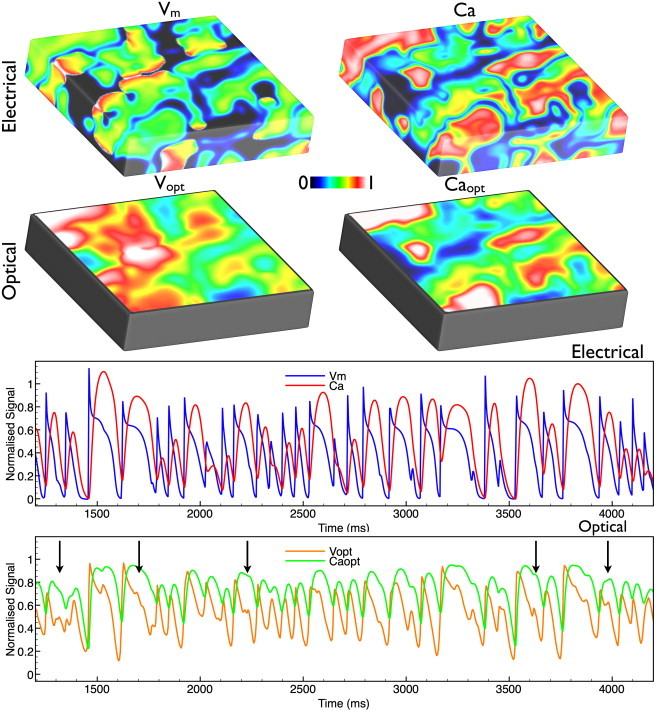
VF dynamics. (Upper) Distributions of V_m, V_opt, Ca, and Ca_opt at the same instance in time (868 ms) into an episode of VF. (Lower) Comparison of V_m/Ca traces (blue/red) and V_opt/Ca_opt traces (orange/green) taken from the central recording site in Fig. 1. Black arrows indicate additional inflections in the V_opt signal. Please see online version for color descriptions.

First, we notice that the amplitude of the V_opt/Ca_opt traces is significantly reduced relative to the electrical traces above, with an elevation in normalized diastolic levels. Next, we can clearly discern a large number of inflections (or humps) in the fluorescent V_opt signal that are not visible in the corresponding V_m trace (Fig. 3, lower). Many of these humps are either undetectable in the corresponding fluorescent Ca_opt signal, or else are present but with a significantly reduced amplitude (black arrows).

Quantitative distortion in voltage and calcium recordings during VF and rapid pacing: MI

We quantify dissociation between V_opt and Ca_opt through application of the MI statistic (3–5). MI was computed between the two pairs of signals (electrical,V_m/Ca, and optical, V_opt/Ca_opt). Fig. 4 a shows how the MI score varies with τ for the electrical and optical traces obtained from the central recording site during the episode of VF. MI peaks at a time lag of ∼25 ms for both pairs of signals. The inset in Fig. 4 a plots the minimum/mean/maximum MI over all τ for the two signals. However, it is important to note that measuring over a range of τ is performed only to remove the inherent physiological time lag between voltage and calcium signals. Thus, recording the maximum MI over τ is the best representation of the dissociation of the two signals. From here on, we therefore focus on using the maximum MI score as a measure of signal dissociation, in accordance with Warren et al. (5).

Figure 4.

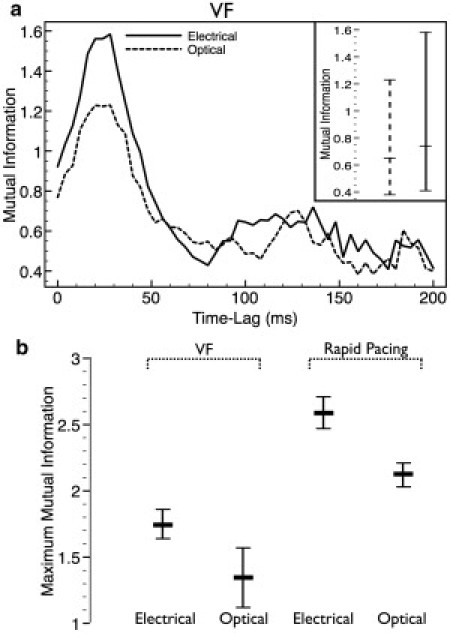
MI scores for VF and rapid pacing. (a) MI scores between V_m/Ca (solid line) and V_opt/Ca_opt (dashed line) signals, plotted as a function of time lag, τ, between voltage and calcium signals, obtained from the central point in Fig. 1 during the episode of VF. (Inset) Minimum/mean/maximum values over the range of τ. (b) Bar graphs of maximum MI scores, averaged across all nine recording sites, for both signals during VF and rapid pacing. Error bars show standard deviation.

Fig. 4 b plots the maximum MI obtained for the electrical and optical signals during both VF and rapid pacing, averaged over all nine recording sites in Fig. 1. During VF, the average maximum MI scores of the optical traces are significantly decreased with respect to the corresponding electrical signals, in agreement with our previous visual identification of dissociation. Most noticeably, the maximum MI falls by 23%, from 1.75 ± 0.11 for V_m/Ca to just 1.35 ± 0.23 for V_opt/Ca_opt. However, the MI score is also seen to fall between electrical and optical cases during rapid pacing, although by less than the fall during VF (maximum MI falls by 18%, from 2.59 ± 0.12 to 2.12 ± 0.09). In this instance, despite the apparent lack of significant visual dissociation between fluorescent V_opt and Ca_opt signals in Fig. 2, it nonetheless appears that the subtle effect of smoothing out the slight Ca_opt alternans (noted above) is responsible for this decrease in MI scores between electrical and optical traces during rapid pacing.

Effect of calcium dye affinity upon optical signal dissociation

The nonlinearity of HA calcium dyes is known to artificially inflate low-amplitude calcium signals (16), providing a possible explanation for the attenuation of Ca_opt alternans and reduction in optical MI scores during rapid pacing described above. Thus, to dissect the relative contribution of the measured dissociation in the optical signals due to the nonlinearity of the HA calcium dye versus dissociation caused by photon scattering, we simulated an additional set of Ca_opt signals using a low-affinity (LA) calcium dye (such as Rhod-FF with K_T = 17 μM (16)), which has an approximately linear relationship between emitted fluorescence and intracellular calcium (Eq. 3).

Fig. 5 plots the temporal Ca_opt traces from the central recording site during rapid pacing (Fig. 5 a) and VF (Fig. 5 b) for the HA (solid line) and LA (dashed line) calcium dyes. Compared to the HA dye, the LA dye generally predicts lower-amplitude oscillations in the calcium signal during VF, as well as more successfully preserving the slight alternans in calcium amplitude present in the electrical Ca signal during rapid pacing (Fig. 2). Thus, during rapid pacing, the Ca_opt signal with the LA dye is more closely associated with the corresponding V_opt trace, which was also seen to display slight alternans (see Fig. 2). This closer association is emphasized in the MI score plots of Fig. 5 c, comparing maximum MI values of V_opt/Ca_opt signals with the LA dye to those of the electrical signals (V_m/Ca, repeated from Fig. 4 b). Here, the use of an LA calcium dye increases the MI scores of the optical rapid pacing signals (relative to the HA dye case of Fig. 4 b) to be in line with the MI scores of the electrical signals; specifically, the maximum MI of the optical signals is now 2.69 ± 0.05, similar to that of the electrical signals (2.59). However, in the case of VF, the MI scores are only marginally increased from the previous HA values; the maximum MI of the optical signals is now 1.46 ± 0.16, still 17% less than the corresponding value for the electrical signals. To further isolate the effects of HA calcium dye from photon scattering on voltage-calcium signal dissociation, we calculated MI for electrical V_m combined with the electrical Ca signal processed by Eq. 3, which simulates the effects of calcium dye nonlinearity on MI only. MI scores for the LA/HA dye were found to be 1.74 ± 0.12/1.69 ± 0.11 during VF and 2.59 ± 0.12/2.09 ± 0.12 during rapid pacing.

Figure 5.

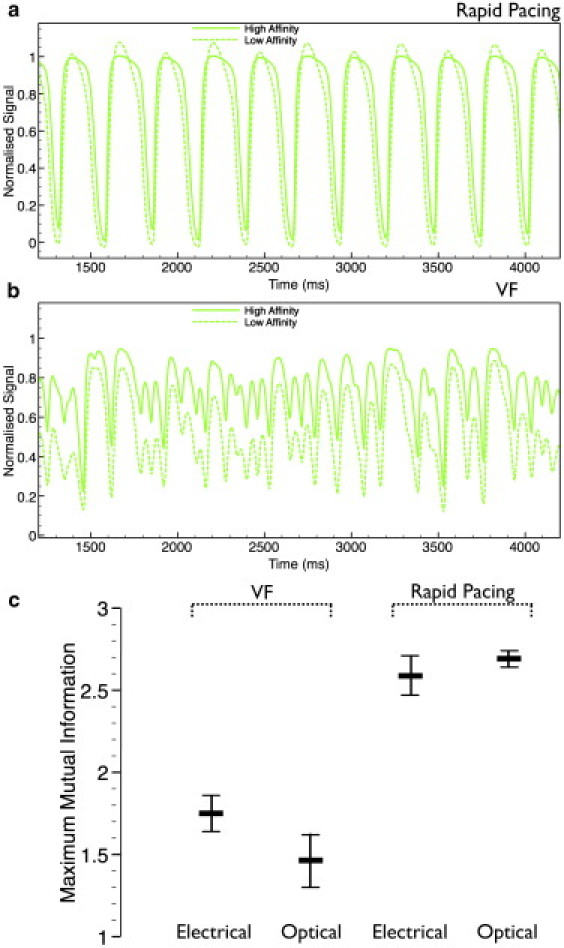
Role of calcium-dye affinity. (a and b) Comparison of optical Ca_opt traces simulated using a HA (solid line) and LA (dashed line) calcium-sensitive dye taken from the central site in Fig. 1 for rapid pacing (a) and VF (b). (c) Bar graphs of maximum MI scores, averaged across all nine recording sites during VF and rapid pacing, showing optical data for the LA calcium dye with the electrical data from Fig. 4b.

Effect of optical penetration depth upon signal dissociation

We have so far demonstrated that recording fluorescent signals from a scattering volume beneath the recording site increases apparent dissociation in optical V_opt/Ca_opt signals during VF but not during rapid pacing. Here, we assess the dependence of the measured dissociation between optical signals on the optical scattering properties (penetration depths) known to govern the dimensions of the respective scattering volumes.

Simulations of optical signals V_opt and Ca_opt were repeated with the optical penetration depths at the respective fluorescent emission wavelengths being varied by 1.5 × δ_default (high) and 0.5 × δ_default (low), using the HA calcium dye. Fig. 6, a and b, shows the corresponding plots of the V_opt and Ca_opt signals from the central recording site (Fig. 1) for both VF (Fig. 6, left column) and rapid pacing (Fig. 6, right column). In the VF traces, the additional inflections in the optical signals (absent from the electrical signals in Fig. 3) are seen to increase in amplitude and number with increasing penetration depth, occurring as the scattering volume from which signals are collected increases in size. However, the rapid pacing traces show relatively little difference as penetration depth is varied.

Figure 6.

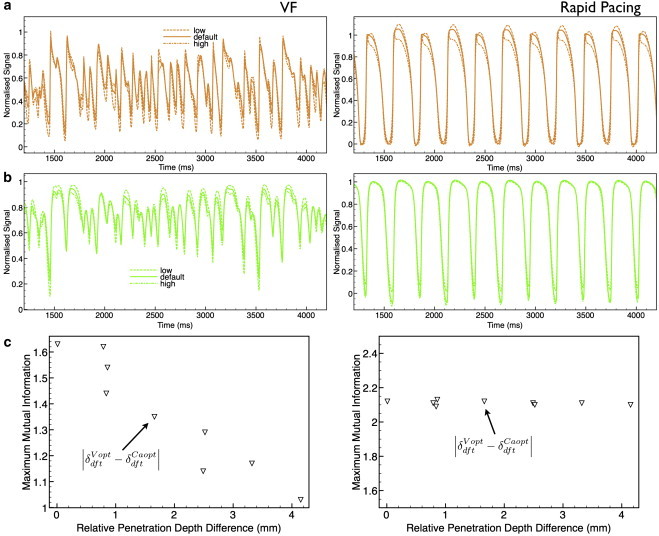
Dependence upon difference in penetration depths for VF (left) and rapid pacing (right). (a and b) Comparison of V_opt (a) and Ca_opt (b) traces obtained upon variation of the penetration depth (δ) of each signal by ${\delta }_{default}^{Vopt}$, 1.5 × ${\delta }_{default}^{Vopt}$(high), and 0.5 × ${\delta }_{default}^{Vopt}$ (low), and by ${\delta }_{default}^{Caopt}$, 1.5 × ${\delta }_{default}^{Caopt}$ (high), and 0.5 × ${\delta }_{default}^{Caopt}$ (low). (c) Variation in maximum MI between the optical (V_opt/Ca_opt) signals as the relative penetration depth (δ) of each signal is varied for all combinations of high, default, and low penetration depths.

Different combinations of the V_opt and Ca_opt signals at the different penetration depths were then combined to calculate MI scores, thus allowing the relative difference in penetration depth between the two signals to be varied. Fig. 6 c plots the maximum MI score as a function of the magnitude of the relative difference in penetration depth between the V_opt and Ca_opt signals, for both VF (left) and rapid pacing (right). The highest MI score in Fig. 6 c corresponds to ${\delta }_{default}^{Vopt}$ × 0.5 and ${\delta }_{default}^{Caopt}$; here, the two signals originate from approximately the same tissue volume, giving a penetration-depth difference close to 0.

Effect of measurement site uncertainty upon optical signal dissociation

Previous experimental studies have highlighted a potential uncertainty in the alignment of V_opt and Ca_opt recording sites (up to ±1 mm separation (3,4)). Here, we assess the effect such misalignment may have on the apparent dissociation between the V_opt and Ca_opt signals.

Fig. 7 plots the maximum MI as a function of the relative separation between V_opt and Ca_opt recording sites during rapid pacing (dashed line) and VF (solid line). The Ca_opt recording site is fixed at the central recording site (Fig. 1), and the V_opt recording site is moved in the positive x-direction. A misalignment of up to 1 mm results in a significant decrease in maximum MI score during VF, falling from 1.23 when the signals are perfectly aligned, to 0.93 at 1 mm misalignment, which further drops to 0.84 at 3 mm. In contrast, during rapid pacing, we see very little change at all in MI, even at 3 mm (maximum MI score falls to only 2.05 from 2.12), due to the higher spatial coherence of the signals during pacing.

Figure 7.

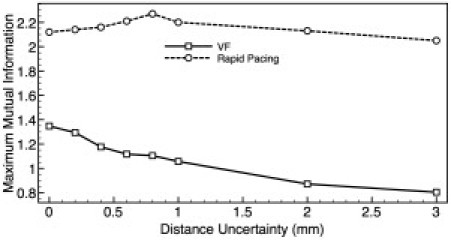
Dependence upon uncertainty in measurement location. Variation in maximum MI in the optical (V_opt/Ca_opt) signals during rapid pacing (dashed line) and VF (solid line) as the relative separation in V_opt and Ca_opt recording site is varied.

Dependence upon specific MI parameters

Finally, we assess whether the specific choice of the different MI parameters (see Measurement of dissociation: mutual information) affects the relative dissociation seen in the electrical and optical signals and thus the conclusions we have drawn up to this point. Fig. S1 in the Supporting Material shows the variation of maximum MI score as we vary the decimation level (Fig. S1 a) and the number of bins (Fig. S1 b) parameters for the case of VF for the electrical (solid line) and optical (dashed line) signals. Note that default values used prior were 15 and 10, respectively. Although the MI score changes significantly in both cases, it is important to note that the relative separation between the electrical and optical signals is preserved (other than at very small decimation levels and bin numbers).

Discussion

It has recently been postulated that the specific interplay between transmembrane voltage and intracellular calcium at the cellular level plays an important role in facilitating wavebreak in intact tissue, thus suggesting a mechanism of VF (2–5). However, reliable measurement of action potentials and calcium transients at the tissue level using the optical mapping technique is difficult due to inherent artifacts introduced by fluorescent photon scattering (6–8,16). In this study, we have demonstrated how such optical distortions interact with the highly complex spatiotemporal dynamics during arrhythmias to reduce the association between fluorescently recorded voltage and calcium signals in VF, an effect which increases with both increasing wavelength separation of voltage/calcium dyes and respective measurement location misalignment. Although such photon scattering effects were not evident during rapid pacing, here, high calcium-dye affinity was seen to increase dissociation by attenuating alternans in the fluorescent calcium signal.

Photon scattering and dual voltage-calcium signal distortion

Previous experimental studies have highlighted the existence of so-called dual-humped action potentials in fluorescent voltage recordings during arrhythmias (9,13,14). Subsequent simulation studies have successfully explained the existence of such anomalous phenomena as being due to the passage of additional wavefronts through the scattering volume of tissue associated with the surface recording site (9,12). Here, we have demonstrated the occurrence of a similar phenomenon during dual voltage-calcium optical mapping recordings of VF, witnessing the occurrence of additional inflections in the fluorescent signals that were not seen in the corresponding electrical signals. During VF, the fractionated nature of the wavefront patterns means that individual wavefronts may propagate within the scattering volume associated with the optical signal, information regarding which is transduced via fluorescent photon scattering resulting in a hump in the optical trace. However, such wavefronts do not propagate directly over the recording site (from which the electrical recordings are directly obtained), thus giving no signal in the electrical trace. It is important to note that we saw a number of such inflections/humps that were present in the V_opt signal but absent from the corresponding Ca_opt signal (Fig. 3). This increase in the number of inflections in the V_opt relative to Ca_opt signal is due to its relatively larger scattering volume (due to longer optical emission wavelength) of the voltage signal relative to the calcium signal. Thus, isolated wavefront events may pass through the larger scattering volume associated with V_opt (giving an inflection in the signal), but not through the smaller Ca_opt volume. Consequently, there was a corresponding significant reduction in the MI score between the optical V_opt/Ca_opt signals, relative to the electrical V_m/Ca signals (Fig. 4 b), decreasing by 23% during VF. It is important that this increase in dissociation between V_opt/Ca_opt signals was magnified as the relative difference in optical scattering-volume dimensions between voltage/calcium signals was increased (Fig. 6 c); furthermore, it was still significantly present when the nonlinearity effects of the HA calcium dye were eliminated (Fig. 5), emphasizing the role played by photon scattering during VF.

During rapid pacing, no such visual dissociation was witnessed in the optical signals (Fig. 2) due to the synchronized nature of the wavefront patterns—the same wavefronts always pass through both the V_opt and the Ca_opt scattering volumes concurrently. Nevertheless, a small reduction was seen in MI score between electrical and optical signals during rapid pacing (Fig. 4 b). However, in contrast to VF, this reduction was eliminated once the nonlinear effects of the calcium dye had been accounted for through use of the LA dye (Fig. 5). Furthermore, no change whatsoever was seen in optical MI score as the optical scattering volumes were varied (Fig. 6 c), again contrary to the case of VF, emphasizing that photon scattering does not contribute to the dissociation of optical voltage/calcium signals during rapid pacing.

Finally, we note that VF, and not rapid pacing, is associated with a decrease in the amplitude and increase in normalized diastolic levels of the V_opt/Ca_opt traces compared to the electrical traces. The fractionated wavefront patterns during VF mean that not all of the tissue within the optical scattering volumes of the V_opt or Ca_opt signals is simultaneously excited (or at rest), as is approximately the case during pacing, with respect to which the signals are normalized, as has been shown previously (9).

Calcium dye affinity

Unlike transmembrane voltage dyes, the calcium-sensitive fluorescent dyes have a nonlinear relationship between the emitted fluorescence and the level of intracellular calcium (Eq. 3). For HA dyes, low-amplitude calcium transients thus appear artificially inflated, whereas for LA dyes, the relatively small value of K_T leads to an approximately linear relationship between emitted fluorescence and intracellular calcium and is thus more correlated with the voltage signal (16). We have found in this study that the association between fluorescent voltage and calcium signals is higher for LA than for HA dyes, as the amplitudes of the voltage and calcium signals track each other more closely. This effect was particularly noticeable during recordings of rapid pacing, where the low amplitude alternans in Ca were reduced in the HA-dye Ca_opt signal, resulting in a lower MI score than when using the LA dye. Note that for lower pacing frequencies, where alternans will not be present in the electrical signals, both LA and HA dyes would yield calcium signals that closely track voltage. However, although eliminating the nonlinearity of the calcium dye is seen to remove the apparent dissociation from the rapid pacing signals, a significant degree of dissociation is still present in the optical signals, relative to the electrical signals, in the case of VF (Fig. 5 b), suggesting that the dissociation due to photon scattering is the dominant factor in this case. Such a result was further emphasized by considering MI scores calculated in the absence of photon scattering, but including the nonlinear effects of the calcium fluorophore.

Dependence of optical dissociation upon optical parameters

The optical penetration depth of biological tissue is a measure of the rate of attenuation of light, and is known to vary strongly with wavelength. As the penetration depth is explicitly related to how easily light both enters and exits the tissue, changes in wavelength either during illumination or fluorescent emission are known to significantly impact the scattering volume of tissue from which optical signals are collected (8,9,15).

By varying the optical penetration depths during fluorescent emission of both V_opt and Ca_opt signals in our optical synthesis model, we were able to conclusively prove our mechanistic description of the role of photon scattering in optical signal dissociation during dual voltage-calcium recordings during VF. Fig. 6 c shows that as the relative difference in the size of the optical scattering volumes associated with V_opt and Ca_opt is increased, the MI score between the two signals decreases. Due to the wide variation in the measured values of optical parameters at particular wavelengths (10,21), we expect that actual effects of photon scattering may be greater than reported here. Thus, Fig. 6 provides a useful guideline to the potential maximum contribution of photon scattering to optical signal dissociation in dual voltage-calcium optical recordings.

Although we have focused here on dual voltage-calcium imaging using a single common excitation wavelength, multiexcitation wavelength modalities have been recently proposed (22,23). As the illumination wavelength strongly influences the depth of tissue excited, and thus also the dimensions of the scattering volume from which signals are collected, careful selection of different excitation wavelengths for the two dyes using such methods could allow the respective dissociation between the voltage and calcium signals to be tuned, in a manner similar to that suggested above during emission. For example, if the calcium dye excitation wavelength were chosen to be less than the voltage excitation wavelength (as is the case in Lee et al. (23)), this would further reduce the volume of the calcium scattering volume relative to that of the voltage, increasing dissociation between the two signals. However, if the calcium wavelength was chosen to be larger than the voltage, the scattering volumes would become similar in size, and dissociation would decrease.

Furthermore, it is intriguing to note that when both scattering volumes of the V_opt and Ca_opt signals are reduced, and thus come relatively closer to one another, we see a reduction in both the number and amplitude of the additional inflections in the fluorescent V_opt/Ca_opt traces (Fig. 6, a and b) in addition to an increase in the MI score (Fig. 6 c), occurring as the two signals are sampling similar wavefront events from similar-sized volumes. (Note that the limit of this is the MI score of the electrical V_m and Ca signals.) This finding has important consequences in relation to a previous experimental study by Warren et al., who used MI to study the dissociation between voltage and calcium optical signals during VF in blood-perfused pig ventricles (5). Blood, however, is known to be a significant absorber of light in the visible spectrum (21), and thus, perfusing the tissue with blood is expected to significantly reduce the penetration depths of the light during both illumination and fluorescent emission (for voltage and calcium signals). Interestingly, the authors found that the fluorescent voltage-calcium signals appeared to be more closely associated overall than had been suggested previously in studies where the tissue was perfused with saline (3,4) Thus, we postulate that the findings from our study provide a plausible explanation for the lack of dissociation in the Warren et al. study (5): specifically, blood perfusion leads to reduced scattering volumes, resulting in the signals being more closely correlated.

Finally, the results from this study also help to suggest ways in which the distortion effects due to scattering might be reduced. For example, using dyes with both lower excitation and lower emission wavelengths, or perfusing the heart with blood instead of saline, will act to reduce the dimensions of the scattering volumes associated with the fluorescent signals. However, note that even if photon scattering effects were completely eliminated, distortion and relative dissociation between the signals may still exist due to the nonlinearity of the calcium dye and potential misalignment errors, as discussed above.

Relation to previous experimental studies

Authors of previous experimental investigations of the dissociation between optically recorded dual voltage-calcium signals during VF reported MI scores significantly lower than those obtained in this study, typically quoting mean MI scores of ≈0.2–0.4 (3,4); they conclude that their recorded voltage and calcium transients are statistically no different from randomly related signals. This was not the case in our study: for comparison, the mean MI in our study was reduced from a value of 0.84 (V_m/Ca) to 0.68 (V_opt/Ca_opt), accounting for the effects of photon scattering.

However, it is important to note that the above values are quoted for mean MI scores over τ, and not maximum MI scores, which we believe to be the most appropriate statistical measure for such analysis, in agreement with Warren et al. (5). Consider, for example, taking the MI of a signal with itself—in this case, the signal is fully associated and a high value of MI is expected. This is provided by the maximum MI, but the minimum and mean MI over τ significantly decrease the apparent association of the signal. The study by Omichi et al. (3) in fact quotes maximum MI scores for individual recording sites (their Fig. 3 D), some of which can be seen to be ∼1. Thus, we believe that a full analysis of maximum MI scores in these studies may lead to different conclusions regarding the association of voltage and calcium signals during VF.

Furthermore, due to the lack of information provided in previous studies (3–5) regarding essential MI parameters (decimation factor and number of bins), direct comparison of MI statistics with our findings proved problematic. However, we show in Fig. S1 that the relative differences in MI scores (between electrical and optical signals) were not sensitive across typical ranges of such parameters; thus, they do not affect the conclusions drawn here regarding the effect of photon scattering upon MI scores. Finally, in contrast to other studies (3,5), we focus here solely on the use of MI as the preferred metric for assessment of dissociation between voltage and calcium signals. We chose not to assess dominant frequency maps or analyze spatial dissociation of propagation wavefronts, as we believe that MI provides the most robust and accurate means of directly investigating the role of photon scattering in optical signal distortion during VF.

Alternative causes of apparent dissociation

Although the inclusion of the effects of photon scattering could not fully explain the previously reported low MI values in optical dual voltage-calcium signals (3,4), other factors may contribute further to the dissociation of the two signals. For example, previous experimental studies have highlighted uncertainty in the alignment of recording sites of V_opt and Ca_opt signals, stating potential uncertainties to be up to ±1 mm separation (3,4). Given the high spatial complexity of VF, it is thought that the impact of measuring V_opt and Ca_opt from different spatial locations will significantly reduce MI scores. This was demonstrated to be the case in Fig. 7, although the MI score during rapid pacing showed little change with measurement uncertainty due to the high coherence of the wavefront. Thus, accounting for the effects of measurement alignment uncertainties, in combination with the effects of photon scattering, reduces MI scores further during VF.

Finally, additional factors, not considered explicitly here, may also accentuate the apparent dissociation seen in optical voltage-calcium signals: for example, pixel resolution, pixel averaging, signal noise, among others. It could be possible that accounting for such factors, which is not possible in this model, may further act to artificially increase the witnessed dissociation between fluorescent voltage-calcium signals, which could bring the MI statistics more in line with previous experimentally measured values (3–5).

Conclusions

In this study, we demonstrated that photon scattering can significantly contribute to experimentally measured dissociation between fluorescent voltage and calcium signals, and thus represents an important consideration in multiparameter optical mapping experiments. This measurement error increased as a function of wavelength separation and degree of misalignment between measurement locations. Furthermore, the affinity of the calcium fluorescent dyes was also seen to play a role in the dissociation of voltage-calcium signals, with dissociation increasing in the case of the highly nonlinear HA dyes, most significantly during rapid pacing, due to the attenuation of alternans. However, photon scattering does not fully account for the experimentally observed dissociation between fluorescent voltage and calcium signals during VF—our simulations do not result in the complete V_m/Ca dissociation reported previously (3,4). It therefore remains to be investigated whether the high level of experimentally measured dissociation can be accounted for by fully incorporating other factors (such as low signal/noise ratio, etc.), or whether experimental observations are in fact caused by uncoupling of voltage and calcium transients at the cellular level during VF.