Substrate Viscosity Enhances Correlation in Epithelial Sheet Movement

Abstract

The movement of the epithelium plays vital roles in the development and renewal of complex tissues, from the separation of tissues in the early embryo, to turnover in the homeostasis of the gastrointestinal mucosa. Yet, despite its importance, a clear interpretation of the mechanism for collective motion in epithelial sheets remains elusive. This interpretation is prohibited by the lack of understanding of the relationship between motion and cell-cell contact, and their mediation by the mechanical properties of the underlying substrate. To better mimic physiological substrates that have inherent viscosity, we probe this relationship using polydimethylsiloxane, a substrate whose mechanical properties can be tuned from predominantly elastic to viscous by altering its cross-linking content. We therefore characterize the comparative spatiotemporal correlations in cell velocity during the movement of an epithelial monolayer as a function of the viscoelasticity of the substrate. Our results show that high correlation in cell velocity is achieved when the substrate G″(ω) is ∼0.4 × G′(ω). This correlation is driven by a balance between cell-cell contact and the adhesion and contraction of the extracellular matrix. For G″(ω) > G′(ω), this balance shifts, and contraction of the tissue drives the substrate to flow, further elevating the correlation in movement.

Introduction

Epithelial sheet motion is involved in fundamental physiological processes such as the development of embryonic tissue (1,2), the movement of cells along mucosal surfaces (3–5), and in wound response (6). Each cell is motile as an individual, and when tightly packed in a group, the cells migrate in synchrony, maintaining their cell-cell contacts. The biochemical factors that regulate this synchronous movement have been investigated extensively (7,8). However, the mechanical influences that guide coordinated sheet motion are less certain.

Tension is generated between cells in a sheet by actomyosin contractility at E-cadherin-based cell-cell junctions (9,10). Tension also exists between cells and the extracellular matrix (ECM) through integrin-based adhesions, and is mediated by the mechanical properties of the substrate itself (11,12). Furthermore, the tension that exists between cells is correlated to the tension between cells and the ECM (13). Therefore, modulation of the tension at the cell-ECM interface, through the mechanical properties of the substrate, will alter cell-cell contact. For mechanically rigid substrates, enhanced integrin-mediated adhesion encourages the breaking of cell-cell contacts (14). For mechanically compliant substrates, cell-cell contacts are retained, and cell migration leads to a global balance of tensile stress (15,16). However, these substrates, although compliant, are essentially purely elastic, unlike many physiological substrates. Thus, the influence of cell-cell and cell-ECM tension on the movement of an epithelial sheet bound to a viscous substrate is less understood.

It has been implied that turnover and flow of the basal lamina, the in vivo substrate for the epithelium, plays a role in the translocation of the epithelium itself (4). The basal lamina is a thin, fibrous layer of protein which separates the epithelium from the lamina propria, the loose connective tissue underneath. It is secreted by the cells as they continuously renew their ECM (17,18). The renewal of the ECM suggests that the basal lamina is dynamic, although there is little evidence supporting its in vivo mobility (19). Thus, translocation due to the turnover of the basal lamina remains uncertain. However, translocation of a cell sheet may be possible, depending upon the mechanical properties of the basal lamina, in particular its viscosity, or its propensity to flow. To date, in vivo rheological measurements of the basal lamina do not exist. We are limited to rheological studies of in vitro networks and analogs of basal lamina (Table 1). These networks contain some of the components that are present in basal lamina, and are highly viscoelastic. By extension, we presume the basal lamina itself to be viscoelastic. As a viscoelastic material, there are timescales over which applied stresses induce the material to flow.

Table 1.

Mechanical properties of epithelial cells and matrix substitutes

Tissue	Constituent or analog	G′(Pa)	G″(Pa)
Epithelial	Kidney epithelial cells (10 rad/s) (27)	72.1	38.2
	Bronchial epithelial cells (10−1 Hz) (26)	450	150
	Alveolar epithelial cells (10−1 Hz) (26)	450	150
	Mammary epithelial cells (indentation) (28)	167 (E∗)
Basal lamina	Collagen, 2.3 mg/ml (10−1 rad/s) (29)	30	4.0
	Collagen, 1.2 mg/ml (1 Hz) (30)	16	4.0
	Collagen, 1.2 mg/ml + 50 μg/mL fibronectin† (1 Hz) (30)	12.9	4.0
	Collagen, 1.2 mg/ml + 50 μg/ml laminin† (1 Hz) (30)	12.9	4.0
	Matrigel (10−1 rad/s)	170.8	21.0
Lamina propria	Fibroblasts (10−2 Hz) (25)	150	50
	Fibroblasts (50 Hz) (31)	1200–2100	900–2000
Other	Smooth muscle airway cells (10−2 Hz) (24)	1000	200

G′ and G″ for cells and biopolymer gels used as analogs to the extracellular matrix.

^∗E refers to the elastic modulus.

^†Addition of fibronectin and laminin formed aggregates in the collagen gel, and were not homogeneously distributed.

We use fluorescence microscopy and computational image analysis to study the dynamics of epithelial sheet movement as a function of the mechanical properties of the substrate. We use polydimethylsiloxane (PDMS) as the cell substrate due to its viscoelasticity. Its mechanical properties can be varied from that of a “liquid-like” gel, to a “solid-like” elastomer, through its curing agent content. As the curing agent is varied, we relate the elastic modulus, G′(ω) and the viscous modulus G″(ω), to the spatial and temporal correlations in cell migration velocity.

In this study, we find that correlation in cell migration velocity is achieved when substrate G″(ω) is equal to ∼0.4 × G′(ω). At this rheology, correlation in motion is conferred by a balance among cell-cell contact and the contraction and remodeling of the ECM. We further show that in a substrate that is not only compliant but viscous, cell movement does not occur through cell migration per se, but rather through a cooperative contraction of the tissue en masse. As the tissue contracts, it is tightly bound to the ECM, and therefore induces a flow in the substrate. As a consequence, the motion of cells on a flowing substrate is further correlated. We therefore propose that correlated movement of a dense epithelial sheet on a viscous surface depends critically on cell-cell contact, and that the viscosity of the ECM facilitates the displacement of the sheet by relaxing passively.

Methods

Substrate composition

Polydimethylsiloxane (PDMS; Sylgard 184 silicone elastomer base; Dow Corning, Midland, MI) is spun onto a 20-mm, Mattek dish (Mattek, Ashland, MA). Before spinning, 0.1-μm rhodamine carboxylated spheres (Invitrogen, Carlsbad, CA) were mixed and degassed with the PDMS polymer solution which contains cross-linker (curing agent) in 0.00625–0.1 cross-linker/polymer weight ratio. The PDMS was then baked at 65°C for 2 h. To calculate G′(ω) and G″(ω), a constant, 1% strain was applied to the PDMS under a cone (2°) and plate rheometer (Advanced Rheometer 2000; TA Instruments, New Castle, DE), for a frequency sweep, ω, between 100 and 0.1 rad/s. The surface of the PDMS is adsorbed with 200 μg/ml fibronectin (Sigma, St. Louis, MO) nonspecifically. This is done as the wettability of the PDMS increases at low cross-linker content (see Fig. S1 in the Supporting Material).

Cell culture

Mouse mammary epithelial cells (CLS-1; American Type Culture Collection, Manassas, VA) were added at >2000 cells/mm² (in DMEM, 10% FBS, 1% pen/strep) to adhere and form a dense monolayer on the coated surface. This is done because the cells do not grow and spread from low densities to form a confluent monolayer on highly viscous substrates (see Fig. S2). To modulate E-cadherin in cell-cell contacts, 50–100 μg/ml of anti-E-cadherin antibody (Invitrogen) was added at seeding.

Image acquisition and analysis

Images were taken at 25× every 1 or 5 min for up to 8 h on an Axiovert 200M/Ultraview Microscope (Carl Zeiss, Jena, Germany, and Perkin-Elmer, Waltham, MA), whereas the cells were maintained at 37°C and 5% CO₂. The cell nuclei were stained by incubating the cells in 1.3 μM SYTO green nuclear dye (Invitrogen) for 15 min and subsequently washed with media. To image the ECM, fibronectin was stained by incubation with 40 μg/ml FITC pig skin gelatin (Invitrogen) at 37°C for 1 h before cell seeding, and subsequently washed with media. MATLAB particle tracking software (http://physics.georgetown.edu/matlab) along with custom-written routines (The MathWorks, Natick, MA), and Imaris (Bitplane, Zurich, Switzerland) were used to track the motion of both cells and PDMS embedded beads. These routines identify the peak fluorescent intensity of the nuclei and the beads for each frame. Trajectories were then assembled to minimize the total squared displacement from frame to frame (20). The tracking of beads may include bead aggregates, as 0.1-μm beads are below the diffraction limit.

Metrics for analyzing cell motion

Migration dynamics are quantified by the mean-squared displacement (MSD) of their movement. A difference in position is taken over an elapsed time t, between the initial position of a cell, ${\overrightarrow{r}}_i\left(0\right)$, and the cell displacement over the elapsed time, ${\overrightarrow{r}}_i\left(t\right)$. Both the magnitude, and the time-scaling coefficient, α, are used to characterize the single-cell, ensemble-averaged dynamics:

$$MSD\left(t\right)=\langle \frac{1}{N}\sum _{i=1}^N{\left({\overrightarrow{r}}_i\left(0\right)-{\overrightarrow{r}}_i\left(t\right)\right)}^2\rangle \sim t^{\alpha }.$$ (1)

The two-point velocity correlation, Cvv(r,τ) (see Eq. 2 below), characterizes the mutual spatial (r, distance between two cells in a pair) and temporal (τ, elapsed time between frames) correlations of movement. It is a pairwise calculation performed in the direction that joins a pair of cells at positions ${\overrightarrow{r}}_i$ and ${\overrightarrow{r}}_j$.

$$C_{\text{vv}}\left(r,\tau \right)=\langle \Delta v_1\left({\overrightarrow{r}}_i,\tau \right)\Delta v_2\left({\overrightarrow{r}}_j,\tau \right)\rangle -\langle \Delta v_1\left({\overrightarrow{r}}_i,\tau \right)\Delta v_2\left({\overrightarrow{r}}_j,\tau \right)\rangle .$$ (2)

The Δv refers to the difference in velocity over the elapsed time, τ for a single cell. The subscripts refer to cell 1 and cell 2 in a pair, separated by r.

The radial distribution function (21), g(r) (see Eq. 3 below) relates the positional organization of cells within the monolayer. We compute the ensemble average for all cells in a 25× field of view with periodic boundary conditions, and correct for decreased intensity at the edges:

$$g\left(r\right)=\frac{1}{\langle n\rangle }\langle \sum _{i\ne j}\delta \left(\left|{\overrightarrow{r}}_i-{\overrightarrow{r}}_j\right|-r\right)\rangle .$$ (3)

The correlation is a delta function (δ) summed over each pair of cells r_i and r_j. The value 〈n〉 is the average number density. This function is proportional to the probability of finding a cell at a radius r away from another reference cell. The fluctuations in density at “large r” (arbitrarily defined at r > 2d, where d is a nuclear diameter) are fit with an exponentially damped oscillatory function F(r) similar to (22)

$$F\left(r\right)\sim \frac{C}{r}\exp \left(-r/\xi \right)\cos \left[K_0\left(r-r_0\right)\right],$$ (4)

where ξ is the characteristic lengthscale of spatial correlation. The coefficients C and K₀ correspond to the amplitude and period of oscillation, respectively.

Metrics for analyzing ECM dynamics

Particle image velocimetry is implemented with the software MATLAB (http://www.oceanwave.jp/softwares/mpiv/). Particle image velocimetry was used on fluorescence images of FITC collagen bound to PDMS and to fluorescent beads embedded inside the PDMS (where the density was high). The vector fields were interpolated using the Kriging method.

The variance in fluorescence intensity of the collagen/fibronectin (i.e., ECM) adsorbed on the surface of the PDMS is given by V:

$$V=\frac{1}{h\times w}\sum _h\sum _w{\left(I\left(x,y\right)-\mu \right)}^2.$$ (5)

The variance is taken over a window of width w, and height h. The difference between the intensity value I at position x,y is compared with the mean over this window, μ. The window for all experiments is for x = y = 10 pixels. This is calculated in ImageJ (National Institutes of Health, Bethesda, MD) and Imaris (Bitplane).

Results

Cell movement induces substrate flow

The mechanical properties of PDMS vary with the cross-linker content. The magnitude of the elastic and viscous moduli, G′(ω) and G″(ω) change, as does their dependence on applied frequency, ω (Fig. 1 A). For low cross-linker content, PDMS is compliant. Thus, the magnitudes of G′(ω) and G″(ω) are low. With increasing cross-linker content, the moduli increase and the PDMS becomes stiffer. However, G′(ω) and G″(ω) also change in proportion to each other (Fig. 1 B). At low cross-linker content, G″(ω) dominates G′(ω), and the PDMS is predominantly viscous. At high cross-linker content, the opposite is true, and the material is predominantly elastic. Likewise, with changes in cross-linker content, the PDMS has a different frequency response (ω^γ) (Fig. 1 C). G′(ω), for example, is relatively insensitive to changes in frequency above a cross-linker/polymer ratio (ζ) of 0.0175 (γ < 0.1). At ζ = 0.0125, the frequency response, as well as the magnitudes of G′(ω) and G″(ω), are roughly equivalent (and similar to that of Matrigel (BD Biosciences, Franklin Lakes, NJ), Fig. 1 D, as shown by η, the ratio of G″/G′). Thus, the mechanical properties of PDMS are highly variable, and may be predominantly elastic (E), equivalently elastic and viscous (VE), or predominantly viscous (V). Here, we summarize the characteristic movement of dense cell sheets on fibronectin-coated PDMS in each of these three regimes (henceforth referred to as E, VE, and V, respectively).

Figure 1.

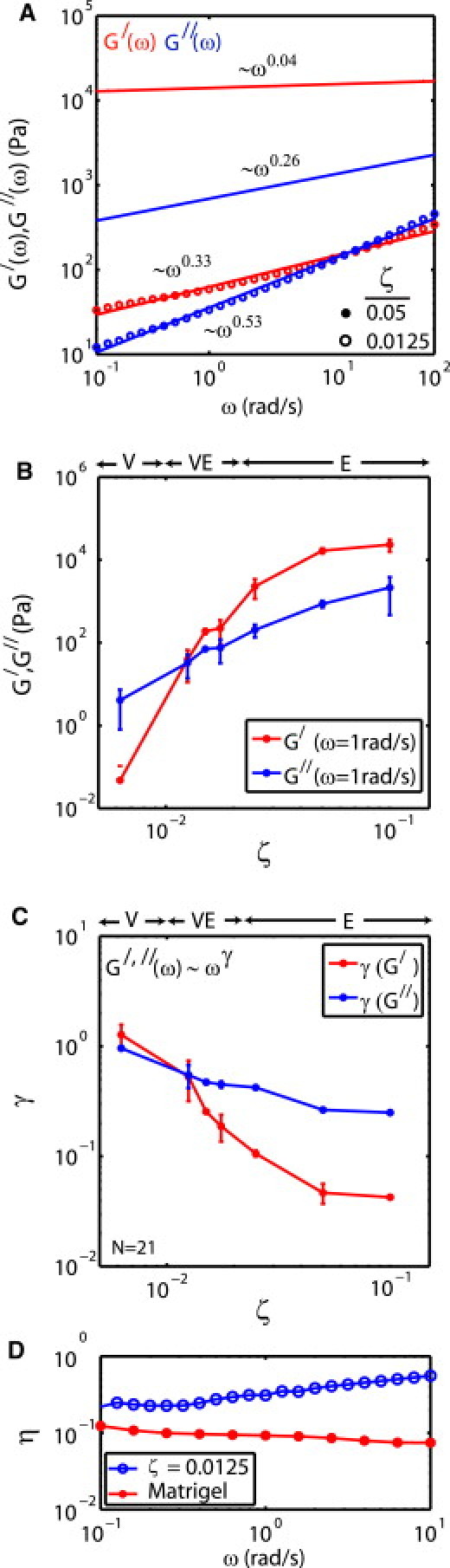
PDMS viscoelasticity varies with cross-linker content. (A) G′(ω) and G″(ω) of PDMS with ζ = 0.05 (solid circle) and 0.0125 (open circle). The dependence on frequency, ω^γ is shown adjacent to each plot. (B) G′(ω) and G″(ω) as a function of ζ (at ω = 1 rad/s). (C) The exponent, γ, as a function of ζ. (D) Loss tangent, η = G″(ω)/G′(ω) of PDMS (ζ = 0.0125) and Matrigel (BD Biosciences).

The epithelial sheet is imaged through the staining of cell nuclei (Fig. 2 A). Tracking of the nuclei show that cells migrate in patterns, as indicated by the mutual direction and magnitude of adjacent vectors in a displacement field (Fig. 2 B). Depending on the stiffness of their underlying substrate, cell traction displaces embedded beads within it (Fig. 2 C).

Figure 2.

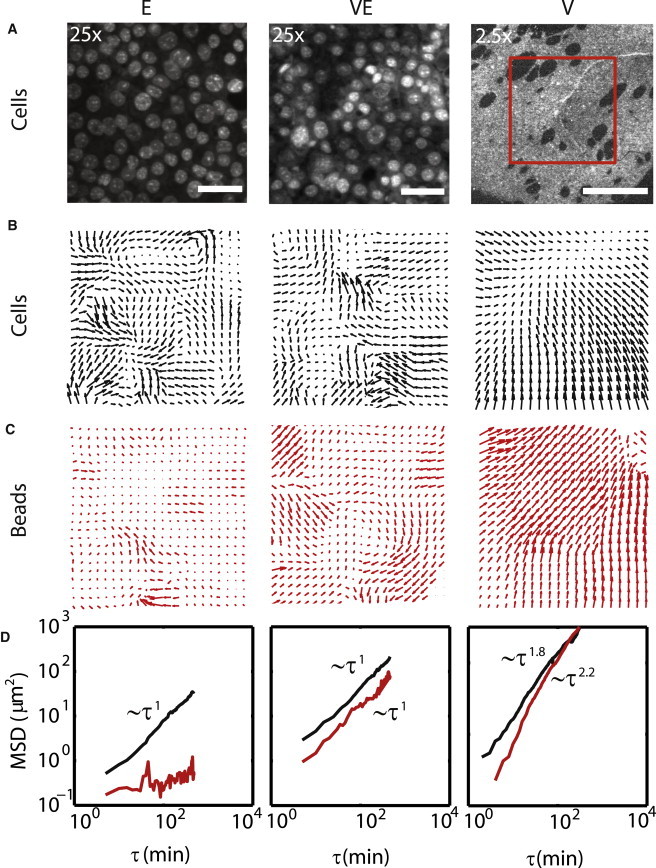
Cell movement induces substrate flow. (A) Stained nuclei of cells in an epithelial sheet adhered to PDMS in regimes E, VE, and V. Scale bars in Regime E and VE are 50 μm. Scale bar in V is 1 mm. (B) The displacement of the cells in panel A over a time period of 25 min (scaled 1.5×). (C) The displacement of beads embedded in the PDMS over the same time period. (D) The mean-squared displacement (MSD) of cells and beads over all time (MSD for cells in regime V are for a different sample than that in A–C).

The lower the cross-linking content, the greater the rate of cell movement (Fig. 2 D). With greater cell movement, the greater the displacement of the underlying substrate. In regime E, there is no macroscopic displacement of the substrate, and cell migration is slow (see Movie S1 in the Supporting Material). In regime VE, the MSD is elevated in contrast to regime E, and there is significant traction-induced displacement of the substrate (see Movie S2). In regime V, the MSD for cells is further elevated in magnitude in contrast to regime VE and E, and highly persistent in time, as the initially fully planar monolayer begins to aggregate (see Movie S3 a). The movement of the cell monolayer induces a persistent flow in the substrate.

Substrate flow enhances correlated cell motion

We quantify how correlated cell migration velocity varies with G′(ω) and G″(ω) of the substrate, and with cell-cell contact. For this, we define an ensemble-averaged pairwise correlation function in velocity, C_vv (Eq. 2), which varies with both r, the distance between cells, and τ, the elapsed time between two images. This is applied to the movement of cells up to 8 h.

For a monolayer on substrates in regime E, C_vv is elevated for only small r and decays quickly in τ (Fig. 3 A). With the addition of antibody against E-cadherin to block cell-cell contact, correlations are similar, with the same pattern of small r and small τ elevation (Fig. 3 A, inset). In regime VE, C_vv is elevated for longer r, to >100 μm (Fig. 3 B). The addition of antibody against E-cadherin in this case reduces the correlation (Fig. 3 B, inset). Finally, in regime V, the epithelial sheet begins to contract macroscopically (Fig. 3 C). In this case, there is little movement relative to the substrate, and nearly all motion is due to contraction of cells and substrate, which locally resembles sheet sliding (Movie S3 b).

Figure 3.

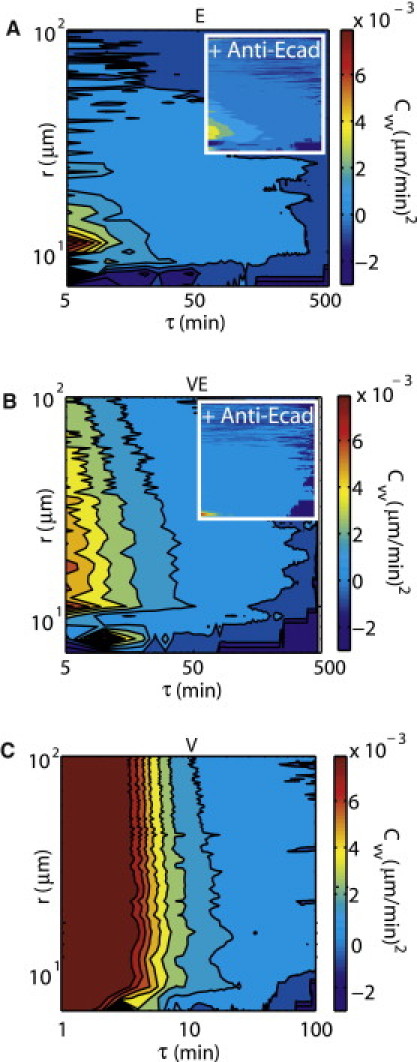
Substrate viscosity increases the range of the correlation in cell velocity C_vv(r, τ). Color map of C_vv in both elapsed time, τ, and separation distance, r for regimes (A) E, (B) VE, and (C) V. C_vv with (A, inset) 100 μg or (B, inset) 200 μg E-cadherin, on PDMS of the same stiffness.

In each of these three regimes of substrate viscoelasticity, the correlated velocity decays as a power law in separation distance, C_vv ∼ r^−α″ (Fig. 4 A). This decay, as indicated by the power-law scaling coefficient α″, is greater for large values of ζ. Taking all measured values of the viscoelastic moduli, G′(ω) and G″(ω) for the corresponding values of ζ, and normalizing G′(ω)/G″(ω), we plot 〈α″〉 (Fig. 4 B). For regime E (G′(ω)/G″(ω) >> 1), cell-cell correlations in velocity are short-ranged, with 〈α″〉 = 1.07 ± 0.12. For regime V (G′(ω)/G″(ω) < 1), the velocity correlation increases as 〈α″〉 = 0.34 ± 0.16, and the epithelial monolayer aggregates. The point where the system transitions between high and low correlation, however, occurs in regime VE, where (G′(ω)/G″(ω) = 1–2.5). In this regime, the velocity correlation is both long-ranged and stable, with 〈α″〉 = 0.81 ± 0.20. In this regime, the sheet does not aggregate. Thus, the scaling coefficient for this power law maps out a sharp transition in the spatial range of correlation in cell movement. This regime corresponds to a G(ω) of 27–100 Pa (Fig. 4 B, inset).

Figure 4.

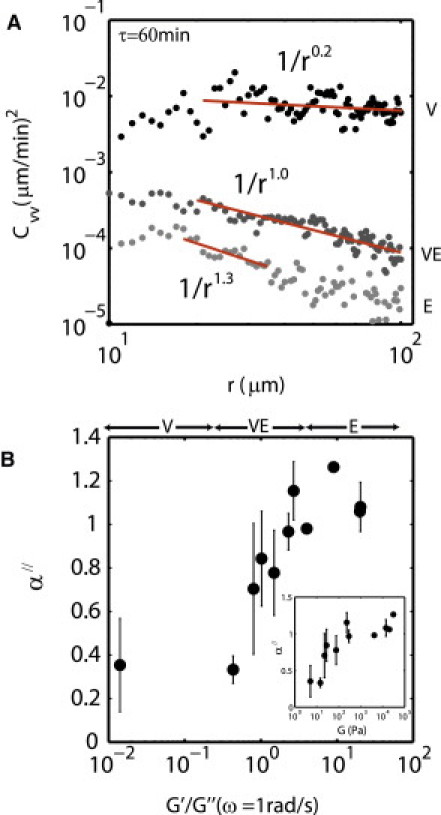
Correlated velocity transitions at G″(ω) ≈ 0.4 × G′(ω). (A) C_vv taken at 1 h for a range of G (ω), fit to the power law, ∼r^−α″. (B) The power-law scaling coefficient, α″ measured for ζ, and plotted against G′(ω)/G″(ω), where ω = 1 rad/s. The same data plotted with the x axis as bulk shear modulus, G (ω) (B, inset).

The blocking of cell-cell contact differentially modulates the correlation in velocity. When E-cadherin is blocked in regime E, α″ drops to 0.90 (p < 0.2686, N = 4, N_Ab = 1). In contrast, in regime VE, α″ rises to 1.24 (p < 0.01, N = 10, N_Ab = 1). Thus, in this regime, correlated motion is reduced. Cells are highly compacted and scatter, but substrate deformation is nominal (see Fig. S3 and Movie S7).

Cells are disordered on a viscous substrate

The radial distribution function, g(r) (Eq. 3), is used in this study to describe the variation in density of the epithelial sheet. Specifically, the g(r) represents the probability of finding a pair of cells separated by a distance r, on average. At short r, the g(r) must be zero, because two cells cannot occupy the same space. As r increases, the g(r) will first peak at the average nearest-neighbor spacing between cells. At larger r, g(r) will peak at the next nearest neighbors. The magnitude of the peaks, as well as how they decay with r, describe the level of positional order in the density of the epithelial sheet (see Fig. S4).

In regime E, the g(r) exhibits regularly spaced peaks at successive cell spacings, which remain pronounced for up to two cell diameters (Fig. 5, A and B). Conversely, in regime VE, cell density is irregular, and correlation is dampened to only a single cell diameter (Fig. 5, C and D). When fit to Eq. 4 for the characteristic amplitude C, we find C reaches a maximum of 0.87 ± 0.64 μm, at >2d (Fig. 5 E) for regime E. For regime VE, C is 0.21 ± 0.26 μm (p = 0.056).

Figure 5.

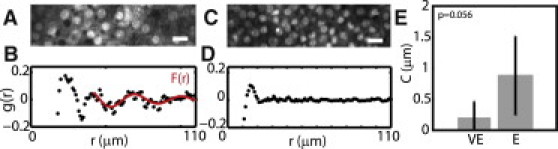
Cells are disordered on a viscous substrate. (A) Image of cells in regime E. Scale bar is 20 μm. (B) The value g(r) corresponding to cells in panel A. (C) Image of cells in regime VE. (D) The value g(r) of cells in panel C. (E) Mean values of the amplitude of oscillations in F(r) for cells in regime VE and E.

ECM remodeling is concomitant with substrate flow

To explore the mechanism by which correlation in motion is conferred, given that it is a function of the mechanical properties of the substrate, we image the ECM that forms the interface between the epithelial monolayer and the substrate. As the medium for how the epithelial sheet interacts with the substrate, we expect visual evidence of collective behavior to manifest in the dynamics of adhesion and traction.

The ECM that forms the interface between the epithelial monolayer and the PDMS surface is nonspecifically adsorbed fibronectin, which is imaged by its complementation with FITC collagen. Cell migration differentially remodels this protein with the mechanical properties of the substrate, as can be seen by the changes in the spatial and temporal distribution of collagen on the surface. In regime E, remodeling of the ECM is minimal (Fig. 6 A, left, and see Movie S4). There are neither significant changes in the spatial or temporal distribution of fluorescence (Fig. 6 A, middle). For regime VE, however, remodeling of the ECM is extensive, and displays highly dynamic behavior. The fluorescence becomes spatially nonuniform (Fig. 6 B, left) and the ECM displaces locally, as shown by the mutual direction and magnitude of the vector fields applied to the fluorescence images (Fig. 6 B, middle). The mechanical properties that characterize this regime are critical, as we approximate that for ζ > 0.0125, the sheet does not aggregate (Fig. 6 B, and see Movie S5). For ζ > 0.0125, there is remodeling of the ECM to the point of complete disassembly. The ECM is stretched, deformed, or degraded over the course of ∼12 h (Fig. 6 C; and see Movie S6).

Figure 6.

ECM remodeling is concomitant with substrate flow. (Left column) FITC collagen labels surface fibronectin, for regimes (A) E; (B) VE (stable); and (C) VE (unstable). Cells remodel the ECM with time, but are unseen. Scale bar is 100 μm. Three images are overlayed, separated by 5 min (red, green, and blue). (Middle column) Displacement of ECM due to cell activity at the surface (zoomed in from the red square in the left column). (Right column) Overlay of the vector fields of ECM displacement with the bead displacement (zoomed in from the red box in the middle column).

Despite the reorganization of the ECM on the surface, there is close coupling between the traction-induced displacement of the ECM and the deformations induced in the underlying substrate. For noncompliant PDMS, there is no traction-induced reorganization or displacement of the ECM, and likewise, no macroscopic displacement of the substrate (Fig. 6 A, right). However, when the PDMS is compliant, the local displacement of the ECM is accompanied by local displacement of the substrate (Fig. 6, B and C, right). Thus, the displacements are similar in direction and magnitude. It should be noted however, that the magnitude of the bead deflection is somewhat less than that for the ECM. We therefore presume there to be a degree of “slip” between the nonspecific adsorption of the ECM, and the underlying substrate.

The remodeling of the ECM after cell seeding and adhesion to a substrate of regime VE is varied, distinct both dynamically and in their influence on the bulk substrate. There are two separate modes, the first of which consists of remodeling of collagen that originates at a central point and spreads radially outwards on the timescale of minutes (Fig. 7 A). Initially homogeneously distributed, the ECM now persists as permanently remodeled for hours, with an overall reduction in fluorescence (Fig. 7 B). Second, the contraction of the surface by cells results in the spatial sequestering of collagen (Fig. 7 C). Also initially homogeneously distributed, the ECM is contracted radially inwards (Fig. 7 D). The rate of remodeling is measured by the variance in the fluorescence intensity, V (Eq. 5). This value is taken for every frame, and plotted for both the waves and for contractions over time (Fig. 7 E). To quantify the rate, we take the slope of the linear regime, m, which occurs at short times (Fig. 7 F). The slope of the outward waves is 6.51 ± 3.36 a.u. (N = 4). The slope of the contractions is 1.80 ± 1.44 a.u. (N = 3, p = 0.062; see Fig. 7 G). The rate of the contraction (Fig. 7 I) is more consistent with the displacement of the embedded beads beneath, than is the wave of fluorescence (Fig. 7 H).

Figure 7.

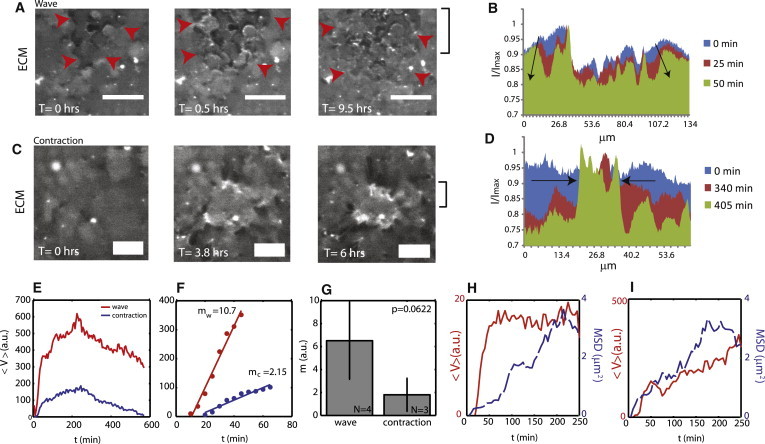
Remodeling of ECM at critical stiffness depends on contraction of the surface. (A) FITC-ECM fluorescence that radiates outward from a central point. Scale bar is 50 μm. Red arrows point to the wave-front. (B) An average and normalized intensity across the x axis of the fluorescence image (y coordinates for average shown in last panel of A). FITC-ECM fluorescence intensity decreases preferentially at the periphery over time. (Arrows) Direction of propagation. (C) Inward sequestering of ECM. Scale bar is 25 μm. (D) The fluorescence begins as uniform across the x axis, and then peaks in a central region. (E) The calculated variance, 〈V〉, in fluorescence intensity over time for both waves and contractions (red, wave; blue, contraction). (F) Short time, linear behavior of the curves in panel E. (G) The mean slopes (a.u.) show a much faster remodeling for what proceeds as a wave, above what proceeds as contraction (p = 0.0622). (H) Fluorescence variance and bead MSD for wave. (I) Fluorescence variance and bead MSD for contraction.

Discussion

We use fluorescence microscopy and computational image analysis to study the dynamics of epithelial sheet movement as a function of the viscoelasticity of the substrate to which they adhere. We find that fast, correlated motion manifests at G″(ω) ≈ 0.4 × G′(ω). At this rheology, the epithelial sheet adheres and contracts the ECM to locally displace the substrate underneath. The correlation in movement and contraction are related, and depend upon cell-cell contact. When G″(ω) > G′(ω), contraction drives the substrate to flow, resulting in fast and correlated movement of cells. This movement, however, is not migration per se, but rather a cooperative contraction of the entire epithelial sheet, which is facilitated by the viscosity of the substrate.

Altering the cross-linking content of PDMS changes both the mechanical properties of the bulk material, as well as the wettability of the surface. Therefore, as changing the cross-linker content is not altering a single variable, PDMS with low cross-linking content has been considered undesirable as a cell substrate. However, the inherent viscosity in PDMS makes it desirable as an analog to basal lamina, the in vivo substrate for epithelial sheets. Therefore, to exploit the unique mechanical properties of the bulk PDMS, we address the changes in the surface in an attempt to rule it out as a governing parameter in the migration response. Specifically, the wettability of the surface increases at low cross-linking content, which in turn, alters the ability for the ECM to stick to it. Thus, we image the ECM that binds the surface, and correlate it with the movement of embedded beads beneath the surface. We presume the coupling between the ECM and the surface to be problematic only to the extent that it is a weak mechanical link between cells and substrate. Although we do find that there is “slip” between the ECM and the substrate (likely facilitating the remodeling of the ECM), the ECM and PDMS surface are still mechanically well-coupled.

The mechanical properties of PDMS are also not univariate. Depending on the cross-linker content, it may be either predominantly elastic, viscous, or equivalently elastic and viscous. However, we find that the migration of cells is differentially coordinated in correspondence with these regimes. Using a two-point correlation function in migration velocity, we see that for the elastic-dominated regime (ζ ≥ 0.0125), correlated movement is shorter-ranged than in the viscoelastic regime, when G′(ω) and G″(ω) are comparable in magnitude (ζ = 0.0125). This is simply explained by the stiffness of the substrate. On stiff substrates that yield no macroscopic deformation by the traction of migrating cells, movement is relative to the substrate. However, when the substrate can be deformed significantly by traction (ζ < 0.0167), movement is a composite between migration relative to the substrate, and the local displacement of the substrate itself. Thus, movement in this sense is unconventional as there are now two separate reference frames. Consequently, local displacement of the substrate enhances the correlation for cells within that local vicinity. This is how we attribute the elevated correlation in movement at ζ = 0.0125. Furthermore, when the substrate is not only compliant but viscous (ζ ≤ 0.0125), the substrate flows, and the correlation becomes long-ranged.

The correlation in this “critical” regime (ζ = 0.0125) is mediated by a balance of cell-cell contact and the adhesion and contraction of the ECM. With the addition of antibody against E-cadherin to block cell-cell contact, the correlation in motion is reduced as cells scatter, and substrate traction is reduced. Furthermore, quantitative analysis of the remodeling of the ECM characteristic to this regime reveals multiple dynamic phenomena. Waves of decreased fluorescence intensity emanate outward quickly, on the order of minutes, whereas contraction of the surface, as indicated by the inward sequestering of fluorescence, is on the order of hours. Correlating the dynamics of this remodeling with deformation into the bulk indicates that only the contraction of the surface occurs in step with the displacement of the substrate-embedded beads.

Tension is generated at cell-cell junctions through actomyosin contractility (9,10). Similarly, tension is generated between the cell and the ECM, and is dependent upon the mechanical properties of the substrate (11,12). Furthermore, cell-cell and cell-ECM tension are related, as illustrated by the reduction in substrate contraction with blocked cell-cell contact. Thus, we propose that the mechanical properties of the “critical” regime occurs at a balance between cell-cell and cell-ECM tension. The sheet neither fully contracts en masse as occurs for G″(ω) > G′(ω), nor is migration independent of contraction of the surface, as occurs for G″ < 0.4 × G′. This intermediate regime is further reflected in the variation in cell density. Although not aggregated, there is disorder in the sheet, as indicated by the g(r) and the magnitude of peaks in F(r). The cells are compacted, with heterogeneity in the shape of the nuclei. We take this as an indication of the onset of cell-cell contraction, which predominates in the viscous regime.

The importance of the relationship between G′(ω) and G″(ω) of the substrate may be underscored by their relationship in cells. For example, it has been shown that the loss tangent, η = G″/ G′, for adherent cells is relatively independent of frequency (below ≈10 Hz) and cell type, at a value of ∼0.3–0.4 (23–26). In our system, correlated behavior manifests in the vicinity of G′/G″ ≈ 2.5, or an η of 0.4. Furthermore, this ratio is also relatively conserved across a wide range of frequency. A relationship between the loss tangent in cells and the loss tangent in the substrate would imply that correlated movement of an epithelial sheet requires the mechanical response of cells to be similar to the mechanical response of the substrate to which they adhere. Thus far, this correspondence may be coincidental, as this ratio also corresponds to a stiffness at which cells can begin to significantly deform the substrate. As previously mentioned, substrate deformations that are sufficiently large as to displace cells locally, will increase the correlation of cells in that vicinity. Thus, an explicit relationship between the loss tangents as they pertain to correlated cell movement, would necessitate controlling G′(ω) or G″(ω) independently of each other. Nevertheless, this superficial correspondence may be indicative of an important relationship between cell and substrate mechanics in controlling the motion of cell sheets.

The cell-contact-dependent motion in vitro as enhanced by the viscosity of the substrate may be analogous to the mechanism used in the in vivo epithelia for achieving fast and uniform cell movement. The in vivo substrate, the basal lamina (or lamina propria), may be considered viscous over times relevant to the migration of an epithelial sheet. Thus the basal lamina may relax, and allow lateral tension as mediated by actomyosin contractility and cell-cell contact, to displace the cell sheet. Thus we believe that our in vitro system, whose critical behavior also occurs at a physiologically relevant rheology, illustrates the feasibility of correlated motion that is facilitated by cell-cell contact when coupled with a viscoelastic substrate.