What's in Gating Currents? Going Beyond the Voltage Sensor Movement

In their article, Lacroix et al. (1) analyzed how the voltage dependence of gating currents in Shaker K⁺ channels is affected by conditioning depolarization. The authors proposed that although a depolarization slows down the kinetics of the voltage sensors' (VS) movement, there is little change in its microscopic voltage dependence. The findings could be fundamental for our understanding of voltage-dependent gating. However, the data can be well accounted for by conclusions other than those drawn by the authors.

The voltage dependence of gating charge in depolarized channels is shifted by –50 to –90 mV, depending on the type of channel and on the specific experimental conditions. The shift occurs during slow inactivation (Na⁺ channels (2)), voltage-dependent inactivation (Ca²⁺ channels (3,4)), and C-type inactivation (Shaker K⁺ channels (5)). Lacroix et al. measured with high precision the gating charge movements in the nonconducting W434F mutant of Shaker K⁺ channel with deleted N-terminus and found only a minor (–10 mV) shift. They explained the much larger shifts seen in previous studies by suggesting that integration periods were too in order to fully capture the slow components of the gating current. The authors assert that the transition of the VS to its relaxed state, which is characterized by slowing of gating currents, is independent from C-type inactivation. According to the authors' view, all observed shifts result from the VS being in the relaxed state. Although not stated directly in the article, this implies that the opposite should also be true: that C-type inactivation is not associated with a change in the VS movement. Below, I present an analysis that rebuts this idea.

The authors' argument follows three major lines of experimental evidence:

• 1.Relaxation is present in transmembrane proteins that do not C-inactivate, and even in those that do not have a pore structure, which is thought to be required for C-type inactivation.
• 2.There is little change in the voltage dependence of gating charge in the nonconducting W434F mutant.
• 3.The drug 4-aminopyridine, which “uncouples” the VS and the pore, removes relaxation.

All of these can be explained by considering that relaxation is an integral part of the inactivation mechanism in the wild-type (WT) channels rather than an independent phenomenon.

Let's first take a quick look at the thermodynamics of coupling between the VS movement and the voltage-independent gating steps. Consider the minimal scheme $\text{A}\stackrel{V_{1/2},q}{\rightleftarrows }\text{B}\stackrel{E}{\rightleftarrows }C$. The microscopic half-transition voltage V_1/2 and the charge q describe equilibrium properties of the voltage-dependent step: ${\text{P}}_{\text{B}}={\text{P}}_{\text{A}}{e}^{q\left(V-V_{1/2}\right)/k_{\text{B}}T}$. The value E is the equilibrium constant of the linked voltage-independent step: ${\text{P}}_{\text{C}}=E{\text{P}}_{\text{B}}$.

The theoretical Q(V) here is: $Q\left(V\right)=q\left({\text{P}}_{\text{B}}+{\text{P}}_{\text{C}}\right)=q{\left(1+{\left(E+1\right)}^{-1}{e}^{q\left(V-V_{1/2}\right)/k_{\text{B}}T}\right)}^{-1}$. Therefore, the voltage at which half of the total charge moves is: $\tilde{V}=V_{1/2}-(k_{\text{B}}T/q)\ln \left(E+1\right)$.

In analogy to ligand-dependent gating, in which the observed binding affinity depends on the efficacy of transition(s) linked to the binding step (6), voltage dependence of gating currents reflects thermodynamics of both the VS movement and the linked transitions. In other words, even when gating charge is measured precisely and completely, so that Q_on equals Q_off, the position of the observed voltage dependence on the voltage axis does not describe only the microscopic properties of the VS. An observed shift of the macroscopic voltage dependence could result partially, or entirely, from changes in the efficacy of linked voltage-independent steps. Specifically, a decrease in the linkage/efficacy of the voltage-independent steps would be observed as a positive shift in the voltage dependence of the gating charge.

A voltage-independent transition might be linked to the VS movement according to the four-step coupling diagram (see Fig. 1 A, and see Brum and Rios (3) and Pizarro et al. (7)). It means that whether or not the voltage-independent transition had occurred, the VS is able to move. In this case, half of the total charge moves at voltage $\tilde{V}=V_{1/2}-(k_{\text{B}}T/q)\ln \left[\right(E+1)/(\alpha E+1\left)\right]\simeq V_{1/2}-(k_{\text{B}}T/q)\ln \left(E+1\right)$. Here, E is the efficacy of the voltage-independent step when the VS in the active (i.e., up) position, and αE (α <<< 1) is the efficacy when the VS is in the resting (i.e., down) position. The theoretical Q(V) relationship (red line in Fig. 1 B) defines the steady-state voltage dependence. This Q(V) corresponds to the condition in which all charge movement is accounted for and, thus, the ON and OFF charges are equal. It can be observed only when integration times are long compared with the kinetics of the slowest gating step. Such a Q(V) is also observed when the kinetics of the voltage-independent step(s) are fast, i.e., comparable with those of the VS movement.

Figure 1.

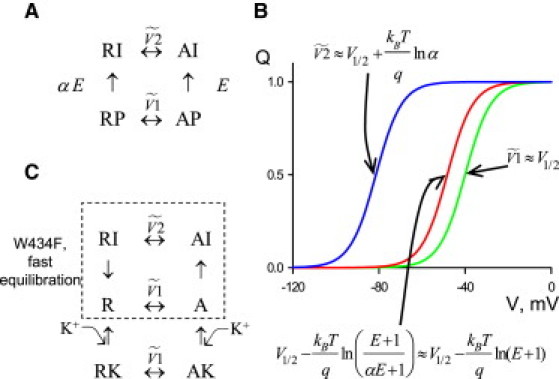
Voltage dependence of gating charge movement is affected by voltage-independent transitions. (A) A four-state diagram describing two coupled processes: movement of the voltage sensor (R↔A) and a voltage-independent (P↔I) step. (B) Voltage dependencies of gating charge movement according to the scheme in panel A. The curves were produced using V_1/2 = −40 mV, k_BT/q = 6 mV, E = 3, α = 0.001. (C) A six-state diagram describing the linkage between gating charge movement, inactivation, and ion occupancy of the pore. In the WT channel in ion-deprived solutions and in the W434F mutant, the inactivating steps are rapid. This causes the slow OFF gating currents and the Q(V) to be like that shown by the red line in panel B. In the WT with permeant ions, the reequilibration between noninactivated and inactivated states is slow. This causes fast OFF gating current transients and the hysteresis/interconversion between the $\widetilde{V1}$ (green line in panel B) and the $\widetilde{V2}$ (blue line in panel B) movements of the voltage sensor.

Relevant to this discussion, a Q(V) close to the theoretical relationship was indeed measured by Lacroix et al. in the W434F mutant. However, when the linked voltage-independent reequilibration is slow in comparison with integration times, the measured charge movement follows the microscopic voltage dependencies of the VS, which are affected by the voltage-independent transitions. The half-charge-movement voltage $\widetilde{V1}$ equals V_1/2 in channels that did not undergo the voltage-independent step, i.e., when gating currents are elicited by a brief depolarization from the negative holding potential (green line in Fig. 1 B). On the other hand, the half-charge-movement voltage after a prolonged depolarization is much more negative, $\widetilde{V2}=V_{1/2}+(k_{\text{B}}T)\ln \alpha$ (blue line in Fig. 1 B), because of a large energy difference between the up- and down-positions of the VS in affected channels. This hysteresis-like behavior was described previously for inactivation (2–5).

To sum up, the observed V_1/2 depends on relative kinetics (and extent of the linkage) between VS movement and those of the linked voltage-independent transition(s). Slow kinetic components of gating currents might reflect voltage-independent steps. When these components are much slower than the kinetics of the unlinked VS, the measured Q(V) is altered by conditioning depolarization. In the studies of the slow OFF gating, the voltage-independent transition of interest might be inactivation.

The experiments of Lacroix et al. clearly demonstrated that the Q(V) shift is much smaller for the nonconducting W434F mutant (8) in K⁺-deprived solutions than that previously described (5). This mutant does not conduct because of its very low open probability due to an alteration of the permeation pathway similar to that observed in C-type inactivated channels (9,10). It is not established whether the W434F is constitutively C-inactivated, or it is ultrafast inactivating. The fact that its ON gating charge is distributed around $\widetilde{V1}$ (8), rather than a much more negative $\widetilde{V2}$, appears to be contradictory to the idea that the W434F is constitutively C-inactivated (see relevant discussions in Olcese et al. (5) and Yang et al. (9)).

The contradiction might be apparent due to an imprecise usage of the term “C-type inactivation”. Strictly speaking, the term “C-type” was coined to describe inactivation of the entire Shaker K⁺ channel without the N-terminus (11). Current consensus is that the selectivity filter is the gate of C-type inactivation. Olcese et al. (5) proposed that, whereas the mutant permanently affects the permeation pathway, it has only a minor effect on the negative shift of the Q(V) due to inactivation. In other words, the W434F mutant might lock the gate in its closed position, but it does not have to lock the VS to the state characterized by the negative $\widetilde{V2}$. Having the inactivation gate in its closed state, whether it is there permanently or occurs ultrafast, would accelerate the equilibration between the up state of the VS and the closed state of the inactivation gate. That would accelerate the OFF gating component due to the voltage-independent step. For the reasons described above, the charge movement would be better characterized by the theoretical steady-state Q(V). A diagram in Fig. 1 C discussed below describes in greater detail the possibility when the inactivation gate is permanently closed.

Kinetics of the OFF gating currents depend on permeating cations and are altered by the W434F mutation. In the presence of permeating cations, the OFF gating currents in the WT are faster than those in the mutant (12,13). Because there is a third critical element, permeant cations, the minimal kinetic scheme should have at least six states (Fig. 1 C). A similar diagram has been proposed to explain the competition between extracellular metal ions and inactivation in skeletal muscle Ca²⁺ channels (7) and it elaborates on the five-state scheme of Chen et al. (12) for K⁺ channels. When the WT channel opens in the presence of permeant ions, it slowly transits to the inactivated state. In this case, the OFF currents are dominated by a fast kinetic component and the voltage dependence of gating currents is described by the hysteresis between the $\widetilde{V1}$ and $\widetilde{V2}$ movements of the VS. When permeant cations are absent, or in the nonpermeant W434F mutant, the voltage-independent transition is fast and the slow OFF gating component becomes faster and, hence, of a greater relative contribution. Because of this rapid equilibration, the voltage dependence of gating currents is described by the steady-state relationship. Importantly, permeant ions, or the W434F mutation, do not need to alter the half-charge-movement for the on-transition. It is worth mentioning that, in contrast to K⁺ channels, intracellular Ca²⁺ ions appear to accelerate the voltage-independent inactivating step in cardiac Ca²⁺ channels (14).

When voltage-independent step(s) are uncoupled from the VS movement (e.g., by applying the drug 4-aminopyridine), the reduction in the efficacy/linkage of voltage-independent step(s) would accelerate the OFF gating and shift positively the Q(V), as observed by Lacroix et al.

Finally, regardless of the mechanism linking voltage-independent steps to movement of the VS, the measured voltage dependence of gating charge movements is almost always apparent rather than true, as it reflects both microscopic properties of the VS and efficacy of linked step(s). The relaxation phenomena in the W434F mutant can be explained by its rapid C-type inactivation. Negative shifts of gating currents in the WT Shaker K⁺ and other channels are more observable because of the slower kinetics of inactivation linked to the VS movement.

The elegant and rigorous experiments of Lacroix et al. provide a valuable closer look into the kinetics and thermodynamics of the processes surrounding the VS movement. As is often the case, the results are subject to different interpretations, consideration of which inspires greater understanding.