Evidence for energy savings from aerial running in the Svalbard rock ptarmigan (Lagopus muta hyperborea)

Abstract

Svalbard rock ptarmigans were walked and run upon a treadmill and their energy expenditure measured using respirometry. The ptarmigan used three different gaits: a walking gait at slow speeds (less than or equal to 0.75 m s⁻¹), grounded running at intermediate speeds (0.75 m s⁻¹ < U < 1.67 m s⁻¹) and aerial running at high speeds (greater than or equal to 1.67 m s⁻¹). Changes of gait were associated with reductions in the gross cost of transport (COT; J kg⁻¹ m⁻¹), providing the first evidence for energy savings with gait change in a small crouched-postured vertebrate. In addition, for the first time (excluding humans) a decrease in absolute metabolic energy expenditure (rate of O₂ consumption) in aerial running when compared with grounded running was identified. The COT versus U curve varies between species and the COT was cheaper during aerial running than grounded running, posing the question of why grounded running should be used at all. Existing explanations (e.g. stability during running over rocky terrain) amount to just so stories with no current evidence to support them. It may be that grounded running is just an artefact of treadmill studies. Research investigating the speeds used by animals in the field is sorely needed.

1. Introduction

When trying to identify the selection pressures that have shaped the terrestrial locomotor system, the currency of most interest is arguably the metabolic cost of transport (COT): the mass-specific energy per unit distance or work (J kg⁻¹ m⁻¹). Variations in the COT with speed (U) are steeped in the optimality approach and may give an indication of evolutionary significant speeds. A similar approach in bird flight uses the theoretical U-shaped power curve (p_met in W kg⁻¹ plotted against U) to predict optimum speeds [1]. The term COT may be used to refer to three different (but related) values: COT (p_met/U), COT_net ([p_met−BMR]/U, where BMR is the basic metabolic rate) and E_met (the slope of the relationship between p_met and U). In practice, COT and COT_net may be used interchangeably when describing broad patterns of variation with U because, for a given U, COT_net simply has lower absolute values than COT. During terrestrial locomotion, as animals increase their speed over the ground, they change gait [2]. Gait changes in several vertebrates are associated with reductions in the COT (e.g. horse Equus ferus caballus [2,3]; red kangaroo Megaleia rufa [4]; camel Camelus dromedaries and donkey Equus asinus [5]; ostrich Struthio camelus and emu Dromaius novaehollandiae [6,7]; and human Homo sapiens [8,9]), supporting the view that energy savings play a role in the evolution of gait changes. However, an abrupt reduction in COT with gait change is not always seen [10]. In addition, if allowed to select their gaits naturally, the trot–gallop transition in the horse [11,12] and walk–run in humans [13] occur at significantly lower speeds than would be expected if energy saving alone was being optimized.

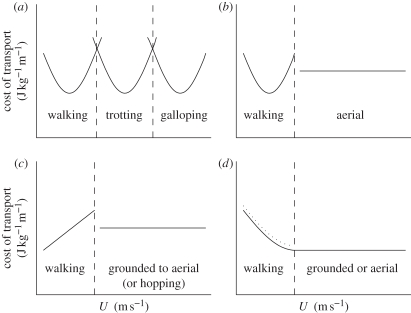
The COT versus U relationship is variable among animals (figure 1). Horses show three U-shaped curves—one each for walking, trotting and galloping (figure 1a)—which overlap, because horses can be forced to extend their gaits into the other gait regimes [2]. Humans [8,9], camels and donkeys [5], and emus and some ostriches [6] also show a U-shaped relationship between COT and U when walking, and when they change gait at higher speeds there is an immediate drop in COT, which remains approximately constant or declines slightly at all successive speeds (figure 1b). In the kangaroo, the relationship between the COT and gait shows a linear increase during slow locomotion (pentapedal gait) followed by an immediate drop in COT at the transition to the fast gait (bipedal hopping; figure 1c). The COT remains approximately constant for the kangaroo at all speeds during bipedal hopping [4]. One study of ostrich terrestrial locomotion [7] reported a pattern between COT and U similar to that for the kangaroo, albeit across different gait changes (figure 1c). In barnacle geese, COT tracks an ever-decreasing smooth curve against U [14] (figure 1d). A similar pattern in the COT is also seen in the platypus Ornithorhynchus anatinus [15], the golden-mantled ground squirrel Spermophilus saturatus [16] and in several other small mammals [17] (figure 1d). Gait changes were not identified for these mammals [17], but would have certainly occurred over the speed ranges used, and yet there was no evidence of a step change downward in COT.

Figure 1.

Generalized relationships between the COT (J kg⁻¹ m⁻¹) and forward speed (U) across different gaits for: (a) horse; (b) human, donkey and camel; (c) ostrich and kangaroo; and (d) barnacle goose (dotted line), and platypus and small mammals (solid line). In (c), grounded and aerial running refers to the ostrich, and hopping refers to the kangaroo. In (d), the type of running (grounded or aerial) is not known.

The variation in the relationship between COT and U suggests that the data for the ostrich and emu [6,7] may not be representative of non-ratite birds. Birds like the barnacle goose, with COT curves that drop during walking [7,17], might not experience a reduction in energy costs with gait changes. As barnacle geese cannot run we selected a galliforme—the Svalbard rock ptarmigan Lagopus muta hyperborea, a non-migratory, ground-dwelling bird [18]—to investigate the COT in a non-ratite. A drop in the metabolic COT in response to a gait change is documented for larger vertebrates [2–5,7–9]. Whether small cursorial animals benefit from similar energy savings with gait changes, or if, like small quadrupeds, they do not, [10] is unclear. Here, we determine the terrestrial locomotion gaits used by the Svalbard rock ptarmigan [18] and measure the metabolic cost of the gaits to test the hypothesis that gait changes are associated with a reduction in the COT in this species.

2. Methods

(a). Study species

Six male Svalbard rock ptarmigans (mean body mass ± s.e. = 0.501 ± 0.009 kg) were housed in the Department of Arctic Biology (The University of Tromsø, Norway) with ad libitum access to food and water. Artificial light and temperature conditions matched those in Tromsø (69°46′ N). Birds were not fasted prior to measurements and were in their summer ‘low body mass’ condition [19,20]. The ptarmigans were trained daily for three months to run on a treadmill for at least 10 min at speeds up to 2.0 m s⁻¹ prior to experimentation.

(b). Indirect calorimetry

An open flow respirometry system was used to measure rates of CO₂ (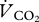) production and O₂ (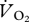) consumption [21,22]. The ptarmigans walked or ran within a 48 l Perspex chamber (30 × 26 × 61.7 cm) mounted upon a treadmill (Bremshey Trail Sport, Finland). The rear and front bottom edges of the box were sealed against the treadmill belt using rubber matting, but a gap of 3 cm was left between the bottom edge of the sides of the box and the treadmill to allow ingress of ambient air. Gases were pulled from the box at a flow rate of 52 l min⁻¹ using a rotary pump (Siemens, Berlin, Germany, model no. 2CH3012). Excurrent air was then sub-sampled into a 0.5 l plastic bottle acting as a carboy at a flow rate of 6 l min⁻¹ using a pump (Charles Austen Pumps Ltd, Surrey, UK, model no. B105DE) and further sub-sampled at 0.115 l min⁻¹ by the Foxbox-C (Sable Systems International, Las Vegas, USA).

The gas sample first passed through a RH300 humidity analyser (Sable Systems International, Las Vegas, USA) where water vapour pressure and relative humidity were measured before CO₂ and O₂ content were recorded. The gas sample was scrubbed of H₂O using a column of calcium chloride prior to passing through the CO₂ analyser and scrubbed of CO₂ using soda lime before entering the O₂ analyser. As H₂O was scrubbed prior to gas analysis, the primary flow rate (FR) of the system was converted to a dry-corrected flow rate (FR_c) using

2.1

where BP is barometric pressure and WVP is water vapour pressure. 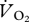was calculated using

2.2

where F_iO₂ is the concentration of O₂ flowing into the respirometry chamber, and F_e″O₂ is that measured in CO₂- and H₂O-free air by the O₂ analyser after leaving the chamber. The difference (fractional change in O₂ concentration) between these two values ranged from 0.000352 ± 0.000033 to 0.000555 ± 0.000068 at the least (0.22 m s⁻¹) and most (1.50 m s⁻¹) metabolically costly speeds, respectively. 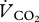was calculated using

2.3

where F_iCO₂ is the concentration of CO₂ in air entering the respirometry chamber and F_e′CO₂ is excurrent CO₂ measured in H₂O-free air by the CO₂ analyser after leaving the chamber. Equations (2.1)–(2.3) are derived from [21]. 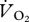was converted into mass-specific power (W kg⁻¹) using the measured respiratory exchange ratio (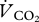/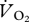) values and thermal equivalents taken from table 12.1 of [23].

The metabolic rate of the ptarmigan was measured at 11 speeds (0.22, 0.5, 0.75, 1, 1.25, 1.39, 1.5, 1.67, 1.75, 1.89 and 2 m s⁻¹; n = 4–6). A bird was placed within the respirometry chamber and left to settle for at least 5 min until the gas concentrations were stable. At each speed, data were collected when a 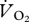trace was achieved that remained level for at least 60 s, which typically took between 3 and 4 min to reach. Birds were then rested for no less than 5 min until a level 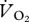trace was again seen before being run at another speed. Birds were run at no more than five speeds during individual trials and were rested for at least a day between successive trials. The order of the birds and the walking/running speeds were randomly selected, and the room temperature was 18.78 ± 0.16°C.

(c). Validation of respirometry chamber

The respirometry set-up was tested for accuracy by leaching N₂ into the respirometry chamber at a known rate, as per our standard protocol [14]. The flow rate of the N₂ in was chosen to approximate the deflection in the 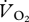trace seen with a bird in the box. Tests were conducted at six speeds between 0 and 2 m s⁻¹ to test for any gas washout caused by the treadmill belt. The pipe emitting the N₂ was positioned at the same height as the ptarmigan beaks and at two positions (the foremost and aftmost position occupied by the ptarmigan during their walking and running trials). The error in 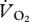measured with the N₂ pipe at the two locations ranged from −1.4 to +2.1% and an ordinary least squares (OLS) regression analysis showed there was no significant effect of treadmill speed on the error (% error in measured 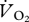= 0.706 − 0.282U, t = −0.831, r² = 0.15, n = 6, p = 0.453).

(d). Kinematics

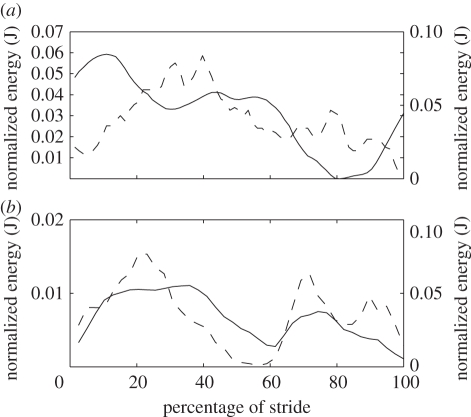
At all speeds, the ptarmigans were filmed in lateral view at 120 frames s⁻¹ with a Handycam HDR-XR520 (Sony, Japan). The video footage was analysed using Tracker software v. 3.1 (Open Source Physics). For each video the left foot (the foot nearest the camera) was tracked over 5–10 strides in order to calculate duty factor (DF), stride frequency (f_stride), stride length (l_stride), and the duration of the swing (t_swing) and stance (t_stance) phases. Three different terrestrial gaits are documented in birds [24–26]: walking; ‘grounded’ running (also referred to as compliant walking [27,28] or ‘Groucho running’ [29]); and aerial running. During walking, the animals' centre of mass (COM) may be modelled as an ‘inverted pendulum’ in which the mechanical energy forms and vectors E_kh (horizontal kinetic energy) and E_p + E_kv (potential energy + vertical kinetic energy) are out of phase, one being exchanged for the other during a stride cycle [30]. In contrast, during both forms of running the two energy forms are in phase. Grounded running and aerial running may be distinguished by DF (greater than 0.5 for grounded and less than 0.5 for aerial) [31]. The kinetic and potential energy fluctuations of the COM were estimated for each bird by tracking the movement of a point on the surface of the bird corresponding to the hip joint throughout a stride. Using only a single video camera is likely to introduce error to the absolute energy values; however, of primary interest here is the phase relationship of the energy forms, which will not be affected.

(e). Data analyses

OLS linear regression was used to test for an association between kinematic variables and U. OLS linear regression was also initially used to determine whether a simple linear relationship described the relationship between 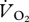or p_met and U. Differences in the nature of the relationship between 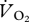or p_met and U for different gaits (walking, grounded running and aerial running) were investigated using ANCOVA. First, both the slopes and the intercept were tested for differences. If the interaction term (gender × U) was non-significant, indicating similar slopes, it was removed from the ANCOVA and the ANCOVA was rerun assuming parallel lines (similar slopes), hence testing for a difference in the intercepts only. All statistical analyses were conducted using the statistics toolbox in Matlab R2007b (The MathWorks, Inc., 3 Apple Hill Drive, Natick, MA, USA) and all means are displayed as ±s.e.

3. Results

(a). Kinematics

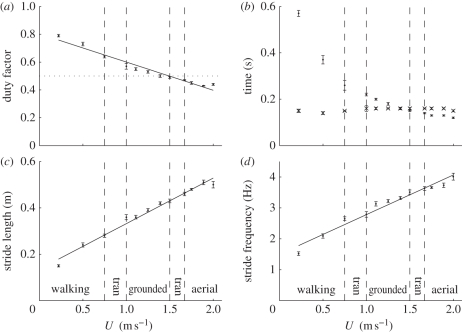
To determine the effect of gait on the energetics of locomotion, the speeds at which a gait change (walking to grounded running to aerial running) occurred were identified. E_kh was out of phase with E_p + E_kv at speeds up to and including 0.75 m s⁻¹, in accordance with pendular walking mechanics (figure 2a). From 1.0 m s⁻¹ onwards, the relationship between E_kh and E_p + E_kv was in phase, indicative of a running gait and spring-associated mechanics (figure 2b). Therefore, the speed at which the ptarmigan changes gait from walking to a grounded run appears to lie between 0.75 and 1.0 m s⁻¹. DF fell significantly below 0.5 (0.47 ± 0.004) at 1.67 m s⁻¹ (figure 3a). Therefore, a transition from grounded to aerial running occurred between 1.5 and 1.67 m s⁻¹.

Figure 2.

Examples of typical COM energy fluctuations for (a) walking at 0.50 m s⁻¹ and (b) grounded running at 1.11 m s⁻¹. The solid lines and right y-axis represent potential plus vertical kinetic energy, and the dashed lines and left y-axis the horizontal kinetic energy of the COM.

Figure 3.

Gait kinematics parameters plotted against forward speed (U). The regression equations describing the relationships represented by the lines are (a) DF = 0.803 − 0.203U (t = −14.78, r² = 0.96, n = 12, p < 0.001), (b) stance phase (circles) and swing phase (crosses) with no lines fitted, (c) stride length = 0.136 + 0.196U (t = 21.98, r² = 0.98, n = 12, p < 0.001), and (d) stride frequency = 1.499 + 1.282U (t = 16.03, r² = 0.96, n = 12, p < 0.001). The areas between the vertical dashed lines (labelled tran) represent the range of speeds where a gait transition occurred.

Both DF and t_stance decreased with increasing speed (figure 3a,b). The relationship between t_stance and U is neither linear nor described very well with a polynomial, so a line has not been fitted. Both l_stride and f_stride increased with forward speed (figure 3c,d). Unlike t_stance, t_swing did not appear to vary predictably with speed (t_swing = 0.148 + 0.007U, t = 2.13, r² = 0.31, n = 12, p > 0.05), only varying between 0.14 and 0.16 s over the entire speed range. t_stance decreased below t_swing at 1.5 m s⁻¹ and at the three highest speeds was less than 82 per cent of t_swing (figure 3b). The highest speed sustainable by the birds (2 m s⁻¹) appeared to be characterized by sharp deviations from the lines of best fit for both DF (an increase) and l_stride (a decrease). There was also a suggestion of a drop in both t_stance and t_swing at 2 m s⁻¹. There was evidence of a discontinuity in the relationship between f_stride and U, with the relationship described by the equation f_stride = 1.043 + 2.130U (t = 36.28, r² = 0.99, n = 3, p = 0.017) during walking and f_stride = 1.892 + 1.030U (t = 12.00, r² = 0.95, n = 9, p < 0.001) during grounded and aerial running, representing a 51 per cent reduction in the slope. It is worth noting that at speeds between those bracketing the gait transitions (0.75–1.0 and 1.5–1.67 m s⁻¹) the ptarmigans were unable to locomote steadily and instead they ‘yo-yoed’ from the front to the back of the box.

(b). Oxygen consumption and power

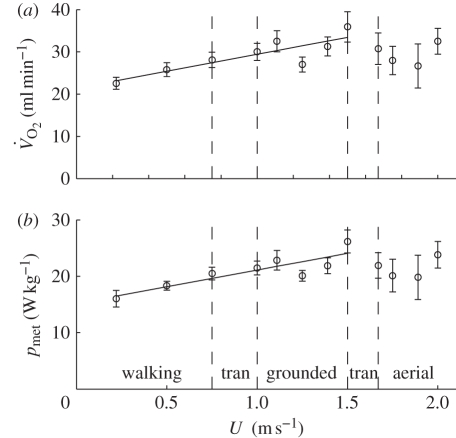
The r² value indicated that an OLS linear regression did not describe the relationship between 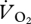and U (figure 4a) adequately (t = 2.058, r² = 0.30, n = 12, p > 0.05). A plot of 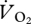and U suggested that the relationship between the variables was continuous across walking and grounded running, but changed at the onset of aerial running (figure 4a). ANCOVA showed that the slope of the relationship between 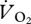and U was not different for walking, grounded running and aerial running (gait × U, F_2,6 = 0.11, p = 0.901). Simplifying the ANCOVA specifying the common slope (8.22 ± 4.29 ml 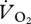min⁻¹ m s⁻¹) also showed no statistically significant difference between the intercepts of the relationship between 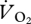versus U for the three different gait regimes (ANCOVA: gait, F_2,8 = 3.44, p = 0.084; U, F_1,8 = 3.67, p = 0.092). Unexpectedly, there also appeared to be no relationship between 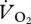and U, suggesting that it was not continuous across gaits. Importantly, the intercept value was very different for aerial running (14.44 ± 2.94 ml 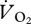min⁻¹) when compared with that for both walking and grounded running, which were very similar (21.45 ± 3.22 and 21.06 ± 1.05 ml 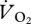min⁻¹, respectively). The intercept values suggested that 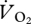increases linearly between 0.22 and 1.5 m s⁻¹, and then drops and flattens out at 1.67–2.0 m s⁻¹, and non-overlapping x-values (U) in each gait indicate that the power of the ANCOVA was compromised here. Therefore, separate regression lines were fitted for walking plus grounded running, and aerial running (figure 4a). As indicated by the ANCOVA, there was a strong linear association (r² = 0.73) showing an increasing 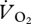with increasing U during walking and grounded running (figure 4a). In contrast, and contrary to the ANCOVA, which suggested common slopes among the three gaits, 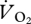did not change predictably with U during aerial running (t = 0.324, r² = 0.05, n = 4, p = 0.767).

Figure 4.

(a) Rate of O₂ consumption (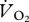, ml min⁻¹) and (b) metabolic power (p_met, W kg⁻¹) plotted against forward speed. The regression lines are (a) = 21.400 + 8.023U (t = 3.99, r² = 0.73, n = 8, p = 0.005) and (b) p_met = 15.195 + 5.917U (t = 4.36, r² = 0.76, n = 8, p = 0.003). The areas between the vertical dashed lines (labelled tran) represent the range of speeds where a gait transition occurred.

Comparing the 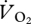at the fastest grounded running speed (1.5 m s⁻¹) and the lowest aerial running speed (1.67 m s⁻¹) showed a 14.3 per cent decrease in gross oxygen consumption (35.9 ± 3.59 versus 30.76 ± 3.74 ml 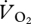min⁻¹), and using the zero-speed intercept from the 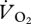versus U relationship (21.4 ml min⁻¹; figure 4a) to correct to net oxygen consumption (locomotion minus basal costs) gave a 35.4 per cent decrease. Because the body masses of the ptarmigan varied little, a pattern between p_met and U was found (figure 4b) similar to that for 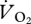versus U (see electronic supplementary material for statistical results). Calculating the minimum COT (E_met) from the relationship between p_met and U for walking and grounded running (figure 4b) gives 5.917 J kg⁻¹ m⁻¹.

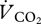followed the same pattern against U as 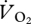, albeit with lower values (respiratory quotient across all speeds = 0.98 ± 0.02).

(c). Cost of transport

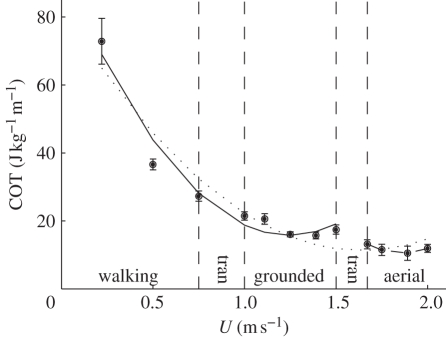
The step change seen in the relationship between 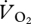and p_met and U was also manifested in the COT (J kg⁻¹ m⁻¹), which decreased curvilinearly with speed up to 1.5 m s⁻¹ and then dropped markedly at 1.67 m s⁻¹ (figure 5). The COT at speeds of 1.67 m s⁻¹ and above is significantly less than the COT at speeds of 1.5 m s⁻¹ and below. The transition from both walking to grounded running and grounded running to aerial running corresponds with a decrease in the COT. Two separate polynomials—one through the walking and grounded running data, and the other through the aerial running data—describe the relationship between COT and U better than a single line (figure 4). COT during the aerial phase varies curvilinearly with speed (r² = 0.99). From these curves, the lowest predicted COT during walking and grounded running is 15.76 J kg⁻¹ m⁻¹ at 1.24 m s⁻¹, and the lowest during aerial running is 10.50 J kg⁻¹ m⁻¹ at 1.86 m s⁻¹. These COT values are higher than those calculated earlier from the slope of the relationship between p_met and U (5.917 J kg⁻¹ m⁻¹) because they are the gross COT (i.e. they incorporate postural costs [32], stress effects [33] and basal metabolism).

Figure 5.

Cost of transport (COT; J kg⁻¹ m⁻¹) plotted against forward speed (U; m s⁻¹). The polynomials are described by the equations COT = 82.835 − 87.175U + 26.564U² (dotted line through all speeds; F_2,9 = 59.564, r² = 0.93, p < 0.001), COT = 94.312 − 126.343U + 50.805U² (solid line through walking and grounded running data only; F_2,5 = 66.193, r² = 0.96, p < 0.001) and COT = 261.525 − 269.598U + 72.386U² (dashed line through aerial running data only; F_2,1 = 110.557, r² = 0.99, p = 0.067). The areas between the vertical dashed lines (labelled tran) represent the range of speeds where a gait transition occurred.

4. Discussion

The Svalbard rock ptarmigan uses three gaits in common with a specialist walking/running bird [7], and therefore experiences two gait change events: walking to grounded running and grounded running to aerial running. Similar to previous findings [25], neither gait change is characterized by an abrupt step change in pelvic limb kinematics. The COT, however, falls after each gait change (figure 5), and in the case of grounded to aerial running there is an obvious step reduction in COT. Our hypothesis is supported and, notably, the data provide the first evidence for a metabolic saving associated with the change from grounded to aerial running.

A stepped reduction in both and p_met at the transition from grounded to aerial running was also found. A decrease in 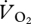with an increment in speed is not necessary for a similar decrease in COT. The ptarmigan is not the first species (though it is the first avian species) to demonstrate a sudden drop and levelling out of 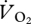at higher speeds. This sudden reduction in 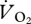was also seen in the kangaroo at the switch between low-speed pentapedal gait and high-speed hopping, where the tendons and ligaments of the pelvic limb are thought to provide significant energy savings, which increase with speed [4]. A closer look at the data in fig. 1b of [34] also suggests that another specialist avian cursor, the roadrunner (Geococcyx californianus), exhibits a similar metabolic pattern against speed, with 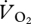dropping and remaining constant after reaching approximately 2.2 km h⁻¹. Other studies of cursorial avian running energetics have not found a drop in 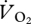or p_met at higher speeds [6,7,35], which may mean the ptarmigan is extraordinary, or may suggest a lack of resolution in previous data (i.e. few increments of U across the speed range), or the use of a limited top speed that does not extend above grounded running.

The E_met of the ptarmigan suggests that they are extremely efficient terrestrial locomotors; currently only the E_met of ratites is known to be lower among avian cursors [6,34,36]. It should be noted that E_met was calculated here from the walking and grounded running data only, because there was no predictable relationship between p_met and U during aerial running. Fitting a linear relationship through all the data would artificially reduce E_met. The data here (figure 4b) and in [6], where the relationship between p_met and U is curvi-linear during walking, suggest that using the slope of a plot of W kg⁻¹ against U to calculate E_met and compare between species may not be appropriate in all cases, because the assumption of linearity is violated. We suggest that E_met should only be compared among species using comparable gaits, as gait-specific locomotor energetics may be a common feature of many animals [6]. If the relationship between p_met and U was curvilinear then the COT would vary with speed and could, in some cases (depending on the curve), be calculated as negative or zero at some speeds: a nonsensical result.

Energy savings during aerial running are usually attributed to elastic storage mechanisms [4]. The Svalbard rock ptarmigan, like other galliformes, has ossified appendicular tendons in the pelvic limb, which enhance elastic storage capabilities [37]. The swing phase of the ptarmigan here was constant across all speeds (figure 3b). With the exception of the mallard, Anas platyrhynchos, which shows an increase in t_swing with increasing speed [38], previous data on a variety of other bird species show a decrease during walking and a constant t_swing over running speeds [14,25,38,39]. The decrease in t_stance with increasing speed is a familiar finding among avian bipeds [14,25,38,39]; generally reductions in DF are facilitated by reductions in t_stance and not increases in t_swing.

Previous studies investigating whether gait changes are associated with energy savings have produced conflicting results [3,11–13,40,41]. Although the transition from walking to grounded running in the ostrich was associated with a reduction in COT, no such saving was found between grounded and aerial running [7]. The primary alternative hypothesis for a mechanism driving gait changes is the reduction of forces applied to the musculoskeletal system [11,42,43], and, again, some support this [11] while others using the same species (horse) conclude the opposite [3]. Interestingly, a study of the small rodent Octodon degus [10] found no evidence for either hypothesis. Unlike horses [2], ptarmigans cannot be made to overlap their gaits. Instead, within the gait transition zones they can only maintain an average velocity by alternating between the slower and faster gait. Similarly, emus were shown to avoid speeds surrounding the gait transition zone when moving along a passageway [6]. Without the ability to overlap gaits it is not possible to say unequivocally that a gait change is made at the ‘energetically optimal transition speed’ as defined by Hreljac [13]. In addition, because neither musculoskeletal force [11] nor bone strain [42] were measured in the ptarmigan, the musculoskeletal system force reduction hypothesis cannot be refuted. It may be that the mechanism behind gait change depends upon the gait shift and there is also no obvious reason why the cue to change gait should be the same for all species. It is striking that the COT against U curves are very different depending upon the organism studied (figure 1)—the ptarmigan adds yet another shape to this list (figure 5)—again suggesting species-specific optimization criteria in terrestrial locomotion and gait selection.

In the absence of measures of the mechanical energy fluctuations of the COM, a gait change may be identified by discontinuities in the relationship between kinematics variables and U [25,44], and there is a discontinuity in f_stride between walking and grounded running here (figure 3d). In contrast, however, and similar to the ostrich [7], none of the kinematics variables show a discontinuity between grounded and aerial running (figure 3). In contrast to both emu and ostrich [6,7], however, the ptarmigan showed a discontinuity in metabolic cost (figures 4 and 5). The ostrich and emu data may lack resolution as metabolic costs were only measured at four speeds for grounded and aerial running, which may have masked a metabolic step between the two gaits. Alternatively, the relationship between metabolic cost and U and gait is potentially species-specific, or perhaps relates to posture: ptarmigans have a crouched posture, whereas the ostrich is more upright.

It is easy to see the evolutionary significance of walking (lowest p_met) and aerial running (cheapest COT). Selecting a walking gait to forage for immobile food items and aerial running to avoid predators (or to travel distance most economically) appears advantageous. The evolutionary significance of grounded running, however, is less obvious. It has been suggested that keeping at least one foot in contact with the ground at all times provides stability that may be of more importance on rough terrain than efficiency or speed [25,45]. Running with a more compliant limb may also increase the control of head movements, enhancing visual stability [46], or reduce the mechanical work of the bouncing non-locomotory body tissues [45]. Unfortunately, data from the field on terrestrial locomotion in birds are sorely lacking, so which gaits they use naturally is currently unknown. Therefore, it is possible that grounded running, and indeed aerial running, are artefacts of being forced to locomote at a set speed upon a treadmill. If so, they have no evolutionary significance.

In conclusion, the ptarmigan experiences an energy saving when it changes gait, and for the first time an energy saving between grounded and aerial running has been identified. It is intuitive to assume that the COT curve is likely to be tuned to an animal's life history, which will influence the optimization criteria (outright speed, stability, foraging vision, economy). The mechanism triggering a gait change could also vary between species and may be an optimized compromise between more than one currency (energy saving, musculoskeletal force reduction and kinematic restriction). What is clear is that we have only just started to scrape the surface of the selection pressures driving the evolution of terrestrial locomotory systems in animals. Without research on what animals do in the field there is a danger that investigations into the energetics and biomechanics of locomotion at different speeds and gaits may have no evolutionary significance, and instead may be confined to understanding laboratory-based treadmill experiments.