Reconciling the influence of predictiveness and uncertainty on stimulus salience: a model of attention in associative learning

Abstract

Theories of selective attention in associative learning posit that the salience of a cue will be high if the cue is the best available predictor of reinforcement (high predictiveness). In contrast, a different class of attentional theory stipulates that the salience of a cue will be high if the cue is an inaccurate predictor of reinforcement (high uncertainty). Evidence in support of these seemingly contradictory propositions has led to: (i) the development of hybrid attentional models that assume the coexistence of separate, predictiveness-driven and uncertainty-driven mechanisms of changes in cue salience; and (ii) a surge of interest in identifying the neural circuits underpinning these mechanisms. Here, we put forward a formal attentional model of learning that reconciles the roles of predictiveness and uncertainty in salience modification. The issues discussed are relevant to psychologists, behavioural neuroscientists and neuroeconomists investigating the roles of predictiveness and uncertainty in behaviour.

1. Introduction

Animals, including humans, spend a great deal of their waking hours learning about and using cues to predict events of motivational significance (reinforcers). One question that has long captivated the imagination of learning theorists is how an organism comes to attend to the appropriate cues. Decades of research have singled out two variables, predictiveness and uncertainty, as playing a key role in determining how much attention a cue will receive [1]. This can be illustrated with a real-life example. Imagine a hungry wetland heron scrutinizing the murky waters of a marsh for cues of fish. Studies of the role of predictiveness in learning suggest that those cues that best predict the location of fish, such as sudden ripples, should possess greater salience¹ than cues that are irrelevant (e.g. the song of a nearby warbler). In the future, sudden ripples will more readily capture the heron's attention, thus helping the bird find its prey. Unfortunately for the heron, ripples are likely to be caused by events other than fish (e.g. the movement of a stealthy alligator), making this cue a rather uncertain predictor of its consequences. Studies of the role of uncertainty in learning suggest that under these circumstances the salience of the ripples should also be high. Attending to them will be equally adaptive because it will allow the heron to acquire ever-finer discriminations between the kinds of ripples given away by fish and, say, those given away by alligators.

While it is clear from behavioural and neurobiological experiments that predictiveness and uncertainty endow cues with high levels of salience, the psychological mechanisms invoked to explain these effects remain contentious [1]. Part of the problem stems from our reliance on two classes of theories of attention in learning which not only fail to account for all the extant data, but which also rest on fundamentally contradictory assumptions. One class of theory, most prominently represented by Mackintosh's model [2], states that good predictors of reinforcement will acquire high salience, while poor predictors should lose salience (see also [3,4]). As a result, good predictors will command substantial attention and poor predictors will come to be ignored. The rival camp, represented by the Pearce–Hall [5] model, rejects this view and assumes that, on the contrary, the salience of good predictors should decrease over the course of learning. Instead, Pearce and Hall propose that increases in salience should be applied where they are most needed—to inaccurate or uncertain predictors of reinforcement, so as to facilitate learning (see also [6,7]).

The purpose of this article is to overcome this theoretical contradiction by providing a proof of concept that the influence of predictiveness and uncertainty on stimulus salience can be reconciled. We begin by briefly reviewing the kinds of evidence that gave rise and lend support to the Mackintosh [2] and Pearce–Hall [5] models. The paradox that unfolds takes us to visit hybrid models that posit the coexistence of Mackintosh and Pearce–Hall mechanisms and which, in a sense, ignore the contradiction [8–10]. Having questioned the hybrid approach, we then advance a possible solution in the form of a new, formal attentional model of learning. To conclude, we contrast some novel predictions and implications from this model with those of hybrid models.

2. Evidence that predictive cues have high salience: the Mackintosh model

The adaptive benefit of a salience-enhancing mechanism that is selective to good predictors of motivationally relevant events (preys, predators, sexual partners, etc.) is evident. In addition to enabling organisms to direct attentional resources towards relevant cues and act upon them with greater efficacy, it also allows them to ‘tune out’ distractors and thus optimize performance. It is no surprise to learn, therefore, that a variety of organisms under a range of conditions exhibit an attentional bias towards cues with predictive significance.

One of the simplest demonstrations that the salience of predictive cues increases is found in studies investigating conditioned orienting responses. In one experiment, for instance, rats were placed in a Skinner box and a localized light was turned on for 10 s without consequences [11]. The animals initially oriented towards the light source, but with repeated presentations this unconditioned response habituated. Interestingly, when the light was subsequently established as a predictor of food, a conditioned orienting response was observed, reflecting a restoration of its salience.

Further evidence for a Mackintosh-type mechanism is provided by studies of attentional-set shifting (also known as intradimensional–extradimensional shift). In this procedure, animals are required to predict a reinforcer on the basis of a relevant dimension (e.g. odour), but not an irrelevant one (e.g. texture). Following this training, a test discrimination is solved more rapidly if the novel cues belong to the previously relevant dimension than if they belong to the previously irrelevant one (for a review, see [12]). This effect is disrupted by lesions of the prefrontal cortex, which has been implicated in salience and attention (for a review, see [13]). Other behavioural techniques have provided similar evidence while circumventing some of the limitations of the attentional set-shift paradigm [14,15].

In humans, evidence of selective attention comes from a variety of behavioural and physiological tests. Relative to poor predictors, good predictors have higher associability [16]; capture more attention by overt and covert measures [17]; are more rapidly recognized [18]; and evoke greater event-related potentials associated with selective attention [19]. Furthermore, individuals with personality characteristics and psychopathology associated with attentional deficits show smaller differences in learning to good relative to poor predictors (e.g. [20]).

This evidence is consistent with Mackintosh's [2] proposals. Formally, the theory states that the salience of a cue will increase if it leads to a smaller prediction error² than all of the other cues in the environment and, conversely, will decline if it leads to a greater prediction error. Since the absence of prediction error is what defines a good predictor, this rule guarantees that good predictors will enjoy greater salience than poor ones. The reader interested in the mathematical instantiation of the model can refer to the electronic supplementary material, S1.

3. Evidence that uncertain cues have high salience: the Pearce–Hall model

In addition to the advantage of selectively attending to predictive cues, it is evident that an organism would also benefit from a mechanism for enhancing the salience of uncertain cues. By directing attentional resources towards such stimuli, the organism should be better placed to discover the relationships between them and their consequences [5,21]. Several lines of evidence suggest that the salience of a cue that predicts a reinforcer with a measure of uncertainty is indeed greater than that of a cue that predicts it with certainty. For instance, the orienting response of a rat towards a visual cue is stronger and more sustained if the cue has been paired with food on a subset of trials (partial reinforcement) rather than on all trials (continuous reinforcement) [22,23]. A similar result has also been revealed in studies of eye movements in humans [24]. In keeping with these findings, we have demonstrated that partially reinforced cues are more readily learned about in a subsequent discrimination than continuously reinforced cues [14].

The influence of uncertainty or surprise on the salience of cues is also demonstrated by the Wilson, Boumphrey and Pearce task [25]. In this procedure, the salience of a cue—as indexed by its associability—is enhanced following the surprising omission of a subsequent event (see also [26]). A well-studied neural circuit comprising attention-related areas such as the amygdala, the substantia nigra, the basal forebrain and the posterior parietal cortex has been identified as critical for this effect [27].

Neural correlates of a greater salience for uncertain rather than certain predictors have also been reported. Ventral midbrain dopamine neurons of monkeys show greater activity in anticipation of a reward that cannot be predicted with certainty [28]. In addition, ventral striatum and orbitofrontal cortex show a strong BOLD response under conditions of uncertainty in functional magnetic resonance imaging studies [29,30]. It has been suggested that these signals may covary with the attention recruited by the experimental events in the way described by the Pearce–Hall [5] model [28,31].

Although none of these phenomena are consistent with the proposals of Mackintosh [2], they can be readily explained by the Pearce–Hall [5] model. Pearce and Hall posit that the salience of a cue is proportional to the aggregate prediction error generated on the last trial in which the cue was present (but see [6]). Under conditions of uncertainty, such as in partial reinforcement, trials will culminate in large aggregate prediction errors and, consequently, the salience of all cues will stay high. In circumstances such as continuous reinforcement, where uncertainty is low by the time learning has reached an asymptote, these errors will be small and so too will be the salience of all cues. As mentioned above, this implies that good predictors should ultimately attract little attention, at least of the kind necessary for learning. A more detailed exposition of the Pearce–Hall model can be found in the electronic supplementary material, S2.

4. A theoretical conundrum (and its implications)

Taken together, the evidence summarized above indicates that both predictiveness and uncertainty lead to high levels of cue salience. As we have pointed out, both effects seem intuitively plausible, albeit for different reasons. Theoretically, however, we are left with a conspicuous contradiction, for if both models were true then, on any given trial, the same cue could potentially undergo simultaneous increments and decrements in salience. Consider the case of a single cue consistently paired with a reinforcer. With sufficient training, Mackintosh predicts that on each trial the salience of this cue should increase, as the cue leads to the smallest prediction error among all stimuli present (i.e. it is the best predictor available). On the very same trial, however, Pearce and Hall anticipate that the cue's salience should decline, for the aggregate prediction error in its presence should approximate zero (i.e. the cue reliably predicts its consequences). For years, this contradiction formed the very substance of the theoretical debate sparked by the two models, and the empirical work they fuelled sought not only to verify their own view but also to dismiss their rival's. As the evidence accumulated, however, a gradual acceptance set in that, puzzling as it might seem, both mechanisms ought to be true at once. This is the central assumption of a family of so-called hybrid models of attention in learning (e.g. [8–10]).

Although varying in detail, hybrid models advocate a dual process of salience modification. One component of the cue's salience is computed for the purpose of stimulus selection according to the principles of Mackintosh's model. Independently, a second salience component is computed for the purpose of learning using the equation provided by Pearce and Hall. The product of these two components then determines the ultimate salience of the cue.

Equipped with these assumptions, hybrid models are able to encompass the two sets of results described above, which hitherto required two different models. This should not be surprising since, by definition, hybrid models incorporate the Mackintosh and Pearce–Hall mechanisms. While acknowledging the success of this approach, some investigators have entertained doubts whether a single mechanism might be able to account for the influence of predictiveness and uncertainty on cue salience [10, p. 32]. Unfortunately, no such mechanism has yet been advanced to challenge hybrid models. This deficiency does more than impoverish the theoretical debate, for a hybrid conception shapes our research hypotheses in very particular ways. In the clinical domain, for instance, applying the hybrid view will inevitably raise the question of which of the two mechanisms, Mackintosh's or Pearce–Hall's, goes awry in disorders with an attentional component, such as schizophrenia, attention deficit hyperactivity disorder and addiction. In studies of the neuroscience of attention in learning, it may lead the investigator to assume the existence of somewhat distinct neural underpinnings for these processes. The possibility remains, however, that the hybrid approach is incorrect, and to this extent our understanding of the processes responsible for variations in cue salience would benefit from competing theories. With this in mind, we have set out to provide an alternative solution to the contradiction.

5. Overcoming the contradiction: a model of attention in learning

(a). Increments in salience

Here, we introduce a formal model of attention in learning that colligates predictiveness- and uncertainty-related attentional phenomena under a single mechanism for increments in cue salience. Decrements in salience are considered separately. While building the model, we have taken recourse to a set of assumptions found already in several influential theories of learning [2,5,32]. Like others, we begin by assuming that the effective salience of a cue (α) is partly determined by sensory attributes, such as its intensity. We shall represent these unacquired properties of the cue with the parameter ϕ, and state, for the sake of simplicity, that ϕ is a constant of range (0–1). For simulation purposes, the absolute value of ϕ is arbitrarily chosen, but its relative value captures the common observation that the salience of a high-intensity stimulus is greater than that of a low-intensity one. Thus, as a first approximation, we shall declare that the level of effective salience, α, is equivalent to ϕ:

5.1

(i). The influence of predictiveness on stimulus salience

To begin to accommodate the evidence summarized above, we shall assume with Mackintosh [2] that a cue acquires additional salience when it predicts motivationally relevant consequences. We shall not, however, adopt Mackintosh's rules for salience modification. Instead, we propose that acquired salience (ɛ) is simply a function of the cue's status as a predictor or, in other words, its associative strength (V):

5.2

In this equation, f refers to a monotonically increasing function. In the absence of any evidence to the contrary, we have assumed in our simulations that f is the identity function (f = 1, see the electronic supplementary material, S4). If the cue becomes associated with several reinforcers at once, then we assume that ɛ is determined by the sum of the cue's associative strengths with those reinforcers, regardless of their motivational sign:

5.3

Factoring in acquired salience, the effective salience of the cue now becomes:

5.4

An example based on the fishing heron of the opening paragraph might help the reader appreciate the implications of the foregoing equations. Equation (5.2) states that the salience of sudden ripples, say, will increase to the extent that they become associated with fish. If similar ripples were also occasionally produced by alligators, then our heron would have two compelling reasons to attend to them, for an error of judgement could make the difference between eating and getting eaten. Equation (5.3) captures this notion by ensuring that fish and alligators both contribute to the salience of the ripples, in proportion to their respective associations with this cue. As will become apparent, this additive assumption is critical for reconciling the roles of predictiveness and uncertainty in salience enhancement.

Equations (5.2) and (5.3) substantially simplify the rules for changes in stimulus salience put forward by Mackintosh [2], the purpose of which is to ensure that the salience of relevant cues increases as the salience of irrelevant cues decreases, thereby achieving selective attention. How else might this be accomplished? Since we assume a direct relationship between salience and associative strength, all that is required is a selective-learning mechanism that grants relevant cues a superior status as predictors to irrelevant cues. An obvious candidate is the delta rule advanced by Rescorla and Wagner [32]. According to this rule, cues conditioned in compound compete for the maximum amount of associative strength supported by the reinforcer (λ), with a fully predicted reinforcer suffering a loss of processing relative to a surprising reinforcer. For each cue, the increment in associative strength (ΔV) on any given trial is proportional to the discrepancy between the value of λ and the aggregate prediction of the reinforcer generated on the basis of all cues present (ΣV). This is captured in the following equation:

5.5

where β is a constant (range 0–1) encapsulating the intrinsic motivational properties of the reinforcer. The larger the λ−ΣV discrepancy in equation (5.5), the more associative learning will take place. Learning ceases as this discrepancy approaches zero. On trials in which the reinforcer is omitted, it is assumed that λ = 0 and the resultant ΔV will be negative, signifying a reduction in the cue's associative strength (i.e. extinction). One consequence of equation (5.5) is that a cue that has a negative correlation with reinforcement (i.e. the reinforcer is more likely to occur in its absence than its presence) will accrue negative associative strength. As will be seen, however, we shall exclude negative cue → reinforcer associations in the particular instantiation of the delta rule presented here.

Application of the delta rule to circumstances in which several cues are present ensures that good predictors will acquire most of the associative strength available at the expense of poor predictors. Equations (5.3) and (5.4) imply that this difference in associative strength will be reflected as a difference in the cues' relative salience. In this manner, the influence of predictiveness on stimulus salience (and allocation of attention) is accounted for, and we shall now turn to examine the relationship between uncertainty and salience.

(ii). The influence of uncertainty on stimulus salience

Equation (5.3) states a simple additive rule according to which a predictor of multiple reinforcers should have more salience than a predictor of just one of these reinforcers. It is interesting to note that, in addition to possessing greater overall motivational significance, a cue in the former case is also, by definition, uncertain as to the particular outcome of each trial. This suggests that it might be possible to explain other instances of uncertainty, such as partial reinforcement, by applying the same additive rule: all one needs to assume is that the omission of reinforcement can itself act as a reinforcer. Before considering this scenario, however, we shall need to say a few words on the notion of ‘no-reinforcer’ representations.

A number of theorists [5,33] have suggested that the surprising omission of a reinforcer is also a motivationally potent event, a proposal that has received empirical support (e.g. [34,35]). Such no-reinforcer representations are assumed to consist primarily of emotional responses opposite in sign to those elicited by the reinforcer itself (e.g. relief if the omitted reinforcer is aversive, disappointment or frustration if it is appetitive). Thus, a cue that is intermittently followed by reinforcement will enter into an association with, respectively, the positive emotional aspects of the reinforcer and the negative emotional aspects of the reinforcer's omission. Theories that incorporate no-reinforcer representations further assume that, when activated, these representations will inhibit their counterpart reinforcer representations [33,36], leading to the commonly observed reduction of responding in partial reinforcement.

In adopting these assumptions, we shall propose, along with others [5,37], that the development of both cue → reinforcer (V) and cue → no-reinforcer (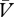) associations are governed by the delta rule. In equation (5.5), we described this rule in relation to the cue → reinforcer association. Acknowledging the contribution of no-reinforcer representations in learning, however, demands some elaboration on this equation. This is because the expectation of no-reinforcement (Σ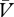) should detract from the expectation of reinforcement (ΣV), to determine the overall prediction of reinforcement (ΣV−Σ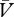). It is this overall prediction that dictates the magnitude and direction of changes in associative strength. Thus, on any given trial, the cue → reinforcer association will change according to:

5.6

If the reinforcer is under-expected (λ > (ΣV−Σ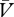)), ΔV will be positive and the association will strengthen (ΔV > 0). Conversely, if the reinforcer is over-expected (λ < (ΣV−Σ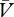)), ΔV will be negative and the association will weaken. In keeping with other theories of associative learning (e.g. [32]), we acknowledge that the strengthening and weakening of the cue→reinforcer association may not occur at the same rate. Consequently, the value of β under circumstances of under-expectation (β_ΔV>0) may be different from the value of β under circumstances of over-expectation (β_ΔV<0; for details about the β-values in our simulations, see figure 1 and the electronic supplementary material, S4).

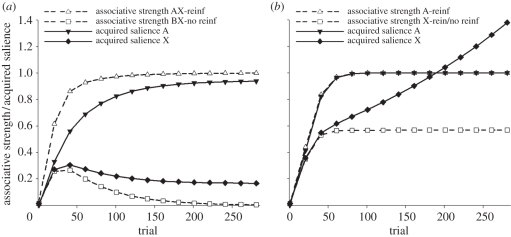
Figure 1.

Simulations of partial reinforcement with the (a) presence and (b) absence of better predictors of trial outcomes. (a) Simulated associative strengths of compounds of cues A and X, and B and X during AX → reinforcer and BX → nothing training; and simulated acquired salience (ɛ) of A and X during the same training. (b) Simulated associative strengths of A and X during continuous and partial reinforcement of these cues, respectively; and simulated acquired salience (ɛ) of A and X during the same training. For both simulations the asymptote of conditioning (λ) = 1, the unacquired salience (ϕ) = 0.2, and the learning rate parameters (β) for, respectively, the acquisition of cue → reinforcer, extinction of cue → reinforcer, acquisition of cue → no-reinforcer and extinction of cue → no-reinforcer learning = 0.07, 0.05, 0.01 and 0.01.

When determining the corresponding equation for the cue → no-reinforcer association, the first step is to define the maximum amount of associative strength that can be supported by this type of learning—that is to say, we must determine its asymptote. This was relatively straightforward for the case of reinforcement, described above, as the reinforcer is a stimulus that is physically present and to which a quantity, λ, could be assigned. The asymptote supported by no-reinforcement, however, requires a different treatment as its quantity is not based upon a physically present stimulus. One simple solution is to suggest that the asymptote of no-reinforcement is equal to the expectation of reinforcement (ΣV). From this, we can then subtract the summed expectation of no-reinforcement (Σ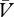) to derive a learning term, ΣV−Σ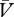, that determines the change in the cue → no-reinforcer association on any one trial. This expression provides an intuition for what should drive cue → no-reinforcer learning. For example, if, our heron repeatedly expects to catch 2 fish (ΣV = 2) but catches none, he will over-expect (and be frustrated or disappointed) by 2 fish, and therefore the cue → no-reinforcer association will tend towards this asymptote. Under some circumstances, however, cue → no-reinforcer learning will take place in the presence of some reinforcement. Thus, if our heron expects to catch 2 fish (ΣV = 2) but catches only 1 (λ = 1), then he will over-expect to the value of 1 fish. In this case, 1 fish will contribute towards the asymptote for the cue → no-reinforcer association. To formalize this notion, we shall draw upon the proposals of Pearce and Hall [5], and suggest that the change in the strength of the cue → no-reinforcer association is determined by

5.7

If the reinforcer is over-expected (λ < (ΣV−Σ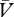)), then Δ 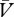will be positive and the cue → no-reinforcer association will strengthen. In contrast, whenever the reinforcer is under-expected (λ > (ΣV−Σ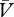)), Δ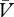 will be negative and the association will weaken. Once again, we acknowledge the possibility that the strengthening and weakening of this association may proceed at different rates ().

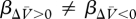It follows from this account that a net conditioned excitor is a cue whose association with reinforcement is greater than its association with no reinforcement (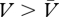) and, conversely, a net conditioned inhibitor is one for which the reverse holds true (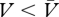). This implies that negative associations, the hallmark of conditioned inhibition according to Rescorla and Wagner [32], are superfluous in the context of this model. Hence, for reasons of parsimony, we shall follow Pearce and Hall [5] and assume that associations between cues and reinforcer or no-reinforcer representations can only be positive, confining instead negative associations to no-reinforcer—reinforcer interactions. For the purposes of simulations provided here, we have assumed that strengths of the cue → reinforcer and cue → no-reinforcer associations range from 0 to 1. A possible architecture of the model is shown in figure 2.

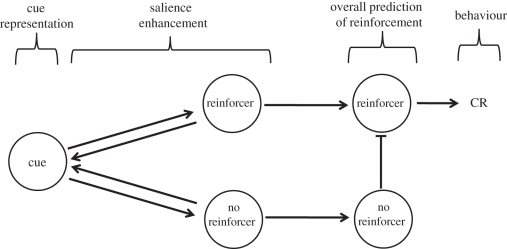
Figure 2.

The associative structure of salience enhancement. Learning: a representation of the cue forms independent associations with representations of the reinforcer and no-reinforcer, according to a version of the delta rule [32]. Salience modification: the degree to which the reinforcer and no-reinforcer representations are each activated by the cue determines feedback to the cue representation, enhancing its salience. Behaviour: downstream, activation of the no-reinforcer representation inhibits activation of the reinforcer representation to determine the overall prediction of reinforcement, which itself dictates conditioned responding.

Let us now return to partial reinforcement. Equations (5.6) and (5.7) correctly predict that a partially reinforced cue should elicit a weaker conditioned response (CR) than would be fostered by continuous reinforcement. Crucially, however, application of equation (5.2) equally predicts, along with Pearce and Hall's model, that the cue should, after sufficient training, acquire substantial salience (see figure 1). This follows from the assumption that the cue will signal two emotionally potent outcomes simultaneously (e.g. food and no-food), which will have additive effects on ɛ (and therefore α):

5.8

It might be profitable to illustrate the significance of equation (5.8) by referring back to our fishing heron. It is probable that the ripples that warn the heron of the presence of fish will not invariably lead to a catch, as occasionally the fish will manage to escape. Casually stated, the mechanism we propose suggests that the harder it is to make a catch, the more frustration and other negative emotions will enhance the acquired salience of the ripples above the level determined by their association with fish. As a result, the chances that the ripples will subsequently capture the heron's attention will also increase, thus improving the likelihood of making a catch. On this view, therefore, it is not the size of the prediction error—as Pearce and Hall [5] posit—that is responsible for the high salience of a partially reinforced cue. Rather, such a high salience derives, in the spirit of Mackintosh's [2] theory, from the cue's associations with emotionally significant events. A similar circumstance will arise if a cue is initially established as a predictor for reinforcement and then established as a predictor for its absence (i.e. extinguished). So long as the (novel) cue → no-reinforcer association grows faster than the (established) cue → reinforcer association is lost, then this procedure will result in the acquisition of both cue → reinforcer and cue → no-reinforcer associations and, consequently a net gain in the acquired salience of the cue. Extant evidence indicates that this is the case [37]. However, as will be appreciated from the next section that considers decrements in salience, extended nonreinforced exposure to a cue should result in a reduction in its salience, thus any gains in salience as a consequence of extinction should not last indefinitely.

Because the amount of salience that a cue will acquire is determined by its relevance, the model successfully accommodates the observation that partial reinforcement will not always result in an increase in salience. Implementation of the delta rule ensures that this will only be the case so long as the cue remains the best available predictor of either outcome. If other cues should signal the presence and absence of reinforcement with greater accuracy, then the partially reinforced cue would ultimately acquire relatively weak associations (low V and low 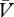), which should limit its acquisition of salience. As a result, the model correctly predicts, with Mackintosh's model, that irrelevant stimuli will normally fail to acquire salience (e.g. [16]; see figure 1 and the electronic supplementary material, S4).

Thus, by assuming that (i) different reinforcers contribute independently to the salience of a cue, and that, in this regard, (ii) no-reinforcer representations can play the part of a reinforcer, it is possible to reconcile the effects of predictiveness and uncertainty on enhancements in cue salience. It is interesting to note that the theoretical notions espoused here are consonant with current thinking and data in behavioural neuroscience, according to which events of opposite motivational significance exert a common influence on salience/arousal neural systems, while having opposing effects on affective-valence systems (e.g. [38]).

(b). Decrements in salience

Thus far, our discussion has focused on the conditions that lead to increments in cue salience as a result of a predictive relationship with reinforcement. It is evident, however, that the salience of a cue may also decline from its initial, novelty level. Phenomena such as habituation and latent inhibition demonstrate that repeated exposure to a cue attenuates unconditioned behaviours directed at the cue (orienting responses, spontaneous exploration [11]) as well as its associability, both commonly used indices of its salience [39,40]. Salience attenuation by exposure, moreover, is not limited to relatively neutral stimuli, but equally affects both reinforcers [41] and their predictors [42].

Decrements in cue salience represent the other side of the contradiction between the Mackintosh [2] and Pearce–Hall models [5]. For Mackintosh, the salience of a cue will decrease if it is a relatively poor predictor of its consequences. In contrast, Pearce and Hall assume that salience will decrease if the cue is a good predictor of its consequences. Both models, however, concur that decrements in salience are determined by the status of the cue as a predictor, an assumption which itself has not gone uncontested [27, p. 343; 43]. Here, we shall abandon this assumption to follow Wagner's [44] proposal that the salience of a cue will drop to the extent that it is itself predicted by (rather than predictive of) other events, including the context. This analysis accommodates the finding that both habituation (e.g. [45]) and latent inhibition (e.g. [46]) are attenuated when the context is changed following exposure. If the extent to which a cue is predicted is represented as the sum of associative strengths between all preceding events and the cue (ΣV_pre→cue), then we can incorporate Wagner's mechanism into the model by assuming that effective salience equals:

5.9

where k is a constant ranging between 0 and 1, the value of which determines the ultimate reduction in the salience of the cue. In keeping with Wagner's [44] proposals, the value of ΣV_pre→cue is determined by the delta rule or, more specifically, by our implementation thereof.

Despite the elegance of this analysis, there is evidence that habituation [47] and latent inhibition [48] may transfer seamlessly across different contexts. It appears therefore that an additional associative structure is required to account for reductions in the salience of a cue as a consequence of exposure. One possibility is that the cue becomes a good predictor of itself. For example, a cue can be regarded as composed of a number of features, each of which possesses a different temporal activation function across the duration of the cue [49]. One implication of this assumption is that, with repeated presentations, later features of the trial will become predicted by earlier features. Although we are aware of at least one study of latent inhibition that is consistent with this analysis [50], we cannot evaluate the influence or generality of this mechanism at this point, and shall therefore refrain from attempting to formalize it.

It is important to realize that, rather than invoking an entirely different mechanism, this analysis of decrements in salience simply applies to cues the processes hitherto applied to reinforcers. That is to say, both cues and reinforcers should suffer a decrement in their processing as a consequence of being predicted. With this addendum to the model, a symmetrical picture emerges according to which every stimulus may simultaneously be signalled by preceding events (detracting from its salience) and a signal of subsequent ones (from which, if motivationally significant, it will derive further salience). Because any stimulus repeatedly presented will to some extent become predicted by itself and the context where it is experienced, stimulus salience should, by default, tend to decline gradually with exposure. We suggest that such a decline forms the backdrop against which the salience-enhancement mechanism described above operates. In the absence of any direct evidence, it is tantalizing to learn that several lesion studies have shown that increments and decrements in cue salience are underpinned by different, non-overlapping neural circuits³ [27].

6. Discussion

This article offers a solution for assimilating predictiveness- and uncertainty-driven attentional phenomena into a coherent salience-changing mechanism. By doing so, it overcomes a long-standing contradiction in the field of associative learning [9,10]. According to the account presented here, increments in the salience of predictive cues underlie the organism's attempt to track events associated with motivationally relevant consequences. Increments in the salience of uncertain cues are seen as a by-product of this process. On the other hand, decrements in salience are otherwise determined: they depend on the status of the cue as an event that is predicted, rather than a predictor of other events, and are thus a natural consequence of exposure. We regard this way of partitioning the salience problem (i.e. incremental versus decremental mechanisms) as more parsimonious than assuming separate, Mackintosh- and Pearce–Hall-type of processes [2,5], each of which can independently (and divergently) produce increments or decrements in salience.

Simulations of the model have confirmed that it successfully handles benchmark cue-interaction effects such as blocking [51], overshadowing and conditioned inhibition [52]. This is a consequence of incorporating the delta rule [32] for determining changes in associative strength, which was designed to explain these phenomena. By the same token, it is obvious that by using this rule the model inherits some of its shortcomings, such as the inadequate account it provides of the role of similarity in learning [53]. Such shortcomings are nonetheless theoretically dissociable from the issue of stimulus salience that concerns us here.

Importantly, the current model represents a departure from existing theories (e.g. [2,5,9,10]) in that it emphasizes the role of associative strength—rather than prediction error—in the determination of stimulus salience. Perhaps the most straightforward implication of this assumption is that a cue that is strongly associated with reinforcement should acquire greater salience than a cue that is only weakly associated. This prediction, which is shared by other attentional theories [2,9,10], has recently received empirical support [54]. A further implication of this analysis is that, under some circumstances, the sum of the associative strengths acquired by a cue whose consequences are uncertain might not exceed the associative strength of a cue whose consequence is certain. From this, it follows that the salience of an uncertain cue may not always be greater than that of a certain cue, a possibility which is not contemplated by hybrid models [55, p. 102]. Although this point warrants further investigation, it is interesting to note that the salience of continuously reinforced cues have occasionally been shown to surpass that of partially reinforced cues (e.g. [56]). One circumstance in which the model predicts this state of affairs is early in training (figure 1b). Evidence in support of this analysis comes from an experiment with pigeons which shows that autoshaped key-pecking, a CR which has been shown to correlate with stimulus salience, is initially higher to a continuously than a partially reinforced cue, but with extended training this pattern of behaviour reverses [57]. While anticipated by the model, these results pose a significant challenge to all other theories discussed above.

Another area where the current model departs substantially from existing models of learning and attention (e.g. [2,5,9,10]) is in its use of cue → reinforcer and cue → no-reinforcer associations to determine the acquired salience of the cue—particularly under conditions of partial reinforcement. An implication of this analysis is that should steps be taken to undermine the contribution of no-reinforcer representations (e.g. frustration) through behavioural or pharmacological interventions, then concomitantly the salience of a partially, but not a continuously reinforced cue should be compromised. This prediction remains to be tested.

To conclude, it has been our aim to show that the roles of predictiveness and uncertainty in stimulus salience can be reconciled and, notably, without departing from conventional assumptions in learning theory. The current model is a case in point that the advent of alternatives to the hybrid approach will refine our research hypotheses, thereby furthering our understanding of the mechanisms involved in salience modification. Elucidation of these mechanisms will benefit the investigation of the neural basis underpinning these changes, and shed light on the nature of disorders characterized by attentional deficits.