The Isolation of Motivational, Motoric, and Schedule Effects on Operant Performance: A Modeling Approach

Abstract

Dissociating motoric and motivational effects of pharmacological manipulations on operant behavior is a substantial challenge. To address this problem, we applied a response-bout analysis to data from rats trained to lever press for sucrose on variable-interval (VI) schedules of reinforcement. Motoric, motivational, and schedule factors (effort requirement, deprivation level, and schedule requirements, respectively) were manipulated. Bout analysis found that interresponse times (IRTs) were described by a mixture of two exponential distributions, one characterizing IRTs within response bouts, another characterizing intervals between bouts. Increasing effort requirement lengthened the shortest IRT (the refractory period between responses). Adding a ratio requirement increased the length and density of response bouts. Both manipulations also decreased the bout-initiation rate. In contrast, food deprivation only increased the bout-initiation rate. Changes in the distribution of IRTs over time showed that responses during extinction were also emitted in bouts, and that the decrease in response rate was primarily due to progressively longer intervals between bouts. Taken together, these results suggest that changes in the refractory period indicate motoric effects, whereas selective alterations in bout initiation rate indicate incentive-motivational effects. These findings support the use of response-bout analyses to identify the influence of pharmacological manipulations on processes underlying operant performance.

Since Skinner (1938/1991), the rate at which an operant is emitted has served as the principal measure of the effectiveness of reinforcement (Killeen & Hall, 2001, but see Hursh & Silberberg, 2008). Free operant response rate, however, is not a unitary phenomenon. Under most contingencies of reinforcement, operant performance seems to be organized in bouts separated by relatively long pauses. Bout-like organization is evident in break-and-run patterns observed under fixed-ratio (FR) schedules of reinforcement (Felton & Lyon, 1966), fixed-interval (FI) schedules (Schneider, 1969), and peak timing procedures (Church, Meck & Gibbon, 1994; Sanabria, Thrailkill & Killeen, 2009). Bout-and-pause patterns are more readily visible in variable-ratio (VR; Reed, 2011) and variable-interval (VI) schedules (Conover, Fulton, & Shizgal, 2001; Shull, Gaynor & Grimes, 2001). These patterns suggest that response rate is constituted by two underlying rates—the rate at which bouts are initiated, and the rate at which responses are emitted while in a bout.

Shull and colleagues (Shull et al., 2001, 2002; Shull, 2004) have shown that the components of operant response rate in VI schedules, bout-initiation rate and within-bout response rate, are differentially sensitive to various experimental manipulations. Bout initiation rate, but not within-bout response rate, positively covaries with rate of reinforcement and level of deprivation (Shull et al, 2001, 2002; Shull, 2004). The addition of an unsignaled ratio requirement at the end of a scheduled interval increases the probability of remaining in a bout after a response (Shull et al., 2001; Shull & Grimes, 2003; Shull, Grimes & Bennett, 2004). The rate of initiation and the length of bouts decrease with time in extinction (Shull et al., 2002). Taken together, these results suggest that, under VI schedules, (1) bout initiation rate depends primarily on rate of reinforcement and deprivation, and (2) within-bout response rate is sensitive to schedule demands such as tandem ratio requirements.

The differential sensitivity of the components of response rate to motivational and schedule manipulations (e.g., deprivation level and tandem ratio requirement, respectively) suggests that important psychological processes may be dissociated in nonhuman animals on the basis of critical aspects of operant performance. Such capability has significant implications in behavioral neuroscience, because the isolation of psychological processes is a prerequisite to the identification of their underlying neural processes and structures. In this regard, it would be ideal if the bout-and-pause analysis could be extended to dissociate motoric effects in addition to its dissociation of motivational and schedule effects. Indeed, motoric effects are of great concern in biopsychological research, because they are often confounded with changes in motivation (Avila et al., 2009; Salamone, Correa, Farrar, Nunes, Pardo, 2009; we refer to the experimental variation in these effort requirements as effort or motoric manipulations).

The present study aimed to replicate the schedule and deprivation-level effects demonstrated by Shull and colleagues (2001, 2002, 2004), and to expand upon them by investigating the effect of effort requirement on response rate. We manipulated effort by varying the height and force requirement of the levers, and motivation for food by implementing a 24-hr deprivation period. Our goal was to use the bout-and-pause analysis to characterize the differential effects of motivational (deprivation level), motoric (lever height and force requirement), and schedule (presence/absence of tandem FR requirement) manipulations on response rate, and to identify performance parameters (bout-initiation rate, within-bout response rate, etc.) that are differentially sensitive to these manipulations. Identifying such effects is critical to establish a means of determining whether changes in response rate caused by a drug are due to an alteration in the motivation for the reinforcer or due to changes in motor capacity. To avoid interactions between the treatment drug and the reinforcer—in particular if the reinforcer is another drug—tests are often conducted under extinction conditions (Fuchs, Tran-Nguyen, Specio, Groff & Neisewander, 1998; Stewart & de Wit, 1987). We therefore introduced a novel, dynamic model to account for changes in model parameters during extinction.

A Bout-and-Pause Model of VI Performance

In a recent series of studies, Shull and colleagues (Shull & Grimes, 2003; Shull, 2004; Shull et al., 2004) analyzed the distribution of VI interresponse times (IRTs) using log survival analyses, and found evidence that such a distribution is more accurately described as a mixture of two exponential distributions—one characterized by very short, burst-like IRTs, and the other characterized by much longer IRTs. This is consistent with the view that a rat can be in either one of two states during a session—an engaged or a disengaged state (see also Heyman, 1988). When the rat is in the engaged state, it responds at a relatively high rate (w, within-bout response rate) according to a Poisson process, generating the exponential distribution of short IRTs. After each response there is a constant probability (1 − q) that the rat will remain in the engaged state and continue to respond at a high rate. There is a complementary probability (q) that the rat will quit the engaged state and enter the disengaged state. In the disengaged state, the rat may perform responses incompatible with the target response (e.g., locomotion, grooming, etc.) or may simply be quiescent for a period of time. Once that period of time elapses, the rat will revisit the target operandum to emit a response, thus reentering the engaged state. The target responses that terminate the disengaged state are therefore called bout-initiation responses. The exponential shape of the distribution of intervals between bouts implies that bout-initiation responses are governed by another Poisson process, albeit one with a much lower rate (b, bout-initiation rate) than the process that controls within-bout responses. Thus, there is evidence that operant responding is not a unitary process, but instead occurs in distinguishable bouts, and that overall response rate is actually a composite of two classes of responses—fast within-bout responses and slower bout-initiation responses.

According to this model, the probability density of an IRT of length τ, p(IRT  =  τ), in VI schedules of reinforcement can be described by the following bi-exponential distribution (Shull & Grimes, 2003; Shull, 2004; Shull et al., 2004):

where w is the mean within-bout response rate; b is the mean bout-initiation rate, and 1 − q is the proportion of IRTs that are emitted during a bout; q is therefore the proportion of IRTs that separate bouts (which is the same as the probability of quitting the engaged state after a response). Overall response rate is thus a composite process controlled by three parameters, q, w, and b. We call this model the bi-exponential model. Note that setting q to zero (or one) reduces Equation 1 to an exponential distribution, which would be a good description of operant performance not organized in groups of bouts.

The Refractory Period

Equation 1 assumes that after a response is made, an animal can instantaneously make another response (i.e., there is no dead time between responses). This is likely to be incorrect— physical limitations impose ceilings on response rates (Killeen, 1994; Killeen & Sitomer, 2003), which yield a dead, or refractory, period after each response during which the animal cannot make another response (Killeen, Hall, Reilly, & Kettle, 2002). This refractory period, which we call δ, is longer for responses that take longer to complete, probably like those that involve a higher workload. We include δ in Equation 1 as

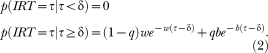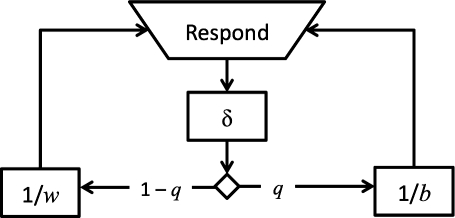
We call Equation 2 the refractory bi-exponential model. Note that fixing δ at zero in Equation 2 reduces it to Equation 1. Figure 1 provides a schematic diagram of the refractory bi-exponential model underlying Equation 2.

Fig 1.

A diagram of the refractory bi-exponential model of operant performance. The lever press requires time δ to complete. Following a response, the rat either remains in the engaged state with probability 1−q and responds on the lever at rate w, or exits the engaged state with probability q and returns at rate b.

Predictions

Prior data suggest that food deprivation covaries with the rate at which response bouts are initiated, but not with response rates within bouts in VI schedules (Shull et al., 2001, 2002; Shull, 2004). Accordingly, we anticipated that depriving rats of food would increase b (bout-initiation rate), but not w (within-bout response rate) or q (probability of quitting an engaged state after a response), in the distribution of food-reinforced VI IRTs. In contrast, prior data suggest that appending a tandem FR requirement at the end of the VI schedule, which increases the response requirement without substantially affecting rate of reinforcement, mainly increases within-bout response rates and not bout-initiation rates (Shull et al., 2001, 2004; Shull & Grimes, 2003). Accordingly, we anticipated that the tandem FR requirement would increase w, possibly decrease q, and would not influence b.

Skjoldager, Pierre and Mittleman's (1993) study provides the most relevant precedent to the motoric manipulation implemented in the present study. They found that increasing the lever height and force requirement prolongs pre-ratio pauses (i.e., reduces rates of engagement) and reduces run rates in a progressive ratio schedule. It is unclear, however, the extent to which the latter effect might have resulted from the longer time it takes to complete more effortful responses, which is reflected in the refractory period δ following each response. We thus anticipated that raising the lever and increasing its force requirement would decrease b, increase δ, and possibly decrease w.

METHOD

Subjects

Six Sprague Dawley rats (Rattus norvegicus, designated 505, 507, 517, 519, 520, and 521) naïve to operant conditioning experimentation served as subjects. They were approximately 90 days old and weighed about 350 g at the start of the study. They were housed individually on a 12∶12 hr reverse light/dark cycle with lights on at 1900 hr, and had free access to food and water in their home cage, unless noted otherwise.

Apparatus

Two experimental chambers (305 mm long, 241 mm wide, and 210 mm high) housed in light- and sound-attenuating compartments were used. The front and rear walls and the ceiling of each experimental chamber were made of clear plastic; the front wall was hinged and functioned as a door to the chamber. The floor consisted of thin metal bars positioned above a catch pan. In the horizontal middle of a side wall (perpendicular to the front and rear walls) was a square aperture (51 mm sides, 15 mm from the chamber floor) to the receptacle for 45-mg sucrose pellets (dustless precision formula F0042; Bio-Serv, Frenchtown, NJ). The chambers were equipped with two retractable levers (MED associates, ENV-112CM) mounted flanking the access to the pellet receptacle. The inside edge of each lever was 8 mm from the closest vertical edge of the receptacle.

One lever (the “low” lever) was located 21 mm above the floor; the other lever (the “high” lever) was 165 mm above the floor and 16 mm below the ceiling. Rats could press the low lever but not the high lever without rearing. Force activation requirements for the low and high lever were 0.05 N and 0.78 N, respectively, except during autoshaping. Force requirements were measured from the tip of the lever using a stylus force gauge and manipulated by adjusting the spring tension of each lever. Henceforth the high height/force lever will be referred to as the high workload lever and the low height/force lever will be referred to as the low workload lever. The assignment of high versus low workload to the lever closest to the door was counterbalanced across chambers and remained fixed for the duration of the experiment. Extraneous noise was masked by a ventilation fan in each chamber. There was no illumination in the chambers during sessions. Data collection and experimental events were handled by MED-PC™ software and hardware.

Procedure

Magazine training and autoshaping

Each subject completed one session of magazine training, in which 60 sucrose pellets were delivered, response-independently, 1 every 60 s. At the end of the training session, it was verified that all rats ate all of the pellets. Nine sessions of autoshaping were then conducted. Each autoshaping trial started with the extension of a lever, which was retracted after 8 s or a lever press, whichever happened first; lever retraction was followed by the delivery of one pellet. The intertrial interval (ITI) was 48 s. During autoshaping, both levers were set at the “low” height; lever force activation requirements were both set at 0.15 N. For all other phases of the experiment the lever work requirements were as described in the apparatus section.

Phase 1: Maintenance

Daily experimental sessions were conducted following the autoshaping phase. Each session began with a 5-min acclimation period in which no experimental events occurred. The remainder of the session was divided into trials, each signaled by the extension of only one of the two levers. The lever closest to the chamber door was always extended for the first trial of each session. The extended lever (high or low) was strictly alternated between trials. Each trial ended and the lever was retracted when a sucrose pellet was delivered or when 300 s had elapsed since the start of the trial, whichever occurred first. Trials were separated by a 15-s ITI during which both levers were retracted.

All experimental sessions lasted for 1 hr or 60 trials, whichever occurred first. Sessions ended only after the end of a trial, never during. Sessions were conducted 7 days a week.

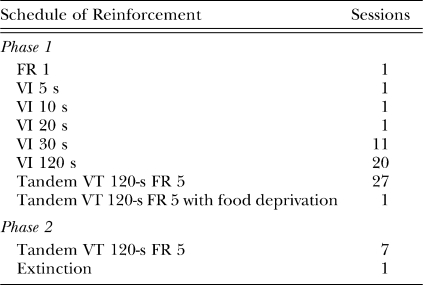
Table 1 lists the experimental conditions in the order in which they were presented. Each condition is identified by the schedule on which pellet deliveries were programmed. During continuous reinforcement (FR 1), pellets were contingent on a single lever press. During VI schedules, pellets were contingent on the first lever press following an unsignaled interval that was randomly sampled without replacement from a flat 48-item distribution of intervals, which had a mean of the stipulated VI duration and ranged between 5 and 240 s. The tandem variable-time (VT) 120 s fixed-ratio 5 (tandem VT 120-s FR 5) schedule was similar to a simple VI 120-s schedule, but pellets were contingent on the fifth lever press following the interval.

Table 1.

Number of sessions in training and experimental conditions, arranged in chronological order.

Acute food deprivation was instated immediately after the 27^th tandem VT 120-s FR 5 session. Chow was removed from the rats' homecage for 24 hr (± 1 hr). One session was conducted on the tandem VT 120-s FR 5 s schedule under food deprivation. Food deprivation was terminated immediately after this session to minimize the possibility of chronic food-restriction effects on operant performance (Epstein, Leddy, Temple & Faith, 2007).

Phase 2: Extinction

Performance was restabilized on the tandem VT 120-s FR 5 schedule for seven sessions, after which one extinction session was conducted. During extinction, only the lever closest to the door was extended after the initial acclimation period; it remained extended for the entire session, with no consequential pellet delivery. The extended lever (high or low workload) was counterbalanced across rats, with 3 rats exposed to each lever.

Data Analysis

Statistical analyses of overall response rates and parameters of the quantitative model were conducted using a within-subject 2 × 3 (workload × condition) ANOVA. The two levels of the workload factor were low and high workload. The three levels of the condition factor were VI 120 s (VI), tandem VT 120-s FR 5 without food deprivation (Tandem), and tandem VT 120-s FR 5 with food deprivation (Food Dep). Dependent measures for each level of the condition factor were the average of the last 4 VI sessions, the average of the last 4 Tandem sessions, and the only Food Dep session. Because the condition factor was a within-subject factor with more than two levels, Mauchly's test of sphericity of the covariance matrix (Mauchly, 1940) was applied. This test verified the homogeneity of variance of the difference scores because violating variance homogeneity can inflate Type I error rates (Myers & Well, 1995). For terms that violated the sphericity assumption, their degrees of freedom were reduced using the Huynh-Feldt epsilon (Huynh & Feldt, 1970), which countered Type I error rate inflation. When the 2 × 3 ANOVA revealed significant main effects or interactions, paired-samples t-tests (pairing within-subject) were conducted on comparisons of interest. More specifically, when an effect involving the condition factor was found to be significant, follow-up paired-samples t-tests were conducted only between VI versus Tandem (to assess the effect of the tandem ratio requirement) and Tandem versus Food Dep (to assess the effect of food deprivation), and not between VI and Food Dep. The times at which responses were emitted during the single extinction session were also collected, but no between-subject statistical inferences were made.

RESULTS PHASE 1: MAINTENANCE

Reinforcement and Response Rate

Panel A in Figure 2 shows daily mean reinforcement rates on both low and high workload levers for each manipulation. Panel B in Figure 2 shows the mean reinforcement rates averaged over the last four training sessions in the VI and Tandem manipulations and the mean reinforcement rates from the single Food Dep manipulation. Reinforcement rate did not appear to be affected by either workload or condition: ANOVA failed to detect a main effect of workload, F(1, 5)  =  1.74, p > .20, condition, F < 1, NS, or a workload × condition interaction, F < 1, NS. This indicates that our schedule successfully controlled for reinforcement rates on both levers across schedule/deprivation manipulations.

Fig 2.

Mean (± SEM) reinforcement rate (Panels A and B) and overall response rate (Panels C and D) for experimental conditions in Phase 1. Left panels show daily means for low and high workload levers. Right panels show means averaged over the last four sessions for VI and Tandem condition and the mean for the single Food Dep session. Asterisks indicate significant (p < .05) effects of condition (schedule/deprivation manipulations).

Panel C in Figure 2 shows daily mean response rates during VI, Tandem, and Food Dep sessions. Panel D in Figure 2 shows mean response rates averaged over the last four VI and Tandem sessions and the mean response rates from the single Food Dep session for each lever. ANOVA found no significant condition × workload interaction effect on response rates, F < 1, NS. ANOVA also found no systematic differences between response rates on the high versus low workload lever (main effect of workload, F < 1, NS). In contrast, ANOVA found a main effect of condition, F(2, 10)  =  18.55, p < .01. A follow-up t-test comparing VI versus Tandem found that subjects responded more during the Tandem condition than during the VI condition, t(5)  =  3.85, p < .02 (left asterisk in Figure 2D). A second follow-up t-test comparing Tandem versus Food Dep found that rats also responded more during Food Dep than during Tandem, t(5)  =  3.87, p < .02 (right asterisk in Figure 2D), in agreement with the hypothesis that motivation is enhanced by increased food deprivation.

Model Selection

Although statistical analysis suggested that response rate was not affected by workload, variability in performance between and within subjects may have obscured systematic changes in more fine-grained parameters that underlie overall response rates. We further explored this possibility by considering four variations of a model of IRT distributions (Equation 2, Figure 1): a single-exponential model, where q  =  0 and δ  =  0; a refractory exponential model, where q  =  0 but δ ≥ 0; a bi-exponential model, where q ≥ 0 but δ  =  0 (Equation 1), and a refractory bi-exponential model, where q ≥ 0 but δ ≥ 0 (Equation 2).

We fitted each model to each rat's daily IRT data on each lever, using the method of maximum likelihood (Myung, 2003). The maximum likelihood estimate (MLE) of each model was the product of the model's daily likelihood estimates across levers and subjects. Akaike Information Criterion (AIC; Burnham & Anderson, 2002; see Appendix A for a brief explanation of the maximum likelihood method, AIC, and ΔAIC) was then used to evaluate the relative goodness of fit of each model. In the present experiment, a trial occasionally timed out before the animal had earned a reinforcer, thus yielding periods that ended without a response. Appendix B provides the expression for the probability that the animal does not emit a response for a given duration for the most general model (i.e., refractory bi-exponential). Parameters were estimated for each of the four models, for each animal, in each experimental condition, based on the joint probability of all IRTs and the “no-response” periods.

Table 2 shows the minimum ΔAIC across daily sessions under each condition for each model. The refractory bi-exponential model (Equation 2) was consistently the best model on every training session. The finding that the next smallest ΔAIC across all sessions was 1097 means that the refractory bi-exponential model was at least e⁵⁴⁸ times more likely than the next best model (nonrefractory bi-exponential model) on any given day.

Table 2.

Minimum daily ΔAIC for each of four models of operant performance, for each experimental condition in Phase 1.

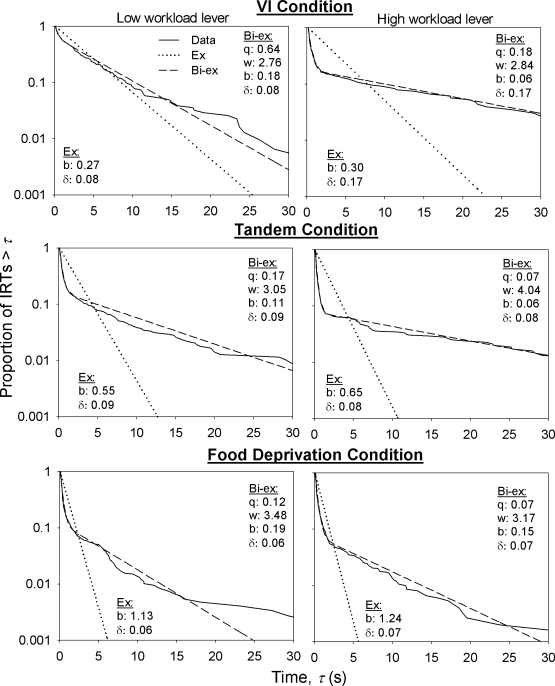
To illustrate the goodness of fit of the selected model, Figure 3 shows log survival plots of IRTs (continuous curves) of a typical rat across experimental conditions, along with fitted refractory exponential (dotted) and refractory bi-exponential (dashed) traces. All plots took the approximate shape of a broken stick: Many IRTs were very short (steep portion of the curve on the left side of each plot); the longer IRTs ranged over much longer intervals (flatter portion of the curve on the right side of each plot). The refractory bi-exponential model fitted the data adequately, and certainly better than the single exponential model. The fitted nonrefractory bi-exponential trace (not shown) was almost identical to the refractory bi-exponential trace, except that the former was shifted to the left by 0.1 s. The similarity of both traces highlights the advantage of using a likelihood-based analysis: AIC clearly showed that the inclusion of the refractory period provided a better description of the data. This advantage would have been missed by both visual inspection of the survival function and by fitting a curve to the function using the method of least squares (Kessel & Lucke, 2008).

Fig 3.

Log survival plots of IRTs produced by a representative rat in all experimental conditions of Phase 1 (continuous curves). Left and right panels show data from low and high workload levers, respectively. The maximum likelihood fits of the refractory single exponential (Ex) and bi-exponential (Bi-ex) models are also shown. The best fitting parameters for the two models are displayed in each graph. q: proportion of IRTs separating bouts; w (responses/sec): within-bout response rate; b (responses/sec): bout-initiation rate; δ (sec): refractory period. The rat was selected by ranking the overall response rate on each lever in the last session of each condition in Phase 1 for each rat, then averaging the rank across levers and conditions, and selecting the rat with the third highest average rank.

Effects on Parameter Estimates

To assess the effect of workload, schedule of reinforcement, and food deprivation on refractory bi-exponential parameters, we compared estimates of these parameters1 across experimental manipulations. This comparison was based on the same 2 × 3 (workload × condition) ANOVA used to analyze overall response rates. The two levels in the workload factors were low and high workload, and the three levels in the condition factor were VI, Tandem, and Food Deprivation (Food Dep). Because our model assumed that each parameter was independent from one another, a separate ANOVA was conducted for each parameter. Estimates for individual rats are shown in Appendix C.

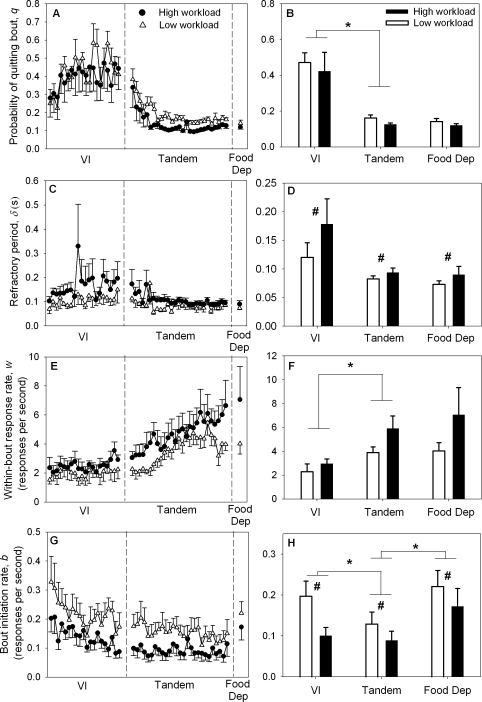
Panels A and B in Figure 4 show the probability of quitting a bout, q, for each of the two levers. ANOVA found no workload × condition interaction effect on q, F < 1, NS. Changing motor workload had no significant effect on q [main effect of workload: F(1, 5)  =  1.07, p > .30]. In contrast, ANOVA found that q was significantly affected by condition [main effect of condition: F(1.0, 5.1)  =  19.64, p <. 01]. A follow-up t-test comparing VI versus Tandem found that increasing ratio requirement reduced q on both levers, t(5)  =  4.54, p < .01, (asterisk in Figure 4B). A second follow-up t-test comparing Tandem versus Food Dep found that food deprivation did not affect q significantly, t(5)  =  1.63, p > .10.

Fig 4.

Mean (± SEM) bi-exponential model parameters: probability of quitting a bout, q (Panels A and B); the refractory period, δ (Panels C and D); within-bout response rate, w (Panels E and F); and bout initiation rate, b (Panels G and H). Left panels show daily means for low and high workload levers. Right panels show means averaged over the last four sessions for VI and Tandem condition and the mean for the single Food Dep session. Asterisks indicate significant (p < .05) effects of condition (schedule/deprivation). Pound signs indicate significant effects of workload.

Panels C and D in Figure 4 show mean estimates of the refractory period, δ, for each of the two levers. On average, δ was systematically higher for the high versus the low workload lever, although the difference was small (pooled average difference  =  0.033 ± 0.009 s)2. ANOVA found no workload × condition interaction effect on δ, F(1.1, 5.3)  =  1.96, p > .20, but it found a significant main effect of workload, F(1, 5)  =  15.38, p < .02 (pound sign in Figure 4D), showing that increasing motor workload increased δ, as predicted. The main effect of condition on δ was not significant, F(1.1, 5.3)  =  3.12, p > .10.

Panels E and F in Figure 4 show mean estimates of the within-bout response rate, w, for the two levers. ANOVA found no significant workload × condition interaction effect on w, F < 1, NS. ANOVA found that the main effect of workload was not significant at the .05 level, F(1, 5)  =  4.50, p > .08, even though differences in mean w between workloads may hint that high workloads maintained higher w. ANOVA found a significant main effect of condition on w, F(2, 10)  =  9.45, p < .01. A follow-up t-test comparing VI versus Tandem found that w increased when ratio requirement was increased, t(5)  =  4.49, p < .01 (asterisk in Figure 4F). A second follow-up t-test comparing Tandem versus Food Dep found that food deprivation did not affect w, t(5)  =  0.92, p > .35.

Panels G and H in Figure 4 show mean estimates of the bout initiation rate, b, for the two levers. ANOVA found no significant workload × condition interaction effect on b, F < 1, NS. ANOVA found a significant main effect of workload on b, F(1, 5)  =  19.83, p < .01, with b being lower on the high workload lever (pound sign in Figure 4H). ANOVA also found a marginally significant main effect of condition at the .055 level, F(1.2, 6.0)  =  5.48, p  =  .054. A follow-up t-test comparing VI versus Tandem found that b was significantly lower under the Tandem condition, t(5)  =  3.40, p < .02 (left asterisk in Figure 4H), suggesting that animals initiated response-bouts less frequently on both levers after ratio requirement increased. A second follow-up t-test comparing Tandem versus Food Dep found that b was increased by food deprivation, t(5)  =  3.19, p < .03 (right asterisk in Figure 4H), in agreement with the hypothesis that food deprivation enhances motivation.

DISCUSSION PHASE 1: MAINTENANCE

A superficial examination of response rate alone indicated that responding on a VI schedule increases if the tandem ratio requirement increases, or if the animals are deprived of food (Figure 2, Panel C and D). Both effects, under conditions of constant rate of reinforcement (Figure 2, Panel A and B), are replications of well-demonstrated phenomena (Ferster & Skinner, 1957; Skinner 1938/1991; Shull et al., 2001). Interestingly, no effect of workload on overall response rate was detected. This result is inconsistent with many reports indicating an inverse relationship between force requirements and response rate (Adair & Wright, 1976; Alling & Poling, 1995; Bradshaw, Szabadi & Ruddle, 1983; Chung, 1965; Posadas-Sanchez, 2005), although support for this relationship is not unequivocal (Collier & Jennings, 1969; Elsmore & Brownstein, 1968; Stanley & Aamodt, 1954; Zarcone, Chen & Fowler, 2007, 2009). Nonetheless, overall response rate is a crude measure of performance: By collapsing all the IRTs into the denominator, response rates neglect the information contained in the distribution of IRTs. We suspected that changes in IRT distribution across conditions would uncover interesting effects, including those produced by changes in workload.

Our first task was to determine the most appropriate characterization of IRT distributions. We thus considered four models, three of which were simplified versions nested within a fourth, more complex model—the refractory bi-exponential model (Equation 2). The complexity of this model was well justified by the variance it accounted for and, therefore, it was adopted. The refractory bi-exponential model assumes that responses occur in bouts; it consists of four parameters: q (the probability of quitting a response bout; its complement, 1− q, is the probability of continuing in a bout), δ (the minimum IRT), w (the rate of responding within a bout), and b (the rate of bout initiation).

Finally, we identified substantial changes in refractory bi-exponential parameters caused by changes in experimental conditions. Consistent with Shull et al. (2001), we found that the tandem VT FR schedule maintained higher response rates than the simpler VI schedule because it sustained longer bouts of fast responding (lower q, higher w), even though these bouts were less frequent (lower b). Food deprivation selectively increased bout frequency, thus yielding even higher response rates; this also replicated Shull's (2004) findings. We also found that mean response rates obscured three mutually compensating effects of workload: Higher workloads yielded less frequent bouts (lower b) of responses that took longer to complete (higher δ), but that tended to be emitted at higher rates (higher w). Although not statistically significant, the workload-induced change in w was sufficient to counteract the depressing influence of b and δ on overall response rate.

Among the factors considered in this study, changes in schedule of reinforcement affected only the probability of staying on the lever (1− q) and the rate of within-bout responding (w), whereas workload uniquely affected the minimum IRT (δ). Thus, evidence presented here supports the use of q and w as indices of schedule effects, and δ as an index of motoric effects in food-maintained behavior. Motivational effects, such as those of food deprivation, may be identified by exclusive changes in the rate of bout initiation b. This means that changes in b that are accompanied by changes in other parameters may be caused by nonmotivational manipulations. As shown in Figure 4 Panel H, a schedule manipulation (tandem FR requirement) and a motoric challenge (higher workload lever) yielded reductions in b. These nonmotivational manipulations also influenced other parameters; only food deprivation influenced b alone.

RESULTS PHASE 2: EXTINCTION

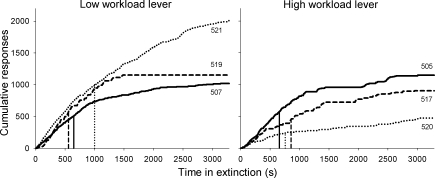
Figure 5 shows, in separate plots for low and high workload, the cumulative lever presses emitted by individual rats and the time when half of those lever presses were emitted during the extinction session. On average, fewer responses appear to be emitted during the extinction of high workload lever pressing, although the variability between subjects precludes any meaningful statistical analysis. In contrast, the rate at which responding decayed during extinction, indexed by the half-life of the cumulative response, was similar across workload levels. As in Phase 1, we anticipated that the analysis of response aggregates provided no more than a general semblance of the extinction process. We thus applied the modeling exercise from Phase 1 to the data from Phase 2.

Fig 5.

Cumulative lever presses emitted during extinction on the low and high workload levers for individual rats. Vertical drop lines indicate the time at which each subject emitted half of its total lever presses in the extinction session. Rat numbers are indicated at the end point of each record.

Because the exponential model is a special case of the bi-exponential model, we focused on generalizing the latter model to extinction performance. Like the maintenance model, the extinction model assumes that responses occur stochastically and independently according to two underlying independent Poisson processes—one with high rate (within-bout) and one with low rate (bout initiation). It is assumed that, during an extinction session, one or more of the following parameters decay exponentially towards zero over time: the probability of remaining in a bout (1 − q), the within-bout response rate (w), and the bout-initiation rate (b). The decay of any one of these parameters would yield longer IRTs, and thus reduced response rates, as a function of time in extinction. The nomination of these decay processes is not motivated by theoretical considerations, but provides reasonable descriptions of the extinction process, given the refractory bi-exponential model.

Specifically, let (1 − q₀) be the baseline probability of remaining in the engaged state at the beginning of the extinction session, w₀ be the baseline within-bout response rate, and b₀ be the baseline bout-initiation rate. Let 1 − q_t be the probability of quitting the engaged state at time t into the extinction session, w_t be the within-bout response rate at time t into the session, and b_t be the bout initiation rate at time t into the session. Then:

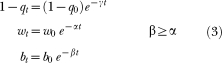where γ, α, and β are the rates of decay of (1 − q₀), w₀, and b₀ respectively. The probability of quitting a bout at time t, q_t, is simply 1 − (1 − q_t). Note that the exponential function is used in Equation 3 to describe the decay of parameters as a function of time in extinction, and not to describe the probability distribution of IRTs (cf. Equations 1–2). For simplicity, we assume that if a rat responded at time t and the next response occurs at t + d, then the parameters q_t, w_t and b_t are given by Equation 3 and they remain constant between t and t + d. Appendix D provides expressions for the probability that the animal does not emit a response between its last emitted response and the end of the session. Parameters were estimated for each animal in each experimental condition, based on the joint probability of all IRTs and the “no-response” periods.

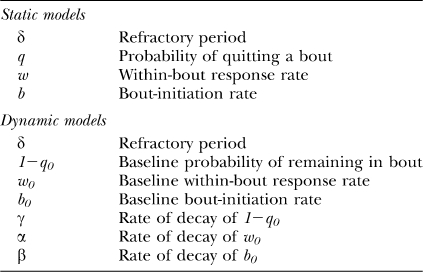
Because parameters q, w, and b change as a function of time in extinction, we call this model the dynamic refractory bi-exponential model, in contradistinction to the static model of Equation 2. Note that if all three decay-rate parameters (γ, α, β) are set to zero, the model reduces to Equation 2. Table 3 lists all the parameters of both static and dynamic refractory bi-exponential models with their meaning, for reference.

Table 3.

List of parameters for the static and dynamic models.

We had no a priori hypothesis as to which of the parameters, (1−q₀), w₀, or b₀, would decay during the extinction session. We therefore used maximum-likelihood estimates and AIC to determine the most efficient model. The following models were compared using AIC: (a) single versus bi-exponential (q₀  =  0 vs. q₀ ≥ 0); (b) nonrefractory versus refractory (δ  =  0 vs. δ ≥ 0); and (c) all possible combinations of decay rate parameters (γ, α, and β) fixed at zero versus not fixed at zero. Models with parameters fixed at zero are more parsimonious and are analogous to the null hypothesis that those parameters are superfluous (Burnham & Anderson, 2002). The AIC scores for these “null” models would be lower, and hence these models would be favored, if alternative models that allow these parameters to be free did not account for substantially more variance. There are a total of four single exponential candidate models: two models with α either free or fixed at zero × two models with δ either free or fixed at zero. There are a total of 16 bi-exponential candidate models: 2³ models with γ, α, and β, each either being free or fixed at zero, and for each bi-exponential model δ can be free or fixed at zero, yielding 2³ × 2  =  16 candidate models. Animals were grouped according to which lever was presented during the extinction session (high vs. low workload); model selection and parameter estimation were conducted for each group separately.

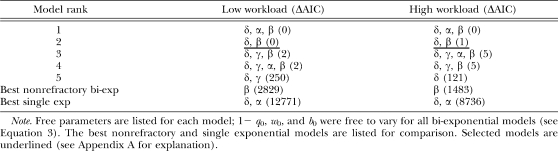
AIC analysis showed that the refractory bi-exponential model fitted extinction data better than both single exponential models and the nonrefractory bi-exponential model. Table 4 shows the five best fitting models for extinction of high versus low workload lever pressing, as well as the best fitting nonrefractory bi-exponential model and the best fitting single exponential model. Model names indicate whether the model is refractory (δ is free) and the decay rate parameters that are allowed to vary freely. Each model's ΔAIC is shown in parentheses. The best fitting refractory bi-exponential models were more than e⁷⁰⁰ times more likely than the best nonrefractory bi-exponential model, which was in turn more than e³⁵⁰⁰ times more likely than the best fitting single exponential model. This provides strong evidence that bout-like responding occurs during extinction, justifying the present fine-grained analysis. The likelihood of each of the top four models for both groups (extinguished on low vs. high workload levers) is fairly similar to each other. In fact, β was the only decay rate parameter that the present data unequivocally suggested needed to be free: For both groups of animals, the best models with β set to zero (ranked fifth in Table 4) were more than e⁵⁸ times less likely than a similar models with β allowed to be free, providing strong evidence that bout-initiation rate declined as extinction progressed. Table 4 also shows that models with γ or α set to zero (ranked second) had low ΔAICs. The present data therefore did not provide substantial evidence that the probability of remaining in a bout or the within-bout response rate declined during an extinction session (for model selection criteria, see Appendix A). The model ranked second, underlined in Table 4, was therefore selected as best balancing parsimony and goodness-of-fit.

Table 4.

Best extinction models according to AIC.

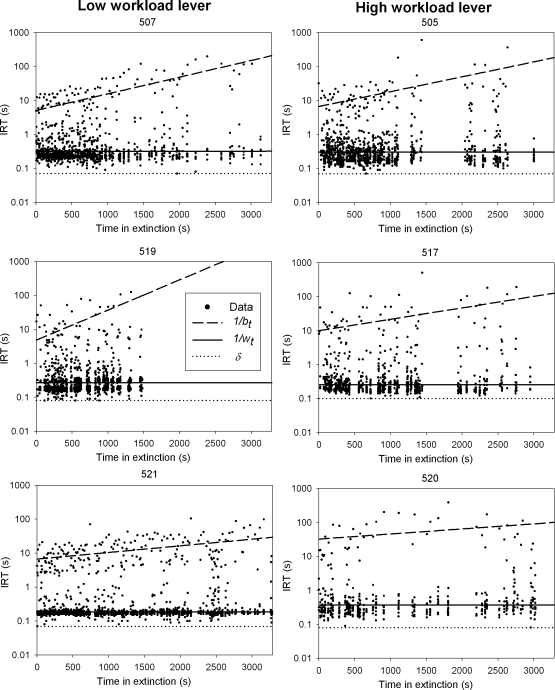
Figure 6 shows how IRTs (pauses between responses) changed as a function of time in extinction. The x-coordinate of each point is the time t when a response was emitted; the y-coordinate shows how long the animal waited until emitting the next response. Note that the y-axis is plotted on a log scale. Also shown are the fitted mean IRTs drawn from the dynamic refractory exponential model selected in Table 4—solid lines represent within-bout IRTs (δ + 1/w_t) and broken lines represent between-bout IRTs (δ + 1/b_t). Note that although the selected dynamic model assumes that b_t remains constant (flat) between consecutive responses and only increases in discrete “jumps”, the mean IRTs in Figure 6 have been joined by a smooth straight line for illustrative purposes. Figure 6 clearly shows clusters of rapid within-bout responses with mean IRT of about 0.3 s, intermixed with much slower bout-initiation responses with mean IRT of about 10 s at the beginning of the extinction session, and rising exponentially to about 100 s by the end of the session. Rat 519 ceased responding completely at about 1500 s into the session; all other rats showed a more gradual decline in bout-initiation rate.

Fig 6.

Interresponse times (IRTs) as a function of time t in extinction. The broken, solid, and dotted lines are, respectively, traces of average bout initiation IRT (1/b_t), average within-bout IRT (1/w_t), and constant minimum IRT (δ), drawn from the dynamic refractory bi-exponential model selected in Table 4 and fitted using the maximum likelihood method. Traces of 1/b_t have been joined by a smooth straight line for illustrative purposes (see main text).

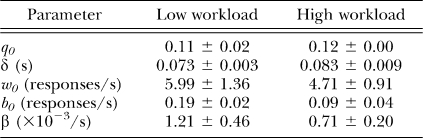
The group mean parameter estimates (±SEMs) of model 2 (Table 4) for each group are presented in Table 5. Due to the small group size (n  =  3), statistical analysis was not conducted on parameter estimates. Nonetheless, there are some noteworthy qualitative inconsistencies and regularities in parameter estimates. The difference in w₀ across workloads was not in the same direction as observed during Phase 1. As the statistical analysis suggested in Phase 1, workload-induced changes in within-bout response rate do not appear reliable. The differences in b₀ and δ across workloads, nonetheless, are consistent with the differences observed during Phase 1, thus confirming that higher workload yields fewer bouts of prolonged responses. Absent reinforcement, bouts of more laborious responses do not appear to decline faster in frequency.

Table 5.

Group mean parameter estimates (±SEMs) of extinction performance from the selected model, which fixed γ and α at zero (Model 2 in Table 3).

DISCUSSION PHASE 2: EXTINCTION

The present experiment complements a previous study by Shull et al. (2002). In their study, extinction sessions were separated into blocks of approximately 20 min, with the assumption that model parameters are constant within a block. Then, two separate analyses were conducted to estimate model parameters for each block, and changes in parameters as a function of block (time in extinction) were visually compared. The first analysis used log survival plots to fit parameters for each block. However, the authors noted that this method was problematic because the number of IRTs per block became increasingly small, which reduced the reliability of parameter estimates in the later blocks. The second technique imposed an arbitrary cutoff-IRT. All IRTs shorter than the cutoff were classified as within-bout, and all IRTs longer than the cutoff were classified as between-bout. Although Shull and colleagues used this method without any reported issues, the selection of the cutoff-IRT has the potential to misclassify pauses between bouts as within-bout IRTs, and vice versa. The present study circumvented these difficulties by generalizing the response-bout model so that any dynamic changes in steady-state parameters can be captured quantitatively. This generalization not only allows parameters to be estimated for individual subjects on a sound theoretical basis, it also has the potential to allow different hypotheses to be explicitly tested using AIC, such as which of the steady-state parameters (q, w, or b) change during extinction. The results from the present extinction experiment supported a relatively simple extension of the static refractory bi-exponential model: when reinforcement is discontinued, only the rate of bout initiation declines exponentially over time. Research elsewhere has shown similar effects of extinction on bout initiation, although small decrements in bout length were also reported (Shull et al., 2002; Podlesnik, Jimenez-Gomez, Ward, & Shahan, 2006).

Overall, these findings are consistent with reports of selective effects of rate of reinforcement on rate of bout initiation (Johnson, Pesek, & Newland, 2009; Shull et al., 2001). The evidence supports the notion that reinforcement operates primarily on the initiation of response bouts (Heyman, 1988), although other studies have shown variations in bout length (Shull et al., 2004) and within-bout response rate (Conover et al., 2001) with rate of reinforcement. The constancy of within-bout “tempo”, for instance, is particularly salient in the flat solid lines of Figure 6. As discussed in Phase 1, however, bout initiation appears to be sensitive also to workload and schedule demands. It is yet unclear whether the workload manipulation implemented in this study influenced the rate at which bout initiation declines during extinction.

GENERAL DISCUSSION

Our results support the notion that free operant responding under VI schedules is organized in bouts separated by pauses. We effectively extended this notion to characterize extinction as an exponential lengthening of the pauses that separate bouts, which is consistent with prior findings (Podlesnik et al., 2006; Shull et al., 2002). Although we considered two models to account for maintenance and extinction performance (the static and dynamic models, respectively), both models may be special cases of a more comprehensive model. In this more general model, operant performance may be characterized as a propensity to initiate response bouts, which increases with reinforcement and declines with time. Alternatively, the decline in bout-initiation may be driven by unreinforced responses, in line with Skinner's (1938/1991) notion of reflex reserve (Catania, 2005). More precisely, the model of bout-initiation decline considered in this study was a hybrid of the time-dependent and response-dependent decline models: We assumed that bout initiations decline as time without reinforcement progress, but the hypothesized clock was only updated with each response. Further research may clarify how the initiation of bouts declines in the absence of reinforcement. We also extended the bi-exponential model to include a refractory period following each response, and demonstrated that it is an informative component of operant performance.

Although the refractory bi-exponential model was capable of describing food-reinforced behavior in rats, it may be somewhat limited in describing the behavior of other species. Pigeon key-pecking has been notoriously resistant to bout-and-pause analyses. Visual inspection of log survival plots of key-pecking IRTs often fail to reveal a distinct inflection point (Bennett, Hughes & Pitts, 2007; Bowers, Hill & Palya, 2008; Podlesnik et al., 2006). This divergence in the performance of rats and pigeons suggests that a more flexible model, of which the refractory bi-exponential is a special case, may be necessary to characterize operant behavior across species.

Motoric Effects

When rats were required to press a higher, heavier lever, bout-initiation rate declined and the minimum time between consecutive responses (the refractory period δ in Equation 2) increased. Bout-initiation rate is also sensitive to deprivation level and rate of reinforcement (Shull, 2004; Shull et al., 2004), but both were kept constant across workload manipulations. Thus, it appears that workload manipulations had an effect similar to that of altering deprivation and rate of reinforcement, aside from the more purely motoric effect of lengthening of the refractory period. This is consistent with Posadas-Sanchez's (2005) finding that a higher lever force requirement decreases indices of motivation while increasing indices of response duration. Skjoldager et al. (1993) reported that an increase in lever height and force requirement prolonged pre-ratio pauses and reduced run rates in a progressive ratio schedule. Alling and Poling (1995) replicated these effects in fixed ratio schedules. Pre-ratio pauses are akin to between-bout IRTs—they indicate periods of disengagement from the operandum, and are particularly attuned to motivational manipulations such as those of deprivation level (Malott, 1966). All this evidence converges on the notion that changes in response cost necessarily influence motivation. Therefore motoric effects, which are embedded within changes in run rates, cannot be empirically isolated; they can only be analytically isolated. That is, motoric effects may not be observed without motivational changes, but they may be estimated on the basis of changes in the shortest IRT. The refractory bi-exponential model provides a means for such estimation.

The hypothesis that motoric manipulations imply motivational effects may explain some weaknesses of extant methods of motor–motivational dissociation. One popular method, for instance, consists of estimating the parameters of Herrnstein's (1970) hyperbola from performance across various VI schedules (Bradshaw, Ruddle & Szabadi, 1981; Glautier, Rigney & Wilner, 2001; Heyman, Kinzie & Seiden, 1986). A common assumption, derived from early interpretations of the hyperbolic parameters (de Villiers & Herrnstein, 1976), is that the asymptotic response rate k attained with very high reinforcement rates should be sensitive only to motoric manipulations, whereas the rate of reinforcement r_e that yields a response rate of k / 2 should only be sensitive to motivational manipulations. A recent review (Dallery & Soto, 2004) suggests that k is sensitive to motoric manipulations, but not selectively: It also appears to be sensitive to changes in deprivation level and reinforcer magnitude. In turn, r_e seems to be sensitive to motoric manipulations under certain circumstances. Motivational effects inherent to motoric manipulations may explain why r_e is sensitive to motoric manipulations, but not why k is sensitive to motivational manipulations. A generalization of Herrnstein's hyperbola (McDowell, 2005), similar to that provided by Baum (1974) for the matching law, appears to account for motivational effects otherwise absorbed by k. This may be a productive development toward a global account of performance in VI schedules. Local mechanisms similar to those suggested here, however, are not specified by the generalized hyperbola.

Schedule Effects

Rats emitted fewer response bouts when a FR requirement was appended at the end of an interval schedule. These bouts, however, were longer and denser in responses (smaller q, higher w), yielding higher overall response rates. If overall response rate was taken as an index of motivation, we would be deceived into believing that the imposition of a tandem FR schedule increased the motivation to engage the operandum. The reduction in bout-initiation rate suggests the contrary: The tandem FR schedule reduced, not increased, motivation. Why would a tandem FR schedule reduce motivation? Longer bouts increase the number of intervening responses between bout-initiating lever presses and reinforcement, and may widen the interval between the two. It is widely acknowledged that delayed reinforcement is less effective in maintaining behavior (e.g., Dickinson, Watt & Griffiths, 1992). More directly relevant to our results, pre-ratio pauses in FR schedules increase with reinforcement delay (Meunier, Starratt & Sergio, 1979; Morgan, 1972). Although the ineffectiveness of delayed reinforcement has a credit-assignment component (Lieberman, McIntosh & Thomas, 1979), it is likely to include also a motivational component: Delayed incentives are less attractive than immediate ones (e.g., Mazur, 2010). Bout initiation rate may thus be reduced by tandem FR schedules because these schedules yield longer bouts that separate their initiation from reinforcement. This explanation has a significant implication: It suggests that, even though the computer recording the rat's activity may count a bout-initiation lever press just as any other lever press, these lever presses are functionally distinct from within-bout lever presses. Despite their topographical similarity, bout-initiating responses and within-bout responses may constitute separate response classes (Schick, 1971). If such were the case, reinforcement of the latter would not completely generalize to the former, and vice versa (see Shull et al., 2004, pp. 76–78, for a related discussion on the bout as a behavioral unit).

Our explanation of reduced bout-initiation rates in tandem FR schedules is based on longer bouts. Why, then, do tandem FR schedules yield longer bouts? Probably because fast response bursts are more likely to be reinforced under tandem VT FR than under VI schedules (Killeen, 1969); schedules with a terminal tandem FR requirement selectively reinforce longer bursts. Interestingly, such reinforcement did not appear to generalize to bout-initiation lever presses in the present study, supporting the notion that bout-initiation and within-bout lever presses are functionally distinct.

Like workload manipulations, schedule manipulations appear to have a motivational and a nonmotivational component. The motivational component is related to the resulting delay between bout initiation and reinforcement. The nonmotivational component is related to the proximity of within-bout responses to reinforcement. The refractory bi-exponential model identifies changes in the former component with changes in parameter b in Equation 2, and changes in the latter component with changes in q and w.

Motivational Effects

Food deprivation selectively increased bout-initiation rate (Phase 1), whereas the elimination of reinforcement selectively reduced bout-initiation rate (Phase 2). Similarly, Podlesnik et al. (2006) found that prefeeding and extinction reduced bout-initiation rate. The results reported here complement the evidence that bout-initiation rate selectively covaries with rate of reinforcement (Shull et al., 2001). They suggest that the rat's willingness to engage the operandum, which is driven by hunger, reinforcer availability, and low “price”, is expressed in the rate of bout initiation (parameter b in Equation 2). Such general willingness may be described as operant motivation, to distinguish it from the more specific notion of incentive motivation (Bindra, 1978).

Incentive motivation refers to the approach or seeking behavior elicited by appetitive or conditional stimuli. Incentive motivation is mostly dependent on the properties of the stimulus and on the state of the animal with respect to the stimulus, and is independent of response cost and the interval between response and reinforcer. Operant motivation, instead, is a function of both incentive and response. Response cost may influence operant motivation, as shown by the effects of motoric manipulations, and longer response–reinforcer intervals are likely to reduce operant motivation, as inferred from the effects of schedule manipulation and rate of reinforcement. Incentive motivation for food, for instance, may be raised by depriving an animal of food or by presenting food (or associated stimuli) to the animal; operant motivation for engaging in food-producing activities may be raised by increasing incentive motivation for food, by reducing the energetic cost of the activities that yield food, or by reducing the time between activities and food. Because incentive motivation is subsumed within operant motivation, changes in incentive motivation may be inferred from concomitant changes in bout-initiation rate, but only when response–reinforcement contingencies are kept constant.

Researchers are often interested in drawing inferences about changes in incentive motivation from operant performance. We may want to demonstrate, for instance, that a particular treatment reduces the incentive motivation for cocaine. One way to perform this demonstration is to compare operant performance for cocaine (under maintenance or extinction schedules) with and without the treatment. Based on the results reported here, one would be advised not to compare overall response rates, but to compare estimates of the rate at which response bouts are initiated. Even then, because bout initiation is an indication of operant, not incentive motivation, one would have to rule out motoric and schedule effects that would indirectly affect operant motivation. That is, if the test indicates that only bout-initiation rates were affected by treatment, it would constitute positive evidence that the treatment reduced the incentive motivation for cocaine, but if it also affected the within-bout response rate or the minimum IRT, reliable inferences on incentive motivation may not be drawn.

The previous example assumes that the inferences we have drawn from food-seeking behavior may be generalized to cocaine self-administration. Whether such generalization is justified or not will require further research with a wider range of reinforcers (e.g., drugs, access to mates, defense against aversive stimuli) and a variety of operants. The present study has laid out the empirical and analytical methods to assess changes in the components of operant performance, even when the reinforcer is absent. We believe these methods are critical to advance our understanding of motivated behavior.

Appendix A

Maximum likelihood method and Akaike Information Criterion (AIC)

The maximum likelihood method consists of maximizing the probability of the data (i.e., the joint probability of all of the observed IRTs and the observed “no-response” periods for each individual rat in a session) given each model, by adjusting model parameters. The maximized probability is known as the maximum likelihood estimate (MLE). The Akaike Information Criterion (AIC) is then used to select between candidate models (Burnham & Anderson, 2002; for examples of its use, see Avila et al., 2009; Killeen, Sanabria & Dolgov, 2009; Sanabria, Acosta, Killeen, Neisewander & Bizo, 2008; Sanabria & Killeen, 2008). The AIC for a model is computed as AIC  =  2k − 2ln(MLE), where k is the total number of free parameters, i.e., the number of parameters allowed to vary in the model, multiplied by the number of subjects. For example, if q, w, b, and δ are allowed to vary freely for 10 subjects, k  =  4 × 10  =  40. The model with the lowest AIC (AIC_MIN) represents the best balance between likelihood (high MLE) and parsimony (low k). ΔAIC was computed for model i as ΔAIC_i  =  AIC_i − AIC_MIN. As a rule of thumb, if ΔAIC_i > 4 the evidence for model i is considered weak relative to the model with the lowest AIC (the best fitting model). This is because the likelihood of model i relative to the best fitting model is exp(ΔAIC_i/2) (Anderson & Burnham, 2002), and with ΔAIC_i > 4, it at least e² ≈ 7 times more likely to observe the data using the best fitting model than using model i. Following this rule, the simplest model (lowest k) with ΔAIC_i < 4 was favored.

Appendix B

Probability of the interval between the last response in a session and the end of the session

Let us assume that the animal emitted its last response of the session at time L, and that the session ended at time S. Then, under the assumption of the dynamic refractory bi-exponential model, the probability that an animal emits no responses between L and S is:

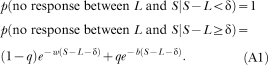For nonrefractory models, fix δ at zero. For single exponential models, fix q at zero.

Appendix C

Refractory bi-exponential model parameters

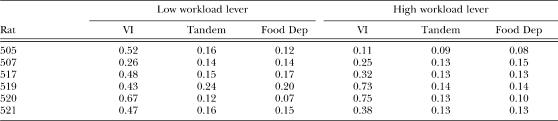
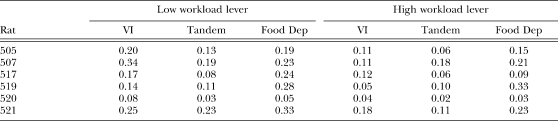
The following tables show estimates of q, δ, w, and b in separate tables. Estimates are shown separately for each individual rat in each experimental condition. Estimates were obtained for each daily session. For the VI and Tandem conditions, the mean estimate of the last four sessions is shown.

Table C1.

Estimates of parameter q (probability of quitting a response bout).

Table C2.

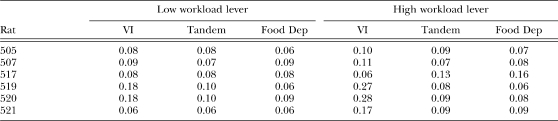
Estimates of parameter δ (minimum IRT duration) in seconds.

Table C3.

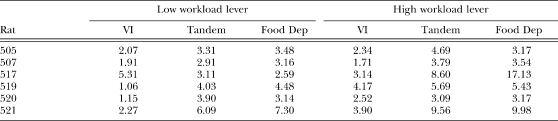
Estimates of parameter w (within-bout response rate) in responses per second.

Table C4.

Estimates of parameter b (rate of bout initiation) in responses per second.

Appendix D

Probability of the interval between the last response in a session and the end of the session, according to the dynamic model

Let us assume that the animal emitted its last response of the session at time L, and that the session ended at time S. Then, under the assumption of the dynamic refractory bi-exponential model, the probability that an animal emits no responses between L and S is:

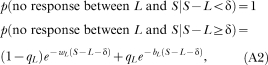where q_L, w_L and b_L are calculated by substituting L into t in Equation 5. For nonrefractory models, fix δ at zero. For single exponential models, fix q at zero.