PROPERTIES OF PHANTOM TISSUE-LIKE POLYMETHYLPENTENE IN THE FREQUENCY RANGE 20–70 MHZ

Abstract

Quantitative ultrasound (QUS) has been employed to characterize soft tissues at ordinary abdominal ultrasound frequencies (2–15 MHz) and is beginning application at high frequencies (20–70 MHz). For example, backscatter and attenuation coefficients can be estimated in vivo using a reference phantom. At high frequencies it is crucial that reverberations do not compromise the measurements. Such reverberations can occur between the phantom's scanning window and transducer components as well as within the scanning window between its surfaces. Transducers are designed to minimize reverberations between the transducer and soft tissue. Thus, the acoustic impedance of a phantom scanning window should be tissue-like; polymethylpentene (TPX) is commonly used because of its tissue-like acoustic impedance. For QUS it is also crucial to correct for the transmission coefficient of the scanning window. Computation of the latter requires knowledge of the ultrasonic properties, viz, density, speed and attenuation coefficients. This work reports values for the ultrasonic properties of two versions of TPX over the high frequency range. One form (TPX film) is used as a scanning window on high frequency phantoms, and at 40 MHz and 22°C was found to have an attenuation coefficient of 120 dB/cm and a propagation speed of 2093 m/s.

INTRODUCTION

Scanning windows on tissue-mimicking phantoms are often Saran Wrap ® (Dow Chemical Company, Midland, Michigan, USA) (Wear et al. 2005) or plastic-coated aluminum foil. (Stiles et al. 2008) Typical thicknesses of Saran Wrap used on phantoms in our lab are 12 μm and 25 μm. At ultrasonic frequencies commonly used in abdominal imaging (2–15 MHz), reverberations between the scanning window and the contacting transducer are shallow enough that they generally do not compromise the usefulness of the phantom. However, at high frequencies (20–70 MHz) such as are used in small animal (preclinical) imaging, ophthalmology or dermatology, depths of penetration are small – a few mm to about 15 mm (Foster et al. 2000; Raju et al. 2001). For these high frequency imagers, even a very thin 12-μm Saran Wrap window can result in reverberations that compromise the usefulness of the phantom. (Madsen et al. 2010) The reverberations probably arise within the transducer which is fabricated of materials to avoid reflections from skin contacting the transducer.

Polymethylpentene, also known as TPX® (Trademark of Mitsui Chemicals America, Inc., Rye Brook, New York, USA), is a plastic known for its tissue-like low acoustic impedance and reasonably low attenuation at low frequencies (about 1.6 dB/cm/MHz in the 2–12 MHz range). (Bloomfield et al. 2000) There are two versions of TPX relevant to ultrasound (US) imaging: film and sheet. The film version is made at thicknesses less than 0.5 mm, while the sheet version is thicker (2.5 mm or greater); the film version is the one we use on high frequency phantoms. Also, the production process is different for the film and sheet versions; viz, the film is extruded onto a cylinder and hardens without compression, whereas the sheet is extruded and then hardens under compression. We have found that scanning windows composed of TPX films cause no significant reverberations detectable in B-scans of phantoms at high frequencies (15–70 MHz). (Madsen et al. 2010)

Some quantitative uses of phantoms require knowledge of the transmission coefficient of the scanning window, e.g., the reference phantom method for estimating the attenuation and backscatter coefficients. (Yao et al. 1990; Lu et al. 1999) The reference phantom method eliminates scanner instrumental factors, but the transmission coefficient of any scanning window on the phantom must be accounted for.

Sufficiently accurate clinical determinations of attenuation and backscatter coefficients could contribute to differentiating benign and malignant tumors. In the low frequency range (2–12 MHz), the reference phantom method has been used to estimate backscatter and attenuation coefficients of liver (Lu et al. 1999), breast (Anderson et al. 2001), brain (Strowitzki et al. 2007), cervix (McFarlin et al. 2010; Labyed et al. 2011), and blood vessel plaque. (Shi et al. 2007)

In the high frequency range the reference phantom method has been used for estimating attenuation coefficients of dermis and subcutaneous fat in the 14–50 MHz range. (Raju and Srinivasan 2001) A laboratory system was used in which the reference phantom had a Saran Wrap scanning window. Reverberation interference was avoided in the 3–mm depth range interrogated by obtaining backscatter data with the transducer face in water at a distance greater than 3 mm from the skin and phantom surfaces; a reference phantom with a well characterized TPX scanning window would not have required a special scanning situation involving an intermediate water path.

Immediate clinical application of the reference phantom method in which the phantom has a TPX scanning window is in determination of high frequency backscatter and attenuation coefficients in dermatology. Distinction between benign and malignant tumors may be possible.

Application of the reference phantom method at high frequencies is being pursued regarding development of an improved technique for breast tumor biopsy. Preliminary to application in patients, a reference phantom with a well-characterized TPX scanning window, produced in our lab, is currently in use over the high frequency range (20–70 MHz) at the University of Illinois to characterize and differentiate in vivo human breast tumors grown in small animal hosts. An ultimate goal is to develop a high frequency ultrasound needle probe for improved biopsies of human breast tumors. The probe will be inserted into the tumor and RF data taken to allow estimation of attenuation and backscatter coefficients of the tumor tissue using the reference phantom method. Transmission through a scanning window without reverberations is necessary, and that window will likely be TPX; using the results of the work reported here, accurate correction of the data to account for transmission is facilitated.

Another high frequency reference phantom with a TPX window has been used for in vitro measurements of backscatter and attenuation coefficients of blood vessel plaque. (McCormick 2011) Using the reference phantom in a similar way could be implemented for intravascular ultrasound (IVUS) which involves frequencies between 20 and 50 MHz.

To characterize a material ultrasonically, the density, propagation speed and attenuation coefficients must be known over the frequency range of concern. Such characterization will allow, e.g., computation of the (linear) transmission coefficient between two media. Therefore, we have measured the attenuation coefficients of TPX film from 20 to 70 MHz. Propagation speed was also determined and the small speed dispersion (about 20 m/s between 20 and 70 MHz) is consistent with the Kramers-Kronig relations. (O'Donnell et al. 1981) Because thicker TPX (a few mm) can be present on medical ultrasound scan heads, e.g., to form lenses or to form transmission covers over mechanically scanned arrays, we also report on the speed and attenuation properties of the sheet form.

Finally, a test of the uncertainty estimates for measured propagation speeds and attenuation coefficients of TPX film was carried out by comparing directly measured transmission coefficients with those predicted using the measured values of propagation speeds and attenuation coefficients. The media separated by the TPX film were different and were representative of clinically relevant media.

MATERIALS

The source (distributor) of the TPX film was the C S Hyde Company (Lake Villa, Illinois, USA), and the manufacturer was Ajedium Films, a division of Solvay Solexis, Inc. (Newark, New Jersey, USA) Raw TPX (for making film or sheet) can be obtained in different grades, and the film we used was made from grade RT-18. The stock sheet form was about 2.4 mm thick and was made from TPX grade DX845; thinner layers of the sheet form were made by milling down sections of the 2.4 mm stock sheet. The distributor – and manufacturer -- of the TPX sheet was Westlake Plastics, Lenni, Pennsylvania, USA. The particular grades of TPX investigated correspond to those we have used on phantoms in our lab; for example, the TPX film has been used as a scanning window on phantoms made for performance testing at high frequencies as well as on high frequency reference phantoms (Yao et al. 1990) currently in use in our lab and a lab at the University of Illinois-Urbana. The cost of 128-μm-thick TPX film is currently about $7.50 per square foot.

MEASUREMENT METHODS

Propagation speeds and attenuation coefficients

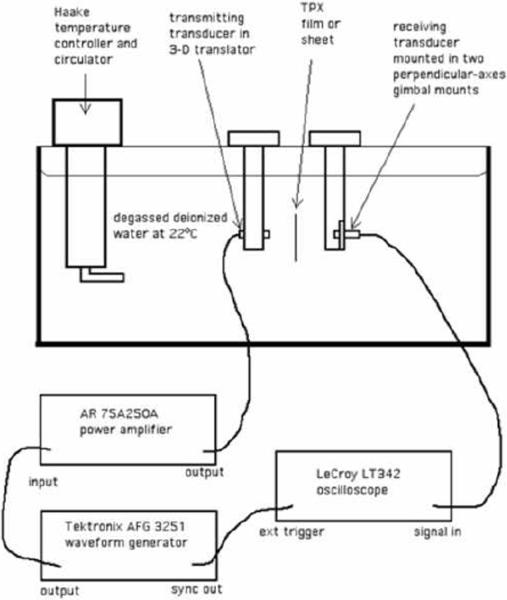
All measurements were made at 22°C except for one set made on TPX sheet at 37°C. Two measurement methods were used in the case of TPX films. The apparatus used in both methods is depicted in Fig. 1. One method (method 1) was the ordinary through-transmission/water-displacement method. (Wear et al. 2005) A film with nominal thickness of 268 μm was used. No thicker film is available from the manufacturer. Ten-cycle sinusoidal bursts with frequencies 20 through 72 MHz – in 1 MHz steps – were employed for a constant amplitude read-out at each discrete frequency. For frequencies between 20 and 40 MHz, only the first four cycles of the received waveform were addressed because of possible interference later in the waveform due to reverberations within the film. The sinusoidal bursts generated by the Tektronix AFG 3251 waveform generator were amplified by the Atlantic Research 75A250A power amplifier and output to the transmitting transducer. For frequencies between 20 and 40 MHz, a matched pair of single-element, unfocused, 6-mm-diameter, −6 dB bandwidth 80%, nominal 30 MHz transducers were employed, one as the transmitter and one as the receiver. (V356, Olympus-Panametrics, Waltham, Massachusetts, USA) For frequencies between 40 and 72 MHz, a matched pair of single-element, unfocused, 6-mm-diameter, −6 dB bandwidth 78%, nominal 50 MHz transducers were employed. (V358, Olympus-Panametrics, Waltham, Massachusetts, USA) The peak-to-peak excitation voltages were set as low as possible while assuring that signal-to-noise ratios (SNR's) were not a source of error. Typically, the excitation voltages were about 100 mV, but at 70 MHz, values as high as 1 V were needed. Because of the high frequencies, it was very important to make sure that the received beam was centered on the receiving element. As shown in Fig. 1, one transducer was mounted on a 3-D translator and the other on a gimbal mount with vertical and horizontal axes of rotation. These translators and rotators allowed peaking of the received signal at each frequency in the absence of the sample (water path only). For each frequency, two signals were monitored: one with the TPX sample absent and one with the sample interposed between the transmitter and receiver. The amplitudes were recorded for each frequency and the arrival time shift (which depends on the sample thickness) at every 5 MHz interval. It was advantageous to employ the random interleave property of the oscilloscope for optimal determinations of the amplitude ratios and time shifts. The distance between the transmitting and receiving elements was between 6 cm and 10 cm, the distance generally decreasing with increasing frequency to allow sufficient signal-to-noise ratios. (At higher frequencies, water attenuation becomes considerable.) As a result, it was not possible for the receiver to be in the far field at all frequencies. Varying the axial position of the sample had no effect on the received signal, however; thus, beam distortions due to the presence of the sample were considered negligible. The propagation speed is given by

$$c_{\mathit{TPX}}=\frac{c_w}{1+\left(c_w\Delta t\right)∕d}$$ (1)

(Kremkau et al. 1981) where c_w = 1488.3 m/s is the propagation speed in pure water at 22°C (Del Grosso VA and Mader CW 1972), d is the thickness of the TPX sample and Δt is the time shift when the sample is inserted. When Δt < 0, c > c_w. The attenuation coefficient in dB per unit length is given by

$${\alpha }_{\mathit{TPX}}=\frac{20}{d}{\log }_{10}\left(\frac{A_0{T}_{\mathit{tot}}}{A}\right)+{\alpha }_w$$ (2)

where A_o is the amplitude in the absence of the sample, A is that when the sample is interposed, T_tot is the amplitude transmission coefficient due to both surfaces of the sample and α_w is the attenuation coefficient in dB per unit length of pure water at 22°C (Kaye and Laby 1973). $T_{\mathit{tot}}=\frac{4r_w{r}_{\mathit{TPX}}}{{(r_w+r_{\mathit{TPX}})}^2}$ (See APPENDIX for derivation.) where r_W is the acoustic impedance of water and rTPX is the acoustic impedance of the sample. The sample density, taken from manufacturer's tabulated data, is 0.833 g/mL.

Fig. 1.

Diagram of apparatus used for speed and attenuation coefficient measurements. For the through-transmission/water displacement method, reverberations within the sample were avoided by measuring the amplitude and arrival time shift using the first few cycles of the waveform, while for the water-TPX-water transmission coefficient method, all significant contributing reverberations were accounted for by using the cycles late in a sufficiently long waveform that amplitudes ceased to vary with time. The distance between transmitting and receiving transducers was 6 to 10 cm.

The other method (method 2) for determining TPX film attenuation coefficients employed the technique described previously for the case of Saran Wrap ® film (Wear et al. 2005). In that technique the modulus of the (water – TPX film – water) transmission coefficient is first determined where all reverberations occurring within the TPX film which are not negligible contribute to the monitored part of the received signal. (In method 1 all reverberations are avoided.) Monitoring the peak-to-peak amplitude using the last 10 cycles of a 40 cycle tone burst will adequately account for all reverberations for the frequencies considered in this work.

That monitoring the peak-to-peak amplitude using the last 10 cycles of a 40 cycle tone burst will adequately account for all possible contributing reverberations can be shown as follows. Each successive reverberation contributes (via interference) no more than R² e^−2dα times the last reverberation where R is the amplitude reflection coefficient at a planar interface between water and TPX (Kinsler et al. 1982), d is the TPX thickness (128 μm) and α = TPX attenuation coefficient at the frequency involved. Considering the TPX propagation speed to be 2090 m/s and its density 0.833 g/mL and the propagation speed in water to be 1488 m/s and density 1 g/mL, R² = 0.00614; thus, the first reverberation will have an amplitude of less than 0.00614 times that of the transmitted wave with no reverberation, and the next reverberation will have an amplitude of less than (0.00614)² = 3.8×10⁻⁵ times that of the transmitted wave with no reverberation, etc. (The attenuation factor, which is always less than 1, is ignored.) Thus, only the first reverberation makes a measurable contribution. The wavelength in TPX at frequency f is λ = 2090 μm μs⁻¹/f, and the number of wavelengths in 2d = 256 μm/λ. For 20 through 72 MHz, the greatest number of wavelengths in 2d is less than 9. Thus, measurement of the peak-to-peak amplitude in the last 10 cycles of a 40 cycle tone burst will assure that all reverberations are adequately accounted for. Note that, even though the first reverberation has a very small amplitude, its effect is demonstrated in Fig. 5 from 20 through about 50 MHz.

Fig. 5.

Measured values of the moduli of the water – TPX film – water transmission coefficient from 20 through 72.5 MHz (x) and the transmission coefficient moduli computed using the mean propagation speed from Fig. 4 and the power law for the attenuation coefficients (solid line), corresponding to Eq. (16), which yields optimal agreement with the measured values. Optimal agreement was determined by iterating the values of α_o and n in the assumed attenuation coefficient relation α = α_o fⁿ, where f is the frequency and α_o and n are constants, until the computed transmission coefficient passed through the middle of the distribution of experimental points over the 20–70 MHz range.

At each frequency, the received amplitudes with and without the TPX film present were determined. The mount for the TPX film is shown in Fig. 2 where water existed both inside and outside of the cylinder and the polyethylene film window was absent to assure equal water pressures on each side of the TPX film. The TPX film was mounted flat on a square acrylic frame which was screwed onto the acrylic cylinder. Data reduction was accomplished using Eq. (1) from Wear et al., viz,

$$T=\frac{2r_w}{2r_w\cos \left(k_{\mathit{TPX}}d\right)+j\left(r_{\mathit{TPX}}+\frac{r_w^2}{r_{\mathit{TPX}}}\right)\sin \left(k_{\mathit{TPX}}d\right)}$$ (3)

where $j=\sqrt{-1}$, r_w, r_TPX and d are defined in the last paragraph, and $k_{\mathit{TPX}}=\frac{2\pi f}{c_{\mathit{TPX}}}-j{\alpha }_{\mathit{TPX}}$. The derivation of Eq. (3) is available in Ford (1971). The modulus, ∥T∥, was measured at each frequency f and then α_TPX was determined over the frequency range by least squares fitting to ∥T∥ values using a power law representation of α_TPX, i.e., α_TPX = B fⁿ where B and n are constants. The TPX propagation speed c_TPX employed in the data reduction was that determined from method 1. TPX film having a nominal thickness of 128 μm was used. Note that the 268-μm-thick film was used in method 1 to avoid reverberation within the film at all frequencies involved, while there was no such restriction for method 2, and the 128-μm film was used in method 2 to optimize received signal-to-noise ratios. Six thickness measurements were made around the area through which the beam passed resulting in a mean and sample standard deviation of 127.8 ± 2.9 μm; a NIST traceable calibrated micrometer was employed. (Code number 293–340, Mitutoyo America Corp., Elk Grove Village, Illinois, USA) The measurement uncertainty for a single measurement at 20°C is ± 1.3 μm for this thickness; thus, by propagation of uncorrellated errors the total uncertainty is ± 3.2 μm. The propagation of uncorrelated errors was employed as applied to calibration (systematic) and random errors. (Taylor 1997)

Fig. 2.

Diagram of liquid barrier apparatus used in measurement of the round-trip “Total” transmission coefficient: water–TPX film–1540 m/s liquid–TPX film– water. The cylinder is fixed in position in the water tank of Fig. 1 and can be rotated about the vertical axis of rotation so that the ultrasound beam from the transmitter to receiver can be aligned perpendicular to either the polyethylene window or the TPX film. Degassed de-ionized tank water surrounds the cylinder, and a solution of propylene glycol and water with a propagation speed of 1540 m/s exists inside the cylinder. Note that the same apparatus was used in method 2 with water inside and outside the cylinder.

Test of the capacity to predict transmission coefficients

Data acquisition

An assessment of the uncertainty estimates for TPX film propagation speeds and attenuation coefficients was carried out by comparing directly measured transmission coefficients for TPX film between two different media with transmission coefficients computed using the measured values of TPX propagation speeds and attenuation coefficients. The two media chosen were water and a solution of propylene glycol and water having a tissue-like propagation speed of 1540 m/s. These two media are relevant to some preclinical laboratory measurements where the reference phantom method is used to estimate the attenuation and backscatter coefficients of tumors hosted by small animals, and a water path exists between the tumor and the transducer. The choice of media is also relevant to clinical skin tissue-characterization in which it may be desirable to include a variable water path stand-off so that the focus of a single element transducer can be positioned at various depths. Application of the reference phantom method in these preclinical and clinical examples would involve production of a matching water path length between the transducer and TPX film.

The apparatus used has been previously described (Stiles et al. 2008). It consists of the same apparatus as in Fig. 1 except that a cylindrical acrylic liquid barrier with vertical TPX and polyethylene windows exists in the water tank of Fig. 1. The barrier is diagrammed in Fig. 2.

Ideally, there would be direct contact between the water and propylene glycol/water solution, but that is impossible since the two would mix. Although the polyethylene (PE) window is thin (13.5 μm = about 2 wavelengths at 70 MHz), its presence nevertheless must be accounted for in the data reduction to determine the modulus of the TPX film total transmission coefficient. The modulus of the PE total transmission coefficient is much closer to 1 than in the case of TPX (see Figs. 11 and 12), so the correction is small (13% or less) but must be included. The matched pair of transducers is first aligned so that their symmetry axes are approximately co-linear and perpendicular to the polyethylene film. Then with 40-cycle sinusoidal ultrasound bursts being generated, the amplitude of the received signal is maximized. (Forty cycles were sufficient that the last part of the received waveform had constant amplitude over all frequencies involved.) Then the cylinder is rotated by a small amount to further maximize the received signal; the later step assures that the film is perpendicular to the ultrasound beam. The peak-to-peak voltage amplitude is recorded and the cylinder rotated so that the beam passes through the TPX film; the received amplitude is again maximized, and the peak-to-peak voltage amplitude is recorded. Then the transmitter/receiver roles of the transducers are switched, peaking of the received signals again done, and peak-to-peak voltage amplitudes recorded with polyethylene and then TPX in position. Seven matched pairs of broadband unfocused transducers were used to span the range of frequencies from 0 to 70 MHz; the nominal frequencies were 2.5, 5, 7, 10, 15, 30 and 50 MHz. Data were obtained in 2 MHz steps.

Fig. 11.

Experimental values for ∥T^TPX_tot∥ (Δ) compared with predicted values (solid line). The predicted ∥T^TPX_tot∥ values were computed with speed and attenuation values determined using method 1; see Eq. (14) for attenuation values. The TPX speed value used was the mean of those in Fig. 4. The ∥T^PE_tot∥ values (dashed line) were computed with a tabulated c_PE = 2000 m/s and attenuation values (α_PE) determined via method 2 (see Eq. (18)).

Fig. 12.

Same as Fig. 11 except that the predicted ∥T^TPX_tot∥ values (solid line) were determined with attenuation coefficient values using method 2 (see Eq. (16)) and the mean speed found using method 1 (see Fig. 4).

Data analysis: accounting for the transmission coefficient of the polyethylene film

Two relations (equations (10 and 13) below) are derived to account for the transmission coefficients of the polyethylene film. The subscript 1 refers to water and the subscript 2 refers to the propylene glycol/water solution. Table 1 lists the definitions of the parameters involved in the derivation. We have moduli of

$$\parallel T_{1\to 2}^{\mathit{TPX}}\parallel =\frac{A_2^{\mathit{TPX}}}{A_1}\mathrm{and}\parallel T_{1\to 2}^{\mathit{PE}}\parallel =\frac{A_2^{\mathit{PE}}}{A_1}.$$ (4)

Assume that the TPX and PE films are sufficiently thin that the diffraction pattern at the receiver is the same for TPX and PE. (This assumption was justified experimentally when no change in received amplitude occurred when the TPX film was moved from being within 1 cm of the transmitter to within 1 cm of the receiver – including 70 MHz.) Then

$$\frac{V_2^{\mathit{TPX}}}{A_2^{\mathit{TPX}}}=\frac{V_2^{\mathit{PE}}}{A_2^{\mathit{PE}}}.$$ (5)

From Eq. (4)

$$\frac{1}{A_1}=\frac{\parallel T_{1\to 2}^{\mathit{PE}}\parallel }{A_2^{\mathit{PE}}}\mathrm{and}\parallel T_{1\to 2}^{\mathit{TPX}}\parallel =\parallel T_{1\to 2}^{\mathit{PE}}\parallel \left(\frac{A_2^{\mathit{TPX}}}{A_2^{\mathit{PE}}}\right).$$ (6)

From Eq. (5)

$$\parallel T_{1\to 2}^{\mathit{TPX}}\parallel =\parallel T_{1\to 2}^{\mathit{PE}}\parallel \left(\frac{V_2^{\mathit{TPX}}}{V_2^{\mathit{PE}}}\right)$$ (7)

Exchanging 1 and 2 in all of the above, we have

$$\parallel T_{2\to 1}^{\mathit{TPX}}\parallel =\parallel T_{2\to 1}^{\mathit{PE}}\parallel \left(\frac{V_1^{\mathit{TPX}}}{V_1^{\mathit{PE}}}\right).$$ (8)

Then the modulus of the total transmission coefficient for TPX in terms of that for polyethylene is

$$\parallel T_{\mathit{tot}}^{\mathit{TPX}}\parallel =\parallel T_{1\to 2}^{\mathit{TPX}}\parallel \times \parallel T_{2\to 1}^{\mathit{TPX}}\parallel =\parallel T_{1\to 2}^{\mathit{PE}}\parallel \times \parallel T_{2\to 1}^{\mathit{PE}}\parallel \left(\frac{V_2^{\mathit{TPX}}}{V_2^{\mathit{PE}}}\right)\left(\frac{V_1^{\mathit{TPX}}}{V_1^{\mathit{PE}}}\right)=\parallel T_{\mathit{tot}}^{\mathit{PE}}\parallel \left(\frac{V_2^{\mathit{TPX}}}{V_2^{\mathit{PE}}}\right)\left(\frac{V_1^{\mathit{TPX}}}{V_1^{\mathit{PE}}}\right);$$ (9)

thus, we have

$$\parallel T_{\mathit{tot}}^{\mathit{TPX}}\parallel =\parallel T_{\mathit{tot}}^{\mathit{PE}}\parallel \left(\frac{V_2^{\mathit{TPX}}}{V_2^{\mathit{PE}}}\right)\left(\frac{V_1^{\mathit{TPX}}}{V_1^{\mathit{PE}}}\right).$$ (10)

The amplitude transmission coefficients T^PE_1→2 and T^PE_2→1 are computed using Eq. (1) in Wear et al. (2005) as follows:

$$T_{1\to 2}^{\mathit{PE}}=\frac{2r_{\mathit{PG}∕\mathit{w}}}{(r_w+r_{\mathit{PG}∕\mathit{w}})\cos \left(k_{\mathit{PE}}{d}_{PE}\right)+j\left(r_{\mathit{PE}}+\frac{r_w{r}_{\mathit{PG}∕\mathit{w}}}{r_{\mathit{PE}}}\right)\sin \left(k_{\mathit{PE}}{d}_{\mathit{PE}}\right)}$$ (11)

and

$$T_{2\to 1}^{\mathit{PE}}=\frac{2r_{\mathit{w}}}{(r_w+r_{\mathit{PG}∕\mathit{w}})\cos \left(k_{\mathit{PE}}{d}_{\mathit{PE}}\right)+j\left(r_{\mathit{PE}}+\frac{r_w{r}_{\mathit{PG}∕\mathit{w}}}{r_{\mathit{PE}}}\right)\sin \left(k_{\mathit{PE}}{d}_{\mathit{PE}}\right)}$$ (12)

where r_W is the acoustic impedance of water, r_PG/w is the acoustic impedance of the propylene glycol/water solution, r_PE is the acoustic impedance of polyethylene, and d_PE is the thickness of the PE film. The complex wave number value is k_PE = 2πf/c_PE + j α_PE, where c_PE = the polyethylene propagation speed and α_PE = the polyethylene attenuation coefficient at the frequency of concern. The value for c_PE was taken from tables (Kaye and Laby 1973), and the values for α_PE were determined experimentally. (See relevant subsection in the RESULTS section below.) Thus, from Eqs. (11) and (12)

$$\parallel T_{\mathit{tot}}^{\mathit{PE}}\parallel =\frac{4r_w{r}_{\mathit{PG}∕\mathit{w}}}{{\parallel (r_w+r_{\mathit{PG}∕\mathit{w}})\cos \left(k_{\mathit{PE}}d\right)+j\left(r_{\mathit{PE}}+\frac{r_w{r}_{\mathit{PG}∕\mathit{w}}}{r_{\mathit{PE}}}\right)\sin \left(k_{\mathit{PE}}d\right)\parallel }^2}$$ (13)

Table 1.

Definitions of parameters involved in the derivation of equations (10) and (13). The subscript 1 refers to water and the subscript 2 refers to the propylene glycol/water solution.

TTPX1→2	amplitude transmission coefficient through TPX from medium 1 to medium 2
TTPX2→1	amplitude transmission coefficient through TPX from medium 2 to medium 1
TPE1→2	amplitude transmission coefficient through polyethylene (PE) from medium 1 to medium 2
TPE2→1	amplitude transmission coefficient through polyethylene (PE) from medium 2 to medium 1
TPEtot	product of TPE2→1 and TPE1→2
An	pressure amplitude of wave incident on TPX or PE from medium n (n = 1 or 2)
ATPXn	pressure amplitude of wave passing from TPX into medium n (n = 1 or 2)
APEn	pressure amplitude of wave passing from PE into medium n (n = 1 or 2)
VTPXn	peak-to-peak voltage amplitude of received signal in medium n when TPX is in place (n = 1 or 2)
VPEn	peak-to-peak voltage amplitude of received signal in medium n when PE is in place (n = 1 or 2)

The mass density of the polyethylene film was measured by submerging an approximately 0.5 cm² piece of the polyethylene film in a solution of 1-bromododecane (density, 1.038 g/mL) and tetradecane (density, 0.763 g/mL). (Sigma Chemical, St. Louis, Missouri, USA) The solution was computed to have a density of about 0.91 g/mL. Addition of small amounts of 1-bromododecane and/or tetradecane, while stirring to make uniform solutions, resulted in the polyethylene film neither rising nor sinking. The density of the final solution (and of the polyethylene film) was then measured with a calibrated hydrometer (Catalog number 11-556D, Fisher Scientific, Pittsburgh, Pennsylvania, USA) with the result of 0.919 g/mL.

Voltages applied to the transmitting transducers

It may be of interest to researchers who would like to employ the measurement methods described to know the peak-to-peak voltages applied to the transmitting transducers. For all measurements described above a six-foot RG 58 immersion coaxial cable connected the output of the power amplifier to the transducer. Since the wavelength of the transmitted voltage at 70 MHz is about 3 meters, the six-foot cable length could result in different peak-to-peak voltages at each end of the cable. Therefore, we measured the voltages using a substitute six-foot RG 58 cable with a T having a UHF connector for the transducer and a BNC connector for the oscilloscope input; the input impedance of the scope was 1 MΩ. (At 70 MHz the peak-to-peak voltage at the transducer was about 90% of that at the power amplifier output.) Also, all peak-to-peak voltages were measured with the emitting end of the transducer immersed in water. Tables 2 and 3 show these voltages for each measurement event.

Table 2.

Transducer models and peak-to-peak voltages applied to transmitting transducers for measurements at 2 MHz intervals (where applicable). For all frequencies of 20–72 MHz, the transmitting and receiving transducers are Panametrics (Olympus) matched pairs. For 2–18 MHz the transmitter is Panametrics, but the receiver is different (Panametrics or AeroTech) and makes and models are given in footnotes to the table.

Frequency (MHz)	Method 1 :TPX film		Method 2 : PE film		Transmission : H2→TPX→propylene glycol solution		Transmission: propylene glycol solution→TPX→H2O
	p-p volts	Transmitter model	p-p volts	Transmitter model	p-p volts	Transmitter model	p-p volts	Transmitter model
2	-	-	-	-	0.857	V306a	0.857	V306a
4	-	-	-	-	0.766	V309b	0.766	V309b
6	-	-	-	-	0.552	V309b	0.552	V309b
8	-	-	-	-	0.656	V320c	0.656	V320c
10	-	-	-	-	0.369	V311d	0.369	V311d
12	-	-	-	-	0.49	A319S	0.49	A319Se
14	-	-	-	-	0.54	A319S	0.54	A319Se
16	-	-	-	-	0.517	A319S	0.353	A319Se
18	-	-	-	-	0.545	A319S	0.442	A319Se
20	29.6	V358	8.34	V358	2.35	V356	0.451	A319Se
22	29.6	V358	8.52	V358	2.42	V356	8.52	V356
24	31.2	V358	8.93	V358	2.51	V356	8.93	V356
26	34.3	V358	9.85	V358	2.66	V356	9.85	V356
28	39.1	V358	11.26	V358	2.79	V356	11.26	V356
30	47.0	V358	13.22	V358	2.87	V356	13.22	V356
32	56.5	V358	16.4	V358	3.05	V356	16.4	V356
34	65.9	V358	19.1	V358	19.1	V358	19.1	V358
36	69.7	V358	20.3	V358	20.3	V358	20.3	V358
38	65.9	V358	19.0	V358	19.3	V358	19.0	V358
40	56.8	V358	16.4	V358	17.5	V358	16.4	V358
42	52.6	V358	22.6	V358	22.6	V358	10.62	V358
44	50.1	V358	21.4	V358	23.7	V358	9.62	V358
46	49.7	V358	28.3	V358	21.2	V358	8.62	V358
48	50.1	V358	28.5	V358	19.1	V358	7.22	V358
50	50.6	V358	57.9	V358	17.1	V358	50.6	V358
52	50.6	V358	57.4	V358	50.6	V358	50.6	V358
54	68.8	V358	55.4	V358	55.4	V358	21.0	V358
56	65.2	V358	52.4	V358	14.63	V358	26.2	V358
58	60.9	V358	49.2	V358	60.9	V358	55.1	V358
60	56.8	V358	45.6	V358	56.8	V358	51.2	V358
62	52.9	V358	88.9	V358	25.4	V358	40.3	V358
64	49.9	V358	84.5	V358	43.5	V358	43.5	V358
66	69.1	V358	47.2	V358	69.1	V358	69.1	V358
68	64.7	V358	44.2	V358	53.6	V358	64.7	V358
70	60.2	V358	73.8	V358	73.8	V358	60.2	V358
72	-	-	69.3	V358	-	-	-	-

^aAerotech Delta PN2794-1

^bAerotech Delta PN2794-3

^cAerotech Delta PN2794-4

^dDelta OOJWM4

^ePanametrics A313S

Table 3.

Transducer models and peak-to-peak voltages applied to transmitting transducers for measurements at 2.5 or 5 MHz intervals. For all frequencies of 20–72.5 MHz, the transmitting and receiving transducers are Panametrics (Olympus) matched pairs. For 10 and 15 MHz the transmitter and receiver are Panametrics, but the receiver model is different as noted in a table footnote.

Frequency (MHz)	Method 2 :TPX film		Method 1 : TPX sheet
	p-p volts	Transmitter model	p-p volts	Transmitter model
10	-	-	2.02	V311a
15	-	-	0.679	A319Sb
20	8.34	V358	8.48	V358
22.5	6.56	V358	-	-
25	7.11	V358	9.39	V358
27.5	8.16	V358	-	-
30	9.98	V358	13.36	V358
32.5	12.9	V358	-	-
35	19.9	V358	20.30	V358
37.5	19.5	V358	-	-
40	16.4	V358	36.60	V358
42.5	22.3	V358	-	-
45	21.3	V358	32.30	V358
47.5	28.5	V358	-	-
50	28.7	V358	32.70	V358
52.5	36.5	V358	-	-
55	40.8	V358	10.35	V358
57.5	49.9	V358	-	-
60	56.8	V358	11.58	V358
62.5	52.2	V358	-	-
65	66.6	V358	14.59	V358
67.5	76.4	V358	-	-
70	73.8	V358	20.40	V358
72.5	75.2	V358	-	-

^aDelta OOJWM4

^bPanametrics A313S

RESULTS

All results correspond to measurements at 22°C except for a set of measurements at 37°C for TPX sheet.

Speed and attenuation coefficients of the TPX film

Method 1

Fig. 3 shows attenuation coefficients from 20 to 70 MHz measured at 1 MHz intervals using method 1 on a nominal 268-μm-thick sample of TPX film. The curve resulting from a least squares fit to a power law is shown in the figure. That power law result is

$${{\alpha }_{\mathrm{TPX}}}^{\mathrm{meth}1}=1.038{\mathrm{f}}^{1.284}\mathrm{dB}{\mathrm{cm}}^{-1}{\mathrm{MHz}}^{-1.284}.$$ (14)

For reference, the value of α_TRX^meth1 at 40 MHz is 118.4 dB cm⁻¹.

Fig. 3.

Attenuation coefficients of TPX film measured using method 1 (♦) and the resulting power law fit (solid line). The power law fit is given in Eq. (14).

Fig. 4 shows measured propagation speeds at 5 MHz intervals with a least squares fitted Kramers-Kronig curve computed using the approximation in Eq. (3b) in O'Donnell et al. (1981), viz,

$$c\left(\omega \right)=c\left({\omega }_0\right)+\frac{2c^2\left({\omega }_0\right)}{\pi }{\int }_{{\omega }_0}^{\omega }\frac{\alpha (\omega \prime )}{\omega {\prime }^2}d\omega \prime$$ (15)

where c(ω_o) is the speed at some angular frequency ω_o and ω is any angular frequency in the range over which the attenuation coefficient α has been measured; c(ω_o) is varied to accomplish the least squares fitting. The error in propagation speeds strongly depends on the sample thickness uncertainty. Thickness measurements at eight positions in the area of the sample where the beam passed through resulted in a mean and sample standard deviation of 269.5 ± 1.6 μm.

Fig. 4.

Propagation speeds of TPX film measured using method 1 (♦). The error bars account for precision and sample thickness uncertainties. The dashed curve is the Kramers-Kronig prediction where least squares fitting using Eq. (15) determined the position of the curve.

Method 2

Fig. 5 shows measured values of the water – TPX film – water transmission coefficient moduli, ‖T^TPX_w→w‖, from 20 through 72.5 MHz in 2.5 MHz increments. The solid curve corresponds to the best fit to the experimental values assuming a power law for TPX film attenuation coefficients and a mean propagation speed of 2093 m/s (see Fig. 4). The resulting power law for TPX film attenuation coefficients is

$${{\alpha }_{\mathrm{TPX}}}^{\mathrm{meth}2}=0.906{\mathrm{f}}^{1.324}\mathrm{dB}{\mathrm{cm}}^{-1}{\mathrm{MHz}}^{-1.324}.$$ (16)

At 40 MHz α_TPX^meth2 = 119.7 dB cm⁻¹ which is within 1.1% of the value obtained using method 1.

A comparison of the attenuation coefficients for TPX film using methods 1 and 2 is shown in Fig. 6. The dotted line corresponds to use of method 1 (Eq. (14)) and the dashed line to use of method 2 (Eq. (16)).

Fig. 6.

Comparison of TPX film attenuation coefficients determined using method 1 (dotted line) and method 2 (dashed line). Also shown are the attenuation coefficients for TPX sheet (solid line) showing the considerable difference between the film and sheet values; e.g., at 50 MHz, the TPX sheet value is 83% of the mean value for the TPX film.

Speed and attenuation coefficients of TPX sheet

Measurements of the attenuation coefficients and propagation speeds on TPX sheet were done using only method 1 since production of sufficiently thin sheets was not practical for application of method 2 due to the high attenuation. Fig. 7 shows measured values of attenuation coefficients from 10 through 70 MHz at 5 MHz intervals. The solid curve results from least squares curve fitting to a power law, which is

$${{\alpha }_{\mathrm{TPX}}}^{\mathrm{meth}1}=0.645{\mathrm{f}}^{1.360}\mathrm{dB}{\mathrm{cm}}^{-1}{\mathrm{MHz}}^{-1.360}.$$ (17)

For comparison with the 118.4 dB cm⁻¹ value for TPX film at 40 MHz, the value for TPX sheet is 97.4 dB cm⁻¹ at 40 MHz; i.e., the sheet value is about 18% less than the film value.

Fig. 7.

Experimental values of attenuation coefficients for TPX sheet (Δ) and least squares curve-fit to the data (solid line). The solid line corresponds to a least squares curve fit to the experimental points (Eq. (17)).

Fig. 8 shows measured propagation speeds at 5 MHz intervals with a least squares fitted Kramers-Kronig relation (Eq. (15)). Two thicknesses (2.39 mm and 1.47 mm) were used, one corresponding to the filled diamonds and the other to the open diamonds. The thickness error propagated into the speed values is the same for all filled diamonds and for all open diamonds; i.e., there are two thickness error values, one for the filled diamonds and another for the open diamonds.

Fig. 8.

Experimental values of propagation speed for 20 – 40 MHz (♦) correspond to a mean sample thickness and standard deviation of 2.3916 ± 0.0041 mm, and values for 40 –70 MHz (◊) correspond to a mean sample thickness and standard deviation of 1.4692 +/− 0.0030 mm. Error bars account for precision and uncertainty in sample thickness. The dashed curve results from least squares fit of Eq. (15).

Because TPX sheet could be used in a transducer in contact with a patient's skin, attenuation coefficients and propagation speeds were measured at 37°C. Regarding temperature dependencies of TPX sheet, it was found that the attenuation coefficients of TPX sheet increase by about 8%, and the propagation speed decreases by about 65 m/s (3%) as the temperature rises from 22°C to 37°C (body temperature). Attenuation coefficient results at 37°C are shown in Fig. 9. Compare with values in Fig. 7. The propagation speed was measured at 40 MHz and was 2073 m/s.

Fig. 9.

Attenuation coefficients of the TPX sheet at 37°C. The solid line corresponds to a least squares fit to the experimental points; the curve-fit equation is also shown in the figure.

Speed and attenuation coefficients of polyethylene film

Only method 2 was used to estimate attenuation coefficients of the polyethylene film since thicker samples than the 13.5 μm form were not available from the manufacturer, and 13.5 μm is too thin to facilitate use of method 1. The propagation speed of 2000 m/s was taken from tables (Kaye and Laby 1973).

Fig. 10 shows data points for the transmission coefficient moduli measured at 2 MHz intervals from 2 through 72 MHz. The solid curve is a graph of the best obtainable fit to the data assuming a power law for the attenuation coefficients. The fit was derived by inserting the speed and trial power law relations for the attenuation coefficients into Eq. (3), where the subscript TPX is replaced with PE (polyethylene). The resulting relation for the attenuation coefficients of the polyethylene film is

$${{\alpha }_{\mathrm{PE}}}^{\mathrm{meth}2}=8.88{\mathrm{f}}^{0.92}\mathrm{dB}{\mathrm{cm}}^{-1}{\mathrm{MHz}}^{-0.92},$$ (18)

and the result of the fit is shown in Fig. 10. For reference, the value of α_PE^meth2 at 40 MHz is 264.4 dB cm⁻¹.

Fig. 10.

Measured values of the water – PE film – water transmission coefficient moduli from 2 through 72 MHz (x) and the transmission coefficient moduli computed using a mean propagation speed of 2000 m/s and a power law for the attenuation coefficients (solid line), corresponding to Eq. (18), which yields optimal agreement with the measured values. Optimal agreement was determined by iterating the values of α_o and n in the assumed attenuation coefficient relation α = α_o fⁿ, where f is the frequency and α_o and n are constants, until the computed transmission coefficient moduli were as close as achievable to the middle of the distribution of experimental points over the 20–70 MHz range. Regarding the “leveling off” of the transmission coefficient moduli above 40 MHz, there are two competing factors. In the absence of attenuation, there would be a minimum value at 37 MHz (at which the film thickness = (1/4)xwavelength) with increase at larger frequencies to 1 again at 74 MHz (at which the film thickness = (1/2)xwavelength); the large attenuation (increasing with frequency) tends to drive the transmission coefficient modulus lower with increasing frequency.

Prediction of round-trip transmission coefficients between different media

Figs. 11 and 12 show comparisons of experimentally determined (Δ) values of ‖T^TPX_tot‖ and predicted – or computed – values (solid lines) of ‖T^TPX_tot‖ from 2 through 70 MHz; Figs. 11 and 12 differ regarding whether method 1 or 2 was used to determine the propagation speeds and attenuation coefficients that were used in the computation of ‖T^TPX_tot‖. The computed values of ‖T^TPX_tot‖ were found using the relation

$$\parallel T_{\mathit{tot}}^{\mathit{TPX}}\parallel =\frac{4r_w{r}_{\mathit{PG}∕\mathit{w}}}{{\parallel (r_w+r_{\mathit{PG}∕\mathit{w}})\cos \left(k_{\mathit{TPX}}d\right)+j\left(r_{\mathit{TPX}}+\frac{r_w{r}_{\mathit{PG}∕\mathit{w}}}{r_{\mathit{TPX}}}\right)\sin \left(k_{\mathit{TPX}}d\right)\parallel }^2}$$ (19)

where r_TPX is the acoustic impedance of the TPX film and $k_{\mathit{TPX}}=\frac{2\pi f}{c_{\mathit{TPX}}}-j{\alpha }_{\mathit{TPX}}$ is the complex wave number. Eq. (19) corresponds to Eq. (13) where PE is replaced with TPX. The dashed lines in Figs. 11 and 12 correspond to application of Eq. (13) and is used in the determination of the experimental values ‖T^TPX_tot‖ as described in section Data analysis: accounting for the transmission coefficient of the polyethylene film.

SUMMARY

Attenuation coefficients and propagation speeds for TPX film were measured using method 1. Propagation speeds are shown in Fig. 4. The errors are dominated by the thickness uncertainty. Conformity to the Kramers-Kronig relations is one test of the accuracy of measurements of these two parameters. Using the Kramers-Kronig relation in Eq. (15) with attenuation coefficients in Eq. (14), a least-squares fit to the measured speed values resulted in the prediction given by dashed line in Fig. 4. Though conformity of the measured values to the Kramers-Kronig prediction is not confirmed, it is also not contradicted.

Method 2 was also used to measure the attenuation coefficients of the TPX film from 20 through 72.5 MHz. Using the mean speed found with method 1 and trial power law representations for the attenuation coefficients in Eq. (3) resulted in the excellent fit to the data seen in Fig. 5. The resulting optimal power law for the attenuation coefficients is given by Eq. (16). In Fig. 6 excellent agreement between results using methods 1 and 2 to measure attenuation coefficients is demonstrated; above 40 MHz, the result for method 1 is slightly lower than that for method 2, the greatest difference being about 2%.

Measurements of the attenuation coefficients and propagation speeds on TPX sheet were done using only method 1 since production of sufficiently thin sheets was not practical for application of method 2 because of the high attenuation values obtained in method 1 (see Fig. 7). Least squares fitting of the attenuation coefficient values yielded Eq. (17). The attenuation coefficients of TPX sheet are considerably less than in the case of the TPX film as shown in Fig. 6 where the solid line corresponds to Eq. (17). For example, at 50 MHz the TPX sheet value is 83% of the mean value for the TPX film.

Measured values of propagation speeds for TPX sheet are shown in Fig. 8 along with the least-squares fitted Kramers-Kronig relation with Eq. (17) inserted. Conformity with the Kramers-Kronig prediction is demonstrated.

Only method 2 was practical for measuring the attenuation coefficients of the polyethylene film used in the apparatus described in the subsection Test of the capacity to predict transmission coefficients. Because of the very thin material (13.5 μm) it was also not practical to estimate a propagation speed so a value from tables was employed. An optimal fit to the water--polyethylene film—water transmission coefficients resulted in Eq. (18) for the polyethylene attenuation coefficients.

Figs. 11 and 12 demonstrate that the prediction of ‖T^TPX_tot‖ using attenuation coefficients measured via method 1 and method 2 – and speed from method 1 -- are nearly identical, as expected. A direct comparison is shown in Fig. 13. Also, agreement with experimental measurements of ‖T^TPX_tot‖ is excellent for both methods. Thus, the validity of using the propagation speed and attenuation coefficients for TPX film to predict transmission coefficients between different media is strengthened.

Fig. 13.

Comparison of ∥T^TPX_tot∥ predicted via from method 1 (solid line) with that predicted via method 2 (dashed line) showing level of agreement between the two.

DISCUSSION

For quantitative ultrasound where corrections for the transmission coefficients of the scanning window are needed when the scanning window exists between different media, prediction of the transmission coefficients in the high frequency range can be made with confidence using the attenuation and speed values reported in this work. However, caution is advised regarding an assumption that the attenuation and speed results presented apply for all TPX film and sheet because it was found that the raw TPX used to manufacture the film or sheet comes in different “grades” and that the process for producing the TPX film is different from that used in the production of TPX sheet. Thus, it is recommended that the results presented in this work be taken to apply only for the particular types of TPX film and sheet investigated.

Clinical implications of this work involve supportive roles. Use of the reference phantom method in the high frequency range may aid in the diagnosis of diseased tissues through knowledge of in vivo attenuation and backscatter coefficients. The success of the reference phantom method will likely require correction for the propagation speed and frequency-dependent attenuation coefficient of a TPX scanning window on the phantom. Knowledge of the high frequency properties of TPX may also be valuable regarding the design of future high frequency scan heads.

Future extensions of this work include characterizing other materials which are – or might – be used by scanner manufacturers in the high frequency range as acoustic lenses or as coupling layers covering transducer arrays. One type of material is Rexolite® which is polypropylene that has been cross-linked in various ways. A form of Rexolite is used on high frequency arrays by VisualSonics®.

APPENDIX

Following is the derivation of the correction factor T_tot in Eq. (2). The amplitude transmission coefficient from medium 1 to medium 2 for normal incidence is T_1→2 = 2r₂/(r₁ + r₂) where r₁ and r₂ are the acoustic impedances of media 1 and 2 (Kinsler et al. 1982), and that for transmission from medium 2 to medium 1 is T_2→1 = 2r₁/(r₁ + r₂). Thus, when the part of the pulse addressed involves no reverberations between two parallel interfaces with medium 2 between medium 1 on either side, we have T_tot = T_1→2 T_2→1 = 4r₁r₂/(r₁ + r₂)². In our case, medium 2 is TPX and medium 1 is water (w), and the relation becomes T_tot = 4r_wr_TPX/(r_w + r_TPX)².