An EM Algorithm for Fitting a 4-Parameter Logistic Model to Binary Dose-Response Data

Abstract

This article is motivated by the need of biological and environmental scientists to fit a popular nonlinear model to binary dose-response data. The 4-parameter logistic model, also known as the Hill model, generalizes the usual logistic regression model to allow the lower and upper response asymptotes to be greater than zero and less than one, respectively. This article develops an EM algorithm, which is naturally suited for maximum likelihood estimation under the Hill model after conceptualizing the problem as a mixture of subpopulations in which some subjects respond regardless of dose, some fail to respond regardless of dose, and some respond with a probability that depends on dose. The EM algorithm leads to a pair of functionally independent 2-parameter optimizations and is easy to program. Not only can this approach be computationally appealing compared to simultaneous optimization with respect to all four parameters, but it also facilitates estimating covariances, incorporating predictors, and imposing constraints. This article is motivated by, and the EM algorithm is illustrated with, data from a toxicology study of the dose effects of selenium on the death rates of flies. Other biological and environmental applications, as well as medical and agricultural applications, are also described briefly. Computer code for implementing the EM algorithm is available as supplemental material online.

1. Introduction

The general problem of modeling binary data as a function of covariates is important in many research areas. This article focuses on the dose-response problem of modeling the probability of a binary response as a function of some measure of dose, which has applications in the biological and environmental sciences, as well as in many other disciplines. The data that motivated this research, and that are used to illustrate the proposed analysis, come from a toxicology study of the dose effects of selenium on the death rates of flies (Jeske et al, 2009). In other areas, one might have a clinical interest in the proportion of subjects experiencing pain relief after ingesting a specific dose of an analgesic drug (Finney, 1978) or an environmental interest in the dose-response relationship between dioxin-like compounds and tumor rates (Walker et al, 2005).

Often, a simple 2-parameter logistic regression model provides an adequate summary of how a binary response relates to dose. This model specifies that the logit-transformed response probability is linear in the dose metric. Consequently, the parameters of interest are an intercept and a slope. Under this model, the dose-response curve has a lower asymptote of zero and an upper asymptote of one, the limits of the expected range of response probabilities.

That [0,1] range may not always be appropriate for modeling response probabilities. For example, some flies may die from causes unrelated to selenium toxicity while others may survive the study no matter how high the dose of selenium. Similarly, some patients may get pain relief from a placebo with no analgesic drug while others may get no pain relief regardless of analgesic dose; and some rodents may develop tumors from non-dioxin causes while others may remain tumor-free despite dioxin exposure. Finney (1978) gives several other biological assay examples and labels such subjects as natural responders and resistants, which we refer to as obligate responders and obligate non-responders, respectively. In these cases, the dose-response probabilities range over a subinterval of [0,1]. Thus, a natural generalization of the 2-parameter logistic model adds two more parameters so that the lower response asymptote may be greater than zero and the upper response asymptote may be less than one. The resulting 4-parameter logistic model provides increased flexibility at the cost of a higher dimensional optimization.

The notion that some subjects will or will not respond, independently of dose, while others have response probabilities that depend on dose suggests reformulating the problem as a mixture model with missing data. One observes indicators of whether or not subjects responded, but not indicators of which subjects were obligate responders and non-responders. Viewing the latter indicators as missing data, we developed an EM algorithm (Dempster et al, 1977) to estimate the proportions of subjects “destined” to respond and “unsusceptible” to response. Under a 2-parameter logistic model for the dose-response relationship among subjects who were neither obligate responders nor obligate non-responders, the EM algorithm provides maximum likelihood estimates (MLEs) of the intercept and slope, plus the destined and unsusceptible proportions, which together constitute the four unknowns in the full 4-parameter logistic model.

In analyzing the selenium data, Jeske et al (2009) applied a probit model, which is similar to a logistic model. They assumed the upper asymptote was one, but allowed for a nonzero lower asymptote representing the proportion of deaths unrelated to selenium toxicity. They obtained an estimate of the lower asymptote from the control (dose zero) data only and treated it as a known value when estimating the intercept and slope in the probit model. Differences between probit and logistic analyses aside, this article extends the basic model of Jeske et al (2009) in three ways. It permits the upper asymptote to be less than one to allow a proportion of “immune” flies to survive the study regardless of the selenium dose; it simultaneously estimates the intercept, slope, and two asymptotes; and it estimates the asymptotes using data from all dose groups.

The proposed EM algorithm is easy to program and can take advantage of existing software for standard logistic regression. Specifically, we show that at each M-step, the estimates of the two asymptotes are simple proportions, and the estimates of the intercept and slope can be obtained via ordinary 2-parameter logistic regression methods. The observed information matrix and the estimated covariance matrix of the estimators are straightforward to compute using the Louis (1982) method. Finally, this EM algorithm performs a pair of 2-parameter optimizations, which may provide computational advantages over simultaneous optimization involving all four parameters. Incorporating covariates in the EM algorithm is straightforward, and perhaps more importantly, some of the required parameter constraints are satisfied automatically. The proposed EM algorithm is illustrated with one of the selenium data sets provided by Jeske et al (2009).

2. Background

2.1 Observed Data

Suppose binary response data are observed from k+1 groups, say a control group and k treated groups, where all N subjects are independent and n_i subjects are randomly assigned to group I and exposed to dose d_i of the test chemical (i=0,1,…,k). Control subjects (i = 0) are unexposed, and thus d₀ = 0. Let Y_ij be a binary indicator of whether subject j (j=1,…,n_i) in group i responds (Y_ij = 1) or not (Y_ij = 0), let Y = {Y_ij: j=1,…,n_i; i=0,1,…,k} be the vector of all responses, and let y be the observed value of Y.

2.2 Hill Model

Assume the probability of response for subject j in group i (j=1,…,n_i; i=0,1,…,k) is given by the Hill (1910) model, a specific form of the 4-parameter logistic model. This non-linear model often is expressed as the following monotone function of dose d_i, with parameters ϕ = (ϕ₁, ϕ₂, ϕ₃, ϕ₄):

$$\mathrm{Pr}(Y_{\mathit{\text{ij}}}-1|d_i)={\varphi }_1+\frac{({\varphi }_2-{\varphi }_1)d_i{}^{{\varphi }_4}}{{\varphi }_3{}^{{\varphi }_4}+d_i{}^{{\varphi }_4}},$$ (1)

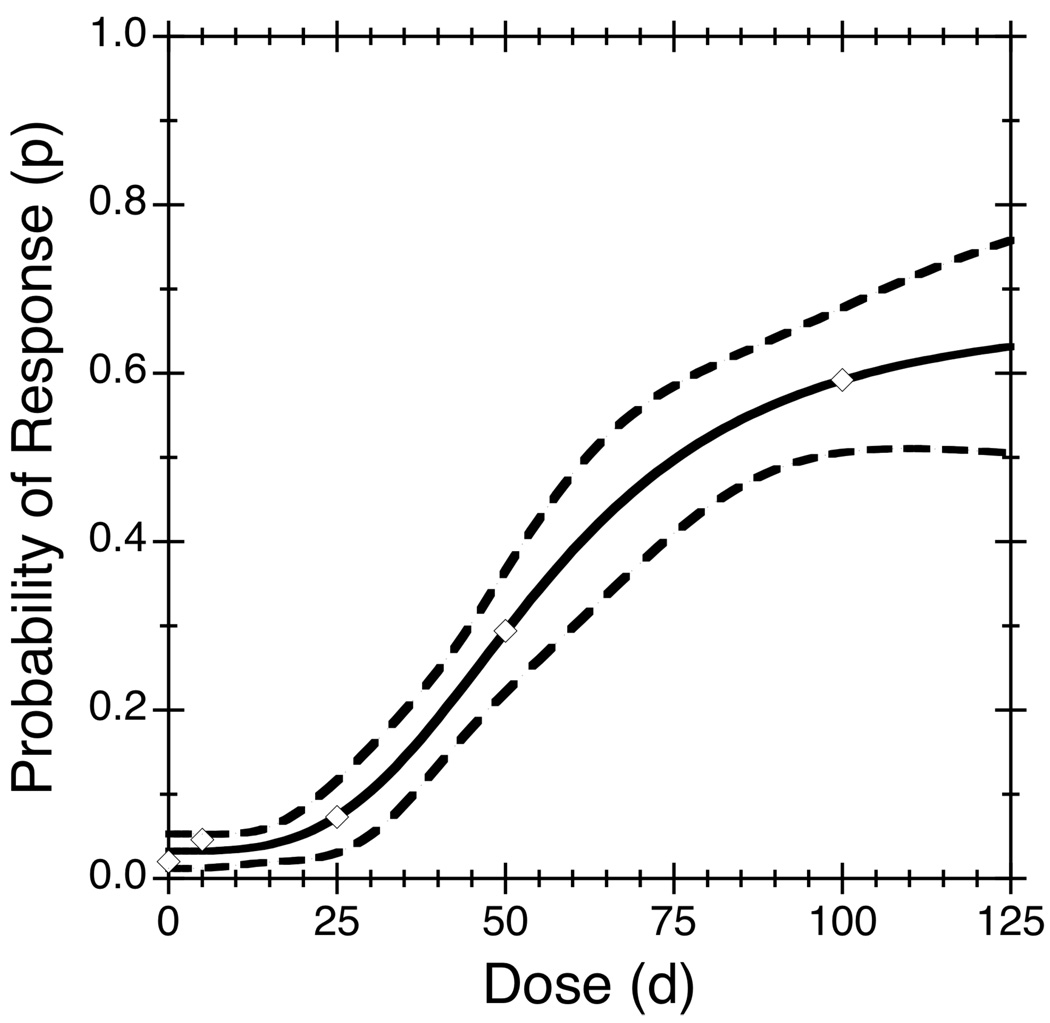
where ϕ₁ is the baseline response probability (at dose 0), ϕ₂ is the maximum response probability (at an infinite dose), ϕ₃ is the dose producing a response probability halfway between ϕ₁ and ϕ₂, and ϕ₄ is a shape parameter. As ϕ₃ is a dose, it must be non-negative. Without loss of generality, assume the probability of response increases with dose, which implies ϕ₄ > 0 and 0 ≤ ϕ₁ < ϕ₂ ≤ 1; otherwise one can simply reverse these constraints or recode Y_ij as 1−Y_ij. The parameter ϕ₃ is typically called the ED₅₀, or the median effective dose, and ϕ₄ is often called the Hill coefficient. The Hill model produces a sigmoidal dose-response curve, such as displayed in Figure 1.

Figure 1.

Probability of response as a function of dose for the selenocysteine data. The empirical response rate for each dose group is shown by a diamond, the dose-response curve fitted under a 4-parameter Hill model is shown by a solid curve, and the pointwise 95% confidence bands are shown by dashed curves.

To see that model (1) is a special case of a 4-parameter logistic model, one can rewrite it in terms of log-dose, z_i = ln(d_i), by substituting d_i = exp(z_i) into (1) and rearranging terms. If one reparameterizes by setting α = −ϕ₄ln(ϕ₃), β = ϕ₄, γ = ϕ₁, and δ = ϕ₂ − ϕ₁, then model (1) becomes

$$\mathrm{Pr}(Y_{\mathit{\text{ij}}}=1|z_i)=\gamma +\frac{\delta }{1+\exp (-\alpha -\beta z_i)},$$ (2)

a 4-parameter logistic model; see Volund (1978) for a discussion of 4-parameter logistic models for continuous responses. Set p_i = Pr(Y_ij = 1|z_i) and note that α and β are an intercept and slope for a response on a modified logit scale, ln[(p_i − γ)/(γ + δ − p_i)]. The bounds on ϕ imply bounds on Ω = (α, β, γ, δ): −∞ < α < ∞, β > 0, and 0 ≤ γ < γ + δ ≤ 1. Note that d₀ = 0 implies z₀ = −∞.

2.3 Likelihood of Observed Data

Conditional on the dose values and ignoring combinatoric factors, the likelihood of the observed response data is proportional to

$${\displaystyle \prod _{i=0}^k\left\{{(p_i)}^{y_{i+}}{(1-p_i)}^{n_i-y_{i+}}\right\},}$$ (3)

where $y_{i+}={\displaystyle {\sum }_{j=1}^{n_i}{y}_{\mathit{\text{ij}}}}$. Note that z₀ = −∞ and β > 0 imply that p₀ = γ. Thus, the log-likelihood of the parameter vector Ω = (α, β, γ, δ), apart from additive constants, is L_Y (Ω; y) = L_Y, where

$$L_y=y_{0+}\ln (\gamma )+(n_0-y_{0+})\ln (1-\gamma )+{\displaystyle \sum _{i=1}^k\left\{y_{i+}\ln \left(\gamma +\frac{\delta }{1+\exp (-\alpha -\beta z_i)}\right)+(n_i-y_{i+})\ln \left(1-\gamma -\frac{\delta }{1+\exp (-\alpha -\beta z_i)}\right)\right\}.}$$ (4)

2.4 Maximum Likelihood Analysis

The maximum likelihood estimates (MLEs) are usually calculated by iteratively optimizing L_Y. For example, one might use a Newton-Raphson method, which requires both first and second derivatives of L_Y; a quasi-Newton method, which only requires first derivatives of L_Y; or a downhill simplex method, which does not require any derivatives. These approaches typically work well unless the data are too sparse and lead to ill-conditioned matrices or the starting values are too far from the MLEs. With any of these methods, however, constraints to honor the bounds on Ω must be imposed explicitly or circumvented through reparameterization.

3. Missing-Data Reformulation

3.1 Complete Data

The original problem can be reformulated into one amenable to EM iterations by incorporating latent variables. Suppose one observes whether or not each subject responded, but not whether a responder was destined to respond, nor whether a non-responder was unsusceptible to response. Thus, each subject is regarded as belonging to one of four mutually exclusive categories, but exact category membership is unknown. Regardless of dose, subjects in Category 1 are destined to respond, whereas subjects in Category 4 are unsusceptible and will not respond. All other subjects are susceptible to response but not destined to respond; they may respond (Category 2) or not respond (Category 3), and the probability of response can depend on dose.

Define a collection of latent indicators (X_1ij, X_2ij, X_3ij, X_4ij), where X_hij is 1 if subject j from group i belongs to Category h (j=1,…,n_i; i=0,1,…,k; h=1,2,3,4) and is 0 otherwise. The observed indicators (Y_ij) and their additive complements (1−Y_ij) can be partitioned into sums of unobserved indicators: Y_ij = X_1ij + X_2ij and 1−Y_ij = X_3ij + X_4ij. One observes whether a subject responded (Y_ij =1) or not (1−Y_ij = 1), but not whether a responder was destined to respond (X_1ij = 1) or not (X_2ij = 1), nor whether a non-responder was susceptible (X_3ij = 1) or not (X_4ij= 1).

3.2 Relationship to Hill Model

Let γ be the proportion of subjects in the population who are destined to respond (Category 1), let δ be the proportion who are susceptible but not destined to respond (Categories 2 and 3), and let 1 − γ − δ be the proportion who are unsusceptible to response (Category 4). Among subjects who are susceptible but not destined to respond, let θ(z_i) and 1 − θ(z_i) denote the dose-dependent proportions who respond (Category 2) and do not respond (Category 3), respectively.

For the j^th subject in the i^th group, the expected values of X_1ij, X_2ij, X_3ij, X_4ij are

$$\mathrm{\gamma },\mathrm{\delta }{\mathrm{\theta }}_{\mathrm{i}},\mathrm{\delta }(1-{\mathrm{\theta }}_{\mathrm{i}}),1-\mathrm{\gamma }-\mathrm{\delta },$$ (5)

respectively, where θ_i = θ(z_i). Note that X_1ij, X_2ij, X_3ij, and X_4ij sum to 1, as do their expected values. Also, the fact that X_1ij and X_2ij are binary and mutually exclusive implies that

$$\mathit{\text{Pr}}(Y_{\mathit{\text{ij}}}=1|z_i)=\mathit{\text{Pr}}(X_{\mathit{1}\mathit{\text{ij}}}+X_{\mathit{2}\mathit{\text{ij}}}=1|z_i)=\mathit{\text{Pr}}(X_{\mathit{1}\mathit{\text{ij}}}=1|z_i)+\mathit{\text{Pr}}(X_{\mathit{2}\mathit{\text{ij}}}=1|z_i)=\mathrm{\gamma }+\mathrm{\delta }{\mathrm{\theta }}_{\mathrm{i},}$$ (6)

which reduces to the Hill model in (2) under the logistic model: θ_i = [1 + exp(−α – βz_i)]⁻¹.

3.3 Likelihood of Complete Data

The likelihood of the complete data is proportional to a product of terms such as those in (5). Note that z₀ = −∞ and β > 0 imply θ₀ = 0 and X_20j = 0 for j=1,…,n₀. Apart from additive constants, the log-likelihood of the complete data is L_X(Ω; x) = L_X, where X = {X_ij: j=1,…,n_i; i=0,1,…,k}, X_ij = (X_1ij, X_2ij, X_3ij, X_4ij), x is a particular realization of X, and

$$L_X={\displaystyle \sum _{j=1}^{n_0}\left\{x_{10j}\ln (\gamma )+x_{30j}\ln (\delta )+x_{40j}\ln (1-\gamma -\delta )\right\}+{\displaystyle \sum _{i=1}^k{\displaystyle \sum _{j=1}^{n_i}\left\{x_{1\mathit{\text{ij}}}\ln (\gamma )+x_{2\mathit{\text{ij}}}\ln (\delta {\theta }_i)+x_{3\mathit{\text{ij}}}\ln [\delta (1-{\theta }_i)]+x_{4\mathit{\text{ij}}}\ln (1-\gamma -\delta )\right\}.}}}$$ (7)

Modeling θ_i by [1 + exp(−α − βz_i)]⁻¹ and collecting terms yields L_X = L_X1 + L_X2, where

$$L_{X1}=-{\displaystyle \sum _{i=1}^k\left\{x_{3i+}\alpha +x_{3i+}{z}_i\beta +(x_{2i+}+x_{3i+})\ln (1+e^{-\alpha -\beta z_i})\right\},}$$ (8)

$$L_{X2}=x_{1++}\ln (\gamma )+(x_{2++}+x_{3++})\ln (\delta )+x_{4++}\ln (1-\gamma -\delta ),$$ (9)

and the “+” subscript indicates summation over the corresponding index. Note that L_X1 and L_X2 are functionally independent, with the former involving only α and β, and the latter involving only γ and δ, which simplifies the maximization of L_X and the calculation of the information matrix. Also, L_X2 does not involve z_i, consistent with the asymptotes being dose-independent.

3.4 EM Algorithm

The MLE of Ω can be obtained via an EM algorithm (Dempster et al, 1977). After choosing a starting value for Ω, the EM algorithm iterates between expectation (E) and maximization (M) steps until convergence. At each iteration, the E-step calculates the expectations of the sufficient statistics for the complete data, conditional on the observed data and the current parameter estimates, and the M-step calculates the value of Ω that maximizes the log-likelihood of the current complete data. Each EM iteration increases the likelihood of the observed data.

At the E-step, conditional on the observed response y_ij and the current parameter estimate Ω̂ = (α̂, β̂, γ̂, δ̂), the expected values E(X_1ij|y_ij, Ω̂) and E(X_4ij|y_ij, Ω̂) are estimated by

$${\widehat{x}}_{1\mathit{\text{ij}}=y_{\mathit{\text{ij}}}}\left(\frac{\widehat{\gamma }}{\widehat{\gamma }+\widehat{\delta }{\widehat{\theta }}_i}\right)\text{\hspace{1em}and\hspace{1em}}{\widehat{x}}_{4\mathit{\text{ij}}}=(1-y_{\mathit{\text{ij}}})\left(\frac{1-\widehat{\gamma }-\widehat{\delta }}{1-\widehat{\gamma }-\widehat{\delta }{\widehat{\theta }}_i}\right),$$ (10)

respectively, where θ̂₀ = 0 and θ̂_i = [1+ exp(−α̂ − β̂z_i)]⁻¹ for i > 0. By subtraction, estimates of the expected values of X_2ij and X_3ij are x̂_2ij = y_ij − x̂_1ij and = x̂_3ij = 1− y_ij − x̂_4ij, respectively.

At the M-step, conditional on x̂_2i+ and x̂_3i+, the estimates of α and β that maximize L_X1 are the MLEs for a 2-parameter logistic regression problem with log-likelihood (8). Furthermore, substituting x̂₁₊₊, x̂₂₊₊, x̂₃₊₊, and x̂₄₊₊ into (9), the estimates of γ and δ that maximize the trinomial log-likelihood L_X2 are

$$\widehat{\gamma }={\widehat{x}}_{1++}/N\text{\hspace{1em}and\hspace{1em}}\widehat{\delta }=({\widehat{x}}_{2++}+{\widehat{x}}_{3++})/N,$$ (11)

where N = n₊ = x̂₊₊₊ is the total number of subjects. Although only two of the four complete-data MLEs (γ̂, δ̂) are available in closed form, the iterative procedure for obtaining the other pair (α̂, β̂) is simpler than maximizing the entire 4-parameter observed-data log-likelihood L_Y.

Continue iterating until successive differences are suitably small for both the observed-data log-likelihood L_Y and the estimate Ω̂, and then declare the latter to be the MLE of Ω.

Computer code for implementing the EM algorithm is available online.

3.5 Variance Estimation

Let G_X(Ω; X) and H_X(Ω; X) be the gradient (first derivative) vector and negative Hessian (second derivative) matrix, respectively, of L_X(Ω; X) with respect to Ω, and define G_Y and H_Y similarly. Louis (1982) showed that the observed information matrix for Y at the MLE Ω̂, say HY(Ω̂; y), is

$${\mathbf{I}}_Y(\widehat{\mathbf{\Omega }})=E_{X|Y}[{\mathbf{H}}_X(\mathbf{\Omega };\mathbf{X})|\mathbf{Y}=\mathbf{y}]|{}_{\mathrm{\Omega }=\mathrm{\Omega ̂}}-E_{X|Y}[{\mathbf{G}}_X(\mathbf{\Omega };\mathbf{X}){\mathbf{G}}_X^T(\mathbf{\Omega };\mathbf{X})|\mathbf{Y}=y]|{}_{\mathrm{\Omega }=\mathrm{\Omega ̂}}.$$ (12)

Simplification of the observed information matrix in (12) is possible because X is a multinomial. The variance-covariance matrix for Ω̂, say Σ, can be estimated by $\widehat{\mathbf{\Sigma }}={\left[{\mathbf{I}}_Y(\widehat{\mathbf{\Omega }})\right]}^{-1}$. This method of estimating Σ involves only L_X and is generally simpler than working with L_Y directly.

4. Application to Selenium Data

Jeske et al (2009) presented data from a toxicology study of the dose effects of four types of selenium on the death rates of flies. We focused on selenocysteine, which they labeled as type 4 selenium, and fitted the Hill model via the EM algorithm. The data are given in Table 1. Of the n_i flies receiving dose d_i of selenocysteine (i = 0,1,2,3,4), let Y_ij indicate whether fly j died during the study (j = 1,…, n_i). Specify the probability of dying during the study by the Hill model in (2), where γ and 1 − γ − δ are the respective proportions of flies destined to die from causes other than selenocysteine toxicity and to survive the study despite selenocysteine toxicity. The remaining proportion δ die during the study with dose-dependent probability θ_i = [1 + exp(−α – βz_i)]⁻¹.

Table 1.

Selenocysteine data from Jeske et al (2009). For group i, d_i is the dose, y_i+ is the observed number of deaths, n_i is the number of subjects, y_i+/n_i is the empirical death rate, P̂_i is the predicted death rate under the Hill model, E_i is the expected number of deaths (rounded) under the Hill model, and the last column is a measure of model goodness-of-fit.

i	di	yi+	ni	yi+/ni	P̂i	Ei	$\frac{{(y_{i+}-E_i)}^2}{E_i}$
0	0	3	152	0.020	0.033	5.0	0.78
1	5	7	152	0.046	0.033	5.0	0.81
2	25	11	150	0.073	0.074	11.1	0.00
3	50	45	153	0.294	0.294	45.0	0.00
4	100	74	125	0.592	0.592	74.0	0.00
		140	732			140.1	1.59

We selected EM starting values for α and β by fitting a 2-parameter logistic model to the observed data, assuming no predestined or unsusceptible subpopulations. However, one cannot set γ=0 and δ=1 as starting values because the EM algorithm will not move from these boundary values. Instead, we defined p̃_i = (y_i++½)/(n_i + 1) to guarantee estimated response rates in (0,1), and then we initially set the lower asymptote (γ) to the smallest p̃_i and the upper asymptote (γ+δ) to the largest p̃_i, with the initial value of δ being the difference. This procedure produced starting values Ω = (−5.814, 1.289, 0.023, 0.568). The resulting MLEs of (α, β, γ, δ) are given in Table 2, along with estimates of their standard errors based on the Louis (1982) method. The MLEs of (ϕ₁, ϕ₂, ϕ₃, ϕ₄), which are simple transformations of (α, β, γ, δ), are also given in Table 2, along with estimates of their standard errors based on applying the delta method (Rao, 1973) to Σ̂.

Table 2.

Maximum likelihood estimates (MLEs) and estimated standard errors (S.E.s) under the Hill model, expressed in terms of either dose or the natural logarithm of dose, for the data of Jeske et al (2009) on the effect of selenocysteine on the death rates of flies.

Hill model (1), in terms of dose di				Hill model (2), in terms of zi = ln(di)
Parameter	MLE	S.E.		Parameter	MLE	S.E.
ϕ1 (min)	0.033	0.010		γ (min)	0.033	0.010
ϕ2 (max)	0.673	0.115		δ (max–min)	0.641	0.118
ϕ3 (ED50)	55.962	9.392		α (intercept)	−13.368	3.923
ϕ4 (shape)	3.322	1.084		β (slope)	3.322	1.084

The parameterizations are related as follows: ϕ₁ = γ, ϕ₂ = γ + δ, ϕ₃ = exp(−α/β), ϕ₄ = β.

The Hill model fits these data well, as seen from the empirical (symbols) and fitted (solid curve) death rates in Figure 1; the dashed curves show pointwise 95% confidence bands obtained by applying the delta method. The usual observed-minus-expected goodness-of-fit statistic is 1.59 (Table 1), which suggests no significant lack of fit (P = 0.21, based on the chi-squared distribution with one degree of freedom). The MLEs of the lower (ϕ̂₁ = 0.033) and upper (ϕ̂₂ = 0.673) asymptotes are more than 1.96 standard errors above zero and below one (Table 2), respectively, suggesting that the full 4-parameter Hill model fits better than a reduced model.

Though Jeske et al (2009) fitted a 3-parameter probit model rather than a 4-parameter logistic model, they obtained similar results for the median effective dose. In their second table, they reported an MLE of 4.42 with a standard error of 0.19 for ln(ED₅₀). After taking natural logs, the MLE and standard error from the EM algorithm are 4.02 and 0.17, respectively.

As a check, a quasi-Newton method gave the same estimate of Ω as the EM algorithm. Also, as a further check, we verified that the first derivative of the observed-data log-likelihood with respect to each parameter was zero when evaluated at the MLE: G_Y(Ω̂; y) = 0.

Optimization procedures can be sensitive to initial values, so we tried several sets. First, we set the lower asymptote (ϕ₁) to 0.023 and the upper asymptote (ϕ₂) to 0.591, which were the starting values used earlier, and then investigated a grid of starting values for the ED₅₀ (ϕ₃) and shape (ϕ₄) parameters. The MLEs of ϕ₃ and ϕ₄ were roughly 56 and 3, so we examined starting values of 40, 60, 80, and 100 for ϕ₃ and values of 1, 2, 3, and 4 for ϕ₄. All 16 combinations of these starting values gave the same final estimates as before, as did several other sets of starting values, suggesting that the EM algorithm is not overly sensitive to the choice of initial values.

5. Discussion

We developed an EM algorithm for fitting a Hill model, or more generally a 4-parameter logistic model, to binary (quantal) dose-response data. The EM algorithm is simple to program and leads to a pair of 2-parameter optimizations at each iteration, one of which has a closed-form solution. Thus, in this non-linear setting, the EM approach may provide computational advantages over conventional iterative approaches that optimize with respect to all 4 parameters simultaneously, at least for some data sets, though a rigorous investigation was not performed. Also, certain constraints that other methods impose explicitly are satisfied automatically in the EM algorithm.

Expanding on this last point, estimates of the lower (ϕ₁) and upper (ϕ₂) asymptotes must satisfy 0 ≤ ϕ₁ < ϕ₂ ≤ 1 if the dose-response curve is increasing, as assumed in the development. The EM algorithm produces estimates of ϕ₁ and ϕ₂ (or γ and δ) that are simple proportions, which always lie in the unit interval. In contrast, conventional methods must either explicitly restrict the asymptotes to fall in [0,1] or else circumvent constraints via reparameterization. For example, ϕ₁ and ϕ₂ can be forced to lie in (0,1) by applying a logistic transform to each. Typically, both EM and conventional methods will satisfy ϕ₁ < ϕ₂ and ϕ₄ > 0 if the observed response rates mostly increase with dose, or ϕ₁ > ϕ₂ and ϕ₄ < 0 if the rates mostly decrease with dose.

This article focused on the Hill model, a special case of the 4-parameter logistic model in which the dose metric is the natural logarithm of dose. The same methods can be applied with other dose metrics, though, such as z_i = d_i or z_i = i. Also, the notation was developed to allow for a control group having a dose of zero (d₀ = 0), but the same methods can be adapted easily to handle studies without a control group by simply ignoring the terms with a subscript of i = 0. Furthermore, although the usual dose-response study involves multiple observations per dose group, the proposed approach can still be applied with only n_i = 1 observation per dose group. Finally, the EM algorithm can be modified trivially to fit a reduced 3-parameter logistic model, such as under the constraint ϕ₂ = 1 (i.e., δ = 1 − γ) used by Jeske et al (2009). However, the 2-parameter model, which constrains ϕ₁ = γ = 0 and ϕ₂ = δ = 1, does not require any EM iterations.

Note that the proposed conceptualization, involving a mixture model with missing data, need not correspond precisely to reality; it is simply a convenient construction for calculating the MLEs under a 4-parameter logistic (or Hill) model. We hypothesize three mutually exclusive groups of subjects: those who always respond, those who never respond, and those who respond with a dose-dependent probability specified by a logistic curve with asymptotes of 0 and 1. This formulation may not mimic reality, but the MLEs it produces are identical to those obtained by other methods under a 4-parameter logistic model with asymptotes that need not equal 0 and 1.

Several extensions of the proposed method are possible. One is the incorporation of additional covariates. The M-step of the EM algorithm maximizes a 2-parameter logistic regression likelihood with an intercept and a slope for a single covariate equal to ln(dose). The incorporation of more covariates is straightforward when modeling response rates of susceptible subjects who are not destined to respond; that is, when maximizing L_X1. Also, since the two pieces of the complete-data log-likelihood are functionally independent, polytomous regression methods can be used to separately maximize L_X2 after modeling the destined and unsusceptible proportions as functions of covariates unrelated to dose. This would allow formal assessment of explanatory variable effects on the destined and unsusceptible proportions, as well as on the response rate of susceptible subjects who are not destined to respond, say through a likelihood ratio test of whether certain regression coefficients are zero.

Another extension is incorporation of survival adjustments in studies where estimation of dose-response relationships might be biased by differential mortality. For example, Walker et al (2005) fitted a 3-parameter logistic model to binary tumor incidence data from a carcinogenicity study and incorporated a poly-3 survival adjustment (Bailer and Portier, 1988) to account for the reduced tumor risk of animals dying before the end of the study. The EM algorithm can be easily adapted to incorporate this same survival adjustment. As an alternative survival adjustment, one could use time as a covariate explaining response. This approach would generalize the nonlethal tumor analysis of Dinse and Lagakos (1983), which applied standard logistic regression methods. By including both dose and time metrics as covariates, one could allow non-boundary values for the asymptotes and also could provide an alternative to the poly-3 correction to adjust for survival effects on the incidence rates of nonlethal tumors. This extension represents ongoing research and will be the subject of a future article.

In summary, the EM algorithm provides a natural solution to the problem of modeling binary responses when some subjects are obligate responders or obligate non-responders. This approach leads to a straightforward way to estimate the covariance matrix of the MLEs and to incorporate explanatory variables. Furthermore, as seen in other contexts (e.g., forcing positive variance component estimates), the EM algorithm automatically satisfies certain constraints that are more complicated to implement with other methods. Though the example and some of the terminology focused on dose-response analysis of toxicology data, the proposed EM algorithm has general applications for various binary outcomes observed in a broad range of research areas. For instance, consider a clinical trial evaluating a new therapy where the probability of disease remission generally increases with dose, but some patients improve even if not treated, while others regress no matter how high the dose. Or, consider an agricultural study of an herbicide, where the death rates of targeted plants generally increase with dose, but some plants may die from causes unrelated to the herbicide, while others may appear resistant within the range of doses applied. The proposed EM algorithm should handle these situations and many others.