Abstract
Maintaining the postural configuration of a limb such as an arm or leg is a fundamental neural control task that involves the coordination of multiple linked body segments. Biological systems are known to use a complex network of inter- and intra-joint feedback mechanisms arising from muscles, spinal reflexes, and higher neuronal structures to stabilize the limbs. While previous work has shown that a small amount of asymmetric heterogenic feedback contributes to the behavior of these systems, a satisfactory functional explanation for this nonconservative feedback structure has not been put forth. We hypothesized that an asymmetric multi-joint control strategy would confer both an energetic and stability advantage in maintaining endpoint position of a kinematically redundant system. We tested this hypothesis by using optimal control models incorporating symmetric versus asymmetric feedback with the goal of maintaining the endpoint location of a kinematically redundant, planar limb. Asymmetric feedback improved endpoint control performance of the limb by 16%, reduced energetic cost by 21% and increased interjoint coordination by 40% compared to the symmetric feedback system. The overall effect of the asymmetry was that proximal joint motion resulted in greater torque generation at distal joints than vice versa. The asymmetric organization is consistent with heterogenic stretch reflex gains measured experimentally. We conclude that asymmetric feedback has a functionally relevant role in coordinating redundant degrees of freedom to maintain the position of the hand or foot.
1. Introduction
Postural control has proven to be a daunting engineering problem, but one that animals solve as a matter of course. Control of multi-link systems is mathematically complicated by dynamic coupling among segments, which introduce torques at the remote joints in response to motion of any segment (Lacquaniti & Soechting, 1986; Sage, De Mathelin & Ostertag, 1999). For kinematically redundant multi-link systems, maintaining the position of the endpoint does not fully constrain the configuration of the joints and this absence of a one-to-one relationship between the control goal of endpoint position and the system state variables further complicates the control problem (Patel & Shadpey, 2005). Despite the computational complexities, biological systems derive striking postural stability and control accuracy from the properties of muscles and proprioceptive reflexes (Kargo & Giszter, 2000; Sinkjaer, 1997).
Biological systems use a complex network of inter- and intra-joint feedback along with intrinsic musculotendon properties to achieve endpoint control. The intrinsic properties of individual muscles provide instantaneous stiffness, viscosity, and interjoint coupling (Hamill & Knutzen, 2003). These mechanisms are amplified by a carefully structured hierarchy of neural feedback mechanisms. At the lowest level, the stretch reflex (Sherrington, 1898) has been considered to provide spring-like or servo-like control of an individual muscle (Merton, 1953; Nichols & Houk, 1976). Feedback from individual muscle spindles was subsequently shown to excite motoneurons of synergistic muscles and to inhibit motoneurons of antagonists (Liddell & Sherrington, 1925; Lloyd, 1946), giving rise to the concept of a myotatic unit comprised of both agonists and antagonists to provide servo-like control of individual joints (Merton, 1953). However, in human subjects, reflex control does not mimic a servo-like system (Crago, Houk & Hasan, 1976), and similarly, in cats the variation in intermuscular feedback gains measured in vivo varies among muscles crossing a single joint (Nichols, 1989). Short latency spindle reflexes modulate activity of many heteronymous muscles (Eccles, 1956; Eccles, Eccles & Lundberg, 1957b; Nichols, 1989), and it seems that reflex mechanisms can provide an integrated control system, spanning and coordinating multiple joints (Nichols, Cope & Abelew, 1999; Perreault & Viant, 2005). This heterogenic feedback can be asymmetric, favoring force generation by one muscle of a pair, or at one joint over another (Bonasera & Nichols, 1994; Eccles & Lundberg, 1958; Nichols et al., 1999; Pratt, 1995).
Asymmetry in heterogenic feedback results in an asymmetric, or non-conservative, system (Hogan, 1985). Hogan raised this point to argue that symmetric or spring-like systems simplify control by allowing higher centers to specify endpoint position in terms of a potential function, the gradient of which defines limb stiffness: the relationship between endpoint displacement and the restoring force. The idea that the human arm stiffness functions as a symmetric system was tested during constrained planar motion in humans and found to hold for only two of the four subjects tested (Mussa-Ivaldi, Hogan & Bizzi, 1985). On average, 6.5% of the forces could not be accounted for under a symmetric assumption, and it is not clear whether this is an important fraction or not, although the authors conclude that it is not. While most studies of human arm stiffness indicate that the system is mostly conservative, or symmetric (Flash & Mussa-Ivaldi, 1990; Franklin & Milner, 2003; Perreault, Kirsch & Crago, 2001; Stroeve, 1999; Tsuji et al., 1995), non-conservative endpoint stiffness has been reported to account for as much as 23% of endpoint forces (Franklin et al., 2003). Moreover, Dolan et al (Dolan, Friedman & Nagurka, 1993) report non-conservative human arm endpoint stiffness for one subject as high as 41% but 25% or less for all other subjects (mean values were not reported). The general interpretation from experiments has been that a symmetric, conservative controller adequately describes the response, despite regular findings of small asymmetries. However, all of these experiments have been conducted in a system where the arm is constrained to move as a planar, two-link system, whereas in most natural movements the arm is a kinematically redundant system where multiple joint configurations can be used to achieve the same endpoint location. The contributions of non-conservative feedback in a kinematically redundant system have not been experimentally measured.
Substantial asymmetries in heterogenic feedback have been predicted using linear musculoskeletal models (Barin, 1989; He, Levine & Loeb, 1991; Park, Horak & Kuo, 2004). He and coworkers (He et al., 1991) used linear optimal control theory to predict length and force feedback between muscles of the feline hind limb and found the heterogenic feedback gains to be asymmetric. Considering higher levels of joint and interjoint feedback, asymmetric controllers were required to match human postural responses modeled using two- (Park et al., 2004) and three- (Barin, 1989) link inverted pendulum models. Asymmetric controllers therefore appear to have performance advantages, despite the added complexity. However, neither experimental observations supporting the importance of asymmetric reflexes, nor a functional explanation of the performance advantages conferred by asymmetric controllers have yet been presented.
We used optimal control theory to investigate the contribution of symmetric and asymmetric feedback control in minimizing a theoretical cost function associated with the control of a multi-joint system. In biomechanical systems, “costs” can include measures of energy and accuracy. The linear quadratic regulator (LQR)(Bryson & Ho, 1975) is ideally suited to this class of problems and has frequently been used to test hypothetical cost functions to probe the organizing principles of the central nervous system (He et al., 1991; Kuo, 1995; Kuo, 2005). One of the strongest advantages of the LQR approach is that it provides a unique, analytical solution. However, previous work has not evaluated the change in cost associated with deviations from the optimal analytical solution, by, for example eliminating the asymmetric components of the feedback controller.
The aim of this paper is to determine whether asymmetric interjoint feedback improves the performance of postural tasks for a generic redundant limb model. We hypothesize that an asymmetric multi-joint control strategy results in lower energetic cost of recovery and reduced endpoint displacement due to perturbations. We use optimal control theory to design specifically structured controllers and measure the effectiveness of each in maintaining postural endpoint control of a multi-link system. We demonstrate that the benefits of asymmetric feedback are dependent upon the task definition. Asymmetric feedback provides no benefit in a system tasked to maintain a specific joint configuration, which provides relatively poor endpoint stability. In a system tasked to maintain the endpoint location, asymmetric feedback improves endpoint stability, reduces energetic cost, and increases coordination among the joints. The biological controller may be structured similarly to the optimal controller to capitalize on these performance advantages. Such a structure would be consistent with the limited experimental data in the literature.
2. Methods
The analytical methods of the paper follow the format of Table 1. First, we define a kinematically redundant multi-link model. Second, two postural tasks (a joint control task and endpoint control task), are specified for the model in the cost function. Third, three controller structures are specified: a diagonal controller (single-joint control, homonymous feedback), a symmetric controller (multi-joint symmetric feedback), and an unconstrained controller (multi-joint asymmetric feedback). We used optimal control to determine the feedback gains of each controller for each task, resulting in a total of 6 optimal controllers. The endpoint stiffness and viscosity characteristics, and dynamic response of the model are reported. To test the hypothesis that asymmetric multi-link strategies improve efficiency and control, the model is subjected to impulse perturbations at the endpoint and kinematic and kinetic performance metrics are reported.
Table 1.
Analytical methods.
| A. Model: | Planar, 3-link, lumped parameter model | ||
| B. Kinematic task specification: | Joint Control, minimize: | Endpoint Control, minimize: | |
| C. Controller constraint (kR,kB): | Diagonal (JD, ED) | Symmetric | Unconstrained (JU, EU) |
| D. Performance evaluation: | Endpoint Viscoelastic Properties | Dynamic response (ξ) | |
2.1 Model
The model simulates a system of three identical links joined by single degree of freedom rotational joints (Figure 1a). Each link of the model is a thin rod of length L and mass m. The nominal joint configuration for simulations was chosen to mimic feline stance posture (θ1 = −51°, θ2 = −86°, θ3 = 35°) based on experimental data (Torres-Oviedo, Macpherson & Ting, 2006). Additional simulations were performed with tree shrew posture (θ1 = −150°, θ2 = 120°, θ3 = −117°) (Schilling, 2005), which is more compact. The equations of motion for the system, expressed in the generalized coordinate system, θ⃑= [θ1, θ2, θ3]T, are
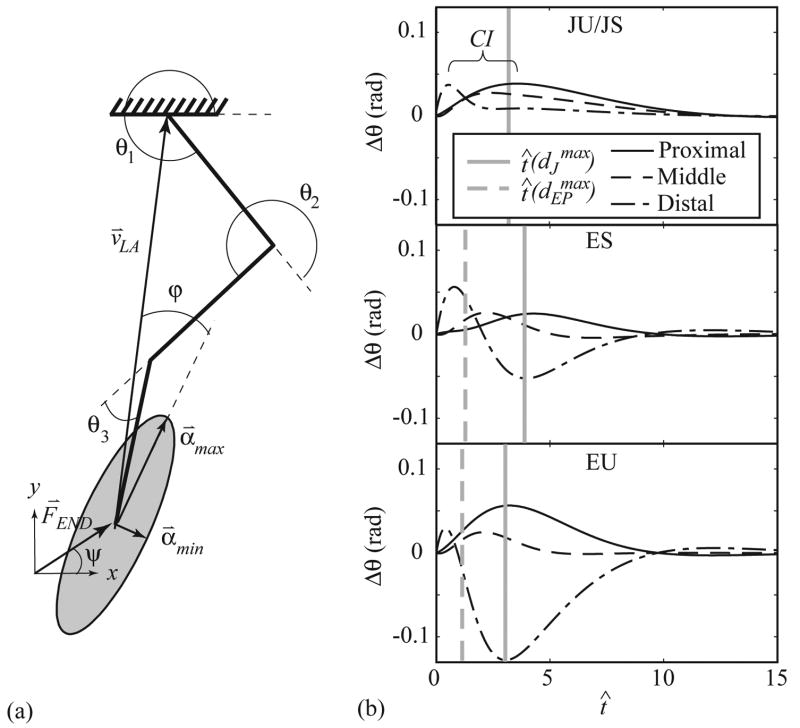
Figure 1.
Model diagram with example endpoint ellipse (A). Three-link model (heavy black lines) with generalized coordinate system (θ⃑ = [θ1, θ2, θ3]T). The limb axis, v⃑LA, is directed from the endpoint to the proximal joint. The endpoint stiffness (kR_END) and viscosity (kB_END) ellipses are characterized by the angle ϕ between the limb axis and direction of maximum stiffness, α⃑MAX. The direction of minimum stiffness is α⃑MIN. Model responses (B) (top: JU/JS, middle: ES, bottom: EU) are shown for a perturbation applied in the x direction (ψ = 0°). The time of maximum endpoint (dashed gray line) and maximum total joint (solid gray line) displacements are indicated.
| (1) |
where M is the inertia matrix, v⃑ is the centrifugal and Coriolis forces, T⃑ is the control joint torques, J is the Jacobian, and F⃑END is an applied force at the endpoint. The equations for M, v⃑ and J were derived in Autolev (Online Dynamics, Sunnyvale, CA).
These equations were derived in non-dimensional units L̂, m̂, and t̂ with the characteristic length L, mass m, and force σ. The characteristic time τ is derived from L, m, and the characteristic force or “effort” of the system (σ),
The effort of the system can be thought of as the ratio of accuracy to energy; for greater effort, accuracy of the system is increased with decreased energetic efficiency. The characteristic force during stance might be the force generated by the triceps surae complex.
The control torque applied to each joint element is determined by a lumped parameter, viscoelastic model,
where, kR is the dimensionless 3×3 joint stiffness matrix and kB the dimensionless 3×3 joint viscosity matrix.
The system described in Eq. 1 was linearized by Taylor series expansion of the model around its nominal configuration with no applied endpoint force. At the zero velocity equilibrium point Coriolis forces are zero, and the governing equations in state space representation become
| (2) |
where . Rearranging terms and defining the state matrix (A), input matrix (B), and state feedback matrix (k) as
| (3) |
allows Eq. (2) to be written in the form, .
2.2 Task Specification and Optimization
The steady-state linear quadratic regulator (LQR) formulation (Bryson & Ho, 1975) was used to uniquely determine the components of the optimal state feedback matrix k. The matrix minimizes a cost function (Ct) of the form
| (4) |
The first term of this expression, z⃑T Qz⃑, is a weighted sum of squares of state errors, and defines the kinematic cost Ck. Two control tasks were defined to specify the kinematic cost. A joint control matrix (QJ) represents the task of holding the limb at its nominal configuration, quantified by simple sum of squares of link displacement:
| (5) |
The accuracy matrix (QEP) was chosen to represent the task of maintaining endpoint position in Cartesian space, and incorporates an internal model in the form of the Jacobian,
| (6) |
This control matrix assumes a constant Jacobian evaluated at the model’s nominal state and is therefore valid only for joint configurations close to this state. In the kinematically redundant system, J is 2×3, and JT I 2x2J has zero determinant. QEP is therefore not positive semi-definite, a requirement for LQR optimization, so the endpoint task is determined by a weighted sum of joint and endpoint control ( ). The accuracy matrix QE for the endpoint task is
The second term, u⃑T Ru⃑, is a weighted sum of squares of the torques. The effort weighting matrix, R = I 3x3, was chosen to equally weight torque production at each joint and results in the sum of the squares of the joint torques, defining an energetic cost (Ce).
The minimum solution of the cost function defined in Eq. (4) for a system of the form and control law, u⃑ = −kz⃑, is
The matrix S is the constant, analytical solution of the matrix algebraic Riccati equation,
| (7) |
and the optimal state feedback matrix is
| (8) |
The control law (k) which minimizes the cost function in equation 4 for the system described by equation 3 is guaranteed to be stable as long as the matrix Q is positive semi-definite, and matrix R is positive definite (Bryson & Ho, 1975). Both criteria are satisfied by all cost functions in this study.
2.3 Controller Constraints
To determine the consequences of structural changes in model stiffness (kR) and viscosity (kB), two matrix constraints were used. First, a constrained controller with diagonal kR and kB produces torque at each joint due to motion of that joint only, representing single joint control. The equivalent biological system would be comprised of only uniarticular muscles with no heterogenic feedback across joints, and is similar to a classic myotatic unit operating about single joints. Second, a constrained controller with symmetric off-diagonal terms causes the torque at a joint to be influenced by motion of remote joints, representing symmetric multi-joint control. The biological equivalent would include biarticular muscles, but is constrained so that net heterogenic feedback is symmetric across joints.
Constrained controllers (k̃) are not guaranteed to produce the absolute minimum S. Optimal constrained controllers are obtained by nonlinear minimization of the Frobenius norm of the difference between the absolute minimum (S) and S̃,
where S̃ is derived from application of the constrained controller (k̃) to Eq. (4). Controllers for both the joint and endpoint tasks were determined subject to no constraints (JU, EU) and to the constraints of diagonal (JD, ED) and symmetric (JS, ES) stiffness and viscosity matrices.
2.4 Analytical Methods
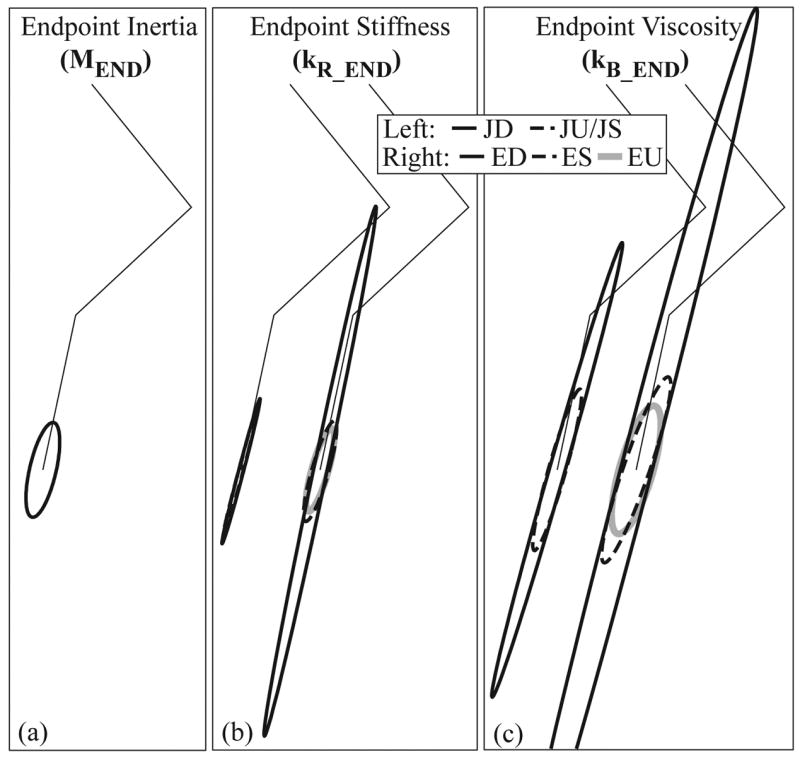
To quantify the global viscoelastic properties of each controller model, endpoint stiffness (kR_END) and viscosity (kB_END) (Fig. 1a) were determined from stiffness and viscosity matrices. The endpoint stiffness is defined by,
for the multi-link model with no background force applied to the endpoint. Endpoint viscosity (kB_END) and endpoint inertia (MEND) matrices are determined by the same transformation of joint viscosity (kB) and inertia (M). It is important to note that the transformation from joint to endpoint matrices is unique and preserves symmetry.
Ellipse eccentricities (s = 1− αMIN/αMAX), areas (A), and the deviation (ϕ) of the direction of maximum stiffness of the ellipse (α⃑MAX) from the vector from the endpoint to the proximal joint center (v⃑LA) are reported (Fig. 1a).
The degree of asymmetry (non-conservativeness) of the endpoint stiffness was measured with the quantity Zmean_R (Mussa-Ivaldi et al., 1985). Zmean_R is the ratio of asymmetric endpoint stiffness to symmetric endpoint stiffness.
The degree of asymmetry of the endpoint viscosity (Zmean_B) was calculated from kB_END in the same way that Zmean_R was determined from kR_END. Note that these metrics of asymetry are determined from endpoint, rather than joint matrices (Mussa-Ivaldi et al., 1985).
Dynamic properties of each model were quantified by the time to maximum endpoint displacement , coordination index (CI) and damping ratios (ξi) of the three primary modes. The coordination index is the maximum time between individual peak joint displacements (Fig. 1b). Damping ratio represents the ratio of actual damping to critical damping of the system. The damping ratios (ξi) are determined according to the method of Inman (1984) as the eigenvalues (ξi) of the matrix ξ,
where the critical damping matrix (kBcr) is defined as
The exponent ½ represents the unique positive-definite square root of a positive-definite matrix. The solution of the Riccati equation (7) is a system with kB equal to 1/√2 kBcr (see Appendix), resulting in damping ratios of 1/√2 for all modes of the unconstrained controllers JU and EU.
To compare the performance of the various controllers in joint and endpoint control, impulse force perturbations of equal magnitude were applied in all directions (y) to the endpoint of the model (Fig 1b). The linear system response to an impulse endpoint force perturbation, assuming a constant Jacobian, is given by
Performance of each controller is quantified by the maximum joint ( ) (Eq. 5) and endpoint ( ) (Eq. 6) displacements experienced by the model and by the energy expenditure of the controller (Ce) (Eq. 4), for a perturbation in a given direction, y. Three sample responses (JU/JS, ES, EU) are shown in Figure 1b for a perturbation applied in the x direction (ψ = 0°). The time of maximum endpoint and joint displacements are shown in Figure 1b. Note that depending on the controller, the maximum endpoint and joint displacements may occur at different times. The endpoint position perturbation magnitude (|F⃑END|= 0.1) was chosen so that no component of the matrix J(θ)TJ(θ) differed by more than 10% from the value at the nominal posture during the perturbation. To evaluate the global performance of the control models, , , and Ce were averaged ( , , ) across perturbation direction, ψ.
An uncertainty analysis was performed to determine the sensitivity of the results to parameter variations. We measured the effect of limb configuration, limb mass and limb length parameters on endpoint asymmetry as quantified by Zmean_R and Zmean_B.
3. Results
3.1 Controller structure
The optimal unconstrained control structure minimizing joint displacement (JU) contains only diagonal elements for kR, and only symmetric components for kB (Table 2) and is therefore identical to JS. The joint control task, therefore, does not benefit from asymmetry in interjoint feedback. The distal joint of the diagonal constrained joint controller (JD) is 45% more stiff and 47% less viscous than the proximal joint, reflecting the lower system inertia below the distal joint.
Table 2.
Model inertia matrix and stiffness (kR) and viscosity (kB) components.
| JD | JU/JS | M | |||||||
|---|---|---|---|---|---|---|---|---|---|
| kR | 1.03 | 0 | 0 | 1.00 | 0 | 0 | 6.41 | 3.41 | 1.31 |
| 0 | 1.15 | 0 | 0 | 1.00 | 0 | 3.41 | 2.99 | 0.99 | |
| 0 | 0 | 1.49 | 0 | 0 | 1.00 | 1.31 | 0.99 | 0.58 | |
|
|
|||||||||
| kB | 4.09 | 0 | 0 | 3.33 | 1.22 | 0.49 | |||
| 0 | 3.27 | 0 | 1.22 | 2.06 | 0.48 | ||||
| 0 | 0 | 2.15 | 0.49 | 0.48 | 0.84 | ||||
| ED | ES | EU | |||||||
|
|
|||||||||
| kR | 2.29 | 0 | 0 | 2.75 | 1.26 | 1.23 | 1.17 | 0.39 | 0.19 |
| 0 | 4.94 | 0 | 1.26 | 1.70 | 0.59 | 0.93 | 1.31 | 0.33 | |
| 0 | 0 | 9.14 | 1.23 | 0.59 | 0.69 | 1.82 | 1.23 | 0.93 | |
|
|
|||||||||
| kB | 6.50 | 0 | 0 | 4.76 | 1.84 | 1.47 | 3.95 | 1.85 | 0.74 |
| 0 | 7.37 | 0 | 1.84 | 2.49 | 0.86 | 2.53 | 2.71 | 0.82 | |
| 0 | 0 | 9.49 | 1.47 | 0.86 | 0.68 | 2.03 | 1.46 | 1.00 | |
In contrast, the optimal unconstrained control structure minimizing endpoint displacement (EU) is asymmetric, with off-diagonal stiffness terms ranging from 0.19–1.82, compared with diagonal stiffness terms of 0.93–1.31. Upper off-diagonal terms are smaller than the lower off-diagonal terms meaning that the torque generated at distal joints due to motion at proximal joints is greater than torque generated at proximal joints due to distal joint motion. For EU, the asymmetry in endpoint stiffness and viscosity is Zmean_ R = 11.5%, and Zmean_ B = 1.5%, respectively. For ED, diagonal joint stiffness terms vary more than for JD, increasing by 300% from proximal to distal while viscosity increases by 46% across joints (Table 2). Addition of symmetric terms inverts this relationship, dramatically decreasing stiffness and viscosity at distal joints. Single joint stiffnesses are decreased by an average of 46%, and viscosities by an average of 62% when symmetric terms are introduced.
3.2 Endpoint characteristics
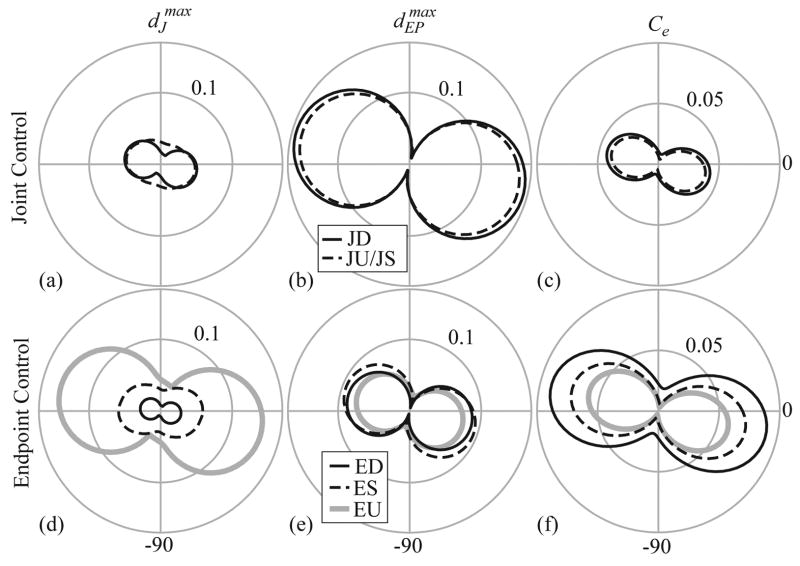
The endpoint stiffness and viscosity ellipses incorporate both controller characteristics and system geometry and provide an integrated measure of the performance of the kinematically redundant system. These ellipses are characterized by their eccentricity (s), which indicates directional sensitivity, and their area, which indicates overall system stiffness. The endpoint stiffness ellipses of the joint control models (Fig. 2b) are highly eccentric (JD: s = 0.967; JU/JS: s = 0.967) (Table 3), with the direction of greatest resistance near the axis of the limb (JD: ϕ = −7.4°; JU/JS: ϕ = −7.9°). In general the direction of maximum stiffness for all controller models is aligned closely with the limb axis (within 9°). The joint control models contain no internal model of the endpoint position, so the eccentricity of the endpoint ellipses reflects geometrical characteristics of the system.
Figure 2.
Endpoint ellipses for the six models (A–C). Ellipses represent the endpoint inertia (A), stiffness (B), and viscosity (C) of the optimal joint (left in B and C), and endpoint (right in B and C) controllers. The stiffness matrix of the JD, and JU/JS model is diagonal resulting in highly eccentric endpoint stiffness ellipses (B), while the addition of symmetric terms to the viscosity matrix for the joint controller JU/JS results in a dramatically less eccentric endpoint viscosity ellipse (C). The addition of symmetric terms to kR and kB in the endpoint controllers ES and EU also result in dramatically less eccentric and smaller endpoint ellipses (B,C). All ellipses are of approximately the same orientation.
Table 3.
Endpoint inertial, stiffness and viscosity ellipse characteristics.
| KR_END | ϕ(°) | s | A | KB_END | ϕ(°) | s | A |
|---|---|---|---|---|---|---|---|
| JD | −7.4 | 0.967 | 1.09 | JD | −8.7 | 0.967 | 10.96 |
| JU/JS | −7.9 | 0.967 | 0.89 | JU/JS | −8.6 | 0.897 | 4.34 |
| ED | −4.6 | 0.975 | 10.91 | ED | −7.4 | 0.968 | 44.21 |
| ES | −8.9 | 0.839 | 2.63 | ES | −11.9 | 0.868 | 7.62 |
| EU | −8.6 | 0.808 | 2.12 | EU | −9.1 | 0.748 | 6.68 |
|
| |||||||
| MEND | −5.7 | 0.727 | 3.84 | ||||
When subject to the diagonal constraint, the endpoint control model (ED) also results in a highly eccentric (s = 0.975) stiffness ellipse (Fig. 2b, Table 3). Relaxing the diagonal constraint to permit symmetric interjoint stiffness (ES) reduces the eccentricity of the stiffness ellipse (s = 0.839). The reduction in stiffness eccentricity is primarily due to decreased stiffness in the direction of maximum stiffness (ED: 11.8, ES: 2.3), resulting in larger displacements in that direction, while the minimum stiffness increases only slightly (ED: 0.29, ES: 0.36). Releasing all constraints on the control model (EU) further reduces endpoint stiffness eccentricity (s = 0.808). The area (A) of the stiffness ellipse decreases dramatically with the addition of symmetric off-diagonal terms (ED: A = 10.91; ES: A = 2.63), and decreases further with the addition of asymmetric off-diagonal terms (EU: A = 2.12).
The endpoint viscosity ellipses demonstrate the same trends (Fig. 2c, Table 3); there is a sharp decrease in eccentricity and area with the addition of symmetric terms for both the joint and endpoint controllers (JD: s = 0.967, A = 10.96; JU/JS: s = 0.897, A = 4.34; ED: s = 0.968, A = 44.21; ES: s = 0.868, A = 7.62, EU: s = 0.748, A = 6.68). The orientation of the endpoint viscosity ellipses is within 12° of the limb axis.
3.3 Dynamic response
To characterize the ability of each controller to maintain endpoint position, we analyzed the response of the system to a force impulse perturbation applied at the endpoint. The dynamic response of JU/JS, ES, and EU models (Fig 1b) demonstrate the different strategies employed to achieve joint and endpoint control. In all responses the distal joint experiences the greatest and most rapid initial displacement in response to the perturbation.
Motion of the JU/JS controller model is dominated by inertia, and joints follow a progressive displacement pattern with individual joints reaching peak displacement successively. Peak endpoint displacement is 0.15, occuring at t̂ = 3.3, and geometric recovery does not begin until substantially after the distal joint has completed its recovery. Maximal joint displacements follow a successive distal-to-proximal pattern (Figure 1b, upper panel) and occur over a dimensionless time of 3.0 (CI).
The endpoint controllers (ED,ES,EU), each of which contains an internal model of endpoint position, all display much better endpoint performance than the joint controllers (JD, JU/JS). The maximal ED controller displacement was 0.09, 43% less than the best joint controller (JU/JS), and geometric recovery began at t̂ = 1.9. For the ES controller, interjoint coupling links the rapid motion of the distal segment to amplified torque generation at the proximal joints. The symmetry of this coupling causes slower displacement of the more proximal joints that poduces a sustained torque generation at the distal joint, which is sufficient to reverse the direction of motion of the distal joint (Fig 1b, middle and lower panels). Interjoint coupling increases the apparent stiffness of proximal joints early in the perturbation, but reverses the apparent stiffness of the distal joint later in the perturbation. This result is due to coupling of the inertially retarded motion of proximal and middle joints to torque generation at the distal joint. The reversal of the distal joint counteracts the continuing motion of the proximal and middle joints to maintain the x-y location of the endpoint. The time to peak endpoint displacement is faster for the ES controller at 1.3, but maximal joint displacements still follow a successive pattern as in the JU/JS controller model and occur within a dimensionless time of 3.5 (CI).
This compensating effect of the distal joint is amplified for the EU controller, where torque generation is coupled asymmetrically. The asymmetry of interjoint coupling permits the distal joint to undergo exaggerated extension without substantially altering proximal joint torque production. Although there is an initial yield as the perturbing force is applied, interjoint elastic coupling results in large distal joint torque generation as the proximal joint begins to yield, and subsequent motion of the distal joint is largely synchronous with the proximal joint (Fig 1b, lower panel). Maximal individual joint displacements do not follow a successive pattern and the coordination index is 1.2, in contrast with 3.0 for the JU/JS model and 3.5 for the ES model. Maximal endpoint displacement of 0.07 occurs at t̂ = 1.1, substantially before any single joint displacement maximum, and geometric recovery begins quickly after cessation of perturbation. Table 4 shows the time to maximum endpoint displacement and coordination index averaged over perturbation direction . The average values follow the trends described for the response to a perturbation in the x-direction (ψ = 0°) with a 7% decrease in and 40% decrease in from ES to EU.
Table 4.
Dynamic properties. Averaging is done across perturbation direction (ψ).
| JD | JU/JS | ED | ES | EU | |
|---|---|---|---|---|---|
| 3.08 ± 0.40 | 3.01 ± 0.66 | 1.83 ± 0.33 | 1.25 ± 0.20 | 1.16 ± 0.10 | |
| 2.59 ± 0.70 | 2.61 ± 0.99 | 1.65 ± 0.39 | 2.90 ± 1.03 | 1.75 ± 0.72 | |
| ξI | 0.59 | 0.71 | 0.67 | 0.41 | 0.71 |
| 1.64 | 0.71 | 1.85 | 0.57 | 0.71 | |
| 2.08 | 0.71 | 3.33 | 0.97 | 0.71 |
The global dynamic response of multi-link systems can be quantified with damping ratio (Table 4). The damping ratio of diagonal controller models vary widely including underdamped (JD: ξ = 0.59, ED: ξ = 0.67) and overdamped (JD: ξ = 2.08, ED: ξ = 3.33) modes. Symmetry allows for a more uniform response for ES for which all modes are underdamped (0.41, 0.57, 0.97). The analytical solution to the matrix algebraic Riccati equation dictates that the damping ratio of EU and JU/JS be 1/√2.
3.4 Cost
Costs associated with endpoint impulse force perturbations are presented in Figure 3. The tradeoff in kinematic and energetic cost can be seen for the joint control model (Fig. 3a–c). The maximum joint displacement averaged over perturbation direction ( ) is 12% higher for the JU/JS controller model than the restricted JD (Fig. 3a, Table 5), while the average energetic cost ( ) is 15% lower for JU/JS than JD (Fig. 3a, Table 5). This means that the symmetric interjoint coupling through the viscosity matrix for JU/JS serves to coordinate joint motions so that the total energetic cost is minimized at the expense of slightly larger joint displacements ( ) compared with JD. The average maximum endpoint displacement ( ) is 4% lower for JU/JS than JD.
Figure 3.
Measures of kinematic and kinetic performance. (A,D) The maximum joint displacement ( ) (Eq. 5), (B,E) maximum endpoint displacement ( ) (Eq. 6), and (C,F) energetic cost (Ce) (Eq. 4) for the optimized models (JD, JU/JS, ED, ES, EU) for impulse perturbations of equal magnitude across perturbation direction (ψ).
Table 5.
The average maximum displacements and energetic cost. Averaging is done across perturbation direction (ψ).
| JD | JU/JS | ED | ES | EU | |
|---|---|---|---|---|---|
| 0.034 ± .014 | 0.039 ± .007 | 0.019 ± .008 | 0.046 ± .010 | 0.096 ± .038 | |
| 0.106 ± .050 | 0.101 ± .046 | 0.057 ± .027 | 0.063 ± .027 | 0.053 ± .019 | |
| 0.026 ± .013 | 0.022 ± .013 | 0.055 ± .026 | 0.040 ± .024 | 0.031 ± .020 |
The kinematic-kinetic tradeoff is also seen for the endpoint controllers (Fig. 3d–f, Table 5). The addition of symmetric off-diagonal terms (ES) results in an 11% increase in , but a 28% decrease in compared with ED. The addition of asymmetric interjoint coupling, however, results in a decrease in both kinematic ( decreased by 16% over ES) and kinetic ( decreased by 21% over ES) quantities. The improvements in endpoint control are achieved by exaggerated joint displacement; is 140% (ES) and 400% (EU) greater for the coupled controllers than ED.
The average displacement magnitudes ( , ) for the two unconstrained optimal controllers (JU/JS and EU) reflect the tasks for which each was optimized. JU/JS has 60% lower than EU, while EU has 47% lower than JU/JS.
To test whether the asymmetry was a coincidental result of the joint configuration, the optimization was repeated for an additional posture (θ1 = −150°, θ2 = 120°, θ3 = −117°) based on the stance phase of locomotion of the tree shrew Tuapaia glis (Schilling, 2005). At the new posture, the equations were re-linearized so that the new optimization represents the optimal behavior of the limb locally at the new posture and is not an extrapolation of the optimization at the previous posture. The optimal endpoint stiffness and viscosity were asymmetric for this posture (Zmean_ R = 20.5%, Zmean_ B = 9.9%) also, but the resulting kinematic and energetic cost improvement ( decreased by 5% from ES to EU; decreased by 11% from ES to EU), and homogenization of endpoint stiffness (ES: s = 0.648, A = 2.16, EU: s = 0.684, A = 2.23), viscosity (ES: s = 0.560, A = 4.62, EU: s = 0.575, A = 5.54), and damping ratios (ES: 0.58, 0.64, 0.77; EU: 0.71) were smaller than seen in the extended posture, indicating that the benefits of asymmetry are limb configuration dependent.
An uncertainty analysis was performed to determine the sensitivity of the results to parameter variations. We measured the effect of limb configuration, limb mass and limb length parameters on endpoint asymmetry as quantified by Zmean_R and Zmean_B. On average, the sensitivity to segment mass or length is about unity in Zmean_R, so that a 10% change in length results in a 10% change (ie: from 11.5% to 10.4% or 12.6%), and about 0.5 in Zmean_B (1.5% to 0.9% or 2.1%). Similarly, a change in joint angle by 10° changes Zmean_R by 4 percentage points and Zmean_B by 2 percentage points. Therefore, changing model parameters does not significantly alter asymmetry in the solutions.
4. Discussion
The goal of this project was to determine whether asymmetric interjoint feedback improved the performance of postural tasks as evaluated by energetic cost and maintenance of endpoint position. The optimal controller for maintaining endpoint position contained substantial asymmetry in the off-diagonal terms, supporting the hypothesis that this structure contributes to endpoint control, and in agreement with similar models (Barin, 1989; He et al., 1991; Park et al., 2004). The results are coherent and testable with uncontrolled manifold (UCM) hypothesis (Scholz & Schoner, 1999; Todorov & Jordan, 2002): EU achieves much greater endpoint control than JU/JS, at the expense of variability in the state. For the cat-like posture, the asymmetry provided an improvement (40% , 16% ) in the recovery from perturbation and a reduction (21%) in energetic cost. These gains were more dramatic when the system was in an extended, cat-like posture than in a compressed, rodent-like posture. The energetic benefit is substantial and likely to contribute to the development of neural control strategies, at least in some areas of the workspace. The same analysis performed on a two degree of freedom model produced optimal asymmetric controllers (EU) that were only slightly better than the symmetric controllers (ES) for both an extended ( : 5%, : 4%) and flexed ( : 3%, : 2%) posture, suggesting that the improvement in control due to asymmetry is specific to kinematically redundant systems (unpublished observations). This result is especially significant when considering the fact that the experiments in each of the cited human arm studies are specifically designed for a constrained two-degree of freedom, non-redundant system where asymmetry is not consistently observed. The degree of asymmetry for a redundant system has not been experimentally measured. It may be that the small amount of endpoint asymmetry will be more consistently measured for experiments using kinematically redundant limbs.
In this study we have demonstrated that a small amount of endpoint asymmetry is required to achieve optimal endpoint control, and that asymmetry as small as 10% can improve endpoint control efficiency by as much as 20%. The degree of asymmetry for the optimal endpoint controller is consistent with experimentally determined magnitudes. Mussa-Ivaldi and coworkers (Mussa-Ivaldi et al., 1985) measured elastic Zmean_R values for human arm ranging from 0.4% to 20.9% with a mean of 6.5% across four subjects and five arm configurations, which is similar to the EU controller Zmean_R of 11.5% in the feline posture and Zmean_R of 20.5% in the shrew-like posture. Mussa-Ivaldi and coworkers concluded that the magnitude of the anti-symmetric part of endpoint stiffness was small compared to the symmetric component.
Interjoint coupling provides substantial improvement in endpoint control, and both symmetric and asymmetric multi-joint control strategies result in greater homogeneity of endpoint properties and dynamic response. The endpoint stiffness ellipse eccentricities of the ES and EU controllers are reduced by 6.4 and 7.7 fold, respectively, over the ED controller. Viscosity endpoint ellipses are reduced 4.1 (ES) and 7.8 (EU) fold. Lower eccentricity means greater similarity in response across perturbations. The dynamic response characteristics also become more uniform with the addition of asymmetric terms for the endpoint model. Damping ratios are all 1/√2 for EU and vary from 0.41 to 0.97 for ES as opposed to ED where damping ratios vary from 0.67 to 3.33.
Damping ratio has been reported previously to be in the range of 0.25 to 0.4 for the ankle joint at various muscle activation levels (Agarwal & Gottlieb, 1977; Weiss, Hunter & Kearney, 1988). Mean wrist joint damping ratio for 4 subjects was calculated at 0.21, and a first attempt at correcting for the inertia of the apparatus resulted in a damping ratio of 0.61 (Sinkjaer & Hayashi, 1989). Median damping ratios for the human arm were reported by Perreault and coworkers (Perreault, Kirsch & Crago, 2004) at 0.25 for the minimally damped mode and 0.47 for the maximally damped mode. These studies demonstrate damping ratios that are consistently lower than the predicted optimal damping ratio of 0.71.
The homogeneity of damping ratio permitted by asymmetric feedback has a dramatic effect on the coordination of the limb. For ES, maximal joint displacements follow a successive pattern, with an average coordination index of 2.9 while maximal joint displacements follow a more coordinated pattern for EU model for the same perturbation, with a of 1.8 ± 0.7 (Table 4). The time course of middle joint displacement varies little between the ES and EU models, and the principal effect of the asymmetry is to impose the kinematics of the proximal joint response on the distal joint. This contributes to the temporal coordination of all of the joints in the limb, consistent with experimental observations of correlated joint motions both in response to perturbation and in voluntary movements (Hogan et al., 1987; Okadome & Honda, 1999).
Two postural tasks were specified to examine two potential mechanisms the central nervous system (CNS) uses to accomplish a stable endpoint posture. The joint control task seeks to minimize the deviation of each specific joint from the initial posture. The optimal controller for this task predicts a myotatic unit-like stiffness component, with no off-diagonal terms, therefore, all interjoint coupling is achieved by the off-diagonal terms in the inertia matrix (M) and joint viscosity matrix kB. Physiologically, the static response is dominated by individual joint or muscle displacements, encoded in the Group I & II spindle response (Matthews & Stein, 1969). The dynamic response, including all of the predicted interjoint coupling, is strongly influenced by velocity, which is encoded in the Group I spindle afferent (Matthews, 1963). The appearance of interjoint coupling only within the viscosity matrix generates torques at remote joints that counteract inertial coupling. This coupling could not be provided by biarticular muscles since they would contribute to both joint viscosity and joint stiffness. This controller, however, presents relatively poor endpoint performance characteristics because of the lack of an internal model (i.e. the Jacobian is not used in the determination of the controller). The displacement of the endpoint in response to a perturbation is highly dependent on perturbation orientation. The system presents excellent resistance along the limb axis, which would provide sound weight support, but poorly resists perpendicular perturbations, and would require a stronger and faster response from higher centers to correct for any non-vertical perturbation. The response of the system to perturbation is also uncoordinated. Individual joints return to their initial configuration as quickly as possible, which would result in segments with lower inertia responding extremely rapidly and a system that responds with time characteristic of the largest segment. In a biological system, in which the distal segments are systematically lighter than proximal segments, the joint control model would predict nearly rigid distal joints and a system response dominated by the hip or shoulder.
The endpoint control task seeks to minimize the deviation of the endpoint from a specified position, regardless of the joint angles necessary to produce that endpoint position. In the endpoint control model, QE contains an internal model of the Jacobian, and the optimal kR depends directly on posture through the Jacobian, and optimal kB depends on posture through both kR and M (see appendix). The shrew-like posture is a more flexed posture and while the degree of asymmetry is increased, the benefits of that asymmetry decrease, indicating that the quantitative benefits of asymmetry are posture dependent. In either of the test postures, the highly extended feline posture or the much more compact shrew posture, the mean energetic cost of recovering from an impulse perturbation was smaller for the EU than ES (11% shrew-like, 21% cat-like).
A proximal to distal gradient exists in the structure of the endpoint controllers. For the symmetric endpoint controller (ES) stiffness and viscosity were higher at proximal than distal joint consistent with the increased musculature in animal limbs at proximal joints compared with distal joints. For the asymmetric endpoint (EU) controller, the proximal distal gradient is mitigated by another gradient in the asymmetry of the feedback. Regardless of posture, the optimal controller was asymmetric in the sense that displacement of the proximal joint resulted in powerful torque production at the distal joint, while displacement of the distal joint induced relatively small torques at the proximal joint. The existence or strength of reflex feedback between hip and ankle muscles in cats is largely unknown, due to the technical difficulties of working with hip muscles (Loeb & Duysens, 1979). Stretch of the hip flexor iliopsoas, representative of a negative θ1 perturbation, has been reported to reduce ankle extensor activity during gait (Hiebert et al., 1996), equivalent to a positive torque at the distal joint as predicted by the optimal controller. Group I feedback from vasti to soleus, which would contribute to kB(3,2), has been measured (Eccles, Eccles & Lundberg, 1957a), although feedback from vasti to gastrocnemius (contributing to both kR,B(3,2) and kR,B(2,2)) is inhibitory (Wilmink & Nichols, 2003). Length changes in soleus have little or no effect on vastus force generation (kR,B(2,3), (Wilmink & Nichols, 2003), which suggests that, in the cat, kR(3,2) would be greater than kR(2,3), as predicted by the optimal control model. EU also contains a strongly asymmetric relationship between proximal and distal joints. For small proximal joint motion the distal joint remains relatively compliant, suitable for rejection of small endpoint perturbations. For large proximal joint motion the asymmetry contributes to greater impedance at the distal joint. This strategy is consistent with an observed role for the ankle in relationship to the hip in human pedaling (Fregly & Zajac, 1996).
The measure of energetic cost used in this analysis is the integrated, squared torque produced during the recovery from perturbation. This differs from work done or absorbed, and it does not account for co-contraction nor energetic savings associated with biarticular muscles. As a biological cost function, it also neglects the higher muscle mass available to the proximal joints, although this may be compensated by structuring the model with non-uniform segmental inertias, where the moment of inertia of distal segments is generally lower than proximal segments. A cat foot, for example, is roughly 12% of the mass of the thigh. A potential alternative measure of energy is stiffness size, since stiffness is proportional to force. The stiffness size is quantified as the area (A) of the endpoint stiffness ellipse (kR_END) reported in table 3. The area of kR_END for EU is 19% smaller than the kR_END for ES, consistent with the original measure of energetic cost ( ).
To determine whether predicted magnitudes of joint stiffness and viscosity are of appropriate physiological magnitude, kR and kB of EU were redimensionalized for average cat (m = 84 g, L = 9.5 cm) and tree shrew (m = 4 g, L = 3 cm) limb dimensions for comparison to measured values. The scaling parameter, σ, was chosen for the cat (σ = 4.0 N; τ = 44.7 msec) so that the limb restores equilibrium on the same order as that measured experimentally (~400 msec) (Macpherson, 1988). Since no data is available for the postural response of a shrew, σ is approximately scaled with muscle force (P0), σSHREW= 0.4 N. Dimensional values of kB/kR range from 0.05 to 0.21 sec for the cat, and from 0.02 to 0.05 sec for the shrew. The viscosity of mammalian muscle increases with animal size, and the prediction that shrew kB/kR is 50–80% smaller than cat is consistent with this scaling. Intrinsic viscosity results from the force velocity relation, and varies from 0.1–2 (P0 sec)/L0, depending on fiber type and species (Close, 1972). The apparent intrinsic stiffness of muscle depends strongly on the length range being considered. The range most relevant to postural perturbations is likely the short range stiffness, resulting from crossbridge elasticity, of 20–100 P0/L0. (Huxley & Simmons, 1971), yielding viscosity to stiffness ratio in the range of 0.001–0.1 sec, which is consistent with the model prediction. Over longer length ranges, stiffness described by the isometric length tension relationship is approximately 0.4 P0/L0. This suggests viscosity to stiffness ratios in the range of 0.25–5 sec, which is only slightly higher than the model prediction.
The lumped parameter approach used in this model cannot distinguish between reflexive and intrinsic mechanisms, with the exception that asymmetries must be reflexive, due to the inherent symmetry of intrinsic mechanisms. Delays associated with neural mechanisms might be destabilizing or might require alterations in the structure of the lumped-parameter control model. This model was inspired by feline postural control, and the characteristic time for the cat hind limb is 45 msec. Redimensionalized, the entire postural response requires 450 ms, which is long relative to reflex responses (25 ms) and suggests that lumping intrinsic and reflexive mechanisms is a reasonable approximation for the gross limb response. The fastest feature of the predicted postural response is a peak displacement of the distal joint around t̂ value of 1 (45 msec, Table 4). This peak occurs on the same time scale as short latency reflexes, and its recovery reflects torque produced at the distal joint as a result of displacement of the proximal joints. This is an interesting coincidence, and suggests that spindle responses from hip muscles might be ideally suited to mediate the strongly asymmetric interjoint coupling predicted by this optimization. Our future work is aimed at investigating similar feedback structures when muscles (and neural delay) are taken into account.
It is worth while to consider the implications of scaling an optimal solution with effort, σ. As pointed out by Kuo (Kuo, 1995), σ has various interpretations, including a measure of the relative cost of kinematic penalty, the speed of system response, and the gain of intrinsic and reflexive impedance properties. The structure of optimal kR and kB matrices are constant for the given parameters. However, to obtain dimensional stiffness and viscosity kR is proportional to σ and kB is proportional to . Thus, the dimensional endpoint ellipses would have the same shape and orientation with the size scaling with σ for stiffness and for viscosity. The scaling also maintains a constant damping ratio across σ. These traits are consistent with observed characteristics of human arms. Mussa-Ivaldi and coworkers (Mussa-Ivaldi et al., 1985) found that adaptive changes in postural stiffness in response to a force in a single direction were accomplished by varying the size rather than the shape or orientation of the ellipses. This is consistent with the idea that the “optimal” solution has the same shape and orientation but different magnitude for varying levels of effort. Perrault and coworkers (Perreault et al., 2004) found that endpoint arm elasticity increased linearly with voluntary force generation while viscosity increased nonlinearly, consistent with σ scaling. The consistency of damping ratios in the human arm (Perreault et al., 2004), wrist (Sinkjaer & Hayashi, 1989), and ankle (Agarwal & Gottlieb, 1977; Weiss et al., 1988) across subjects and effort level is also in agreement with σ scaling.
Since the magnitude of the optimal controllers scale not only with the physical size of the model (mass and length) but with a voluntary force or effort, both intrinsic and reflex properties of the limb must also scale with effort. The force of a reflex can vary even with a constant stimulus. Descending neurons from higher centers make synaptic connections at the alpha motor neurons, interneurons and presynaptic terminals of the afferent fibers, changing the tonic activity of the cell to modulate the sensitivity of reflex response. Alpha-gamma coactivation may be responsible for coordinated increases of intrinsic and reflexive components of muscle impedance; in general gamma motor neurons are set at higher levels as the speed of movement increases (Hulliger et al., 1989). Prochazka and coworkers (Prochazka, 1989) describe significant changes in monosynaptic reflex pathways (tendon and H-reflex) in anticipation of co-activation, so that the reflex and intrinsic magnitudes may scale together.
We have tested the hypothesis that an asymmetric multi-joint control strategy would confer both energetic and stability advantages in maintaining endpoint position in a kinematically redundant system. We have demonstrated that asymmetric feedback improved endpoint control performance of the limb by 16%, reduced energetic cost by 21%, and increased interjoint coordination by 40%, compared to the symmetric feedback system. The performance gains were achieved by a joint coordination strategy where perturbations to proximal joint angles produced more torque generation in distal joints than vice versa. This organization is consistent with heterogenic stretch reflex gains measured experimentally. We conclude that asymmetric feedback has a functionally relevant role in coordinating redundant degrees of freedom in maintaining the position of the hand or foot.
Acknowledgments
This work was supported by NIH grant HD46922 to LHT.
Appendix
Using LQR theory to determine optimal stiffness and viscosity matrices results in an optimal viscosity matrix that is 1/√2 times the critical damping matrix. This appendix contains the derivation of this result from the matrix algebraic Riccati equation (7) and the optimal state feedback matrix Eq. (8). Matrices R, Q, M and S are symmetric. Applying Eq. (8) to Eq. (7) yields
Matrix S is symmetric and divided into components,
Substituting the definitions of S, as well as A, k, and Q, Eqs. (3–5),
simplifying, yields
| (9) |
Equation (8) can be written as
| (10) |
Solving the left hand side of the matrix equality in Eq. (10) for SB and applying to the lower left hand matrix equality of Eq. (9),
Pre-multiplying both sides by and simplifying
| (11) |
Which is symmetric, by the relationships in Eq. (9). Taking the transpose of the left side
| (12) |
Pre-multiplying both sides of Eq. (12) by
| (13) |
Pre- and post-multiply Eq. (13) by the unique positive definite square root (M−1/2) of positive definite matrix M−1,
| (14) |
If kR and kB are positive definite, then
| (15) |
Solve for kB.
References
- Agarwal GC, Gottlieb GL. Compliance of the human ankle joint. J Biomech Eng. 1977;99:166–170. [Google Scholar]
- Barin K. Evaluation of a Generalized-Model of Human Postural Dynamics and Control in the Sagittal Plane. Biological Cybernetics. 1989;61:37–50. doi: 10.1007/BF00204758. [DOI] [PubMed] [Google Scholar]
- Bonasera SJ, Nichols TR. Mechanical actions of heterogenic reflexes linking long toe flexors with ankle and knee extensors of the cat hindlimb. J Neurophysiol. 1994;71:1096–110. doi: 10.1152/jn.1994.71.3.1096. [DOI] [PubMed] [Google Scholar]
- Bryson AE, Ho Y-C. Applied optimal control: optimization, estimation, and control. Rev. printing. Hemisphere Pub. Corp.; New York: 1975. [Google Scholar]
- Close RI. Dynamic properties of mammalian skeletal muscles. Physiol Rev. 1972;52:129–97. doi: 10.1152/physrev.1972.52.1.129. [DOI] [PubMed] [Google Scholar]
- Crago PE, Houk JC, Hasan Z. Regulatory Actions of Human Stretch Reflex. Journal of Neurophysiology. 1976;39:925–935. doi: 10.1152/jn.1976.39.5.925. [DOI] [PubMed] [Google Scholar]
- Dolan JM, Friedman MB, Nagurka ML. Dynamic and Loaded Impedance Components in the Maintenance of Human Arm Posture. Ieee Transactions on Systems Man and Cybernetics. 1993;23:698–709. [Google Scholar]
- Eccles JC. Excitatory and Inhibitory Synaptic Action. Harvey Lectures. 1956:1–24. [PubMed] [Google Scholar]
- Eccles JC, Eccles RM, Lundberg A. The convergence of monosynaptic excitatory afferents on to many different species of alpha motoneurones. Journal of Physiology. 1957a;137:22–50. doi: 10.1113/jphysiol.1957.sp005794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eccles JC, Eccles RM, Lundberg A. Synaptic Actions on Motoneurones in Relation to the 2 Components of the Group-I Muscle Afferent Volley. Journal of Physiology-London. 1957b;136:527–546. doi: 10.1113/jphysiol.1957.sp005778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eccles RM, Lundberg A. Significance of Supraspinal Control of Reflex Actions by Impulses in Muscle Afferents. Experientia. 1958;14:197–199. doi: 10.1007/BF02159082. [DOI] [PubMed] [Google Scholar]
- Flash T, Mussa-Ivaldi F. Human arm stiffness characteristics during the maintenance of posture. Exp Brain Res. 1990;82:315–26. doi: 10.1007/BF00231251. [DOI] [PubMed] [Google Scholar]
- Franklin DW, Burdet E, Osu R, Kawato M, Milner TE. Functional significance of stiffness in adaptation of multijoint arm movements to stable and unstable dynamics. Exp Brain Res. 2003;151:145–57. doi: 10.1007/s00221-003-1443-3. [DOI] [PubMed] [Google Scholar]
- Franklin DW, Milner TE. Adaptive control of stiffness to stabilize hand position with large loads. Exp Brain Res. 2003;152:211–20. doi: 10.1007/s00221-003-1540-3. [DOI] [PubMed] [Google Scholar]
- Fregly BJ, Zajac FE. A state-space analysis of mechanical energy generation, absorption, and transfer during pedaling. J Biomech. 1996;29:81–90. doi: 10.1016/0021-9290(95)00011-9. [DOI] [PubMed] [Google Scholar]
- Hamill J, Knutzen K. Biomechanical basis of human movement. 2. Lippincott Williams & Wilkins; Philadelphia: 2003. [Google Scholar]
- He JP, Levine WS, Loeb GE. Feedback gains for correcting small perturbations to standing posture. IEEE Trans Autom Control. 1991;36:322–32. [Google Scholar]
- Hiebert GW, Whelan PJ, Prochazka A, Pearson KG. Contribution of hind limb flexor muscle afferents to the timing of phase transitions in the cat step cycle. J Neurophysiol. 1996;75:1126–37. doi: 10.1152/jn.1996.75.3.1126. [DOI] [PubMed] [Google Scholar]
- Hogan N. The mechanics of multi-joint posture and movement control. 1985;52:315–31. doi: 10.1007/BF00355754. [DOI] [PubMed] [Google Scholar]
- Hogan N, Bizzi E, Mussa-Ivaldi FA, Flash T. Controlling multijoint motor behavior. Exerc Sport Sci Rev. 1987;15:153–90. [PubMed] [Google Scholar]
- Hulliger M, Durmuller N, Prochazka A, Trend P. Flexible fusimotor control of muscle spindle feedback during a variety of natural movements. Prog Brain Res. 1989;80:87–101. 57–60. doi: 10.1016/s0079-6123(08)62202-5. [DOI] [PubMed] [Google Scholar]
- Huxley AF, Simmons RM. Mechanical properties of the cross-bridges of frog striated muscle. J Physiol. 1971;218:59P–60P. [PubMed] [Google Scholar]
- Kargo WJ, Giszter SF. Afferent roles in hindlimb wipe-reflex trajectories: free-limb kinematics and motor patterns. J Neurophysiol. 2000;83:1480–501. doi: 10.1152/jn.2000.83.3.1480. [DOI] [PubMed] [Google Scholar]
- Kuo AD. An optimal control model for analyzing human postural balance. IEEE Trans Biomed Eng. 1995;42:87–101. doi: 10.1109/10.362914. [DOI] [PubMed] [Google Scholar]
- Kuo AD. An optimal state estimation model of sensory integration in human postural balance. J Neural Eng. 2005;2:S235–49. doi: 10.1088/1741-2560/2/3/S07. [DOI] [PubMed] [Google Scholar]
- Lacquaniti F, Soechting JF. EMG responses to load perturbations of the upper limb: effect of dynamic coupling between shoulder and elbow motion. Exp Brain Res. 1986;61:482–96. doi: 10.1007/BF00237573. [DOI] [PubMed] [Google Scholar]
- Liddell EGT, Sherrington C. Further observations on myotatic reflexes. Proceedings of the Royal Society of London Series B-Containing Papers of a Biological Character. 1925;97:267–283. [Google Scholar]
- Lloyd DPC. Facilitation and Inhibition of Spinal Motoneurons. Journal of Neurophysiology. 1946;9:421–438. doi: 10.1152/jn.1946.9.6.421. [DOI] [PubMed] [Google Scholar]
- Loeb GE, Duysens J. Activity patterns in individual hindlimb primary and secondary muscle spindle afferents during normal movements in unrestrained cats. J Neurophysiol. 1979;42:420–40. doi: 10.1152/jn.1979.42.2.420. [DOI] [PubMed] [Google Scholar]
- Macpherson JM. Strategies that simplify the control of quadrupedal stance. I. Forces at the ground. J Neurophysiol. 1988;60:204–17. doi: 10.1152/jn.1988.60.1.204. [DOI] [PubMed] [Google Scholar]
- Matthews PB. The Response of De-Efferented Muscle Spindle Receptors to Stretching at Different Velocities. J Physiol. 1963;168:660–78. doi: 10.1113/jphysiol.1963.sp007214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews PB, Stein RB. The regularity of primary and secondary muscle spindle afferent discharges. J Physiol. 1969;202:59–82. doi: 10.1113/jphysiol.1969.sp008795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merton PA. Slowly Conducting Muscle Spindle Afferents. Acta Physiologica Scandinavica. 1953;29:87–88. doi: 10.1111/j.1748-1716.1953.tb01003.x. [DOI] [PubMed] [Google Scholar]
- Mussa-Ivaldi FA, Hogan N, Bizzi E. Neural, Mechanical, and Geometric Factors Subserving Arm Posture in Humans. Journal of Neuroscience. 1985;5:2732–2743. doi: 10.1523/JNEUROSCI.05-10-02732.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols TR. The organization of heterogenic reflexes among muscles crossing the ankle joint in the decerebrate cat. J Physiol. 1989;410:463–77. doi: 10.1113/jphysiol.1989.sp017544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols TR, Cope TC, Abelew TA. Rapid spinal mechanisms of motor coordination. Exerc Sport Sci Rev. 1999;27:255–84. [PubMed] [Google Scholar]
- Nichols TR, Houk JC. Improvement in linearity and regulation of stiffness that results from actions of stretch reflex. J Neurophysiol. 1976;39:119–42. doi: 10.1152/jn.1976.39.1.119. [DOI] [PubMed] [Google Scholar]
- Okadome T, Honda M. Kinematic construction of the trajectory of sequential arm movements. Biol Cybern. 1999;80:157–69. doi: 10.1007/s004220050514. [DOI] [PubMed] [Google Scholar]
- Park S, Horak FB, Kuo AD. Postural feedback responses scale with biomechanical constraints in human standing. Exp Brain Res. 2004;154:417–27. doi: 10.1007/s00221-003-1674-3. [DOI] [PubMed] [Google Scholar]
- Patel RV, Shadpey F. Control of Redundant Robot Manipulators - Theory and Experiments. Control of Redundant Robot Manipulators: Theory and Experiments. 2005;316:Vii-+. [Google Scholar]
- Perreault EJ, Kirsch RF, Crago PE. Effects of voluntary force generation on the elastic components of endpoint stiffness. Exp Brain Res. 2001;141:312–23. doi: 10.1007/s002210100880. [DOI] [PubMed] [Google Scholar]
- Perreault EJ, Kirsch RF, Crago PE. Multijoint dynamics and postural stability of the human arm. 2004;157:507–17. doi: 10.1007/s00221-004-1864-7. [DOI] [PubMed] [Google Scholar]
- Perreault EJ, Viant TL. Neural coordination of multijoint stretch reflexes in the human arm. Conf Proc IEEE Eng Med Biol Soc. 2005;4:4389–92. doi: 10.1109/IEMBS.2005.1615438. [DOI] [PubMed] [Google Scholar]
- Pratt CA. Evidence of Positive Force Feedback Among Hindlimb Extensors in the Intact Standing Cat. Journal of Neurophysiology. 1995;73:2578–2583. doi: 10.1152/jn.1995.73.6.2578. [DOI] [PubMed] [Google Scholar]
- Prochazka A. Sensorimotor gain control: a basic strategy of motor systems? Prog Neurobiol. 1989;33:281–307. doi: 10.1016/0301-0082(89)90004-x. [DOI] [PubMed] [Google Scholar]
- Sage HG, De Mathelin MF, Ostertag E. Robust control of robot manipulators: a survey. International Journal of Control. 1999;72:1498–1522. [Google Scholar]
- Schilling N. Ontogenetic development of locomotion in small mammals--a kinematic study. J Exp Biol. 2005;208:4013–34. doi: 10.1242/jeb.01875. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Schoner G. The uncontrolled manifold concept: identifying control variables for a functional task. Exp Brain Res. 1999;126:289–306. doi: 10.1007/s002210050738. [DOI] [PubMed] [Google Scholar]
- Sherrington CS. Experiments in examination of the peripheral distribution of the fibers of the posterior roots of some spinal nerves. Part II. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences. 1898;190:45–86. [Google Scholar]
- Sinkjaer T. Muscle, reflex and central components in the control of the ankle joint in healthy and spastic man. Acta Neurol Scand Suppl. 1997;170:1–28. [PubMed] [Google Scholar]
- Sinkjaer T, Hayashi R. Regulation of wrist stiffness by the stretch reflex. J Biomech. 1989;22:1133–40. doi: 10.1016/0021-9290(89)90215-7. [DOI] [PubMed] [Google Scholar]
- Stroeve S. Impedance characteristics of a neuromusculoskeletal model of the human arm I. Posture control. Biol Cybern. 1999;81:475–94. doi: 10.1007/s004220050577. [DOI] [PubMed] [Google Scholar]
- Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nature Neuroscience. 2002;5:1226–1235. doi: 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
- Torres-Oviedo G, Macpherson JM, Ting LH. Muscle synergy organization is robust across a variety of postural perturbations. J Neurophysiol. 2006;96:1530–46. doi: 10.1152/jn.00810.2005. [DOI] [PubMed] [Google Scholar]
- Tsuji T, Morasso PG, Goto K, Ito K. Human hand impedance characteristics during maintained posture. Biol Cybern. 1995;72:475–85. doi: 10.1007/BF00199890. [DOI] [PubMed] [Google Scholar]
- Weiss PL, Hunter IW, Kearney RE. Human ankle joint stiffness over the full range of muscle activation levels. J Biomech. 1988;21:539–44. doi: 10.1016/0021-9290(88)90217-5. [DOI] [PubMed] [Google Scholar]
- Wilmink RJ, Nichols TR. Distribution of heterogenic reflexes among the quadriceps and triceps surae muscles of the cat hind limb. 2003;90:2310–24. doi: 10.1152/jn.00833.2002. [DOI] [PubMed] [Google Scholar]