Simulation of blood flow in deformable vessels using subject-specific geometry and spatially varying wall properties

SUMMARY

Simulation of blood flow using image-based models and computational fluid dynamics has found widespread application to quantifying hemodynamic factors relevant to the initiation and progression of cardiovascular diseases and for planning interventions. Methods for creating subject-specific geometric models from medical imaging data have improved substantially in the last decade but for many problems, still require significant user interaction. In addition, while fluid–structure interaction methods are being employed to model blood flow and vessel wall dynamics, tissue properties are often assumed to be uniform. In this paper, we propose a novel workflow for simulating blood flow using subject-specific geometry and spatially varying wall properties. The geometric model construction is based on 3D segmentation and geometric processing. Variable wall properties are assigned to the model based on combining centerline-based and surface-based methods. We finally demonstrate these new methods using an idealized cylindrical model and two subject-specific vascular models with thoracic and cerebral aneurysms.

1. INTRODUCTION

Hemodynamic factors, including pressure, flow rate, and shear stress, have been shown to play an important role in vascular diseases, such as atherosclerosis [1, 2] and aneurysms [3, 4]. Recent advances in medical imaging techniques, such as magnetic resonance imaging (MRI) and computed tomography (CT), can provide exquisite anatomical information of the vasculature. However, local in vivo hemodynamics is difficult to measure noninvasively [5]. Based on computational fluid dynamics (CFD), blood flow simulation provides a unique way to quantify hemodynamics in high spatial and temporal resolution [6-8]. This information could be employed in the future to guide decision making of alternative options prior to interventional procedures [9].

While, initially, blood flow simulations were performed using idealized geometric models, in the last decade the majority of papers report results using image-based, subject-specific models [10, 11]. Subject-specific geometry is crucial in predicting hemodynamics because of the large anatomic and physiologic variations amongst individuals. Many of the early tools for image-based modeling of blood flow were based on 2D segmentation of vessel lumen boundary [12] and solid model generation by ‘lofting’ from a series of these 2D segmentations [7, 13]. Although these methods can be used to create complex geometric models, there are some shortcomings of this approach which limit its use for certain applications. Diseased vessels are often not tubular and sometimes exceedingly difficult to segment in 2D. In addition, anatomical information in images between two neighboring segmentations is not utilized in the constructed model. Moreover, this approach is largely manual and thus very time-consuming.

More recently, some authors have proposed model construction in a direct 3D fashion [14, 15]. This approach is attractive because it makes use of more anatomical information and reduces human labor. In general, 3D model construction includes two major steps: image segmentation and surface modeling. A thorough review of methods for image segmentation is not possible in this paper. Therefore, we restrict our review to some recent work with the same goal of this paper—image-based modeling of blood flow. There are two major approaches in image segmentation that have been employed for vascular modeling: deformable models (also known as active surfaces) and the level set method. In the former approach [16, 17], a surface mesh is deformed by internal forces computed from surface features, e.g. curvature, as well as external forces computed from the image, e.g. gradient. This approach has limitations when segmenting large portions of the vasculature because of its inflexibility to handle complex shape and topology changes, although merging of smaller segmentations is possible [18]. The level set method overcomes this difficulty by implicitly representing the surface as the zero level of a higher dimension (level set) function [19] and has been successfully applied to segment vascular images [20-22]. Since the initialization of the level set function, ideally close to the target segmentation, is crucial to robustness and convergence, it is usually achieved by means of a fast marching method (FMM) due to its computational efficiency [19]. An improved initialization strategy, known as ‘colliding fronts’, is also proposed in [23]. Once the final segmentation is obtained, it is converted into a triangulated surface representation, generally using the marching cubes algorithm [24]. Because this surface mesh cannot be directly used for flow computation, mesh processing operations, such as smoothing, prolongation, subdivision, and remeshing, are necessary [21-23]. Finally, there have been techniques to convert the discrete surface triangulation from a mesh to NURBS [22, 25]. Nevertheless, for finite element flow computations, this final step is optional since the NURBS representation will be discretized for flow computation. In summary, for rigid wall models and segmentation of the luminal surface, current direct-3D segmentation and model construction methods have greatly improved the utility of image-based modeling of blood flow. However, further developments are still needed, especially as these methods move from research to clinical settings where robustness, accuracy, and speed are essential. The first goal of this paper is to describe a new workflow to construct models from medical images. We have linked the output of this workflow to the automatic mesh generator and CFD solver used in our group.

Blood does not flow in static, rigid vessels. In fact, the motion of the vessel wall and surrounding tissue affects the blood flow and vice versa, both in normal and diseased states. Furthermore, wave propagation phenomena in the cardiovascular system can only be modeled by taking the deformability of the vessel wall into account. To date, the vast majority of blood flow simulations have assumed rigid walls, due in no small part to the difficulties in formulating and solving the coupled problem of fluid and solid, i.e. blood flow and vessel wall deformation. However, in recent years, significant progress has been made in solving blood flow in deformable walls using the Arbitrarily Lagrangian-Eularian method [26-28], the immersed boundary method [29], and space-time finite element methods [30]. Our group previously proposed a new method, the Coupled Momentum method (CMM) for fluid–solid interaction to model blood flow and vessel wall dynamics [31]. While this method is currently restricted to small displacements and thin-walled structures, it is highly efficient with only minimal additional computational cost as compared to rigid wall simulations. We previously reported simulations of blood flow and vessel wall dynamics in subject-specific models with uniform mechanical wall properties, i.e. Young's modulus and thickness. Clearly, these properties are highly variable in the vasculature [32]. Normal, healthy large arteries reduce in diameter and thickness and become stiffer with increasing distance from the heart. Furthermore, diseased blood vessels can have properties that are highly inhomogeneous, e.g. aneurismal blood vessels become stiffer due in part to an increased collagen/elastin ratio. In order to account for the variability of wall property, we extended our implementation of the CMM to incorporate spatial variations in vessel wall properties and reported simulations using idealized geometric models [33]. The second goal of this paper is to describe a novel technique we developed to assign variable wall properties in subject-specific models. To our knowledge, this paper is the first to describe simulations of blood flow and vessel wall dynamics employing large-scale 3D-based subject-specific models and assigned variable mechanical wall properties. We believe that the combination of these two features will make our simulation results closer to the reality of blood flow in humans.

The remainder of this paper is organized as follows. We first present our workflow for constructing vascular models from medical images through 3D modeling. We then present our approach of assigning variable wall properties on the constructed model by combining centerline-based and surface-based methods. A new centerline extraction algorithm from the model is proposed. Next we briefly review the CMM for fluid–structure interaction. We then present the results for a demonstrative idealized model followed by two different subject-specific models. Finally, we discuss the significance of the results obtained and limitations of our methodology.

2. VASCULAR MODEL CONSTRUCTION

2.1. Overview

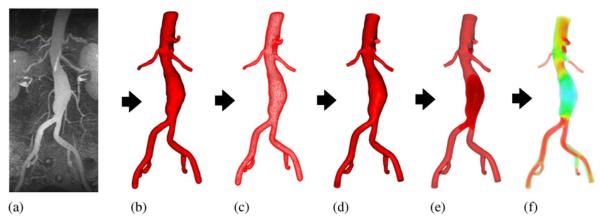
Construction of a vascular geometric model is a prerequisite for blood flow simulation. This task is difficult because of the complex nature of the vasculature. It is desired to obtain a model which reflects the real geometry, is suitable for simulation, and yet requires minimal user intervention for construction. Figure 1 is a graphical overview of the workflow proposed in this paper for this purpose. From the medical image data, we perform a 3D segmentation using a level set method. A triangular surface mesh is extracted from the segmentation. The surface is then enhanced to get a computational domain by a combination of five geometric processing operations: smoothing, pruning, trimming, circularization, and elongation. Further, the domain bounded by the surface mesh is discretized into a tetrahedral volumetric mesh and boundary conditions are specified. Finally computer simulations are carried out to obtain hemodynamic data.

Figure 1.

Schematic of the proposed workflow. From the medical image data (a), we perform a 3D segmentation (b) using level set method. A triangular surface mesh (c) is extracted from the segmentation. The surface is then enhanced to get a discrete model (d) as the computational domain. Further, the domain is discretized into a tetrahedral volumetric mesh (e) and boundary conditions are specified. Finally computer simulations (f) are carried out to predict hemodynamic variables.

2.2. 3D image segmentation

Segmentation of vessels from medical images is a challenging task. Although modern medical imaging modalities can acquire images of relatively high resolution, this resolution may still not be enough to resolve small vessels or differentiate two vessels which are close to each other. Undesired anatomical features, such as veins and bones, often surround arteries of interest but do not have a clear boundary between them. In addition, the vessels vary greatly in diameter: we need to represent both large and small vessels. Noise and limited resolution may lead to coarse and irregular surfaces which may not be realistic and cause detrimental effects on subsequent geometric processing and blood flow simulations.

We employ a 3D level set method to segment arteries in a scalar image I(x),ℝ³ ↦ℝ. The vessel surface is represented by the zero level set of a function ϕ(x),ℝ³ ↦ℝ . The surface then deforms with the level set function evolution governed by a partial differential equation [34, 35]:

$${\varphi }_t\left(\mathit{x}\right)+\underset{\text{propagation term}}{\underbrace{\alpha \mathit{P}\left(\mathit{x}\right)|\mathrm{\nabla }\varphi \left(\mathit{x}\right)|}}+\underset{\text{advection term}}{\underbrace{\beta \mathit{A}\left(\mathit{x}\right)\cdot \mathrm{\nabla }\varphi \left(\mathit{x}\right)}}=\underset{\text{curvature term}}{\underbrace{\gamma \mathit{Z}\left(\mathit{x}\right)\kappa \left(\mathit{x}\right)|\mathrm{\nabla }\varphi \left(\mathit{x}\right)|}}$$ (1)

Here α, β, and γ are user-selected coefficients. The propagation term αP(x)|▽ϕ(x) drives the surface inflation, where P(x)=1/(1+|▽I(x)|) is the inflation speed, which is high in regions with flat intensity values, but low in regions with high gradient magnitude, or edges. The advection term βA(x)·∇ϕ(x) attracts the surface to edges, where A(x)=−∇P(x) is a vector field which aligns with and points to edges. The curvature term γZ(x)k(x)|∇ϕ(x)| ensures the smoothness of the surface, where Z(x)= P(x) allows the surface to have high curvature only on edges and k(x)=∇·(∇ϕ(x)/|ϕ(x)|) is the mean curvature of the surface. The level set function ϕ(x) is in general chosen to be the signed distance function to enable further simplification. The level set evolution equation can be solved efficiently using a narrow-band method [19]. In order to address the issues of nonuniform intensity and large variations of vessel sizes often encountered in the segmentation, the original image I(x) can be subdivided into multiple sub-images I_i(x), i =1,2, …,n. Although user interaction involved in this subdivision is not a major issue in research settings, we note that it is necessary to be minimized for use in clinical settings. The level set functions resulting from segmenting these sub-images can be merged into a single function by

$$\mathrm{\Phi }\left(\mathit{x}\right)=\min {\varphi }_i\left(\mathit{x}\right),i=1,2,\dots ,n.$$ (2)

To initialize the level set functions for vessel segmentation, an initial seed region must be specified inside the vessel to represent the initial surface. In some cases, several seeds are necessary to speed up the segmentation or drive the surface across a noisy region. While the level set function is evolving, the actual surface can be reconstructed by marching cubes method [24] to enable real-time visualization of segmentation results. Finally the user can stop the segmentation when the results are satisfactory.

2.3. Geometric processing

Level set segmentation provides a good approximation of the vessel lumen boundaries in the image. It implicitly represents the vessel surface as a zero level of the level set function. However, in order to simulate blood flow using numerical methods, we need to generate a volumetric mesh. Although there are methods to generate volumetric meshes directly from the level set function, such as the isosurface stuffing method [36], we choose to generate a surface mesh, in particular a triangular mesh before the volumetric mesh for several reasons. First, the segmentation will not yield a perfectly correct or smooth model due to limited resolution and noise of the images. Further mesh processing is necessary to remove those artifacts. Second, boundary condition specification for the inlets and outlets is usually prescribed on a plane perpendicular to the main axis of the vessel. The trimming operation is also more easily performed on a surface mesh than on a volumetric mesh. Finally, in some cases, we need to combine the results of a direct 3D segmentation approach with a traditional 2D lofting approach [37]. It is straightforward to have surface meshes from both approaches and then merge them.

The well-known surface mesh generation method, marching cubes, is very robust and fast. However, it is generally not suitable to generate the mesh with the ultimate goal of simulation since the quality of the mesh is poor in terms of triangle shape and angle. In addition, a good quality surface triangulation makes the further processing of the mesh more robust. In our approach, we adopt the method described by Boissonnat and Oudot which produces provable good sampling and meshing of isosurfaces [38]. This meshing algorithm is based on the notion of the restricted Delaunay triangulation. The algorithm computes a set of sample points on the surface and extracts an interpolating surface mesh from the 3D triangulation of these sample points. Points are iteratively added to the sample, as in a Delaunay refinement process, until some size and shape criteria, such as a lower bound on the minimum degrees of mesh facets, are satisfied.

To account for the nonsmooth artifacts, we can either smooth the level set function or perform a smoothing operation on the surface mesh. The former is more suitable to smooth globally by utilizing only the curvature term in the level set evolution (see previous description). The latter works best to smooth the surface locally. We adopt the method by Desbrun et al. in which the surface mesh is faired by a curvature flow [39]:

$${\mathit{x}}_{\mathrm{t}}=-\lambda \kappa \left(\mathit{x}\right)\mathit{n}\left(\mathit{x}\right).$$ (3)

Here, x_t is the time-dependent change of a vertex x on the mesh, k(x)and n(x) are the mean curvature and normal at this vertex, respectively, and λ is a user-defined coefficient controlling the smoothing strength. Such an equation can be solved efficiently using a sparse matrix solver. The effect of the smoothing operation is demonstrated in Figure 2(a).

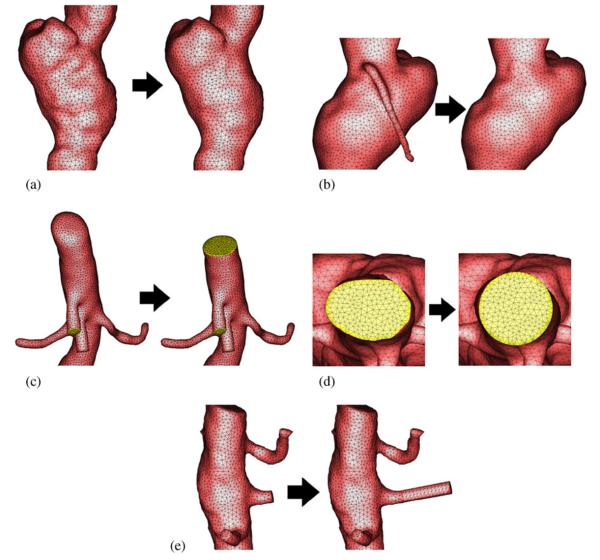
Figure 2.

Geometric operations on surface meshes: (a) smoothing; (b) pruning; (c) trimming; (d) circularization; and (e) elongation. In each subfigure, left is before the operation and right is after.

In some cases, the segmentation can include unwanted vessels which are not desirable for the simulation. The vessel can be interactively pruned by first selecting it as a region of interest (ROI) on the surface mesh. Then, the triangles can be deleted within the ROI. Next, a triangulation of the 3D polygon bounded by the vertex list of the open boundary is performed. Finally, the newly generated triangles are re-meshed to maintain a high quality mesh. The effect of the pruning operation is illustrated in Figure 2(b).

In order to specify boundary conditions, trimming operations of all the inlets and outlets are performed to obtain a planar surface. The user defines a cutting plane by selecting a vertex and a normal direction. Note that in general this plane can cross not only the vessel to be trimmed but also other vessels in the mesh. Therefore, a procedure must be developed rather than just simply deleting all the triangles on one side of the plane. Starting from an initial vertex, we trace a loop around the vessel until this vertex is encountered again. In the meantime, we determine which edge of the triangles neighboring the current vertex is intersected by the plane in the direction of forward tracing. The closer vertex of the edge is projected onto the plane and chosen to be the next vertex of the tracing process. When the tracing finishes, all the triangles that are connected to the vertices encountered during the tracing, and are on one side of the plane, are removed. This removal results in a hole that is surrounded by encountered vertices. The hole is then filled by a 2D constrained Delaunay triangulation with the edges on the open boundary as the constraints. The effect of the trimming operation is shown in Figure 2(c).

We have developed two other operations on the inlets or outlets which can be performed during trimming to make them suitable for prescribing boundary conditions, e.g. Womersley's velocity profile. One operation is to circularize the inlets or outlets. This operation is necessary if the cross section is far from a circle such that the assumptions of an analytical velocity profile are violated. We perform circularization after the trimming operation but before filling the hole. The user specifies a distance that is inwards from the trimming plane. The vessel surface within this distance is then smoothly morphed. This is achieved by weighting between the original vessel surface and a perfect cylinder. The weight is linearly varied within the distance in order to perfectly circularize at the trimming plane while keeping the vessel surface intact beyond the distance. We choose the radius of the circular cross section that preserves the area of the original noncircular section. The effect of the circularization operation is shown in Figure 2(d). A final additional operation that is needed in some cases is to elongate the inlets or outlets further. This can be particularly useful when the branch vessel is very short such that the boundary conditions may introduce instabilities in the computation or the solution of interest is overly influenced by the boundary conditions. We perform the elongation operation by attaching a cylinder with a radius comparable to that of the cross section. The orientation is chosen according to the normal direction of the trimming plane. The length of the cylinder is specified by the user. The junction between the original surface and the cylinder is locally smoothed. The effect of the elongation operation is demonstrated in Figure 2(e). In practice, the operations of circularization and prolongation should be used with caution since they may disturb the true geometry of the blood vessel and thus the flow solution. In addition, short branch vessels are inevitable due to the difficulty of segmentation for limited spatial resolution and the necessity of trimming before sharp turns to avoid the solution instability. In this case, prolongation is preferred to circularization because one does not need to assume an analytical profile at the original cross section. Instead, the artificial profile at the prolonged cross section will adjust naturally at the original cross section.

3. VESSEL WALL MECHANICAL PROPERTY ASSIGNMENT

As previously noted, the vessel wall mechanical properties, in particular elastic modulus and thickness cannot be assumed to be uniform throughout the model, especially when the model is composed of several branch vessels and/or diseased region such as aneurysms. It is crucial when modeling the blood flow in deformable vessels to take the variable nature of the vessel properties into account and for these properties to be as realistic as possible. One may get information for vessel properties from tissue experiments or from the literature data. However, it is infeasible to obtain property values resolved to every node of the model. In general, only values for a limited number of locations are known. Therefore, it is necessary to assign properties by interpolating and/or extrapolating known values throughout the entire model. The assigned properties should match the known values at these prescribed locations and have smooth transitions in between. In addition, as a first approximation, these properties should be roughly circumferentially symmetric over cross sections for most normal vessels. For diseased vessels, these properties could vary significantly over cross sections.

3.1. Centerline-based and surface-based assignments

Considering the requirements described above, we propose a novel technique which combines a centerline-based and a surface-based technique (shown in Figure 3) for assigning vessel wall mechanical properties. The centerline-based method is mainly used for normal or symmetric vessels, whereas the surface-based method is suitable for diseased and nonsymmetric vessels. In general, we first assign the properties on the entire model using a centerline-based method and then overwrite certain regions which have abnormal values.

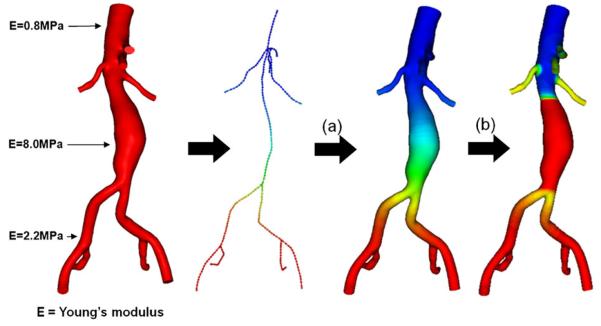
Figure 3.

Centerline-based (a) and surface-based (b) methods to assign variable wall properties. We assume there are certain locations where wall properties are known, e.g. Young's modulus in this case. In the centerline-based method, the wall properties are first assigned to the centerline and then mapped out to the vessel surface. In the surface-based method, the wall properties are directly assigned to the surface. Although the two methods can be used separately, we found it is usually helpful to assign by a centerline-based method and overwrite some regions using the surface-based method.

The centerline-based method assumes that a centerline of the model is already extracted (described in next subsection). The basic idea is to first propagate known values on the centerline. Values at a node can be thus influenced by values at nodes with known values. The relative influences are determined by the distance between the node of interest and the nodes with known values. Next, the assigned property values on the centerline are mapped onto the nodes of the model from values at the nearest centerline nodes. Different properties, such as Young's modulus and thickness, will be assigned separately. The detailed algorithm for property assignment is as follows:

1. Set a default value for each node on the centerline. The value is often the average of known values.

2. Select a node on the centerline where the value of the property p_known is known and assign pknown to the node.

   1. For each unknown node, obtain the curve distance d on the centerline from the known node.
   2. Calculate the contributing weighting w of the known node to the unknown node by a relation w = exp(−d^k/D^k), where D is the influential distance of the known node and k controls the attenuation of the influence. To limit the influential extent of a known node, we set w = 0 if d > D_max,where D_max is the maximal influential extent. Note, D_max needs to be properly defined to ensure that every unknown node is at least covered by a known node.
   3. Update the value at this unknown node to a new value p_new by weighting between the current value p_current and the value from the known node p_known,i.e. p_new = p_current(1 − w)+p_known^w.

3. Repeat after selecting another known node by going to (2).

4. Map the assigned values on the centerline onto the surface of the model by searching for the nearest node on the centerline to the node on the model.

The surface-based method works similarly to the centerline-based method except that we directly propagate values on the surface nodes of the model. The algorithm for the centerline-based method can be adapted with the following changes:

1. Properties are set and updated on the surface of the model rather than on the centerline.

2. The distance d is now given by the geodesic distance on the surface which is computed by solving the Eikonal equation |∇d(x)|= 1 using the FMM [19].

3.2. Centerline extraction

Centerlines (also known as skeletons or medial axes) are useful in representation of the topology of vasculature. While our goal here is to employ a centerline as the basis for wall property assignment, the usage of centerlines is not limited only to this application. One example of other applications is to quantify longitudinal deformation of arteries [40]. Although there are many centerline extraction algorithms designed for various applications, the definition of the centerline and also the input and output of the algorithm are possibly distinct from one algorithm to another [41]. For material property assignment, efficient extraction of a centerline from the constructed model with the following features is desirable:

1. Thin: The centerline should be as thin as a list of nodes.

2. Centered: The nodes should be locally centered with respect to the surface of the model.

3. Connected: All nodes should be connected. No gaps are allowed.

4. Topologically equivalent to the model: The centerline represents the topology of the model. Most importantly, the centerline should have the same number of inlets and outlets as the model.

We propose a new algorithm for extracting centerlines that takes as input the volumetric meshes of vascular models used for blood flow simulation. The output of the algorithm will be a centerline that satisfies the above criteria. The basic idea is to utilize two distance transforms with respect to two types of model surfaces: inlet/outlet and wall. We use the distance to inlet/outlet to divide the model longitudinally following the different vessel branches of the model. Within each subdivision, the distance to the wall suggests the location of centerline nodes. The detailed algorithm (illustrated in Figure 4) is described as follows:

1. Input the volumetric mesh of a vascular model.

2. Compute distance to the wall (DW) using the FMM.

3. Compute distance to the inlet/outlet (DL) using FMM.

4. Divide the model into subdivisions based on the equal split of the range of DL.

5. Within each subdivision, choose the centerline node as the node with maximal DW among all nodes.

6. Link all centerline nodes to get a raw centerline.

7. Calculate node valences or degrees to divide the raw centerline into segments.

8. Re-sample each segment to improve the centerline such that it is given by evenly distributed nodes.

9. Super-sample the centerline by sampling a fitted spline for every segment.

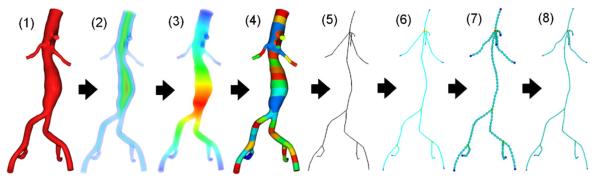
Figure 4.

The proposed algorithm to extract the centerline from the model. From the input model (1), we compute two types of distances: (2) the distance to the wall (DW) and (3) the distance to the in/outlet (DL). The model is then subdivided (4) by splitting the range of DL. A raw centerline (5) is generated by choosing a node for each piece which has the maximal DW. The raw centerline is divided (6) into segments using node valences. The final centerline is obtained by re-sampling (7) and then super-sampling (8) to improve nodal distribution.

3.3. Blood flow simulation with deformable walls using variable wall properties

Although the method described in the previous section can be used to assign wall properties for many fluidstructure interaction methods employing a thin-walled approximation, we employ the CMM as an example for deformable wall simulation with variable wall properties [31]. We refer the readers to the original paper for the details of CMM. The method is based on a conventional stabilized finite element method for the Navier–Stokes equation and adapted to consider compliant vessel walls by embedding a description of wall motion in the formulation. The degrees-of-freedom (or displacements) for the wall are described as a function of the fluid velocities at the fluid–solid interface, using a transverse-shear enhanced linear membrane model. The effects of vessel compliance are then incorporated by embedding the model of deformable walls in the weak form representing the blood flow. In this paper, we assume that the wall is incompressible and isotropic. Therefore, the wall properties of interest are Young's modulus E and thickness ζ, although it is straightforward to generalize to anisotropic cases. The nonuniformity of wall properties can be taken into account during system matrix assembly at the element level.

4. RESULTS

4.1. Simulation of blood flow in an idealized cylindrical model

In order to test the feasibility of our method to simulate blood flow in deformable arteries using variable wall properties, we first considered a simple cylindrical model with radius 0.3 cm and length 12.6 cm. At the inlet of the model, we prescribed a Womersley flow profile with period 1.1 s. For the outlet, we used a three-element Windkessel model with a proximal resistance R_p=1.16×10³ dynes·s/cm⁵, a capacitance C=2.30×10⁻⁵ cm⁵/dynes, and a distal resistance R_d=1.96×10⁴ dynes·s/cm⁵ [42]. The solutions were obtained using a linear tetrahedral mesh of 101 510 nodes and 489 159 elements, using a time step size of 1.1 ms, for five cardiac cycles. Blood was assumed to behave as a Newtonian fluid with density 1.06 g/cm³ and dynamic viscosity 0.04 poise. The vessel wall was assumed to be linear elastic with density 1.0g/cm³, Poisson's ratio 0.5, and thickness 0.03 cm. The Young's modulus of the vessel wall, E_Y, was assumed to follow one of three spatial distributions assigned using the centerline-based method:

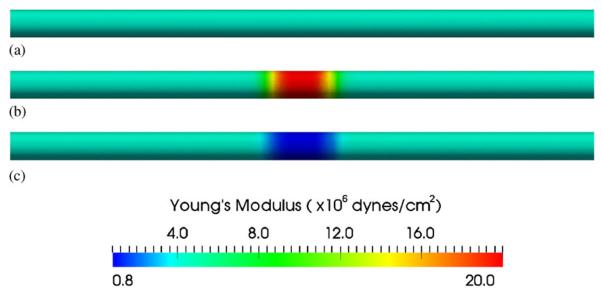
1. Uniform case: E_Y=4.0×10⁶ dynes/cm² (Figure 5(a));

2. Stiffer case: E_Y = 4.0×10⁶ dynes/cm² at two sides; E_Y 20.0 × 10⁶ dynes/cm² in the middle (Figure 5(b));

3. Softer case: E_Y = 4.0×10⁶ dynes/cm² at two sides; E_Y = 0.8×10⁶ dynes/cm² in the middle (Figure 5(c)).

Figure 5.

Assigned Young's modulus for an idealized cylindrical model: (a) uniform Young's modulus 4.0×10⁶ dynes/cm² everywhere; (b) Young's modulus 4.0×10⁶ dynes/cm² at two ends but 20.0×10⁶ dynes/cm² in the middle (stiffer); and (c) Young's modulus 4.0×10⁶ dynes/cm² at two ends but 0.8×10⁶ dynes/cm² in the middle (softer).

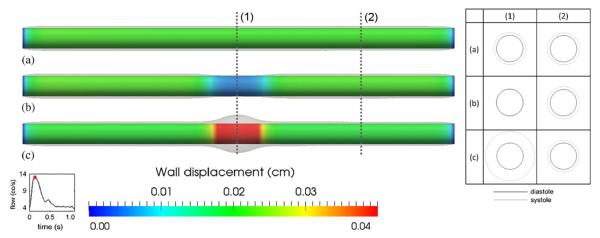
For all simulations, the geometry and boundary conditions were identical. The simulated wall displacements obtained in the three cases are shown in Figure 6. Note that the wall was held fixed at both ends and the vessel displacement is visualized using mesh warping with a magnification factor of 3. Outside the vicinity of the inlet and outlet, the wall indeed deformed uniformly in the case of a uniform Young's modulus. The deformation is smaller in the case with a larger Young's modulus in the central region. In contrast, more deformation is observed in the central region for the softer wall case. Furthermore, the deformation is quite similar in the regions with constant Young's modulus for all three cases. We probed the averaged radial displacement (Δr) over a circumference at two locations (1) and (2) shown in Figure 6. In the uniform case, $\mathrm{\Delta }{r}_{\text{uniform}}^{\left(1\right)}=0.0209\mathrm{cm}$ and $\mathrm{\Delta }{r}_{\text{uniform}}^{\left(2\right)}=0.0212\mathrm{cm}$. In the stiffer case, $\mathrm{\Delta }{r}_{\text{stiffer}}^{\left(1\right)}=0.0047\mathrm{cm}$ and $\mathrm{\Delta }{r}_{\text{stiffer}}^{\left(2\right)}=0.0221\mathrm{cm}$.. In the softer case, $\mathrm{\Delta }{r}_{\text{softer}}^{\left(1\right)}=0.0873\mathrm{cm}$ and $\mathrm{\Delta }{r}_{\text{softer}}^{\left(2\right)}=0.0191\mathrm{cm}$. The ratios $\mathrm{\Delta }{r}_{\text{uniform}}^{\left(1\right)}∕\mathrm{\Delta }{r}_{\text{stiffer}}^{\left(1\right)}=4.45$ and $\mathrm{\Delta }{r}_{\text{softer}}^{\left(1\right)}∕\mathrm{\Delta }{r}_{\text{uniform}}^{\left(1\right)}=4.18$ are close to the inverse of the ratios of Young's modulus, which are both 5.

Figure 6.

Simulated wall displacement for the idealized cylindrical model. (a) The case of uniform Young's modulus (uniform case) as in Figure 5(a); (b) The case of larger Young's modulus (stiffer case) in the middle as in Figure 5(b); (c) The case of smaller Young's modulus (softer case) in the middle as in Figure 5(c). Notice both ends were held fixed for all three cases. Overlays are warped vessel wall by nodal displacements (magnified three times for ease of visualization). Labels (1) and (2) mark the locations where radial deformations are probed. The table on the right shows the cross sections of these locations (also magnified three times) at end diastole (black) and peak systole (gray).

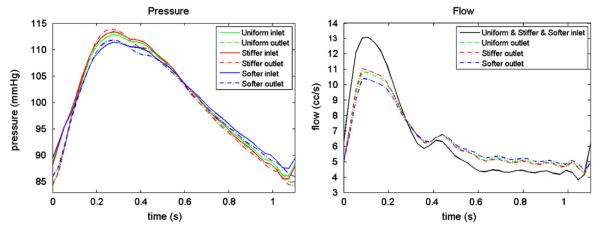
In Figure 7, we show the pressure and flow waves for the three cases. For the pressure field measured at both the inlets and outlets, the stiffer case presents a higher pressure pulse (Δp) than the uniform case which is in turn higher than the softer case. At the inlets, Δp_stiffer=27.86 mmHg>Δp_uniform=26.69mmHg>Δp_softer=23.89 mmHg, whereas at the outlets, Δp_stiffer=29.60mmHg>Δpuniform=28.49 mmHg>Δp_softer=25.82 mmHg. This result agrees with the wellknown phenomenon in the cardiovascular system: stiffer vessels tend to experience higher pressure pulses. The flow waves (Q) measured at the inlets are identical since we prescribed the same inlet boundary condition in all three cases. At the outlets, Q_stiffer>Q_uniform>Q_softer in the systolic phase, whereas Q_stiffer>Q_uniform>Q_softer in the diastolic phase. The stiffer vessel stores less blood in systole so that the outflow is higher in the systolic phase but lower in the diastolic phase. The amount of blood volume stored (ΔV) in systole is ΔV_stiffer=0.4077cc>V_uniform=0.4455cc>ΔV_softer=0.5336cc.

Figure 7.

Pressure and flow at the inlet and outlet of the idealized cylindrical model for all three cases. From the pressure plot, pulse pressure: stiffer case > uniform case > softer case at both inlet and outlet. From the flow plot, outlet flow: stiffer case > uniform case > softer case at systolic phase, but in reversed order at diastolic phase.

4.2. Simulation of a subject-specific model with thoracic aortic aneurysm

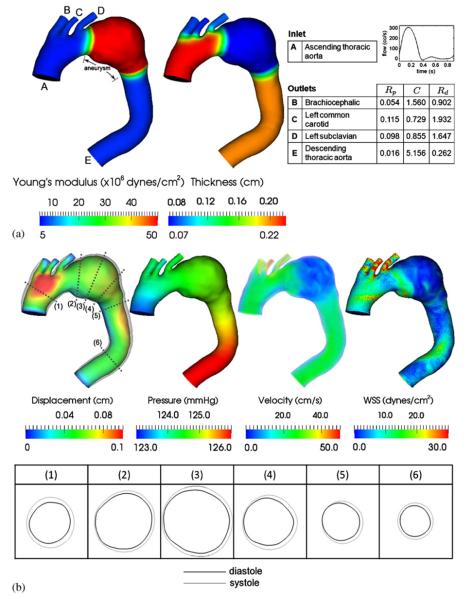
We next consider a subject-specific model of a thoracic aortic aneurysm constructed from cardiac-gated CT data (image resolution: 0.58×0.58×0.7 mm) of a 76-year-old patient. The end-diastolic frame was used to construct the model due to its minimal motion artifact. Variable wall properties, i.e. Young's modulus and thickness, were employed in the deformable wall simulation as shown in Figure 8(a). These values were taken from the literature data [32] and assigned using the proposed centerline- and surface-based methods. The vessel gets stiffer and thinner from proximal to distal locations. In the aneurismal region, we assume that the wall is eight times stiffer and three times thinner than its neighboring regions. For the inlet, we prescribed a Womersley velocity profile with period 0.9 s, with mean flow of 4.9 L/min. For each outlet, a three-element Windkessel model was used with parameters given in Figure 8(a). These parameters were obtained by tuning for flow split and a physiologic pressure range. The shape of outlet velocity profile was constrained using an Augmented Lagrangian method to avoid instabilities due to the large retrograde flow in diastole [43]. The solutions were obtained using a linear tetrahedral mesh of 471 408 nodes and 2 479 570 elements, with a time step size of 0.9 ms, for six cardiac cycles.

Figure 8.

(a) Wall property and boundary condition of the thoracic aortic aneurysm model. The units of the three-element Windkessel model are R_p (×10⁴ dynes·s/cm⁵), C(×10⁻⁴ cm⁵/dynes), R_d (×10⁴ dynes·s/cm⁵). (b) Simulated wall displacement, blood pressure, velocity, and wall shear stress at peak systole. Overlays on the displacement are the vessel wall warped using nodal displacements (magnified three times). Numbered labels mark the locations where radial deformations are probed. The table on the bottom shows the cross sections of these locations (also magnified three times) at end diastole (black) and peak systole (gray).

In Figure 8(b), we present the simulated wall displacement, blood pressure, velocity, and wall shear stress at peak systole. Overlays on the displacement are a warped vessel wall according to the calculated nodal displacements (magnified three times for ease of visualization). For quantification purpose, we probed the maximal radial displacement (Δr) over a circumference at the numbered locations. The corresponding maximal circumferential strain (ε_θθ) can be calculated by considering the circumference of the cross section. At the proximal location (1), Δr⁽¹⁾=0.1014 cm and ${\epsilon }_{\theta \theta }^{\left(1\right)}=0.0578$. At the aneurysmal locations (2), (3), and (4), Δr⁽²⁾=0.0630 cm, Δr⁽³⁾=0.0752 cm, Δr⁽⁴⁾ = 0.0739 cm, and ${\epsilon }_{\theta \theta }^{\left(2\right)}=0.0257,{\epsilon }_{\theta \theta }^{\left(3\right)}=0.0271,{\epsilon }_{\theta \theta }^{\left(4\right)}=0.0339$. At the distal locations (5) and (6), Δr⁽⁵⁾=0.0682 cm, Δr⁽⁶⁾=0.0549 cm, and ${\epsilon }_{\theta \theta }^{\left(5\right)}=0.0435,{\epsilon }_{\theta \theta }^{\left(6\right)}=0.0403$. From the warped vessel wall in Figure 8(b) and from these strain values, we demonstrate that the use of variable wall properties indeed yield desired effects: proximal vessels in general deform more than distal vessels, whereas a stiffened aneurysm leads to smaller deformations.

4.3. Simulation of a subject-specific model with cerebral aneurysm

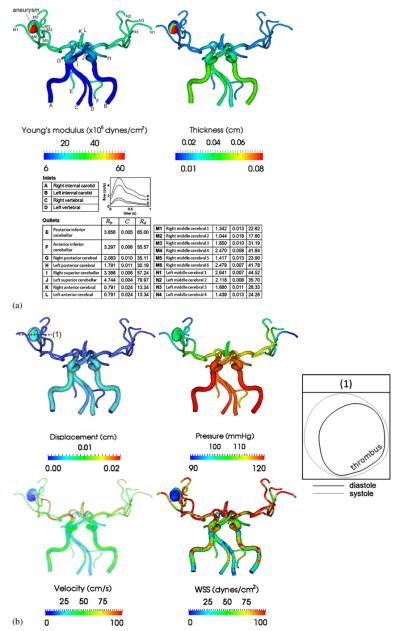
Lastly, we consider a subject-specific model of the cerebral vasculature of an 83-year-old male patient with a cerebral aneurysm. The model was constructed from CT data (image resolution: 0.38×0.35×0.5 mm) and it includes the full circle of Willis. The aneurysm is located in the right middle cerebral artery of the patient. Furthermore, there is a prominent thrombus on one side of the aneurysm. Vessel wall properties, i.e. Young's modulus and thickness, obtained from the literature [44] were assigned as shown in Figure 9(a). Distal vessels are stiffer and thinner than the proximal vessels. In the aneurysmal region, the thrombus side was assigned to have a greater Young's modulus and thickness. There are four inlets for this model: two internal carotid arteries and two vertebral arteries. The inflow conditions were obtained from a previous simulation result that accounted for the carotid vasculature as proximal as the aortic arch [11]. For each outlet, a three-element Windkessel model was used with parameters given in Figure 9(a). The solutions were obtained using a linear tetrahedral mesh of 295 415 nodes and 1 313 482 elements, with a time step size of 0.9 ms, for six cardiac cycles.

Figure 9.

(a) Wall property and boundary condition of the cerebral aneurysm model. The units of three-element Windkessel model are R_p (×10⁴ dynes·s/cm⁵), C(×10⁻⁴ cm⁵/dynes), R_d (×10⁴ dynes·s/cm⁵). Note that one side of the aneurysm is both stiffer and thicker than the other side since there is a thrombus on that side and (b) simulated wall displacement, blood pressure, velocity, and wall shear stress at peak systole. Overlays on the displacement are warped vessel wall by nodal displacements (magnified six times). Label (1) marks the location where a cross section of the aneurysm is obtained. The table on the right shows the cross section (also magnified six times) at end diastole (black) and peak systole (gray).

In Figure 9(b), we present the simulated wall displacement, blood pressure, velocity, and wall shear stress at peak systole. Similar to the previous example, we found that the proximal vessels deformed more than distal vessels due to changes in geometry and wall properties. The thrombotic side deforms much less than the opposite side because it is stiffer and thicker. Quantitatively, the maximal magnitude of displacement of the thrombotic side is 0.0634 cm, as opposed to 0.0211 cm on the opposite side.

5. CONCLUSION

We have successfully developed and implemented a complete workflow that enables the simulation of blood flow in deformable arteries with 3D subject-specific geometry and spatially varying variable wall properties. The workflow to construct subject-specific geometry from medical images includes 3D image segmentation, geometric processing, meshing, and interfaces to a mesh generator and flow solver. In particular, we implemented a set of geometric operations with customuser interfaces. The balance between automation and interactivity dramatically improved the efficiency of model construction while preserving user control. In the applications presented here, we have demonstrated that this workflow is sufficiently robust to handle complex vascular geometry. Our novel techniques may help to reduce the workload and subjectivity involved in the process of image-based cardiovascular modeling, especially in the context of population-based studies, where hundreds or even thousands of models need to be constructed. In addition, the workflow is also generic, so that it is possible to apply it to other image-based biomechanical studies.

Future efforts in geometry construction could include investigation into the influences of small changes, i.e. perturbations, of the geometry to the hemodynamic variables of interest, e.g. pressures and wall shear stresses. Uncertainties in constructed geometry arise either from an uncontrolled source, e.g. original images, or a controlled source, e.g. the level of smoothing. Another future development could include a study of the effects of large changes, such as for the purpose of surgical planning, of the geometry to the hemodynamic variables or treatment goals, e.g. pressure drops across stenoses or flow through bypass grafts.

We also described centerline-based and surface-based methods to assign variable wall properties for deformable wall simulations. In general, these two methods can be combined for vessel wall mechanical property assignment for both healthy and diseased vessels. We have shown that it is crucial to employ the variability of wall properties to replicate desired effects of vessel wall motion, e.g. the proximal vessels in general deform more than the distal vessels and the aneurysms show smaller strain. Furthermore, the use of variable wall properties can result in differences in blood flow itself. Therefore, it is important to employ wall properties as close to reality as possible. One of the limitations of our current study is that the wall properties are not subject-specific. Indeed, it is difficult to measure in vivo wall properties noninvasively, although recent studies in parameter estimation could be extended to estimate wall properties from the observed motion of the vessel wall [37]. However, the degree of estimation accuracy needs to be thoroughly evaluated prior to its actual use. More importantly, the benefit of obtaining these estimations should be well justified on account of the burden and/or radiation dose resulting from the measurements, especially for cardiac-gated CT. For many cases considered in image-based modeling for blood flow, 3D, time-resolved measurements of vessel geometry are still intractable in practice. Therefore, the approach adopted herein could fill the gap from using constant wall properties to using truly subject-specific wall properties.

In this paper, we also described a novel method to extract a centerline from the constructed model. The merit of this method is that it guarantees that the centerline is thin, centered, connected, and with the number of inlets/outlets identical to that of the original model. Therefore, this centerline, representing the topology of the vessel, can be used in 1D blood flow simulation. In addition, it has been used in quantification of vascular geometry, such as length and curvature changes of the coronary arteries [38].

In summary, image-based modeling of blood flow in arteries requires robust and efficient methods for geometric model construction. As research efforts shift from a focus on velocity and shear fields obtained using simulations of blood flow in rigid wall models to fluidstructure interaction methods capable of obtaining velocity, pressure, shear stress and tensile stress in deformable models, methods for ‘image-based fluid-structure interaction’ such as those described in this paper will be essential for attaining realistic solutions.