Adding Subjects or Adding Measurements in Repeated Measurement Studies Under Financial Constraints

Abstract

Budget constraint is a challenge faced by investigators in planning almost every clinical trial. For a repeated measurement study, investigators need to decide whether to increase the number of participating subjects or to increase the number of repeated measurements per subject, with the ultimate goal of maximizing power for a given financial constraint. This financially constrained design problem is further complicated when taking into account things such as missing data and various correlation structures among the repeated measurements. We propose an approach that combines a GEE estimator of slope coefficients with the cost constraint. In the case where we have no missing data and the compound symmetric correlation structure, the optimal design is derived analytically. In the case where we have missing data or other correlation structures, the optimal design is identified through numerical search. We present an extensive simulation study to explore the impacts of cost ratio, missing pattern, dropout rate, and correlation structure. We also present an application example.

1. Introduction

Budget constraint is a challenge faced by investigators in planning almost every clinical trial. When designing a repeated measurement study, investigators need to decide how to make full use of the limited financial resources: increasing the number of participating subjects (n) or increasing the number of repeated measurements per subject (m). The ultimate goal is to maximize the testing power. The selection of n and m in repeated measurement studies has been discussed by many authors (Snedecor and Cochran 1989; Fleiss 1986; Maxwell 1998; Arndt et al. 2000; Ahn and Jung 2003, 2004). Ahn and Jung (2003, 2004) presented a method to assess the relative benefit of adding subjects versus adding measurements in terms of the efficiency of the generalized estimating equation (GEE) estimator of slope coefficients. Without taking cost into account, such methods effectively assume an infinite financial resource.

In relatively short-term efficacy clinical trials of perhaps a 6–8 weeks duration, a linearly divergent treatment effect is often expected, where the expected difference between the treatment groups increases linearly over time, possibly after a data transformation (Winkens et al. 2005a,b; Overall and Doyle 1994; Jennrich and Schluchter 1986; DeGruttola, Lange, and Dafni 1991; Frison and Pocock 1997). The analysis of data from the randomized parallel-group design often focuses on the difference between treatment groups in the average rate of changes as represented by the slopes of regression lines fitted to the response measurements. In this article, we propose an approach that combines a GEE estimator of the slope coefficients with the cost constraint in clinical trials with a linearly divergent treatment effect.

The cost incurred by an additional subject is usually different from that by an additional measurement. Several papers have provided the sample size estimate for repeated measurement studies incorporating costs for recruiting and measuring subjects (Bloch 1986; Lai et al. 2003; Lui and Cumberland 1992; Winkens et al. 2006, 2007).

The determination of n and m is further complicated in the presence of missing data and different types of correlation structures among repeated measurements. The GEE method (Liang and Zeger 1986) has been widely used for the evaluation of treatment effects in controlled clinical trials because it does not require the restrictive compound symmetric (CS) correlation structure and it accommodates missing data. In this article, we derive the optimal combination of n and m where the GEE estimator of the treatment effect yields the smallest variance within a particular budget. In other words, the optimal combination of n and m maximizes the testing power when making inference about the treatment effect under a budget constraint.

In Section 2, we briefly review the GEE sample size formula (Jung and Ahn 2003), which provides a closed form sample size solution for comparing the rates of changes in repeated measurement studies. In Section 3, we introduce how to find the optimal combination of n and m to maximize power under a budget constraint. In Section 4, we introduce how to find the optimal choice of n and m to minimize cost for a prespecified power. An example is provided in Section 5. We conclude with a brief discussion in Section 6.

2. Sample Size Estimation Using GEE

We introduce the following notation. For subject i (1 ≤ i ≤ n), let y_ij be the continuous response variable obtained at time t_j (1 ≤ j ≤ m). Here we assume a common measurement schedule for all the subjects and m ≥ 2 is the number of repeated measurements. We assume a fixed follow-up period T, and assume t_j to be equally spaced time points in [0, T]. Thus,

$$t_j=\frac{j-1}{m-1}T\text{for}j=1,\dots ,m.$$

We consider a linear regression model

$$y_{ij}={\beta }_1+{\beta }_2{r}_i+{\beta }_3{t}_j+{\beta }_4{r}_i{t}_j+{\epsilon }_{ij},$$ (1)

where ε_ij is the error term with mean zero and variance σ². Serial correlation may exist among ε_i1, …, ε_im. We define ρ_jj′ = corr(ε_ij, ε_ij′) for j ≠ j′ and ρ_jj = 1. Here r_i is the treatment indicator taking 0 for the control group and 1 for the treatment group. Our primary interest lies in β₄, which models the difference in slopes between the control and treatment groups.

Let δ_ij = 0/1 denote that y_ij is missing/observed. We define p_j = E(δ_ij) to be the proportion of subjects with measurement at t_j, and p_jj′ = E(δ_ijδ_ij′) to be the proportion of subjects with measurements at both t_j and t_j′. Note that p_jj = p_j.

Jung and Ahn (2003) investigated the experimental design problem for clinical trials with repeated measurements using the GEE method under the assumption of missing completely at random (MCAR). Different missing patterns and correlation structures have been considered. In this study we assume the missing data mechanism to be MCAR. Letting β̂₄ be the GEE estimator of β₄, $\sqrt{n}({\widehat{\beta }}_4-{\beta }_4)$ is approximately normal with mean 0 and variance ${\sigma }_4^2$, where

$${\sigma }_4^2=\frac{{\sigma }^2{s}_t^2}{{\mu }_0^2{\sigma }_r^2{\sigma }_t^4},$$ (2)

and ${\mu }_0={\sum }_{j=1}^m{p}_j,{\mu }_k={\mu }_0^{-1}{\sum }_{j=1}^m{p}_j{t}_j^k$ for k = 1, 2, ${\sigma }_t^2={\mu }_2-{\mu }_1^2,\overline{r}={\sum }_{i=1}^n{r}_i/n,{\sigma }_r^2=\overline{r}(1-\overline{r}),s_t^2={\sum }_{j=1}^m{\sum }_{j^{\prime }=1}^m{p}_{j{j}^{\prime }}{\rho }_{j{j}^{\prime }}(t_j-{\mu }_1)(t_{j^{\prime }}-{\mu }_1)$. Here r̄ is the proportion of subjects who receive the experimental treatment. Different missing patterns and correlation structures are accounted for by p_j, p_jj′, and ρ_jj′. Details of derivation can be found in Jung and Ahn (2003). With a two-sided α and a power 1 − γ, the required sample size to test H₀: β₄ = 0 versus H_a: β₄ = β₄₀ is

$$n=\frac{{\sigma }^2{s}_t^2{(z_{1-\alpha /2}+z_{1-\gamma })}^2}{{\beta }_{40}^2{\mu }_0^2{\sigma }_r^2{\sigma }_t^4}.$$ (3)

We reject H₀ if $\sqrt{n}{\widehat{\beta }}_4/{\sigma }_4>Z_{1-\alpha /2}$, where Z_{1 − α/2} is the 100(1 − α/2)th percentile of the standard normal distribution. Equivalently, given (n, m, α), we can compute the power of the test,

$$\begin{array}{l}1-\gamma =\mathrm{\Phi }\left(\sqrt{\frac{n{\beta }_{40}^2{\mu }_0^2{\sigma }_r^2{\sigma }_t^4}{{\sigma }^2{s}_t^2}}-Z_{1-\alpha /2}\right)\\ \equiv \mathrm{\Phi }\left(\sqrt{\frac{{\beta }_{40}^2}{{\sigma }_4^2/n}}-Z_{1-\alpha /2}\right),\end{array}$$ (4)

where Φ(·) is the cumulative distribution function of the standard normal distribution. Expression (4) suggests that the power 1 − γ is maximized when ${\sigma }_4^2/n$ is minimized.

3. Maximizing Power Under a Budget Constraint

In practice, the number of subjects and the number of repeated measures per subject are often restricted by budget constraints. In this article, we assume that C₁ and C₂ are the costs of recruiting one study subject and the cost of making one measurement on a subject for both control and treatment groups. For simplicity, we further assume that there is no overhead cost. We denote the total budget by C. Thus, the budget constraint is presented as ${nC}_1+n({\sum }_{j=1}^m{p}_j)C_2\le C$, which takes into account that some measurements might be missing. The goal is to find (n^o, m^o), the optimal combination of (n, m), that minimizes ${\sigma }_4^2/n$ within a budget of C. The computation of ${\sigma }_4^2$ in (2) does not involve sample size n, which indicates that, for a given m, a larger n always leads to a smaller ${\sigma }_4^2/n$ and a greater power. We define an integer function of m such that

$$n(m)=\underset{n\in I^{+}}{max}\left\{n:n\le C/(C_1+\sum _{j=1}^m{p}_j{C}_2)\right\}.$$ (5)

Here I⁺ denotes the set of positive integers. Thus, for investigators, the action space determined by the budget constraint is {(n(m), m): m ≥ 2}. Furthermore, in medical studies investigators might also face logistic constraints. For example, within the study period T, the maximum number of measurements is limited at m_max. Then we have

$$(n^o,m^o)\in \mathcal{R},\text{where}\mathcal{R}\equiv \{(n(m),m):2\le m\le m_{max}\}.$$ (6)

In Equation (2), the terms that are affected by m include $s_t^2,{\mu }_0^2$, and ${\sigma }_t^2$. Thus, to find (n^o, m^o), our goal of minimizing ${\sigma }_4^2/n$ is equivalent to minimizing

$$Q=\frac{s_t^2}{{\mu }_0^2{\sigma }_t^{4}n},$$ (7)

under constraint (6). For the time being we ignore the integer constraint for n, and plug $n=C/(C_1+{\sum }_{j=1}^m{p}_j{C}_2)$ into (7). We have

$$Q=\frac{s_t^2}{{\mu }_0^2{\sigma }_t^4\frac{C}{C_1+{\sum }_{j=1}^m{p}_j{C}_2}}=\frac{C_2}{C}·\frac{s_t^2({\sum }_{j=1}^m{p}_j+V)}{{\mu }_0^2{\sigma }_t^4},$$ (8)

where V = C₁/C₂. Thus, (n^o, m^o) can be obtained by first identifying m^o which minimizes $s_t^2({\sum }_{j=1}^m{p}_j+V)/({\mu }_0^2{\sigma }_t^4)$, and then solving n^o by n^o = n(m^o). From (8) we have the following fact.

Fact 1. For a financial constraint represented by (C, C₁, C₂), the optimal number of repeated measurements (m^o) is only affected by the cost ratio (C₁/C₂). Changing the total budget C only affects the sample size n^o.

Proof. See Appendix A.1.

3.1 No Missing Data and CS Correlation Structure

Under no missing data (p_j = 1, j = 1, …, m) and the CS correlation structure (ρ_jj′ = ρ for j ≠ j′), (n^o, m^o) can be obtained analytically. Specifically, m^o is determined by the cost ratio V =C₁/C₂,

$$m^o=\{\begin{array}{lll}2,\hfill & \text{if}\hfill & V\le 2,\hfill \\ 2\text{or}{m}_{max},\hfill & \text{if}\hfill & V>2,\hfill \end{array}$$

and n^o = n(m^o). When C₁/C₂ ≤ 2, the testing power is always maximized when investigators take m^o = 2 measurements from each subject. WhenC₁/C₂ > 2, the maximum power is achieved either at m = 2 or at m = m_max. More details can be found in Appendix A.2.

3.2 Numerical Analyses Under Other Scenarios

Under missing data or other correlation structures such as AR(1), the expression of Q in (8) is too complicated to find (n^o, m^o) analytically. We conduct numerical analyses to explore the factors that impact (n^o, m^o).

Since the optimal combination of (n^o, m^o) depends on the relative costs of subjects and repeated measures, a large range for the cost ratio, V =C₁/C₂ = 1, 10, 100, is considered. For practical reasons, the number of repeated measures is bounded by m ≤ m_max = 10. Without loss of generality, we fix the length of the study period at T = 1 and the true value of the slope coefficient at β₄ = 0.1. We search for the optimal choice of m and n that maximizes the testing power under the budget constraint. The combinations of the following factors are considered:

• Three cost ratios between recruiting a subject and making a measurement:C₁/C₂ =1, 10 and 100.

• Two missing patterns: random missing (RM) and monotone missing (MM). Under the RM pattern, missing value occurs independently among the m measurements, with p_jj′ = p_jp_j′ for j ≠ j′. On the other hand, in some studies subjects missing at a measurement time miss all the subsequent measurements, which is called an MM pattern. In this case we have p_jj′ = p_j′ for j < j′ (p₁ ≥ ··· ≥ p_m).

• Two correlation structures: CS or AR(1). Since the length of the study period is fixed at T = 1, for easy comparisons, we fix the correlation between the first and last measurements at ρ, that is, ρ_1m = ρ. Thus, under CS, we have ρ_jj′ = ρ for j ≠ j′. Under AR(1), we have ρ_jj′ = ρ^{|j−j′|/(m−1)}.

• The range of ρ: 0.2 to 0.8. A baseline-to-end-point correlation of 0.5 has been considered realistic in clinical trials with symptom rating scales in a clinical psychopharmacology research (Poktin and Siu 2009). In order to explore the impact of ρ, we conduct numerical analysis under a wide range of ρ.

• Three dropout levels: no dropout (no missing data), moderate dropout or high dropout. We assume p_j = 1 − t_jθ. That is, a linear trend in the observation probability. Thus, the dropout rate at the end of study is T θ = θ. In the labor pain study provided in the Example section, the dropout rate was 59% (Davis 1991). Most psychiatric clinical trials report dropout rates of >20% (Poktin and Siu 2009). Here, we consider three values for θ: 0, 0.30, and 0.60, corresponding to no dropout, moderate dropout and high dropout.

For a particular combination of (C₁/C₂, missing pattern, correlation structure, θ, ρ), we evaluate the relative efficiency (RE) of the β₄ estimator for every plausible number of repeated measurements to that under m = 2. Specifically, RE is defined as

$$\text{RE}(m)=\frac{{\sigma }_4^{2(m=2)}/n(2)}{{\sigma }_4^{2(m)}/n(m)}.$$

Recall that n(m) is the sample size given m under a cost constraint, as defined in (5), and the superscript (m) of ${\sigma }_4^2$ indicates that it is obtained based on the design with m repeated measurements. We interpret RE as follows: In order to achieve the same testing power, a trial with m measurements per patient needs to enroll 1/RE times as many patients as a trial with two measurements per patient. Thus, the m with the highest RE is the optimal number of repeated measurements (m^o) under a certain design configuration. Using Fact 1, it can be shown that RE is independent from the total budget C.

Tables 1–3 list the optimal numbers of repeated measurements and their RE, m^o (RE(m^o)), under various combinations of designing factors. We have several observations. First, when C₁/C₂ = 1, we have m^o = 2 regardless of missing pattern, correlation structure, dropout rate, and ρ. Second, the RE’s have a range of 1 to 2.63, indicating that the choice of m can greatly impact the efficiency of a clinical trial. Third, under the CS correlation structure, the results are identical under various combinations of missing pattern, dropout rate, and ρ. Fourth, m^o is affected by every factor considered in the numerical study. It is difficult to summarize a single rule to describe the relationship between m^o and the factors. However, one reasonable intuition is that as V = C₁/C₂ increases, the optimal m value is nondecreasing for any given combination of other factors, the reason being that it becomes more expensive to enroll a new subject than to obtain an additional measurement. Such a nondecreasing behavior is observed across Tables 1–3. We have conducted simulations under other values of V, which also confirm this intuition (results not shown).

Table 1.

The m^o(RE(m^o)) under no dropout (θ= 0)

	C1/C2	ρ = 0.2	ρ = 0.4	ρ = 0.6	ρ = 0.8
CS	1	2(1.00)	2(1.00)	2(1.00)	2(1.00)
	10	10(1.22)	10(1.22)	10(1.22)	10(1.22)
	100	10(1.87)	10(1.87)	10(1.87)	10(1.87)
AR(1)	1	2(1.00)	2(1.00)	2(1.00)	2(1.00)
	10	2(1.00)	2(1.00)	2(1.00)	2(1.00)
	100	2(1.00)	2(1.00)	2(1.00)	2(1.00)

Table 3.

The m^o(RE(m^o)) under high dropout (θ = 0.60)

	C1/C2	ρ = 0.2	ρ = 0.4	ρ = 0.6	ρ = 0.8
(a) RM
CS	1	2(1.00)	2(1.00)	2(1.00)	2(1.00)
	10	10(1.59)	10(1.65)	10(1.74)	10(1.88)
	100	10(2.23)	10(2.31)	10(2.43)	10(2.63)
AR(1)	1	2(1.00)	2(1.00)	2(1.00)	10(1.39)
	10	3(1.05)	4(1.10)	6(1.18)	2(1.00)
	100	9(1.26)	9(1.37)	10(1.56)	10(1.94)
(b) MM
CS	1	2(1.00)	2(1.00)	2(1.00)	2(1.00)
	10	10(1.40)	10(1.24)	7(1.09)	3(1.04)
	100	10(1.95)	10(1.73)	10(1.50)	9(1.27)
AR(1)	1	2(1.00)	2(1.00)	2(1.00)	2(1.00)
	10	3(1.02)	3(1.02)	3(1.03)	3(1.04)
	100	4(1.06)	4(1.06)	4(1.07)	4(1.09)

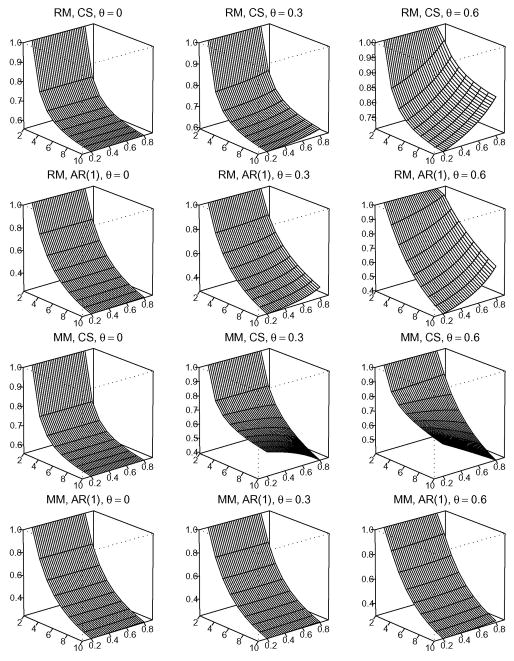
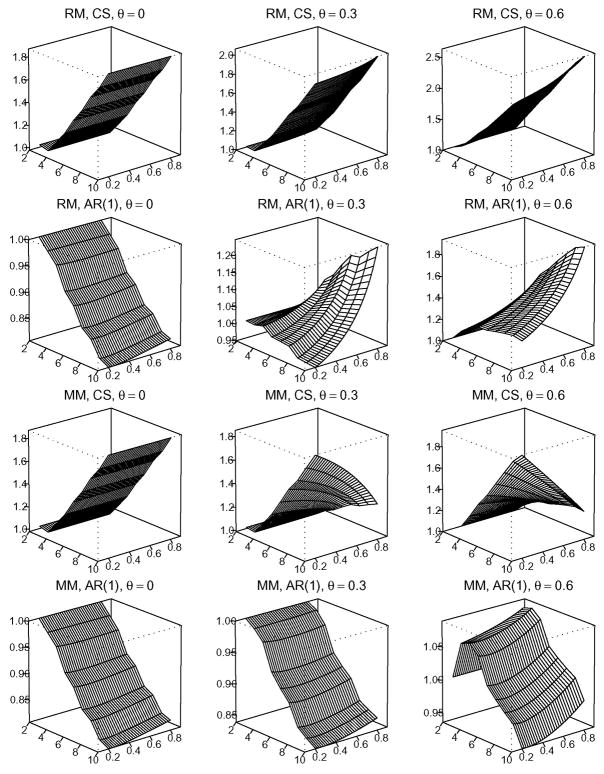
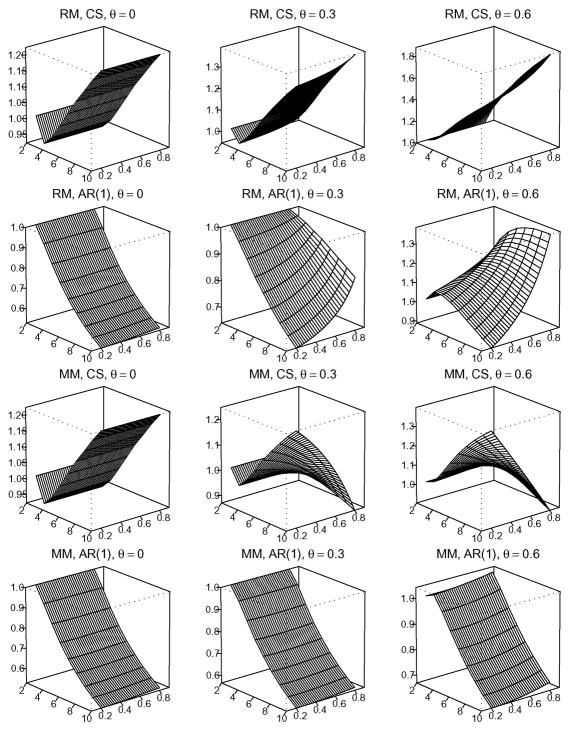
In order to provide a global view of the association between m^o and the various factors, we plot Figures 1–3. Figures 1–3 show the numerical analysis under C₁/C₂ = 1, 10, and 100, respectively. From top to bottom, the four rows in each figure show results under the configurations of (RM, CS),(RM, AR(1)),(MM, CS) and (MM, AR(1)). From left to right, the three columns in each figure correspond to dropout rate θ = 0, 0.30, and 0.60, respectively. In each of the three-dimensional graphs, the x-axis indicates m, the number of repeated measurements. Note that under the cost constraint, n(m) is a one-to-one function of m. Thus, the x-axis effectively denotes choices of (n(m), m). The y-axis indicates correlation ρ, ranging from 0.2 to 0.8. The z-axis corresponds to the RE under different values of m and ρ, given the assumed missing pattern, correlation structure, and dropout rate θ. Thus, each vertical slice parallel to the x-axis provides a curve of RE versus m for a given configuration of (C₁/C₂, missing pattern, correlation structure, θ, ρ). Note that in each graph we employ a different scale on the z-axis to provide maximum detail in the change of RE.

Figure 1.

Under the cost ratio of C₁/C₂ = 1, the relative efficiency of the GEE treatment effect estimate with m repeated measurements against that with two repeated measurements.

Figure 3.

Under the cost ratio of C₁/C₂ = 100, the relative efficiency of the GEE treatment effect estimate with m repeated measurements against that with two repeated measurements.

For C₁/C₂ = 1, Figure 1 shows a decreasing trend in RE as m increases (or as n decreases), over all missing pattern, correlation structure, ρ*, or θ. It is consistent with the observation in Tables 1–3 that m^o = 2 for C₁/C₂ = 1 under all designing configurations. In Appendix A.2 we have proved that under no missingness and the CS correlation structure, the power (or RE) decreases with m when C₁/C₂ ≤ 2. Figure 1 suggests that this conclusion applies to situations with missing data or AR(1) correlation structure. We have tried different cost ratios, such asC₁/C₂ =0.5, 1.5, and 2, and obtained similar results (omitted due to space limitations). This suggests that the above conclusion holds generally for C₁/C₂ ≤ 2. Thus, when C₁/C₂ ≤ 2, the optimal strategy is to maximize the number of subjects. That is, to use combination (n(2),2).

Figures 2 and 3, on the other hand, suggest that the identification of m^o is much more complicated under greater cost ratios (C₁/C₂ = 10 or 100). There is no simple rule to locate m^o under different configurations and a numerical search is required. Note that the unsmoothness in Figure 3 is due to the integer constraint on m and n.

Figure 2.

Under the cost ratio of C₁/C₂ = 10, the relative efficiency of the GEE treatment effect estimate with m repeated measurements against that with two repeated measurements.

The RE in Figures 1–3 is helpful to locate the optimal number of repeated measurements. It does not, however, directly show how the choices of (n(m), m) under a cost constraint affect the testing power. In Figure 4 we present the power curves against m under combinations of RM/MM patterns, CS/AR(1) correlation structures, and different values of ρ*, given C = 2000, C₁ = 10, C₂ = 1, and θ = 0.60. We observe two features in Figure 4. First, in general we observe an upward shifting in the power curves as ρ increases. One explanation is that, given a high dropout rate (θ= 0.60), if the data are highly correlated, the missingness results in less information loss. Second, Figure 4 demonstrates the importance of studying the optimal design under a cost constraint. In the first graph (ρ = 0.2), the solid curve (RM and CS) has a range of 0.62 to 0.81 depending on the choice of m. In practice, it will make the difference between an under-powered and an adequately powered clinical trial.

Figure 4.

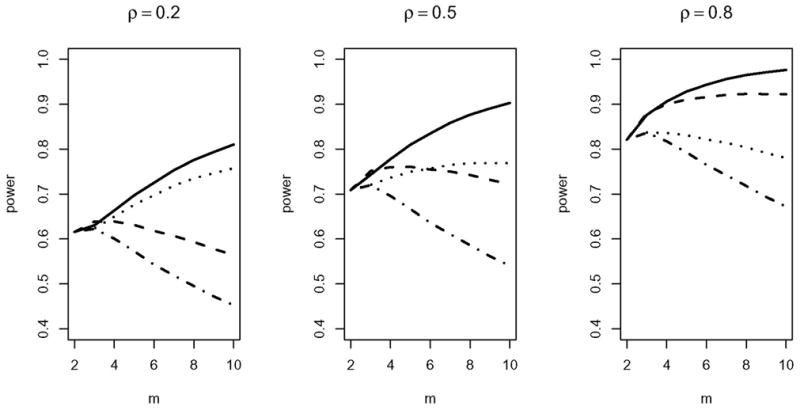
The power curves against m, fixing C = 2000, C₁ = 10, C₂ = 1, θ = 0.60. The three graphs are under ρ = 0.2, 0.5, and 0.8, respectively. The solid line corresponds to (RM, CS), the dashed line to (RM, AR(1)), the dotted line to (MM, CS), and the dashed-and-dotted line to (MM, AR(1)).

4. Minimizing the Budget for a Given Power

In other studies (Moerbeck, van Breukelen, and Berger 2000), investigators might have a prespecified power requirement, and a desire to find (n^o, m^o) that minimizes the total cost, $C={nC}_1+n{\sum }_{j=1}^m{p}_j{C}_2$. Plugging in the equation of n as given in (3), we can show that

$$C=\frac{{\sigma }^2{(z_{1-\alpha /2}+z_{1-\gamma })}^2{C}_2}{{\beta }_{40}^2{\sigma }_r^2}·\frac{s_t^2({\sum }_{j=1}^m{p}_j+V)}{{\mu }_0^2{\sigma }_t^4}.$$ (9)

Note that the first term does not depend on m and the second term is proportional to Q in (8). Thus, the m^o that minimizes Q also minimizes C in (9). In other words, whether to maximize power for a given budget or to minimize the total cost for a given power, the search for m^o is the same. The difference lies in the computation of n^o after m^o is identified. When maximizing power for a given budget, we find n^o by n^o = n(m^o), which incorporates the cost constraint. When minimizing cost for a given power, we compute n^o by (3), which incorporates the power requirement.

5. An Example

We apply the sample size method to a labor pain study (Davis 1991). In this study, 83 women in labor were randomly assigned to the pain medication group (43 women) or the placebo group (40 women). Within a three-hour period, the self-reported amount of pain was assessed repeatedly using a 100mm line, with 0 for no pain and 100 for extreme pain. We assume that the cost to recruit a subject is C₁ = $300, the cost to obtain a self-reported pain measurement is C₂ = $20, the standard deviation of measurement error is 30, the repeated measurements follow a monotone missing pattern, and the correlation structure is AR(1) with ρ = 0.2. The researchers adopted a balanced experimental design (r = 0.5) and the total budget constraint is set at C = $80, 000. For practical reasons, m is bounded to a maximum of six measurements. The goal is to find the optimal m and n to maximize the power in detecting the difference in slopes between the two treatment groups. Assuming that the dropout rate at the end of study is 48%, to detect a difference in slope of 3 points per hour with 5% two-sided Type I error, the optimal combination is m^o = 2 and n^o = 242. The achieved power is 83.6%. If the observations follow an RM pattern, then the optimal combination is m^o = 3 and n^o = 231, with a power of 84.0% and an RE of 1.01. When there are no missing data (p_j = 1), the optimal combination is m^o = 2 and n^o = 235, achieving a power of 0.95.

6. Discussion

In this article we take financial constraints into account in the design of repeated measurement studies. We have shown that for a given configuration of missing pattern, correlation structure, ρ, and dropout rate, m^o is determined by cost ratio C₁/C₂. That is, no matter how we change the overall cost constraint C, the optimal number of repeated measurements will remain the same as long as the cost ratio C₁/C₂ is unchanged. Zhang and Ahn (2010) evaluated the effects of correlation and missing data with MCAR and nonignorable missing on sample size estimation without financial constraints in repeated measurement studies. Further study is needed to investigate the effect of misspecified correlation structure and missing data on the determination of optimal combination of n and m under financial constraints.

This study has several limitations. First, it focuses on a linear regression model estimating the difference in slopes between treatment groups. In many clinical trials, researchers are often interested in the time-averaged difference in a response between groups (Diggle et al. 2002), in which case this approach is not applicable. Second, it identifies the optimal number of repeated measurements based on a “statistical” criterion of maximizing the power. Under this criterion, the simulation study suggests that given many test configurations the preferred design is the one with only m = 2 observations. In many longitudinal drug studies, however, researchers follow patients at intervals not only to estimate the slope in treatment effect, but also to monitor the patients over time with respect to safety and other endpoints. That is, the schedule of assessments is determined not only by the cost, but also by regulatory implications. For example, patients might require one or more follow-up visits after the primary assessments are completed. Blindly adopting the statistically optimal design might prevent researchers from addressing these important questions. One solution is to specify the minimal number of repeated measurements that is required by clinical goals, and then conduct statistical searching to identify the optimal design that maximizes power.

The computation of this study is performed in R. The program is available upon request from the first author.

Table 2.

The m^o(RE(m^o)) under moderate dropout (θ = 0.30)

	C1/C2	ρ = 0.2	ρ = 0.4	ρ = 0.6	ρ = 0.8
(a) RM
CS	1	2(1.00)	2(1.00)	2(1.00)	2(1.00)
	10	10(1.32)	10(1.33)	10(1.35)	10(1.39)
	100	10(1.96)	10(1.98)	10(2.01)	10(2.07)
AR(1)	1	2(1.00)	2(1.00)	2(1.00)	2(1.00)
	10	2(1.00)	2(1.00)	2(1.00)	2(1.00)
	100	4(1.01)	4(1.02)	10(1.07)	10(1.25)
(b) MM
CS	1	2(1.00)	2(1.00)	2(1.00)	2(1.00)
	10	10(1.25)	10(1.16)	10(1.04)	2(1.00)
	100	10(1.85)	10(1.73)	10(1.55)	10(1.29)
AR(1)	1	2(1.00)	2(1.00)	2(1.00)	2(1.00)
	10	2(1.00)	2(1.00)	2(1.00)	2(1.00)
	100	2(1.00)	2(1.00)	2(1.00)	2(1.00)

Appendix A.1

Proof

From (8), it is obvious that Q is proportional to C₂/C, and that where Q reaches the maximum is solely determined by the term $s_t^2({\sum }_{j=1}^m{p}_j+V)/({\mu }_0^2{\sigma }_t^4)$. Thus the financial constraint affects the value of m^o through V =C₁/C₂, the cost ratio.

Because changing the total budget C does not affect m^o, it only affects sample size n^o through the function n(m), as defined in (5).

Appendix A.2

Under no missing data (p_j = 1 for j = 1, …, m) and homogeneous correlation structure, we have μ₀ = m,

$$\begin{array}{l}{\mu }_1={\mu }_0^{-1}\sum _{j=1}^m{p}_j{t}_j\\ ={\mu }_0^{-1}[0+T/(m-1)+2T/(m-1)+\cdots +T]\\ ={\mu }_0^{-1}\frac{T}{m-1}(0+1+\cdots +(m-1))\\ =\frac{1}{m}\frac{T}{m-1}\frac{m(m-1)}{2}=\frac{T}{2},\end{array}$$

and

$$\begin{array}{l}{\mu }_2={\mu }_0^{-1}\sum _{j=1}^m{p}_j{t}_j^2\\ ={\mu }_0^{-1}[0+T^2/{(m-1)}^2+{(2T)}^2/{(m-1)}^2+\cdots +T^2]\\ ={\mu }_0^{-1}\frac{T^2}{{(m-1)}^2}[0+1+2^2+\cdots +{(m-1)}^2]\\ =\frac{1}{m}\frac{T^2}{{(m-1)}^2}\frac{(m-1)m(2m-1)}{6}=\frac{(2m-1)T^2}{6(m-1)}.\end{array}$$

Thus

$${\sigma }_t^2={\mu }_2-{\mu }_1^2=\frac{m+1}{12(m-1)}{T}^2.$$

We also need $s_t^2={\sum }_{j=1}^m{\sum }_{j^{\prime }=1}^m{p}_{j{j}^{\prime }}{\rho }_{j{j}^{\prime }}(t_j-{\mu }_1)(t_{j^{\prime }}-{\mu }_1)$. Note that p_jj′ = 1, and ρ_jj′ = ρ for j ≠ j′ and ρ_jj′ = 1 for j = j′. Thus

$$\begin{array}{l}{s}_t^2=\rho \sum _{j=1}^m\sum _{j^{\prime }=1}^m(t_j-{\mu }_1)(t_{j^{\prime }}-{\mu }_1)+(1-\rho )\sum _{j=1}^m{(t_j-{\mu }_1)}^2\\ =(1-\rho )(\sum t_j^2-m{\mu }_1^2)\\ =(1-\rho )\frac{(m+1){mT}^2}{12(m-1)}.\end{array}$$

Plugging μ₀, $s_t^2$, and ${\sigma }_t^2$ into (8), we have

$$\begin{array}{l}Q=\frac{C_2}{C}\frac{(1-\rho )\frac{(m+1){mT}^2}{12(m-1)}({\sum }_{j=1}^m{p}_j+V)}{m^2{\left[\frac{m+1}{12(m-1)}{T}^2\right]}^2}\\ \equiv \frac{(m-1)(m+V)}{m(m+1)}.\end{array}$$

We have the ≡ sign because (1− ρ), T, C, and C₂ do not depend on (n, m). Recall that V = C₁/C₂ ≥ 0 is the cost ratio between an additional subject and an additional measurement. Setting

$$\begin{array}{l}\frac{\partial log(Q)}{\partial m}=\frac{1}{m-1}+\frac{1}{m+V}-\frac{1}{m}-\frac{1}{m+1}\\ =\frac{(2-V)m^2+2Vm+V}{(m-1)m(m+1)(m+V)}=0,\end{array}$$

we have roots

$$m=\frac{-V\pm \sqrt{2V^2-2V}}{2-V}\text{when}V\ge 1.$$

For m ≥ 2, the denominator of (A.1) is always positive. For the numerator of (A.1), we define f(m) = (2−V)m²+2Vm+V and discuss several scenarios.

• When 0 < V < 1, f(m) is a U-shape curve above 0. Thus, ∂log(Q)/∂m > 0 for m ≥ 2. That is, Q is increasing with m and the minimum is achieved at m^o = 2.

• When 1 ≤ V <2, f(m) is a U-shape curve centered at −V/(2−v) < 0. Thus we have f(m) > f(2) = 8+v > 0 for m ≥ 2. As a result, Q is also increasing over m ≥ 2 and the minimum is achieved at m^o = 2.

• When V = 2, f(m) = 4m+2 is an increasing function of m. For m ≥ 2, we have f(m) > f(2) = 10> 0. Thus Q is increasing over m ≥ 2 and the minimum is achieved at m^o = 2.

• When V > 2, f(m) is a reversed U-shape curve with two roots

  $$m=\frac{-V\pm \sqrt{2V^2-2V}}{2-V}.$$

Lemma 1

$$\frac{-V+\sqrt{2V^2-2V}}{2-V}\le 2\le \frac{-V-\sqrt{2V^2-2V}}{2-V}.$$

Proof

Suppose Lemma 1 does not hold. Then solving inequality

$$\frac{-V+\sqrt{2V^2-2V}}{2-V}\ge 2$$

yields that −8 ≤ V ≤ 2, which contradicts with the requirement that V ≥ 2. On the other hand, solving

$$\frac{-V-\sqrt{2V^2-2V}}{2-V}\le 2$$

given V > 2 also yields an empty set. Thus we finish the proof of Lemma 1.

Lemma 1 suggests that f(m) or ∂log(Q)/∂m changes from positive to negative at

$$m^{\ast }=\frac{-V-\sqrt{2V^2-2V}}{2-V},$$

that is, Q increases on the left of m* and decreases on the right of m*. Because 2 ≤ m* ≤ m_max, the maximum of Q is achieved at m*, and the minimum of Q is achieved at one of the two extreme values of m (2 or m_max).