Biomechanical capabilities influence postural control strategies in the cat hindlimb

Abstract

During postural responses to perturbations, horizontal plane forces generated by the cat hindlimb are stereotypically directed either towards or away from the animal’s center of mass, independent of perturbation direction. We used a static, three-dimensional musculoskeletal model of the hindlimb to investigate possible biomechanical determinants of this “force constraint strategy” (Macpherson, 1988). We hypothesized that directions in which the hindlimb can produce large forces are preferentially used in postural control. We computed feasible force sets (FFS) based on hindlimb configurations of three cats during postural equilibrium tasks (Jacobs and Macpherson, 1996) and compared them to horizontal plane postural force directions. The grand mean FFS was bimodal, with maxima near the posterior-anterior axis (−86±8° and 71±4°), and minima near the medial-lateral axis (177±8° and 8±8°). Postural force directions clustered near both maxima; there were no medial postural forces near the absolute minimum. However, the medians of the anterior and posterior postural force direction histograms in the right hindlimb were rotated counter-clockwise from the FFS maxima (p<0.05; Wilcoxon signed-rank test). Because the posterior-anterior alignment of the FFS is consistent with a hindlimb structure optimized for locomotion, we conclude that the biomechanical capabilities of the hindlimb strongly influence, but do not uniquely determine the force directions observed in the force constraint strategy. Forces used in postural control may reflect a balance between a neural preference for using forces in the directions of large feasible forces and other criteria, such as the stabilization of the center of mass, and muscular coordination strategies.

1 Introduction

Forces generated by each limb of the cat during postural equilibrium tasks are characterized by a “force constraint strategy” whereby the directions of forces produced by each limb are more constrained than the directions of net force produced together by all of the limbs (Macpherson, 1988). A similar force constraint strategy has also been identified during bipedal postural control (Henry et al., 2001; Fung et al., 1995). It has been suggested by Macpherson (1988) that such a strategy simplifies the coordination problem faced by the nervous system (i.e., the “degrees of freedom problem,” Bernstein, 1967), because an appropriate net postural response force is achieved by modulating the amplitudes of the individual limb forces without altering their directions. The stereotypical force directions observed in the force constraint strategy are as follows: during quiet standing, limb forces are directed downward and away from the center of mass, acting along diagonal axes when viewed in the horizontal plane (Fung and Macpherson, 1995). Following horizontal plane translation perturbations of the support surface, or rotation of the support surface about the pitch or roll axis, active postural response forces in each limb act along the same diagonal axes, regardless of the direction of the perturbation (see Fig. 1; Macpherson, 1988; Ting and Macpherson, 2004).

Fig. 1.

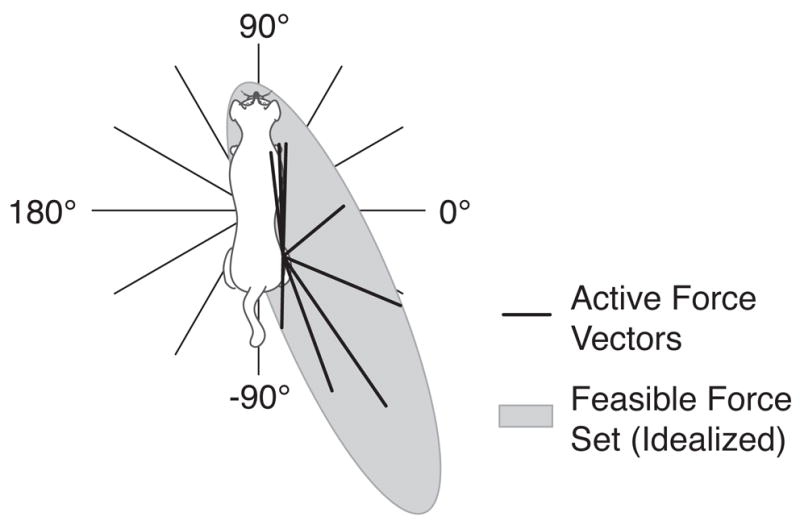
The force constraint strategy (Macpherson, 1988). Perturbations in 12 directions in the horizontal plane (thin lines) elicit postural response forces that are more constrained in direction (thick lines). Postural response forces exerted by the hindlimb act along a diagonal axis, regardless of perturbation direction. We hypothesized that this behavior reflects a neural preference for using directions of maximum feasible force, represented by the idealized feasible force set (“FFS,” gray oval) (Valero-Cuevas et al., 1998; Gruben et al., 2003; Schmidt et al., 2003).

We hypothesized that the limited directions of force produced by the cat hindlimb during postural responses are preferentially chosen because they are biomechanically favorable. Previously, acute studies have demonstrated the diagonal axis used in the force constraint strategy is also a primary torque direction for single muscles activated through direct nerve stimulation (Lawrence et al., 1993) or spinal reflexes (Nichols et al., 1993), and for ensembles of muscles activated through reflex mechanisms (Bonasera and Nichols, 1996; Siegel et al., 1999; Nichols, 2002). Similarly, forces produced during static and dynamic pedaling reflect biomechanically favorable force directions in the human lower limb. A static musculoskeletal model demonstrated the set of feasible forces (“feasible force set,” or FFS) that can be produced by the limb is elongated, with the orientation of the maximal possible force coinciding with the stereotypical force directions observed experimentally (Gruben et al., 2003; Schmidt et al., 2003). Although it may be possible to produce forces in other directions, this study showed that biomechanical factors influence self-selection of force directions when they are not explicitly specified by the task.

We tested our hypothesis by quantifying the FFS of the cat hindlimb and comparing it to the directions of observed postural response forces in three cats performing postural equilibrium tasks (Jacobs and Macpherson, 1996). The FFSs were based on experimentally measured kinematic configurations and constraints on individual muscle forces (Kuo and Zajac, 1993; Valero-Cuevas et al., 1998; Schmidt et al., 2003). Because sagittal plane models (He et al., 1991; Prilutsky et al., 1997; Hof, 2001; Kaya et al., 2005) were inadequate for investigating horizontal plane forces, we created a three-dimensional model based on the measurements of Burkholder and Nichols (2000, 2004). Our hypothesis that biomechanically favorable force directions are preferentially used during postural control would be supported if the FFS were elongated along the same axes as the force directions observed experimentally (e.g., Fig. 1, solid oval).

2 Methods

We constructed FFSs using a model of the cat hindlimb in postures based on kinematic data taken from 412 individual trials of three cats during translation perturbations of the support surface in 12 directions (Fig. 1). We then compared active postural response force directions to the average FFS over all trials. Simulations and subsequent analyses were conducted in Matlab (The Mathworks, Natick, Mass., USA).

2.1 Model of the cat hindlimb

A three-dimensional static model of the cat hindlimb was developed based on the measurements of Burkholder and Nichols (2000, 2004). The model consists of seven rotational degrees of freedom (q) and 31 muscles. The hip joint was modeled as a ball joint, and the knee and ankle were each modeled using two non-intersecting, nonorthogonal axes. Muscles were modeled as straight lines between origin and insertion points, with via points. Muscle moment arm values were determined with SIMM software (Musculographics, Inc., Santa Rosa, CA).

The transformation between a 31-element input vector of muscle excitations e (0 ≤ e_i ≤ 1) and the (6 × 1) force and moment system F ([f_x f_y f_z m_x m_y m_z]^T) produced at the endpoint (approximated as the metatarsal-phalangeal joint; Jacobs and Macpherson, 1996) is defined as:

$$\mathit{F}={\mathit{J}}^{\mathbf{T}}\mathit{R}{\mathit{F}}_{\mathit{o}}{\mathit{F}}_{\mathit{AFL}}\mathit{e}$$ (1)

All factors in Eq. (1) except F_o vary with the limb posture q; this dependence is omitted for clarity. The last four factors map muscle excitations e to a net joint torque vector through F_AFL, the (31 × 31) diagonal matrix of scaling factors based on active muscle force-length characteristics, F_o, the (31 × 31) diagonal matrix of maximal muscle forces, (Zajac, 1989; Valero-Cuevas et al., 1998) and R, the (6 × 31) moment arm matrix (Valero-Cuevas et al., 1998). All muscles were assumed to be at 95% optimum fiber length for the mean posture of each cat (Burkholder and Lieber, 2001).

J^−T maps the net joint torque vector to the endpoint force and moment system. A closed-form solution for the (6 × 7) system geometric Jacobian J(q) was developed with Autolev software (Online Dynamics, Inc., Stanford, CA). All seven degrees of freedom were used to establish the limb postures (see Section 2.3). The degree of freedom corresponding to internal/external rotation of the femur was neglected (“locked”) during endpoint force calculation so that J^T was (6 × 6) and directly invertible. This degree of freedom was chosen because it contributed primarily to the generation of moments rather than forces in the horizontal plane.

The complete model includes passive muscle forces F_PFL 1, where F_PFL is a (31 × 31) diagonal matrix of passive force-length scaling factors and 1 is a vector of ones:

$$\mathit{F}={\mathit{J}}^{\mathbf{T}}\mathit{R}{\mathit{F}}_{\mathit{o}}{\mathit{F}}_{\mathit{AFL}}\mathit{e}+{\mathit{F}}_{\mathit{PFL}}1$$ (2)

2.2 Postural response data

The kinematic and kinetic data used in this study have been presented previously (Jacobs and Macpherson, 1996). Briefly, three cats (Bi, Ni, and Ru) were trained to stand on a moveable platform equipped with four triaxial force plates. Postural perturbations consisted of ramp-and-hold translations of the platform in one of 12 directions uniformly spaced in the horizontal plane (Fig. 1). Although the perturbations were destabilizing, they resulted only in small changes in joint angles (≤ 5°), suggesting that a static musculoskeletal model is adequate to estimate feasible forces. The positions of the hip, knee, ankle, and metatarsal-phalangeal (MTP) joint centers were estimated from kinematic marker data (Fung and Macpherson, 1995).

For the current analysis, we obtained the average kinematic configuration of the hindlimb in an 80 ms window before the onset of the perturbation in each trial (Fig. 3, gray lines). We also obtained the active postural response force vector, which was computed as the difference in force direction between the active force response period during an 80 ms window 120 ms following perturbation onset, and the background period (Jacobs and Macpherson, 1996).

Fig. 3.

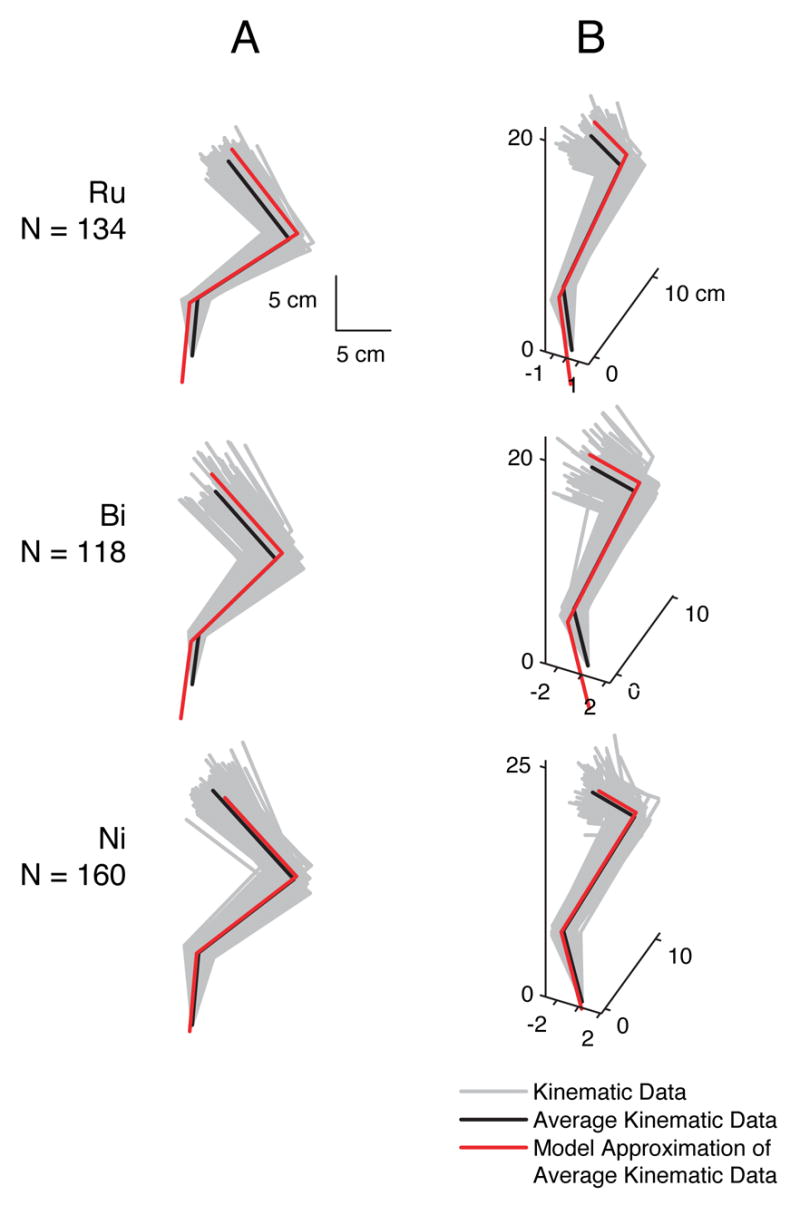
Model postures were based on kinematic data of three cats. Column A: sagittal view. Column B: posterior-lateral view. Light gray traces are kinematic data from each trial (Ru: N=134, Bi: N=118, Ni: N=160), used in the FFS computation. Black traces are the average kinematic data for each cat. Red traces illustrate the best fit of the model to the average segment angles in the frontal and sagittal planes for each cat (see Section 2.4).

2.3 Feasible force sets

Feasible force sets were constructed for each of the 412 trials using linear programming. For each trial, numerical optimization was used to calculate the limb posture q that minimized the mean squared error between the sagittal and posterior plane femur, shank, and foot angles of the model and those of the kinematic data; all residual segment angle errors were ≤ 10⁻⁴ ° (Fig. 3).

After the best-match q was established, the muscle excitation vector e producing the maximal biomechanically feasible force projection in each of 520 directions on the unit sphere was calculated subject to the constraint that all muscle excitations varied between 0 and 1. The FFS was then defined as the smallest convex polygon in the dorsal plane that encompassed the projections of these 520 forces. The vertices of this polygon represent unique e; the distance from each point on the boundary of the polygon to the origin is the maximal biomechanically feasible force magnitude in that direction (Valero-Cuevas et al., 1998; Kuo and Zajac, 1993). We have found that this method produces results identical to exact solutions produced with computational geometry tools (Avis and Fukuda 1992; e.g., cdd, K. Fukuda; cddmex, F. Torrisi and M. Baotic) when the dimension of e is ≤ 13 (data not shown). Exact solutions of this type are not feasible for larger numbers of muscles because computation time increases exponentially with the dimension of e.

2.4 Sensitivity analysis

We tested the sensitivity of the FFS to morphological parameters and model architecture. A FFS was constructed based on the mean kinematic data of each cat. We then examined the changes in the maximal directions of these FFSs due to perturbations of ±50% to all nonzero muscle moment arms, perturbations of ±50% to the maximum force value for each muscle, and 1° perturbations to each joint angle (cf., Lehman and Stark, 1982; Scovil and Ronsky, 2006). In addition, we tested the influence of an externally applied moment limit, the use of the pseudoinverse of the full seven degree of freedom system Jacobian (J^T)⁺, and of scaling individual segment lengths to match the kinematic data.

3 Results

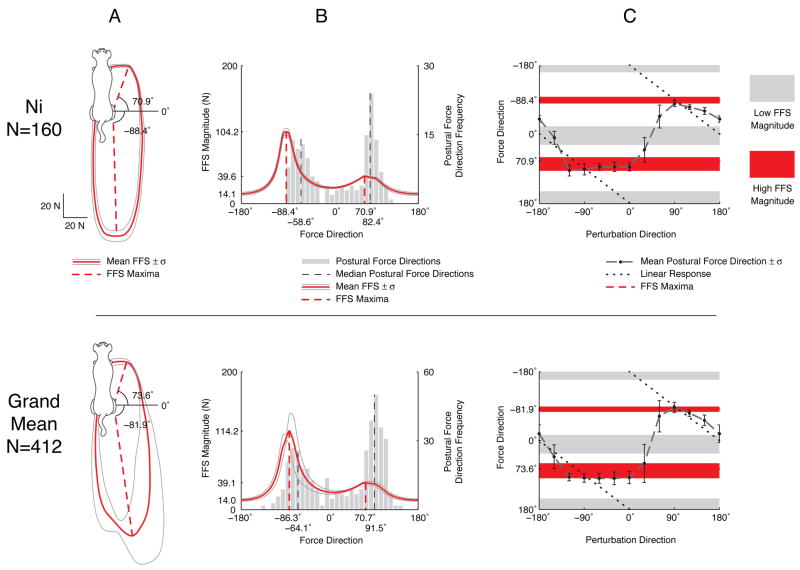
All simulations exhibited strongly anisotropic FFS with maxima in both the posterior and anterior half-planes, (Fig. 4A, solid red lines) consistent with stereotypical force directions observed in the force constraint strategy (Macpherson, 1988). Inter-trial variance of the FFS was minimal; maximum coefficients of variation for points on the FFS were 9.0%, 15.5%, and 15.3% for cats Ru, Bi, and Ni (Fig. 4, upper row), respectively. Because of this small variability and the general similarity of FFS shape across cats, all FFSs were combined into a grand mean for subsequent analysis (Fig. 4, lower row) except for the sensitivity analyses, which were performed about the mean posture of each cat. Sensitivity analysis results based on the mean posture of Ru are reported in detail here because they were the most sensitive.

Fig. 4.

FFSs and active postural force directions for cat Ni (top row), and the grand mean across all cats (bottom row). Angle conventions are defined in Fig. 1. A: Dorsal plane FFS mean ±SD (red thick and thin lines, respectively). FFS maxima (dashed lines) are directed either posteriorly or anteriorly with small lateral components. FFS minima are in the medio-lateral directions. The mean FFS of the individual animal and the grand mean are bimodal, similar to the two-vector force constraint strategy. B: FFS magnitude from A (solid red line, left hand scale), plotted against force direction and histogram of active postural response forces (gray bars, right hand scale). Postural force directions are bimodal with peaks (dashed gray lines) clustered near the maxima of the FFS (dashed red lines). No active forces were directed medially, near the FFS minima. C: Active postural forces generated by the hindlimb (black circles) are not directly opposite to the perturbation direction (dotted black line). Instead, forces tend towards directions of high feasible force magnitude (red shaded area) and away from regions of low feasible force magnitude (gray shaded area). The FFS maxima therefore act as attractors of force direction that have stronger influence on lateral perturbation directions (−90° to 90°) than medial perturbations (≤ −90° or ≥ 90°).

The grand mean FFS was bimodal, with maxima nearly aligned with the posterior-anterior axis (−87±8° and 71±4°; mean ± SD); the anterior maxima had a small lateral component (Fig. 4A, red dashed lines). The absolute minimum of the FFS was directed medially (177±8°), and a second minimum was directed almost exactly laterally (8±8°). The magnitude of the posterior maximum was 8.2 times the absolute minimum, while anterior magnitude was 2.8 times the absolute minimum (Fig. 4B, solid red line).

The histogram of the active postural force directions was also bimodal (Fig. 4B, gray bars), with peaks located near the FFS maxima (Fig. 4B, compare red and black dashed lines), consistent with the hypothesis that biomechanically favorable force directions are preferentially used. The medians of the posterior and anterior postural force direction histograms were rotated counter-clockwise relative to FFS maxima by a moderate but statistically significant amount (−22° and −21°, respectively; Wilcoxon signed-rank test, p<0.05). There were few directly lateral forces where FFS magnitude was small (Fig. 4B, near 0°), and notably, no medial forces near the absolute minimum of the FFS (Fig. 4B, near 180°).

The anisotropic shape of the FFS qualitatively predicted the nonlinear relationship between perturbation direction and active postural force direction (Fig. 4C) first reported by Macpherson (cf., 1988, Fig. 8B). Active force directions in response to a specific perturbation direction were not directly opposite to the perturbation direction (Fig. 4C, dotted line). Instead, the active forces tended to gravitate towards directions where feasible forces were high (Fig. 4C, red shaded area) and away from directions where feasible forces were low (Fig. 4C, gray shaded area). Deviations from the linear response were more acute for perturbations directed laterally; postural forces either clustered around the anterior FFS maxima (−90° to 0°) or were dispersed (0° to 90°; notice the larger error bars in this region in Fig. 4).

The FFS was robust to various perturbations to the model parameters. The results of the sensitivity analysis performed about the mean posture of Ru are summarized in Table 1; results for Bi and Ni were equally or less sensitive in general. The FFS maxima were insensitive to ±50% perturbations to individual muscle moment arms and maximum muscle forces, eliciting maxima direction changes of ≤ 14° and magnitude changes of ≤ 27% across all cats. Sensitivity to individual joint angles was ≤ 3.5° for posterior maxima and ≤ 10.2° for anterior maxima; the increased sensitivity of anterior maxima is not critical because the anterior maxima were more broadly tuned in general. We found only small changes in FFS maximum directions (≤ 9.1°) when we scaled the model segment lengths to each cat, and comparably small changes (≤ 9.8°) when we recreated the analysis using the pseudoinverse (J^T)⁺ of the full seven degree of freedom system Jacobian in Eq. (2). The largest sensitivity values were associated with external limits placed on the endpoint moment. FFS maxima directions were moderately affected by moment limits ranging between 0.001 N-m and 10 N-m (≤ 17.6°), but the FFS magnitude was scaled considerably (≤ 85.3%). In all cases, however, FFSs retained their bimodal shape, and FFS magnitudes exceeded observed postural force magnitudes.

Table 1.

Sensitivity of FFS maxima (cat Ru) to model architectural and morphological parameters

	Direction		Magnitude
	posterior	anterior	posterior	anterior
Moment limit = 0.001 N-m	1.0°	−0.3°	−42.5%	−82.7%
Moment limit = 1 N-m	3.8	−17.6	−31.2	−64.9
Moment limit = 10 N-m	−3.4	9.6	3.6	−0.8
Pseudoinverse	−3.4	9.8	3.6	−0.1
Altered segment lengths	−3.3	9.1	14.1	8.0
1° perturbations to joint coordinates	≤ 3.5	≤ 10.2	≤ 3.8	≤ 1.7
±50% perturbations to moment arms	≤ 5.1	≤ 13.6	≤ 23.9	≤ 6.8
±50% perturbations to Fo values	≤ 4.9	≤ 13.5	≤ 15.8	≤ 12.0

Note: Sensitivity of posterior and anterior maxima directions and magnitudes are expressed separately; in general anterior maxima directions are more sensitive but are also less acutely tuned. This analysis was conducted about the mean limb posture for cat Ru; sensitivity values for Bi and Ni were similar or less sensitive in general.

4 Discussion

We used a musculoskeletal model of the cat hindlimb to assess the possible biomechanical determinants of the stereotypical force directions observed during postural control. We hypothesized that postural forces are preferentially chosen in directions of biomechanically favorable force production. Experimental horizontal plane force directions were distributed bimodally, with peaks near the directions of maximum force predicted by the model. However, they were consistently rotated with respect to these maxima, which were almost directly anterior and posterior. Thus, the anisotropy of the FFS may influence, but does not completely determine the choice of force direction during postural control.

The elongated shape and orientation of the FFS was consistent between animals, across all trials, and was insensitive to variations in model parameters, including maximum muscle forces, moment arms, kinematic configuration, segment lengths, and endpoint moment constraints. Similarly, Kuo and Zajac (1993) reported minimal sensitivity of their feasible acceleration sets to morphological parameters and variations among standing postures in the human. The FFS shape is probably most strongly influenced by the kinematic description of the model (Valero-Cuevas et al., 1998), however, altering the number of kinematic degrees of freedom (via the use of the pseudoinverse of the full rank system Jacobian) did not significantly alter our results. Similarly, scaling the model segment lengths to match the morphology of each cat had little influence. Therefore, it is not likely that using a subject-specific model (Zajac et al., 2002), rather than our generic, unscaled model of the cat hindlimb would alter our results. Because endpoint moment data are unavailable, we could not estimate the exact effects of endpoint moment on the FFS (cf., Valero-Cuevas et al., 1998). However, the high sensitivity to limits on endpoint moment is not considered to be critical because the bimodal structure of the FFS was unchanged even for the most extreme limits on endpoint moment.

The external force and moment during a postural task could affect the peak force directions predicted by the FFS. The endpoint forces and moments during standing result from gravitational forces, muscular forces from the other limbs and trunk, and forces due to unmodeled muscles in the hindlimb. Adding the background force during standing would effectively translate the origin of the FFS in a posterior and lateral direction, increasing the maximum force magnitude in the anterior direction. This could account for the relatively small anterior force peak (Fig. 4B) in the FFS compared to the experimental force directions, which were measured during active unloading on a background of extensor activity (Macpherson 1988). The addition of unmodeled pelvic muscles that contribute to flexion could also increase the anterior force magnitudes. As discussed above, maximum endpoint moment constraints affect FFS magnitude more than shape. The largest changes to force maximum directions were ≤17.6°, when a moderate constraint was applied (≤ 1 N-m). Therefore, the addition of more realistic external forces and moments are not predicted to significantly alter force maximum directions, only magnitudes.

It is possible that the large number of muscles in our model decreased the sensitivity of the FFS to individual model parameters. For example, while single muscle forces predicted by optimization have been reported to be highly sensitive to parameter values (Raikova and Prilutsky, 2001; Kaya et al., 2005), multiple muscle activation patterns have not (Raikova and Prilutsky, 2001; van Bolhuis and Gielen, 1999). Similarly, in dynamic simulations of the human leg, Scovil and Ronsky (2006) report considerable sensitivity of single muscle forces to muscle model parameter perturbations, but reduced sensitivity of the overall model behavior (e.g., the ground reaction force during walking). In contrast to maximal effort tasks (e.g., Valero-Cuevas et al., 1998; Pandy et al., 1990), the postural task presented here imposed no explicit biomechanical constraint on single limb force direction. While total force generated by all four limbs must oppose the perturbation direction, the nervous system is free to choose single limb force directions that may optimize arbitrary criteria (cf., Crowninshield and Brand, 1981; Kaya et al., 2005; Harris and Wolpert, 1998; Todorov, 2004; Scott, 2004).

Using a diagonal axis of force production may simplify the neural control mechanism required to coordinate force direction and amplitude during postural responses, but is not imposed by biomechanical limitations in hindlimb force production. The force of each limb could be controlled by modulating a limited number of muscle activation patterns (Ting and Macpherson, 2005) that produce forces in an equally limited number of directions. Although postural force magnitudes (≈ 1–2 N) are small, using a biomechanically favorable force direction may also be energetically advantageous, and beneficial in an uncertain environment when the magnitude of the postural perturbation is unpredictable. Valero-Cuevas et al. (1998) has suggested that solutions to “maximal effort” tasks may represent functional units of neuromechanical organization applicable to tasks requiring submaximal effort. Scaled versions of the muscle excitation patterns determined by the maxima of the FFS of the human index finger are used over the entire voluntary range (Valero-Cuevas, 2000).

Other factors not modeled here that could influence the choice of force directions used in postural control include interlimb coordination and stability criteria. The considerable anisotropy of the FFS may reflect hindlimb biomechanical capabilities tuned for locomotion, and not necessarily postural control. Large posterior forces are consistent with propulsion during locomotion, and anterior forces are used in the deceleration phase of gait. The maximal force directions of the FFS would have limited capacity to resist lateral perturbations. While the use of the diagonal force direction is not explicitly predicted by the FFS, the diagonal forces are still consistent with biomechanically favorable directions of force production, with the added benefit that lateral force components can also be generated. Moreover, rotation of the force vectors in each limb towards the center of mass is consistent with a self-stabilization strategy (Holmes et al., 2006; Kubow and Full, 1999; Bauby and Kuo, 2000), reducing torques about the center of mass.

Fig. 2.

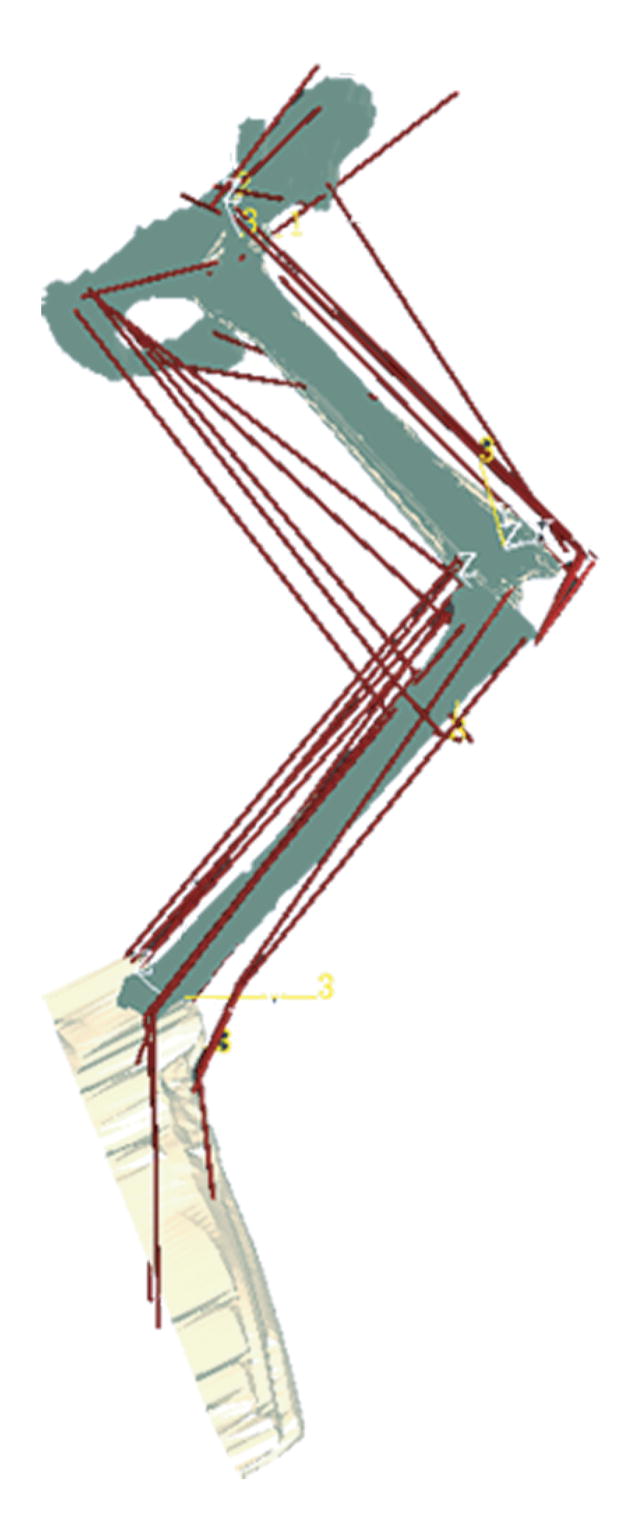
A three-dimensional model of the cat hindlimb. SIMM software (Musculographics, Inc., Santa Rosa, CA) was used to determine muscle moment arms for each of the 412 simulations. The model consists of seven rotational degrees of freedom and 31 muscles, based on the measurements of Burkholder and Nichols (2004).