Abstract
Optimizing the function of tissue engineered cardiac muscle is becoming more feasible with the development of microfabricated scaffolds amenable to mathematical modeling. In the current study, the elastic behavior of a recently developed poly(glycerol sebacate) (PGS) accordion-like honeycomb (ALH) scaffold [Engelmayr et al., 2008. Nature Materials 7 (12), 1003–1010] was analyzed. Specifically, 2D finite element (FE) models of the ALH unit cell (periodic boundary conditions) and tessellations (kinematic uniform boundary conditions) were utilized to determine a representative volume element (RVE) and to retrospectively predict the elastic effective stiffnesses. An RVE of 90 ALH unit cells (≃3:18×4:03mm) was found, indicating that previous experimental uni-axial test samples were mechanically representative. For ALH scaffolds microfabricated from PGS cured 7.5 h at 160 1°C, FE predicted effective stiffnesses in the two orthogonal material directions (0.081±0.012 and 0.033±0.005 MPa) matched published experimental data (0.083±0.004 and 0.031±0.002 MPa) within 2.4% and 6.4%. Of potential use as a design criterion, model predicted global strain amplifications were lower in ALH (0.54 and 0.34) versus rectangular honeycomb (1.19 and 0.74) scaffolds, appearing to be inversely correlated with previously measured strains-to-failure. Important in matching the anisotropic mechanical properties of native cardiac muscle, FE predicted ALH scaffolds with 50μm wide PGS struts to be maximally anisotropic. The FE model will thus be useful in designing future variants of the ALH pore geometry that simultaneously provide proper cardiac anisotropy and reduced stiffness to enhance heart cell-mediated contractility.
Keywords: Tissue engineered myocardium, Poly(glycerol-co-sebacate), PGS, Periodic finite element modeling, Anisotropy
1. Introduction
Cardiac muscle contracts via the interaction between cardiomyocytes and their hierarchically structured collagen network. As such, an ideal scaffold for forming tissue engineered cardiac muscle would promote aligned cardiomyocytes, offer minimal resistance to cardiomyocyte-mediated contraction, and provide mechanical properties closely matched to those of native myocardium (Freed et al., 2009). Building upon the significant advances made using traditional approaches (Eschenhagen and Zimmermann, 2005; Vunjak-Novakovic et al., 2009), more recent scaffold designs have emphasized biomimicry (Ott et al., 2008), microfabrication (Yeong et al., 2009), and in particular their combination (Engelmayr et al., 2008). For example, in Ott et al. (2008) decellularization of native heart tissue itself yielded a scaffold capable of supporting contractility and nascent pump function upon repopulation with neonatal cardiomyocytes. Rendered by selective laser sintering of poly(caprolactone), a microfabricated scaffold by Yeong et al. (2009) consisting of square pyramid cellular units was designed to enhance nutrient transport to C2C12 cells seeded within the microporous struts. Combining the precision of microfabrication with cardiac biomimicry, Engelmayr et al. (2008) developed an accordion-like honeycomb (ALH) scaffold toward replicating aspects of cardiac structural mechanics.
The anisotropic unit cell of the ALH scaffold was generated by overlapping two 200 × 200 μm square pores oriented at 45° to yield an undulated network of 50 μm wide struts (Fig. 1). Rendered in the bioresorbable elastomer poly(glycerol sebacate) (PGS) (Wang et al., 2002) by excimer laser microablation, tensile mechanical testing demonstrated the ALH scaffold to exhibit anisotropy similar to native right ventricular (RV) myocardium. In particular, preferred (PD) and orthogonal cross-preferred (XD) material directions were defined and matched to the circumferential and longitudinal directions of the heart, respectively. Of particular importance in scaffold design, Kemppainen and Hollister (2010) demonstrated the utility of homogenization finite element analysis in predicting the elastic modulus of microfabricated scaffolds. While the empirical design approach in Engelmayr et al. (2008) was effective in matching the anisotropic scaffold stiffnesses to those of native myocardium, it involved a time-consuming and costly sequence of iterative fabrication and characterization steps. Further, while the empirical design approach allowed for prediction of macroscale scaffold effective stiffness, it yielded no information regarding structural deformations at the microscale.
Fig. 1.

Scanning electron micrograph of an ALH scaffold (unpublished image from studies presented in Engelmayr et al., 2008). Scale bar = 500 μm.
In the current study finite element (FE) simulations and a homogenization approach were used to retrospectively predict the anisotropic effective stiffnesses of the ALH PGS scaffold. FE simulations were conducted using Zset finite element code (Mines-ParisTech, 2003) as published previously for heterogeneous materials (Barbe et al., 2001a, b; Diard et al., 2005; Kanit et al., 2006; Zeghadi et al., 2007; Musienko et al., 2007; Madi et al., 2007; Osipov et al., 2008; Gerard et al., 2009). Elastic constants obtained by FE simulations were compared to the effective stiffnesses measured for ALH scaffolds microfabricated from PGS cured for either 7.5 h or 16 h at 160 °C, as well as used to calculate associated anisotropy indices. Toward developing a better understanding of the failure properties of microfabricated PGS scaffolds, strain amplification within the PGS struts were computed and ALH scaffolds were compared with square or 2:1 aspect ratio rectangular honeycomb scaffolds.
2. Mathematical framework and methods
2.1. Experimental methods and data for PGS ALH scaffold
Experimental methods and data for microfabricated PGS ALH scaffold and associated mechanical properties were previously published (Engelmayr et al., 2008). In brief, in Engelmayr et al. (2008) PGS polymer was synthesized by reacting glycerol and sebacic acid (1:1 molar ratio, Sigma) under heat (120 °C) and vacuum ≃15 mTorr for 72 h (Wang et al., 2002), cast into 250 μm–thick sheets by curing (7.5 and 16 h at 160 °C) on sucrose-coated silicon wafers in a vacuum oven (Fidkowski et al., 2005), and microfabricated using a Rapid X 1000 system (Resonetics, Nashua, NH) with a 248 nm krypton fluoride LPX200 excimer laser (Coherent-lambda Physik). Following fabrication, ALH scaffold microstructures were imaged by scanning electron microscopy (Fig. 1). Additional samples (25 × 5 mm) were prewetted for 24 h in water and subjected to uniaxial tensile testing (Electroforce ELF 3200; Bose Enduratec, Framingham, MA) to obtain the scaffold stiffnesses in the PD and XD directions. Mechanical properties were similarly measured for native adult rat right ventricular myocardium.
2.2. Description of the unit cell and periodic tessellation
The periodic ALH scaffold was defined by the translation of a unit cell (Fig. 2) along a combination of vectors of periodicity. The unit cell consists of a pore space surrounded by PGS with a width one-half that of the strut. In the following, the inside length and the width of the struts are denoted l and w, respectively (Fig. 2). According to Engelmayr et al. (2008), the ratio w/l is equal to 0.25, corresponding with a PGS area fraction VsPGS of 31.2%. As depicted in Fig. 2, the ALH unit cell is symmetric about the PD and XD axes, theoretically allowing development of analytical expressions for the ALH scaffold effective stiffnesses in the two orthogonal directions, as shown previously for hexagonal honeycombs (Gibson et al., 1982). However, because the PD and XD axes do not coincide with the directions of the vectors of periodicity (Fig. 3), such an analysis is not straightforward. As such, here 2D FE simulations under plane strain conditions with homogeneous boundary conditions were used to compute the effective mechanical behavior.
Fig. 2.
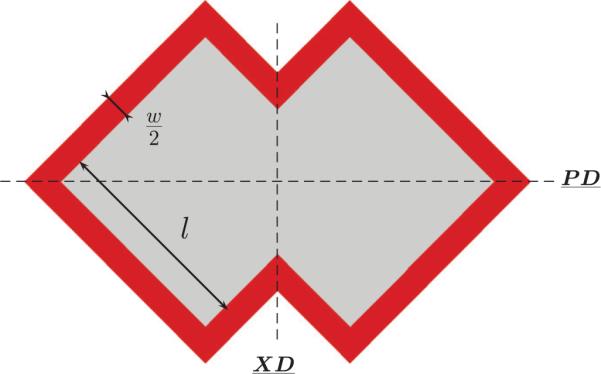
Unit cell used to derive the effective elastic behavior of the infinite scaffold from periodic finite element computations.
Fig. 3.
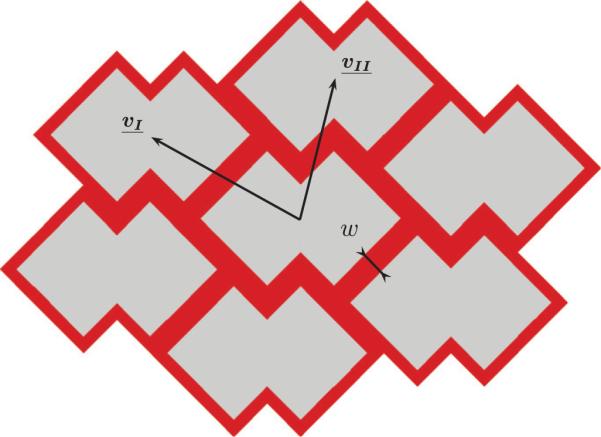
A scaffold periodic tessellation consisting of seven cells generated by translating the unit cell to its first neighbors along a combination of periodicity vectors (vI, vII).
2.3. Homogeneous boundary conditions
Consider S the surface of the heterogeneous unit cell (i.e., S = SPGS⋃Svoid) or the heterogeneous periodic tessellation and ∂S the outer boundary and x the position of any point belonging to S. To compute the effective stiffness, a displacement u is prescribed on ∂S:
- for kinematic uniform boundary conditions (KUBC):
(1) - • for periodic boundary conditions (PBC):
(2)
where is the homogeneous strain tensor:
| (3) |
For periodic conditions, v is the periodic fluctuation that takes the same value at two homologous nodes N− and N+:
| (4) |
Let n be a normal vector to ∂S. The periodic unit cell is in equilibrium, hence the traction vector takes opposite values at two homologous nodes:
| (5) |
Let be the local fourth-rank tensor field of elastic moduli. In linear elasticity, the constitutive equation is
| (6) |
with and the local stress tensor and local strain tensor, respectively. The effective global fourth-rank tensor of elasticity is expressed in terms of the average strain and average stress :
| (7) |
where
| (8) |
The Voigt notation of the effective fourth-rank tensor of elasticity is
| (9) |
For PBC, the effective fourth-rank tensor of elasticity is obtained on the representative volume element (RVE) unit cell. By contrast, for KUBC, the effective elastic tensor is obtained once the RVE is reached (i.e., for a large enough tessellation) and coincides with the effective response from PBC (Sab, 1992).
The FE simulations of the ALH scaffold were carried out using the Zset FE code (Mines-ParisTech, 2003). Because the geometry of the ALH unit cell results from the union of two overlapping squares, the mesh consisted of square elements with a quadratic interpolation of the displacement field. A mesh density of 20 square elements per edge was determined from a mesh independence study (data not shown).
2.4. Computation of ALH scaffold effective stiffnesses
The PGS structural elements and void space were assumed to exhibit isotropic linear elastic behavior based on published mechanical data (Engelmayr et al., 2008). The scaffold effective stiffnesses in the two orthogonal directions, EPD and EXD, corresponded to the components and , respectively, for prescribed displacements along the PD and XD directions.
For the PGS phase, Young's moduli were assigned based on Engelmayr et al. (2008), in which mechanical testing yielded Young's moduli equal to 0.825±0.062 and 2.116±0.1 MPa for 7.5 and 16 h of curing at 160 °C, respectively. For the void space, a Young's modulus near zero (0.0001 MPa) was assigned in order to obtain a condition number amenable to stiffness matrix inversion during the FE code execution. For both phases, a Poisson ratio equal to 0.45 was assumed.
Both EPD and EXD are computed on various size tessellations using KUBC until an RVE is reached and on the unit cell using PBC. The tessellation structures were generated iteratively by a custom C++ program.
2.5. Prediction of strain amplification and ALH scaffold anisotropy
To gain insight into the failure behavior of the ALH scaffold observed in Engelmayr et al. (2008), for 7.5 h cured PGS the spatial distribution of equivalent strain in the PGS phase was plotted. Equivalent strain plots were generated for prescribed macroscopic strains of (E11=10%, E22=0, E12=0) and (E11=0, E22=10%, E12=0). To quantify the influence of unit cell geometry, corresponding plots were generated for square and rectangular honeycombs. The equivalent strain was calculated from the deviatoric part of the strain tensor:
| (10) |
The local strain amplification in the PGS phase, , was calculated by normalizing the local equivalent strain to the average equivalent strain over the whole scaffold:
| (11) |
The global strain amplification in the PGS, , was also calculated for the PD and XD loading directions by dividing the average equivalent strain in the PGS by the average equivalent strain over the whole scaffold:
| (12) |
Assuming the mechanical behavior of each phase (i.e., PGS and void) is linear elastic and isotropic, the anisotropy depends on the geometry of the unit cell. In order to compare the FE predicted anisotropy to that calculated from experimental data in Engelmayr et al. (2008), the ratio of EPD to EXD (hereby denoted r) was calculated:
| (13) |
To provide an additional measure of anisotropy, the Zener (1948) coefficient α was calculated based on the components of the effective fourth-rank elasticity tensor:
| (14) |
It should be noted that while the Zener coefficient provides a useful benchmark of scaffold anisotropy from a pure mechanics perspective, from a tissue engineering perspective, the anisotropy ratio r is of paramount importance, as it provides a direct basis for matching the PD and XD mechanical properties of an ALH scaffold to the circumferential and longitudinal mechanical properties of native myocardium, respectively (Engelmayr et al., 2008).
To quantify the influence of structural element dimensions on ALH scaffold anisotropy, for 7.5 h cured PGS the effective stiffnesses EPD and EXD were predicted for a range of w/l ratios in which l was held constant at 200μm and w was varied from 0 to 160μm. To quantify the influence of unit cell geometry, r and α values predicted for the ALH scaffold were compared with those for scaffolds comprised of 200 × 200μm square unit cells (VsPGS=36%) and 400 × 200μm (i.e., 2:1 aspect ratio) rectangular unit cells (VsPGS=29%).
3. Results
3.1. Determination of an RVE for the ALH scaffold
For 7.5 h cured PGS, Fig. 4 illustrates the evolution of KUBC predicted elastic stiffnesses in the two orthogonal directions as a function of the number of cells in the tessellation. The KUBC predicted stiffnesses asymptotically approached the PBC predicted values and coincided (within 2%) for a tessellation, an RVE, containing at least 90 cells (i.e., 3.18 × 4.03mm, Fig. 5). Despite an ≃2.5–fold higher EPGS under 16 h curing, a similar RVE of ≃90 unit cells was obtained. Of note, the FE predicted effective stiffnesses were systematically lower than the Voigt bound of 0.261MPa (first order bound in the homogenization theory).
Fig. 4.
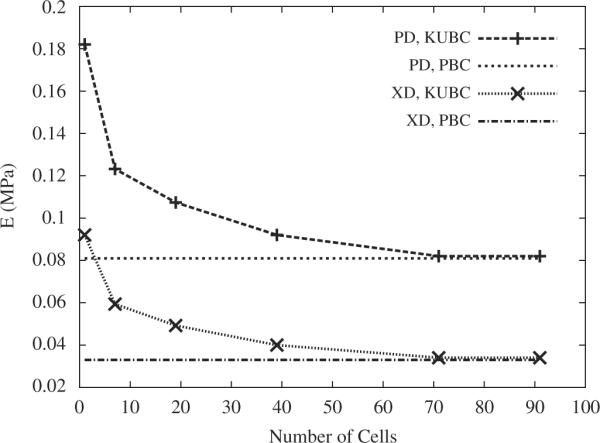
Stiffnesses of the scaffold in the orthogonal PD and XD directions as a function of the number of cells in the tessellation, obtained from KUBC and PBC FE computations for 7.5 h of curing at 160 °C.
Fig. 5.
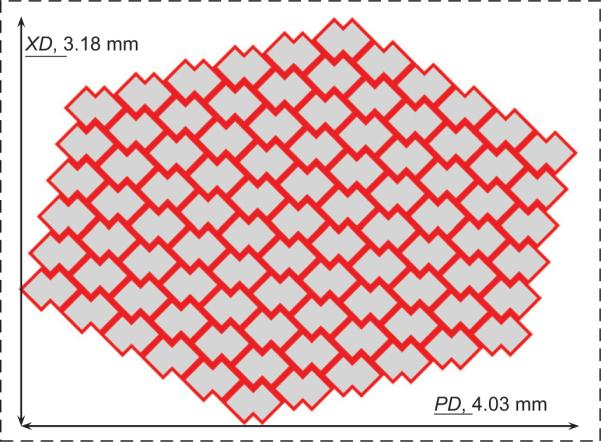
The RVE of the ALH tessellation was found to contain 90 unit cells based on KUBC simulations in the PD and XD loading directions.
3.2. Comparison of experimental and FE predicted effective stiffnesses
The ALH scaffold stiffnesses in the two orthogonal directions obtained from uniaxial tensile tests (Engelmayr et al., 2008) and FE computations are plotted in Fig. 6 for both 7.5 and 16 h of curing and summarized in Table 1.
Fig. 6.
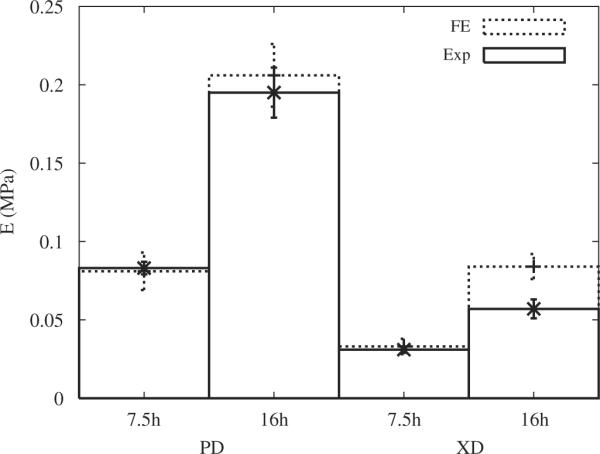
Stiffnesses of ALH scaffolds in the two orthogonal directions PD and XD obtained from FE computations (FE) and from experimental data (Exp) for 7.5 and 16 h of curing of the PGS at 160 °C (Engelmayr et al., 2008).
Table 1.
Stiffnesses (E) of ALH scaffolds obtained in the PD and XD directions by FE computations and experimentally (Exp) for 7.5 and 16 h of curing of the PGS at 160 °C (Engelmayr et al., 2008).
| Curing time | 7.5 h |
16 h |
||
|---|---|---|---|---|
| Stiffness (MPa) | EPD | EXD | EPD | EXD |
| Exp | 0.083 ± 0.004 | 0.031 ± 0.002 | 0.195 ± 0.016 | 0.057 ± 0.006 |
| FE | 0.081 ± 0.012 | 0.033 ± 0.0049 | 0.206 ± 0.02 | 0.084 ± 0.008 |
Experimental data represent mean ± s.e.m (n=3).
For 7.5 h of curing, deviations relative to the experimental data of 2.4% and 6.4% were observed for the PD and XD directions, respectively. By contrast, for 16 h of curing, deviations relative to the experimental data of 5.6% and 47% were observed for the PD and XD directions, respectively.
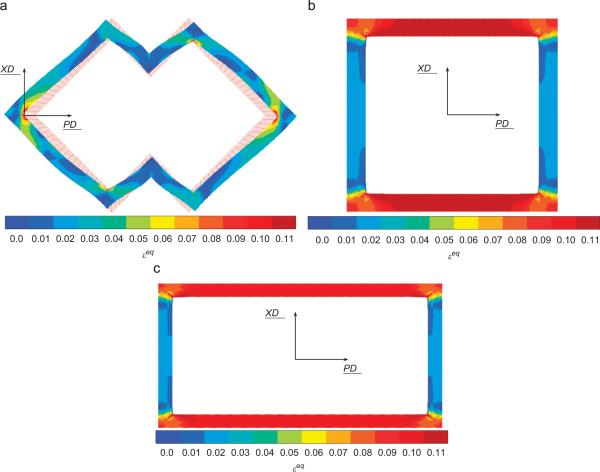
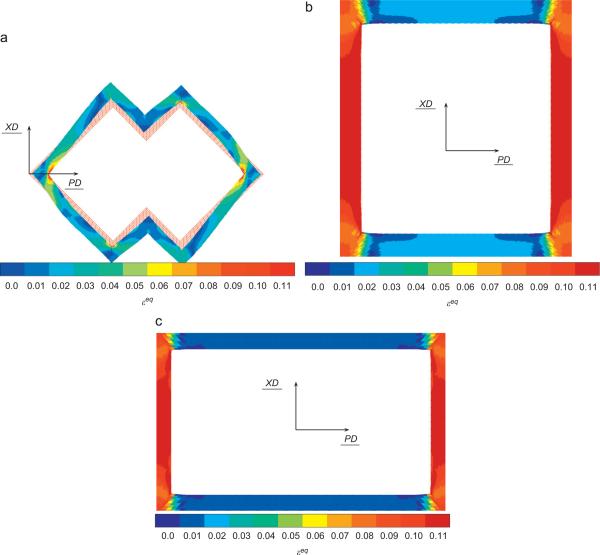
For prescribed macroscopic strains of (E11=10%, E22=0, E12=0) and (E11=0, E22=10%, E12=0), the field of equivalent strain, εeq, was plotted in the PGS phase in Figs. 7 and 8, respectively. In both the PD and XD loading cases, the highest equivalent strain values were localized to the inside corners coincident with the pore long axis (i.e., the PD direction).
Fig. 7.
Equivalent strain εeq in the PGS phase for 10% macroscopic strain E11=10% (i.e., in the PD direction) prescribed on the cell (7.5 h of curing) for ALH (a), square (b) and rectangular (c) unit cells.
Fig. 8.
Equivalent strain εeq in the PGS phase for 10% macroscopic strain E22=10% (i.e., in the XD direction) prescribed on the cell (7.5 h of curing) for ALH (a), square (b) and rectangular (c) unit cells.
3.3. Prediction of strain amplification in the PGS phase
For the two loading directions (Table 2), the ALH scaffold leads to the least global amplification of the equivalent strain. Locally, different regions of the PGS struts forming the ALH scaffold will experience different magnitudes of equivalent strain (Figs. 7(a) and 8(a)). The influence of unit cell geometry can be observed in corresponding plots for square (Figs. 7(b) and 8(b)) and rectangular (Figs. 7(c) and 8(c)) unit cells. In other words, the magnitude of the local equivalent strain amplification (Eq. (11)) varies locally throughout the PGS, and may take the same value at spatially disparate locations. These areas of PGS manifesting the same local equivalent strain amplification can be summed and divided by the total area of PGS to obtain the fraction of PGS at each local equivalent strain amplification magnitude. A histogram depicting the fraction of PGS at each magnitude of local equivalent strain amplification is presented in Fig. 9. The ALH exhibited a relatively broad distribution compared to the square and rectangular honeycombs which exhibited two distinct peaks. The highest local values of amplification were 1.4, 1.6 and 1.7 for the ALH, square and rectangular tessellations, respectively.
Table 2.
Global strain amplification obtained in the case of square, rectangular and ALH tessellations in the PGS for both PD and XD loading directions.
| PGS | ALH | Square | Rectangular |
|---|---|---|---|
| PD | 0.54 | 0.98 | 1.19 |
| XD | 0.34 | - | 0.74 |
Fig. 9.
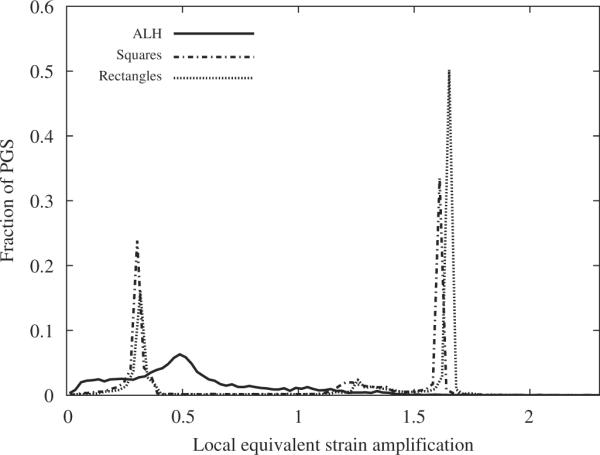
Histogram depicting the fraction of PGS at each magnitude of local equivalent strain amplification for 10% macroscopic strain in the PD direction (7.5 h of curing).
3.4. Prediction of ALH scaffold elastic anisotropy
Fig. 10 illustrates the evolution of the anisotropy ratio r as a function of the ratio w/l. For a null or infinite ratio, the unit cell would be homogeneous (consisting of void or PGS only) and lead to isotropic elastic behavior (r=1). Incidentally, the ALH scaffold was found to have the highest anisotropy ratio r for the published w/l ratio of 0.25 (Fig. 10, dashed line). The FE predicted value of r for the ALH scaffold was close to that measured experimentally (and that of native RV myocardium), and higher than the values predicted for square or rectangular scaffolds (Table 3). Providing an additional measure of scaffold anisotropy, FE predicted value of the Zener coefficient α were 1.6, 17.48 and 48.39 for the ALH, square and rectangular tessellation, respectively.
Fig. 10.
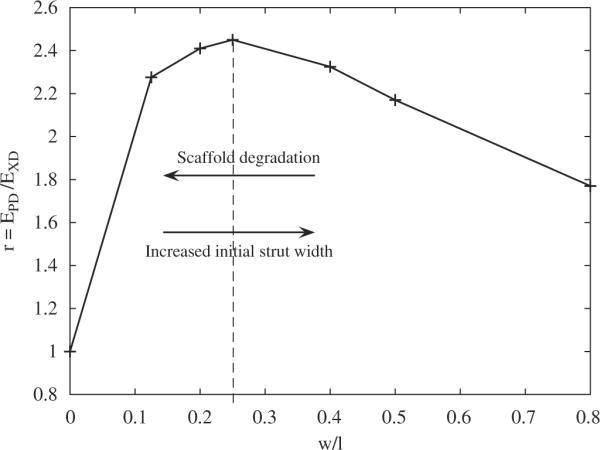
Evolution of the ratio r=EPD/EXD as a function of the ratio of the width over the inside length of the structural element of the ALH unit cell, w/l. The dashed line indicates the maximum anisotropy, which occurred at the ratio w/l=0.25 published in Engelmayr et al. (2008). Conceptually, the two arrows illustrate the possible changes in ALH scaffold anisotropy with changes in initial strut width (i.e., a design parameter) or scaffold degradation.
Table 3.
Anisotropy ratio r obtained for each tessellation: ALH, square and rectangular.
| Native RV myocardium | ALH Exp | ALH FE | Square FE | Rectangular FE | |
|---|---|---|---|---|---|
| r | 2.8 ± 0.5 | 2.7 ± 0.1 | 2.5 | 1.0 | 1.8 |
For comparison, experimental data (mean × s.e.m (n=3)) for the ALH scaffold and native RV myocardium are presented (Engelmayr et al., 2008).
4. Discussion
While native tissue properties often yield an intuitive target, the most appropriate initial scaffold mechanical properties for forming biomimetic tissue engineered cardiac muscle remain unknown. Of note, recent studies by Jacot et al. (2008) and Bhana et al. (2010) reported optimal differentiation of neonatal rat cardiomyocytes on polyacrylamide substrates ranging in stiffness from 10 to 50 kPa. Toward investigating permutations of the ALH scaffold structural–mechanical parameters (e.g., strut width, pore shape), the primary goal of the current study was to develop an accurate FE model of the published ALH scaffold structure (Engelmayr et al., 2008). The advantages of combining FE modeling and microfabrication in scaffold design are particularly highlighted by the work of Hollister (2009). In conjunction with the broadly tunable mechanical properties of PGS and the inherent flexibility of the laser microablation process, the FE model would allow for rapid testing of a variety of feasible ALH microstructures prior to physical fabrication.
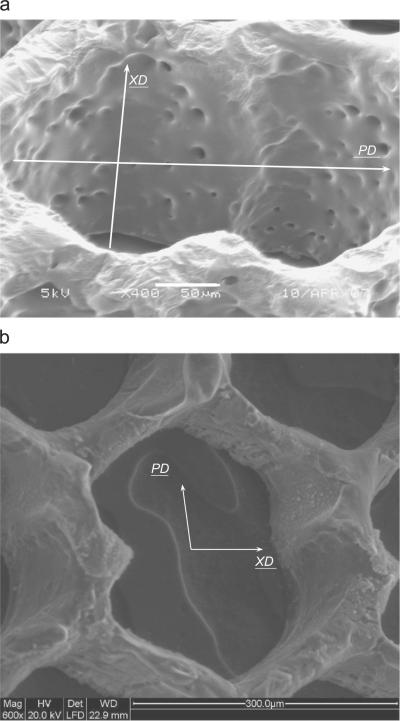
In this paper, the stiffnesses of the ALH scaffold were computed with KUBC prescribed on increasingly larger sized tessellations and compared to the PBC response in order to arrive at an RVE for the two PGS materials (i.e., cured 7.5 and 16h at 160 °C). The RVE, for which the two responses coincided within 2%, contained 90 cells (3.18×4.03mm) (Fig. 5). Hence, the experimental samples subjected to uniaxial testing in Engelmayr et al. (2008) (5mm ≤gage length ≤10mm; width=5mm) were representative mechanically. Comparing the experimental stiffnesses with the computed data (Table 1 and Fig. 6), the current model enabled us to estimate with good accuracy the elastic behavior of the ALH scaffold in the two orthogonal directions for a PGS cured 7.5 h at 160 °C. Regarding ALH scaffolds fabricated from PGS cured 16 h at 160 °C, the significant deviation observed between experiments and FE simulations in the XD loading direction suggests at least two possibilities. One possibility is that one or more of the ALH scaffolds tested in Engelmayr et al. (2008) were not representative, and that testing of additional samples may have yielded a higher mean EXD value. Another possibility is that the current model, under elastic assumptions, does not take into account all the physical phenomena. As observed by SEM (Fig. 11(a)), the 16h/160 °C PGS struts exhibited evidence of microporosity, possibly due to the longer curing time and/or the higher excimer laser burst frequency (500 s−1 versus 25 s−1) and/or burst count (1000 versus 100) used to process the 16h versus 7.5 h (Fig. 11(b)) cured PGS. Simulating the effects of microporosity warrants further investigation and could be explored in future studies via a 3D model of the ALH scaffold.
Fig. 11.
High magnification scanning electron micrograph of a 16 h/160 °C PGS ALH scaffold demonstrating evidence of micropores ((a) unpublished image from studies presented in Engelmayr et al., 2008). Scale bar = 50 μm. For comparison, a representative scanning electron micrograph of a 7.5 h/160 °C PGS ALH scaffold is presented (b). Scale bar = 300 μm.
In order to gain insight into the failure properties of the ALH scaffold, the global and local strain amplifications in the PGS phase were compared to those of the square and rectangular honeycombs (Table 2 and Fig. 9). Notably, the ALH tessellation led to the least global strain amplification (0.54 and 0.34 when loaded in the PD and XD directions, respectively) while the rectangular tessellation had the highest amplification in the associated directions of loading (1.19 and 0.74, respectively). Tentatively, these FE predicted global strain amplifications appear to be inversely correlated with experimentally measured strains-to-failure (unpublished observations from studies presented in Engelmayr et al., 2008). For example, for scaffolds fabricated from 16 h/160 °C PGS and tested dry, the strains-to-failure for ALH scaffolds (n=3) were 0.50±0.05 and 0.81±0.13 when loaded in the PD and XD directions, respectively. By contrast, the associated strains-to-failure for rectangular honeycomb scaffolds (n=3) were 0.39±0.005 and 0.52±0.1, respectively. In future studies, analysis and minimization of strain amplification will be useful in designing honeycomb structures with improved failure properties.
The morbidity and mortality associated with myocardial infarction are often concomitant to pathological remodeling of infarct anisotropy and composition (Holmes et al., 2005; Fomovsky and Holmes, 2010). Of note, Badie and Bursac (2009) recently reported a microfabricated 2D culture system capable of recapitulating variations in cardiac cellular and electrical anisotropy through ventricular cross-sections (i.e., orthogonal to both the circumferential and longitudinal directions of the heart). Based on observations of fibroblast alignment on non-degradable, honeycomb scaffold structures (Engelmayr and Sacks, 2006), it is clear that cellular alignment within 3D pore structures evolves over time. Recognizing that the ALH scaffold material of construction, PGS, degrades over time by surface hydrolysis (Wang et al., 2003; Pomerantseva et al., 2008), it is clear that the diminished effective stiffness and anisotropy observed in Engelmayr et al. (2008) for ALH scaffolds following 1 week heart cell culture (i.e., EPD = 0.032±0.002 MPa, EXD = 0.019±0.004 MPa; r=1.9±0.3) must have been due to the combined effects of scaffold degradation and the formation and alignment of cells and tissue. Importantly, FE predictins suggest that the time evolution of tissue engineered cardiac muscle anisotropy could be optimized by the choice of initial strut width (Fig. 10). In particular, in combination with exogenous biochemical (Cheng et al., 2007) or biophysical (Boublik et al., 2005; Tandon et al., 2009) stimuli capable of promoting tissue maturation, the decrease in ALH scaffold anisotropy with degradation could theoretically be offset by a commensurate increase in tissue anisotropy within the ALH pores.
5. Conclusion and prospects
Toward optimizing PGS scaffold microstructures for cardiac muscle tissue engineering applications, in the current study a FE model was developed to retrospectively predict the anisotropic effective stiffnesses of the ALH PGS scaffold presented in Engelmayr et al. (2008). The FE model will be useful in designing future ALH scaffolds that simultaneously provide proper cardiac anisotropy and reduced stiffness to enhance heart cell-mediated contractility. In addition, the FE model developed herein is amenable to simulating the evolution of cardiac muscle tissue formation within the ALH pores. Thus, future studies will aim to integrate cell and ECM orientation data into the model such as to predict the mechanical behavior of the composite engineered tissue, as well as the transfer of macroscale stresses and strains into the developing tissue at the microscale.
Acknowledgments
Funding for this work was provided by National Institutes of Health (NIH) Grant 1-R01-HL086521-01A2 (PI Lisa E. Freed, Subaward PI GCE). This funding was made possible by the American Recovery and Reinvestment Act. The authors gratefully acknowledge Dr. Lisa E. Freed (The Charles Stark Draper Laboratories and Massachusetts Institute of Technology, Cambridge, MA) for providing experimental data and for helpful discussions in preparing the manuscript. The authors also gratefully acknowledge Dr. Lorna J. Gibson (Massachusetts Institute of Technology) for helpful discussions regarding the modeling of honeycomb structures and Dr. Ted Sussman (Adina R&D, Inc, Watertown, MA) for critically reviewing the manuscript.
Footnotes
Conflict of interest statement The authors have no conflicts of interest to disclose.
References
- Badie N, Bursac N. Novel micropatterned cardiac cell cultures with realistic ventricular microstructure. Biophysical Journal. 2009;96(9):3873–3885. doi: 10.1016/j.bpj.2009.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbe F, Decker L, Jeulin D, Cailletaud G. Intergranular and intragranular behavior of polycrystalline aggregates. Part 1: F.E. model. International Journal of Plasticity. 2001a;17(4):513–536. [Google Scholar]
- Barbe F, Forest S, Cailletaud G. Intergranular and intragranular behavior of polycrystalline aggregates. Part 2: results. International Journal of Plasticity. 2001b;17(4):537–563. [Google Scholar]
- Bhana B, Lyer RK, Chen WL, Zhao R, Likhitpanichkul M, Simmons CA, Radisic M. Influence of substrate stiffness on the phenotype of the heart cells. Biotechnology and Bioengineering. 2010;105(6):1148–1160. doi: 10.1002/bit.22647. [DOI] [PubMed] [Google Scholar]
- Boublik J, Park H, Radisic M, Tognana E, Chen F, Pei M, Vunjak-Novakovic G, Freed LE. Mechanical properties and remodeling of hybrid cardiac constructs made from heart cells, fibrin, and biodegradable, elastomeric knitted fabric. Tissue Engineering. 2005;11(7/8):1122–1132. doi: 10.1089/ten.2005.11.1122. [DOI] [PubMed] [Google Scholar]
- Cheng M, Park H, Engelmayr GC, Jr., Moretti M, Freed LE. Effects of regulatory factors on engineered cardiac tissue in vitro. Tissue Engineering. 2007;13(11):2709–2719. doi: 10.1089/ten.2006.0414. [DOI] [PubMed] [Google Scholar]
- Diard O, Leclercq S, Rousselier G, Cailletaud G. Evaluation of finite element based analysis of 3D multicrystalline aggregates plasticity. Application to crystal plasticity model identification and the study of stress and strain fields near grain boundaries. International Journal of Plasticity. 2005;21(4):691–722. [Google Scholar]
- Engelmayr GC, Jr., Cheng MY, Bettinger CJ, Borenstein JT, Langer R, Freed LE. Accordion-like honeycombs for tissue engineering of cardiac anisotropy. Nature Materials. 2008;7(12):1003–1010. doi: 10.1038/nmat2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engelmayr GC, Jr., Sacks MS. A structural model for the flexural mechanics of nonwoven tissue engineering scaffolds. Journal of Biomechanical Engineering. 2006;128(4):610–622. doi: 10.1115/1.2205371. [DOI] [PubMed] [Google Scholar]
- Eschenhagen T, Zimmermann WH. Engineering myocardial tissue. Circulation Research. 2005;97(12):1220–1231. doi: 10.1161/01.RES.0000196562.73231.7d. [DOI] [PubMed] [Google Scholar]
- Fidkowski C, Kaazempur-Mofrad MR, Borenstein J, Vacanti JP, Langer R, Wang Y. Endothelialized microvasculature based on a biodegradable elastomer. Tissue Engineering. 2005;11(1/2):302–309. doi: 10.1089/ten.2005.11.302. [DOI] [PubMed] [Google Scholar]
- Fomovsky GM, Holmes JW. Evolution of scar structure, mechanics, and ventricular function after myocardial infarction in the rat. American Journal of Physiology—Heart and Circulatory Physiology. 2010:H221–H228. doi: 10.1152/ajpheart.00495.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freed LE, Engelmayr GC, Jr., Borenstein JT, Moutos FT, Guilak F. Advanced Material Strategies for Tissue Engineering Scaffolds. Advanced Materials. 2009;21(32–33):3410–3418. doi: 10.1002/adma.200900303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerard C, N'Guyen F, Osipov N, Cailletaud G, Bornert M, Caldemaison D. Comparison of experimental results and finite element simulation of strain localization scheme under cyclic loading. Computational Materials Science. 2009;46(3):755–760. [Google Scholar]
- Gibson LJ, Ashby MF, Schajer GS, Robertson CI. The mechanics of two-dimensional cellular materials. Proceedings of the Royal Society A. 1982;382(1782):25–42. [Google Scholar]
- Hollister SJ. Scaffold design and manufacturing: from concept to clinic. Advanced Materials. 2009;21(32–33):3330–3342. doi: 10.1002/adma.200802977. [DOI] [PubMed] [Google Scholar]
- Holmes JW, Borg TK, Covell JW. Structure and mechanics of healing myocardial infarcts. Annual Review of Biomedical Engineering. 2005;7:223–253. doi: 10.1146/annurev.bioeng.7.060804.100453. [DOI] [PubMed] [Google Scholar]
- Jacot JG, McCulloch AD, Omens JH. Substrate stiffness affects the functional maturation of neonatal rat ventricular myocytes. Biophysical Journal. 2008;95(7):3479–3487. doi: 10.1529/biophysj.107.124545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanit T, N'Guyen F, Forest S, Jeulin D, Reed M, Singleton S. Apparent and effective physical properties of heterogeneous materials: representativity of samples of two materials from food industry. Computer Methods in Applied Mechanics and Engineering. 2006;195(33–36):3960–3982. [Google Scholar]
- Kemppainen JM, Hollister SJ. Tailoring the mechanical properties of 3D-designed poly(glycerol sebacate) scaffolds for cartilage applications. Journal of Biomedical Materials Research A. 2010;94(1):9–18. doi: 10.1002/jbm.a.32653. [DOI] [PubMed] [Google Scholar]
- Madi K, Forest S, Boussuge M, Galliègue S, Lataste E, Buffière J-Y, Bernard D, Jeulin D. Finite element simulations of the deformation of fused-cast refractories based on X-ray computed tomography. Computational Materials Science. 2007;39(1):224–229. [Google Scholar]
- Mines-ParisTech Zset. Mines ParisTech, ONERA, NWNumerics. 2003 <http://zebulon.onera.fr/English/index.html>.
- Musienko A, Tatschl A, Schmidegg K, Kolednik O, Pippan R, Cailletaud G. Three-dimensional finite element simulation of a polycrystalline copper specimen. Acta Materiala. 2007;55(12):4121–4136. [Google Scholar]
- Osipov N, Gourgues-Lorenzon AF, Marini B, Mounoury V, N'Guyen F, Cailletaud G. FE modelling of bainitic steels using crystal plasticity. Philosophical magazine. 2008;88(30–32):3757–3777. [Google Scholar]
- Ott HC, Matthiesen TS, Goh SK, Black LD, Kren SM, Netoff TI, Taylor DA. Perfusion-decellularized matrix: using nature's platform to engineer a bioartificial heart. Nature Medicine. 2008;14(2):213–221. doi: 10.1038/nm1684. [DOI] [PubMed] [Google Scholar]
- Pomerantseva I, Krebs N, Hart A, Neville CM, Huang AY, Sundback CA. Degradation behavior of poly(glycerol sebacate) Journal of Biomedical Materials Research A. 2008;91A(4):1038–1047. doi: 10.1002/jbm.a.32327. [DOI] [PubMed] [Google Scholar]
- Sab K. On the homogenization and the simulation of random materials. European Journal of Mechanics and Solids. 1992;11(5):585–607. [Google Scholar]
- Tandon N, Cannizzaro C, Chao P, Marsano A, Au H, Radisic M, Vunjak-Novakovitch G. Electrical stimulation systems for cardiac tissue engineering. Nature Protocol. 2009;4(2):155–173. doi: 10.1038/nprot.2008.183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vunjak-Novakovic G, Tandon N, Godier A, Maidhof R, Marsano A, Martens TP, Radisic M. Challenges in cardiac tissue engineering. Tissue Engineering B Review. 2009 doi: 10.1089/ten.teb.2009.0352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Ameer GA, Sheppard BJ, Langer R. A tough biodegradable elastomer. Nature Biotechnology. 2002;20(6):602–606. doi: 10.1038/nbt0602-602. [DOI] [PubMed] [Google Scholar]
- Wang Y, Kim YM, Langer R. In vivo degradation characteristics of poly (glycerol sebacate) Journal of Biomedical Materials Research A. 2003;66(1):192–197. doi: 10.1002/jbm.a.10534. [DOI] [PubMed] [Google Scholar]
- Yeong WY, Sudarmadji N, Yu HY, Chua CK, Leong KF, Venkatraman SS, Boey YC, Tan LP. Porous polycaprolactone scaffold for cardiac tissue engineering fabricated by selective laser sintering. Acta Biomateriala. 2009:713–724. doi: 10.1016/j.actbio.2009.12.033. [DOI] [PubMed] [Google Scholar]
- Zeghadi A, Forest S, Gourgues AF, Bouaziz O. Ensemble averaging stress-strain fields in polycrystalline aggregates with a constrained surface microstructure—part 2: crystal plasticity. Philosophical Magazine. 2007;87(8–9):1425–1446. [Google Scholar]
- Zener C. Elasticity and Anelasticity of Metals. University of Chicago Press; 1948. Chapter II; p. 16. [Google Scholar]