Demographic Processes Underlying Subtle Patterns of Population Structure in the Scalloped Hammerhead Shark, Sphyrna lewini

Holly A Nance; Peter Klimley; Felipe Galván-Magaña; Jimmy Martínez-Ortíz; Peter B Marko

doi:10.1371/journal.pone.0021459

. 2011 Jul 14;6(7):e21459. doi: 10.1371/journal.pone.0021459

Demographic Processes Underlying Subtle Patterns of Population Structure in the Scalloped Hammerhead Shark, Sphyrna lewini

Holly A Nance ^1,^*, Peter Klimley ², Felipe Galván-Magaña ³, Jimmy Martínez-Ortíz ⁴, Peter B Marko ¹

Editor: Sharyn Jane Goldstien⁵

PMCID: PMC3137562 PMID: 21789171

Abstract

Genetic diversity (θ), effective population size (N_e), and contemporary levels of gene flow are important parameters to estimate for species of conservation concern, such as the globally endangered scalloped hammerhead shark, Sphyrna lewini. Therefore, we have reconstructed the demographic history of S. lewini across its Eastern Pacific (EP) range by applying classical and coalescent population genetic methods to a combination of 15 microsatellite loci and mtDNA control region sequences. In addition to significant population genetic structure and isolation-by-distance among seven coastal sites between central Mexico and Ecuador, the analyses revealed that all populations have experienced a bottleneck and that all current values of θ are at least an order of magnitude smaller than ancestral θ, indicating large decreases in N_e (θ = 4N_eμ), where μ is the mutation rate. Application of the isolation-with-migration (IM) model showed modest but significant genetic connectivity between most sampled sites (point estimates of Nm = 0.1–16.7), with divergence times (t) among all populations significantly greater than zero. Using a conservative (i.e., slow) fossil-based taxon-specific phylogenetic calibration for mtDNA mutation rates, posterior probability distributions (PPDs) for the onset of the decline in N_e predate modern fishing in this region. The cause of decline over the last several thousand years is unknown but is highly atypical as a post-glacial demographic history. Regardless of the cause, our data and analyses suggest that S. lewini was far more abundant throughout the EP in the past than at present.

Introduction

Modern fishing practices have led to declines in numerous marine species [1]–[3], with long-lived fish and mammals particularly susceptible to over-harvesting [4], [5]. Among the most affected and ecologically important species are sharks [6], [7], which sit atop marine food webs, providing significant top-down control over many other pelagic and benthic marine species [8]. Due to declines in other fin-fishes and the high demand for shark fins [9], [10], sharks are among the most sought-after harvested marine species. At the same time, however, sharks (particularly large sharks), remain highly enigmatic, with relatively little known about their population structure, life-histories, and recent demographic histories in comparison to analogous apex predators on land, but see [11].

Mark-and-recapture studies have figured prominently in estimating long-range movements, behaviors, and survival in sharks [12]. In many cases, genetic data have been collected from threatened or declining marine species [13], [14] with the idea that those data will provide information about important demographic parameters and processes relevant to conservation, like genetic diversity (θ), effective population size (N_e), and interpopulation connectivity [15]. For the 11 largest or “great” species of sharks, population genetic data are particularly limited, with the majority having been collected over large geographic scales with an analytical focus on global phylogeography and delineation of evolutionary distinct units (ESUs) for conservation [16]–[20]. We have therefore used a combination of classical and coalescent population genetic methods to reconstruct the regional demographic history of the IUCN globally endangered scalloped hammerhead shark, Sphyrna lewini, across its Eastern Pacific (EP) range. S. lewini is a large, highly-mobile circumtropical marine predator found along continental margins and oceanic islands [21] that forms large and conspicuous aggregations, particularly in the tropical EP [22]–[24]. This shark is caught both intentionally and as by-catch throughout its range [7] and Western North Atlantic stocks alone have experienced an estimated 83% reduction between 1981 and 2005 [25]. Previous genetic work on S. lewini has yielded estimates of population structure, female effective population size (N_ef) and gene flow that vary widely among different regions across the globe [17], [26], [27]. Although some of this variability could be real, contrasting patterns among recent studies could also reflect a combination of significant differences in the spatial scale of analysis, large differences in sample sizes (of individuals), and the predominant use of only a single (mtDNA) locus.

To reconstruct the demographic history of S. lewini, detect changes in N_e, and estimate levels of contemporary gene flow, we have used a combination of mtDNA sequences and 15 microsatellite loci. Currently, only the isolation-with-migration (IM) class of models [28]–[31] lacks the assumption that gene flow and genetic drift are in an evolutionary equilibrium, and have therefore become valuable tools for disentangling the effects of ancestral polymorphism and contemporary gene flow in a statistically robust way. These analytical methods allowed us to consider patterns of genetic differentiation from a temporal perspective and delineate current populations for our estimates of N_e, as well as estimate change in N_e over time to help interpret levels of genetic diversity. Low diversity has been found in several species of sharks [32]–[35] and therefore may be common in this group, or alternatively, could be the result of population decline.

Methods

Ethics Statement

No ethical or institutional approval was required for the field-based zoological and genetical research described in this paper. No live specimens were obtained or used.

Sampling, DNA extraction, sequencing, and genotyping procedures

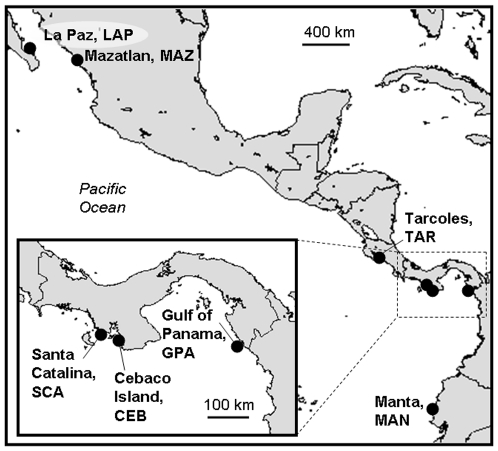
We collected 221 tissue samples from artisanal fishers at six Eastern Pacific sites between 2007 and 2008 (Fig. 1, Table S1, Table S2). With the exception of Manta, Ecuador, all samples came from sharks caught in close proximity to the fish camps where they were collected (<40 km from shore [36]); samples collected in Manta were caught farther off shore, between mainland Ecuador and the Galapagos Islands. This likely explains why Manta was the only sample with adults; all other samples were comprised of 1–3 year old juveniles. Samples were stored in 90% ethanol and genomic DNA was isolated with proteinase K tissue digestion in 2× CTAB, followed by two chloroform∶isoamyl alcohol (24∶1) extractions and precipitation with ethanol. DNA was dried, re-suspended in 50 µL water, and frozen.

Sample localities and their associated abbreviations indicated by black dots. The three Panamanian sites are enlarged due to their close proximity to one another.

We amplified and scored 15 microsatellite loci from all 221 individuals. Thirteen were developed for S. lewini [37] and two (Cli-12 and Cli-100) for the blacktip shark [38]. All PCR reactions [37] were conducted using a DNA Engine DYAD Peltier Thermal Cycler (MJ Research, Inc.) and visualized on an ABI 3130 (Applied Biosystems, Inc.) sequencer. We scored individual genotypes with GeneMapper v. 3.7 (Applied Biosystems, Inc.).

We also sequenced a 548 bp fragment of the mtDNA control region from 126 individuals with the Pro-L and SLcr-H primers [17] using the following cycling temperature profile: 95°C for 4 minutes, 40 cycles of 95°C for 1 minute, 57°C for 1 minute, slow ramp (1°C/s) to 72°C for 1 minute, 30 seconds, followed by an extension at 72°C for 10 minutes. Each reaction contained 1× GoTaq buffer, 0.16 µM Pro-L primer, 0.16 µM SLcr-H primer, 0.1% Triton X-100, 1.25 mM dNTPs, 0.7 U GoTaq polymerase (Promega), and 0.5 µl genomic DNA, in a total volume of 25 µl. Because all of the informative sites were at one end of the fragment [17], we only sequenced with the Pro-L primer. However, any chromatograms with ambiguous base calls were also sequenced in the opposite direction with the SLcr-H primer. Sequences were visualized on an ABI 3130 sequencer, chromatograms edited with Sequencher v.4.2.2 (Gene Codes Corp.), aligned using CLUSTAL-X v.1.81 [39], and checked by eye.

Microsatellite and MtDNA diversity

Microsatellite loci were checked for evidence of nulls using MICRO-CHECKER v. 2.2.3 [40], tested for linkage disequilibrium and deviations from Hardy-Weinberg equilibrium (HWE) with ARLEQUIN v. 3.11 [41], and effective numbers of alleles (A_E) per sample were calculated in Genalex [42]. For the mtDNA, we calculated Fu's F_s [43] in ARLEQUIN, and Fu and Li's D* [44] in DNAsp v. 4.90 [45] using 10,000 simulations (conditional on θ).

Kinship Analyses

Because of the high number of juveniles, we estimated relatedness among individuals within samples using COLONY2 [46], which searches for the maximum likelihood configuration of sibship assignments for all individuals in a sample based on microsatellite genotypes. We then calculated the percentage of half- or full-sibling pairings with ≥95% probability. Low haplotype diversity prohibited the identification of maternal siblings based on mtDNA. Because COLONY2 will overestimate the proportion of siblings when sample sizes are small with respect to the total population [47], [48], as a control comparison, we also estimated the proportion of half- and full-siblings among the combined La Paz and Tarcoles samples. These two nurseries are separated by over 3000 km of coastline, so we expected sibling pairs between these two sites to be much less frequent than within an individual site if sibship estimates within each sample were meaningful.

Genetic structure

For the microsatellites, we estimated F_ST and R_ST among sites with a locus-by-locus Analysis of Molecular Variance (AMOVA) in ARLEQUIN. Confidence intervals for F_ST were generated by bootstrapping over loci (20,000 replicates). For the mtDNA, we created a haplotype network with statistical parsimony in TCS v.1.21 [49], [50]. We then used MODELTEST v. 3.8 [51] to identify the best-fitting substitution model [HKY model selected over HKY+G (LLR = 2.62, P = 0.05) and HKY+I (LLR = 5.08, P = 0.01)]. We then estimated F_ST and Φ_ST, the latter with an AMOVA using the best-fitting model available in ARLEQUIN [52].

Although population differentiation was low, we also used STRUCTURE v. 2.3.3 [53] to infer the number of discrete populations. We set K = 1–20 for each run, assuming prior population information and an admixture model allowing for mixed ancestry of individuals [54]. Each run was repeated three times with independent allele frequencies, 100,000 steps, and a burn-in of 10,000 steps.

Demographic analyses

We used several different methods to investigate past changes in N_e, utilizing approaches that employ different assumptions and different combinations of the nuclear and cytoplasmic markers. First, we conducted mtDNA mismatch analyses in ARLEQUIN under a model of sudden demographic expansion. To determine how well the sudden expansion model fit our data, we calculated Harpending's raggedness index, r [55] and assessed the significance of r with 1000 parametric bootstrap replicates. For samples not deviating significantly from the expansion model, we then estimated the time since the start of expansion using the formula τ = 2 µt, where t is the number of years since expansion and μ is the per locus, per year mutation rate. Confidence intervals for τ were estimated with 1000 parametric bootstrap replicates.

We then calculated the M-ratio statistic with the software M_P_val [56] to test for evidence of a recent population bottleneck in each sample of microsatellites. The empirical value of M was compared to a simulated equilibrium distribution based on the two-phase model of microsatellite mutation. This simulated critical value (M_C) was calculated with 10,000 replicates in critical_M [56]. We analyzed our data using two different values for p_s, the percentage of mutations that follow the single-step mutation model, and Δ_g, the mean size of larger mutations; p_s = 0.88 and Δ_g = 2.8, and then more conservative values p_s = 0.90 and Δ_g = 3.5 [56]. Because empirical values of M were equal for both, we only showed M-ratios calculated for the latter p_s and Δ_g values.

To test for significance of the M-ratios, we used a range of values for pre-bottleneck θ = 4N_eμ (0.01, 0.1, 1.0, 10.0), yielding pre-bottleneck N_e of 250, 2500, 25,000, and 250,000, respectively. To calculate θ for these tests, we chose a microsatellite mutation rate (μ) of 1×10⁻⁵, which is the slower end of the range estimated in mammals [57]–[60], since mitochondrial and nuclear markers mutate roughly an order of magnitude slower in sharks than in mammals [61], [62]. We used values of p_s = 0.90 and Δ_g = 3.5 to calculate M_C [56]. Because outlier alleles and violations to the single-step mutation (SSM) model can bias values of M [56], we ran all tests with the full data set, and then re-ran tests after removing outlier alleles (those at the ends of the size range that were separated by more than 10 bp from the next allele) and loci that had at least one allele not conforming to a di-nucleotide repeat pattern.

We also tested for evidence of a recent reduction in N_e in the microsatellite dataset with BOTTLENECK [63] using the Wilcoxon sign-rank test under the infinite alleles model (IAM), the two-phase model (TPM), and the single-step model (SSM), given that all of the loci we developed had point mutations and therefore did not conform to the strict SSM. Changes in N_e were also estimated with MSVAR v. 1.3 [64], which applies MCMC simulations of the mutation-coalescent history to present day genotypes in a sample by characterizing the posterior distribution of the parameters N₀ (current population size), N₁ (ancestral population size), μ (mean mutation rate of all loci), and t (time since population size change) for each population (GPA was too small for this analysis). We varied priors for each locus for N₀, N₁, μ, and t, [64]. We chose a range of microsatellite mutation rates (μ), as recommended by the authors [64], between 1.0×10⁻⁵ and 2.0×10⁻⁴, given that, 1) the estimated microsatellite μ is 1.5×10⁻⁴ in zebra fish [65] and 5.56×10⁻⁴ in the common carp [66], and 2) the range of μ in mammals is 10⁻⁵ to 10⁻² [67] and both mtDNA and nuclear markers mutate roughly an order of magnitude slower in sharks than in mammals [61], [62]. Prior values were updated throughout the analysis, and modeled with an exponential change in population size. Each run was 200 million steps, with a burn-in of 10,000 steps and output every 10,000 steps. We used TRACER v. 1.4.1 [68] to graph posterior distributions of N₀, N₁, μ, and t, and to calculate the 95% mean probability densities of each parameter.

Although age at first reproduction (roughly 15 years in S. lewini [53], [54]) is typically used as a proxy for generation time [17], coalescent estimates of N_e require an estimate of G, the average age of breeding adults [69]. To estimate G, we used a method [69] requiring life history data, and since none exists for EP populations, we used survival rates for S. lewini in the East Atlantic [70]. For age specific reproductive rates, we used 15 years as the age of first reproduction [71], [72], and a mean litter size of 23 pups, which remains relatively constant throughout adulthood (Nguyen and Piercy unpub. data). From these data, we calculated l_i (age-specific survival rates), b_i (birth rates), and p_i (probability of a gene being inherited from a parent of age i), for all age classes, I [69], and then used these data to calculate G (Table S3). We used MATLAB v. 2007a on a Windows XP operating system to calculate mean generation time (G) based on the equation of Felsenstein [73].

Population divergence times and migration rates

We estimated genetic diversities (θ₁, θ₂, and ancestral θ_A), migration rates (m₁ and m₂), and time since population divergence (t) for all pairs of samples using the program IMa [29] on the CBSU computing clusters at Cornell University. The “isolation with migration” model in IMa does not assume gene flow and genetic drift are in equilibrium, making it most appropriate for recently diverged populations that share haplotypes and alleles due to both gene flow and ancestral polymorphism. Although IMa2 [74] can handle multiple populations at once, we analyzed all possible pairs of populations separately in IMa because IMa2 requires a well-supported phylogeny of the groups of individuals being analyzed [74].

We started with analyses in “MCMC Mode” (M-Mode) using the full complement of model parameters (i.e., θ₁≠θ₂≠θ_A, and m₁≠m₂), with broad priors for all, reducing them in repeated runs to more densely sample the posterior distribution. Once several replicates converged on the same answer, we used the saved genealogies from three separate M-Mode runs in a new analysis using the nested models option in “Load Trees Mode” (L-Mode) to determine if the fully parameterized IMa model was a significantly better fit to the data than a series of simpler models with fewer parameters, based on log-likelihood ratio tests [29]. We converted migration parameters m₁ and m₂ into the number of migrants per generation (Nm) using the equation Nm = (θ m)/4.

To convert divergence times from IMa scaled by mutation (t/μ) into units of years, μ of at least one locus must be known. Given that microsatellite mutation rates are unknown for sharks and can vary by an order of magnitude within individual species [75], we used only mtDNA substitution rates calculated specifically for hammerhead sharks (below) and allowed IMa to infer separate rate scalars for the microsatellite loci [76]. To estimate the substitution rate of mtDNA control region, we built a phylogeny for all eight sphyrnid species using BEAST v. 1.5.4 [77] based on previously published [78] nuclear (ITS2, Dlx1, and Dlx2) and mitochondrial (NADHd2, D-loop, Cyt-b, and CO1) genes. Using Carcharhinus acronotus as the outgroup [78], we chose lognormal priors for a 40.4 (+/−1.05) million years (my) divergence time between Carcharhinus and Sphyrnidae [79], and a 21.5 (+/−1.05) my divergence time for species within Sphyrnidae (based on the first sphyrnid in the fossil record [79]) to calibrate the substitution rate for each gene. Five runs, totaling 225 million MCMC steps resulted in a divergence rate of 1.21% per million years (my) for Sphyrnidae D-loop, corresponding to a mutation rate of 6.03×10⁻⁹ substitutions per site per year. This is only slightly faster than a divergence rate of 0.8% per my, which was based on the assumption that Western Atlantic and Eastern Pacific populations of S. lewini separated three million years ago by the Isthmus of Panama [17].

Results

Microsatellite and mtDNA diversity

Average observed and expected heterozygosity across all loci and populations were 0.770 and 0.792, respectively (Table S1), and across all loci in all populations, the number of effective alleles (A_E) was distinctly less than the total number of alleles (Table S1). After Bonferroni correction of alpha [80], four loci deviated significantly from HWE in one or two populations (Table S1). Two loci (Cli-12 and Cli-100) were in linkage disequilibrium in two of seven samples. Micro-Checker showed five loci had no nulls in any of the samples, and ten had potential nulls in one or two samples.

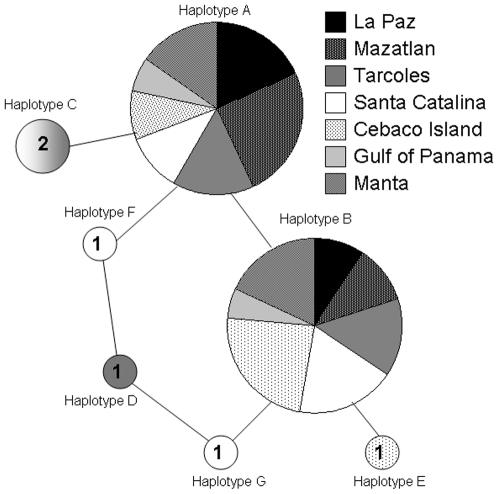
As with previous analyses of mtDNA in the Pacific, we found low levels of diversity in the EP: seven mtDNA control region haplotypes that differed by a maximum of two base pair changes. Haplotypes A and B were common to all locations, C and D were found in one to two locations, respectively (Fig. 2). D and E were novel to this study (GenBank accession numbers HQ916311 and HQ916312, respectively). Fu's F_s was positive for each sample, though none were significant (Table S2). Fu and Li's D* was negative for three samples: TAR, SCA and CEB, though none were significant (Table S2).

Haplotypes A and B are common to all populations. Haplotype C is shared by TAR and SCA (hence, the two shades), haplotypes D and E are unique to TAR and CEB, respectively, and haplotypes F and G are unique to SCA. Numbers inside haplotypes C through G indicate the number of haplotypes present in our sampled individuals.

Relatedness

We estimated that only 3.7% of individuals per sample were members of a full-sibling pair. Half-sibs were more frequent, with a mean of 59.2% of individuals being half-sibs. However, when we estimated sibship in the La Paz and Tarcoles samples combined (two sites separated by more than 3000 km), we found similar proportions of siblings: 7.8% and 59.4% for full- and half-sib pairs, respectively, suggesting our sample sizes are too small to recover meaningful estimates of kin. All proportions of siblings reported were recovered with a likelihood >95%.

Genetic structure

For the microsatellites, all R_ST estimates were insignificant (not shown), but the global estimate of F_ST was highly statistically significant (F_ST = 0.005, P<0.001; see Table 1). Pairwise estimates of F_ST (ranging from 0.015 – 0.002; Table 2) were also significant for most comparisons. Correlation between geographic distance and genetic differentiation was marginally insignificant for F_ST (r = 0.302, P = 0.063) and marginally significant for R_ST (r = 0.422, P = 0.032).

Table 1. AMOVA results for all sites, characterizing spatial structure with both mtDNA (Φ_ST) and microsatellites (F_ST).

Marker	Source of variation	d.f.	SS	Variance components	Φ_ST/F_ST
mtDNA	among pops	6	2.746	Va 0.009	0.031
	within	119	34.57	Vb 0.291
msats	among pops	6	43.293	Va 0.024	0.005^*
	within	599	3147.3	Vb 5.254

Open in a new tab

*indicates significant at α = 0.05.

Table 2. Pairwise locus-by-locus AMOVA results characterizing structure based on microsatellites (F_ST) between all Eastern Pacific sites.

	LAP	MAZ	TAR	SCA	CEB	GPA	MAN
LAP	*
MAZ	0.000	*
TAR	0.010	0.007	*
SCA	0.005	0.005	0.007	*
CEB	0.015	0.012	0.013	0.011	*
GPA	0.012	0.014	0.009	0.005	0.000	*
MAN	0.006	0.004	0.009	0.002	0.007	0.009	*

Open in a new tab

Values significant at α = 0.05 are indicated in bold.

For the mtDNA sequences, neither F_ST nor Φ_ST across all sites were statistically significant (only Φ_ST values shown in Table 1) and no pairwise F_ST estimates were significant. However, pairwise estimates of Φ_ST were significant between one central Panama sample (SCA) and both Mexico samples (SCA-LAP Φ_ST = 0.17, P = 0.03 and SCA-MAZ Φ_ST = 0.21, P = 0.01). The Mantel test showed a marginally significant correlation between Φ_ST and geographic distance (r = 0.523, P = 0.039), though no correlation was detected with the frequencies of haplotypes (F_ST).

STRUCTURE showed that K = 1 had the highest probability, indicating no differentiation among samples (plots of assignment for K = 1 to 20 showed no evidence of subdivision, not shown). With such low F_ST estimates, however, STRUCTURE v. 2.3.3 is not expected to be informative [53].

Demographic analyses

MtDNA mismatch distributions showed evidence of relatively ancient demographic expansions across all populations (Table 3): the model of sudden demographic expansion was only rejected for MAN. For all populations, the modal number of nucleotide differences between haplotypes peaked between zero and one (graphs not shown), indicating relatively recent expansions. After conversion with the mtDNA substitution rate from BEAST, point estimates of time since expansion among all populations (excluding MAN) were between 90,606 and 136,061 years ago (Table 3).

Table 3. Mismatch distribution results.

Sample	Coordinates	τ	90% CI	r	t (years)	90% CI t (years)
LAP	N 24.20, W 110.40	0.641	0.042–1.277	0.208	97,121	6364–193,485
MAZ	N 23.20, W 106.40	0.598	0.105–1.191	0.201	90,606	15,909–180,455
TAR	N 9.80, W 84.80	0.898	0.336–1.617	0.140	136,061	50,909–245,000
SCA	N 7.56, W 81.30	0.867	0.375–1.578	0.149	131,364	56,818–239,091
CEB	N 7.55, W 81.00	0.812	0.281–1.559	0.201	123,030	42,576–236,212
GPA	N 7.01, W 78.19	0.898	0–22.75	0.347	136,061	0–3,446,970
MAN	S 1.10, 84.95	0.814^†	0.313–1.414	0.280	NA	NA

Open in a new tab

†indicates significance at α = 0.05.

Tau (τ) and 90% confidence intervals of simulations under the model of sudden expansion for each population are shown. Harpending's raggedness index (r), time since population expansion in years (t), and associated 90% confidence intervals are shown for all populations where the sudden expansion hypothesis could not be rejected. Time since expansion (t) was estimated using the fossil-calibrated substitution rate (6.03×10⁻⁹ subs/yr). Site abbreviations correspond to locations in Figure 1.

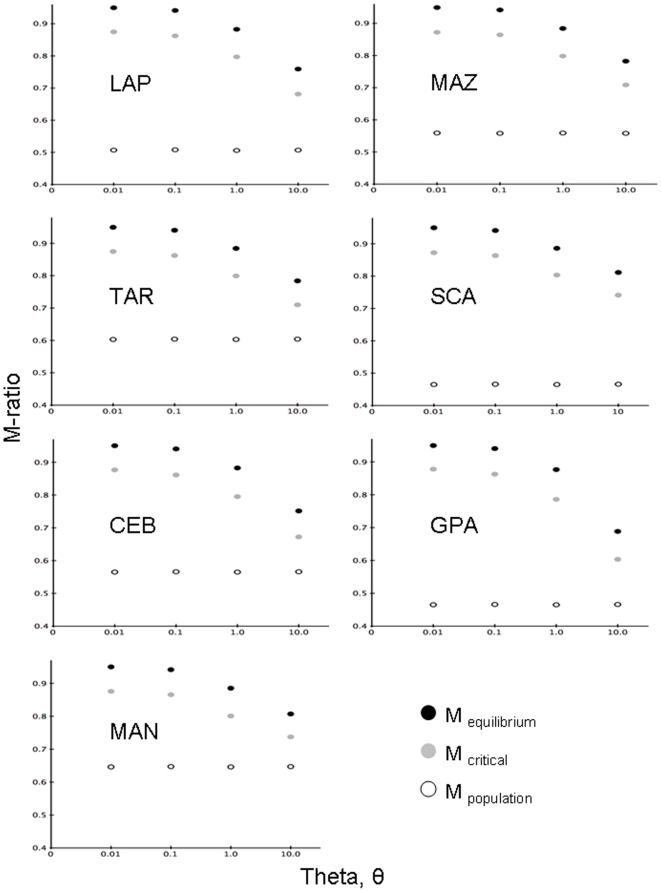
Using the full microsatellite data set, the M-ratio for each population was lower than the simulated critical M_C value for each value of θ (Fig. 3) providing evidence of recent population declines. Removal of outlier alleles and loci not conforming to the di-nucleotide repeat pattern (see Methods), resulted in only the Manta population lacking evidence of decline, and only when tested with a pre-bottleneck value of θ = 10 (M_MAN = 0.845). Results from BOTTLENECK depended on the model of microsatellite mutation: under the IAM model alone, the results showed a significant excess in gene diversity, and therefore a recent bottleneck, for all populations (p-value for one-tail test<0.05), except Cebaco Island (CEB) and Manta (MAN).

The population-specific M ratio (open circles), average M from simulations assuming each population is in drift-mutation equilibrium (black circles), and critical M_c based on these simulations (gray circles) are shown. M values below M_c indicate a population has undergone a recent bottleneck. All data shown here were calculated with a proportion of single step mutations (p_s) of 0.90 and an average size of mutations evolving more than one repeat unit (Δ_g) of 3.5. All M values were calculated with θ = 0.01, 0.1, 1.0, and 10.0, corresponding to N_e = 1445, 14,451, 144,509, and 1,445,087, respectively.

MSVAR also showed population declines, showing that current N_e at each sample site was at least two orders of magnitude smaller than historic N_e, with point estimates of the onset of decline ranging between 3600 and 12,000 years ago (Table 4). Results from IMa (below) also showed that current θ is smaller than ancestral θ_A by 1–3 orders of magnitude (Table 5, 6). Although 95% posterior probability densities (PPDs) of these estimates were wide, both coalescent methods show significant decline, with no overlap between most (23 of 30 from IMa and 3 of 6 from MSVAR) 95% PPDs of current and ancestral N_e.

Table 4. Results from MSVAR (Beaumont 1999) analyses using only microsatellite data.

Population	N_e0	N_e1	t (in years)
LAP	435.51	39,627.80	8452.79
95% HPD	(36.16–4717.37)	(4718.46–324,041.03)	(493.06–117,733.49)
MAZ	384.68	43,551.19	6181.59
95% HPD	(28.89–4627.01)	(4927.20–365,426.47)	(386.99–81,320.49)
TAR	481.95	34,994.52	5766.34
95% HPD	(49.57–4607.87)	(4102.99–289,867.82)	(347.46–86,616.37)
SCA	284.32	39,728.30	5870.84
95% HPD	(28.66–2777.15)	(4822.80–326,061.90)	(562.99–59,278.88)
CEB	226.67	38,256.04	3639.15
95% HPD	(8.00–4952.22)	(4463.75–333,042.76)	(116.33–79,031.46)
MAN	604.09	35,958.37	11,917.91
95% HPD	(50.14–6428.36)	(4303.28–296,619.70)	(830.42–145,378.40)

Open in a new tab

Current (N_e0) and historic (N_e1) estimates of effective population size, and time in years (t) since the onset of population decline are shown. All point estimates are followed by 95% highest posterior density intervals, as calculated in Tracer v. 1.4.1 [51].

Table 5. IMa results.

Samples	θ₁	θ₂	θ_A	m₁	m₂	t/μ	t, years
LAP-MAZ	0.04	0.40	87.50	184.40	35.55	0.006	51.16
95% HPD	(0.01–4.00)	(0.08 - ∞)	(51.70–129.70)	(96.4 - ∞)	(13.05 - ∞)	(0.005–0.110)	(38.17–895.77)
LAP-TAR	0.11	0.37	74.69	51.03	9.00	0.010	243.45
95% HPD	(0.06–3.84)	(0.17–5.00)	(48.07–138.05)	(25.68–484.58)	(1.56–202.20)	(0.008–0.217)	(186.73–5117.27)
LAP-SCA	0.04	0.17	31.73	105.00	15.95	0.003	159.50
95% HPD	(0.03–0.87)	(0.07–8.39)	(23.54–58.28)	(33.0–1079.40)	(7.15–894.85)	(0.001–0.033)	(66.0–1831.50)
LAP-CEB	0.02	0.79	49.21	23.40	85.25	0.004	86.53
95% HPD	(0.02–0.99)	(0.29 - ∞)	(33.61–83.14)	(21.0–1107.0)	(23.65–987.25)	(0.003–0.099)	(55.07–1945.03)
LAP-MAN	0.02	0.18	36.55	170.1	32.80	0.002	36.55
95% HPD	(0.01–0.59)	(0.08 - ∞)	(24.95–69.45)	(90.90 - ∞)	(26.40–1469.6)	(0.001–0.022)	(24.95–69.45)
MAZ-TAR	0.05	1.15	89.55	57.05	14.63	0.012	287.15
95% HPD	(0.02–1.76)	(0.09 - ∞)	(56.85–150.45)	(16.45–353.85)	(0.23–449.78)	(0.008–0.314)	(187.27–7828.00)
MAZ-SCA	0.04	0.16	35.6	95.4	67.65	0.002	124.36
95% HPD	(0.02–0.58)	(0.05–1.85)	(26.51–71.87)	(40.20 - ∞)	(12.65–805.75)	(0.001–0.027)	(46.64–1399.09)

Open in a new tab

Table 6. IMa results (continued).

Samples	θ₁	θ₂	θ_A	m₁	m₂	t/μ	t, years
MAZ-CEB	0.02	0.14	43.19	127.00	82.45	0.002	35.64
95% HPD	(0.01–0.40)	(0.07 - ∞)	(29.47–74.55)	(63.0 - ∞)	(31.45–1481.55)	(0.001–0.025)	(17.82–447.24)
MAZ-MAN	0.01	0.13	32.83	241.5	145.21	0.001	13.83
95% HPD	(0.01–0.23)	(0.05–13.70)	(21.0–57.40)	(151.5 - ∞)	(55.26–2198.64)	(0.001–0.009)	(6.38–98.92)
TAR-SCA	0.61	1.26	85.41	30.38	4.42	0.029	19,968.14
95% HPD	(0.13–2.13)	(0.33–3.01)	(47.90–132.84)	(6.83 - ∞)	(0.05–41.09)	(0.021–0.377)	(14,363.05–263,789.59)
TAR-CEB	0.05	0.55	64.4	29.75	52.88	0.010	375.7
95% HPD	(0.05–1.88)	(0.47–19.45)	(35.76–127.12)	(14.75–450.75)	(10.58–420.98)	(0.007–0.276)	(261.2–109,26.87)
TAR-MAN	0.01	0.09	44.14	162.35	41.3	0.003	88.32
95% HPD	(0.01–0.30)	(0.06–6.39)	(31.53–86.13)	(75.65 - ∞)	(21.70–1305.50)	(0.001–0.023)	(37.37–777.91)
SCA-CEB	0.02	0.09	41.52	74.75	78.75	0.002	110.02
95% HPD	(0.01–0.25)	(0.02 - ∞)	(29.36–62.16)	(12.65 - ∞)	(1.05–1288.35)	(0.000–0.017)	(18.34–1026.84)
SCA-MAN	0.07	0.35	88.27	81.25	15.23	0.017	513.52
95% HPD	(0.06–2.73)	(0.29–11.42)	(50.83–173.03)	(37.25–455.75)	(6.13–331.63)	(0.012–0.212)	(348.35–6357.42)
CEB-MAN	0.20	0.53	83.07	66.75	19.21	0.057	857.77
95% HPD	(0.05 - ∞)	(0.11–8.30)	(58.11–122.07)	(14.75–241.75)	(0.115–166.64)	(0.019–0.226)	(280.86–3423.5)

Open in a new tab

θ = 4N_eμ for populations 1, 2, and the ancestral population from which they arose, migration parameters m₁ and m₂, and time in years (t) since populations diverged using the fossil-calibrated substitution rate (6.03×10⁻⁹ subs/year) are shown. 95% HPDs (highest probability densities) represents the interval on the x-axis where 95% of the area under the posterior probability density curve lies. Upper boundaries of ∞ indicate the HPD had not yet reached zero, though was approaching it. In each pair of populations, population 1 is listed first.

Population divergence times and migration

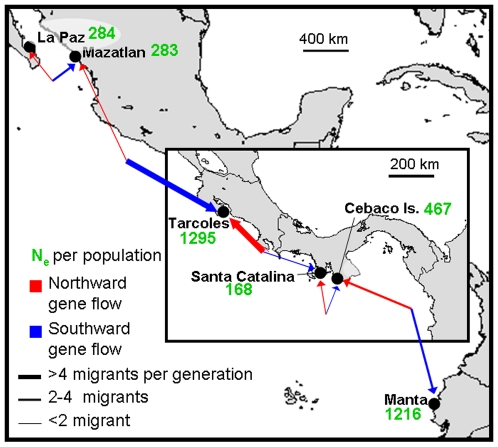
For each comparison of adjacent samples, simpler demographic models in IMa were rejected in favor of the fully parameterized model (Table S4). Estimates of t for all population pairs were significantly greater than zero, given that the posterior probability distributions (PPDs) drop to zero as t approaches zero. Using our conservative fossil-based estimate of the mtDNA control region mutation rate from BEAST, 95% PPDs were large for all estimates of t, although the majority (13 of 15) were completely contained within the Holocene (Table 5, 6). The posteriors for migration showed that gene flow was also greater than zero among all comparisons. Maximum likelihood estimates (MLEs) of Nm = θm/4 (the number of migrants per generation) between all possible population pairs ranged between 0.1 and 16.7 (Fig. 4).

Nm refers to the number of migrants per generation. Red arrows indicate northward gene flow; blue indicate southward flow. Thickness of arrows corresponds to magnitude of flow, or number of migrants per generation. Values in green indicate current N_e, as averaged from estimates of MSVAR and IMa. N_e from IMa was calculated with the equation θ = 4N_eμ.

Discussion

Current and ancestral population sizes

The most consistent and statistically significant result from our analyses of 15 microsatellite loci and mtDNA control region sequences from S. lewini was that current population size (N_e) is substantially (1–3 orders of magnitude) smaller than ancestral N_e among all Eastern Pacific (EP) sites studied, indicating that the demographic history of S. lewini in the EP is marked by statistically significant declines in N_e. Although 95% posterior probability distributions (PPDs) from both MSVAR (microsatellites) and IMa (microsatellites and mtDNA) were wide, the majority of the credibility intervals for current and ancestral estimates of N_e from IMa (23 of 30 comparisons) and MSVAR (3 of 6 comparisons) did not overlap, and where there was overlap among the three MSVAR comparisons, it was less than 5% of the area under the curves. Though we varied the priors for the microsatellite mutation rate (μ) of each locus (as recommended for MSVAR [64]), the range (μ between 1.0×10⁻⁵ and 2.0×10⁻⁴) included rates for bony fish [65], [66] and the slower end of known rates for mammals [67]. Whether our range of prior μ is too fast or too slow, error in the estimation of μ by the MSVAR method will not change the fact that current and ancestral estimates of N_e in general do not overlap – a faster or slower μ would bias the two parameters equally.

Although the upper bounds on our estimates of current N_e are substantially smaller than what has been reported previously for S. lewini in the EP [17] and for other large sharks elsewhere [20], the larger number of loci in our study should result in more accurate N_e estimates. However, an additional reason why we obtained smaller estimates of N_e is likely related to our use of a newer method (MSVAR) with an underlying demographic model that specifically includes changes in N_e over time; methods that assume a static population size across the entire coalescent history of the sample are expected to yield upwardly biased estimates if N_e has recently declined in the past.

Although MSVAR, IMa, and M-ratio tests suggested EP populations of S. lewini have declined, mismatch distributions (mtDNA) showed that most populations in this region also experienced expansion, with point estimates of time since expansion (t) ranging from 90,606 to 136,061 years. While these two results may seem contradictory – signals of both expansion and decline – mismatch distributions are robust to subsequent change in N_e for a long time after the initial expansion [55], [81] whereas the coalescent structure of more rapidly evolving microsatellites likely track more recent demographic events [82].

Population differentiation and divergence

Both nuclear and mitochondrial markers showed evidence of population subdivision: we found subtle but significant genetic differentiation among our sampled populations (global AMOVA for the microsatellites was statistically significant, F _ST = 0.005, P<0.001), most pairwise microsatellite F _ST estimates (between 0.002 and 0.014) were statistically significant, and both estimates of Φ_ST from mtDNA (r = 0.51, P = 0.05) and R_ST from microsatellite data (r = 0.42, P = 0.03) showed significant evidence of isolation by distance (IBD). Although the biological significance of subtle patterns of genetic differentiation as measured by F _ST can be difficult to evaluate on their own [83], [84], IMa posterior distributions for estimates of the time since population separation (t) had strong peaks (Fig. 5) and differed fundamentally from the uniform priors, with probabilities dropping to zero as t approached zero, indicating that each EP location is a sample from a separate population. Although the peaks in most of the PPDs for t were surprisingly recent (tens to hundreds of years), the upper bound on the 95% PPDs for 13 of 15 pairwise estimates of t fell within the Holocene. However, distributions were quite broad, indicating considerable uncertainty despite the use of 16 loci.

The posterior probability density (PPD) of time (t), in years, is based on the fossil-calibrated substitution rate (6.03×10⁻⁹ subs/year).

Gene flow

Rates of gene flow (i.e., the number of migrants per generation, Nm = θm/4) between EP populations inferred from IMa (ranging from 0.1 to 16.7 migrants per generation, Fig. 4) were less than 10% of point estimates of N_e, suggesting the potential for demographic asynchrony [85], [86]. However, it is difficult to fully evaluate the demographic interdependence of populations without knowledge of population growth rates [87]. Nevertheless, an average of 2.4 migrants per generation probably provides little exogenous demographic input given the slow growth and maturation of S. lewini.

Because we did not sample all populations that could be exchanging migrants, our estimates of migration may be biased upwards. Simulations have shown that a third, unsampled population exchanging migrants with one of the two focal (sampled) populations considered in an IMa analysis will upwardly bias estimates of migration and θ [88]. Therefore, both connectivity and N_e may actually be lower than our data suggest. Gene flow from other regions is probably very low given that previous work ([17], Daly-Engel et al (unpublished data)) has shown that Nm based on both mtDNA and microsatellites from Hawaii and Indo-Pacific populations into Eastern Pacific populations is less than one. Therefore, given that the effects of ‘ghost populations’ are minimal when migration rates are low [89], and any upward bias in N_e would be evident in both current and ancestral estimates, it is unlikely that gene flow from central and western Pacific populations alone caused the large difference we observed between current and ancestral N_e.

Demographic history of Sphyrna lewini in the Eastern Pacific

Taken together, our data and analyses suggest that in the EP, S. lewini currently exists as a series of separate and potentially very small populations. Although low molecular diversity in sharks [32]–[35] is often attributed to low mutation rates in elasmobranchs [61], our analyses suggest that small N_e may be a significant factor contributing to low mtDNA (mean π = 0.0011, mean h = 0.5338; Table S3) and low microsatellite (mean H_o = 0.770, mean H_e = 0.792; A_E<A, Table S2) diversity in S. lewini. However, it remains to be seen if small N_e is characteristic of other sharks with low levels of diversity. In addition to contributing to low diversity, small N_e could be an important evolutionary force driving population differentiation, rather than just restricted gene flow, given that some IMa estimates of gene flow were large enough (Nm>10) to maintain genetic homogeneity among populations [87].

Potential factors contributing to population decline

Whether or not the decline in EP S. lewini is typical of other elasmobranchs, a history of decline following the last glacial maximum (LGM) 18,000–20,000 years ago in S. lewini is highly unusual considering warming after the LGM likely caused population expansions in many marine and terrestrial organisms [90]–[93]. Although precipitation decreased off the coast of Chile during the mid-Holocene (∼7700 – 4000 ybp; [94]), potentially reducing terrestrial run-off and nearshore productivity, mid-Holocene conditions in the equatorial EP were marked by increased upwelling and productivity [95]. Though these latter conditions are not expected to induce widespread decline in a marine apex predator, it is unclear how Holocene climate conditions affected coastal marine species throughout the EP. Another possibility is disease, which has been responsible for recent declines in several marine species [96]–[98]. However, little is known about the impacts of diseases in natural populations of sharks other than in general, they are thought to have robust immune systems [99]–[102].

An additional hypothesis is that prehistoric fishing practices initiated the decline [103], [104], which was later exacerbated by modern fishing. Archaeological remains from 14 sites along the EP coasts of Costa Rica, Panama, and Ecuador show that fishers using primitive nets and watercrafts as early as 6,000 years ago were catching sharks [105], with 3–5% of aboriginal middens comprised of shark remains (Richard Cooke, pers. comm.). Although fish comprised over 50% of edible meat remains in some places [106] and large inshore schools of juvenile hammerheads (typically in shallow embayments) are particularly vulnerable to even the simplest fishing methods, the extent of the potential impact of prehistoric fishing remains difficult to evaluate [107]–[111].

Considering alternative hypotheses regarding the cause for decline in EP S. lewini depends on the timing of decline as estimated with MSVAR, which is contingent on the rate and model of microsatellite mutation. It is difficult to speculate whether our prior range (including the known rates of bony fish and the slow end of the range of mammals) is too fast or too slow, which would either downwardly bias or upwardly bias our estimates of the time (t) since the start of decline, respectively. Departures from the simple SSM model of microsatellite evolution might also upwardly bias estimates of t from MSVAR because large mutations (addition or deletion of >1 repeat unit) will be modeled as a series of single steps [112]. However, a recent simulation study showed that MSVAR is robust to moderate departures from the SSM model [113], and this method has detected recent declines among mouse lemur populations (500 years before present (ybp); [114]) and among giant pandas (1000 ybp; [82]). Thus, while this method is capable of detecting change in N_e initiating as early as the Holocene, serious consideration of possible causes for decline will require further refinement of the timing of this demographic event as inferred from genetic data.

Conclusions

Our use of coalescent methods to estimate current and historic N_e based on data from 16 independent loci suggests that scalloped hammerheads may have been far more abundant in the past than they are today. Low levels of genetic diversity in EP S. lewini may be a consequence of small N_e, and genetic drift, rather than restricted gene flow, may be an important force causing population divergence. Our use of non-equilibrium models, which enabled us to estimate past population parameters for a globally endangered shark, has shed light on this vulnerable species' demographic history, providing a deeper understanding of the processes that led to existing levels and patterns of genetic diversity.

Supporting Information

Table S1

Microsatellite statistics per locus, per population. A = total number of alleles per locus across all populations. A_E = effective number of alleles. A_p = private alleles per locus, per population. H_o = observed heterozygosity per locus, per population, and H_e = expected heterozygosity per locus, per population, as calculated in Arlequin v. 3.11 [32]. P-values in bold were significant after sequential Bonferroni correction of alpha (α). Number next to population abbreviation indicates number of samples.

(PDF)

Click here for additional data file.^{(1,007KB, pdf)}

Table S2

Diversity statistics for mtDNA per population. Nucleotide (π) and haplotype (h) diversities, and neutrality statistics (Fu's F_s and Fu and Li's D*) are shown. Though neither neutrality statistic was significant at α = 0.05, only samples TAR and SCA show an increase in new mutations with negative D* values.

(PDF)

Click here for additional data file.^{(126.8KB, pdf)}

Table S3

Life history data used for generation time ( G ) estimates. Values of li (age-specific survival rates), bi (birth rates), and pi (probability of a gene being inherited from a parent of age i), for all age classes, i, used to calculate the mean age of breeding adults, G [55].

(PDF)

Click here for additional data file.^{(216.6KB, pdf)}

Table S4

Log-likelihood ratio test (LLRT) results from IMa analyses. For each adjacent population pair, the likelihood of a simpler, alternative model where θ1 = θ2 = θA is shown [log(P)], the degrees of freedom for the LLRT of the full and alternative model, results from the test (2LLR), and the probability of achieving the test statistic by chance under the null model (P-value) are shown. All alternative models where population size has not changed were rejected in favor of the full model at α = 0.05.

(PDF)

Click here for additional data file.^{(534KB, pdf)}

Acknowledgments

We are extremely grateful to M. Hoyos, Y. Torres, M. Garcia, A. Polanco, I. Zanella, D. Chacon-Rojas, A. Vega, H. Guzman, P. Ahuja, O. Escobar, S. Jorgensen, S. Torres, L. Mejia, V. Alatorre, D. Ramírez, L. Castillo, M. Angel, and Chuy, Coochie, and other fishermen who generously cooperated with us and were instrumental in sample collection. All sequencing was done at CUGI – we thank J. Troutman, K. Brown, and R. Ackerman. S. Emme, the Marko Lab, and M. Marsh provided valuable technical support. F. Galván-Magaña thanks Instituto Politécnico Nacional (COFAA and EDI) for their support. This is a technical contribution no. 5942 of the Clemson University Experiment Station.

Footnotes

Competing Interests: The authors have declared that no competing interests exist.

Funding: Funds for this work were provided by National Science Foundation (http://www.nsf.gov/) grants DEB03-44419 and OCE05-50526 to Peter B. Marko, a Cooperative State Research, Education, and Extension Service/United States Department of Agriculture grant under project number SC-1700342, and a University of North Carolina Smith Graduate Research grant (http://gradschool.unc.edu/funding/) to Holly A. Nance. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

1.Rose GA, deYoung B, Kulka DW, Goddard SV, Fletcher GL. Distribution shifts and overfishing the northern cod (Gadus morhua): a view from the ocean. Can J Fish Aquat Sci. 2000;57:644–663. [Google Scholar]
2.Porch CE, Eklund AM, Scott GP. A catch-free stock assessment model with application to goliath grouper (Epinephelus itajara) off southern Florida. Fish Bull. 2006;104:89–101. [Google Scholar]
3.MacKenzie BR, Myers RA. The development of the northern European fishery for north Atlantic bluefin tuna Thunnus thynnus during 1900–1950. Fish Res. 2007;87:229–239. [Google Scholar]
4.Holt T, Medley P, Rice J, Cooper J, Hough A. Certification report for South Georgia Patagonian Toothfish longline fishery. 2001. Moody Marine, Ltd., Birkenhead.
5.Kraus SD, Brown MW, Caswell H, Clark CW, Fujiwara M, et al. North Atlantic right whales in crisis. Science. 2005;309:561–562. doi: 10.1126/science.1111200. [DOI] [PubMed] [Google Scholar]
6.Baum JK, Myers RA, Kehler DG, Worm B, Harley SJ, et al. Collapse and conservation of shark populations in the Northwest Atlantic. Science. 2003;299:389–392. doi: 10.1126/science.1079777. [DOI] [PubMed] [Google Scholar]
7.Dulvy NK, Baum JK, Clarke S, Compagno LJV, Cortés E, et al. You can swim but you can't hide: the global status and conservation of oceanic pelagic sharks and rays. Aqua Conserv: Mar Fresh Ecosys. 2008;18:459–482. [Google Scholar]
8.Myers RA, Baum JK, Shepherd TD, Powers SP, Peterson CH. Cascading effects of the loss of apex predatory sharks from a coastal ocean. Science. 2007;315:1846–1850. doi: 10.1126/science.1138657. [DOI] [PubMed] [Google Scholar]
9.Fong QW, Anderson JL. International shark fin markets and shark management: an integrated market preference-cohort analysis of the blacktip shark (Carcharhinus limbatus). Ecol Econ. 2002;40:117–130. [Google Scholar]
10.Clarke SC, Magnussen JE, Abercrombie DL, McAllister MK, Shivji MS. Identification of shark species composition and proportion in the Hong Kong shark fin market based on molecular genetics and trade records. Conserv Biol. 2006;20:201–211. doi: 10.1111/j.1523-1739.2005.00247.x. [DOI] [PubMed] [Google Scholar]
11.Bradshaw CJA, Fitzpatrick BM, Steinberg CC, Brook BW, Meekan MG. Decline in whale shark size and abundance at Ningaloo Reef over the past decade: the world's largest fish is getting smaller. Biol Conserv. 2008;141:1894–1905. [Google Scholar]
12.Jorgensen SJ, Reeb CA, Chappel TK, Anderson S, Perle C, et al. Philopatry and migration of Pacific white sharks. Proc R Soc B. 2010;277:679–688. doi: 10.1098/rspb.2009.1155. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Roman J, Palumbi SR. Whales before whaling in the North Atlantic. Science. 2003;301:508–510. doi: 10.1126/science.1084524. [DOI] [PubMed] [Google Scholar]
14.Chevolot M, Ellis JR, Rijnsdorp AD, Stam WT, Olsen JL. Temporal changes in allele frequencies but stable genetic diversity over the past 40 years in the Irish Sea population of thornback ray, Raja calvata. Heredity. 2008;101:120–126. doi: 10.1038/hdy.2008.36. [DOI] [PubMed] [Google Scholar]
15.Hoelzel AR. Looking backwards to look forwards: conservation genetics in a changing world. Conserv Genet. 2010;11:655–660. [Google Scholar]
16.Pardini AT, Jones CS, Noble LR, Kreiser B, Malcolm H, et al. Sex-biased dispersal of great white sharks. Nature. 2001;412:139–140. doi: 10.1038/35084125. [DOI] [PubMed] [Google Scholar]
17.Duncan KM, Martin AP, Bowen BW, De Couet HD. Global phylogeography of the scalloped hammerhead shark (Sphyrna lewini). Mol Ecol. 2006;15:2239–2251. doi: 10.1111/j.1365-294X.2006.02933.x. [DOI] [PubMed] [Google Scholar]
18.Quattro JM, Stoner DS, Driggers WB, Anderson CA, Preide KA, et al. Genetic evidence of cryptic speciation within hammerhead sharks (Genus Sphyrna). Mar Biol. 2006;148:1143–1155. [Google Scholar]
19.Castro ALF, Stewart BS, Wilson SG, Hueter RE, Meekan RE, et al. Population genetic structure of the Earth's largest fish, the whale shark (Rhinocdon typus). Mol Ecol. 2007;16:5183–5192. doi: 10.1111/j.1365-294X.2007.03597.x. [DOI] [PubMed] [Google Scholar]
20.Karl SA, Castro ALF, Lopez JA, Charvet P, Burgess GH. Phylogeography and conseration of the bull shark (Carcharhinus leucas) inferred from mitochondrial and microsatellite DNA. Conserv Genet. 2011;12:371–382. [Google Scholar]
21.Compagno LJV. FAO Species catalogue. 1984. Vol. 4, Parts 1 & 2, Sharks of the World. FAO Fisheries Synopsis.
22.Torres-Huerta AM. Observaciones sobre la biologia reproductiva de la cornuda barrosa, Sphyrna lewini (Griffith y Smith, 1834) (Pisces: Sphyrnidae) en aguas del noroeste de Mexico. 1999. Bachelor Sciences. UNAM. Escuela Nacional de Estudios Profesionales, Iztacala.
23.Martínez-Ortíz J, Galván-Magaña F, Carrera-Fernández M, Mendoza-Intriago D, Estupiñán-Montaño C, et al. Abundancia estacional de tiburones desembarcados en Manta – Ecuador. In: Martínez-Ortíz J, Galván-Magaña F, editors. Tiburones en el Ecuador: Casos de Estudio. Manta: EPESPO-PMRC; 2007. pp. 9–27. [Google Scholar]
24.Zanella I. Caracterización de la pesca y algunos aspectos sobre la reproducción, alimentación y distribución del tiburón martillo Sphyrna lewini, Sphyrnidae, en el Pacífico de Costa Rica. 2008. Tesis de M. en C., Universidad Nacional de Costa Rica, Instituto Internacional de Conservacion y Manejo de Vida Silvestre.
25.Hayes CG, Jiao Y, Cortés E. Stock assessment of scalloped hammerheads in the Western North Atlantic Ocean and Gulf of Mexico. N Am J Fish Manag. 2009;29:1406–1417. [Google Scholar]
26.Chapman DD, Pinhal D, Shivji MS. Tracking the fin trade: Genetic stock identification in western Atlantic scalloped hammerhead sharks Sphyrna lewini. Endang Species Res. 2009;9:221–228. [Google Scholar]
27.Ovenden JR, Kashiwagi T, Broderick D, Giles J, Salini J. The extent of population genetic subdivision differs among four co-distributed shark species in the Indo-Australian archipelago. BMC Evol Biol. 2009;9:40–55. doi: 10.1186/1471-2148-9-40. [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Hey J, Nielsen R. Multilocus methods for estimating population sizes, migration rates and divergence time, with applications to the divergence of Drosophila pseudoobscura and D. persimilis. Genetics. 2004;167:747–760. doi: 10.1534/genetics.103.024182. [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Hey J, Nielsen R. Integration with the Felsenstein equation for improved Markov chain Monte Carlo methods in population genetics. Proc Natl Acad Sci. 2007;104:2785–2790. doi: 10.1073/pnas.0611164104. [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Becquet C, Przeworski M. A new approach to estimate parameters of speciation models with application to apes. Genome Res. 2007;17:1505–1519. doi: 10.1101/gr.6409707. [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Becquet C, Przeworski M. Learning about modes of speciation by computational approaches. Evol. 2009;63:2547–2562. doi: 10.1111/j.1558-5646.2009.00662.x. [DOI] [PubMed] [Google Scholar]
32.Hoelzel AR, Shivji MS, Magnussen J, Francis MP. Low worldwide genetic diversity in the basking shark (Cetorhinus maximus). Biol Lett. 2006;2:639–642. doi: 10.1098/rsbl.2006.0513. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Schultz JK, Feldheim KA, Gruber SH, Ashley MV, McGovern TM. Global phylogeography and seascape genetics of the lemon sharks (genus Negaprion). Mol Ecol. 2008;17:5336–5348. doi: 10.1111/j.1365-294X.2008.04000.x. [DOI] [PubMed] [Google Scholar]
34.Dudgeon CL, Broderick D, Ovenden R. IUCN classification zones concord with, but underestimate, the population genetic structure of the zebra shark Stegostoma fasciatum in the Indo-West Pacific. Mol Ecol. 2009;18:248–261. doi: 10.1111/j.1365-294X.2008.04025.x. [DOI] [PubMed] [Google Scholar]
35.Pereyra S, Garcia G, Miller P, Oviedo S, Domingo A. Low genetic diversity and population structure of the narrownose shark (Mustelus schmitti). Fish Res. 2010;106:468–473. [Google Scholar]
36.Torres-Rojas YE, Hernández-Herrera A, Galván-Magaňa F, Alatorre-Ramírez V. Stomach content analysis of juvenile, scalloped hammerhead shark Sphyrna lewini captured off the coast of Mazátlan, Mexico. Aquat Ecol. 2010;44:301–308. [Google Scholar]
37.Nance HA, Daly-Engel TS, Marko PB. New microsatellite loci for the endangered scalloped hammerhead shark, Sphyrna lewini. Mol Ecol Res. 2009;9:955–957. doi: 10.1111/j.1755-0998.2008.02510.x. [DOI] [PubMed] [Google Scholar]
38.Keeny DB, Heist EJ. Characterization of microsatellite loci isolated from the blacktip shark and their utility in requiem and hammerhead sharks. Mol Ecol Notes. 2003;3:501–504. [Google Scholar]
39.Thompson JD, Gibson TJ, Plewniak F, Jeanmougin F, Higgins DG. Multiple sequence alignment with Clustal X. Trends Biochem Sci. 1998;23:403–405. doi: 10.1016/s0968-0004(98)01285-7. [DOI] [PubMed] [Google Scholar]
40.Van Oosterhout C, Hutchinson WF, Wills DPM, Shipley P. Micro Checker: software for identifying and correcting genotyping errors in microsatellite data. Mol Ecol Notes. 2004;4:535–538. [Google Scholar]
41.Excoffier L, Laval G, Schneider S. ARLEQUIN ver. 3.0: An integrated software package for population genetics data analysis. Evol Bioinforma Online. 2005;1:47–50. [PMC free article] [PubMed] [Google Scholar]
42.Peakall R, Smouse PE. GenAlEx 6: genetic analysis in excel – Population genetic software for teaching and research. 2005. Australian National University, Canberra. [DOI] [PMC free article] [PubMed]
43.Fu YX. New statistical tests of neutrality for DNA samples from a population. Genetics. 1996;143:557–570. doi: 10.1093/genetics/143.1.557. [DOI] [PMC free article] [PubMed] [Google Scholar]
44.Fu YX, Li WH. Statistical tests of neutrality of mutations. Genetics. 1993;133:693–709. doi: 10.1093/genetics/133.3.693. [DOI] [PMC free article] [PubMed] [Google Scholar]
45.Rozas JJ, Sánchez-DelBarrio C, Messeguer X, Rozas R. DnaSP, DNA polymorphism analyses by the coalescent and other methods. Bioinforma. 2003;19:2496–2497. doi: 10.1093/bioinformatics/btg359. [DOI] [PubMed] [Google Scholar]
46.Wang J. A new method for estimating effective population sizes from a single sample of multilocus genotypes. Mol Ecol. 2009;18:2148–2164. doi: 10.1111/j.1365-294X.2009.04175.x. [DOI] [PubMed] [Google Scholar]
47.Wang J. Estimation of effective population sizes from data on genetic markers. Phil Trans R Soc B. 2005;360:1395–1409. doi: 10.1098/rstb.2005.1682. [DOI] [PMC free article] [PubMed] [Google Scholar]
48.Ashley MV, Berger-Wolf TY, Caballero IC, Chaovalitwongse W, DasGupta B, et al. Full sibling reconstruction in wild populations from microsatellite genetic markers. In: Russe AS, editor. Computational Biology: New Research. Nova Science Publishers, Hauppauge; 2008. pp. 231–258. [Google Scholar]
49.Clement MD, Posada D, Crandall KA. TCS: a computer program to estimate gene geneologies. Mol Ecol. 2000;9:1657–1660. doi: 10.1046/j.1365-294x.2000.01020.x. [DOI] [PubMed] [Google Scholar]
50.Templeton AR, Crandall KA, Sing CF. A cladistic analysis of phenotypic associations with haplotypes inferred from restriction endonuclease mapping and DNA sequence data. III Cladogram estimation. Genetics. 1992;132:619–633. doi: 10.1093/genetics/132.2.619. [DOI] [PMC free article] [PubMed] [Google Scholar]
51.Posada D, Crandall KA. Modeltest: testing the model of DNA substitution. Bioinforma. 1998;14:817–818. doi: 10.1093/bioinformatics/14.9.817. [DOI] [PubMed] [Google Scholar]
52.Tajima F, Nei M. Estimation of evolutionary distance between nucleotide sequences. Mol Biol Evol. 1984;1:269–285. doi: 10.1093/oxfordjournals.molbev.a040317. [DOI] [PubMed] [Google Scholar]
53.Hubisz MJ, Falush D, Stephens M, Pritchard JK. Inferring weak population structure with the assistance of sample group information. Mol Ecol Res. 2009;9:1322–1332. doi: 10.1111/j.1755-0998.2009.02591.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
54.Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
55.Rogers AR, Harpending H. Population growth makes waves in the distribution of pairwise genetic differences. Mol Biol Evol. 1992;9:552–569. doi: 10.1093/oxfordjournals.molbev.a040727. [DOI] [PubMed] [Google Scholar]
56.Garza JC, Williamson EG. Detection of reduction in population size using data from microsatellite data. Mol Ecol. 2001;10:305–318. doi: 10.1046/j.1365-294x.2001.01190.x. [DOI] [PubMed] [Google Scholar]
57.Dallas JF. Estimation of microsatellite mutation-rates in recombinant inbred strains of mouse. Mamm Genome. 1992;3:452–456. doi: 10.1007/BF00356155. [DOI] [PubMed] [Google Scholar]
58.Weber JL, Wong C. Mutation of short human tandem repeats. Hum Mol Gen. 1993;2:1123–1128. doi: 10.1093/hmg/2.8.1123. [DOI] [PubMed] [Google Scholar]
59.Ellengren H. Mutation-rates in porcine microsatellite loci. Mamm Genome. 1995;6:376–377. doi: 10.1007/BF00364807. [DOI] [PubMed] [Google Scholar]
60.Yue GH, Beeckmann P, Geldermann H. Mutation rate at swine microsatellite loci. Genetica. 2002;114:113–119. doi: 10.1023/a:1015189921578. [DOI] [PubMed] [Google Scholar]
61.Martin AP, Naylor GJP, Palumbi SR. Rates of mitochondrial evolution in sharks are slow compared with mammals. Nature. 1992;357:153–155. doi: 10.1038/357153a0. [DOI] [PubMed] [Google Scholar]
62.Martin AP. Substitution rates of organelle and nuclear genes in sharks: implicating metabolic rate (again). Mol Biol Evol. 1999;16:996–1002. doi: 10.1093/oxfordjournals.molbev.a026189. [DOI] [PubMed] [Google Scholar]
63.Cornuet JM, Luikart G. Description and power analysis of two tests for detecting recent population bottlenecks from allele frequency data. Genetics. 1996;144:2001–2014. doi: 10.1093/genetics/144.4.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
64.Beaumont MA. Detecting population expansion and decline using microsatellites. Genetics. 1999;153:2013–2029. doi: 10.1093/genetics/153.4.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
65.Shimoda N, Knapik EW, Ziniti J, Sim C, Yamada E, et al. Zebrafish genetic map with 2000 microsatellite markers. Genomics. 1999;58:219–232. doi: 10.1006/geno.1999.5824. [DOI] [PubMed] [Google Scholar]
66.Yue GH, David L, Orban L. Mutation rate and pattern of microsatellites in common carp (Cyprinus carpio L.). Genetica. 2007;129:329–331. doi: 10.1007/s10709-006-0003-8. [DOI] [PubMed] [Google Scholar]
67.Schug MD, Mackay TFC, Aquadro CF. Low mutation rates of microsatellite loci in Drosophila melanogaster. Nature Gen. 1997;15:99–102. doi: 10.1038/ng0197-99. [DOI] [PubMed] [Google Scholar]
68.Rambaut A, Drummond AJ. 2007. Tracer v1.4, Available: http://beast.bio.ed.ac.uk/
69.Jorde PE, Ryman N. Temporal allele frequency change and estimation of effective size in populations with overlapping generations. Genetics. 1995;139:1077–1090. doi: 10.1093/genetics/139.2.1077. [DOI] [PMC free article] [PubMed] [Google Scholar]
70.Cortés E, Arocha F, Beerkircher L, Carvalho F, Domingo A, et al. Ecological risk assessment of pelagic sharks caught in Atlantic pelagic longline fisheries. Aquat Living Res. 2010;23:25–34. [Google Scholar]
71.Branstetter S. Age, growth and reproductive biology of the silky shark, Carcharhinus falciformis, and the scalloped hammerhead, Sphyrna lewini, from the northwestern Gulf of Mexico. Enviro Biol Fish. 1987;19:161–173. [Google Scholar]
72.Piercy AN, Carlson JK, Sulikowski JA, Burgess GH. Age and growth of the scalloped hammerhead shark, Sphyrna lewini, in the north-west Atlantic Ocean and Gulf of Mexico. Mar Freshw Res. 2007;58:34–40. [Google Scholar]
73.Felsenstein J. Inbreeding and variance effective numbers in populations with overlapping generations. Genetics. 1971;68:581–597. [Google Scholar]
74.Hey J. Isolation with migration models for more than two populations. Mol Biol Evol. 2010;27:905–920. doi: 10.1093/molbev/msp296. [DOI] [PMC free article] [PubMed] [Google Scholar]
75.Bulut Z, McCormick CR, Gopurenko D, Williams RN, Bos DH, et al. Microsatellite mutation rates in the eastern tiger salamander (Ambystoma tigrinium tigrinium) differ 10-fold across loci. Genetica. 2009;136:501–504. doi: 10.1007/s10709-008-9341-z. [DOI] [PubMed] [Google Scholar]
76.Hey J. On the number of New World founders: a population genetic portrait of the peopling of the Americas. PLoS Biol. 2005;3:e193. doi: 10.1371/journal.pbio.0030193. [DOI] [PMC free article] [PubMed] [Google Scholar]
77.Drummond AJ, Rambaut A. BEAST: Bayesian evolutionary analysis by sampling trees. BMC Evol Biol. 2007;7:241–248. doi: 10.1186/1471-2148-7-214. [DOI] [PMC free article] [PubMed] [Google Scholar]
78.Lim DD, Motta P, Mara K, Martin AP. Phylogeny of hammerhead sharks (Family Sphyrnidae) inferred from mitochondrial and nuclear genes. Mol Phylogenetics Evol. 2010;55:572–579. doi: 10.1016/j.ympev.2010.01.037. [DOI] [PubMed] [Google Scholar]
79.Cappetta H. Chondrichthes II. Mesozoic and Cenozoic Elasmobranchii; vol. 3B. Handbook Paleoichthyology. Stuttgart: Fisher; 1987. [Google Scholar]
80.Rice WR. Analyzing tables of statistical tests. Evol. 1989;43:223–225. doi: 10.1111/j.1558-5646.1989.tb04220.x. [DOI] [PubMed] [Google Scholar]
81.Lavery S, Moritz C, Fielder DR. Genetic patterns suggest exponential population growth in a declining species. Mol Biol Evol. 1996;13:1106–1113. [Google Scholar]
82.Hu Y, Qi D, Wang H, Wei F. Genetic evidence of recent population contraction in the southernmost population of giant pandas. Genetica. 2010;138:1297–1306. doi: 10.1007/s10709-010-9532-2. [DOI] [PubMed] [Google Scholar]
83.Hedrick PW. Highly variable loci and their interpretation in evolution and conservation. Evol. 1999;53:313–318. doi: 10.1111/j.1558-5646.1999.tb03767.x. [DOI] [PubMed] [Google Scholar]
84.Palumbi SR. Population genetics, demographic connectivity, and the design of marine reserves. Ecol Appl. 2003;13:S146–S158. [Google Scholar]
85.Hastings A. Complex interactions between dispersal and dynamics: lessons from coupled logistic equations. Ecology. 1993;74:1362–1372. [Google Scholar]
86.Waples RS, Gaggiotti O. What is a population? An empirical evaluation of some genetic methods for identifying the number of gene pools and their degree of connectivity. Mol Ecol. 2006;15:1419–1439. doi: 10.1111/j.1365-294X.2006.02890.x. [DOI] [PubMed] [Google Scholar]
87.Lowe WH, Allendorf FW. What can genetics tell us about population connectivity? Mol Ecol. 2010;19:3038–3051. doi: 10.1111/j.1365-294X.2010.04688.x. [DOI] [PubMed] [Google Scholar]
88.Strasburg JL, Rieseberg LH. How robust are “Isolation with Migration” analyses to violations of the IM model? A simulation study. Mol Biol Evol. 2010:297–310. doi: 10.1093/molbev/msp233. [DOI] [PMC free article] [PubMed] [Google Scholar]
89.Beerli P. Effect of unsampled populations on the estimation of population sizes and migration rates between sampled populations. Mol Ecol. 2004;13:827–836. doi: 10.1111/j.1365-294x.2004.02101.x. [DOI] [PubMed] [Google Scholar]
90.Wares JP, Cunningham CW. Phylogeography and historical ecology of the North Atlantic intertidal. Evol. 2001;55:2455–2469. doi: 10.1111/j.0014-3820.2001.tb00760.x. [DOI] [PubMed] [Google Scholar]
91.Uthicke S, Benzie JAH. Gene flow and population history in high dispersal marine invertebrates: mitochondrial DNA analysis of Holothuria nobilis (Echinodermata: Holothuroidea) populations from the Indo-Pacific. Mol Ecol. 2003;12:2635–2648. doi: 10.1046/j.1365-294x.2003.01954.x. [DOI] [PubMed] [Google Scholar]
92.Liu JX, Gao TX, Zhuang ZM, Jin XS, Yokogawa K, et al. Late Pleistocene divergence and subsequent population expansion of two closely related fish species, Japanese anchovy (Engraulis japonicus) and Australian anchovy (Engraulis australis). Mol Phylogenet Evol. 2006;40:712–723. doi: 10.1016/j.ympev.2006.04.019. [DOI] [PubMed] [Google Scholar]
93.Marko PB, Hoffman JM, Emme SA, McGovern TM, Keever C, et al. The expansion-contraction model of Pleistocene demography: rocky shores suffer a sea change? Mol Ecol. 2010;19:146–169. doi: 10.1111/j.1365-294x.2009.04417.x. [DOI] [PubMed] [Google Scholar]
94.Lamy F, Hebbeln D, Rohl U, Wefer G. Holocene rainfall variability in southern Chile: a marine record of latitudinal shifts of the Southern Westerlies. Earth Planet Sci Lett. 2001;185:369–382. [Google Scholar]
95.Koutavas A, Lynch-Stieglitz J, Marchitto TM, Sachs JP. El Nino-like pattern in ice age tropical Pacific sea surface temperature. Science. 2002;297:226–230. doi: 10.1126/science.1072376. [DOI] [PubMed] [Google Scholar]
96.Lessios HA, Cubit JD, Robertson DR, Shulman MJ, Parker MR, et al. Mass mortality of Diadema antillarum on the Caribbean coast of Panama. Coral Reefs. 1984;3:173–182. [Google Scholar]
97.Cook T, Folli M, Klinck J, Ford S, Miller J. The relationship between increasing sea-surface temperature and the northward spread of Perkinsus marinus (Dermo) disease epizootics in oysters. Estuar Coast Shelf Sci. 1998;46:587–597. [Google Scholar]
98.Aronson RB, Precht WF. White-band disease and the changing face of Caribbean coral reefs. Hyrdobiol. 2001;460:25–38. [Google Scholar]
99.Stoskopf MK. Fish Medicine. Philadelphia: W.B. Saunders Company; 1993. 882 [Google Scholar]
100.Smith AG, Muhvich AG, Muhvich KH, Wood C. Fatal Fusarium solani infections in baby sharks. Med Mycol. 1989;27:83–91. [PubMed] [Google Scholar]
101.Crow GL, Brock JA, Kaiser S. Fusarium solani fungal infection of the lateral line canal system in captive scalloped hammerhead sharks (Sphyrna lewini) in Hawaii. J Wildl Dis. 1995;31:562–565. doi: 10.7589/0090-3558-31.4.562. [DOI] [PubMed] [Google Scholar]
102.Walsh CJ, Luer CA, Bodine AB, Smith CA, Cox HL, et al. Elasmobranch immune cells as a source of novel tumor cell inhibitors: implications for public health. Integr Comp Biol. 2006;46:1072–1081. doi: 10.1093/icb/icl041. [DOI] [PMC free article] [PubMed] [Google Scholar]
103.Jackson JBC, Kirby MX, Berger WH, Bjorndal KA, Botsford LW, et al. Historical overfishing and the recent collapse of coastal ecosystems. Science. 2001;293:629–638. doi: 10.1126/science.1059199. [DOI] [PubMed] [Google Scholar]
104.Pinnegar JK, Engelhard GH. The ‘shifting baseline’ phenomenon: a global perspective. Rev Fish Biol Fish. 2008;18:1–16. [Google Scholar]
105.Cooke R. Prehistoric nearshore and littoral fishing in the eastern Tropical Pacific: An ichthyological evaluation. J World Prehist. 1992;6:1–49. [Google Scholar]
106.Rick TC, Erlandson JM, Vellanoweth RL. Paleocoastal marine fishing on the Pacific coast of the Americas: Perspectives from Daisy Cave California. Am Antiq. 2001;66:595–613. [PubMed] [Google Scholar]
107.Butler VL. Changing fish use on Mangaia, Southern Cook Islands: resource depression and the prey choice model. Int J Osteoarchaeol. 2001;11:88–100. [Google Scholar]
108.Allen MS. resolving long-term change in Polynesian marine fisheries. Asian Perspect. 2002;41:195–212. [Google Scholar]
109.Allen MS, Ladefoged TN, Wall JJ. Traditional Rotuman fishing in temporal and regional context. Int J Osteoarchaeol. 2001;11:56–71. [Google Scholar]
110.Fitzpatrick SM, Donaldson TJ. Anthropogenic impacts to coral reefs in Palau, Western Micronesia during the Late Holocene. Coral Reefs. 2007;26:915–930. [Google Scholar]
111.Erlandson JM, Rick TC. Archaeology meets marine ecology: The antiquity of maritime cultures and human impacts on marine fisheries and ecosystems. Annu Rev Mar Sci. 2005;2:231–251. doi: 10.1146/annurev.marine.010908.163749. [DOI] [PubMed] [Google Scholar]
112.Gonser R, Donnelly P, Nicholson G, Di Rienzo A. Microsatellite mutations and inferences about human demography. Genetics. 2000;154:1793–1807. doi: 10.1093/genetics/154.4.1793. [DOI] [PMC free article] [PubMed] [Google Scholar]
113.Girod C, Vitalis R, Leblois R, Freville H. Inferring population decline and expansion from mimcorsatellite data: a simulation-based evaluation of the MSVAR method. Genetics. 2011 doi: 10.1534/genetics.110.121764. [DOI] [PMC free article] [PubMed] [Google Scholar]
114.Olivieri GL, Sousa V, Chikhi L, Radespiel U. From genetic diversity and structure to conservation: genetic signature of recent population declines in three mouse lemur species (Microcebus spp.). Biol Conserv. 2008;141:1257–1271. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Table S1

(PDF)

Click here for additional data file.^{(1,007KB, pdf)}

Table S2

(PDF)

Click here for additional data file.^{(126.8KB, pdf)}

Table S3

(PDF)

Click here for additional data file.^{(216.6KB, pdf)}

Table S4

(PDF)

Click here for additional data file.^{(534KB, pdf)}

[pone.0021459-Rose1] 1.Rose GA, deYoung B, Kulka DW, Goddard SV, Fletcher GL. Distribution shifts and overfishing the northern cod (Gadus morhua): a view from the ocean. Can J Fish Aquat Sci. 2000;57:644–663. [Google Scholar]

[pone.0021459-Porch1] 2.Porch CE, Eklund AM, Scott GP. A catch-free stock assessment model with application to goliath grouper (Epinephelus itajara) off southern Florida. Fish Bull. 2006;104:89–101. [Google Scholar]

[pone.0021459-MacKenzie1] 3.MacKenzie BR, Myers RA. The development of the northern European fishery for north Atlantic bluefin tuna Thunnus thynnus during 1900–1950. Fish Res. 2007;87:229–239. [Google Scholar]

[pone.0021459-Holt1] 4.Holt T, Medley P, Rice J, Cooper J, Hough A. Certification report for South Georgia Patagonian Toothfish longline fishery. 2001. Moody Marine, Ltd., Birkenhead.

[pone.0021459-Kraus1] 5.Kraus SD, Brown MW, Caswell H, Clark CW, Fujiwara M, et al. North Atlantic right whales in crisis. Science. 2005;309:561–562. doi: 10.1126/science.1111200. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Baum1] 6.Baum JK, Myers RA, Kehler DG, Worm B, Harley SJ, et al. Collapse and conservation of shark populations in the Northwest Atlantic. Science. 2003;299:389–392. doi: 10.1126/science.1079777. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Dulvy1] 7.Dulvy NK, Baum JK, Clarke S, Compagno LJV, Cortés E, et al. You can swim but you can't hide: the global status and conservation of oceanic pelagic sharks and rays. Aqua Conserv: Mar Fresh Ecosys. 2008;18:459–482. [Google Scholar]

[pone.0021459-Myers1] 8.Myers RA, Baum JK, Shepherd TD, Powers SP, Peterson CH. Cascading effects of the loss of apex predatory sharks from a coastal ocean. Science. 2007;315:1846–1850. doi: 10.1126/science.1138657. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Fong1] 9.Fong QW, Anderson JL. International shark fin markets and shark management: an integrated market preference-cohort analysis of the blacktip shark (Carcharhinus limbatus). Ecol Econ. 2002;40:117–130. [Google Scholar]

[pone.0021459-Clarke1] 10.Clarke SC, Magnussen JE, Abercrombie DL, McAllister MK, Shivji MS. Identification of shark species composition and proportion in the Hong Kong shark fin market based on molecular genetics and trade records. Conserv Biol. 2006;20:201–211. doi: 10.1111/j.1523-1739.2005.00247.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Bradshaw1] 11.Bradshaw CJA, Fitzpatrick BM, Steinberg CC, Brook BW, Meekan MG. Decline in whale shark size and abundance at Ningaloo Reef over the past decade: the world's largest fish is getting smaller. Biol Conserv. 2008;141:1894–1905. [Google Scholar]

[pone.0021459-Jorgensen1] 12.Jorgensen SJ, Reeb CA, Chappel TK, Anderson S, Perle C, et al. Philopatry and migration of Pacific white sharks. Proc R Soc B. 2010;277:679–688. doi: 10.1098/rspb.2009.1155. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Roman1] 13.Roman J, Palumbi SR. Whales before whaling in the North Atlantic. Science. 2003;301:508–510. doi: 10.1126/science.1084524. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Chevolot1] 14.Chevolot M, Ellis JR, Rijnsdorp AD, Stam WT, Olsen JL. Temporal changes in allele frequencies but stable genetic diversity over the past 40 years in the Irish Sea population of thornback ray, Raja calvata. Heredity. 2008;101:120–126. doi: 10.1038/hdy.2008.36. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Hoelzel1] 15.Hoelzel AR. Looking backwards to look forwards: conservation genetics in a changing world. Conserv Genet. 2010;11:655–660. [Google Scholar]

[pone.0021459-Pardini1] 16.Pardini AT, Jones CS, Noble LR, Kreiser B, Malcolm H, et al. Sex-biased dispersal of great white sharks. Nature. 2001;412:139–140. doi: 10.1038/35084125. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Duncan1] 17.Duncan KM, Martin AP, Bowen BW, De Couet HD. Global phylogeography of the scalloped hammerhead shark (Sphyrna lewini). Mol Ecol. 2006;15:2239–2251. doi: 10.1111/j.1365-294X.2006.02933.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Quattro1] 18.Quattro JM, Stoner DS, Driggers WB, Anderson CA, Preide KA, et al. Genetic evidence of cryptic speciation within hammerhead sharks (Genus Sphyrna). Mar Biol. 2006;148:1143–1155. [Google Scholar]

[pone.0021459-Castro1] 19.Castro ALF, Stewart BS, Wilson SG, Hueter RE, Meekan RE, et al. Population genetic structure of the Earth's largest fish, the whale shark (Rhinocdon typus). Mol Ecol. 2007;16:5183–5192. doi: 10.1111/j.1365-294X.2007.03597.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Karl1] 20.Karl SA, Castro ALF, Lopez JA, Charvet P, Burgess GH. Phylogeography and conseration of the bull shark (Carcharhinus leucas) inferred from mitochondrial and microsatellite DNA. Conserv Genet. 2011;12:371–382. [Google Scholar]

[pone.0021459-Compagno1] 21.Compagno LJV. FAO Species catalogue. 1984. Vol. 4, Parts 1 & 2, Sharks of the World. FAO Fisheries Synopsis.

[pone.0021459-TorresHuerta1] 22.Torres-Huerta AM. Observaciones sobre la biologia reproductiva de la cornuda barrosa, Sphyrna lewini (Griffith y Smith, 1834) (Pisces: Sphyrnidae) en aguas del noroeste de Mexico. 1999. Bachelor Sciences. UNAM. Escuela Nacional de Estudios Profesionales, Iztacala.

[pone.0021459-MartnezOrtz1] 23.Martínez-Ortíz J, Galván-Magaña F, Carrera-Fernández M, Mendoza-Intriago D, Estupiñán-Montaño C, et al. Abundancia estacional de tiburones desembarcados en Manta – Ecuador. In: Martínez-Ortíz J, Galván-Magaña F, editors. Tiburones en el Ecuador: Casos de Estudio. Manta: EPESPO-PMRC; 2007. pp. 9–27. [Google Scholar]

[pone.0021459-Zanella1] 24.Zanella I. Caracterización de la pesca y algunos aspectos sobre la reproducción, alimentación y distribución del tiburón martillo Sphyrna lewini, Sphyrnidae, en el Pacífico de Costa Rica. 2008. Tesis de M. en C., Universidad Nacional de Costa Rica, Instituto Internacional de Conservacion y Manejo de Vida Silvestre.

[pone.0021459-Hayes1] 25.Hayes CG, Jiao Y, Cortés E. Stock assessment of scalloped hammerheads in the Western North Atlantic Ocean and Gulf of Mexico. N Am J Fish Manag. 2009;29:1406–1417. [Google Scholar]

[pone.0021459-Chapman1] 26.Chapman DD, Pinhal D, Shivji MS. Tracking the fin trade: Genetic stock identification in western Atlantic scalloped hammerhead sharks Sphyrna lewini. Endang Species Res. 2009;9:221–228. [Google Scholar]

[pone.0021459-Ovenden1] 27.Ovenden JR, Kashiwagi T, Broderick D, Giles J, Salini J. The extent of population genetic subdivision differs among four co-distributed shark species in the Indo-Australian archipelago. BMC Evol Biol. 2009;9:40–55. doi: 10.1186/1471-2148-9-40. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Hey1] 28.Hey J, Nielsen R. Multilocus methods for estimating population sizes, migration rates and divergence time, with applications to the divergence of Drosophila pseudoobscura and D. persimilis. Genetics. 2004;167:747–760. doi: 10.1534/genetics.103.024182. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Hey2] 29.Hey J, Nielsen R. Integration with the Felsenstein equation for improved Markov chain Monte Carlo methods in population genetics. Proc Natl Acad Sci. 2007;104:2785–2790. doi: 10.1073/pnas.0611164104. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Becquet1] 30.Becquet C, Przeworski M. A new approach to estimate parameters of speciation models with application to apes. Genome Res. 2007;17:1505–1519. doi: 10.1101/gr.6409707. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Becquet2] 31.Becquet C, Przeworski M. Learning about modes of speciation by computational approaches. Evol. 2009;63:2547–2562. doi: 10.1111/j.1558-5646.2009.00662.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Hoelzel2] 32.Hoelzel AR, Shivji MS, Magnussen J, Francis MP. Low worldwide genetic diversity in the basking shark (Cetorhinus maximus). Biol Lett. 2006;2:639–642. doi: 10.1098/rsbl.2006.0513. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Schultz1] 33.Schultz JK, Feldheim KA, Gruber SH, Ashley MV, McGovern TM. Global phylogeography and seascape genetics of the lemon sharks (genus Negaprion). Mol Ecol. 2008;17:5336–5348. doi: 10.1111/j.1365-294X.2008.04000.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Dudgeon1] 34.Dudgeon CL, Broderick D, Ovenden R. IUCN classification zones concord with, but underestimate, the population genetic structure of the zebra shark Stegostoma fasciatum in the Indo-West Pacific. Mol Ecol. 2009;18:248–261. doi: 10.1111/j.1365-294X.2008.04025.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Pereyra1] 35.Pereyra S, Garcia G, Miller P, Oviedo S, Domingo A. Low genetic diversity and population structure of the narrownose shark (Mustelus schmitti). Fish Res. 2010;106:468–473. [Google Scholar]

[pone.0021459-TorresRojas1] 36.Torres-Rojas YE, Hernández-Herrera A, Galván-Magaňa F, Alatorre-Ramírez V. Stomach content analysis of juvenile, scalloped hammerhead shark Sphyrna lewini captured off the coast of Mazátlan, Mexico. Aquat Ecol. 2010;44:301–308. [Google Scholar]

[pone.0021459-Nance1] 37.Nance HA, Daly-Engel TS, Marko PB. New microsatellite loci for the endangered scalloped hammerhead shark, Sphyrna lewini. Mol Ecol Res. 2009;9:955–957. doi: 10.1111/j.1755-0998.2008.02510.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Keeny1] 38.Keeny DB, Heist EJ. Characterization of microsatellite loci isolated from the blacktip shark and their utility in requiem and hammerhead sharks. Mol Ecol Notes. 2003;3:501–504. [Google Scholar]

[pone.0021459-Thompson1] 39.Thompson JD, Gibson TJ, Plewniak F, Jeanmougin F, Higgins DG. Multiple sequence alignment with Clustal X. Trends Biochem Sci. 1998;23:403–405. doi: 10.1016/s0968-0004(98)01285-7. [DOI] [PubMed] [Google Scholar]

[pone.0021459-VanOosterhout1] 40.Van Oosterhout C, Hutchinson WF, Wills DPM, Shipley P. Micro Checker: software for identifying and correcting genotyping errors in microsatellite data. Mol Ecol Notes. 2004;4:535–538. [Google Scholar]

[pone.0021459-Excoffier1] 41.Excoffier L, Laval G, Schneider S. ARLEQUIN ver. 3.0: An integrated software package for population genetics data analysis. Evol Bioinforma Online. 2005;1:47–50. [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Peakall1] 42.Peakall R, Smouse PE. GenAlEx 6: genetic analysis in excel – Population genetic software for teaching and research. 2005. Australian National University, Canberra. [DOI] [PMC free article] [PubMed]

[pone.0021459-Fu1] 43.Fu YX. New statistical tests of neutrality for DNA samples from a population. Genetics. 1996;143:557–570. doi: 10.1093/genetics/143.1.557. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Fu2] 44.Fu YX, Li WH. Statistical tests of neutrality of mutations. Genetics. 1993;133:693–709. doi: 10.1093/genetics/133.3.693. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Rozas1] 45.Rozas JJ, Sánchez-DelBarrio C, Messeguer X, Rozas R. DnaSP, DNA polymorphism analyses by the coalescent and other methods. Bioinforma. 2003;19:2496–2497. doi: 10.1093/bioinformatics/btg359. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Wang1] 46.Wang J. A new method for estimating effective population sizes from a single sample of multilocus genotypes. Mol Ecol. 2009;18:2148–2164. doi: 10.1111/j.1365-294X.2009.04175.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Wang2] 47.Wang J. Estimation of effective population sizes from data on genetic markers. Phil Trans R Soc B. 2005;360:1395–1409. doi: 10.1098/rstb.2005.1682. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Ashley1] 48.Ashley MV, Berger-Wolf TY, Caballero IC, Chaovalitwongse W, DasGupta B, et al. Full sibling reconstruction in wild populations from microsatellite genetic markers. In: Russe AS, editor. Computational Biology: New Research. Nova Science Publishers, Hauppauge; 2008. pp. 231–258. [Google Scholar]

[pone.0021459-Clement1] 49.Clement MD, Posada D, Crandall KA. TCS: a computer program to estimate gene geneologies. Mol Ecol. 2000;9:1657–1660. doi: 10.1046/j.1365-294x.2000.01020.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Templeton1] 50.Templeton AR, Crandall KA, Sing CF. A cladistic analysis of phenotypic associations with haplotypes inferred from restriction endonuclease mapping and DNA sequence data. III Cladogram estimation. Genetics. 1992;132:619–633. doi: 10.1093/genetics/132.2.619. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Posada1] 51.Posada D, Crandall KA. Modeltest: testing the model of DNA substitution. Bioinforma. 1998;14:817–818. doi: 10.1093/bioinformatics/14.9.817. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Tajima1] 52.Tajima F, Nei M. Estimation of evolutionary distance between nucleotide sequences. Mol Biol Evol. 1984;1:269–285. doi: 10.1093/oxfordjournals.molbev.a040317. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Hubisz1] 53.Hubisz MJ, Falush D, Stephens M, Pritchard JK. Inferring weak population structure with the assistance of sample group information. Mol Ecol Res. 2009;9:1322–1332. doi: 10.1111/j.1755-0998.2009.02591.x. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Pritchard1] 54.Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Rogers1] 55.Rogers AR, Harpending H. Population growth makes waves in the distribution of pairwise genetic differences. Mol Biol Evol. 1992;9:552–569. doi: 10.1093/oxfordjournals.molbev.a040727. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Garza1] 56.Garza JC, Williamson EG. Detection of reduction in population size using data from microsatellite data. Mol Ecol. 2001;10:305–318. doi: 10.1046/j.1365-294x.2001.01190.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Dallas1] 57.Dallas JF. Estimation of microsatellite mutation-rates in recombinant inbred strains of mouse. Mamm Genome. 1992;3:452–456. doi: 10.1007/BF00356155. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Weber1] 58.Weber JL, Wong C. Mutation of short human tandem repeats. Hum Mol Gen. 1993;2:1123–1128. doi: 10.1093/hmg/2.8.1123. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Ellengren1] 59.Ellengren H. Mutation-rates in porcine microsatellite loci. Mamm Genome. 1995;6:376–377. doi: 10.1007/BF00364807. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Yue1] 60.Yue GH, Beeckmann P, Geldermann H. Mutation rate at swine microsatellite loci. Genetica. 2002;114:113–119. doi: 10.1023/a:1015189921578. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Martin1] 61.Martin AP, Naylor GJP, Palumbi SR. Rates of mitochondrial evolution in sharks are slow compared with mammals. Nature. 1992;357:153–155. doi: 10.1038/357153a0. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Martin2] 62.Martin AP. Substitution rates of organelle and nuclear genes in sharks: implicating metabolic rate (again). Mol Biol Evol. 1999;16:996–1002. doi: 10.1093/oxfordjournals.molbev.a026189. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Cornuet1] 63.Cornuet JM, Luikart G. Description and power analysis of two tests for detecting recent population bottlenecks from allele frequency data. Genetics. 1996;144:2001–2014. doi: 10.1093/genetics/144.4.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Beaumont1] 64.Beaumont MA. Detecting population expansion and decline using microsatellites. Genetics. 1999;153:2013–2029. doi: 10.1093/genetics/153.4.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Shimoda1] 65.Shimoda N, Knapik EW, Ziniti J, Sim C, Yamada E, et al. Zebrafish genetic map with 2000 microsatellite markers. Genomics. 1999;58:219–232. doi: 10.1006/geno.1999.5824. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Yue2] 66.Yue GH, David L, Orban L. Mutation rate and pattern of microsatellites in common carp (Cyprinus carpio L.). Genetica. 2007;129:329–331. doi: 10.1007/s10709-006-0003-8. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Schug1] 67.Schug MD, Mackay TFC, Aquadro CF. Low mutation rates of microsatellite loci in Drosophila melanogaster. Nature Gen. 1997;15:99–102. doi: 10.1038/ng0197-99. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Rambaut1] 68.Rambaut A, Drummond AJ. 2007. Tracer v1.4, Available: http://beast.bio.ed.ac.uk/

[pone.0021459-Jorde1] 69.Jorde PE, Ryman N. Temporal allele frequency change and estimation of effective size in populations with overlapping generations. Genetics. 1995;139:1077–1090. doi: 10.1093/genetics/139.2.1077. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Corts1] 70.Cortés E, Arocha F, Beerkircher L, Carvalho F, Domingo A, et al. Ecological risk assessment of pelagic sharks caught in Atlantic pelagic longline fisheries. Aquat Living Res. 2010;23:25–34. [Google Scholar]

[pone.0021459-Branstetter1] 71.Branstetter S. Age, growth and reproductive biology of the silky shark, Carcharhinus falciformis, and the scalloped hammerhead, Sphyrna lewini, from the northwestern Gulf of Mexico. Enviro Biol Fish. 1987;19:161–173. [Google Scholar]

[pone.0021459-Piercy1] 72.Piercy AN, Carlson JK, Sulikowski JA, Burgess GH. Age and growth of the scalloped hammerhead shark, Sphyrna lewini, in the north-west Atlantic Ocean and Gulf of Mexico. Mar Freshw Res. 2007;58:34–40. [Google Scholar]

[pone.0021459-Felsenstein1] 73.Felsenstein J. Inbreeding and variance effective numbers in populations with overlapping generations. Genetics. 1971;68:581–597. [Google Scholar]

[pone.0021459-Hey3] 74.Hey J. Isolation with migration models for more than two populations. Mol Biol Evol. 2010;27:905–920. doi: 10.1093/molbev/msp296. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Bulut1] 75.Bulut Z, McCormick CR, Gopurenko D, Williams RN, Bos DH, et al. Microsatellite mutation rates in the eastern tiger salamander (Ambystoma tigrinium tigrinium) differ 10-fold across loci. Genetica. 2009;136:501–504. doi: 10.1007/s10709-008-9341-z. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Hey4] 76.Hey J. On the number of New World founders: a population genetic portrait of the peopling of the Americas. PLoS Biol. 2005;3:e193. doi: 10.1371/journal.pbio.0030193. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Drummond1] 77.Drummond AJ, Rambaut A. BEAST: Bayesian evolutionary analysis by sampling trees. BMC Evol Biol. 2007;7:241–248. doi: 10.1186/1471-2148-7-214. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Lim1] 78.Lim DD, Motta P, Mara K, Martin AP. Phylogeny of hammerhead sharks (Family Sphyrnidae) inferred from mitochondrial and nuclear genes. Mol Phylogenetics Evol. 2010;55:572–579. doi: 10.1016/j.ympev.2010.01.037. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Cappetta1] 79.Cappetta H. Chondrichthes II. Mesozoic and Cenozoic Elasmobranchii; vol. 3B. Handbook Paleoichthyology. Stuttgart: Fisher; 1987. [Google Scholar]

[pone.0021459-Rice1] 80.Rice WR. Analyzing tables of statistical tests. Evol. 1989;43:223–225. doi: 10.1111/j.1558-5646.1989.tb04220.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Lavery1] 81.Lavery S, Moritz C, Fielder DR. Genetic patterns suggest exponential population growth in a declining species. Mol Biol Evol. 1996;13:1106–1113. [Google Scholar]

[pone.0021459-Hu1] 82.Hu Y, Qi D, Wang H, Wei F. Genetic evidence of recent population contraction in the southernmost population of giant pandas. Genetica. 2010;138:1297–1306. doi: 10.1007/s10709-010-9532-2. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Hedrick1] 83.Hedrick PW. Highly variable loci and their interpretation in evolution and conservation. Evol. 1999;53:313–318. doi: 10.1111/j.1558-5646.1999.tb03767.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Palumbi1] 84.Palumbi SR. Population genetics, demographic connectivity, and the design of marine reserves. Ecol Appl. 2003;13:S146–S158. [Google Scholar]

[pone.0021459-Hastings1] 85.Hastings A. Complex interactions between dispersal and dynamics: lessons from coupled logistic equations. Ecology. 1993;74:1362–1372. [Google Scholar]

[pone.0021459-Waples1] 86.Waples RS, Gaggiotti O. What is a population? An empirical evaluation of some genetic methods for identifying the number of gene pools and their degree of connectivity. Mol Ecol. 2006;15:1419–1439. doi: 10.1111/j.1365-294X.2006.02890.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Lowe1] 87.Lowe WH, Allendorf FW. What can genetics tell us about population connectivity? Mol Ecol. 2010;19:3038–3051. doi: 10.1111/j.1365-294X.2010.04688.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Strasburg1] 88.Strasburg JL, Rieseberg LH. How robust are “Isolation with Migration” analyses to violations of the IM model? A simulation study. Mol Biol Evol. 2010:297–310. doi: 10.1093/molbev/msp233. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Beerli1] 89.Beerli P. Effect of unsampled populations on the estimation of population sizes and migration rates between sampled populations. Mol Ecol. 2004;13:827–836. doi: 10.1111/j.1365-294x.2004.02101.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Wares1] 90.Wares JP, Cunningham CW. Phylogeography and historical ecology of the North Atlantic intertidal. Evol. 2001;55:2455–2469. doi: 10.1111/j.0014-3820.2001.tb00760.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Uthicke1] 91.Uthicke S, Benzie JAH. Gene flow and population history in high dispersal marine invertebrates: mitochondrial DNA analysis of Holothuria nobilis (Echinodermata: Holothuroidea) populations from the Indo-Pacific. Mol Ecol. 2003;12:2635–2648. doi: 10.1046/j.1365-294x.2003.01954.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Liu1] 92.Liu JX, Gao TX, Zhuang ZM, Jin XS, Yokogawa K, et al. Late Pleistocene divergence and subsequent population expansion of two closely related fish species, Japanese anchovy (Engraulis japonicus) and Australian anchovy (Engraulis australis). Mol Phylogenet Evol. 2006;40:712–723. doi: 10.1016/j.ympev.2006.04.019. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Marko1] 93.Marko PB, Hoffman JM, Emme SA, McGovern TM, Keever C, et al. The expansion-contraction model of Pleistocene demography: rocky shores suffer a sea change? Mol Ecol. 2010;19:146–169. doi: 10.1111/j.1365-294x.2009.04417.x. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Lamy1] 94.Lamy F, Hebbeln D, Rohl U, Wefer G. Holocene rainfall variability in southern Chile: a marine record of latitudinal shifts of the Southern Westerlies. Earth Planet Sci Lett. 2001;185:369–382. [Google Scholar]

[pone.0021459-Koutavas1] 95.Koutavas A, Lynch-Stieglitz J, Marchitto TM, Sachs JP. El Nino-like pattern in ice age tropical Pacific sea surface temperature. Science. 2002;297:226–230. doi: 10.1126/science.1072376. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Lessios1] 96.Lessios HA, Cubit JD, Robertson DR, Shulman MJ, Parker MR, et al. Mass mortality of Diadema antillarum on the Caribbean coast of Panama. Coral Reefs. 1984;3:173–182. [Google Scholar]

[pone.0021459-Cook1] 97.Cook T, Folli M, Klinck J, Ford S, Miller J. The relationship between increasing sea-surface temperature and the northward spread of Perkinsus marinus (Dermo) disease epizootics in oysters. Estuar Coast Shelf Sci. 1998;46:587–597. [Google Scholar]

[pone.0021459-Aronson1] 98.Aronson RB, Precht WF. White-band disease and the changing face of Caribbean coral reefs. Hyrdobiol. 2001;460:25–38. [Google Scholar]

[pone.0021459-Stoskopf1] 99.Stoskopf MK. Fish Medicine. Philadelphia: W.B. Saunders Company; 1993. 882 [Google Scholar]

[pone.0021459-Smith1] 100.Smith AG, Muhvich AG, Muhvich KH, Wood C. Fatal Fusarium solani infections in baby sharks. Med Mycol. 1989;27:83–91. [PubMed] [Google Scholar]

[pone.0021459-Crow1] 101.Crow GL, Brock JA, Kaiser S. Fusarium solani fungal infection of the lateral line canal system in captive scalloped hammerhead sharks (Sphyrna lewini) in Hawaii. J Wildl Dis. 1995;31:562–565. doi: 10.7589/0090-3558-31.4.562. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Walsh1] 102.Walsh CJ, Luer CA, Bodine AB, Smith CA, Cox HL, et al. Elasmobranch immune cells as a source of novel tumor cell inhibitors: implications for public health. Integr Comp Biol. 2006;46:1072–1081. doi: 10.1093/icb/icl041. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Jackson1] 103.Jackson JBC, Kirby MX, Berger WH, Bjorndal KA, Botsford LW, et al. Historical overfishing and the recent collapse of coastal ecosystems. Science. 2001;293:629–638. doi: 10.1126/science.1059199. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Pinnegar1] 104.Pinnegar JK, Engelhard GH. The ‘shifting baseline’ phenomenon: a global perspective. Rev Fish Biol Fish. 2008;18:1–16. [Google Scholar]

[pone.0021459-Cooke1] 105.Cooke R. Prehistoric nearshore and littoral fishing in the eastern Tropical Pacific: An ichthyological evaluation. J World Prehist. 1992;6:1–49. [Google Scholar]

[pone.0021459-Rick1] 106.Rick TC, Erlandson JM, Vellanoweth RL. Paleocoastal marine fishing on the Pacific coast of the Americas: Perspectives from Daisy Cave California. Am Antiq. 2001;66:595–613. [PubMed] [Google Scholar]

[pone.0021459-Butler1] 107.Butler VL. Changing fish use on Mangaia, Southern Cook Islands: resource depression and the prey choice model. Int J Osteoarchaeol. 2001;11:88–100. [Google Scholar]

[pone.0021459-Allen1] 108.Allen MS. resolving long-term change in Polynesian marine fisheries. Asian Perspect. 2002;41:195–212. [Google Scholar]

[pone.0021459-Allen2] 109.Allen MS, Ladefoged TN, Wall JJ. Traditional Rotuman fishing in temporal and regional context. Int J Osteoarchaeol. 2001;11:56–71. [Google Scholar]

[pone.0021459-Fitzpatrick1] 110.Fitzpatrick SM, Donaldson TJ. Anthropogenic impacts to coral reefs in Palau, Western Micronesia during the Late Holocene. Coral Reefs. 2007;26:915–930. [Google Scholar]

[pone.0021459-Erlandson1] 111.Erlandson JM, Rick TC. Archaeology meets marine ecology: The antiquity of maritime cultures and human impacts on marine fisheries and ecosystems. Annu Rev Mar Sci. 2005;2:231–251. doi: 10.1146/annurev.marine.010908.163749. [DOI] [PubMed] [Google Scholar]

[pone.0021459-Gonser1] 112.Gonser R, Donnelly P, Nicholson G, Di Rienzo A. Microsatellite mutations and inferences about human demography. Genetics. 2000;154:1793–1807. doi: 10.1093/genetics/154.4.1793. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Girod1] 113.Girod C, Vitalis R, Leblois R, Freville H. Inferring population decline and expansion from mimcorsatellite data: a simulation-based evaluation of the MSVAR method. Genetics. 2011 doi: 10.1534/genetics.110.121764. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0021459-Olivieri1] 114.Olivieri GL, Sousa V, Chikhi L, Radespiel U. From genetic diversity and structure to conservation: genetic signature of recent population declines in three mouse lemur species (Microcebus spp.). Biol Conserv. 2008;141:1257–1271. [Google Scholar]

PERMALINK

Demographic Processes Underlying Subtle Patterns of Population Structure in the Scalloped Hammerhead Shark, Sphyrna lewini

Holly A Nance

Peter Klimley

Felipe Galván-Magaña

Jimmy Martínez-Ortíz

Peter B Marko

Roles

Abstract

Introduction

Methods

Ethics Statement

Sampling, DNA extraction, sequencing, and genotyping procedures

Figure 1. Map of Eastern Pacific range of Sphyrna lewini and study area.

Microsatellite and MtDNA diversity

Kinship Analyses

Genetic structure

Demographic analyses

Population divergence times and migration rates

Results

Microsatellite and mtDNA diversity

Figure 2. Haplotype network showing proportion of haplotypes per population.

Relatedness

Genetic structure

Table 1. AMOVA results for all sites, characterizing spatial structure with both mtDNA (ΦST) and microsatellites (FST).

Table 2. Pairwise locus-by-locus AMOVA results characterizing structure based on microsatellites (FST) between all Eastern Pacific sites.

Demographic analyses

Table 3. Mismatch distribution results.

Figure 3. M ratio test results based on microsatellite data for each population.

Table 4. Results from MSVAR (Beaumont 1999) analyses using only microsatellite data.

Table 5. IMa results.

Table 6. IMa results (continued).

Population divergence times and migration

Figure 4. Map showing relative migration rates (Nm) between only adjacent pairs of EP populations.

Discussion

Current and ancestral population sizes

Population differentiation and divergence

Figure 5. Posterior probability density of time since divergence for each population pair analyzed in IMa.

Gene flow

Demographic history of Sphyrna lewini in the Eastern Pacific

Potential factors contributing to population decline

Conclusions

Supporting Information

Acknowledgments

Footnotes

References

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Table 1. AMOVA results for all sites, characterizing spatial structure with both mtDNA (Φ_ST) and microsatellites (F_ST).

Table 2. Pairwise locus-by-locus AMOVA results characterizing structure based on microsatellites (F_ST) between all Eastern Pacific sites.