Automated computation of functional vascular density using laser speckle imaging in a rodent window chamber model

Abstract

We report a methodology for computing functional vascular density within a rodent dorsal window chamber model based on long-exposure laser speckle imaging (LSI). This technique relies on the presence of flow to create detailed vasculature maps. Employing this contrast mechanism is not possible using conventional imaging methods. Additionally, a freeware algorithm for computing functional vascular density (FVD) from images acquired using long-exposure LSI is also described to facilitate ease in adopting this method. We demonstrate that together these tools can be used to compute FVD nearly twelve times faster than manual computation, yet with with comparable accuracy.

INTRODUCTION

For in vivo vascular research, it is often necessary to utilize a simple but informative metric for quantifying the dynamic features of angiogenesis, including flow and vessel density. Functional vascular density (FVD) frequently is used to assess changes in blood and lymphatic vessel density (Dellian et al., 1996; Fukumura et al., 2001; Padera et al., 2002). FVD is defined as the total length of perfused vessels within a region of interest in a two-dimensional image, divided by the area of that region (Schmid-Schoenbein et al., 1977). FVD measurements can be acquired noninvasively and are independent of changes in vessel diameter that result from vasodilation and vasoconstriction. For these reasons, measuring FVD in a tissue of interest over time serves as a simple and robust method for tracking tissue perfusion.

FVD is typically calculated in a manual fashion from images of vasculature. With this approach, the researcher must visually determine the extent of all perfused vessels within an image. This process is time intensive, and introduces errors due to the difficulty in discriminating between vessels and artifacts and selecting the vessel midline for length summation. A robust, automated method for calculating FVD from images of vessels would improve computational accuracy, consistency, and speed.

To this end, we describe a new methodology for measuring FVD using images acquired with long-exposure laser speckle imaging (LSI) (Boas and Dunn, 2010; Briers, 2001; Choi et al., 2004). LSI is a full-field imaging technique used to create in vivo maps of relative blood flow. This is achieved by illuminating a sample that contains moving optical scatterers such as red blood cells, with a diffuse laser beam. A time-varying speckle pattern is created due to scatterer motion. When this speckle pattern is imaged using a CCD camera with a finite exposure time, the movement of scatterers causes blurring of the speckle pattern in the acquired image. The degree of blurring can be quantified at each pixel as a speckle contrast value, K, which is correlated with relative flow dynamics. K is defined as

$$K=\frac{\sigma }{<I>}$$ (1)

where σ is the standard deviation and <I> the average intensity of a group of pixels.

We demonstrate that high-resolution images of perfused vessels can be acquired with long-exposure LSI using common laboratory equipment, and that these images can be used to compute FVD. We additionally show that this method for computing FVD is faster than, yet has comparable accuracy to manual computation.

MATERIALS AND METHODS

Collection of raw speckle images

Raw speckle images were collected by transilluminating the dorsal window chambers of anesthetized mice with the expanded beam of a 30 mW 633 nm HeNe laser. Images of the speckle pattern were acquired with a CCD camera (Nuance, Cambridge Research Instruments, Woburn, MA). Image exposure time was adjusted manually and illumination intensity was adjusted with a polarizer-analyzer setup to utilize the full dynamic range of the camera for the given exposure time. Care was taken to assure that each speckle at the detector was sampled by at least two CCD pixels, to satisfy the Nyquist criterion (Kirkpatrick et al., 2008).

Generation of speckle contrast maps

K typically is computed from raw speckle images with algorithms based on either the temporal or spatial statistics of the imaged speckle pattern. With temporal analysis, multiple images of the sample are acquired in series. The intensity of a single pixel, I(i,j,n), is chosen for n collected images and used to compute K using Eq. (1). This operation is performed at each pixel coordinate (i,j) to create a single map of K. This temporal method was used for all FVD computations because it results in maps of K which exhibit higher spatial resolution compared to the spatial analysis method (Cheng et al., 2003). All computation was performed using custom-written MATLAB software (m-file available online at http://choi.bli.uci.edu/software.html).

Computation of functional vascular density

Following generation of maps of K, FVD of each map was computed using an image processing algorithm written in MATLAB (m-file available online at http://choi.bli.uci.edu/software.html). Briefly, the vessel edges in a given image are first accentuated by using a low-pass filter and the resultant image subtracted from the original image. The result is then thresholded for intensity and object size to isolate vessels and remove noise. A median filter to smooth vessel edges is then applied to the binary image. The resulting image is then skeletonized so that all objects are reduced to one pixel in diameter along the medial axis, and FVD is computed by summing the length of all vessels divided by the area of the region of interest. The steps of this algorithm are outlined in Fig. 1.

Figure 1.

Steps for calculating FVD from map of K. (a) original map of K, (b) edge emphasis, (c) intensity thresholding, (d) size thresholding, (e) skeletonization. Computed FVD value is 0.347 μm⁻¹. Scale bar = 500 μm.

Verification of functional vascular density computation algorithm

For verification of the FVD computation algorithm, three mouse dorsal window chambers were imaged using long-exposure LSI. Three regions of interest in each window chamber were selected and used to compute FVD both manually and using the FVD computation algorithm. A paired t-test was used to assess the significance of the difference between these two methods.

RESULTS AND DISCUSSION

Imaging of functional blood vessels using laser speckle imaging

Maps of K generated using both temporal and spatial statistics for various exposure times can be seen in Fig. 2. Maps of K generated using temporal statistics exhibit vessel contrast comparable to the white light transillumination image (Fig. 2C and G) and exhibit higher spatial resolution than the corresponding maps of K generated using spatial statistics (Fig. 2H and I). This higher resolution facilitates accurate FVD computation. The resolution difference in the maps of K generated using spatial versus temporal statistics arises from the need to use a sliding window operator to compute K, which inherently decreases spatial resolution when using spatial statistics.

Figure 2.

Maps of K generated using temporal (a–c) and spatial (d–f) correlation. The corresponding white light transillumination image can be seen in (g). The red circle in (g) indicates the area treated with a pulsed laser to induce the cessation of flow via photocoagulation. Highlighted sections of (c) and (f) (size: 1.23 × 1.12 mm) can be seen magnified (h) and (i), respectively. Exposure times are: (a) and (d), 10 ms, (b) and (e), 100 ms, (c) and (f), 1000 ms. Scale bar = 1 mm.

Contrast in maps of K results from the movement of red blood cells. Vessels that do not exhibit flow are therefore not visualized using LSI, unlike what is observed with either white light reflectance or transillumination images in which contrast is achieved via optical absorption. This principle is demonstrated in Fig. 2C and G, where vessels within the red circle in G have been photocoagulated to induce cessation of blood flow. The treated vessels remain visible in the white light transillumination image in G, but are not present in the LSI image and thus do not contribute to the FVD calculation. By definition, FVD considers only vessels that are actively contributing flow at a particular point in time; thus, selecting only perfused vessels is imperative for the accurate calculation of FVD. This is particularly important because vessels, especially in tumors, can exhibit intermittent or complete cessation of flow (Vaupel et al., 1989).

Fig. 2A–F demonstrate that maps of K exhibit increased vessel resolution for increased image exposure time. Exposure times used in LSI typically range from 1 to 10 ms and generally are chosen to match the correlation time of the intensity fluctuations in the imaged speckle pattern (Briers, 2001). The rationale for such a choice is elucidated by analyzing the following equation for K (Bandyopadhyay et al., 2005; Fercher and Briers, 1981):

$$K^2=\frac{2}{T{\langle I\rangle }^2}\underset{0}{\overset{T}{\int }}\left(1-\frac{\tau }{T}\right)C_t(\tau )d\tau$$ (2)

where T is the camera exposure time and C_t(τ) is the autocovariance of the temporal fluctuations in the intensity of a single speckle. If the following definition of speckle correlation time is used (Mandel, 1981):

$${\tau }_c=\underset{-\infty }{\overset{\infty }{\int }}{\mid \gamma (t)\mid }^{2}dt$$ (3)

where is γ(t) the normalized autocorrelation function of the laser light remitted from the sample and is chosen as a Gaussian velocity distribution appropriate for describing ordered flow within blood vessels (Ramirez-San-Juan et al., 2008), we can then describe K as:

$$K={\left[\frac{1}{2}\frac{{\tau }_c}{T}\mathit{erf}\left({\pi }^{1/2}\frac{T}{{\tau }_c}\right)\right]}^{1/2}$$ (4)

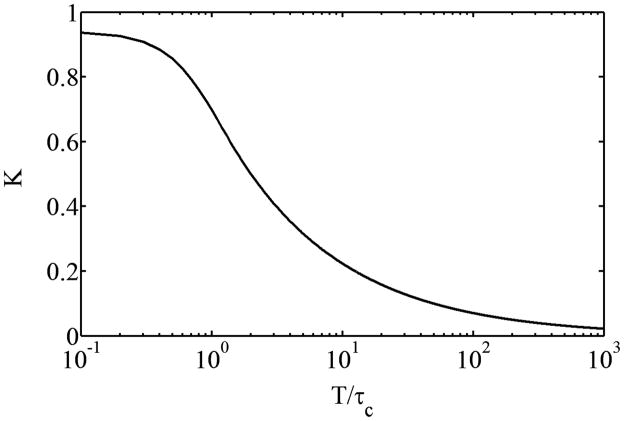
A plot of T/τ_c versus K is shown in Fig. 3 and demonstrates that maximum sensitivity of K to changes in τ_c, or specifically changes in flow, is achieved when T is chosen to be comparable to τ_c.

Figure 3.

Plot of K versus T/τ_c based on Eq. 4.

Accurate FVD calculation relies on identification of all functional vessels within a region of interest. The slower flow (and hence longer τ_c) in vessels such as capillaries and venules necessitates the use of longer exposure times to achieve an adequate decrease in K. The use of long exposures (T>100 ms) during LSI therefore is appropriate for visualizing vessels with a larger range of sizes than conventional LSI. We have found that an exposure time of 1000 ms is adequate for imaging all resolvable vasculature in the rodent dorsal window chamber. Longer exposure times do not enhance the ability to resolve vessels and thus increase FVD (data not shown). The use of long exposure times, however, minimizes the sensitivity of K to relatively high flows in a region of interest, making long-exposure LSI appropriate only for analyzing vessel structure and not for quantification of flow within identified vessels. Additionally, the use of long exposure times during LSI also increases sensitivity to Brownian motion both within vessels and the surrounding tissue. This effect is small enough, however, that occluded blood present in the window shown in Fig. 2 did not contribute to the computed FVD, indicating that the correlation time of the blood within occluded vessels remained longer than that of the surrounding functional vessels.

Although the quantitative nature of LSI is limited due to simplifying assumptions associated with describing the dynamic interaction between scattered light and tissue, inaccuracies resulting from these assumptions are mitigated by analyzing only vessel structure rather than relative flow. For example, the effects of scattering from static features, which is not accounted for in Eq. 4, are largely reduced by utilizing temporal statistics rather than spatial statistics when computing K because their temporal contribution is ideally zero (Li et al., 2006). Additionally, the effect of photons undergoing multiple scattering events may affect the apparent size of vessels (Zakharov et al., 2006), but this effect is minimized during the skeletonization step of FVD computation using the described algorithm provided that vessel resolution is not lost.

Automated computation of functional vascular density using speckle contrast maps

Nine maps of K were acquired as described above and used to compute FVD manually and using an automated algorithm. A paired t-test indicated that the difference in the computed FVD values was not statistically significant (p = 0.571). The average difference between these methods was 6.1 ± 3.3%, indicating a small positive systematic bias that resulted in slightly larger algorithm-computed FVD values compared to the corresponding manually-computed values. However, unlike manual FVD computation, which introduces inter-user bias as well as variable bias from a single user, the presented algorithm exhibits repeatable bias. This error likely arises from imperfect intensity and size thresholding, which causes background pixels to be registered as vessel pixels, thus artificially increasing the computed FVD. Such artifacts can be reduced by using more complex image processing techniques which are less sensitive to noise such as utilizing matched filters for vessel isolation (Chaudhuri et al., 1989). However, the slight reduction in noise would come at the expense of computation time and simplicity. Finally, manual computation of FVD in the three analyzed window chambers took an average of 21.3 ± 3.8 min, whereas automated FVD computation took an average of 1.8 ± 0.3 min, a nearly 12-fold improvement in time.

CONCLUSIONS

In conclusion, we have demonstrated a novel method for calculating FVD in a rodent dorsal window chamber based on long-exposure LSI. This method is capable of producing detailed maps of functional vessels at a spatial resolution ranging from capillaries to venules via selection of proper CCD camera exposure time, magnification, and lens numerical aperture. Because vessel visualization with LSI is dependent on moving particles, discrimination of vessels with and without flow can be achieved, which is not possible using conventional transmission and reflectance imaging. Finally, this method can be easily adopted due to the relatively small cost, wide availability of the equipment required (laser, diffuser, and CCD camera), and ease and flexibility in image acquisition (reflection geometry, transmission geometry, lack of stringent alignment requirements).

• Long-exposure laser speckle imaging used to create detailed vasculature maps.

• Flow detection facilitates accurate computation of functional vascular density.

• Presented algorithm computes functional vascular density from vasculature maps.

• Algorithm is nearly 12-fold faster and comparably accurate to manual computation.