Rigid substructure search

Abstract

Motivation: Identifying the location of binding sites on proteins is of fundamental importance for a wide range of applications, including molecular docking, de novo drug design, structure identification and comparison of functional sites. Here we present Erebus, a web server that searches the entire Protein Data Bank for a given substructure defined by a set of atoms of interest, such as the binding scaffolds for small molecules. The identified substructure contains atoms having the same names, belonging to same amino acids and separated by the same distances (within a given tolerance) as the atoms of the query structure. The accuracy of a match is measured by the root-mean-square deviation or by the normal weight with a given variance. Tests show that our approach can reliably locate rigid binding scaffolds of drugs and metal ions.

Availability and Implementation: We provide this service through a web server at http://erebus.dokhlab.org.

Contact: dokh@unc.edu

1 INTRODUCTION

The protein crystal structures database contains a number of proteins whose functional role is not fully understood. Identifying potential binding sites of small molecules or metal ions will allow optimizing docking protocols and may also help to elucidate the unknown protein functions. Here we introduce a server for identifying similar 3D protein substructures via direct comparison with a query structure.

Analogous studies have targeted the identification of protein folding motifs (Kato and Takahashi, 1997; Shi et al., 2007), protein similarity detection (Stivala et al., 2009), search of protein docking and ligand binding sites (Capra et al., 2009; Konc and Janežič, 2010) and search of protein surface motifs (Yin et al., 2009). Here we focus on the search of a unique substructure of a larger protein with a known crystal structure.

The problem of substructure search is a special case of the subgraph isomorphism (SI) problem (Ullmann, 1976). The SI problem is well studied, and optimized algorithms have been proposed to solve it (Eppstein, 1999; Ullmann, 1976). However, here we incorporate tolerance to deviations from the query substructure, possibly at the cost of speed or specificity. We permit small differences between the pairwise distances of atoms in the query and the target structures, or allow some query atoms to be absent in the identified substructure. In order to achieve this aim, we capitalize on the properties of proteins graphs to significantly simplify the subgraph search. We make use of (i) the minimal degeneracy of atom pairs in a protein, that is, a small number of identical atoms in identical residues separated by the same distance, if this distance is much larger than a covalent bond length and (ii) the fact that both query substructure and protein structure are represented by complete graphs, that is, have known distances between all pairs of atoms. In other words, when searching for the matching substructure, we need to look only among a small number of atoms, additionally constrained by atom names and residue types. These properties reduce the SI problem complexity as compared to the NP-hard general SI problem, so that utilization of Ullmann's algorithm is not required, although in the future it may be used to improve performance.

The limitation of our method is its focus on the search of rigid structures, as it does not enumerate rotational isomers or account for backbone flexibility. Our approach is also not a strict solution, in the sense that it may report a noticeable amount of poor matches, especially in the case of loose search conditions. However, high-quality matches will not be omitted, irrespective of their relative orientation to the query structure. Another important benefit of our approach is its high performance (see inset in Fig. 2).

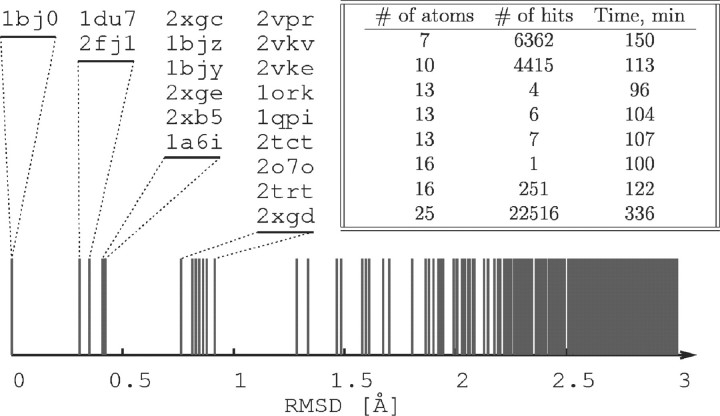
Fig. 2.

Root mean square deviation (RMSD) of seven query atoms in substructures found in various proteins. All substructures found in tetracycline repressors have RMSD < 1 Å. The corresponding PDB IDs are listed in the order of increasing RMSD. The inset shows run times as a function of the number of query atoms and the number of matches. The run times were measured on a 16-core 2.1 GHz workstation.

2 DESCRIPTION

The web interface is written in a combination of PHP and Java-script. The input consists of the query structure in Protein Data Bank (PDB) format, which must list heavy atoms (hydrogen atoms are ignored) in ATOM or HETATM records. Important fields are: atom name, residue ID, residue name, coordinates and atom occupancy. Order of atoms and residues is not important. Numeric id of a residue is used only to define whether the corresponding atoms must belong to the same or different residues. A special wild-card residue name ‘ANY’ may be used to match atoms irrespective of residue type, e.g. when the query includes backbone atoms. Chain ID and atom ID are not used in the search, but are saved and copied to the output files. The guidelines for designing a query structure are: (i) minimize the number of query atoms by selecting only those atoms critical for pocket or scaffold formation; and (ii) choose atoms with large pairwise distances. The occupancy field is interpreted as the relative weight w_j of the atom when search conditions allow for one or more query atoms to be missing in the identified substructure.

The other parameters are matching precision (σ) and weight threshold (W_min). These parameters control the accuracy of matching by affecting the atom pair selection criterion; a pair of atoms j in the target structure is considered to be a potential match for a pair i in the query, if:

(1)

where Δq_i is the distance between the i-th pair of atoms in the query, Δt_j is the distance between the j-th pair of atoms in the target structure and W_i is the weight of i-th pair in the matching substructure.

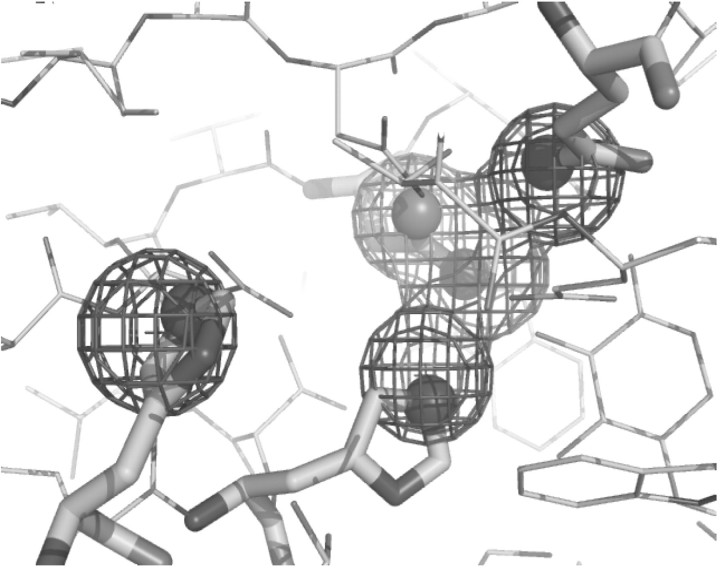
Program output is provided in two formats: plain text and PyMOL script. The plain text output gives the PDB ID of the structure containing the matching substructure, the model index, the substructure atoms and residues, the root-mean-square deviation from the query, the subgraph weight and the transformed coordinates of the query atoms. The PyMOL script contains instructions for the PyMOL viewer to download the crystal structure, select the matching substructure atoms and show them as spheres, load the transformed query atoms and show them as a mesh surface, and orient the protein for the best view of the identified substructure, as shown in Figure 1.

Fig. 1.

The identified target substructure. Query atoms are indicated by a mesh surface, and their matching target atoms are shown as spheres.

3 DISCUSSION

Our implementation of the substructure search avoids the use of any SI algorithms, as the incorporation of tolerance to variations in atom identities and interatomic distances is not readily compatible with these algorithms. Instead, we employ an iterated sorting and filtering scheme, which first scans the target structure and collects those atom pairs that have an equivalent pair of atoms with matching distance as in the query structure. These collected candidate pairs are then used to construct candidate substructures, followed by the selection of the best matching substructures based on their weights. Substructure weight is defined as the geometric mean of weights W_i of all N atom pairs in the substructure, multiplied by an additional penalty (1 − w_j), where w_j is the weight of a missing atom, to account for up to M of such atoms:

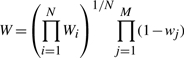(2)

The tolerance to deviations in atom pair distances is an important requirement, as the available crystal structures have limited resolution and the conformation of a binding pocket undergoes constant thermal fluctuation. Available computational power imposes a practical limit on the tolerance that can be handled by our algorithm; a higher tolerance results in a larger number of matches, and therefore an increased structure processing time. We show that we can accurately locate the binding pockets for small molecules (drugs, poisons and ADP), scaffolds for metal ions and, in certain cases, the binding sites of short peptides. To illustrate these results, we have prepared a test query structure using the following seven atoms of the tetracycline binding pocket from tetracycline repressor (PDB ID 1BJ0): H64 NE2, N82 ND2, N82 OD1, F86 CE1, F86 CE2, H100 NE2 and Q116 NE2. We perform a search for this substructure with a tolerance of σ = 2 Å on the entire PDB, current as of October 12, 2010, which at this time contains a total of 20 tetracycline repressor structures and 68 000 protein structures (2 × 10⁵ models) overall. Our method locates 18 of these structures (Fig. 2), and it is interesting to note that not all of these structures have tetracycline bound. The two tetracycline repressor structures (2NS7 and 2NS8) that we did not identify have active site conformations very different from other tetracycline repressors, most likely caused by mutations introduced in residues near the binding site.

Finally, we point out that our method is not limited to the detection of surface features, and can also detect buried substructures. By providing information on proteins containing specified atoms and residues in the given spatial arrangement, Erebus may serve as the first step in many structure analysis protocols.

Funding: National Institutes of Health (grant numbers R01GM080742, ARRA supplements GM080742-03S1 and GM066940-06S1 to N.V.D.).

Conflict of Interest: none declared.