COSINE: COndition-SpecIfic sub-NEtwork identification using a global optimization method

Abstract

Motivation: The identification of condition specific sub-networks from gene expression profiles has important biological applications, ranging from the selection of disease-related biomarkers to the discovery of pathway alterations across different phenotypes. Although many methods exist for extracting these sub-networks, very few existing approaches simultaneously consider both the differential expression of individual genes and the differential correlation of gene pairs, losing potentially valuable information in the data.

Results: In this article, we propose a new method, COSINE (COndition SpecIfic sub-NEtwork), which employs a scoring function that jointly measures the condition-specific changes of both ‘nodes’ (individual genes) and ‘edges’ (gene–gene co-expression). It uses the genetic algorithm to search for the single optimal sub-network which maximizes the scoring function. We applied COSINE to both simulated datasets with various differential expression patterns, and three real datasets, one prostate cancer dataset, a second one from the across-tissue comparison of morbidly obese patients and the other from the across-population comparison of the HapMap samples. Compared with previous methods, COSINE is more powerful in identifying truly significant sub-networks of appropriate size and meaningful biological relevance.

Availability: The R code is available as the COSINE package on CRAN: http://cran.r-project.org/web/packages/COSINE/index.html.

Contact: hongyu.zhao@yale.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Various statistical methods exist for comparative analysis of two or more sets of microarray data. Based on how prior knowledge is utilized, these methods can be generally classified into four categories [a similar classification scheme was presented in Nacu et al. (2007)]: (i) single gene-based differential expression analysis. These methods start by quantifying the level of differential expression of individual genes using various statistics [for a comprehensive review, see Dudoit et al. (2002)]. Genes with significant P-values are then checked for enrichment in predefined biological processes or pathways using annotation tools such as DAVID (Dennis et al., 2003; Huang et al., 2009). This approach is simple and intuitive. However, the choice of a significance level for the P-values can be arbitrary, and this approach ignores the dependency between genes. (ii) Gene set-based differential analysis, among which the Gene Set Enrichment Analysis (Subramanian, et al., 2005) is a well-known example. For a good review and method comparison, see Ackermann and Strimmer (2009). This class of approaches has the advantage of clear biological interpretation; however, it relies on the prior knowledge of gene sets (genes in the same pathway or related to the same disease), which is still far from being complete and accurate. Moreover, under many circumstances, only a subset of genes in a pathway exhibit expression alterations, and testing on the whole set may give rise to false negatives (Yan and Sun, 2008). (iii) Topology-based gene co-expression network analysis. Horvath and colleagues developed the weighted gene co-expression network analysis, WGCNA (Langfelder and Horvath, 2008), which is a clustering method taking into account topological similarity between genes. However, for high-dimensional datasets (e.g. > 1000 genes), clustering methods may lead to very large modules, making interpretation based on gene ontology (GO) annotation less informative. (iv) Responsive sub-network identification using graph search methods. Here the goal is to identify a subset of genes showing condition-specific changes. This class of methods has two main components: a scoring function quantifying the alternation of a given sub-network between different conditions, and a search algorithm to extract the highest scoring sub-networks. The seminal work of Iderker et al. (2002) used sum of z-score (which is the standard normal inverse of a single gene's P-value) adjusted for the size of the sub-network as the scoring function, and employed simulated annealing to search for the best sub-networks. Guo et al. (2007) used an edge-based scoring function rather than node score to account for gene–gene correlation. Due to the non-deterministic polynomial-time hard (NP-hard) nature of the problem of finding the maximal-scoring connected sub-graph, it can only be approached by heuristic or approximate methods. Apart from simulated annealing, previous studies have also employed local greedy search algorithms (Breitling et al., 2004; Nacu et al., 2007; Rajagopalan and Agarwal, 2005; Ulitsky et al., 2008) and various mathematical programming or graph theory-based exact approaches. For example, Qiu et al. (2009) used a mixed integer linear programming model to identify differentially expressed pathways. Dittrich et al. (2008) transformed the problem into the well-known prize-collecting Steiner tree problem (PCST). Wang and Xia (2008) incorporated both nodes and edges in their scoring function and used an iterative algorithm to solve the local optimization problem. Qiu et al. (2010) exploited a regression model with diffusion kernel to detect disease-associated modules and to prioritize responsive genes.

The last category of methods requires little prior knowledge and has great flexibility in terms of differential expression analysis. However, except for Wang and Xia (2008), methods in this class consider either node or edge, but not both, in their scoring functions (Wu et al., 2009). This can be inefficient since many studies have demonstrated that disease conditions are marked not only by differential expression of single genes, but also by alterations in the gene pair correlation or other higher order topologies (Barrenas et al., 2009; Feldman et al., 2008; Franke et al., 2006; Goh et al., 2007; Kohler et al., 2008; Krauthammer et al., 2004; Lee et al., 2008; Linghu et al., 2009; Park et al., 2009; Wu et al., 2008). The necessity of taking a network perspective in identifying disease-related sub-networks was also implicated in a study of type 2 diabetes (Liu et al., 2007), in which the authors failed to detect transcriptionally altered insulin-signaling gene sets using single gene-based state of the art methods such as DEA and GSEA. As for the method of (Wang and Xia, 2008), it was not designed for expression data analysis and it aims at identifying many small locally optimal sub-networks rather than a globally optimal one.

The proposed method COSINE is, to our knowledge, the first algorithm (i) that considers the weighted contribution of both nodes and edges inspired by network alignment studies; and (ii) that searches for the single globally optimal sub-network, which may perform better than those selecting many locally optimal sub-networks. In the following, we first describe the basic methodology of COSINE and then show its applications to both simulated and real datasets.

2 METHODS

2.1 The scoring function of COSINE

Given two or more microarray expression profiles under different conditions (several tissue types, normal versus diseased samples, etc.), COSINE aims to identify a sub-network of genes showing maximal alternation in terms of the holistic expression pattern. The whole background network is represented as a graph G = (V, E), where V represents all the nodes and E represents all the edges. For each node, the F-statistic is used to measure the differential expression of each gene. Let g denote the number of different groups, x_ij denote the j-th observation of gene X in the i-th group, n_i denote the sample size of the i-th group, be the sample mean of gene X of the i-th group, be the sample mean of all observations, where i = 1, 2,…, g and j = 1, 2,…, n_i and n is the total number of observations. The F-statistic is computed as:

For each edge, the Expected Conditional F-statistic (ECF-statistic) is used to measure the differential gene–gene co-expression across different groups. For a detailed derivation of the ECF-statistic, see Lai et al. (2004). Assuming a bivariate normal distribution of two genes X and Y in the i-th group,

The ECF-statistic of gene X given the expression value of gene Y E_Y(F_X|Y=y) is calculated as:

The ECF-statistic of an edge linking genes X and Y is defined as:

The F-statistic and ECF-statistic are then standardized against the whole pool of nodes/edges to generate the node score and edge score used in the scoring function as follows:

Let G′ = (V′, E′) denote a sub-network of G with size k, where E′ represents all the edges connecting the k nodes in V′. The score of G′ is:

λ(0 ≤ λ ≤ 1) is a weight parameter controlling the respective contribution of the edge score and node score, whereas the denominator adjusts for the size of the sub-network. In cases where the protein–protein interaction (PPI) network is used to define the existence of an edge, we simply change the denominator of the edge score term to the square root of the total number of edges in the selected sub-network.

2.2 Using the genetic algorithm to search for the highest scoring sub-network

Extraction of the highest scoring sub-network is identical to the global optimization problem of finding a binary vector of length p (the total number of genes) where the i-th element in the vector being 1 corresponds to this gene being included in the sub-network; and 0 otherwise. Since the size of the search space is 2^p, it is computationally prohibitive to perform an exhaustive search when p is large. The genetic algorithm is a global search algorithm commonly used on high-dimensional binary optimization. It takes the binary vectors as chromosomes and mimics the genetic recombination, mutation and other evolutionary processes to search for the highest scoring binary vector. Important parameters in the genetic algorithm include: (i) mutation rate: the probability that a gene in the chromosome mutates; (ii) zero to one ratio: the ratio of number of 0s to number of 1s on the binary chromosome for mutations and initiation, which is used to control the number of genes selected; (iii) population size: the number of individuals in each iteration; and (iv) elitism: the number of chromosomes kept into next generation. The function ‘rbga.bin’ in the R package ‘genalg’ is used in our application of the genetic algorithm.

2.3 Simulated data

To investigate the performance of our approach, we simulated seven datasets, including one reference dataset (called control in the following) and six datasets to be compared to the control dataset (called case datasets in the following), from multivariate normal distributions. These seven datasets had different means and covariance matrices, where the variances were fixed at 1. Each dataset consists of 500 genes and 20 samples. We use μ to denote mean and ρ to denote correlation coefficient. Compared to the control dataset, a total of 50 genes formed the condition-specific sub-network for case datasets 2, 3, 4, 5 and the sub-network consisted of 40 genes in the case dataset 6. The case dataset 1 serves as the negative control where the data were generated in the same way as the control dataset. More details are given below for these seven datasets.

Control group: μ = ρ = 0 for all genes (to be compared with each of the six case sets for the identification of the optimal sub-network).

Case set 1: μ = ρ = 0 for all genes (negative control).

Case set 2 (both differential expression and differential correlation): Gene 1 to Gene 50 have μ = 0.75, and ρ = 0.6 between each gene pair; the other 450 genes have μ = ρ = 0.

Case set 3 (only differential expression, no differential correlation): Gene 1 to Gene 50 have μ = 0.75, and ρ = 0 between each gene pair; the other 450 genes have μ = ρ = 0.

Case set 4 (only differential correlation, no differential expression): Gene 1 to Gene 50 have μ = 0, and ρ = 0.6 between each gene pair; the other 450 genes have μ = ρ = 0.

Case set 5: Gene 1 to Gene 25 have μ = 0.75, and ρ = 0.6 between each pair; Gene 26 to Gene 50 have μ = −0.75 and ρ = 0.6 between each pair of them; ρ = −0.6 between any gene from 1 to 25 and any gene from 26 to 50. The other 450 genes have μ = 0 and ρ = 0 (differential correlation and differential expression with both up and down regulation).

Case set 6: 10 genes from each of set 2, set 3, set 4 and set 5, the other 460 genes from set 1 (mixed pattern of differential expression and differential correlation).

We also conducted simulations based on the observed covariance matrices from the obesity dataset and this is described in the Supplementary Material.

2.4 Real data

1. PPI data: we used the database of HPRD (Human Protein Reference Database, http://www.hprd.org/download), Release 9, 2010 (Keshava Prasad et al., 2009; Mishra et al., 2006; Peri et al., 2003). After excluding self-interactions, there remained 37 080 binary PPIs involving 9465 genes.

2. Prostate cancer (PC) data: this gene expression omnibus (GEO) dataset, GSE3933 (Lapointe et al., 2004), contains the gene expression profiles of 71 prostate tumor samples and 41 normal samples. First, we selected the common probes covered by the three arrays. Then within each array, we imputed missing values for each probe using the mean of available observations and the data was normalized to have mean 0 and SD 1. We computed the expression of genes as the mean value of the expression level of probes mapped to that gene. For the following analysis, we only considered the genes that are also included in the PPI network, which consists of 5335 genes (nodes) and 18 249 interactions (edges).

3. Genes for analysis in (4) and (5): since the original dataset contained a large number of genes (> 10 000), it is computationally too demanding to analyze them all. Meanwhile, we are more interested in the genes related to various diseases and quantitative traits. Therefore, we collected a candidate gene list from ‘A Catalog of Published Genome-Wide Association Studies’ at the National Human Genome Research Institute (http://www.genome.gov/gwastudies/). We used all the annotated genes in this catalog as of 2/1/2010, which consists of 1667 genes associated with 265 traits.

4. Tissue expression data of morbidly obese patients: this dataset collects the whole genome expression profile of liver, omental and subcutaneous adipose tissues of a large sample of morbidly obese individuals [more details can be found in Zhong et al. (2010)]. The original data were measured on 40 638 probes. For simplicity, we focused on the 456 subjects with data available for all three tissue types and the subset of 1667 genes in (3) covered by the probes (when one gene is covered by more than one probe, we used the mean expression value of the multiple probes to represent the expression levels of that gene). We then excluded genes with > 10% missing observations and subjects with > 10% missing genes. The remaining missing values were imputed using the mean of available samples. After processing, there remained 420 subjects and 1327 genes for analysis.

5. HapMap expression data of Asian (CHB+JPT) (ASN), CEUP and YRIP samples: expression data of Epstein-Barr virus (EBV)-transformed lymphoblastoid cell lines of individuals used in the phases I & II of the HapMap project (Stranger et al., 2007). We considered the populations of ASN [combination of 45 Han Chinese in Beijing, China (CHB) and 45 Japanese in Tokyo, Japan (JPT) individuals], CEPH (Utah residents with ancestry from northern and western Europe) (CEU)-parents (60 individuals) and Yoruba in Ibadan, Nigeria (YRI)-parents (60 individuals) because they are genetically unrelated. We first conducted rank and inverse standard normal transformations of the data within each population while keeping the original mean and SD of each gene, using the method described by (Li, 2002). The total number of probes is 40 273. After a data filtering procedure similar to that described above, there remained 1145 genes to be analyzed for the 210 subjects.

2.5 Choice of weight parameter λ

An appropriate choice of λ is essential for the scoring function and optimization result. In order to achieve a reasonable balance between the node and edge scores, we first compared the magnitude of the ‘edge_score_term’ and ‘node_score_term’:

using the Case set 1 and the Control Group simulated as described in Section 2.3. For each of the 11 k values ranging from 25 to 75 by a step size of 5, 2000 sub-networks were randomly sampled from the background pool of 500 genes, generating 11 populations of both score terms. The distribution plots (Supplementary Figures S1 and S2) show that sub-networks of different sizes share similar distributions for the two score terms. A further look at the distribution of (Supplementary Figure S3) shows that the majority (> 95% of the 2000 log-ratio values for each k) fall in the region of (−0.5, 1.5). We then calculated the five quantiles (minimum, 25%; median, 75%; and maximum) of the log-ratios for each population, and averaged each quantile across the 11 populations, denoted as vector r, in order to get a reasonable estimate of the quantiles for networks of different sizes. Accordingly, we set . See Table 1 for the values of r and λ used in this article.

Table 1.

Quantiles of and λ

Log-Ratio	Min.	1st Qu.	Median	3rd Qu.	Max.
Set 1	−2.50	0.48	0.59	0.69	3.36
Prostate	−3.12	−0.35	0.03	0.41	3.09
new_simu	−1.81	0.44	0.68	0.87	2.98
LO	−2.54	0.13	0.52	0.95	3.64
LOS	−2.12	0.35	0.73	1.14	3.52
ACY	−2.26	0.42	0.81	1.19	3.89
Lambda	Min.	1st Qu.	Median	3rd Qu.	Max.
Set 1	0.0004	0.17	0.21	0.25	0.9968
Prostate	0.0008	0.28	0.48	0.69	0.9992
new_simu	0.0010	0.13	0.17	0.27	0.9848
LO	0.0002	0.10	0.23	0.43	0.9971
LOS	0.0003	0.07	0.16	0.31	0.9925
ACY	0.0001	0.06	0.13	0.28	0.9946

new_simu: new simulation dataset with real covariance matrices; LO: liver–omental data comparison; LOS: three tissue data comparison; ACY: ASN–CEUP–YRIP data comparison. The size of randomly sampled sub-networks for LO/LOS/ACY is from 100 to 150 by the interval of five.

As to the final choice of λ among the five quantiles, we used the following procedure: (i) randomly sample a large number (e.g. 10 000) of sub-networks with sizes ∼10% of the entire background gene pool (or some other percentage based on how large a sub-network the user intends to extract); (ii) derive the averaged five quantiles of λ, and use each λ to identify a sub-network. Denote the scores of the selected sub-network as f; (iii) for each of the five λs, randomly sample 1000 sub-networks of the same size with the one chosen by COSINE, and calculate their scores, thereby generating five score populations; (iv) compute the mean μ and standard deviation s of each score population, then the adjusted score = (f − μ)/s; and (v) Choose the λ whose corresponding sub-network has the highest adjusted score. As to the analysis combining PPI data and gene expression data, the choice of quantile values is the same. For the final choice of λ, we randomly sampled the same number of nodes and the same number of edges as the selected sub-network, and repeated the sampling for ∼10 000 times to derive the mean and SD of the scores.

2.6 Performance assessment

Recall, precision and the combined F-measure were used to evaluate the performance of different methods. Let TP denote the number of correctly identified genes, FP denote the number of falsely identified genes and FN denote the number of falsely unidentified genes. The traditional F-measure or balanced F-score (F₁-score) is the harmonic mean of precision and recall, and can be used as a measure of total accuracy when equal importance is attached to recall and precision (Van Rijsbergen, 1979). Then,

2.7 Analysis of various topological measures of single trait-associated gene networks

For genes associated with each of the 265 traits [as described in (1) of Section 2.4], we constructed co-expression networks for the liver/omental/subcutaneous data, as well as the ASN/CEUP/YRIP data, resulting in six groups of co-expression networks. Five representative topological metrics were computed for these networks of different sizes, including (i) mean connectivity, (ii) mean clustering coefficient, (iii) density, (iv) heterogeneity and (v) centralization, using the function ‘fundamentalNetworkConcepts’ in the R package WGCNA (Langfelder and Horvath, 2008). We then derived the across-tissue and across-population variance of each metric for each co-expression network. In order to assess the significance of these variances, 1000 sub-networks of the same size with each trait-associated gene network were randomly sampled from the background gene pool to form a null distribution of the variances. A P-value was then computed based on how frequently we observed a variance larger than the original one.

3 RESULTS

3.1 Method comparison on simulated data

To test COSINE on the simulated data, each of the six case datasets was compared with the Control Group to identify condition specific sub-networks. For the parameters of the genetic algorithm, we set mutation rate to 0.005 and the iteration number to 300. The results of COSINE using five different λ's for each set are summarized in Figure 1. It can be seen from the plots that the λ allows the fine-tuning of the relative contribution of edge and node, thus favoring the selection of different types of sub-networks: smaller λ (more weight on the node term) favors the selection of sub-networks with significant differential expression (DE), such as set 3; whereas larger λ (more weight on the edge term) shows better performance for identifying sub-networks with differential gene–gene correlation patterns (DC), such as set 4. For sets showing both DE and DC (set 2, set 5 and set 6), the performance of COSINE is more consistent for different λs. In the case of set 1 (negative control), the identified sub-networks are not enriched for Genes 1 to 50, as expected.

Fig. 1.

Performance of COSINE on simulated datasets. X-axis displays the grouping by the five λ values in increasing order. Y-axis shows the values of recall, precision and F-measure using each λ.

We then compared the sub-network with the highest adjusted score (as described in Section 2.5; see Supplementary Table S1 (a) for detailed results) with the result of ‘jActiveModules’ (Ideker et al., 2002), the edge-based method (Guo et al., 2007) and the combined method of (Wang and Xia, 2008), as shown in Table 2 (see ‘Supplementary Material: Methods’ for further details of method implementation). Since the method of Wang and Xia (2008) aims to identify a series of locally optimal sub-networks rather than a single globally optimal one (which is different from the objective of COSINE), the comparison with their result is not that straightforward. In each iteration of the local search, their method identifies a small sub-network (usually <5 genes), extracts this sub-network, eliminates the affiliated nodes from the background pool and then starts a new iteration. We chose to look at the union of the genes identified in the first 13 iterations of local search in order to obtain approximately the same number of genes in the sub-network to assess the selection performance of their method.

Table 2.

Performance comparison of COSINE and with three other methods

Set	Best λ for COSINE	Size of selected sub-network			Recall			Precision			F-measure
		COSINE	jAM	Local	COSINE	jAM	Local	COSINE	jAM	Local	COSINE	jAM	Local
1	0.17	58	419	51	0.12	0.9	0.12	0.1	0.11	0.12	0.11	0.19	0.12
2	0.987	57	417	63	0.98	1	0.82	0.86	0.12	0.65	0.92	0.21	0.73
3	0.0009	13	385	51	0.24	0.98	0.7	0.92	0.13	0.69	0.38	0.23	0.69
4	0.994	95	421	75	0.86	0.86	0.06	0.45	0.1	0.04	0.59	0.18	0.05
5	0.973	75	400	44	0.92	1	0.74	0.61	0.125	0.84	0.74	0.22	0.79
6	0.0005	25	417	52	0.55	0.9	0.65	0.88	0.086	0.5	0.68	0.16	0.57

Edge: the method of Guo et al. (2007); Local: the method of Wang and Xia (2008).

Compared with the other three methods, COSINE achieves higher recall, precision and F-measure in most cases except for the negative control set 1. The sub-network chosen by jActiveModules (jAM) is generally too large. Therefore, although the recall of jAM is satisfactory, its precision is very low. As for the edge-based method, it fails to select a sub-network for all six datasets (all 500 nodes are still retained after 10 000 iterations). The rationale of the edge-based method is to eliminate the edges in the original network one by one and then remove all the nodes with degree of 0 in each iteration of simulated annealing. Although it can be applied to the analysis of PPI networks which are highly sparse, its performance on gene–gene co-expression networks is poor because the co-expression networks are complete, thus even removing a large number of edges may not reduce the number of connected nodes. In fact, the output network of the edge-based method does contain much fewer edges than that of the input background network [which has C (500, 2) = 124 750 edges], ranging from 62 159 to 62 353. Nevertheless, no nodes can be removed since their degrees are still non-zero. The local method of Wang and Xia (2008) performs better than both jAM and the edge-based method. However, as for set 4, which has only differential correlation to a modest extent (ρ = 0.6) and no differential expression; COSINE's performance is significantly better than all the other methods.

3.2 Method comparison on PC data with integration of PPIs

We then compared the performance of COSINE with other methods on the real data of PC, in combination of the PPI network information. The parameter setting of COSINE was: number of iteration = 5000; mutation Rate = 0.05; and zero to one ratio = 30. For all the other three methods, we used the default parameter settings in their software or program code and set iteration = 5000 for jAM and the edge-based method. As in the case for simulated data, in each iteration of the local method, only a very small sub-network was extracted, so we combined the genes selected in the first 33 iterations in order to make the total number of selected genes roughly equal to that of COSINE (the original paper of the local method did not describe how to choose the number of iterations). Using the five quantiles of λ, COSINE selected sub-networks with sizes 98, 142, 199, 243, 232, with the fourth quantile giving rise to the highest adjusted score. For method evaluation, we collected genes related to PC from the Dragon Database of Genes associated with Prostate Cancer (DDPC) (Maqungo et al., 2011). We chose this database because: (i) genes included in DDPC are all experimentally verified to be associated with PC, providing clear molecular context for the gene's function; (ii) it is much more comprehensive (including 704 PC genes in all) and updated than previous databases such as Prostate Gene Database (PGDB) (Li et al., 2003), containing only 162 PC genes. Among the 704 genes, 400 are included in the 5335 genes of our dataset. The sub-network selection results of different methods are shown in Table 3. Consistent with previous comparison on simulated data, the jAM and edge-based method extracted too large a sub-network, 1669 and 4339 out of 5335 genes, respectively. Fold enrichment shows that COSINE performs the best in identifying PC genes, followed by the edge-based method, whereas the fold enrichment of jAM and the local method is only slightly > 1.

Table 3.

Performance comparison on PC data

Method	COSINE	jAM	Edge	Local
No. of nodes selected	243	1669	4339	230
No. of edges (PPI) selected	102	3283	16 576	32
No. of PC genes recovered	23	133	373	18
Fold enrichment	1.262	1.063	1.147	1.044

Fold enrichment is calculated as follows: No. PC genes recovered / (400*No. ofnodes selected/5335).

We also checked kyoto encyclopedia of genes and genomes (KEGG) pathway enrichment using DAVID. It turned out that most PC-related pathways could be identified via all the four methods, such as ‘Regulation of actin cytoskeleton’, ‘MAPK signaling pathway’, ‘Chemokine signaling pathway’, etc. However, jAM and the edge-based method returned too long a list of enriched pathways, a significant proportion of which show little relation to PC. Therefore, the fold enrichment statistic is a more objective criterion for comparison. Although it is possible that gene expression in PC might be widely changed, and whether the extracted sub-network is biologically meaningful should not be judged based on its size, it is still preferred for feature selection methods (including all the sub-network extraction methods discussed here) to retrieve a small subset of the original features with the best discriminative power, which is exactly the goal of COSINE.

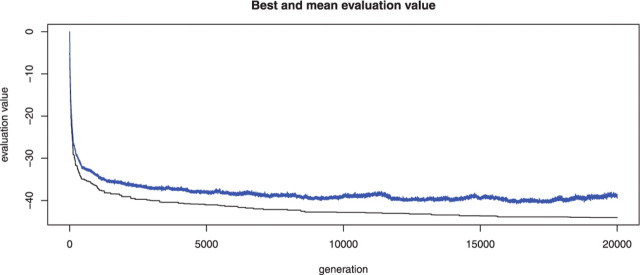
Analysis in this article was done on a Dell PowerEdge 1955 server containing two-dual core 3.0 GHz Xeon 64 bit EM64T Intel cpus model 5160, 16 GB RAM. For the PC dataset of 5335 genes and 18 249 PPIs, it took about 6.5 h to finish 5000 iterations. In order to test the convergence of the genetic algorithm, we reran the program with the fourth quantile of λ, and iteration = 10 000 and 20 000. The fold enrichment for PC-related genes increases with more iterations of the genetic algorithm, which is 1.317 and 1.328, respectively. Figure 2 shows the convergence of the mean and best scores in each iteration of the genetic algorithm (because the R package ‘genalg’ used for implementing the genetic algorithm aims to minimize the objective function, the scores on the plot are minus the actual scores of selected sub-network). It can be seen that after 15 000 iterations, the mean score stabilizes and the best score also approaches a constant. In terms of practical use, we recommend that the iteration number to be set around the total number of genes in the dataset for balance between time and performance.

Fig. 2.

Convergence of the genetic algorithm during 20 000 iterations for the analysis of PC data. X-axis shows the iteration number, Y-axis shows the value of (−1)*the mean(above) or best(below) scores of the objective function in each iteration (since each iteration consists of a population of 200 ‘chromosomes’—binary vectors).

Gene prioritization within the selected sub-network can be easily achieved by sequentially excluding each gene from the sub-network, and calculating the decrease in the network score. The larger the score loss, the higher ranked in the sub-network the excluded gene. For example, applying the above procedure to the 243 genes selected with iteration = 5000 shows that the top three genes are ‘TGFBR1’, ‘PAFAH1B1’ and ‘COL17A1’. Their scaled node score is 8.299, 10.351 and 10.343, indicating that the differential expression of ‘TGFBR1’ is less significant than the other two genes. However, ‘TGFBR1’ participates in 50 edges within the sub-network, whereas ‘PAFAH1B1’ and ‘COL17A1’ both have only nine edges. Therefore, the contribution of ‘TGFBR1’ is larger, which makes sense considering the wide-range impact of the transforming growth factor beta (TGF-β) signaling pathway.

3.3 Application to liver and omental gene expression data of morbidly obese individuals

We then applied COSINE to the real dataset of the liver and omental tissue expression profile of morbidly obese patients, which contains 1327 genes after the pre-processing described in Section 2.4. The mutation rate was set to 0.05 and iteration number to 1000. For the five values of λ, the sizes of the identified sub-networks are 80, 73, 41, 32 and 31 (the complete lists of selected genes are in Supplementary Table S2), respectively. Supplementary Table S3 shows the pairwise intersection of the five sub-networks and corresponding fold enrichment compared to the expected number of common genes of two randomly chosen sub-networks of the same size out of the whole pool of 1327 genes. For example, the sizes of sub-networks 1 and 2 are 80 and 73, respectively, so the expected number of common genes is 80*73/1327 = 4.4, whereas the actual intersection consists of 36 genes with a fold enrichment of 36/4.4 = 8.18. As expected, the intersection of sub-networks identified by adjacent λ values is larger than that of distant λ values. No gene is selected by all the five different λ's. Another interesting observation is that the sub−networks identified by λ₃, λ₄ and λ₅ have significantly higher overlap compared with that of λ₁ and λ₂, which indicates that for this dataset, when more weight is attached to differential correlation (edges) rather than differential expression (nodes), the extracted tissue-specific sub-network tends to be more consistent. For this dataset, jAM selects a sub-network of size 677, which is about half the size of the background gene pool.

The sub-network with the highest adjusted score is given by λ₅. Functional annotation of the 31 genes using DAVID (Dennis et al., 2003; Huang, et al., 2009) identifies several enriched biological pathways, as shown in Supplementary Table S4. These pathways are consistent with previous biological studies of tissue-specific gene expression of obesity, as reviewed by (Kim and Park, 2010), including pathways of ‘inflammation, immune response, adhesion molecules, lipid metabolism, adipocyte differentiation, defense, and stress responses’. We then compared our approach with traditional separate DE and differential correlation (DC) analysis. After ranking the 1327 genes solely based on the node score (F-statistic) or mean edge score (averaged ECF-statistic with the other 1326 genes), we looked at the top 31 genes based on such single measures. Since we are doing two group comparison (liver tissue versus omental tissue), the F-statistic is actually the square of the Student's t-statistic. There is no overlap between the 31 genes identified by COSINE and single DE analysis, but 13 genes in common between COSINE and DC analysis, which is expected since for this pair of datasets, the best λ is the largest one, so more weight is given to the edge score term measuring differential correlation. Functional annotation results for the genes are shown in Supplementary Table S4. Compared with separate DE/DC analysis, COSINE assigns higher ranks and significantly smaller P-values to the obesity-related pathways. Therefore, the joint consideration of both differential expression and differential correlation has a higher potential in revealing unexpected or less well-studied biological pathways which are deregulated in diseases.

We then took a further look at selected edges exhibiting significant differential correlation between the liver and omental data. We ranked the 465 edges among the 31 genes based on their scaled ECF scores and found that the top 10 edges all include the gene ‘CRP’, although the differential expression of this gene is not significant (scaled F-statistics = −0.43). C-reactive protein (CRP) is synthesized by the liver in response to factors release by fat cells. Its function is to recognize foreign pathogens and damaged cells of the host and to initiate their elimination by interacting with humoral and cellular effector systems in the blood. Partners of CRP for the top 10 edges are: ‘FGB’, ‘CYP2C9’, ‘ITIH1’, ‘CYP4F2’, ‘APOC3’, ‘ANGPTL3’, ‘CYP2C8’, ‘ADH6’, ‘SLCO1B1’ and ‘APOC1’. Among these genes: (i) ‘FGB’ is the β component of fibrinogen, an important player in blood coagulation; ‘ITIH1’ is the heavy chain of a serine protease inhibitor involved in the inflammatory response; ‘ANGPTL3’ is a member of the angiopoietin-like family of secreted factors. Differential correlation of these three edges (correlation with CRP is higher in omental tissue than in liver, data not shown) are consistent with the fact that in the omental adipose tissue, the large number of fat cells enhance the interaction between CRP and the immune system. (ii) ‘CYP2C9’, ‘CYP4F2’ and ‘CYP2C8’ are involved in synthesis of cholesterol, steroids and other lipids, whereas ‘ADH6’ and ‘SLCO1B1’ function in the metabolism of many substrates including alcohol and lipids. Differential correlations of these five edges (correlation with CRP is positive in omental tissue yet negative in liver, data not shown) are consistent with the fact that under the pathological condition of morbid obesity, the liver is oversupplied with free fatty acid whereas omental adipose tissue shows over-expression of lipid metabolism genes. (iii) ‘APOC3’ and ‘APOC1’ are apolipoproteins thought to delay catabolism of triglyceride-rich particles. Their correlation with CRP is also negative in liver but positive in omental tissue, contributing to the deregulation of lipid metabolism in liver of obesity patients.

We also compared the topological difference of this sub-network in liver versus omental tissues. After constructing the co-expression network of the 31 genes (as detailed in the Section 2.7), we calculated four representative topological measures. In order to achieve a fair comparison, we randomly sampled 1000 sub-networks of size 31 and derived the null distribution of the four topological measures in the liver as well as omental data. We then normalized the original values using the mean and SD of the null distribution and the results are shown in Table 4. It can be seen that the sub-network is denser (higher mean connectivity, higher mean clustering coefficient) in the omental tissue than that in liver. The heterogeneity (a measure of the variance of connectivity of each node) of this sub-network is not significant in either liver or omental tissues. The big difference in centralization indicates that this co-expression sub-network is much more like star topology in the omental tissue but not in the liver.

Table 4.

Topological comparison of selected sub-network of the liver–omental datasets

Tissue	Mean connectivity	Mean clustering coefficient	Heterogeneity	Centralization
Liver	8.5	5.8	−1.2	2.7
Omental	247.9	52.0	−1.5	51.1

We explored the effect of different parameter settings on the genetic algorithm using a new simulated dataset with real covariance matrices extracted from the liver–omental data. We also showed the reasonability of the proposed procedure for the final choice of λ via calculation of adjusted score using this dataset; please see ‘Supplemental Material’ for details.

3.4 Extension to sub-network identification across multiple gene expression datasets

As both the F-statistic and ECF-statistic can measure DE and DC across more than two conditions, COSINE can be easily applied to multiple network comparisons. As an example here, we used COSINE to identify the condition-specific sub-network across the expression profile of three HapMap sample populations: ASN, CEUP and YRIP. To our knowledge, this is the first between-population study on the expression of genome wide association studies (GWAS) genes using an integrated approach. In this analysis, we set the mutation rate to 0.05, iteration number to 1000 and ZeroToOne ratio to 5. The k-values used for random sampling to derive the λ quantiles are 100–150 by the interval of 5. The size of the identified sub-network is 122, 164, 196, 178 and 198, for the five λs, respectively. The best and mean scores in each iteration of the genetic algorithm are shown in Supplementary Figure S5. There is a significant overlap between the latter three sub-networks, with 84 genes shared among them. We then looked at the sub-network identified by λ₄, which gave rise to the highest adjusted score (the number of random sampling to get the null distribution of sub-network scores was set to 10 000). The results for the adjusted sub-network scores are shown in Supplementary Table S1(c).

Functional annotation of the 178 genes indicates the enrichment for many immune-related pathways, such as ‘Viral myocarditis’, ‘Type 1 diabetes mellitus’ and ‘Graft-versus-host disease’, as well as several non-immune pathways including ‘Pathways in cancer’, ‘Oocyte meiosis’ and ‘MAPK signaling pathway’. For the detailed annotation list, see Supplementary Table S7. The significance of immune-related pathways has been shown in a number of studies on gene expression variation across different ethnic groups (Storey et al., 2007; Zhang et al., 2008). We also compared the results of COSINE with those of separate analysis of differential expression or differential correlation. In this case, DE analysis fails to identify several immune pathways that are known to show racial difference [e.g. ‘Type 1 diabetes mellitus’ (Lorenzi et al., 1985) and ‘chemokine signaling pathway’ (Storey et al., 2007)]; and for the identified ones (e.g. ‘Viral myocarditis’), it assigns much larger P-values. The pathways identified via DC analysis are almost exclusively immune pathways. Since the racial/ethnic difference in the risk of lung cancer (Haiman et al., 2006) and PC (Wells et al., 2010) has been extensively studied and well recognized, this comparison shows that COSINE has the advantage of identifying a more comprehensive condition-specific sub-network than traditional approaches based on single criterion, which is not surprising since the best parameter λ for this dataset is neither the minimum nor the maximum among the five quantiles, indicating that a weighted combination of DE and DC does a better job for the search of the most significant sub-network.

3.5 Comparison with higher order topological measure-based analysis

In order to compare COSINE with analysis based on non-local network characteristics, we calculated five topological measures for each of the 265 trait-associated gene networks (as described in Section 2.4). For some traits, the associated genes collected from the GWAS catalog were not covered by the probes of the microarray platform, and thus were not included in the co-expression network construction. After this filtering, 189 traits remained for the tissue data analysis and 150 traits for the HapMap data. We then calculated the P-value of each topological measure's variance across different tissues and different populations, respectively, as described in Section 2.7. For the HapMap data, only a few trait networks showed significant P-values (<0.05) of the variance (six traits for mean clustering coefficient, five traits for centralization/density/heterogeneity/mean connectivity), thus prohibiting a reasonable comparison. In contrast, the topological metrics of many trait networks vary significantly across tissues (Supplementary Table S8). Among these, three traits, ‘Cholesterol, total’, ‘LDL cholesterol’ and ‘Triglycerides’, exhibit significant variance for all the five topological metrics and have > 15 associated genes. Figure 3 shows the heatmap of the co-expression patterns. It turns out that there is always an apparent co-expression cluster in the omental tissue but not in the other two tissues. From a biological point of view, these three traits are closely related to obesity pathology, and their gene expression profiles are expected to differ between liver and adipose tissues (Kim and Park, 2010).

Fig. 3.

Heatmap plots of gene co-expression for three traits with significant across-tissue topological variance.

The adjusted scores of the five sub-networks are shown in Supplementary Table S1 (d), with the highest one given by λ₄, although it is very close to that of λ₅. This again suggests that although the major variation in the expression pattern across three tissues is on the side of DC rather than DE, taking a weighted combination of both aspects can identify a sub-network with better discriminative performance. It also shows that COSINE is able to recover not only the genes with significant alternation in DE/DC, but also the ones with higher order topological variations.

We then used COSINE to analyze the liver–omental–subcutaneous data. The λ quantiles are listed in Table 1, mutation rate = 0.05, iteration number = 1000, ZeroToOne ratio = 7. We then checked how many of the union of the three trait networks (48 genes) were recovered by COSINE. As shown in Table 5, the best performance was achieved by λ₅(0.992547), which is expected because the five topological metrics mainly reflect the gene–gene correlation patterns rather than the variation of single gene expression.

Table 5.

Recovery of genes associated with the three obesity-related traits

Weight parameter	λ1	λ2	λ3	λ4	λ5
Size of selected sub-network	114	151	155	110	126
Number of genes recovered	2	5	4	3	7
Fold enrichment	0.49	0.92	0.71	0.75	1.54

Fold enrichment is calculated as follows: number of genes recovered/(48*size of selected sub-network/1327).

4 DISCUSSION

The advantages of COSINE include: (i) the scoring function is a weighted combination of both the node score and the edge score. In this way, COSINE takes into account not only the alteration in the expression level of individual genes, but also the variation of gene–gene correlation, which is the building block of other higher order topological metrics, so that it can better reflect the integrative changes of a sub-network. (ii) COSINE uses the genetic algorithm, which is efficient for global optimization involving binary variables. For practical use, we recommend using the default parameter setting in the COSINE package. (iii) COSINE can be easily applied to gene prioritization within the extracted sub-network. (iv) COSINE naturally eases the issue of scoring over more than two conditions, since both the F-statistic and the ECF-statistic are defined for multiple groups. In contrast, previous methods use either P-value or signal-to-noise ratio to measure the differential gene expression, which requires additional transformation when scoring over multiple conditions (Idekers et al., 2002) and thus may lead to misinterpretation of the original information. (v) Distinct from various clustering methods, the goal of COSINE is not to assign each gene to a specific module. It aims at extracting the most variable sub-networks which are of real biological interest. (vi) COSINE uses a simple empirical procedure to select weight parameter λ, making it adaptive to the specific datasets being analyzed.

An issue of note is the effect of gene positions in the binary vector on the genetic algorithm. It has been reported that the ordering of genes on the chromosome can affect the convergence of the genetic algorithm (Sehitoglu and Ucoluk, 2003). In future studies, we would like to compare genetic algorithm with other global optimization algorithms to perform more efficient sub-graph search. We also note that appropriate scoring function is essential for sub-network identification. Apart from our proposed procedure to select λ, there have been numerous studies in the field of network alignment (Flannick et al., 2009) as well as structural alignment in biophysics (Zien et al., 2000) on parameter optimization for an objective function. Therefore, it would be interesting to test other more sophisticated parameter learning algorithms in COSINE. Last but not the least, COSINE can be easily applied to other types of networks, such as PPI network and gene regulatory networks, to search for altered gene interaction patterns in case–control groups.

5 CONCLUSION

In this article, we have proposed a new method, COSINE, to identify condition-specific sub-network across two or more gene expression datasets. Different from previous methods, COSINE coordinately considers single gene's expression variation and gene-pair's differential correlation, in order to extract a globally optimal sub-network which can maximize the across-group difference. We have shown using both simulated and real datasets that COSINE can successfully identify biologically meaningful sub-networks that exhibit significant alterations across a set of phenotypes.