A Hierarchical Whole-body Modeling Approach Elucidates the Link between in Vitro Insulin Signaling and in Vivo Glucose Homeostasis

Abstract

Type 2 diabetes is a metabolic disease that profoundly affects energy homeostasis. The disease involves failure at several levels and subsystems and is characterized by insulin resistance in target cells and tissues (i.e. by impaired intracellular insulin signaling). We have previously used an iterative experimental-theoretical approach to unravel the early insulin signaling events in primary human adipocytes. That study, like most insulin signaling studies, is based on in vitro experimental examination of cells, and the in vivo relevance of such studies for human beings has not been systematically examined. Herein, we develop a hierarchical model of the adipose tissue, which links intracellular insulin control of glucose transport in human primary adipocytes with whole-body glucose homeostasis. An iterative approach between experiments and minimal modeling allowed us to conclude that it is not possible to scale up the experimentally determined glucose uptake by the isolated adipocytes to match the glucose uptake profile of the adipose tissue in vivo. However, a model that additionally includes insulin effects on blood flow in the adipose tissue and GLUT4 translocation due to cell handling can explain all data, but neither of these additions is sufficient independently. We also extend the minimal model to include hierarchical dynamic links to more detailed models (both to our own models and to those by others), which act as submodules that can be turned on or off. The resulting multilevel hierarchical model can merge detailed results on different subsystems into a coherent understanding of whole-body glucose homeostasis. This hierarchical modeling can potentially create bridges between other experimental model systems and the in vivo human situation and offers a framework for systematic evaluation of the physiological relevance of in vitro obtained molecular/cellular experimental data.

Introduction

The incidence of type 2 diabetes is rapidly increasing in many parts of the world, to a large extent the result of overeating and a sedentary life style. The disease is characterized by malfunctioning energy homeostasis, in particular glucose homeostasis, which is due to both insulin resistance in insulin-responding tissues and to insufficient insulin release by the pancreatic β-cells. Insulin controls the flow of energy substrates between its target tissues (adipose, muscle, and liver), during both eating and fasting states, through the insulin signaling network. Insulin signaling in adipocytes is of special interest because resistance of the adipose tissue appears to influence other target tissues of the hormone, in particular muscle and liver, to become insulin-resistant (1). This insulin resistance in the target organs progresses to type 2 diabetes when the insulin-producing β-cells fail to compensate by releasing more insulin. Energy homeostasis is a complex process, involving several layers of regulation, multiple organs, different cell types, and many hormones and metabolites. This complexity has hampered progress toward understanding the pathogenesis and treatment of the disease. This complexity is also the main reason why mathematical modeling increasingly is used as a tool to complement and analyze experimental results when untangling various biological subsystems. Nevertheless, although such modeling is mainstream in physics and engineering, its application to biology and medicine is still in its infancy.

Insulin signaling is initiated by insulin binding to the insulin receptor (IR),³ which has been modeled to some extent (2–5). These modeling efforts have considered nonlinear behaviors, such as cooperativity (4) and the effects of more than one insulin molecule binding to the IR (5). Binding of insulin leads to rapid autophosphorylation and endocytosis of the insulin-autophosphorylated insulin-IR complex and an increased receptor tyrosine protein kinase activity toward downstream signal mediators, such as the insulin receptor substrate-1 (IRS1). The dynamics of the IR-IRS1 interaction have also been modeled (6, 7), and we recently completed a comprehensive and integrated experimental/modeling-based analysis of the early molecular events in IR signal transduction (8). Therein, we sorted out the importance of different possible feedback mechanisms during the first phase of the signaling and concluded that a negative feedback mechanism that requires endocytosis of IR is an essential part of the first 5 min of signaling. Notably, these conclusions were drawn without relying on known or uniquely estimated parameter values. Furthermore, many other plausible mechanisms, such as insulin degradation, competitive inhibition, and endocytosis or feedbacks on their own, could be rejected as sole mechanistic explanations for the experimental observations. Note that such rejections are strong conclusions and at least as important as the ultimately proposed model (8).

More downstream events in insulin signaling have been less modeled, but one earlier model by Sedaghat et al. (7) involves many of the most studied signaling intermediates. However, the model suffers from problems such as unrealistic parameters and concentrations. There are also some similarly detailed models that have been developed using alternative frameworks, in particular Boolean networks (9, 10). Boolean networks are good for preliminary modeling of a system, but Boolean networks do not make use of the full information content in data and cannot accurately investigate either gradual and quantitative changes or feedbacks and other cyclic mechanisms. Regarding connection of intracellular signaling with whole-body glucose homeostasis, Chew et al. (11) have connected the Sedaghat model (7) with a previously published whole-body model (12). They link the two levels simply by scaling up cellular glucose uptake to the whole-body level. A more detailed description of that link is included in the multilevel model by Kim et al. (13), but this model is based on little data, especially compared with the high complexity of the model. The discrepancy between the complexity in the model by Kim et al. (13) and the information content in the data severely limits the possibilities to validate the model and to use their modeling approach to draw conclusions. Another potentially interesting multilevel modeling initiative is the PhysioLab platform, developed by the company Entelos (14). This platform is, however, commercial and therefore not available to the scientific community. An interesting recent model by Dalla Man et al. (15) describes whole-body glucose homeostasis in an organ-based manner. The glucose and insulin fluxes in this model are particularly interesting because they are based on virtually model-independent measurements in more than 200 healthy human subjects. Notably, a type 1 diabetes version of this model has been accepted by the Food and Drug Administration as a possible replacement for studies on animals when certifying certain insulin treatments. The Dalla Man model is nevertheless of limited use in, for example, drug screening or identification of drug targets because it lacks intracellular details regarding signaling and metabolic pathways. In summary, existing models for insulin signaling and whole-body glucose homeostasis are either focusing on one level only or are so overparameterized that they fail to draw the kind of strong conclusions that can be drawn from minimal models and a hypothesis-testing approach.

Most modeling of energy homeostasis and insulin signaling is, moreover, based on data obtained in cell lines or animals, and the relevance of these model systems for the true in vivo situation in human beings is usually not known. Isolated primary human cells from biopsies or surgery, such as isolated adipocytes, arguably constitute a highly relevant experimental model system to study the molecular and cellular basis of human physiology and human disease, such as type 2 diabetes. These model systems are nonetheless in vitro models, and the relation between an isolated cell system and the same cells in the intact organism (i.e. in vivo) has to be sorted out to fully exploit the understanding and therapeutic potential of experimental research at the molecular/cellular level. Linking the two levels is important in drug development because the intracellular level is where metabolic and other types of dysfunctions occur and where drugs act, whereas the whole-body level is where diseases are manifested and clinical diagnosis is possible.

Herein, we extend our previously developed parameter-free modeling approach (8) to a hierarchical multilevel modeling framework, which we use to link insulin signaling in isolated human adipocytes with whole-body glucose homeostasis. In this process, we can reach strong conclusions because of already published high quality data of the in vivo organ fluxes in response to a meal (15). In our new modeling framework, these in vivo fluxes serve as constraints to an adipocyte-based organ model and allow us to conclude (as opposed to just propose) that in vitro insulin signaling and control of glucose uptake in isolated adipocytes is insufficient to explain the in vivo glucose uptake profile of the adipose tissue. We also propose mechanistic explanations for the observed discrepancy, which are presented in a minimal acceptable model. We also extend this minimal model into a detailed hierarchical model where differently detailed submodules of the insulin signaling network can be turned on or off and which also allows for future inclusion of more details as new knowledge and data are obtained. Our work demonstrates for the first time a methodology to (i) assess the physiological relevance of molecular/cellular data obtained in in vitro experimental model systems and (ii) merge such data in an expandable and internally consistent body of knowledge for whole-body glucose homeostasis.

MATERIALS AND METHODS

Subjects

Informed consent was obtained from all participating individuals. The procedures were approved by the Regional Ethics Committee at Linköping University and were performed in accordance with the Declaration of Helsinki. Abdominal subcutaneous fat was obtained, during elective surgery with general anesthesia, from female patients recruited consecutively at the Clinic of Obstetrics and Gynecology at the University Hospital in Linköping. The patients were usually subjected to hysterectomy and they were not diagnosed with diabetes.

Glucose uptake (see below) was determined at 0.5 mm 2-deoxyglucose in adipocytes obtained from subjects 39–76 years in age (average 50 years) with body mass index (BMI) of 19.2–28.2 kg/m² (average 23.0 kg/m²) and at 5 mm 2-deoxyglucose from subjects 35–74 years in age (average 55 years) with BMI of 23.2–36.2 kg/m² (average 27.2 kg/m²).

We calculated percentage of body fat from BMI, body weight, age, and gender according to Ref. 16 and thus obtained each individual's volume of adipose tissue. We then calculated the whole-body glucose uptake in mg of glucose/kg of body weight/min (same unit as in the Dalla Man model (15)) by accounting for the adipose tissue volume and the body weight of each subject.

Isolation and Incubation of Adipocytes

Adipocytes were isolated from subcutaneous adipose tissue by collagenase (type 1; Worthington) digestion as described previously (17). Cells were washed in Krebs-Ringer solution (0.12 m NaCl, 4.7 mm KCl, 2.5 mm CaCl₂, 1.2 mm MgSO₄, and 1.2 mm KH₂PO₄) containing 20 mm HEPES, pH 7.40, 1% (w/v) fatty acid-free bovine serum albumin, 100 nm phenylisopropyladenosine, and 0.5 units/ml adenosine deaminase with 2 mm glucose, at 37 °C on a shaking water bath (18). After overnight incubation (18) cells were washed and incubated with insulin (19).

Protein Phosphorylation

The protein phosphorylation data used were compiled from previous (18, 20) and unpublished work. In brief, cell incubations were terminated by separating cells from medium using centrifugation through dinonylphtalate. To minimize postincubation signaling modifications in the cells and protein modifications, which can occur during immunoprecipitation, the cells were immediately dissolved in SDS and β-mercaptoethanol with protease and protein phosphatase inhibitors, frozen within 10 s, and thawed in boiling water for further processing (17). Equal volumes of cells as determined by lipocrit (i.e. total cell volume) were subjected to SDS-PAGE and immunoblotting (18). The phosphorylation of IRS1, IR, and protein kinase B (PKB) was normalized to the amount of IRS1, IR, and PKB protein, respectively, in each sample.

Determination of Glucose Transport

After transfer of cells to medium without glucose, cells were incubated with the indicated concentrations of insulin for 15 min, when glucose transport was determined as uptake of 0.05 mm or 0.5 mm 2-deoxy-d-[1-³H]glucose (18, 21), as indicated, during 30 min. To determine the transport at 5 mm of 2-deoxy-d-[1-³H]glucose, cells were incubated with or without 100 nm of insulin for 20 min, when glucose uptake was determined every minute for 5 min. The slope of the linear uptake curve was used to calculate the rate of uptake. 2-Deoxyglucose at 5 mm had no untoward effects on the cells because we ascertained that the uptake of 2-deoxyglucose at 5 mm was comparable with 2-deoxyglucose at 50 μm in the presence of 5 mm glucose.

Modeling

We used a model-based approach to elucidate the relation between in vitro insulin signaling in primary human adipocytes and the in vivo whole-body glucose homeostasis. We thus did not aim to develop a single model but rather to utilize many models to analyze, evaluate, and compare different hypotheses regarding how a link between intracellular insulin signaling and whole-body glucose homeostasis can and cannot be constructed. In a first phase, we developed models that link insulin signaling in the adipocytes with the adipose tissue level. In this phase, conclusions were drawn, and it resulted in a number of rejections and a minimal model that can explain the link. In a second phase, we inserted the minimal adipose tissue model as a module in the whole-body Dalla Man model (15) and also added more signaling details obtained from other studies. The resulting model thus bridges all three levels (whole-body, organ, and intracellular), although the model from the first phase only bridges the organ and intracellular levels.

Hypothesis, Model Structure, and Model

We follow the notations of Ref. 8 and distinguish between a hypothesis, a model structure, and a model. A hypothesis corresponds to an overall property of the studied set of assumptions (models), usually corresponding to the presence or absence of a specific mechanism. We study four hypotheses, which are denoted Ma, Mb, Mc, and Md, and which correspond to the assumption that only insulin signaling (Ma), insulin signaling plus handling-induced effects on basal GLUT4 translocation (Mb), insulin signaling plus insulin effects on the blood flow (Mc), or insulin signaling plus both handling-induced effects on GLUT4 translocation and insulin effects on blood flow (Md) is sufficient to explain the link between the intracellular and organ level. A model structure is a collection of a set of ordinary differential equations,

where x represents the states (concentrations of substances), p represents the kinetic rate constants, y contains the measurement signals (determined, for example, by SDS-PAGE and immunoblotting), and f and g are nonlinear functions, which describe a set of specific dynamic/mechanistic assumptions. A model structure is hence a specific instance of a hypothesis, and the model structures for hypothesis Ma are denoted Ma1, Ma2, Ma3, etc. A model is a model structure with specified initial conditions and with values for the kinetic and measurement parameters. The hypotheses, model structures, and models are introduced under “Results” and in supplemental Tables S1 and S2. All model structures are specified in full detail in supplemental Figs. S1 and S2, and the principles of constructing and simulating a model from these are given in the supplemental Methods. All model equations and simulations files are available as supplementary material.

Optimization and Statistical Testing

The optimization is centered on a cost function, V(p), that is given by the sum of least squares,

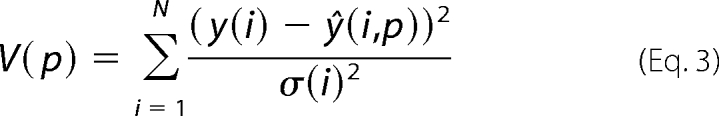where y(i) is the measured signal, ŷ(i,p) is the simulated curve, and this summation is done over all measured mean points, where the index i runs both over different time points and measurement signals. For the optimization, we used the Systems Biology Toolbox for Matlab (22) and its simannealingSBAO function, which is a combination of a global simulated annealing approach with a local, but not gradient-based, downhill simplex approach. For the uncertainty analysis of the predictions, we also performed a modified approach, simannealingSBAOclustering (8, 23), giving widely different but still acceptable parameters. Note that shared properties among all found acceptable parameters, also when the parameters are unidentifiable, indicate uniquely identified predictions (referred to as core predictions) (8). In the figures, we show simulations of models for each of the found extreme acceptable parameter sets (i.e. the ones that contain a maximum or a minimum value). In other words, in our approach, we do not deal with parameter values for the rate constants (for instance describing the rate of phosphorylation of IR) but circumvent the problem of determining these parameters by examining a point approximation of all parameters that give an acceptable agreement with the measurement data.

The statistical tests were performed primarily using χ² tests, but we also used a likelihood ratio test (8, 24) to characterize significant differences between models/model structures. Regarding degrees of freedom in the χ² test, we tested N-6 and tested N-9 and N-12, corresponding to a compensation for the normalization of data and corresponding to normalization plus an additional three and six identifiable parameters, respectively; N denotes the number of data points. Regarding significance, we tested both 95 and 99%. The uncertainties in the data and in the adipose tissue module constraints were estimated by the S.E. because we worked with models for an “average subject.” The results of the optimizations and statistical tests are summarized under “Results” and in supplemental Tables S1 and S2, and all Matlab files used for the optimizations and statistical tests are available as supplemental material.

Differences between Our Approach and Traditional Large Scale Gray Box Modeling

Our minimal modeling approach is described in detail elsewhere (8). The approach differs in several ways from traditional systems biology approaches. These differences are summarized in Table 1, where it should be noted that we have taken a simplified view of traditional modeling in order to make the main points clear (e.g. also traditional modeling may involve more than one model, but our point is that in our approach we examine more models than are common; herein we examined >15 model structures corresponding to four different hypotheses). The focus of our approach is to identify models that can be rejected because rejections are one of the two main conclusions in our approach. The other type of main conclusions are made up by the core predictions, which are shared properties among all acceptable parameters. The handling of parameter values is a key difference between our approach and most others because (i) parameter values are usually not known and not uniquely identifiable based on existing data, and (ii) such non-identifiability implies that corresponding predictions are weak and non-final. In contrast, the two types of conclusions we seek, model rejections and core predictions, are strong because they are valid for the entire model structure (instead of for a model; i.e. a model structure with specified parameters) and because they will not be revised in the future, as long as the existing data are not erroneous.

TABLE 1.

Characterizing features of traditional large scale gray box modeling and the conclusive minimal modeling approach demonstrated herein

Feature	Traditional modeling	Our approach
Number of models	One	Many
Mechanistically based model structures	Yes	Yes
Included mechanisms	All known and relevant	As few as possible, only those necessary
Main insights from comparing with data	Model can explain the data	Something crucial is missing
Parameter values	A single set of values, from literature and fitting	All acceptable parameters
Prediction identification	Simulation	Shared properties among all acceptable parameters
Type of predictions	Non-unique suggestions	Uniquely identified
Finality of conclusions	No, will be revised in the future	Yes, both rejections and core predictions are final

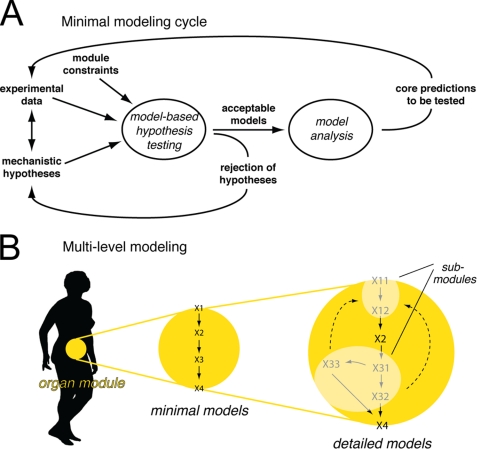
Hierarchical Modeling

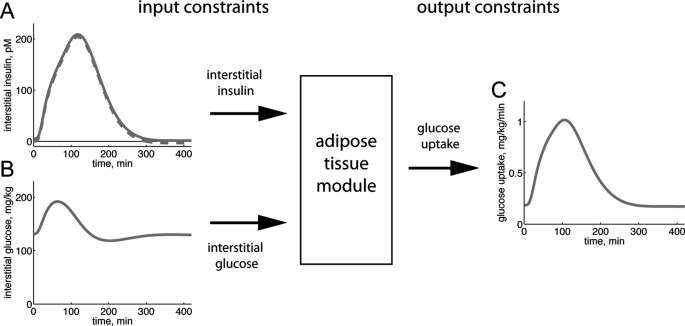
Herein we extended our previously developed modeling framework to be able to obtain similarly strong conclusions in multilevel hierarchical modeling. The multilevel models (denoted M¹–M³) have different extents of detail included as submodules. To be able to connect the models consisting of different scales and levels of details, we used a hierarchical, module-based approach. The technical term for this approach is object-oriented modeling, and we used one of the most common object-oriented languages, Modelica, which can handle multiple domains. An object (which we will refer to as a module or a submodule) is a replaceable unit with input and output signals that must be fulfilled, to maintain the correct communication with the other objects in the model. We refer to such input and output signals as module constraints (Fig. 1), where the input signal parts of module constraints are referred to as input constraints and where the outputs that should be produced by the module are referred to as output constraints. (In our case, the input-output constraints correspond to interstitial insulin and glucose concentrations and to glucose uptake, respectively.) These module constraints were used in the minimal modeling cycle while testing hypotheses (Fig. 2A).

FIGURE 1.

Module constraints. The behavior of an adipose tissue module inserted in a whole-body model is governed by input and output constraints. Input constraints are used as inputs to the module, and the resulting output of the model must fit the output constraints. A and B, input constraints from the Dalla Man model in response to a meal (15). A, dashed line, interstitial insulin concentration; solid line, our modified interstitial insulin concentration that is restricted to positive values. B, interstitial glucose concentration. C, output constraints calculated from the Dalla Man model in response to a meal; rate of glucose uptake by the adipose tissue module.

FIGURE 2.

Modeling strategy. In the minimal modeling cycle (A), mechanistic hypotheses are tested against experimental data sets, and conclusions are drawn. Conclusions are in the form of core predictions (uniquely identified predictions) and rejected hypotheses. Non-rejected (i.e. acceptable) minimal models can be included as organ modules when creating multilevel models (B), provided that the module constraints are fulfilled. The minimal model can further be extended with more details, as long as the submodules fit their relevant module constraints. The result is a hierarchical multilevel model with optional submodules of varying complexity.

The main idea in extending our previous approach (8) was to develop a minimal model for the adipose tissue that bridges insulin signaling with the adipose tissue input-output profiles (Fig. 2A). Then, in the second phase (Fig. 2B), we included the adipose tissue module in the whole-body Dalla Man model (15) and added details corresponding to previous knowledge. In the first phase, we can draw strong conclusions, and in the second phase, we can achieve a detailed and multilevel model.

To simulate the Modelica code, we used the software MathModelica (by MathCore Engineering AB, SE58330 Linköping, Sweden), which is a modeling tool for analysis of dynamical systems, traditionally used in the field of mechanics. MathModelica is built up by component libraries for matching applications. By gathering the components in libraries, it is easy to reuse and replace the created components and to develop new ones that fit into an existing hierarchical model. For modeling of biological systems, there is a recently developed BioChem library available (available on the Mathcore Web site). Both MathModelica and the Systems Biology Toolbox for Matlab support the systems biology markup language (SBML), and it is thus possible to transfer created models to other software applications.

RESULTS

We developed a mathematical model for insulin signaling in the adipose tissue, which we inserted as a dynamic module in an existing model for whole-body glucose homeostasis by Dalla Man et al. (15). Because of our modified hypothesis-testing approach depicted in Fig. 2, this resulted in a detailed model that, nonetheless, allows conclusions to be drawn, rather than mere suggestions and descriptions. An important addition to our earlier approach (8) was that inputs consist of both experimental data and module constraints (Figs. 1 and 2). These constraints are mandatory for the dynamic fitting of the organ module to the rest of the whole-body model. The constraints allowed for a conventional hypothesis-testing approach during model development (i.e. despite a high complexity of the combined multilevel model, the constraints allowed for the study of isolated subsystems and subproblems, with real conclusive statements, such as rejections of hypotheses, core predictions, and minimal models). Once found, the minimal model was inserted as a module in the whole-body model (Fig. 2B). Where detailed data or prior models are available, these could subsequently be filled in as submodules to various parts of the minimal model to obtain a more detailed version of the model (Fig. 2B).

Identification of the Adipose Tissue Module Constraints

We first identified the input and output module constraints that ensure that our developed adipose tissue models fit in with the whole-body level. For this, we made use of the organ fluxes of insulin and glucose that have been obtained experimentally in the modeling effort by Dalla Man et al. (15, 26, 27). These data provide the glucose uptake of the combined insulin-sensitive tissues, mainly corresponding to muscle and fat, which in that model is described by one entity. To relate our insulin signaling to these data, we determined the adipose tissue contribution to the combined tissue data. Previous studies in humans have shown that in the fasting state and in the postprandial insulin-stimulated states, ∼20% of the glucose consumption by insulin-responding tissues can be attributed to the adipose tissue, and 80% is attributable to muscle tissues (Table 2). This fraction was preserved between the two relevant physiological states (fasting and eating) covered by the Dalla Man model (15). We therefore subdivided the Dalla Man model's insulin-responding glucose uptake entity in two parts, muscle and adipose tissue, with static 80/20 proportions. The glucose uptake profile of the adipose tissue module, when the Dalla Man model simulates the breakdown of a meal, is depicted in Fig. 1C. Fig. 1C thus depicts the output constraints of the module (i.e. the mandated output of the developed adipose tissue module to which the model is fitted). The glucose uptake by the adipose tissue module should be obtained with the corresponding tissue concentrations of glucose and insulin (Fig. 1, A and B) as input constraints. These adipose tissue module constraints (Fig. 1) are part of all three data sets (Z_1–3) used below.

TABLE 2.

Adipose tissue glucose uptake compared with muscle glucose uptake

Nutritional state	Total adipose tissue glucose uptake	Total muscle glucose uptake	Ratio of adipose tissue/muscle	Reference
Postabsorptive state	5% of total glucose uptake	20% of total glucose uptake	20/80	40
Postprandial state	7–15% of total glucose uptake	35–40% of total glucose uptake	15–30/70–85	40
Euglycemic hyperinsulinemia	9.5% of total glucose uptake	52.5% of total glucose uptake	15/85	41
Postprandial state	120 μmol/min	650 μmol/min	16/84	25

There are two additional concerns regarding the module constraints. First, the reported proportions for glucose uptake by the adipose and muscle tissues range between 15 and 30% (Table 2). We therefore tested also other proportions in this range, and none of the key conclusions herein were affected by such changes to the organ constraints (see below). Second, the interstitial concentration of insulin has in the Dalla Man model an unrealistic behavior when approaching steady state; it becomes very slightly negative (Fig. 1A, broken line). Because the sizes of the negative concentrations are small, unrealistic, and lead to numerical and interpretation problems, we shifted the curve to positive values (Fig. 1A, continuous line).

Accounting for Adiposity, Gender, Age, and Insulin Sensitivity

This study centers on the combination of two data sets (one in vivo set and one in vitro set) that have been obtained for two different populations. Differences in populations include gender, body weight, body constitution (fat/muscle proportions), etc. and require a careful choice of scaling and conversion into a common unit when comparing the data. The derivation of a common unit for total uptake of glucose by the adipose tissue is obviously dependent on the amount of adipose tissue; more adipose tissue can take up more glucose. However, insulin resistance in the adipose tissue is manifested in a reduced maximal rate of glucose uptake by the adipocytes (19, 28). The overall effect of increased adiposity is thus the result of these two opposing effects. We therefore examined how adiposity correlated to glucose uptake in adipocytes isolated from subjects exhibiting a wide range of obesity (measured as BMI). The rate of glucose uptake by the adipocytes significantly decreased with increasing BMI of the cell donor, both maximal rate in response to insulin and basal rate in the absence of the hormone (Fig. 3A). Thus, both insulin-stimulated and basal glucose uptake were negatively correlated with obesity. Interestingly, this effect of obesity on glucose uptake disappeared by unit conversion from uptake per cell, or a volume of cells, to whole-body uptake (Fig. 3B) (see “Materials and Methods”). This means that per kg of body weight, the increased amount of fat is exactly compensated for by the insulin resistance. We thus used this unit (mg of glucose/kg of body weight/min) in linking the adipocyte in vitro and in vivo data.

FIGURE 3.

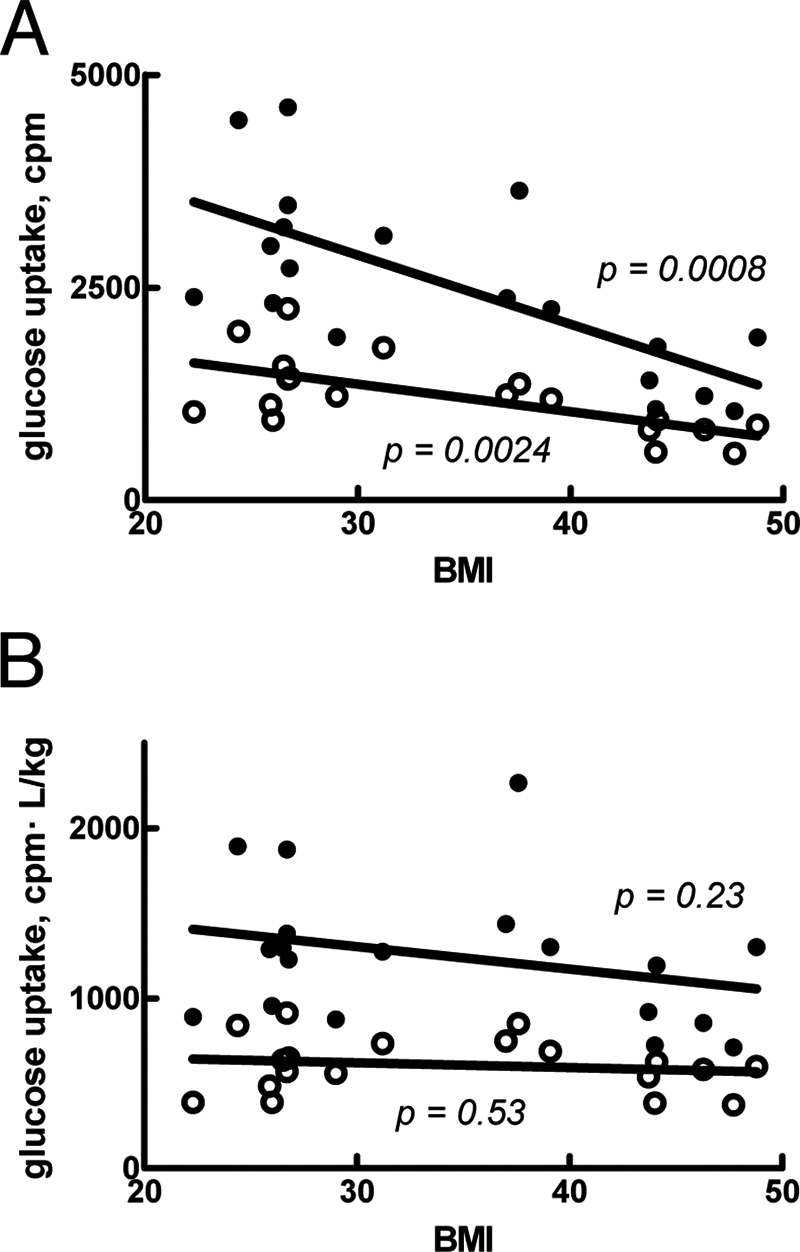
Glucose uptake by isolated adipocytes in relation to BMI. A, rate of glucose uptake, with (filled circles) or without (open circles) 100 nm insulin, in relation to BMI of the individual cell donor. B, rate of glucose uptake, with (filled circles) or without (open circles) 100 nm insulin, multiplied by the fat tissue volume (in liters, calculated as described under “Materials and Methods”) and divided by body weight (in kg) of the individual cell donor. Indicated are p values for correlation between rate of glucose uptake and BMI.

A First Attempt at a Minimal Adipose Tissue Model

To create a minimal, insulin signaling-controlled adipose tissue module for glucose uptake, we included insulin activation of IR, which via phosphorylation of IRS1 and protein kinase B/Akt (PKB) enhances glucose uptake through the insulin-regulated glucose transporter (GLUT4). This signaling sequence is perhaps the most established path between insulin binding and glucose uptake. The actual situation involves multiple feedbacks, branch points, dependences on location, and cross-talk with other regulatory subsystems, but, as we will show, many of our important conclusions hold also for this simplified signaling network. In addition to glucose uptake by GLUT4, we included glucose transporter-1 (GLUT1)-catalyzed uptake of glucose, which is not significantly stimulated by insulin. The resulting model structure is denoted Ma1 (supplemental Fig. S1) because it is the first model that belongs to our first hypothesis, Ma (Table 3). The Ma hypothesis has as the common denominator that model structures only include insulin effects on glucose uptake via the insulin signaling cascade, which is assumed to be independent of whether the cells are in an in vivo or in an in vitro situation. The differential equations of a model structure are given in Fig. 4. All model structures are graphically depicted in supplemental Figs. S1 and S2, and the model equations are available as supplemental material.

TABLE 3.

Summary of tested hypotheses

Hypothesis	Data set
	Z1	Z2
Ma, intracellular signaling	OK	Rejected
Mb, in vitro/in vivo different basal GLUT4 translocation	OK	Rejected
Mc, in vitro/in vivo different blood flow	OK	Rejected
Md, multiple in vitro/in vivo differences	OK	OK

FIGURE 4.

Example of model equations. The model equations for Ma2 demonstrate how the models are formulated. The states are the simulated signaling proteins that are phosphorylated (indicated with p) or non-phosphorylated. Insulin and glucose, the input constraints, are functions of time. Glucose uptake, the output constraint, is given by an expression depending both on insulin (via GLUT4 in the plasma membrane (GLUT4pm)) and glucose. The model parameters (i.e. the rate constants) are searched for in the optimization process while fitting models to experimental data and output constraints. The complete model equations for all models are available as supplemental material.

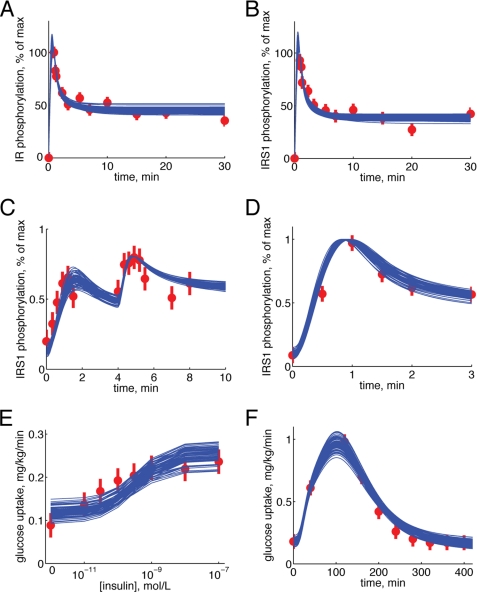
We complemented the input and output module constraints described above (Fig. 1) with experimental dose-response data for insulin stimulation of IR autophosphorylation (Fig. 5A), receptor phosphorylation of IRS1 (Fig. 5B), phosphorylation of PKB at threonine 308 (Fig. 5C), and glucose uptake by isolated primary human adipocytes (Fig. 5D). This combined data set is referred to as data set Z₁ (Table 4).

FIGURE 5.

Simulations by model Ma2 in comparison with data sets Z₁ and Z₂. A–D, dose response to increasing concentrations of insulin. A, IR phosphorylation; B, IRS1 phosphorylation; C, PKB phosphorylation; D, glucose uptake. Simulated results are depicted as blue solid lines (one line for each extreme acceptable parameter set), and experimental data are depicted as red filled circles with error bars (±S.E.). Experimental data are from isolated adipocytes. E, glucose uptake of the adipose tissue in response to a meal. Simulated results are depicted as blue solid lines (one line for each extreme acceptable parameter set), and experimental data are depicted as red filled circles with error bars (±S.E.). Experimental data are from the Dalla Man model (15). F, predicted glucose uptake (blue solid lines) with 5 mm glucose in the medium. G, experimentally determined (red bars, ±S.E.) versus fitted/simulated (blue bars) glucose uptake for the isolated adipocytes in the presence of 5 mm glucose, with or without 100 nm insulin, as indicated.

TABLE 4.

Contents of data sets Z₁–Z₃

Data set	Adipose tissue module constraints	Dose-response phosphorylation data	Glucose uptake (0.5 mm glucose)	Glucose uptake (5 mm glucose)	Dynamic phosphorylation dataa
Z1	X	X	X
Z2	X	X	X	X
Z3	X	X	X	X	X

^a Data from Ref. 8.

We fitted the model Ma1 to the data set Z₁ (see “Materials and Methods”), but despite extensive searches in the parameter space, we could not find an acceptable fit. That even the best fits were unacceptable was formally tested using a χ² test (see “Materials and Methods”), which rejected the model Ma1 with a significance of <0.05. We examined several variations of the same hypothesis, involving feedbacks (models Ma2 and Ma3, supplemental Fig. S1), Hill equations (model Ma4, supplemental Fig. S1), a basal translocation of GLUT4 (model Ma5, supplemental Fig. S1), more signaling intermediates (models Ma6 and Ma7, supplemental Fig. S1), more complex signaling involving branch points (model Ma7, supplemental Fig. S1), and IR endocytosis (model Ma6, supplemental Fig. S1). Different significance levels and degrees of freedom were tested (see “Materials and Methods”), and the results are summarized in Table 3 and Table S1. Some of the tests are on the border of rejections (Ma4 passes a test with 31 but not with 28 degrees of freedom; Ma3 is rejected with a significance of p < 0.05 but not p < 0.01). Because of these ambiguities, we complemented the χ² test with a likelihood ratio test, which indicates that the two nested models Ma1 and Ma2 are significantly different (χ²(Ma1) − χ²(Ma2) = 54.2 − 40.9 = 13.3 > χ² (1, α = 0.01) = 6.63). In other words, the added parameter in model Ma2 corresponding to the positive feedback contributes significantly to the fit of the model to data. In summary, the two models Ma2 and Ma6 pass all tests and thus move to the next step: identification of experimentally testable core predictions (Fig. 2A).

The Minimal Modeling Reveals That Insulin-stimulated Glucose Uptake in Isolated Adipocytes Cannot Account for the Observed in Vivo Glucose Uptake by the Adipose Tissue

We sought to identify an approximation of all acceptable parameters for Ma2, using as threshold a χ² test with significance level of 0.05 and 34 degrees of freedom (Fig. 5, A–E). The glucose uptake data in data set Z₁ were determined at 0.5 mm glucose, a subphysiological concentration (29–31). The predicted dose-response curves by Ma2 for glucose uptake by the adipose tissue at physiological (5 mm) glucose are shown in Fig. 5F. As can be seen, also when accounting for the uncertainty in the prediction due to the lack of specific parameter values, a distinct curve is obtained. A similar prediction is also produced by the model structure Ma6 (supplemental Fig. S3). These predictions thus fulfill the conditions for an experimental test; they are core predictions (8) that are physiologically relevant/interesting and that can be experimentally tested.

We thus determined glucose uptake by isolated adipocytes at 5 mm glucose (Fig. 5G). The expanded data set containing these new glucose uptake data plus data set Z₁ is denoted Z₂ (Table 4). In the next step of the minimal modeling cycle (Fig. 2A), we tested the model structures Ma2 and Ma6 with the expanded data set Z₂. Optimization plus statistical tests showed that none of these models were acceptable with 36 degrees of freedom, even for α = 0.01 (Table 3 and supplemental Table S1). We further examined models Ma2 and Ma6 with a modified data set Z₂, using two different subdivisions of the adipose/muscle tissue compartments (15/85 or 30/70), and this also led to rejections of both Ma2 and Ma6.

Extension of the Model to Include Effects Other than Insulin Signaling for Control of Glucose Uptake

The above analysis showed that all models corresponding to hypothesis Ma are rejected. The rejection of Ma means that something more than mere in vitro intracellular insulin signaling to increased glucose uptake is needed to obtain an adipose tissue module compatible with in vivo determination of adipose tissue glucose fluxes. We refer to such differences as in vitro/in vivo differences, and they can correspond to different mechanisms. Basal translocation of GLUT4, and thus basal glucose uptake, is a possible in vitro/in vivo difference because it has been reported that GLUT4 can artifactually translocate to the plasma membrane in response to cell handling (32). It is also possible that the lack of counterregulatory factors in the isolated cell system can cause an increased translocation of GLUT4 in the absence of insulin. We refer to a model incorporating this GLUT4 translocation hypothesis as Mb (Table 3 and supplemental Fig. S2). Another possibility is that insulin signaling to enhanced glucose uptake by the adipocytes is not the only effect of insulin in the adipose tissue that enhances glucose uptake. Insulin has, for instance, effects on the blood flow (33) that could affect the availability of glucose and insulin in the local interstitial tissue surrounding the adipocytes, which in turn would effect glucose uptake by the adipocytes. We refer to this blood flow hypothesis as Mc (Table 3 and supplemental Fig. S2).

The results from optimization of model structures belonging to hypotheses Mb or Mc with respect to data set Z₂ are summarized in Table 3 and supplemental Table S2. Mb and Mc were implemented by six model structures together, whereof all are rejected. We thus rejected both hypotheses Mb and Mc. A shared property among Mb and Mc is the single included in vitro/in vivo difference. The next step was therefore to create variants of the hypotheses with more than one in vitro/in vivo difference. We refer to the multiple in vitro/in vivo difference hypothesis as Md. None of the model structures in Md were rejected when fitting them to the data set Z₂ (Table 3 and supplemental Table S2). Additionally, the best model from the hypothesis Md, Md3, is significantly better than the best models from the hypotheses Ma, Mb, and Mc (χ²(Ma2) − χ²(Md3) = 66.8 − 33.8 = 33 > χ²(2, α = 0.01) = 9.2; χ²(Mb2) − χ²(Md3) = 54.6 − 33.8 = 20.8 (equal number of parameters); χ²(Mc2) − χ²(Md3) = 49.5 − 33.8 = 15.7 > χ²(1, α = 0.01) = 6.6). For our further multilevel modeling, we thus chose Md3 as our minimal model.

Construction of Hierarchical Multilevel Models with Plug-in Submodules for Greater Mechanistic Detail in Insulin Signaling

At this point, we had obtained a minimal model (Md3) and left the iterative scheme in Fig. 2A in order to progress to the next phase (Fig. 2B). Here we added more known signaling intermediates and more mechanistic details, as plug-in submodules, to the minimal model Md3. For more mechanistic details in upstream insulin signaling, we used a previously developed model (see Ref. 8; therein referred to as Mifa). Mifa describes the first few min of the IR-IRS1 phosphorylation dynamics, which involve IR endocytosis and generation of a negative feedback. The Mifa model can explain all of our available data for this subsystem, including time series to single and multiple insulin stimulations at different concentrations, responses to inhibition of endocytosis, and measurements of the amount of internalized receptors (8). We merged this data set for the IR-IRS1 subsystem with the data set Z₂ and denoted the resulting data set Z₃ (Table 4). We then merged the Mifa model as a submodule within the minimal model Md3 and referred to the resulting detailed model as M¹ (Table 5). Fitting the parameters in M¹ showed that it can explain the Z₃ data set (supplemental Fig. S4).

TABLE 5.

Summary of the detailed hierarchical models

The model equations are available upon request.

Detailed model	Included modules/submodules
M1	Md3 + Mifa (from Ref. 8)
M2	M1 + downstream signaling details
M3	M2 + Kiselyov model (from Ref. 5)

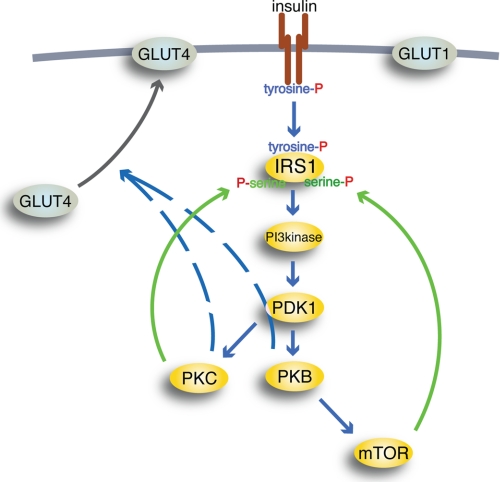
Downstream insulin signaling to control of glucose uptake involves branching and feedbacks; we therefore next included more details regarding some of the most well established such mechanisms (Fig. 6). First, the signaling from IRS1 to PKB involves several steps, in particular the phosphoinositide 3-kinase (PI3K) and phosphoinositide-dependent kinase-1 (PDK1). Second, signaling from PDK1 to GLUT4 has two branches: one involving PKB and one involving protein kinase Cλ/ζ (PKCλ/ζ). Finally, some of the known or hypothesized feedbacks include feedback from PKB, via the mammalian target of rapamycin (mTOR) to serine phosphorylation of IRS1, and another one from PKCλ/ζ to serine phosphorylation of IRS1; serine-phosphorylation of IRS1 is believed to increase or decrease the tyrosine phosphorylation of IRS1 and thus affect the insulin signaling through IRS1 (19, 34, 35). All of these mechanisms were added to M¹, and the resulting model denoted M² (Table 5) can also explain the Z₃ data set (supplemental Fig. S5). At this point, we thus had a detailed hierarchical model of glucose homeostasis with optional adipose tissue plug-in submodules, representing different extents of mechanistic detail in the insulin signaling.

FIGURE 6.

Schematic outline of insulin signaling pathways. Insulin binding to the IR (brown) causes autophosphorylation of IR at tyrosine; thus activated, IR will phosphorylate IRS1 at tyrosine to create binding sites for Src homology 2 domain-containing proteins, such as PI3K (PI3kinase). Thus activated, PI3K will phosphorylate phosphoinositides in the cell membrane, allowing PDK1 to phosphorylate and activate PKB and PKCλ/ζ (PKC). Thus activated, PKB can activate mTOR in complex with raptor, through which insulin can control protein synthesis, autophagy, and mitochondrial function. mTOR and protein kinase PKCλ/ζ relay feedback signals (green) to phosphorylation of IRS1 at serine residues. Blue arrows, downstream signaling by insulin; black arrow, translocation of insulin-regulated GLUT4 from an intracellular location to the plasma membrane (thick gray line); hatched lines, poorly defined signal paths; P, phosphate. GLUT1 is not affected by insulin.

Merging of our Hierarchical Model with Models of Others

We next continued to show how we could further expand the hierarchical model M² by merging it with models and insights obtained by others.

In a recent work by Kiselyov et al. (5), the binding of insulin to IR, with a focus on the importance of double and triple binding of insulin to its receptor, has been modeled. That model contains a more comprehensive description of the insulin-IR binding dynamics than we have tested (8), and it would thus be valuable to incorporate that model in our adipose tissue module. The model by Kiselyov et al., however, has been developed for other cell types (IM9 and 293EBN cells) and for low temperatures to reduce the effect of endocytosis. It is therefore not possible to use that model's data or parameter values, but only the underlying model structure, in our adipose tissue module. We thus replaced the structure of the insulin binding reactions in M² with those in the Kiselyov model, resulting in a final detailed model M³ (Fig. 7 and Table 5; see supplemental material) and fitted that model to the data set Z₃ (Fig. 8, A–F). As can be seen, also M³ can describe all our data. Hence, it is now possible to translate the effects of multiple insulin-IR binding (5) to the corresponding whole-body effects in response to a meal (Fig. 9, A–F). We thus have three multilevel models with differently detailed versions of an adipose tissue module (M¹, M², and M³) that all can explain the complete data set Z₃. This was possible because the differences between the different detailed models are restricted to certain well defined areas in the adipose tissue module. Note also that these localized switches are easy to turn on or off using our object-oriented software environment (see “Materials and Methods”). We can therefore refer to the models (M¹, M², and M³) as the same hierarchical model with modules and submodules of different levels of detail.

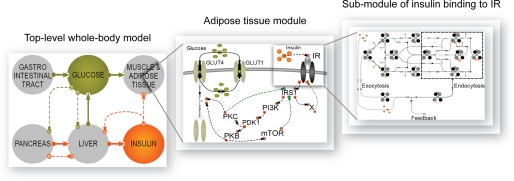
FIGURE 7.

Hierarchical, module-based modeling; the final multilevel model M³. The left panel depicts the top level part of the model, which is the glucose/insulin whole-body model from Ref. 15, but with an adipose tissue module extracted from the original single insulin-dependent tissue. The adipose tissue module in the middle panel is expanded to show the next level of the model, insulin signaling to enhanced glucose uptake via the GLUT4 translocation. In the right panel, insulin binding to IR is expanded with the insulin-IR binding model from Ref. 5 and the insulin-IR internalization/feedback model from Ref. 8. Together, all three panels constitute the final hierarchical model, M³.

FIGURE 8.

Simulations of the final hierarchical model M³ compared with data set Z₃. Simulated results are depicted as blue solid lines (one line for each extreme acceptable parameter set), and experimental data are depicted as red filled circles with error bars (±S.E.). A, IR phosphorylation in response to 100 nm insulin. Experimental data are from isolated adipocytes. B, IRS1 phosphorylation in response to 100 nm insulin. Experimental data are from isolated adipocytes. C, IRS1 phosphorylation in response to the first 1.2 nm at 0 min and then 10 nm insulin at 4 min. Experimental data are from isolated adipocytes. D, IRS1 phosphorylation in response to 10 nm insulin. Experimental data are from isolated adipocytes. E, dose response for glucose uptake in response to increasing concentrations of insulin. Experimental data are from isolated adipocytes. F, glucose uptake by the adipose tissue in response to a meal. Experimental data are from the Dalla Man model (15).

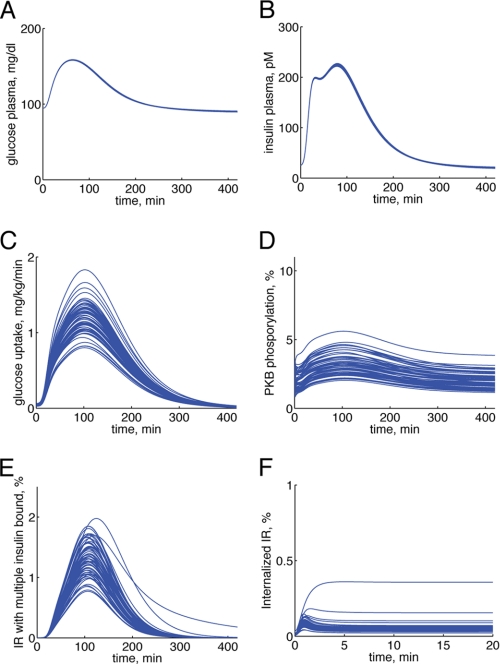
FIGURE 9.

Simulations/core predictions of the final hierarchical model M³. Simulations of the final hierarchical model (M³) for each extreme acceptable parameter set of the adipose tissue module can be used as core predictions (uniquely identifiable predictions) to draw conclusions. Here are some examples of such simulations (one blue line for each extreme acceptable parameter set) from different levels of the model: plasma glucose concentration (A), plasma insulin concentration (B), glucose uptake in the adipose tissue module (C), PKB phosphorylation in adipose tissue module (D), the fraction of IR states with two or three insulin molecules bound in the submodule of insulin binding to IR (E), and the fraction of internalized IR in the submodule of insulin binding to IR (F).

DISCUSSION

We have herein extended a previous model for insulin signaling, which focused on the early response of the IR/IRS1 subsystem to insulin (8), to include more mechanistic and downstream details and a link to whole-body glucose homeostasis. This has required a closer examination of the data from the two levels.

Most modeling of energy homeostasis and insulin signaling is based on data obtained in cell lines or animals, and the relevance of these model systems for the true in vivo situation is poorly understood. Our experimental model system, primary human cells from biopsies or surgery, is arguably an unusually realistic model system. Nonetheless, ours is also an in vitro system because the cells have been isolated from their native environment in the living human body, the consequences of which we know little. Our herein presented hierarchical modeling approach is a first attempt to create a bridge between this in vitro and the whole-body in vivo situation.

The modeling analysis revealed that the GLUT1- and insulin signaling-enhanced GLUT4-mediated uptake of glucose by isolated human adipocytes cannot simply be scaled up to explain the glucose uptake by the adipose tissue in the intact body. This is a conclusive statement, and it is supported by different types of arguments. (i) All models belonging to the hypothesis Ma (i.e. models that scale up the insulin signaling-mediated glucose uptake by the isolated adipocytes to the corresponding uptake by the adipose tissue) fail to describe the data set Z₂ and are rejected by statistical tests. Also, all models from the hypotheses Mb and Mc, which include single in vitro/in vivo differences, are rejected. (ii) Acceptable models from the hypothesis Md (which include multiple in vitro/in vivo differences) are significantly better than the best models from the hypotheses Ma, Mb, and Mc, as measured using likelihood ratio tests with a high significance (p < 0.01). (iii) We have sought to make our conclusions independent of a specific model structure, by analyzing a family of models corresponding to each rejected or acceptable hypothesis. Also, the conclusions are independent of specific parameter values because model rejections reject the whole model structure. This parameter value-independent aspect also holds for core predictions because they are shared properties among all acceptable parameters (8). The conclusions, however, rely on the assumption that we have not overlooked any crucial acceptable parameters or model structures.

The strength of these conclusions can be illustrated by comparison with previously published modeling efforts. Concerning models that include both a whole-body and an intracellular level, we are not aware of any previous examples that could draw the types of conclusions described herein. Although the model by Kim et al. (13) includes such additional factors that we have concluded are necessary, Kim et al. have not demonstrated that these factors are required. On the contrary, they have constructed a complete model at once. Such a one-model/one-parameter value approach allows neither for rejection conclusions nor, because of the extremely high dimensionality of the parameter space, nor for reliable core predictions. Another example is the modeling by Chew et al. (11), which is based on a model where the insulin-stimulated glucose uptake has been scaled in exactly such a way that we show is not possible. They have not detected the problem because they have not used input-output constraints, such as those from the Dalla Man model; this comparison thus clearly demonstrates the importance of including such module constraints (Fig. 1).

Although several of the models studied in this paper utilize previously published model structures, all analyzed models are in fact new. In particular, we have made use of the Dalla Man model (in M¹–M³), the Mifa model from (8) (in Ma6, Mb3, and M¹–M³), the Sedaghat model (in Ma7), and the Kiselyov model (in M³), but these borrowed models only appear in certain well defined areas. More specifically, the Dalla Man model only appears in M¹–M³ at the whole-body level (i.e. the organ and subcellular levels are new). Similarly, the Mifa and Sedaghat models only describe the initial insulin signaling (i.e. the parts of the models describing downstream links to the glucose uptake and to the organ level are new). The Kiselyov model appears in the insulin binding level, and the links from insulin binding to internalization to downstream signaling are new. This indeed illustrates one of the strengths of our approach, that different existing or new models are easily incorporated in the model as defined submodules.

There are different possible candidates for what mechanisms the in vitro/in vivo differences might represent. We examined in detail two possible mechanisms, blood flow (Mc) and an increased in vitro basal GLUT4 translocation (Mb). Neither of those fundamentally different mechanistic hypotheses are sufficient to explain the experimental data set Z₂, but multiple in vitro/in vivo differences, as in the hypothesis Md, are required. The model structures of both Mb and Mc correspond to fairly loosely specified mechanisms, and therefore there are other possible interpretations to the same model equations. For instance, cell-intercellular matrix interactions in situ have been reported to affect glucose uptake (36), and this might be another explanation for the in vitro/in vivo differences. There are also hormones and metabolites other than insulin with a regulatory function in the control of glucose homeostasis that are not included in the Dalla Man model and thus also not in our model. Such missing entities could serve as alternative interpretations of the models corresponding to the Mc hypothesis. Irrespective of the actual responsible mechanism(s), our modeling analysis demonstrates the inadequacy of cell-based data only to describe insulin-controlled uptake of glucose by the adipose tissue in vivo. As an important corollary, it was not possible to simply scale glucose uptake by the isolated adipocytes to match the glucose uptake profile of the adipose tissue in an in vivo setting. Such simple scaling was precluded because the in vitro cell-based data and the in vivo whole-body data had been obtained under fundamentally different conditions, such as the addition of insulin to cells versus consumption of a meal, with very different time scales and insulin concentration profiles over time. It is, for instance, not feasible to mimic ingestion of a meal by increasing and decreasing the concentration of insulin added to isolated adipocytes. In contrast, modeling is well suited to deal with such differences by requiring that a model explain both the in vitro and in vivo uptake of glucose, given the corresponding inputs. The rejection of a simple scaling, moreover, is not trivial because some of the model structures can explain data set Z₁ but not Z₂, indicating that details of the model structure are critical.

These conclusions could not have been drawn from a direct inspection of data, because the in vitro cell-based data and the in vivo whole-body data were obtained under fundamentally different conditions, such as the addition of a constant amount of insulin (cellular data) versus consumption of a meal leading to time-varying insulin stimulation (whole-body data). Modeling is well suited to deal with such differences by simply requiring that a model explain both the in vitro and in vivo uptake of glucose, given the corresponding inputs. Moreover, some of the model structures can explain data set Z₁ but not Z₂, demonstrating that details of the model structure and the details in the data series are critical and that the rejection conclusion is non-trivial.

A further, potentially alternative interpretation to the data comes from the differences in the subjects examined. The Dalla Man data are from non-diabetic, healthy middle-aged men, whereas the adipocytes examined herein were obtained from non-diabetic, middle-aged women undergoing abdominal surgery. Such gender differences implicate differences in the amount and location of body fat, which could have a role in the observed in vitro/in vivo differences. We have, however, compensated for the extent of obesity and for the fact that we study women, when translating adipocyte glucose uptake to the whole-body units of measure used in the Dalla Man model (see “Accounting for Adiposity, Gender, Age, and Insulin Sensitivity”). Likewise, our testing of muscle/adipose tissue proportions for glucose uptake other than 80/20 means that the key rejections herein probably hold despite the gender difference. To summarize, we have identified an important object for further research: to untangle the quantitative role of these potentially important components that, in addition to insulin signaling in the adipocytes, may regulate the glucose uptake in the adipose tissue. In the future, the model will also have to account for different fat locales and their properties. In particular, it will have to account for abdominal subcutaneous versus visceral adipose tissue (37), the latter of which drains to the portal vein and the liver and may therefore directly affect liver metabolism through increased fatty acid release. Future models should also include data obtained during physical exercise, which entails insulin-independent stimulation of glucose uptake in muscle.

Finally, insulin signaling is one of many subsystems involved in whole-body glucose homeostasis. There is currently no consensus regarding which of these subsystems is actually most important for the overall regulation and which of these subsystems are most decisive for the malfunctioning in type 2 diabetes. We have here demonstrated how pieces of knowledge can be merged together using a hierarchical modeling approach and also how such an approach efficiently can pinpoint important missing components. Therefore, we believe that our hierarchical multilevel modeling is an important step toward the achievement of more comprehensive and internally consistent views of cellular level and whole-body glucose and energy homeostasis, which will be required for the eventual understanding and sound treatment of type 2 diabetes, in line with the Tokyo Declaration from 2008 (38, 39).