Frailty-Based Competing Risks Model for Multivariate Survival Data

SUMMARY

In this work, we provide a new class of frailty-based competing risks models for clustered failure times data. This class is based on expanding the competing risks model of Prentice et al. (1978, Biometrics 34, 541–554) to incorporate frailty variates, with the use of cause-specific proportional hazards frailty models for all the causes. Parametric and nonparametric maximum likelihood estimators are proposed. The main advantages of the proposed class of models, in contrast to the existing models, are: (1) the inclusion of covariates; (2) the flexible structure of the dependency among the various types of failure times within a cluster; and (3) the unspecified within-subject dependency structure. The proposed estimation procedures produce the most efficient parametric and semiparametric estimators and are easy to implement. Simulation studies show that the proposed methods perform very well in practical situations.

1. Introduction

In many experimental settings, survival data arise in a clustered form. For example, in multicenter clinical trials, where failure times are observed for multiple patients in each center, and in family studies, where ages at onset of a disease are recorded for multiple members of the same family. Frequently, factors that vary by clusters may exert a powerful influence on study outcomes. Such cluster effects lead to dependencies among outcomes within each cluster. It is well known that inferences that ignore the clustering effect can be seriously misleading (Hougaard, 2000, and references therein). Frailty models (Clayton and Cuzick, 1985) are becoming increasingly popular for analyzing clustered survival data. In this approach, the frailties (the random effects) often enter the model multiplicatively to the hazard function in order to model the correlation among outcomes within a cluster.

Most of the published works dealing with clustered survival data concentrate on estimating the parameters of one type of event at a time, under the assumption that the censoring mechanism is independent of the event type of interest conditional on the covariates. However, this assumption is violated when multiple types of events occur and follow-up of some of the events is censored by the onset of the other events. For example, consider a breast cancer family study with BRCA1 mutation as a covariate. The BRCA1 mutation is known to markedly increase the risk of multiple cancers: breast, ovarian, and testis cancers (Risch et al., 2006). Thus, in estimation of breast cancer risk, for example, a subject may be censored due to death from ovarian cancer or other related causes that occur before the onset of breast cancer that might otherwise occur. It is well known (Prentice et al., 1978; Kalbfleisch and Prentice, 2002, Chapter 8, and references therein) that violation of the independent censoring mechanism as described above may produce biased estimates of cause-specific marginal hazard function. A possible way to address this problem is to use a competing risks framework (Kalbfleisch and Prentice, 2002) where the observable information for a subject is the time to first event among the possible competing events or censoring for noncompeting reasons.

Limited work has been done on clustered failure time data with competing risks. Bandeen-Roche and Liang (2002) presented statistical methods for analyzing multivariate failure times in the presence of competing risks with no covariates and under a multiplicative frailty effect. Their idea is to model the time to the earliest failure from any cause so that the overall hazard, which is the summation over the type-specific hazards, equals the standard frailty model with no competing risks. As a result, the type-specific hazards are being interpreted as the partition of the overall hazard to the various causes. The work of Chatterjee, Hartge, and Wacholder (2003) deals with competing risks kin-cohort data where the covariate of the relatives is unobserved. A piecewise constant nonparametric model of the cause-specific hazard functions with dichotomous covariate is used. The cause-specific hazard function is of Prentice et al. (1978). The estimation technique is based on the “composite-likelihood” approach, where it is assumed that the relatives are independent given the proband’s covariate. By using the composite-likelihood, the problem is being simplified to a competing risks problem with no clustered data, and that can be solved by the method presented in Prentice et al. (1978). Hence, the cause-specific hazards are consistently estimated, however, the dependence of various competing risks among cluster members, which is of interest by itself, is not estimated. Katki, Chen, and Parmigiani (2007) considered a competing risks model for family data with the use of positive-stable copula model for modeling the dependence among the possible outcomes. However, this specific choice of copula function induces identical dependence parameters for any pair of outcomes, an assumption that would likely be violated. Chen et al. (2008) developed a nonparametric estimator of the cumulative incidence functions under a cause-specific hazard model of Prentice et al. (1978) with no covariates. The estimators are based on the nonparametric Nelson–Aalen (Aalen, 1978) estimator of each cause-specific hazard function. It is shown that the estimators are consistent to the true cumulative incidence functions under the competing risks model even if event times within cluster are correlated. As in Chatterjee et al. (2003), the dependence of various competing risks among cluster members is not estimated.

In this work, we propose a new class of flexible frailty models for competing risks analysis of clustered survival data with covariates, and proportional hazards frailty model for each failure type. Flexibility is in the manner of a flexible correlation structure being allowed among failure types within a cluster. It will be shown that this class of models includes the model of Bandeen-Roche and Liang (2002) as a special case. Section 2 describes the model and Section 3 provides examples for the frailty process. The likelihood function and the parametric and nonparametric maximum likelihood estimators (parametric maximum likelihood estimators (PMLEs) and nonparametric maximum likelihood estimators (NPMLEs)) are presented in Section 4. Simulation results are presented in Section 5, where the proposed PMLEs and NPMLEs are being contrasted with a “naive” approach in which the competing risks are mistakenly considered as independent censoring. A data example is given in Section 6 and a short discussion is given in Section 7.

2. The Proposed Model

We adopt the competing risks model of Prentice et al. (1978) and Kalbfleisch and Prentice (2002) with the required modifications under a frailty model setting. By this, we avoid determining the joint distribution of all failure types for a subject, as required by the approach that uses latent or potential failure times. As a result, our current approach will not address the question, for example, whether the failure times of different failure types within a subject are associated, as we are mainly concerned about the cluster-level associations of failure times of the same or different failure types between subjects. For details regarding completely modeling the probability laws for competing failure times, readers are referred to Crowder (2001) and references therein.

Consider n independent clusters, with cluster i, i = 1, …, n, having m_i members. For subject k of cluster i, let $T_{\mathit{\text{ik}}}^o$ and C_ik be the time to the first failure and the censoring time, respectively, and Z_ik be a vector of time-independent covariates. For simplicity, we assume time-independent covariates, but all the developments presented in this article can be extended readily to the case of time-dependent covariates. Let J_ik ∈ {1, …, L} be the type of the first observed failure and J_ik = 0 if censored. Define $T_{\mathit{\text{ik}}}=\text{min}(T_{\mathit{\text{ik}}}^o,C_{\mathit{\text{ik}}})\text{ and }{\delta }_{\mathit{\text{ik}}}=I(T_{\mathit{\text{ik}}}^o\le C_{\mathit{\text{ik}}})$. For cluster i, let ε_i (t) = {ε_i1 (t), …, ε_iL (t)} be a vector-valued random process, t ∈ [0, τ] where τ is the maximal follow-up time. Define ℱ_it to be the σ-algebra generated by ε_i (t) through its history up to and including time t: ℱ_it = {ε_i (u), 0 ⩽ u ⩽ t}.

The overall hazard function of the kth member of cluster i at time t, given the regression vector Z_ik and the cluster-level σ-algebra ℱ_it, is given by

$${\lambda }_{\mathit{\text{ik}}}(t|{\mathbf{Z}}_{\mathit{\text{ik}}},{ℱ}_{\mathit{\text{it}}})=\underset{h\downarrow 0}{\text{lim}}\frac{1}{h}{P}_r\left(t\le T_{\mathit{\text{ik}}}^o<t+h|T_{\mathit{\text{ik}}}^o⩾t,{\mathbf{Z}}_{\mathit{\text{ik}}},{ℱ}_{\mathit{\text{it}}}\right).$$

The cause-specific hazard functions are defined by

$$\begin{array}{cc}{\lambda }_{\mathit{\text{jik}}}(t|{\mathbf{Z}}_{\mathit{\text{ik}}},{ℱ}_{\mathit{\text{it}}})\hfill & =\underset{h\downarrow 0}{\text{lim}}\frac{1}{h}{P}_r\left(t⩽T_{\mathit{\text{ik}}}^o<t+h,\times J_{\mathit{\text{ik}}}=j|T_{\mathit{\text{ik}}}^o\ge t,{\mathbf{Z}}_{\mathit{\text{ik}}},{ℱ}_{\mathit{\text{it}}}\right)\hfill \\ \hfill & ={\lambda }_{0j}(t)\text{ exp }\{{\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+{\epsilon }_{\mathit{\text{ij}}}(t)\}\hfill \end{array}$$

for j = 1, …, L, where β₁, …, β_L and λ₀₁ (·), …, λ_0L (·) are cause-specific regression coefficients’ vectors and cause-specific baseline hazard functions, respectively. Although the vector of covariates Z_ik is the same for all the failure types, the regression coefficients’ vector can vary among the failure types. Thus, a coefficient can be set to 0 in case its respective covariate is absent for a particular event. For simplicity of presentation, we assume that the regression coefficients’ vectors and the cause-specific baseline hazard functions are identical among a cluster’s members.

If only one of the failure types can occur, then ${\lambda }_{\mathit{\text{ik}}}(t|{\mathbf{Z}}_{\mathit{\text{ik}}},{ℱ}_{\mathit{\text{it}}})={\displaystyle {\sum }_{j=1}^L}{\lambda }_{\mathit{\text{jik}}}(t|{\mathbf{Z}}_{\mathit{\text{ik}}},{ℱ}_{\mathit{\text{it}}})$. It follows that the cause-specific densities equal f_jik (t | Z_ik, ℱ_it) = λ_jik (t | Z_ik, ℱ_it) S_ik (t | Z_ik, ℱ_it), j = 1, …, L, where $S_{\mathit{\text{ik}}}(t|{\mathbf{Z}}_{\mathit{\text{ik}}},{ℱ}_{\mathit{\text{it}}})=\text{exp}\{-{\displaystyle {\int }_0^t}{\displaystyle {\sum }_{j=1}^L}{\lambda }_{\mathit{\text{jik}}}(u|{\mathbf{Z}}_{\mathit{\text{ik}}},{ℱ}_{\mathit{\text{it}}})\mathit{\text{du}}\}$. Hence, the likelihood function can be written in terms of the cause-specific hazards. For the cause-specific survival function, we have $S_{\mathit{\text{jik}}}(t|{\mathbf{Z}}_{\mathit{\text{ik}}},{ℱ}_{\mathit{\text{it}}})=1-{\displaystyle {\int }_0^t}{f}_{\mathit{\text{jik}}}(u|{\mathbf{Z}}_{\mathit{\text{ik}}},{ℱ}_{\mathit{\text{iu}}})\mathit{\text{du}}$.

The associations between outcomes of members of cluster i are induced by the latent cluster-specific frailty process history up to the cluster’s maximum observed time, denoted by ℱ_it̃. Conditional on the cluster’s frailty process history and the observed covariates, the survival times within cluster i are assumed to be independent. At any given time t_i = (t_i1, …, t_imi), ε_i (t_i) = {ε_i (t_i1)^T, …, ε_i (t_imi)^T}^T i = 1, …, n are assumed to be independent with density denoted by f{ε_i (t_i) | θ(t_i)} where θ(t) is a vector of unknown parameters.

A multivariate competing risks model involves three types of dependence: (i) Dependence of failure times of the same failure type between cluster members (e.g., mother and her daughter with breast cancer). (ii) Dependence of failure times of different failure types between cluster members (e.g., mother with breast cancer and her daughter with ovarian cancer). (iii) Dependence of failure times of different failure types within a subject (e.g., a mother with breast cancer and ovarian cancer). With the above proposed formulation, associations of types (i) and (ii) are determined by the random process ε_i (t). The dependency of type (iii) could come from different sources. Each source can be classified into one of two types: (a) risks that are being shared by all the family members (e.g., exposure to air pollution), and (b) risks that are subject-specific (e.g., average number of cigarettes smoked per day). The type (a) risks are at the cluster level, and those of type (b) are at the subject level. The cluster-level dependency is defined by ε_i (t), however, the subject-level dependency structure is left unspecified.

3. Examples

Various models can be considered for the distribution of ε_i (t) i = 1, …, n. Each model imposes different dependency structure within a cluster. Four examples are presented below.

• Example 1: In the special case where β_j = 0 for all j = 1 …, L, λ_0j (t) = λ₀ (t) and exp{ε_ij (t)} = ω_iν_ij (t) for all j = 1 …, L and t ∈ [0, τ] such that ω_i is a single nonnegative random variable and independent of the nonnegative random vector {ν_i1 (t), …, ν_iL (t)}, the above cause-specific hazard model becomes the model provided by Bandeen-Roche and Liang (2002, equation (6)).

• Example 2: If we impose ε_i (t) = ε_i, ε_ij = ε_i for all t ∈ [0, τ] and j = 1, …, L and let ε_i be a positive-stable random variable, then the model reduces to the one considered by Katki et al. (2007) with identical dependence parameters for any pair of outcomes.

• Example 3: As a practical motivating example, consider the case where for each j = 1, …, L, ${\epsilon }_{\mathit{\text{ij}}}(t)={\epsilon }_{\mathit{\text{ij}}}^{(1)}$ if the observed time is smaller than or equal to a pre-specified constant, $t_o^{(j)},\text{ and }{\epsilon }_{\mathit{\text{ij}}}(t)={\epsilon }_{\mathit{\text{ij}}}^{(2)}$ otherwise. Let $\mathit{\epsilon }={({\epsilon }_1^{(1)},{\epsilon }_1^{(2)},\dots ,{\epsilon }_L^{(1)},{\epsilon }_L^{(2)})}^T$ with density function f (ε | θ) and unknown vector of parameters θ. Then, for each family i, ε_i is being determined by the observed data of the family and its distribution, f (ε_i | θ_i)—the marginal distribution of f (ε | θ), since ε_i and θ_i are subvectors of ε and θ, respectively (including ε and θ). In family studies, this corresponds to a situation that early onset cases (e.g., breast or ovarian cancers) may have a different etiology from cases with late onset.

• Example 4: Let ε_i (t) ≡ ε_i for all t ∈ [0, τ], and consider a multivariate normal distribution for ε_i, which provides a flexible and unrestricted covariance matrix. Since this case is considered in the simulation study and the real data analysis, we explore our proposed model under the multivariate normal frailty distribution, by using the cause-specific cross-ratio of Bandeen-Roche and Liang (2002). This provides us a simple tool in understanding the dependency imposed by this specific frailty model.

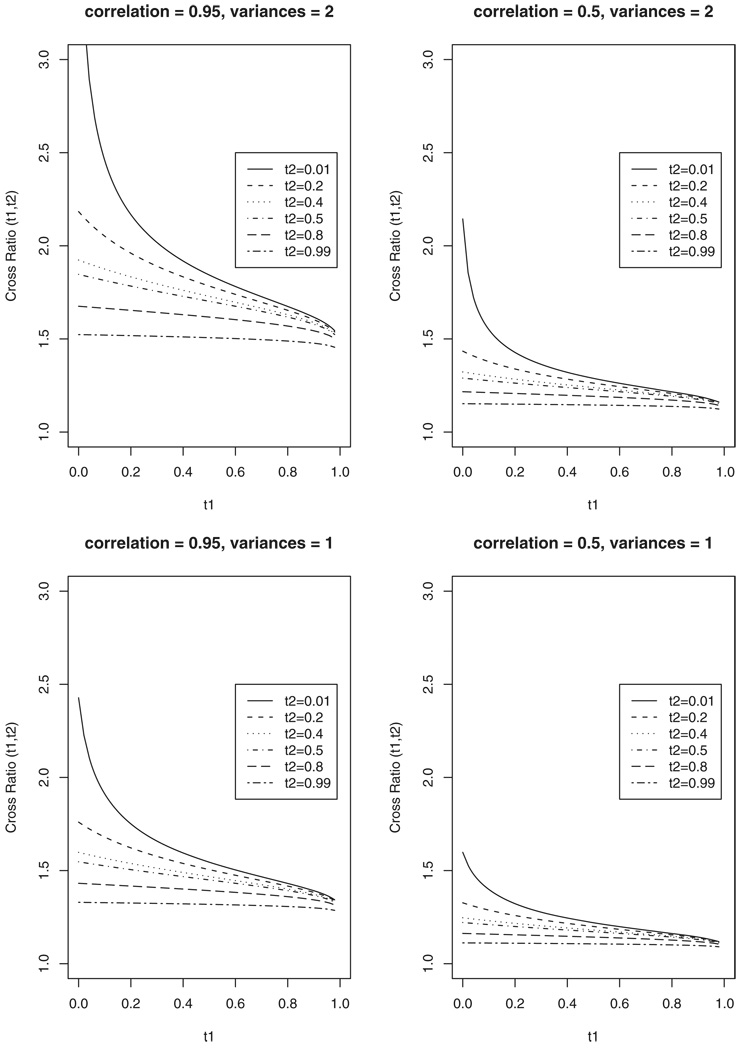
The cross-ratio function of Bandeen-Roche and Liang (2002) can be interpreted as a local dependency measure of two failure times of different types. Specifically, let $(T_{i1}^o,T_{i2}^o)$ and (J_i1, J_i2) be survival times and failure types of two cluster members, respectively. The cause-specific cross-ratio of $T_{i1}^o\text{ and }{T}_{i2}^o$ of types J_i1 = j₁ and J_i2 = j₂ is defined as

$${\mathit{\text{CR}}}_{j_1,j_2}(t_1,t_2)=\frac{S(t_1,t_2)f(t_1,t_2,j_1,j_2)}{{\displaystyle {\int }_{t_2}^{\mathrm{\infty }}}{\displaystyle \sum _{j=1}^L}f(t_1,u,j_1,j)\mathit{\text{du}}{\displaystyle {\int }_{t_1}^{\mathrm{\infty }}}{\displaystyle \sum _{j=1}^L}f(u,t_2,j,j_2)\mathit{\text{du}}},$$

where S (·, ·) denotes the survival function of $(T_{i1}^o,T_{i2}^o)$ and f (·, ·, j₁, j₂) denotes the density function of $(T_{i1}^o,T_{i2}^o)$ of types (j₁, j₂). Hence, CR_{j1, j2} (t₁, t₂) is the ratio of the risk of one member to fail at t₁ due to cause j₁ given the other member failed at t₂ due to cause j₂ to the risk given the other member not yet failed at all by t₂. CR_{j1, j2} (t₁, t₂) = 1 indicates independence of $(T_{i1}^o,T_{i2}^o)$ of j₁ and j₂ failure types at (t₁, t₂), and CR_{j1, j2} (t₁, t₂) > 1(<1) indicates positive (negative) correlated $(T_{i1}^o,T_{i2}^o)$ of j₁ and j₂ failure types at (t₁, t₂). Straightforward algebra shows that under the multivariate normal frailty model, if corr (ε_j1, ε_j2) = 0, CR_{j1, j2} (t₁, t₂) = 1 for all t₁, t₂ ∈ [0, τ]. Figure 1 depicts the above cross-ratio function of two failure types, j₁ = 1 and j₂ = 2, under the multivariate normal frailty model with mean zero and various covariance matrices. For simplicity, there are no covariates in the model and each conditional hazard function at time t, given the frailty variates, equals 1/(1 − t)0 ⩽ t ⩽ 1. It is evident that the cross ratio is a nonlinear decreasing function of t₁ and t₂ as often the situation in family studies (Fan, Prentice, and Hsu, 2000). The cross-ratio function is also a nonlinear increasing function of the variances/covariance components of the covariance matrix. The above conclusions hold for any multivariate normal frailty model, and the hazard functions and the regression coefficients affect the slopes of the CR curves. It should also be noted that the covariance components of the covariance matrix are allowed to be negative, yielding CR_{j1, j2} (t₁, t₂) < 1.

Figure 1.

The cross-ratio function under the multivariate normal frailty model with various covariance matrices.

4. The Likelihood Function, PMLEs, and NPMLEs

Denote the observed data of cluster i, i = 1, …, n, by (T_i, Z_i, J_i, δ_i) where T_i = (T_i1, …, T_imi), ${\mathbf{Z}}_i={({\mathbf{Z}}_{i1}^T,\dots ,{\mathbf{Z}}_{{\mathit{\text{im}}}_i}^T)}^T$, J_i = (J_i1, …, J_imi), and δ_i = (δ_i1, …, δ_imi). For the construction of the likelihood function, we assume the following: (1) Conditional on Z_i and ℱ_it̃, the censoring times are independent of the failure times and noninformative for the frailty process and {β_j, λ_0j, j = 1, …, L}. (2) The frailty process is independent of Z_i. (3) The covariates’ effect is subject specific, namely f_{Tik, Jik | Zi, εi} (t, j | Z_i, ℱ_it̃) = f_{Tik, Jik | Zik, εi} (t, j | Z_ik, ℱ_it̃). Hence, the likelihood function, under any choice of distributions f{ε_i (t_i) | θ(t_i)}, is proportional to

$$L={\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{{\mathbf{t}}_i>\mathbf{0}}}{\displaystyle \int }{\displaystyle \prod _{k=1}^{m_i}}\times {\left[{\lambda }_{0J_{\mathit{\text{ik}}}}(t_{\mathit{\text{ik}}})\text{ exp }\{{\mathit{\beta }}_{J_{\mathit{\text{ik}}}}^T{\mathbf{Z}}_{\mathit{\text{ik}}}+{\epsilon }_{{\mathit{\text{iJ}}}_{\mathit{\text{ik}}}}(t_{\mathit{\text{ik}}})\}\right]}^{{\mathit{\text{dN}}}_{\mathit{\text{ik}}}(t_{\mathit{\text{ik}}})}\text{ exp }\left[-{\displaystyle \sum _{j=1}^L}\text{exp }\{{\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+{\epsilon }_{\mathit{\text{ij}}}(t_{\mathit{\text{ik}}})\}{\lambda }_{0j}(t_{\mathit{\text{ik}}}){\mathit{\text{dt}}}_{\mathit{\text{ik}}}\times \{1-{\mathit{\text{dN}}}_{\mathit{\text{ik}}}(t_{\mathit{\text{ik}}})\}{Y}_{\mathit{\text{ik}}}(t_{\mathit{\text{ik}}})\right]f\{{\mathit{\epsilon }}_i({\mathbf{t}}_i)|\theta ({\mathbf{t}}_i)\}d{\mathit{\epsilon }}_i({\mathbf{t}}_i),$$ (1)

where N_ik (t) = δ_ik I (T_ik ⩽ t) and Y_ik (t) = I (T_ik ⩾ t) are the failure counting process and the at-risk process, respectively. Alternatively, let the counting processes $\{N_{\mathit{\text{ik}}}^{(j)}(t),t\ge 0\}$ be defined at time t by $N_{\mathit{\text{ik}}}^{(j)}(t)=N_{\mathit{\text{ik}}}(t)I(J_{\mathit{\text{ik}}}=j)$, j = 1, …, L. Then, the above likelihood can also be written as

$$L={\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{{\mathbf{t}}_i>\mathbf{0}}}{\displaystyle \int }{\displaystyle \prod _{k=1}^{m_i}}{\displaystyle \prod _{j=1}^L}\times {\left[{\lambda }_{0j}(t_{\mathit{\text{ik}}})\text{ exp }\{{\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+{\epsilon }_{\mathit{\text{ij}}}(t_{\mathit{\text{ik}}})\}\right]}^{{\mathit{\text{dN}}}_{\mathit{\text{ik}}}^{(j)}(t_{\mathit{\text{ik}}})}\text{ exp }\left[-\text{exp }\{{\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+{\epsilon }_{\mathit{\text{ij}}}(t_{\mathit{\text{ik}}})\}{\lambda }_{0j}(t_{\mathit{\text{ik}}}){\mathit{\text{dt}}}_{\mathit{\text{ik}}}\times \{1-{\mathit{\text{dN}}}_{\mathit{\text{ik}}}^{(j)}(t_{\mathit{\text{ik}}})\}{Y}_{\mathit{\text{ik}}}(t_{\mathit{\text{ik}}})\right]f\{{\mathit{\epsilon }}_i({\mathbf{t}}_i)|\theta ({\mathbf{t}}_i)\}d{\mathit{\epsilon }}_i({\mathbf{t}}_i).$$ (2)

It is easy to see that if the ε_ij (·)’s, j = 1, …, L, are independent, the above likelihood function factors into a separate components for each cause-specific hazard function λ_j {t | Z, ε_j (t)}. The jth factor is precisely the likelihood that would be obtained if failures of types other than j were regarded as being censored and the time-dependent frailty variate ε_ij (·) accounts for the unobservable cluster-level effect related to failure type j. This result is in the spirit of Prentice et al. (1978, Section 2). However, the case of independent ε_ij (·)’s does not imply that the L risks are not competing with each other. It only means that the failure time of type j of one cluster member is independent of the failure time of type k ≠ j of any other cluster member. However, different failure types can still compete with each other at subject level.

Based on the above likelihood function, various estimation procedures can be proposed. In what follows, we provide two estimation techniques, one that yields PMLEs for the case where λ₀₁ (·), …, λ_0L (·) are of a parametric form, and another that provides NPMLEs when the baseline hazard functions are left unspecified.

4.1 PMLEs

In parametric regression models, where the baseline hazard functions follow a parametric form such as the generalized gamma, log-normal, or log-logistic, one may maximize the likelihood function (2) directly with respect to β_j j = 1, …, J, the parameters of the frailty process and the parameters involved with Λ_0j j = 1, …, J, by using numerical integration. Alternatively, we provide a simple EM-algorithm for computing the PMLEs: (1) Estimate the conditional expectation of exp{ε_ij (t)} given the observed data and the current parameters’ values, denoted by μ̂_ij (t). This conditional expectation can be written explicitly for each specific density f{ε_i (·) | θ(·)} by using Bayes’ theorem. (2) Estimate β_j j = 1, …, J and the parameters involved with λ_0j (·)j = 1, …, J by maximizing

$${\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{{\mathbf{t}}_i>\mathbf{0}}}{\displaystyle \prod _{k=1}^{m_i}}{\displaystyle \prod _{j=1}^L}{[{\lambda }_{0j}(t_{\mathit{\text{ik}}})\text{exp}\{{\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+\text{log}{\widehat{\mu }}_{\mathit{\text{ij}}}(t_{\mathit{\text{ik}}})\}]}^{{\mathit{\text{dN}}}_{\mathit{\text{ik}}}^{(j)}(t_{\mathit{\text{ik}}})}\text{ exp }\left[-\text{ exp }\right\{{\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+\text{log}{\widehat{\mu }}_{\mathit{\text{ij}}}(t_{\mathit{\text{ik}}})\}{\lambda }_{0j}(t_{\mathit{\text{ik}}}){\mathit{\text{dt}}}_{\mathit{\text{ik}}}\{1-{\mathit{\text{dN}}}_{\mathit{\text{ik}}}^{(j)}(t_{\mathit{\text{ik}}})\}{Y}_{\mathit{\text{ik}}}(t_{\mathit{\text{ik}}})].$$

(3) Estimate θ(·) by maximizing ${\displaystyle {\sum }_{i=1}^n}\widehat{\mathrm{E}}[\text{log}f\{{\mathit{\epsilon }}_i(·)|\theta (·)\}]$, where Ê is defined as the conditional expectation given the observed data and the current parameters’ estimated values. Again, this conditional expectation can be written explicitly for each specific density by using Bayes’ theorem. (4) Repeat Steps (1)–(3) until convergence is reached with respect to all the parameters’ estimates.

Continuing Example 3 above, for each i = 1 …, n, k = 1, …, m_i, and j = 1, …, L, let ${\tilde{\epsilon }}_{\mathit{\text{ikj}}}={\epsilon }_j^{(1)}I(T_{\mathit{\text{ik}}}⩽t_o^{(j)})+{\epsilon }_j^{(2)}I(T_{\mathit{\text{ik}}}>t_o^{(j)}),{\delta }_{\mathit{\text{ik}}}^{(j)}={\delta }_{\mathit{\text{ik}}}I(J_{\mathit{\text{ik}}}=j)$ and

$$V_i=\text{exp}\left({\displaystyle \sum _{k=1}^{m_i}}{\displaystyle \sum _{j=1}^L}[{\tilde{\epsilon }}_{\mathit{\text{ikj}}}{\delta }_{\mathit{\text{ik}}}^{(j)}-\text{exp}\{{\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+{\tilde{\epsilon }}_{\mathit{\text{ikj}}}\}{\mathrm{\Lambda }}_{0j}(T_{\mathit{\text{ik}}})]\right).$$

Then, the conditional expectation of exp{ε_ij (t)} becomes

$$\frac{{\displaystyle \int }\text{exp}\left({\epsilon }_j^{(h)}\right)V_{i}f\left({\epsilon }_j^{(h)},{\mathit{\epsilon }}_i|\tilde{\theta }\right)d{\epsilon }_j^{(h)}d{\mathit{\epsilon }}_i}{{\displaystyle \int }{V}_{i}f({\mathit{\epsilon }}_i|{\theta }_i)d{\mathit{\epsilon }}_i}$$

with h = 1 if $t⩽t_o^{(j)}$, and h = 2 otherwise, where θ̃ is a subvector of θ and is being determined by the joint distribution of $({\epsilon }_j^{(h)},{\mathit{\epsilon }}_j)$. In addition, let θ^(r−1) be the current estimated values of θ. Then, the rth estimate of θ is the solution of the following equations:

$$\frac{1}{{\displaystyle \int }{V}_{i}f\left({\mathit{\epsilon }}_i|{\theta }_i^{(r-1)}\right)d{\mathit{\epsilon }}_i}{\displaystyle \sum _{i=1}^n}{\displaystyle \int }\frac{\partial \text{ log }f\left({\mathit{\epsilon }}_i|{\theta }_i\right)}{\partial {\theta }_i}{V}_{i}f\left({\mathit{\epsilon }}_i|{\theta }_i^{(r-1)}\right)d{\mathit{\epsilon }}_i=\mathbf{0}.$$

Usually, the integrals in the above calculations require numerical integration procedures such as Gaussian quadrature approximations.

It is well known (Kalbfleisch and Prentice, 2002, among many others) that parametric regression models often involve stronger distribution assumptions regarding the baseline hazard function than it is suitable to make. If the parametric models of the baseline hazard functions are incorrect, the above PMLEs are inconsistent. Therefore, in the following section, we provide an estimation technique for unspecified baseline hazard functions that is expected to suffer from some efficiency loss in comparison to the PMLEs, as long as the baseline hazards are correctly specified.

4.2 NPMLEs

The following NPMLEs is based on the seminal paper of Zeng and Lin (2007). That is, we regard the maximum partial likelihood estimators and the associated Breslow (1972) estimators of the cumulative baseline hazard functions as NPMLEs in that they maximize the nonparametric likelihood where the cumulative baseline hazard functions are regarded as infinite dimensional parameters.

Specifically, the NPMLEs can be obtained by the following EM algorithm. For j = 1, …, L define

$$S_j^{(0)}({\mathit{\beta }}_j,t)={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{k=1}^{m_i}}{Y}_{\mathit{\text{ik}}}(t)\text{ exp }\{{\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+{\epsilon }_{\mathit{\text{ij}}}(t)\}$$

and

$$S_j^{(1)}({\mathit{\beta }}_j,t)={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{k=1}^{m_i}}{Y}_{\mathit{\text{ik}}}(t){\mathbf{Z}}_{\mathit{\text{ik}}}\text{ exp }\{{\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+{\epsilon }_{\mathit{\text{ij}}}(t)\}.$$

In the M-step, we solve the complete-data score equation conditional on the observed data and the current parameter estimates. Hence for the estimation of $ℬ=({\mathit{\beta }}_1^T,\dots ,{\mathit{\beta }}_L^T)$ we solve

$${\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{k=1}^{m_i}}{\displaystyle {\int }_0^{\mathrm{\infty }}}\left[{\mathbf{Z}}_{\mathit{\text{ik}}}-\frac{{\widehat{S}}_j^{(1)}({\mathit{\beta }}_j,t)}{{\widehat{S}}_j^{(0)}({\mathit{\beta }}_j,t)}\right]{\mathit{\text{dN}}}_{\mathit{\text{ik}}}^{(j)}(t)=\mathbf{0}j=1,\dots ,L,$$ (3)

where ${\widehat{S}}_j^{(m)}({\mathit{\beta }}_j,t)m=0,1$ are defined analogously to $S_j^{(m)}({\mathit{\beta }}_j,t)$ while replacing the unknown exp{ε_ij (t)} by its conditional expectation given the observed data and the current parameters’ values, μ̂_ij (t) of Step (1) of the PMLEs algorithm.

For the estimation of the cumulative baseline hazard functions, ${\mathrm{\Lambda }}_{0j}(t)={\displaystyle {\int }_0^t}{\lambda }_{0j}(u)\mathit{\text{duj}}=1,\dots ,L$, we define the estimator of the jth cumulative baseline hazard by a step function with jumps at the observed failure times of type j, and is given by

$${\widehat{\mathrm{\Lambda }}}_{0j}(t)={\displaystyle {\int }_0^t}\frac{{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{k=1}^{m_i}}{\mathit{\text{dN}}}_{\mathit{\text{ik}}}^{(j)}(s)}{{\widehat{S}}_j^{(0)}({\mathit{\beta }}_j,s)}j=1,\dots ,L.$$ (4)

Finally, we estimate θ(·) as in Step (3) of the PMLEs algorithm.

To summarize, the following is our proposed NPMLE estimation procedure: (i) Given the values of θ and Λ_0j, j = 1, …, L, estimate β_j, j = 1 …, L, by solving (3). (ii) Given the values of θ and β_j, j = 1, …, L, estimate Λ_0j, j = 1, …, L, by using (4). (iii) Given the values of β_j and Λ_0j, j = 1, …, L, estimate θ by maximizing ${\displaystyle {\sum }_{i=1}^n}\widehat{\mathrm{E}}[\text{log}f\{{\mathit{\epsilon }}_i(·)|\theta (·)\}]$. (iv) Repeat Steps (i)–(iii) until convergence is reached with respect to all the parameters’ estimates.

Denote the true values of ℬ, θ, and 𝒜 = (Λ₀₁, …, Λ_0L) by ℬ^o, θ^o, and 𝒜^o and their NPMLEs by ℬ̂, θ̂, and 𝒜̂. Based on Zeng and Lin (2007), it can be shown that for bounded cluster size m_i as the total number of clusters n goes to infinity: (i) ℬ̂ is strongly consistent for ℬ^o. (ii) θ̂ is strongly consistent for θ^o. (iii) 𝒜̂(·) uniformly converges to 𝒜^o (·). (iv) n^1/2{ℬ̂ − ℬ^o, θ̂ − θ^o, 𝒜̂ − 𝒜^o} converges weakly to a zero-mean Gaussian process, and the limiting covariance matrix of {ℬ̂, θ̂} achieves the semiparametric efficiency bound. A detailed list of the technical conditions required for the above asymptotic results can be found in Zeng and Lin (2007, Appendix B, Conditions D1–D4 and D6–D8).

For the variance and covariance estimates, we treat the likelihood as a parametric likelihood of the regression coefficients and the jump sizes of the baseline hazard functions. Hence, the inverted observed information matrix is the variance–covariance estimated matrix of all the parameters’ estimates {ℬ̂, θ̂, 𝒜̂}. However, in practice, this procedure often does not work because of the large dimension of the observed information matrix. When the interest lies only in the regression coefficients and the frailty process parameters, the profile likelihood approach of Murphy and van der Vaart (2000) is recommended. For estimating the variance of the cumulative baseline hazard estimator as well, the bootstrap approach is recommended (e.g., Kosorok, Lee, and Fine, 2004), with cluster as the sampling unit.

5. Simulation Study

The following simulation studies are aimed to evaluate the finite-sample properties of the proposed model and estimation procedure. We considered L = 2 competing risks, 500 and 1000 clusters and two members within each cluster. The cluster-level dependency was constructed through a zero-mean multivariate normal distribution of the frailty variate ε(t) ≡ ε = (ε₁, ε₂) with $\theta =({\sigma }_1^2,{\sigma }_2^2,{\rho }_{12})=(1,1.5,0.5)$. In addition, we considered a single U[0, 1] distributed covariate with regression coefficients β₁ = 0.5 and β₂ = 2.5 for the two failure types, respectively. Given (β₁, β₂, ε₁, ε₂) and the covariate, we generated the earliest failure time, T^o, of each cluster member, from an exponential distribution with parameter γ = ∑_j exp(β_j Z + ε_j). Note that Pr (J = j | T^o = t) = γ_j/γ where γ_j = exp(β_j Z + ε_j). Hence, for generating the failure type of each cluster member, a Bernoulli random value, x, was sampled with probability of success γ₁/γ, so that x = 1(x = 0) implies J = 1(J = 2). In addition, independent censoring times were generated from U[0, 0.3]. The integrals were approximated by a two-dimensional Gauss–Hermite quadrature with 20 × 20 function evaluations from a one-dimensional Gauss–Hermite quadrature. Results are based on 200 simulated data sets. Table 1 summarizes the censoring rates and the average number of observed events under each scenario.

Table 1.

Summary of simulation settings: censoring rates and average (standard deviation, SD) number of observed events under the ρ₁₂ = 0.5. Each cluster consists of two members.

	500 clusters	1000 clusters
Censoring rate	48%	48%
Average (SD) number of individuals with observed event type j = 1	135.0 (12.30)	268.6 (16.26)
Average (SD) number of individuals with observed event type j = 2	376.5 (17.9)	754.9 (22.88)
Average (SD) number of families with two different types of observed events	47.7 (6.60)	94.8 (9.25)
Average (SD) number of families with two identical observed events of type j = 1	14.7 (3.80)	28.2 (5.35)
Average (SD) number of families with two identical observed events of type j = 2	93.7 (8.85)	188.4 (12.19)

We contrasted the proposed PMLEs and NPMLEs with those of the naive analysis that treats competing risks as independent censoring (see Appendix for details). It should be noted that the naive estimation procedure coincides with the proposed PMLE and NPMLE in case the frailty variates ε_j j = 1, …, J are independent, which in the current context, ρ₁₂ = 0.

The results are presented in Table 2 which include the empirical means and standard deviations of the estimates. It is evident that both PMLEs and NPMLEs perform very well in terms of bias and PMLEs are generally more efficient than NPMLEs. In contrast, the naive approach suffers from substantially biased estimate of the regression coefficient β₁ and some bias in estimation of ${\sigma }_1^2$ and Λ₀₁. Almost no bias is presented in the estimates of β₂, ${\sigma }_2^2$, and Λ₀₂. This can be explained by the sampling design in which we set β₁ = 0.5 and β₂ = 2.5, so that event type j = 2 is rarely censored by event type j = 1, while event type j = 1 is often censored by event type j = 2.

Table 2.

Summary of simulation results: the proposed NPMLEs and PMLEs for competing risks versus the naive approach that ignores competing risks under ρ = 0.5

	True value	Proposed NPMLE		Proposed PMLE		j = 2 as Censored				j = 1 as Censored
						NPMLE		PMLE		NPMLE		PMLE
		Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
500 clusters
β1	0.5	0.4790	0.2875	0.4881	0.3674	0.2857	0.3420	0.3293	0.3652	–	–	–	–
β2	2.5	2.4720	0.2792	2.4850	0.2323	–	–	–	–	2.4610	0.2709	2.5110	0.2383
${\sigma }_1^2$	1.0	1.0000	0.3724	1.0490	0.3491	0.9384	0.3878	1.1420	0.4038	–	–	–	–
${\sigma }_2^2$	1.5	1.4590	0.3369	1.4850	0.2362	–	–	–	–	1.4340	0.3209	1.5330	0.2458
ρ12	0.5	0.4833	0.2132	0.4878	0.2059	–	–	–	–	–	–	–	–
ψ1	1.0	–	–	1.0110	0.2252	–	–	0.9352	0.2240	–	–	–	–
ψ2	1.0	–	–	1.0280	0.1797	–	–	–	–	–	–	0.7330	0.1758
Λ01(0.10)	0.10	0.1002	0.0243	0.1011	0.0225	0.1013	0.0257	0.0935	0.0224	–	–	–	–
Λ01(0.15)	0.15	0.1497	0.0347	0.1516	0.0338	0.1466	0.0358	0.1403	0.0336	–	–	–	–
Λ01(0.20)	0.20	0.1969	0.0447	0.2022	0.0450	0.1883	0.0446	0.1870	0.0448	–	–	–	–
Λ01(0.25)	0.25	0.2397	0.0559	0.2527	0.0563	0.2253	0.0541	0.2338	0.0560	–	–	–	–
Λ02(0.10)	0.10	0.1036	0.0212	0.1028	0.0179	–	–	–	–	0.1013	0.0210	0.0973	0.0176
Λ02(0.15)	0.15	0.1529	0.0289	0.1542	0.0269	–	–	–	–	0.1479	0.0284	0.1460	0.0264
Λ02(0.20)	0.20	0.2025	0.0379	0.2056	0.0359	–	–	–	–	0.1939	0.0368	0.1947	0.0352
Λ02(0.25)	0.25	0.2493	0.0464	0.2570	0.0449	–	–	–	–	0.2367	0.0442	0.2433	0.0439
1000 clusters
β1	0.5	0.5008	0.2636	0.4971	0.2567	0.3080	0.2563	0.3423	0.2619	–	–	–	–
β2	2.5	2.4890	0.1817	2.4960	0.1751	–	–	–	–	2.4790	0.1814	2.5230	0.1782
${\sigma }_1^2$	1.0	0.9558	0.2765	0.9656	0.2508	0.8838	0.2892	1.0640	0.2856	–	–	–	–
${\sigma }_2^2$	1.5	1.4770	0.2002	1.4890	0.1495	–	–	–	–	1.4510	0.2017	1.5360	0.1542
ρ12	0.5	0.5014	0.1499	0.4943	0.1412	–	–	–	–	–	–	–	–
ψ1	1.0	–	–	1.0150	0.1637	–	–	0.9330	0.1555	–	–	–	–
ψ2	1.0	–	–	1.0070	0.1232	–	–	–	–	–	–	0.9633	0.1171
Λ01(0.10)	0.10	0.1011	0.0179	0.1018	0.0164	0.1007	0.0183	0.0933	0.0155	–	–	–	–
Λ01(0.15)	0.15	0.1512	0.0258	0.1527	0.0246	0.1461	0.0254	0.1399	0.0233	–	–	–	–
Λ01(0.20)	0.20	0.2006	0.0333	0.2036	0.0328	0.1891	0.0316	0.1866	0.0311	–	–	–	–
Λ01(0.25)	0.25	0.2465	0.0423	0.2545	0.0410	0.2282	0.0386	0.2333	0.0389	–	–	–	–
Λ02(0.10)	0.10	0.1014	0.0129	0.1017	0.0122	–	–	–	–	0.0990	0.0126	0.0963	0.0117
Λ02(0.15)	0.15	0.1524	0.0185	0.1525	0.0183	–	–	–	–	0.1471	0.0179	0.1444	0.0176
Λ02(0.20)	0.20	0.2019	0.0249	0.2034	0.0244	–	–	–	–	0.1929	0.0239	0.1927	0.0234
Λ02(0.25)	0.25	0.2513	0.0315	0.2543	0.0305	–	–	–	–	0.2380	0.0298	0.2408	0.0293

In order to evaluate the efficiency loss due to the unnecessary modeling of the dependency between the frailty variates, we provide, in Table 3, simulation results of the above setting but with ρ₁₂ = 0 and (β₁, β₂) = (1, 1) or (β₁, β₂) = (0.5, 2.5). Under (β₁, β₂) = (1, 1), we observed negligible efficiency loss, if any, with respect to all the parameters for both PMLEs and NPMLEs. With (β₁, β₂) = (0.5, 2.5), where event of type j = 2 tends to censor the other event type but not vice versa, the NPMLE of β₁ corresponds to j = 1 suffers from some efficiency loss (relative efficiency is about 80%) in comparison to the other regression coefficient β₂ (relative efficiency is about 109%). In all the other cases, the efficiency loss, if any, is very small.

Table 3.

Summary of simulation results: the proposed NPMLEs and PMLEs for competing risks versus the naive approach that ignores competing risks under ρ = 0

	True value	Proposed NPMLE		Proposed PMLE		j = 2 as Censored				j = 1 as Censored
						NPMLE		PMLE		NPMLE		PMLE
		Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
1000 clusters
β1	1.0	1.0020	0.1990	1.0080	0.1963	0.9946	0.1983	1.0080	0.1959	–	–	–	–
β2	1.0	0.9944	0.1863	0.9846	0.1894	–	–	–	–	1.0060	0.1901	0.9846	0.1896
${\sigma }_1^2$	1.0	0.9523	0.2142	0.9797	0.1842	0.9998	0.2308	0.9737	0.1839	–	–	–	–
${\sigma }_2^2$	1.5	1.4890	0.2546	1.4920	0.2186	–	–	–	–	1.4720	0.2715	1.4870	0.2151
ρ12	0.0	−0.0106	0.1537	−0.0125	0.1429	–	–	–	–	–	–	–	–
ψ1	1.0	–	–	1.0040	0.1363	–	–	1.0070	0.1342	–	–	–	–
ψ2	1.0	–	–	1.0240	0.1434	–	–	–	–	–	–	1.0260	0.1407
Λ01(0.10)	0.10	0.1012	0.0153	0.1004	0.0142	0.1001	0.0255	0.1007	0.0134	–	–	–	–
Λ01(0.15)	0.15	0.1507	0.0212	0.1506	0.0213	0.1501	0.0230	0.1510	0.0201	–	–	–	–
Λ01(0.20)	0.20	0.1999	0.0280	0.2008	0.0273	0.2004	0.0301	0.2014	0.0268	–	–	–	–
Λ01(0.25)	0.25	0.2464	0.0349	0.2510	0.0341	0.2483	0.0384	0.2517	0.0336	–	–	–	–
Λ02(0.10)	0.10	0.1018	0.0150	0.1024	0.0143	–	–	–	–	0.1013	0.0143	0.1026	0.0141
Λ02(0.15)	0.15	0.1528	0.0216	0.1536	0.0215	–	–	–	–	0.1512	0.0202	0.1539	0.0211
Λ02(0.20)	0.20	0.2039	0.0299	0.2048	0.0287	–	–	–	–	0.2007	0.0269	0.2052	0.0281
Λ02(0.25)	0.25	0.2523	0.0368	0.2560	0.0359	–	–	–	–	0.2479	0.0343	0.2565	0.0352
1000 clusters
β1	0.5	0.5156	0.2422	0.5143	0.2357	0.4890	0.2151	0.5181	0.2349	–	–	–	–
β2	2.5	2.4830	0.1751	2.4890	0.1696	–	–	–	–	2.4760	0.1833	2.4890	0.1692
${\sigma }_1^2$	1.0	0.9880	0.2632	0.9434	0.2372	0.9970	0.2702	0.9316	0.2393	–	–	–	–
${\sigma }_2^2$	1.5	1.4790	0.2048	1.4920	0.1565	–	–	–	–	1.4860	0.2097	1.4880	0.1536
ρ12	0.0	−0.0099	0.1726	−0.0130	0.1604	–	–	–	–	–	–	–	–
ψ1	1.0	–	–	1.0170	0.1556	–	–	1.0210	0.1503	–	–	–	–
ψ2	1.0	–	–	1.0200	0.1231	–	–	–	–	–	–	1.0220	0.1212
Λ01(0.10)	0.10	0.1022	0.0173	0.1017	0.0155	0.1010	0.0168	0.1021	0.0150	–	–	–	–
Λ01(0.15)	0.15	0.1525	0.0246	0.1525	0.0233	0.1520	0.0245	0.1531	0.0226	–	–	–	–
Λ01(0.20)	0.20	0.2012	0.0316	0.2034	0.0311	0.2015	0.0323	0.2042	0.0300	–	–	–	–
Λ01(0.25)	0.25	0.2477	0.0391	0.2542	0.0389	0.2462	0.0381	0.2553	0.0376	–	–	–	–
Λ02(0.10)	0.10	0.1020	0.0132	0.1020	0.0123	–	–	–	–	0.1028	0.0139	0.1022	0.0121
Λ02(0.15)	0.15	0.1527	0.0190	0.1530	0.0185	–	–	–	–	0.1539	0.0197	0.1533	0.0182
Λ02(0.20)	0.20	0.2036	0.0240	0.2040	0.0246	–	–	–	–	0.2032	0.0257	0.2044	0.0242
Λ02(0.25)	0.25	0.2514	0.0313	0.2550	0.0308	–	–	–	–	0.2512	0.0335	0.2555	0.0303

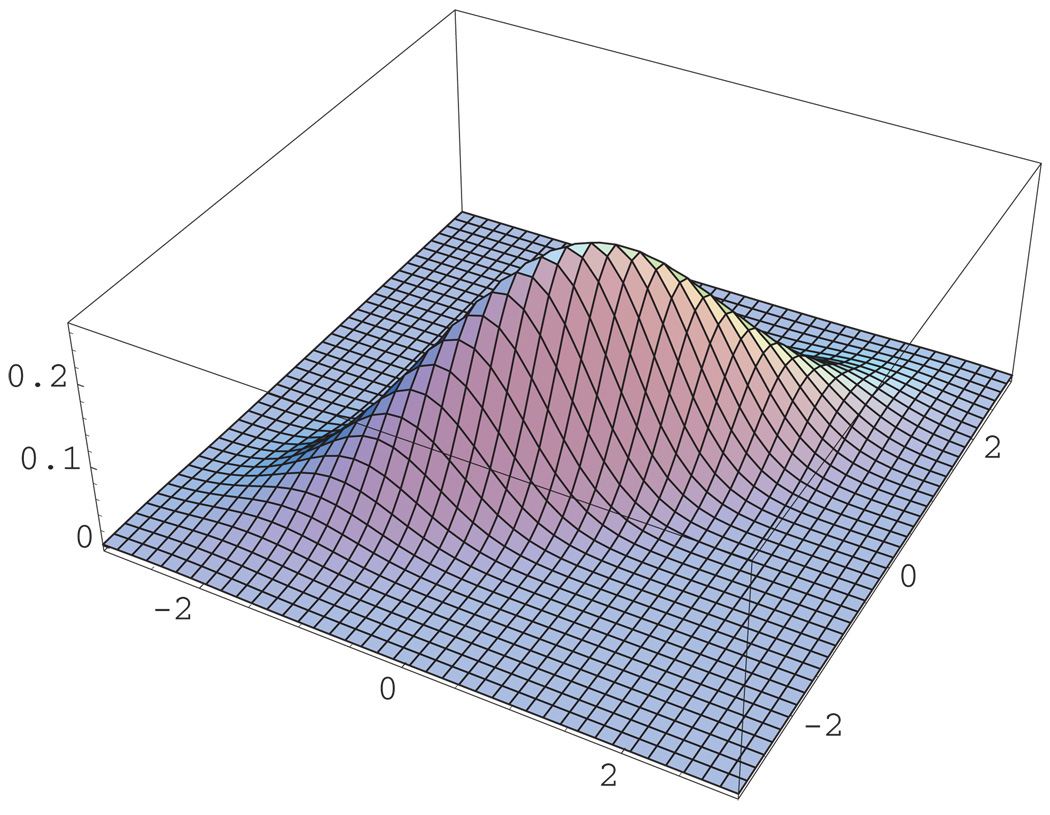
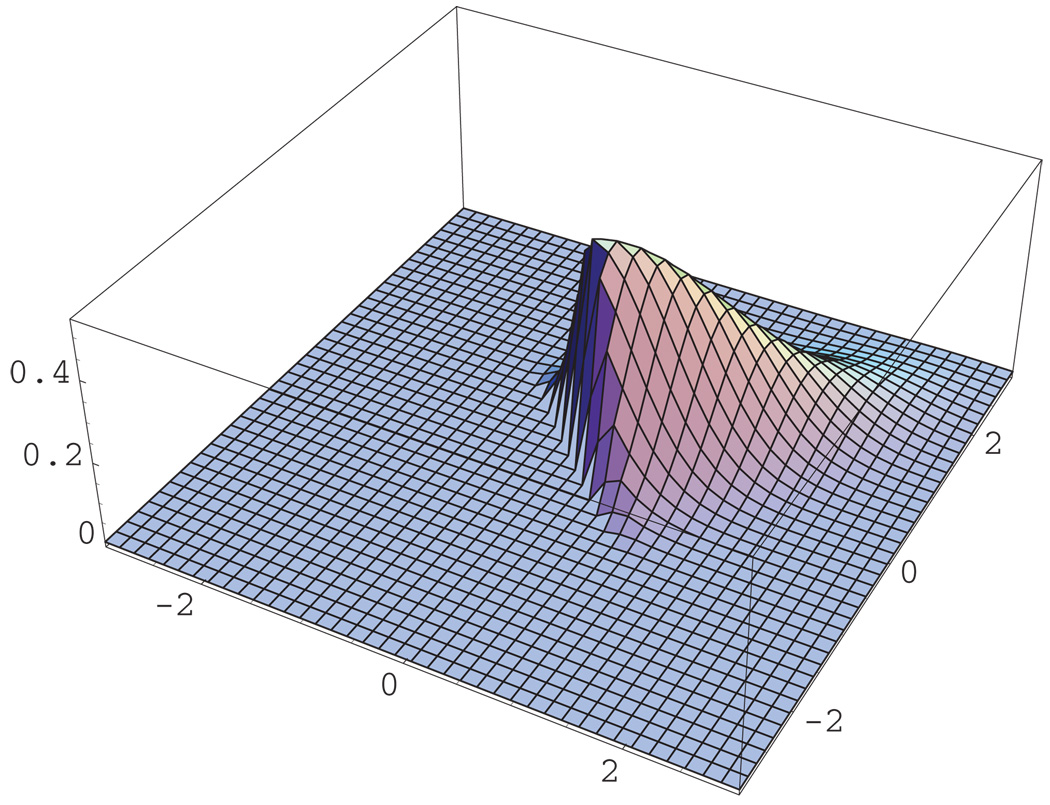
Next, we consider the robustness of the proposed model and the estimation technique when the frailty distribution of ε is misspecified. Specifically, we assumed a multivariate normal frailty model but the true frailty variates were generated from a multivariate skewed-normal distribution (Azzalini and Dalla Valle, 1996). An L-dimensional random variable X is said to have a multivariate skewed-normal distribution if it is continuous with density function 2ϕ_L (x; Ω)Φ(α^T x) where x ∈ ℛ^L, ϕ_L (x; Ω) is the L-dimensional normal density with zero mean and correlation matrix Ω, Φ(·) is the standard normal distribution function, and α is a L-dimensional vector. When the shape parameter α, which regulates skewness, equals zero, the above density reduces to the multivariate normal density with zero mean and correlation matrix Ω. Figures 2 and 3 provide a graphical demonstration of the discrepancy between the bivariate normal distribution and the skewed-normal distribution with α = (50, 50)^T and correlation parameter of 0.8, used in the following simulation results. Table 4 presents simulation results under the skewed-normal distribution with shape parameter of α = (50, 50)^T and the correlation parameter value of Ω equals 0.8. The rest of the sampling design is the same as of Table 2. The results indicate that even under misspecification of the frailty distribution the PMLEs and NPMLEs of ℬ and 𝒜, based on the multivariate normal distribution, introduce only a small bias in contrast to the naive approach treating the other event as censored.

Figure 2.

The bivariate normal density function with mean zero and correlation parameter of 0.8. This figure appears in color in the electronic version of this article.

Figure 3.

The bivariate skewed-normal density function with correlation parameter of 0.8 and α = (50, 50)^T. This figure appears in color in the electronic version of this article.

Table 4.

Summary of simulation results: misspecification of the frailty distribution. The true frailty distribution is a multivariate skewed-normal and the assumed distribution is a multivariate normal.

	True value	Proposed NPMLE		Proposed PMLE		j = 2 as Censored				j = 1 as Censored
						NPMLE		PMLE		NPMLE		PMLE
		Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
500 clusters
β1	0.5	0.4823	0.3246	0.4858	2.5140	0.2587	0.2983	0.3026	0.3070	–	–	–	–
β2	2.5	2.4880	0.2488	2.5140	0.2360	–	–	–	–	2.4670	0.2444	2.5450	0.2379
ψ1	1.0	–	–	0.9554	0.2012	–	–	0.8868	0.2013	–	–	–	–
ψ2	1.0	–	–	0.9670	0.1533	–	–	–	–	–	–	0.9057	0.1437
Λ01(0.10)	0.10	0.0939	0.0213	0.0955	0.0201	0.0966	0.0231	0.0887	0.0201	–	–	–	–
Λ01(0.15)	0.15	0.1405	0.0309	0.1433	0.0302	0.1392	0.0318	0.1330	0.0302	–	–	–	–
Λ01(0.20)	0.20	0.1864	0.0408	0.1911	0.0402	0.1796	0.0409	0.1774	0.0403	–	–	–	–
Λ01(0.25)	0.25	0.2285	0.0519	0.2389	0.0503	0.2153	0.0498	0.2217	0.0503	–	–	–	–
Λ02(0.10)	0.10	0.0972	0.0171	0.0967	0.0153	–	–	–	–	0.0951	0.0167	0.0906	0.0144
Λ02(0.15)	0.15	0.1447	0.0247	0.1451	0.0229	–	–	–	–	0.1396	0.0237	0.1359	0.0216
Λ02(0.20)	0.20	0.1933	0.0310	0.1934	0.0307	–	–	–	–	0.1841	0.0293	0.1811	0.0287
Λ02(0.25)	0.25	0.2390	0.0389	0.2418	0.0383	–	–	–	–	0.2253	0.0359	0.2264	0.0359
1000 clusters
β1	0.5	0.4723	0.2462	0.4841	0.2333	0.2476	0.2277	0.2948	0.2341	–	–	–	–
β2	2.5	2.1550	0.2005	2.5300	0.1813	–	–	–	–	2.4990	0.1999	2.5650	0.1833
ψ1	1.0	–	–	0.9521	0.1432	–	–	0.8742	0.1425	–	–	–	–
ψ2	1.0	–	–	0.9514	0.1120	–	–	–	–	–	–	0.8868	0.1063
Λ01(0.10)	0.10	0.0950	0.0159	0.0951	0.0143	0.0967	0.0170	0.0874	0.0143	–	–	–	–
Λ01(0.15)	0.15	0.1413	0.0216	0.1428	0.0215	0.1387	0.0224	0.1311	0.0214	–	–	–	–
Λ01(0.20)	0.20	0.1888	0.0282	0.1904	0.0286	0.1799	0.0282	0.1748	0.0285	–	–	–	–
Λ01(0.25)	0.25	0.2334	0.0376	0.2380	0.0356	0.2175	0.0364	0.2186	0.0356	–	–	–	–
Λ02(0.10)	0.10	0.0947	0.0130	0.0951	0.0111	–	–	–	–	0.0924	0.0128	0.0887	0.0106
Λ02(0.15)	0.15	0.1422	0.0182	0.1427	0.0168	–	–	–	–	0.1366	0.0175	0.1330	0.0159
Λ02(0.20)	0.20	0.1914	0.0238	0.1903	0.0224	–	–	–	–	0.1815	0.0225	0.1774	0.0213
Λ02(0.25)	0.25	0.2394	0.0306	0.2379	0.0280	–	–	–	–	0.2244	0.0283	0.2217	0.0266

Table 5 aimed to study the effect of misspecification of the baseline hazard functions. The true baseline hazard functions are Λ_0j (t) = ψ_j t^2/3 with ψ_j = 1, j = 1, 2, and the analysis was performed as if Λ_0j (t) = ψ_j t, j = 1, 2. As expected, the PMLEs are severely biased with respect to all the parameters, while the NPMLEs are not.

Table 5.

Summary of simulation results: misspecification of the parametric baseline hazard functions. The true baseline hazard functions are Λ_0j (t) = ψ_j t^2/3j = 1, 2 and the assumed functions (under PLMEs) are Λ_0j (t) = ψ_j tj = 1, 2.

	True value	Proposed NPMLE		Proposed PMLE		j = 2 as Censored				j = 1 as Censored
						NPMLE		PMLE		NPMLE		PMLE
		Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
1000 clusters
β1	0.5	0.5065	0.2303	1.4070	0.3159	0.3813	0.2666	0.6406	0.3209	–	–	–	–
β2	2.5	2.4880	0.1729	3.2670	0.2252	–	–	–	–	2.4740	0.1731	3.5426	0.2387
${\sigma }_1^2$	1.0	0.9606	0.2383	2.7130	0.3267	0.8576	0.2073	2.8230	0.3065	–	–	–	–
${\sigma }_2^2$	1.5	1.4740	0.1699	3.1090	0.2115	–	–	–	–	1.4410	0.1714	3.5870	0.2102
ρ12	0.5	0.4984	0.1303	0.8997	0.1065	–	–	–	–	–	–	–	–
ψ1	1.0	–	–	1.8870	0.2790	–	–	1.4090	0.2491	–	–	–	–
ψ2	1.0	–	–	1.9630	0.2866	–	–	–	–	–	–	1.4200	0.2041
Λ01(0.10)	0.2154	0.2165	0.0303	0.1887	0.0279	0.0988	0.0181	0.1409	0.0249	–	–	–	–
Λ01(0.15)	0.2823	0.2818	0.0378	0.2831	0.0418	0.1443	0.0236	0.2113	0.0374	–	–	–	–
Λ01(0.20)	0.3420	0.3374	0.0463	0.3740	0.0558	0.1879	0.0306	0.2818	0.0498	–	–	–	–
Λ01(0.25)	0.3969	0.3833	0.0549	0.4718	0.0697	0.2274	0.0377	0.3523	0.0623	–	–	–	–
Λ02(0.10)	0.2154	0.2181	0.0235	0.1963	0.0287	–	–	–	–	0.2086	0.0227	0.1420	0.0204
Λ02(0.15)	0.2823	0.2854	0.0307	0.2945	0.0429	–	–	–	–	0.2700	0.0290	0.2130	0.0306
Λ02(0.20)	0.3420	0.3433	0.0379	0.3926	0.0573	–	–	–	–	0.3220	0.0352	0.2840	0.0408
Λ02(0.25)	0.3969	0.3918	0.0441	0.4908	0.0716	–	–	–	–	0.3652	0.0407	0.3550	0.0510

In the Web Appendix we present additional simulation results for the following cases: (1) small number of clusters, such as 100; (2) two independent covariates; (3) two dependent covariates; and (4) skewed covariate. In short, it is evident that our methods performs reasonably well under these scenarios as well.

6. Real Data Analysis: The Washington Ashkenazi Kin-Cohort Study

To illustrate the utility of our proposed model and estimation procedure, we analyze data from the Washington Ashkenazi Kin-Cohort Study (WAS; Struewing et al., 1997). In this study, blood samples and questionnaires were collected from Ashkenazi Jewish men and women volunteers living in the Washington, DC area. Based on blood samples, volunteers were tested for specific mutations in BRCA1 and BRCA2 genes. The questionnaire included information on cancer and mortality history of the first-degree relatives of the volunteers.

Currently, we consider a subset of the data consisting of female first-degree relatives of volunteers (mother, sisters and daughters); two competing events: breast (j = 1) and ovarian (j = 2) cancers; and a binary covariate that takes a value of 1 or 0 according to presence or absence of any BRCA1/2 mutations in the volunteer’s blood sample. The data consists of 4153 families with 2–8 relatives (12206 subjects). A total of 896 and 99 subjects were observed with breast cancer and ovarian cancer, respectively, as their first event. Only 10 families were observed with the two types of events among the relatives (exactly one event of each type). For the analysis of these data we used only the nonparametric approach as it is not obvious which parametric form would fit best for the misspecified baseline hazard functions, if any. Given our simulation results for the misspecified baseline hazard function, the NPMLEs may be more appropriate here.

Table 6 presents the NPMLEs based on the two-dimensional normal frailty model for the association of outcomes of family members. Namely, (ε_i1, ε_i2)^T are bivariate time-independent normally distributed with mean zero and the covariance matrix consists of the parameters $({\sigma }_1^2,{\sigma }_2^2,{\rho }_{12})$. We used a time-independent distribution for the frailty process due to the small number of families with two types of events. The weighted bootstrap approach of Kosorok et al. (2004, Section 4) was used for calculating the standard errors and a total of 50 bootstrap data sets were generated. It is evident that the presence of any BRCA1/2 mutation in the volunteer’s blood sample increases the risk of breast or ovarian cancers among her first-degree relatives, and the cumulative baseline hazard of breast cancer is much higher than that of ovarian cancer. In addition, the familial dependence of relatives’ ovarian cancer ages at onset $({\widehat{\sigma }}_2^2=1.7240)$ is much stronger than that of breast cancer $({\widehat{\sigma }}_1^2=0.8718)$. The familial dependence between age at breast cancer onset of one relative and age at ovarian cancer onset of another relative was observed to be relatively weak (ρ̂₁₂ = 0.1247). Without adjusting for the volunteer’s BRCA1/2 mutations’ status, the familial dependencies for breast cancer, ovarian cancer, and the correlation between ovarian and breast cancer are 0.9404, 1.7527, and 0.2099, respectively, indicating that volunteer’s BRCA1/2 mutations’ status explained partly the familial dependence of breast and ovarian cancers and particularly the correlation between breast and ovarian cancers. Two possible naive analyses exist, where in each analysis the risk’s parameters of one type of cancer are being estimated and the other type of cancer is being considered as independent censoring. In these data, the estimates of the naive models are fairly close to those based on the proposed competing risks model. For example, β̂₁ and β̂₂ were 1.4055 (SD 0.2239) and 1.5118 (SD 0.4695), respectively, and ${\widehat{\sigma }}_1^2\text{ and }{\widehat{\sigma }}_2^2$ were 0.9416 (SD 0.5285) and 1.6436 (SD 0.7454), respectively. This is probably because ρ̂₁₂ is close to zero. However, it can be seen that the competing risks modeling provides a more comprehensive analysis of multiple failure types in cluster settings than the analysis that deals with one failure type at a time. It can also be seen that the efficiency loss due to estimation of ρ₁₂, when this parameter is close to zero, is very small. This result strengthens our confidence in the general usage of competing risks modeling for this type of data.

Table 6.

Analysis of the Washington Ashkenazi Kin-Cohort Data using the proposed NPMLE approach

	Estimator	Bootstrap SD
	Breast cancer
β1	1.3910	0.2167
${\sigma }_1^2$	0.8718	0.5362
Λ01(50)	0.0298	0.0061
Λ01(60)	0.0578	0.0108
Λ01(70)	0.0966	0.0165
Λ01(80)	0.1395	0.0215
	Ovarian cancer
β2	1.5420	0.4361
${\sigma }_2^2$	1.7240	0.7811
Λ02(50)	0.0014	0.0006
Λ02(60)	0.0035	0.0014
Λ02(70)	0.0067	0.0028
Λ02(80)	0.0096	0.0038
	Familial correlation between breast and ovarian cancers
ρ12	0.1247	0.0981

7. Discussion

The proposed class of models can be easily extended to the case in which the regression coefficients’ vectors or the cause-specific hazard functions also vary among individuals within a cluster. For example, in a family study, mothers and daughters may not have the same regression coefficients or cause-specific baseline hazard functions.

The proposed PMLEs and NPMLEs can be easily implemented. For example, for NPMLEs, within each maximization step of the EM algorithm, the estimates of the regression coefficients and the cumulative baseline hazard functions can be computed by using built-in statistical packages such as coxph of R with an offset term.

Our proposed approaches require numerical integration for which many numerical routines have been developed. We used the Gauss–Hermite quadrature. For this method, it is generally recommended that the nodes are symmetric about zero and 15^L function evaluations from one-dimensional Gauss–Hermite quadrature usually provide a very good approximation in most applications, as long as L ⩽ 5. Most statistical and mathematical software packages provide one-dimensional Gauss–Hermite quadrature calculations, which can be easily adopted for the multivariate case.

Fine, Jiang, and Chappell (2001) proposed a semi-competing risks model, in which one event may censor another event, but not vice versa. In continuation of the BRCA1 example in the Introduction, the semi-competing risks model describes more precisely the situation where the onset of breast cancer does not prevent the death from ovarian cancer, but the death from ovarian cancer or any other related cause precludes the onset of breast cancer. The development of our multivariate frailty model to semi-competing risks situation is worth pursuing and could be a topic of future work.

Frailty models require the specification of the distribution of the random effects. Hougaard (2000) provides a comprehensive discussion of the theoretical properties and the fit of various frailty distributions for a noncompeting risks setting. Hsu, Gorfine, and Malone (2007) show by simulation that the bias in the marginal parameters, under a noncompeting risks setting, are generally 10% or lower under the assumed Gamma model and misspecification of the frailty distribution. We also showed here that our model is robust under the assumed multivariate normal frailty model when the true distribution is skewed. However, it is worthwhile to develop diagnostic approaches, tests, and graphical procedures for model checking and model selection to ensure the fitted model is as close to the true model as possible.

APPENDIX

Estimation Procedures for the Naive PMLEs and NPMLEs

Consider the situation where the jth failure type is of interest and all other failure types are considered as independent censoring events, under a time-independent multivariate normally distributed frailty variate. The naive PMLEs and NPMLEs are obtained by the following steps: (1) Estimate exp{ε_ij} by μ̂_ij which are defined as

$$\frac{{\displaystyle \int }\text{exp}({\epsilon }_j)\text{ exp }\left[{\displaystyle \sum _{k=1}^{m_i}}\{{\epsilon }_j{\delta }_{\mathit{\text{ik}}}^{(j)}-\text{exp}({\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+{\epsilon }_j){\mathrm{\Lambda }}_{0j}(T_{\mathit{\text{ik}}})\}\right]f({\epsilon }_j|\theta )d{\epsilon }_j}{{\displaystyle \int }\text{exp}\left[{\displaystyle \sum _{k=1}^{m_i}}\{{\epsilon }_j{\delta }_{\mathit{\text{ik}}}^{(j)}-\text{exp}({\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+{\epsilon }_j){\mathrm{\Lambda }}_{0j}(T_{\mathit{\text{ik}}})\}\right]f({\epsilon }_j|\theta )d{\epsilon }_j}$$ (A.1)

while replacing the unknown parameters with their current estimated values. (2) Estimate β_j and the parameters involved with λ_0j (·) by maximizing

$${\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{k=1}^{m_i}}{[{\lambda }_{0j}(T_{\mathit{\text{ik}}})\text{ exp }\{{\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+\text{log}{\widehat{\mu }}_{\mathit{\text{ij}}}\left\}\right]}^{{\delta }_{\mathit{\text{ik}}}^{(j)}}\text{ exp }[-\text{exp}\{{\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+\text{log}{\widehat{\mu }}_{\mathit{\text{ij}}}\}{\mathrm{\Lambda }}_{0j}(T_{\mathit{\text{ik}}})]$$

for PMLE, and estimate β_j and λ_0j (·) by maximizing

$${\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{k=1}^{m_i}}{\displaystyle \int }{\{{\lambda }_{0j}(T_{\mathit{\text{ik}}})\text{ exp }({\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+{\epsilon }_j\left)\right\}}^{{\delta }_{\mathit{\text{ik}}}^{(j)}}\text{ exp }\{-\text{exp}({\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+{\epsilon }_j){\mathrm{\Lambda }}_{0j}(T_{\mathit{\text{ik}}})\}f({\epsilon }_j|\theta )d{\epsilon }_j$$

for NPMLE. (3) Estimate $\theta ={\sigma }_j^2$ by

$$\frac{{\displaystyle \int }{\epsilon }_j^2\text{exp}\left[{\displaystyle \sum _{k=1}^{m_i}}\{{\epsilon }_j{\delta }_{\mathit{\text{ik}}}^{(j)}-\text{exp}({\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+{\epsilon }_j){\mathrm{\Lambda }}_{0j}(T_{\mathit{\text{ik}}})\}\right]f({\epsilon }_j|\theta )d{\epsilon }_j}{{\displaystyle \int }\text{exp}\left[{\displaystyle \sum _{k=1}^{m_i}}\{{\epsilon }_j{\delta }_{\mathit{\text{ik}}}^{(j)}-\text{exp}({\mathit{\beta }}_j^T{\mathbf{Z}}_{\mathit{\text{ik}}}+{\epsilon }_j){\mathrm{\Lambda }}_{0j}(T_{\mathit{\text{ik}}})\}\right]f({\epsilon }_j|\theta )d{\epsilon }_j}$$ (A.2)

while replacing the unknown parameters with their current estimated values. (4) Repeat steps (1)–(3) until convergence.