Particle Based Shape Regression of Open Surfaces with Applications to Developmental Neuroimaging

Abstract

Shape regression promises to be an important tool to study the relationship between anatomy and underlying clinical or biological parameters, such as age. In this paper we propose a new method to building shape models that incorporates regression analysis in the process of optimizing correspondences on a set of open surfaces. The statistical significance of the dependence is evaluated using permutation tests designed to estimate the likelihood of achieving the observed statistics under numerous rearrangements of the shape parameters with respect to the explanatory variable. We demonstrate the method on synthetic data and provide a new results on clinical MRI data related to early development of the human head.

1 Introduction

Technologies for shape representation and statistical shape analysis are important for several problems in medical imaging including image segmentation, quantitative analysis of anatomy, and group comparisons. A widely used approach is to evaluating shapes is assign correspondences or landmarks to shapes (curves, or surfaces) and to compare the positions or configurations of these landmarks. This approach has benefitted in recent years from methods for the automatic placement of landmarks in a way that captures the statistical properties of an ensemble of images [1,2,3]. Finding correspondences that minimize description length [2] or entropy [1] has been shown to generate shape models that systematically capture the underlying variability of the population and conform, qualitatively, to the underlying anatomy. This paper extends the method of Cates et al. [1], which uses an variational formulation of ensemble entropy to position dense collections of landmarks, or particles.

On the clinical front, quantitative magnetic resonance imaging has significantly advanced our understanding of brain development during childhood and adolescence. Courchesne et al. [4] describe differences in growth patterns in autism compared to controls. However, these studies do not include children below the age of 4 years. Data measured in infants from birth to 4 years are mostly volumetric measurements, such as intracranial volume and volumes of brain lobes and subcortical structures [5]. Whereas this selection of previous work demonstrates very active research towards determining brain growth at early stage of development, there is little data on modelling head and brain growth across a continuum of time and almost no work on the study of how development influences shape.

In developmental analyses, such as paediatric neurodevelopment, shape regression gives aggregate models of growth, with variability. Thus shape analysis promises to give not only basic insights into the process of development, but also allow comparisons of individuals against normative models. Of course, precise characterizations of these relationships will require shape models that can tease apart those aspects of shape variability that are explained by the underlying variables and those that are not. Likewise, in order to understand the statistical significance of such relationships we will need a systematic, unbiased method for testing these correlations. These are the topics addressed in this paper.

2 Methodology

This section gives a brief overview of the particle-system correspondence optimization method, which is first described in [1]. The general strategy of this method is to represent correspondences as point sets that are distributed across an ensemble of similar shapes by a gradient descent optimization of an objective function that quantifies the entropy of the system. Our proposed extension to this method incorporates a linear regression model into the correspondence optimization. We also present a new methodology for correspondence optimization on open surfaces where surface boundaries are defined by arbitrary geometric constraints—which is important for studying paediatric head shape.

Correspondence Optimization

We define a surface as a smooth, closed manifold of codimension one, which is a subset of ȑ^d (e.g., d = 3 for volumes). We sample a surface 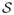⊂ ȑ^d using a discrete set of N points that are considered random variables Z = (X_1, X_2, …, XN )^T,X ∈ ȑ ^d drawn from a probability density function (PDF), p(X). We denote a realization of this PDF with lower case, and thus we have z = (x₁,x₂, …, x_N )^T, where z ∈ 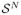. The probability of a realization x is p(X = x), which we denote simply as p(x).

The amount of information contained in such a random sampling is, in the limit, the differential entropy of the PDF, which is

$$H[\mathbf{X}]=-{\int }_{S}p(\mathbf{x})logp(\mathbf{x})dx=-E\{logp(\mathbf{X})\},$$ (1)

where E{·} is the expectation. Approximating the expectation by the sample have mean, we have $H[\mathbf{X}]\approx -\frac{1}{Nd}{\sum }_{i}logp({\mathbf{x}}_i)$ To estimate p(x_i), we use a non-parametric Parzen windowing estimation, modified to scale density estimation in proportion to local curvature magnitude. The kernel width σ is chosen adaptively at each x_i to maximize the likelihood of that position. We refer to the positions x as particles, and a set of particles as a particle system.

Now consider an ensemble 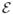, which is a collection of M surfaces, each with their own set of particles, i.e., 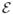= z¹, …, z^M. The ordering of the particles on each shape implies a correspondence among shapes, and thus we have a matrix of particle positions $P={\mathbf{x}}_j^k$, with particle positions along the rows and shapes across the columns. We model z^k ∈ȑ^{N d} as an instance of a random variable Z, and minimize a combined ensemble and shape cost function

$$Q=H(\mathbf{Z})-\sum _{k}H(P^k),$$ (2)

which favors a compact ensemble representation balanced against a uniform distribution of particles on each surface. Given the low number of samples relative to the dimensionality of the space, we use a parametric approach described in [1] for density estimation in the space of shapes. The entropy cost function Q is minimized using a gradient descent strategy to manipulate particle positions (and, thus, also correspondence positions). The surface constraint is specified by the zero set of a scalar function F (x). This optimization strategy balances entropy of individual surface samplings with the entropy of the shape model, maximizing the former for geometric accuracy (a good sampling) and minimizing the latter to produce a compact model.

Any set of implicitly defined surfaces is appropriate as input to this framework. For this paper, we use binary segmentations, which contain an implicit shape surface at the interface of the labeled pixels and the background. To remove aliasing artifacts in these segmentations, we use the r-tightening algorithm given by Williams et al. [6]. Correspondence optimizations are initialized with the splitting strategy described in [1], starting with a single particle on each object. We use a Procrustes algorithm, applied at regular intervals during the optimization, to align shapes with respect to rotation and translation, and to normalize with respect to scale.

Correspondence with Regression Against Explanatory Variables

With the assumption of a Gaussian distribution in the space of shapes, we can introduce a generative statistical model

$$\mathbf{z}=\mu +\epsilon ,\epsilon \sim \mathcal{N}(\mathbf{0},\mathrm{\sum })$$ (3)

for particle correspondence positions, where μ is the vector of mean correspondences, and ε is normally-distributed error. Replacing μ in this model with a function of an explanatory variable t gives the more general, regression model

$$\mathbf{z}=f(t)+\widehat{\epsilon },\widehat{\epsilon }\sim \mathcal{N}(\mathbf{0},\widehat{\mathrm{\sum }}).$$ (4)

The optimization described in the previous section minimizes the entropy associated with ε, which is the difference from the mean. In this paper, we propose to optimize correspondences under the regression model in Eqn. 4 by instead minimizing entropy associated with ε̂, the residual from the model. Considering particle correspondence to be a linear function of t, given as f (t) = a + bt, we need an estimate of parameters a and b to compute ε̂. We estimate these with a least-squares fit to the correspondence data,

$$arg\underset{\mathbf{a},\mathbf{b}}{min}E(\mathbf{a},\mathbf{b})=\frac{1}{2}\sum _k{[(\mathbf{a}+\mathbf{b}{t}_k)-{\mathbf{z}}_k]}^T{\mathrm{\sum }}^{-1}[(\mathbf{a}+\mathbf{b}{t}_k)-{\mathbf{z}}_k].$$ (5)

Setting $\frac{\delta E}{\delta \mathbf{a}}=\frac{\delta E}{\delta \mathbf{b}}=0$ and solving for a and b, we have $\mathbf{a}=\frac{1}{n}({\sum }_k{\mathbf{z}}_k-{\sum }_k\mathbf{b}{t}_k)$, and $\mathbf{b}=({\sum }_k{t}_k{\mathbf{z}}_k-{\sum }_k{\mathbf{z}}_k{\sum }_k{t}_k)/({\sum }_k{t}_k^2-{(\sum t_k)}^2)$.

The proposed regression model optimization algorithm then proceeds as follows. Correspondences are first optimized under the nonregression model (Eqn 3) to minimize the entropy associated with the total error ε, and to establish an initial estimate for a and b. We then follow the same optimization procedure as described in Section. 2, but replace the covariance of the model with the covariance of the underlying residual relative to the generative model. We interleave the two estimation problems, and thus the parameters a and b are re-estimated after each iteration of the gradient descent on the particle positions.

Correspondences on Open Surfaces

To compute correspondence positions on a set of open surfaces, we propose an extension to the sampling method reviewed in Section. 2. The proposed method is to define the boundary as the intersection of the surface 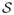with a set of geometric primitives, such as cutting planes and spheres. Our goal is to formulate the interactions with these boundaries so that the positions of these constraints has as little influence as possible on the statistical shape model.

For each geometric primitive, we construct a virtual particle distribution that consists of all of the closest points on its surface to the particles x_i on 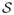. During the gradient descent optimization, particles x_i interact with the virtual particles, and are therefore effectively repelled from the geometric primitives, and thus from the open surface boundary. The virtual distributions are updated after each iteration as the particles on 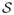redistribute under the optimization. Because the virtual particles are allowed to factor into the Parzen windowing kernel size estimation, particles x_i maintain a distance from the boundary proportional to their density on the surface . In this way, features near the boundary may be sampled, but particles are never allowed to lie on the actual boundary itself. One such configuration is shown in Figure. 1

Fig 1.

Particle system with geometric primitives defining the boundary

Permutation Test of Significance

Analysis of variance (ANOVA) is the standard parametric test for testing if the explanatory variables have a significant effect in a linear regression. The test statistic used is

$$T=\frac{R^2/(m-1)}{(1-R^2)/(n-m)},$$ (6)

where R² is Pearson’s coeffcient of regression, generally defined as $R^2=1-\frac{{SS}_{\text{err}}}{{SS}_{\text{tot}}}$ ,where SS _err is the sum-squared residual error, and SS _tot represents total variance in the data. In general, R² can be related to the unexplained variance of the generated model, and is used to measure the goodness-of-fit for the regression model. When the residuals of the linear model are iid Gaussian, the statistic T follows an F distribution with m − 1 and n − m degrees of freedom under the null hypothesis.

In this case where the outcome variables are correspondence-optimized shape parameters, the underlying assumptions of the parametric F -test may not hold. Furthermore, optimization with knowledge of the underlying parameter could lead to optimistic estimates of significance, because we are explicitly minimizing the residual. To overcome this, we propose a nonparametric permutation test for significance. Permutation tests for regression work by permuting the values of the explanatory variables. This allows us to compute a distribution of our test statistic under the null hypothesis that the explanatory variable has no relationship to the dependent variable. Given data (z_i, t_i), we generate the kth permuted data set as (z_i, t_π^k(i)), where π _k is a permutation of 1, …, n. For each permutation we compute a test statistic T_k using (6). Then comparing our unpermuted test statistic T to the distribution of T_k, we can compute the p-value as the percentage of T_k that are greater than T. Notice, that for the case of regression-optimized correspondences, described in Section 2, we perform a the correspondence optimization on each permutation separately, and thus the results of our permutation test are not biased by the correspondence method.

3 Results and Discussion

This section details experiments designed to illustrate and validate the proposed method. First, we present an experiment with synthetically generated tori to illustrate the applicability of the method and validation based on permutation tests. Next, we present an application to the study of early growth of head shapes extracted from structural MRI data.

To illustrate and validate the proposed methods, we performed two experiments on sets of 40 synthetically generated tori, parameterized by the small radius r and the large radius R. The values for the shape parameters were chosen as independent functions of a uniformly distributed explanatory variable t. The definition of R², used to compute the test statistic as explained in Section. 2, is extended to include the two independent variables for this experiment:

$$R^2=1-\frac{{({SS}_{\mathit{err}})}_r+{({SS}_{\mathit{err}})}_R}{{({SS}_{\mathit{tot}})}_r+{({SS}_{\mathit{tot}})}_R}.$$ (7)

We examine sets of time-dependent shapes with p-values {0.01, 0.1} in order to examine the performance of the system with and without significance. To construct these example data sets, we use the value for the statistic T (look up from the F -distribution) to generate a target R². The values of r and R are chosen such that the R² of the generated set is approximately equal to the target R² for that experiment. Along with explicit correspondences generated from the standard torus parametrization, we use the correspondence methods from Section. 2, optimization with and without an underlying regression model, to optimize correspondences using 256 particles on each shape. An analysis of the resulting models showed that all three sets of correspondences exhibited two pure modes of variation.

Synthetic Data (Tori)

Here we present the results of the statistical analysis of the tori test data using permutation tests consisting of 1000 permutations of the explanatory variable t. For the correspondences we compute the test statistics using the two dominant modes from a PCA on the set of correspondences. The procedure described in Section. 2 is then applied to get the corresponding p-values. Table. 1 shows the results of the two permutation tests for the explicit correspondences, and correspondences generated using the proposed methods. A comparison of the parametric p-value with the p-values obtained by the permutation tests confirms that the proposed methods preserve the relationship between the explanatory variable and the dependent variables. The correspondence-based approaches, particularly with the regression model, show greater significance than the parametric case. This might be an inherent property of the statistic or it could be an artifact due to the limited number of example datasets and the limited number of permutations. Future work will include more datasets, more permutations, and a bootstrapping procedure to analyze variability of the p-values computed by the various methods.

Table 1.

Results of permutation tests (1000 permutations)

p-value (theory)	p-value(parametric)	Correspondence Type
		Explicit Min.	Entropy	Regression-based
0.01	0.011	0.011	0.007	0.004
0.1	0.095	0.095	0.067	0.066

Head Shape Regression

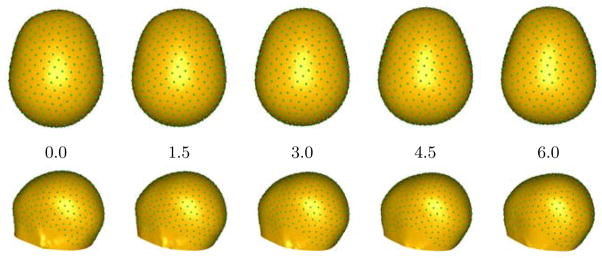
The proposed regression-based correspondence method is also used to study the growth of head shape from structural MRI data obtained from clinical studies spanning the age range from neonate to 5 year old. The 40 cases include 1.5T, T1-weighted MRI scans with resolutions of 1mm ×1mm ×1mm and 0.4mm ×0.4mm ×3.6mm. The scans are preprocessed and segmented to obtain the head surfaces, which are input to the optimization process. Manually placed landmarks on the bridge of the nose and the openings of the left and right ear canals define a cutting plane and a pair of spheres that we use as constraints, as in Section. 2, to repel the correspondences from the neck, face, and ears, in order to restrict the analysis to the cranium, which is most interesting from a neurological point of view. Figure. 1 shows the particle system distributed across one of the head shapes after optimizing 500 particles.

Head size, measured in volume or circumference is well known to correlate with age. This is confirmed by the linear regression plot (size versus log of age) with p < 2 × 10⁻¹⁶, shown in Figure. 2. Next, the shapes were preprocessed using methods mentioned in Section. 2 to remove the effects of size. Changes in head shape along the linear regression line (shape versus log of age) are shown in Figure. 3. Note the relative lengthening of the head, and the narrowing at the temples with increasing age. These shape changes are consistent with clinical observations that neonatal brain growth proceeds more rapidly in the forebrain. These results tie head shape to age in the paediatric setting.

Fig 2.

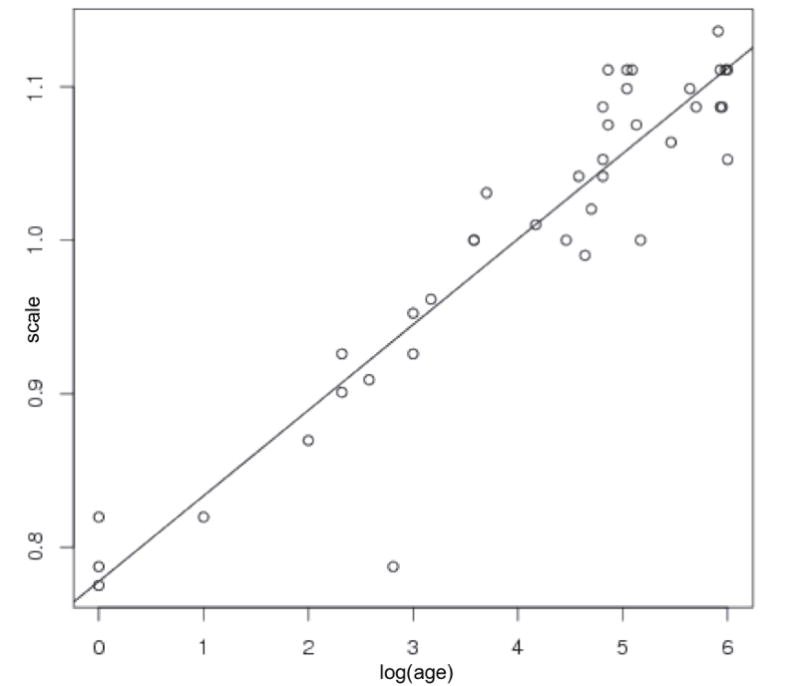
Changes in head size with age

Fig 3.

Overview of head shape regression: Changes in head shape with age

The permutation tests for both the proposed methods for this example showed that none of 1000 permutations gave a better correlation than the input data. While this p = 0 result is not conclusive, it does give strong evidence for significance. Future work will include more permutations to more accurately evaluate the significance.

The experiments were run on a 2GHz processor with run times of approximately 15 minutes for the tori (256 particles) and 40 minutes for the head shapes (500 particles). The permutation tests (1000 permutations) were run as parallel processes on a 16-processor machine.

4 Conclusion

This paper describes a method for shape regression that accounts for explanatory variables in the placement of correspondences and allows for open surfaces with arbitrary geometric constraints, and presents a mechanism for hypothesis testing of the role of underlying variables in shape. Results from a study of head shape growth indicate that the proposed method can be applied to quantitative characterization of the relationship between age and head shape in young children. Such analysis will generate data beyond the currently established standard of head circumference measurements as an index of growth. Moreover, it will generate normative data as a continuous growth model of shape, which can be useful in building optimal MRI head coils for young infants. The continuous shape model could also find use in population studies where two groups are compared with respect to growth trajectory rather than differences at individual time points.