The shape of mammalian phylogeny: patterns, processes and scales

Abstract

Mammalian phylogeny is far too asymmetric for all contemporaneous lineages to have had equal chances of diversifying. We consider this asymmetry or imbalance from four perspectives. First, we infer a minimal set of ‘regime changes’—points at which net diversification rate has changed—identifying 15 significant radiations and 12 clades that may be ‘downshifts’. We next show that mammalian phylogeny is similar in shape to a large set of published phylogenies of other vertebrate, arthropod and plant groups, suggesting that many clades may diversify under a largely shared set of ‘rules’. Third, we simulate six simple macroevolutionary models, showing that those where speciation slows down as geographical or niche space is filled, produce more realistic phylogenies than do models involving key innovations. Lastly, an analysis of the spatial scaling of imbalance shows that the phylogeny of species within an assemblage, ecoregion or larger area always tends to be more unbalanced than expected from the phylogeny of species at the next more inclusive spatial scale. We conclude with a verbal model of mammalian macroevolution, which emphasizes the importance to diversification of accessing new regions of geographical or niche space.

1. Introduction

As our ability to reconstruct phylogenies has developed, it has become clear that the Tree of Life's structure is much less regular than most early depictions: proliferation has been much more rapid in some branches and at some times than others (reviewed by [1–3]). In mammals, for instance, a recent taxonomy listed 2277 species of rodent and 1166 species of bat, but only one aardvark, two flying lemurs and three elephants [4]—even though all these clades are tens of millions of years old. There is a long history of both deterministic and stochastic explanations for such diversity differences, both in general (e.g. [5–7]) and in mammals (e.g. [6,8,9]).

Phylogenies of present-day species provide two valuable—though still incomplete—lines of evidence that can be analysed to gain more precise insight into macroevolution [1–3]. First, analysing the temporal spacing of nodes can reveal changes in diversification rates over time. Such an analysis of mammalian phylogeny found evidence for a pulse of early radiation about 100–85 Ma, followed by low rates until about 10 Myr after the cretaceous–paleogene (or K–Pg) boundary, when diversification again sped up [10]. However, analyses of nodes ages depend on the adequacy of the methods used to estimate dates—still a contentious area (e.g. [11,12])—and are unlikely to estimate extinction history accurately [13–15].

In this paper, we therefore focus on the second line of evidence—the phylogeny's asymmetry or imbalance. If two sister clades have diversified to very different extents, their species have probably had different underlying probabilities of diversifying [16]. Measures of imbalance seek to capture the difference in species-richness between sister clades [1], and are commonly used to test whether contemporaneous species could all have had the same chances of diversification, a null model known as the equal-rates Markov (ERM) model. We begin by analysing the overall imbalance of mammalian phylogeny before using a range of empirical and simulation approaches to try to understand mammalian macroevolution.

2. The shape of mammalian phylogeny

We used a modification [17] of Bininda-Emonds et al.'s [10] phylogeny because it adopts a more recent taxonomy [4]. We excluded four domesticated species, generated by artificial rather than natural selection, from all of our analyses. The resulting tree has 925 bifurcations with enough present-day descendants to be informative about imbalance. Importantly, it contains the great majority (5016/5416) of the recognized species: the imbalance of highly incomplete phylogenies will be an unbiased estimate of the true imbalance if sampling is random, but strict randomness may be unlikely [18]. Wilkinson et al. [19] noted that the method used to construct the supertree is biased with respect to tree shape, tending to favour more unbalanced topologies. We therefore also analysed two near-complete, well-resolved, species-level ‘supermatrix’ Bayesian phylogenies of orders—Carnivora [20] and Cetartiodactyla [21]: comparing the imbalance of these trees with the relevant portions of the supertree provides a preliminary assessment of whether the supertree's imbalance could be artifactual.

We characterized imbalance in two ways. The first is a purely phenomenological measure of pattern. We used Fusco & Cronk's [22] approach to compute an imbalance score, I, for each of the 925 informative nodes, according to

where B is the number of species in the more diverse sister clade, m is the smallest value B could take and M the largest possible value for B. These I values range from zero (as symmetric as possible) to one (completely asymmetric). We applied weights as in Purvis et al. [23] such that, under ERM, the weighted mean I (hereafter, I_w) has an expectation of 0.5 for any node size (i.e. total number of extant descendant species). The empirical I_w for the whole set of nodes was compared with the null expectation using a weighted t-test. We likewise tested marsupials, all placentals and four placental superorders separately. On rejecting ERM, we then constructed imbalance signatures to provide a richer description of imbalance; we grouped nodes into 10 bins of equal width on the log(node size) axis between the clade's minimum and maximum node size, computed I_w within each bin and regressed I_w against mean log(node size) among bins. Although the nodal I values have a strongly non-normal distribution, use of within-bin I_w gives regressions a much more normally distributed error term. In these regressions, node size might be acting as a proxy for node age—whatever processes are causing imbalance can operate for longer in older clades. We tested this possibility using weighted multiple regression of nodal I on log(node size) and log(clade age). The R package caper (C. D. L. Orme 2011, unpublished data, http://caper.r-forge.r-project.org/) was used to compute nodal imbalance scores.

We also used a process-based measure of imbalance, namely the estimate of β from Aldous's [24] β-split model of clade growth. The range of β is from –2 to +∞; trees where β < 0 are more unbalanced than average ERM trees, and those with β > 0 are more balanced. Two trees that grew under the same β-split model should yield very similar β estimates. Aldous [24] was motivated by mathematical simplicity rather than biological considerations, and biological meaning of particular β values remains opaque [25]. Nonetheless, a β of approximately –1 has been found to provide a good fit to a wide range of (incomplete) published phylogenies [25], perhaps implying a common macroevolutionary process. At the very least, β reflects tree shape pattern differently from I_w. To estimate β, we modified the function maxlik.betasplit in the R package apTreeshape [26] in two ways. First, we removed the requirement for a fully resolved phylogeny. (We used simulations, not shown, to check that estimates of β were not systematically biased by randomly collapsing branches in ERM phylogenies.) Second, to avoid underflow errors, we amended one of the internal functions to work with the log(beta) distribution rather than the beta distribution. We then optimized β for the whole tree and for the same subtrees and binned sets of nodes as identified above.

Both I_w and β indicate that chances of diversification have varied among contemporaneous species (table 1; first row). The values of I_w and β are very similar for marsupials and placentals separately, and for three of the four placental superorders (table 1), the exception being Xenarthra, which had only seven informative nodes. The cyt b phylogenies were slightly more unbalanced than the corresponding portions of the supertree (table 1), suggesting that the supertree's imbalance is not artifactual.

Table 1.

Estimates of I_w and β for portions of mammalian phylogeny. n = number of informative nodes. Significance of departure from the equal-rates Markov expectation is assessed by weighted t-test for I_w and from 1000 parametric bootstrap replicates for β. 95% CI, confidence interval for β from bootstrapping.

clade	n	Iw ± s.e.	β	95% CI
Mammalia	925	0.631 ± 0.013***	−0.857***	−0.974 to −0.710
Marsupialia	110	0.650 ± 0.038***	−0.904***	−1.215 to −0.392
Eutheria	812	0.627 ± 0.014***	−0.847***	−0.985 to −0.684
Afrotheria	15	0.657 ± 0.090	−0.878	−1.671 to 6.113
Xenarthra	7	0.420 ± 0.160	7.264	−2.000 to >500
Laurasiatheria	398	0.603 ± 0.020***	−0.765***	−0.955 to −0.498
Euarchontoglires	389	0.653 ± 0.020***	−0.938***	−1.110 to −0.731
Carnivora: supertree	108	0.590 ± 0.040	−0.752***	−1.104 to −0.137
Carnivora: cyt b tree	140	0.672 ± 0.033	−1.102***	−1.276 to −0.855
Cetartiodactyla: supertree	69	0.616 ± 0.032	−0.770	−1.216 to 0.014
Cetartiodactyla: cyt b tree	148	0.662 ± 0.032	−1.002***	−1.186 to −0.732

*p < 0.05; **p < 0.01, ***p < 0.001.

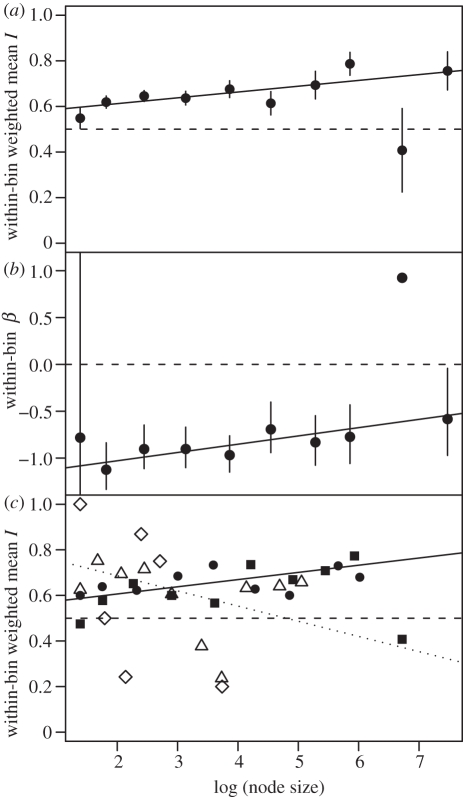
The imbalance signature in figure 1a shows that I_w increases with node size across the whole phylogeny. The regressions of I_w on log(node size) did not differ significantly among placental superorders (omitting Xenarthra on grounds of sample size; F_2,21 = 1.67, p > 0.2), but placental and marsupial imbalance signatures do differ significantly (F_1,31 = 4.83, p = 0.04). However, a clearer distinction is that I_w increases more with log(node size) in the two more diverse placental superorders (Laurasiatheria and Euarchontoglires) than in Afrotheria or Marsupialia (F_1,31 = 6.25, p = 0.02; figure 1c). ANCOVA showed no differences between the imbalance signatures of cyt b tree and supertree for either order (Carnivora: F_2,244 = 1.30, p > 0.2; Cetartiodactyla: F_2,213 = 0.61, p > 0.5).

Figure 1.

(a) I_w signature for the whole mammalian phylogeny. Points are within-bin I_w; vertical lines indicate ± 1 s.e. (Note the large s.e. of the second point from the right, associated with a small sample size.) Horizontal dashed line, ERM expectation. Solid line is weighted regression, with sample sizes as the weights: slope = 0.025, t₈ = 2.573, p = 0.03. (b) β signature for the whole tree. Points are within-bin estimates of β; vertical lines are confidence intervals under a χ² approximation. (The second point from the right is again unusual but uncertain.) Horizontal dashed line, ERM expectation. Solid line is weighted regression, with the inverse of the confidence interval width as weights: slope = 0.088, t₈ = 2.238, p = 0.06. (c) I_w signature for each of four superorders. Points are within-bin mean I_w. Triangles, Marsupialia; diamonds, Afrotheria; squares, Laurasiatheria; circles, Euarchontoglires. Dotted line is regression through Marsupialia and Afrotheria (slope = −0.067, t₁₄ = −1.768, p = 0.1); solid line is regression through Laurasiatheria and Euarchontoglires (slope = 0.032, t₁₇ = 2.685, p = 0.02); regressions weighted as in (a).

Multiple regression suggests that node age does not confound the relationship seen in figure 1a: nodal I does not depend on log(node age) (t₉₂₂ = −1.085, p > 0.2) but increases weakly with log(node size) (slope = 0.024, t₉₂₃ = 2.418, p = 0.02). Although the two predictors are correlated, variance inflation factors were less than 2, indicating no strong collinearity. Contrary to expectation, β shows a weak tendency (p = 0.06) to become less negative—closer to ERM—for larger nodes (figure 1b).

The finding that mammalian phylogeny is too unbalanced for ERM is unsurprising: analyses of large individual trees (e.g. [27,28]) and collections of smaller trees (e.g. [18,29–31]) have repeatedly shown that complete or nearly complete empirical phylogenies are markedly too asymmetric for ERM. The estimate of β is significantly less negative than the value of −1 suggested by Blum & Francois [25] for their smaller, incomplete trees, but very close to the estimate derived from their largest fully bifurcating trees (−0.89).

The dependence of I_w on node size is in line with some previous studies. Purvis & Agapow [31], analysing a set of 61 phylogenies across a wide range of taxa, found that nodes with a given number of higher taxa (e.g. genera) descended from them were more unbalanced on average than nodes having the same number of species descended from them. Holman [32] showed that I_w increased roughly linearly with log(node size) across the same set of phylogenies, and a similar pattern was also reported for a collection of highly incomplete trees [33]. Freckleton et al. [34] showed I_w to rise with log(node size) in carnivora but to decrease in New World primates. An increase in I_w with node size indicates the presence of small basal clades; however, clades are unlikely to persist for long at low numbers under diversity independent dynamics. The frequency of small, old clades (especially in Laurasiatheria and Euarchontoglires) therefore suggests either that their dynamics are diversity-dependent or that they are now declining deterministically (having previously grown deterministically). The surprising finding that—unlike I_w—β becomes closer to ERM expectations at deeper nodes suggests that it is best not to view the value of β as a process parameter; it is not constant. A possible mechanism is if many clades having a greatly reduced diversification rate die out before they become old, making the tree self-pruning.

The overall shape of mammalian phylogeny is complex, reflecting a mixture of diversification rates. The next section is to identify clades that stand out as unusual compared with the tree as a whole.

3. Winners and losers: pinpointing shifts in diversification rate

Here, we distinguish between two kinds of deviation from the tree-wide imbalance signature. Individual nodes with unusual imbalance can suggest which intrinsic and extrinsic phenomena may have regulated diversification [16,22]. On the other hand, consistent variation in imbalance—i.e. a whole subtree with imbalance differing from the parental phylogeny—is analogous to non-stationarity in models of spatial or time-series data: it suggests that different processes have been operating in different parts of the phylogeny.

To locate individual changes in diversification rate, we used the Δ₁ statistic [35,36] as implemented in apTreeshape [26]. Δ₁ considers two pieces of evidence in deciding whether diversification rate has increased along a branch: the imbalance of the ancestral node and the imbalance of the descendant. Nodal imbalance is expressed as the ratio between the likelihood of the observed split under a single-rate ERM process, and the likelihood of the same split if the larger daughter clade had diversified with a 100-fold higher rate; larger likelihood ratios therefore indicate higher imbalance. Δ₁ is simply the difference between the likelihood ratios of the nodes at the start and the end of a branch; significance is assessed by simulating a single-rate ERM process. An upshifted descendant clade will tend to make the parental clade appear to be upshifted too (a phenomenon known as ‘trickle down’; [37]). In such cases, both likelihood ratios will be large but the Δ₁ between them relatively small. Consequently (following the contingency table in [36]), here we ascribe an increase in diversification rate only to branches where a significant Δ₁ is observed between an unbalanced ancestral node and a more balanced descendant. Of 1335 bifurcating nodes in the supertree, 15 provided such evidence of an increase in diversification rate. These nodes are presented in table 2, and depicted with an upward-facing black triangle on figure 2.

Table 2.

Rate-shifted clades. MSW taxon = name of clade in Wilson & Reeder [4]. n = number of species in clade, n_sister = number of species in sister clade, n_ancs = number of species in sister group to ancestral node.

MSW taxon (3rd edn)	age (Myr)	n	nsister	nancs	node label
(a) Clades arising from significant (p ≤ 0.05) upshifts in diversification rate (100-fold shift in λsister) as measured by Δ1 [37]
‘Boreoeutheria’	96.2	4614	29	69	8
Dipodomyinae + Perognathinae + some Geomyidae (Rodentia)	35.9	96	2	1456	443
Sciurinae + Xerinae + Calloscurinae (Rodentia; Sciuridae)	40.2	275	1	1	585
Sciurinae (Rodentia; Sciuridae)	18.2	80	4	7	681
within Sylvivagus (Lagomorpha; Leporidae)	8.3	10	1	2	809
Simiiformes	52.4	265	7	79	885
Carnivora	64.1	282	8	325	1330
Hipposideridae + Rhinolophidae (Chiroptera)	47.5	147	16	5	1702
Artibeus (Chiroptera; Phyllostomidae)	8.6	17	1	26	1845
Molossus and allies (Chiroptera; Molossidae)	22.8	58	4	10	1898
Subgenus Sorex (Soricomorpha; Soricidae)	24	47	3	3	2162
Phalangeriformes + Macropodiformes (Diprotodontia)	45.8	122	4	1	2285
Macropus (Diprotodontia; Macropodidae)	10.1	13	1	2	2357
Dasyuridae (Dasyuromorphia)	25.4	63	1	2	2391
Didelphinae (Didelphimorphia; Didelphidae)	51.6	79	5	216	2464
(b) Clades tentatively identified as resulting from downshifts in diversification rate
Monotremata	63.6	4	5012	n/a	2
Anomaluromorpha (Rodentia)	54.9	9	1447	98	15
Castoridae (Rodentia)	12.1	2	96	1456	442
Sciurotamias (Rodentia; Sciuridae)	5	2	120	6	674
Dermoptera	12.8	2	351	20	1115
Giraffidae + Antilocaprinae (Cetartiodactyla)	20.2	3	189	8	1251
Camelidae (Cetartiodactyla)	21.8	3	306	16	1315
Harpionycteris (Chiroptera; Pteropodidae)	3.8	2	85	12	1617
Noctilionidae (Chiroptera)	3.5	2	158	1	1763
Desmodontinae (Chiroptera; Phyllostomidae)	26.8	3	147	8	1772
Solenodeontidae (Soricomorpha)	40.5	2	390	1669	2216
‘Afrotheria’	89.5	69	4643	300	2236

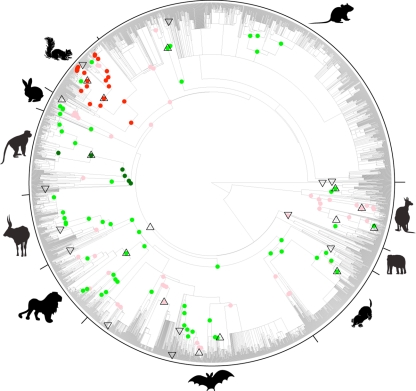
Figure 2.

Diversification rate shifts localized on the supertree. Major clades are summarized with pictograms (clockwise from top: Rodentia, ‘Marsupials’, ‘Afrotheria’, ‘Eulipotyphyla’, Chiroptera, Carnivora, Cetartiodactyla, Primates, Lagomorpha, Sciuridae). Filled circles indicate subtrees with betas different from that of the whole tree (see text for details). More unbalanced: red (non-overlapping CI) and pink (maximum-likelihood estimate of β for subtree outside whole-tree CI); more balanced: green (non-overlapping CI) and light green (ML estimate of β for subtree outside whole-tree CI). Triangles indicate nodes with significant (p ≤ 0.05) upshifts as indicated by Δ₁ (upwards pointing) and putative downshifts (downwards pointing).

Moore et al. [37] argue that Δ₁ can only detect increases in diversification rate, because clades undergoing a decrease are unlikely to survive to be observed. We suggest that Δ₁ can also be used to pinpoint some decreases in diversification rate (‘downshifts’), albeit with caveats. For small clades, the likelihood under a single-rate ERM process will be similar to that under a heterogenous rate, as there is little evidence to differentiate between the two: small clades have inherently low likelihood ratios. As a result, a significant Δ₁ can be found along a branch between an unbalanced ancestral node and a smaller descendant. If imbalance at the ancestral node cannot be ascribed to an increase in rate on the branch leading to its larger daughter, and if a significant Δ₁ is observed on the branch leading to its smaller daughter, we contend this to suggest a decrease in net diversification rate in the smaller daughter clade. Such downshifted clades are depicted with downward triangles in figure 2 and table 2 gives details. We caution that our evidence is only suggestive, and note that our approach does not permit the identification of single species as downshifts.

Δ₁ localizes rate shifts to an individual branch, but its performance is yet to be evaluated in the context of gradual changes across the phylogeny. These would probably best be detected using the temporal spacing of nodes, but the supertree's incomplete resolution and dating complicates such an analysis. Instead, we used local variation in Aldous' β to paint a wider picture of variation in imbalance across the supertree, and to look for subtrees having consistent but unusual imbalance signatures. Our motivation is that any whole-tree imbalance statistic, while useful, is a measure of the central tendency of imbalance for a set of nodes and can therefore average away interesting biological patterns. We therefore calculated the maximum-likelihood estimate of β for every subtree in the phylogeny. Several subtrees yield β values whose confidence intervals do not overlap with those of the whole-tree estimate. Primates are significantly more balanced and sciurids significantly more unbalanced, as shown by the coloured circles in figure 2 (red subtrees are unbalanced, dark green are balanced). Figure 2 also shows that variation in imbalance is not randomly located around the phylogeny: many other clades have imbalance signatures that differ consistently, although not significantly, from the whole-tree imbalance (pink and mint green subtrees have a β outside the 95% CI for the whole-tree estimate). Whole-tree imbalance measures do seem to obscure interesting variation, although in mammals the effect size may be slight.

What mechanisms might underlie this variation in imbalance across mammalian phylogeny? Comparing the topologies of Primates and Sciuridae—the clades with the most extreme balance and imbalance, respectively—suggests that the answer could lie in the interaction of historical biogeography and biotic responses to global change. The differing geographical nature of diversification in response to global change has, we suspect, played a large part in generating the observed differences in imbalance.

Crown-group Primates are old for their habitat. We infer Simiiformes to be a significant radiation, at about 52.4 Ma, a timing that closely matches the first appearance of crown-group Primates (Euprimates) in the fossil records of Europe, Asia and North America at the onset of the Eocene [38,39]. However, by the Mid-Eocene, Primates as a whole were beginning to decline even as crown-group Simiiformes were diversifying. Simiiformes radiated in a world that was cooling and drying throughout the Eocene [40], as the area of habitat similar to modern tropical forests was declining [41] and possibly filling up with competitors such as arboreal rodents [42]. New World primates, in particular, show an extremely balanced topology. Repeated variation in the availability of tropical forest has been suggested to govern diversification regimes in South American vertebrates [43] and specifically the topological balance of Primates (the ‘simultaneous across-lineage vicariance’ of Heard & Cox [44]). We suggest that the balanced phylogeny of Primates is a consequence of such vicariant speciation within a limited geographical region, throughout much of the history of crown-group Primates (and speculate that Xenarthra—also an unusually balanced clade (table 1)—may have had a similar history). Towards the end of the Eocene, sciurids experienced the flip side of the same coin, as xeric habitats, savannah and temperate forest all increased rapidly in area leading, we speculate, to a diffusion of lineages through newly available space and a resulting unbalanced topology. Many of the diversification rate upshifts in table 2 can be argued to correspond to sudden access to novel geographical or habitat space, although palaeontological data are patchy, limiting the scope for meta-analysis. Kisel et al. [45] present evidence that, in mammals, colonization of new geographical areas usually elevates diversification.

Downshifts in diversification rate are even harder than upshifts to infer or date reliably, so interpretation of the clades in table 2 is necessarily more speculative. Limited geographical space, geographical isolation or disproportionate extinction can all be expected to lead to a depauperate extant clade [46,47]. In some cases, extinction does appear to be a contributory factor, either in deep time—Afrotherians, and perhaps monotremes—or more recently—camelids, giraffids (e.g. [48]) and solenodons [49]. Most of the downshifted clades are moderately widespread and some (e.g. Castoridae and Camelidae) are very wide-ranging. From an ecological perspective, many seem to be highly unusual mammals: vampire and fishing bats, high-altitude xeric artiodactyls, lodge-building riparian rodents, toothless monotremes and non-chiropteran gliders (including one highly balanced clade in the otherwise universally unbalanced Sciuridae). Unusualness is a statistical concept, of course, and species-rich groups are bound to appear typical, but specialization to a narrow adaptive zone may be the best predictor of species-poverty. We speculate that such specializations may reduce the likelihood of radiation—because the niches are not broad enough to support multiple species in sympatry—but at the same time confer a strong incumbency advantage [50] that reduces the per-species background extinction rate if niches are stable over time [51]. Such a mechanism would lead to species in relictual groups tending to be highly specialized, which is certainly true for some of the species-poor basal clades (e.g. Monotremata, Xenarthra).

If biogeographic history has been important in shaping mammalian diversity [52], then it should be considered alongside ecological or life-history differences when trying to understand clade-richness patterns [53]. It may also explain why ecological or life-history differences alone have so far explained little of the variance in species-richness among mammalian clades in phylogenetic comparative analyses. A test of whether dispersal ability is associated with richness in mammals, as it is in birds [54], would be of great interest.

4. Is mammalian phylogeny unusual?

How common is the shape of mammalian phylogeny? Previous studies suggest that tree shape may be consistent (and consistently too unbalanced for ERM) among groups as different as plants, insects and vertebrates [29,30,55]. However, these studies had low power: they all reduced each phylogeny's shape to a single number, and the largest compilation had 120 trees. More recent suggestions of a general shape for phylogenies [25,56] have been based on incomplete trees. To provide a more stringent test, we compare the mammalian imbalance signature to that of a compilation from the literature of 243 non-overlapping and non-mammalian near-complete phylogenies. The compilation includes all the non-mammalian trees analysed previously by Purvis & Agapow [31] and Holman [32], supplemented by some more recent phylogenies [57,58]. All trees selected met the criteria used in Purvis & Agapow [31], excepting that Bayesian trees (summarized as the maximum clade credibility tree from the posterior distribution) were also used. Outgroups were removed prior to analysis.

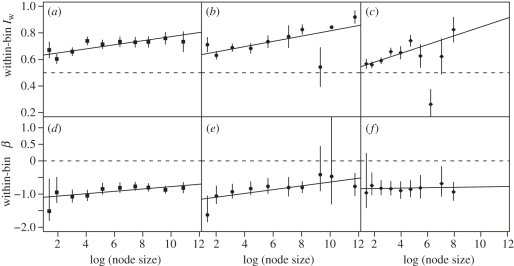
The phylogenies provided 2496 informative nodes, representing many groups from three major clades—arthropods (73 trees, 582 informative nodes); plants (66 trees, 812 nodes); and non-mammalian vertebrates (102 trees, 1102 nodes). Figure 3 shows how I_w and β vary with log(node size) in these three groups. The I_w regression lines for plants and arthropods are not statistically distinct (ANCOVA: F_2,16 = 0.511, p > 0.6; pooled intercept = 0.622 ± 0.0167 s.e., pooled slope = 0.0159 ± 0.0034 s.e.); neither are the mammalian and non-mammalian vertebrate lines (ANCOVA: F_2,16 = 1.355, p > 0.2; pooled intercept = 0.532 ± 0.0217 s.e.; pooled slope = 0.0306 ± 0.0077 s.e.). Vertebrates (mammals + non-mammals) and non-vertebrates (plants + arthropods) do not reject a pooled slope (ANCOVA: F_1,36 = 3.402, p = 0.07; slope = 0.0194 ± 0.0035) but their intercepts differ significantly (non-vertebrates 0.607 ± 0.0179 s.e.; vertebrates 0.561 ± 0.0145 s.e.; F_1,37 = 10.09, p = 0.003). This overall model explains 61.5 per cent of the variance in I_w among bins with three parameters, providing a succinct phenomenological description of imbalance.

Figure 3.

I_w and β signatures for (a,d) plants, (b,e) arthropods and (c,f) non-mammalian vertebrates. Top row as in figure 1a. Bottom row as in figure 1b. One point in f lies well above the plotting region (β = 3.54), and is also an outlier in c.

The relationship between β and log(node size) is harder to model because of β's asymmetric error distribution and apparent nonlinearity in plants (figure 3d) and arthropods (figure 3e). A least-squares regression, weighted by the inverse of the confidence interval width, has a significantly positive slope within plants (slope = 0.036 ± 0.014 s.e.; t₈ = 2.62, p = 0.03) and arthropods (slope = 0.057 ± 0.021 s.e., t₈ = 2.73, p = 0.03; these regressions are not distinct: F_2,16 = 0.713, p > 0.5) but not in non-mammalian vertebrates (t₈ = 0.106, p > 0.9). Like I_w, β is consistent with a model having a pooled slope (0.094 ± 0.0424 s.e.) but an intercept that is further from ERM expectation for the non-vertebrates (−1.466 ± 0.304 s.e.) than for the pooled vertebrates (−1.040 ± 0.241 s.e.).

The supertree's shape is not particularly unusual compared with the other vertebrate phylogenies in our dataset. However, vertebrate imbalance patterns differ from those seen in plants and arthropods. This difference was not detected in the previous comparisons of phylogeny shape [25,29,55,56], but emerges from using more informative summaries of shape and from analysing near-complete phylogenies. The difference parallels one in the temporal spacing of nodes reported by McPeek [59], who found that molecular phylogenies of chordates showed more evidence of slowdown than did those of arthropods or an angiosperm group (we are unable to repeat McPeek's test as our non-mammalian phylogenies mostly lack timescales). The parallel may simply be coincidence, but both a slowdown and relatively balanced nodes near the tips of the tree are to be expected if competition with closely related species inhibits speciation; perhaps this situation is more common in vertebrates than in arthropods or plants.

Whether competition is or is not part of why these groups show different imbalance signatures, it cannot explain why phylogenies are unbalanced relative to ERM expectations. Why is imbalance so widespread? Many models of clade growth have been proposed that, when simulated, generate trees that are more unbalanced than ERM (reviewed by Mooers et al. [3]). In the next part of the paper, we simulate several of these models and analyse the phylogenies they produce. If only some models produce trees whose imbalance patterns resemble those in figure 3, we may be closer to understanding the sorts of processes that have structured diversity.

5. What simple processes can produce realistic tree shapes?

We simulated the growth of 100 phylogenies to 1000 ‘species’ each under six stochastic macroevolutionary models, detailed in table 3 (this is obviously not an exhaustive set: e.g. [3]), and constructed imbalance signatures using the pooled data from each model. The first three models have speciation probabilities depending on a slowly evolving key trait, a class of models first simulated by Heard [60]; in the fourth, the binary trait that determines speciation rate evolves so rapidly that it changes along most of the phylogeny's branches. The fifth model (first simulated by [61], see also [62]) has speciation rates depending not on species' traits but on their ages, declining smoothly from a high value straight after speciation to a background rate; we term this model patency to contrast it with Losos & Adler's [63] latency model in which newly speciated lineages are unable to speciate again for a while. Although it is implausible that species age per se determines speciation rate, age could be proxy for a macroecological trait that does itself change as species age, like global population or geographical range size [64,65]. The last process we simulate is a spatial model in which species occupy squares in a grid and can speciate only if they are next to empty squares. In this model, species are selected at random to speciate and, if they are able to do so, the new species is placed in a randomly chosen adjoining empty cell. The axes can be viewed as latitude and longitude or dimensions of niche space.

Table 3.

Details of the six macroevolutionary models that were simulated. X₀ = ancestral value of trait X; X_i = value of trait X in species i; λ_i = instantaneous speciation rate in species i; λ₀, λ₁ = instantaneous speciation rate for species in the 0 state or 1 state, respectively; r_ab = per-lineage rate of transition of X from state a to state b; t_i = time since species i was last involved in a speciation event. Models 1–5 were simulated using MeSA (www.agapow.net/software/mesa), model 6 with PhyloGen (tree.bio.ed.ac.uk/software/phylogen/).

model	details
1. punctuationally evolving key trait [60,61]	X0 = 100; Xi changes (in both daughters) only at speciation events; changes are drawn from a normal distribution, μ = 0, σ = 50. If Xi becomes negative it is set to 0. λi = 0.001 + Xi/100 000
2. gradually evolving key trait [60,61]	X0 = 100; X changes continuously by Brownian motion with μ = 0, σ = 5 per time unit; Xi and hence λi were assessed every 0.1 time units and at every speciation event. Negative Xi were truncated to 0. λi = 0.0001 + Xi /10 000
3. binary key trait	X0 = 0, λ0 = 1, λ1 = 10. r01 = r10 = 0.05. States and rates were assessed every time unit and at every speciation event
4. fast-evolving binary key trait	X0 = 0, λ0 = 1, λ1 = 10. r01 = r10 = 10. States and rates were assessed every time unit and at every speciation event
5. patency [61]	λi = max(5–15ti, 0.6); ages and rates were assessed every 0.001 time units and at every speciation event
6. spatial model	Initial λ = 1. Ancestral species placed on an infinite square grid (i.e. each cell is adjacent to four others). Species occupy only one cell; they are selected at random to speciate but can do so only if they are adjacent to at least one empty cell

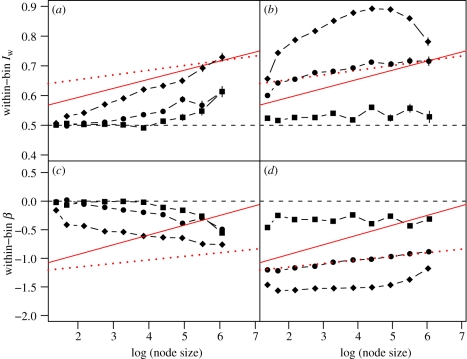
Figure 4 shows the I_w and β signatures from each of the six models. The models in which speciation rates depend on slowly evolving traits produce qualitatively different signatures (figure 4a,c) from those seen in our empirical phylogenies (figure 3). These models generated pronounced imbalance only deep within the phylogeny: near the tips, nodes are consistent with the ERM (because there is little or no interspecies variation in the key trait on which clade selection can act: [60,66]). The remaining three processes produce more realistic signatures, with significant imbalance even among small nodes (figure 4b,d).

Figure 4.

I_w and β signatures for six simulation models, which are described fully in the text. (a,c) Instantaneous speciation rate depends linearly on the values of an evolving trait (squares, binary trait; circles, gradually evolving trait; diamonds, punctuational trait). (b,d) Models in which close relatives often have very different speciation rates. Squares, rates depend on a fast-evolving binary trait; circles, rates decline exponentially with time since speciation; diamonds, spatial model; dashed line, ERM expectation. Best-fit lines for vertebrate data (solid lines) and non-vertebrate data (dotted lines) are provided for comparison.

The poor fit of models in which speciation rates evolve only slowly suggests that (i) the relationship between diversification rate and phenotype is more complex than that simulated, (ii) different traits affect diversification in different clades, or (iii) most variation in diversification rate near the tips of the phylogeny does not depend on slowly evolving traits. A previous simulation study [60] concluded that models with slowly evolving traits could produce imbalance comparable to that seen in empirical phylogenies, but that study measured the shape of each simulated or empirical tree using an index that is most sensitive to imbalance at the root.

The patency model can produce trees similar to the empirical data for non-vertebrates (dotted line in figure 4b,d). A slightly more complex spatial model might produce quantitatively as well as qualitatively realistic imbalance signatures: unrealistic features of our simulation include that the initial ancestor could diversify equally in every direction (leading to balanced nodes at the root of the tree), and that space was divided into contiguous equal-sized units. Patency's relatively good fit adds to growing evidence that many clades may be at or near equilibrium diversity. The North American Cenozoic mammalian fossil record shows negative diversity-dependence [67] at the species level, as does Phanerozoic marine macroinvertebrate genus-level diversity [68]. Complete molecular phylogenies with timescales typically indicate that speciation rates have declined as clades have grown [58,59]. More generally, numbers of species in non-nested clades usually do not depend strongly on their ages (e.g. [15,27,46,69]). Mammalian lineages that disperse successfully to a different biogeographic realm tend to be more diverse than their sister clades in their ancestral regions [45]. Dispersal ability is the strongest known predictor of clade richness among bird families [54], but good broad-scale data on dispersal ability are not, so far as we are aware, available for mammals (or indeed for many non-avian groups).

Taken together, our results may explain why studies finding significant correlates of diversity (reviewed by Coyne & Orr [70]) have nearly all compared old, rather than young, lineages. They may also help to explain the dearth of significant correlates, and why the explanatory power has typically been low. We suggest that study of lineages' opportunity for diversification, as well as their intrinsic attributes, is likely to prove fruitful. The next section therefore considers the spatial context of mammalian faunas alongside the imbalance patterns they show.

6. The geographical scale of phylogenetic imbalance

Phylogenies arise through ecology and evolution over long time periods and, crucially, in a geographical context. Despite the importance of geography, only one study has so far analysed phylogeny shape geographically. Heard & Cox [44], in a study of primates in African and South American nature reserves, showed how imbalance can be partitioned into a hierarchy of spatial scales. The shape of the phylogeny of a local assemblage can be compared with that of the regional source pool, and the latter compared with global imbalance. Such a decomposition can shed light on the spatial scale at which imbalance is generated, and perhaps on the processes that produce it. The approach has strong conceptual links with community phylogenetics [71,72]. However, we are trying not only to see how the local community is assembled from a source pool, but also whether local processes scale up to shape species diversity at larger scales.

We considered four spatial scales: global, ‘biorealm’ (a convenient shorthand for unique combinations of World Wide Fund for Nature (WWF) biome and biogeographic realm: definitions from Olson et al. [73]), WWF ecoregion [73] and local assemblage (from local species checklists). We computed β for the phylogeny of mammals within each unit (e.g. each biorealm) at each level; we chose β over I_w because it varies less with node size (figure 1). We also compared the imbalance of each unit with a biogeographic null expectation [44]—the value expected if the unit's species were drawn at random from the species within the next spatial scale up. For example, an ecoregion's β would be compared with the distribution of β values obtained from 1000 randomizations, each of which samples the ecoregion's number of species from the biorealm that contains it. As a summary statistic, we subtract from each observed β the mean of the corresponding null distribution; we term this difference β_dev. If ecoregions' species are random subsets of those in the corresponding biorealms, the β_dev will be centred around 0.

Cooper et al. [72], in a community phylogenetic analysis, found that mammalian assemblages tended to contain fewer closely related species than predicted under the biogeographic null model, consistent with competitive exclusion among close relatives. Given that mammalian phylogeny overall is unbalanced, an overdispersed sample—in which species-rich groups will tend to be under-represented—will tend to be less unbalanced. We therefore predict that the β_dev for assemblages within ecoregions will tend to be positive (i.e. assemblages more balanced than ecoregions), though we note that Cooper et al. [72] restricted their analyses to species within the same family. At large scales, in situ diversification presumably becomes an important process [74], leading to diversifying clades being over-represented relative to the biogeographic null. However, the same pattern could be caused by habitat filtering—a top-down rather than bottom-up process, whereby some clades are under-represented because ecological conditions do not suit them. For both processes, we expect β_dev at the large scale to be negative, as spatial units should be more unbalanced than the biogeographic null. Competitive exclusion might also be more likely in species-rich, energy-poor or ecologically uniform systems.

Species lists for biorealms and ecoregions were generated by overlaying maps of the units (downloaded from www.worldwildlife.org/science/ecoregions/item1267.html, accessed August 2006) with distribution maps from the Global Mammal Assessment [75]; historical, uncertain or introduced species ranges were excluded, and only extant non-marine species present in the phylogeny were considered. The final dataset contained 4846 mammalian species within 62 biorealms and 796 ecoregions. Assemblage data came from a literature compilation of 242 species checklists [76,77] containing a total of 1911 species and representing 140 ecoregions; the lists were for non-volant mammals only, so Chiroptera (bats) were pruned from the trees prior to randomizations of assemblages within ecoregions. Because estimates of β from small datasets seemed highly variable, we excluded all samples with fewer than 20 species, leaving us with 59 biorealms, 728 ecoregions and 233 assemblages.

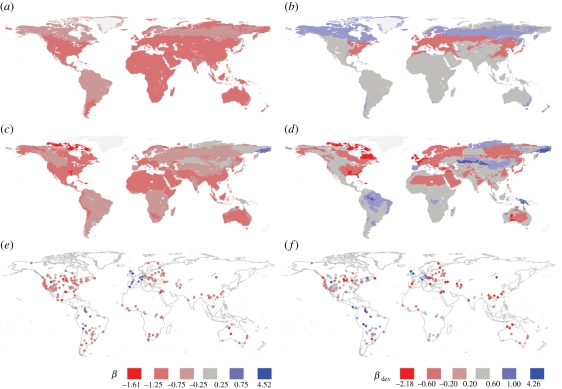
Figure 5 presents maps of β and β_dev at each spatial scale. As expected, we find that strong imbalance at the largest spatial scale (biorealms) largely reflects the global imbalance of mammalian phylogeny. All 59 biorealms yielded negative estimates of β, 37 of them significantly negative (figure 5a), whereas the mean β_dev for biorealms (figure 5b) was not significantly different from 0 (mean = 0.02; Wilcoxon signed-rank test, V = 943, p > 0.05). Eight biorealms had phylogenies significantly more unbalanced than the biogeographic null while four biorealm phylogenies were significantly more balanced.

Figure 5.

Maps of (a,c,e) β and (b,d,f) β_dev for (a,b) biorealms, (c,d) ecoregions and (e,f) assemblages. See text for explanation.

Imbalance was again ubiquitous at the intermediate scale of ecoregions within biorealms: the estimate of β was positive in only 19 of the 728 ecoregions (none significantly), and was significantly negative in 112 (figure 5c). Furthermore, the mean β_dev showed significant imbalance when compared with the biorealm source pools (mean = −0.07; Wilcoxon signed-rank test, V = 101 487, p < 0.001). The biogeographic null model was rejected in 82 of the 720 ecoregions where it could be tested (the ecoregion and biorealm had the same set of species in the other eight ecoregions); of these, 56 ecoregion phylogenies were more balanced than expected and 26 more unbalanced (figure 5d).

Moving to the level of assemblages within ecoregions, β was negative in 209 of 233 assemblages but significantly so in only two (figure 5e); this lack of significance is unsurprising given that the assemblage phylogenies are seldom large. However, contrary to our expectations, β_dev is significantly negative on average (mean = –0.12; Wilcoxon signed-rank test, V = 8503, p < 0.001), indicating that assemblage phylogenies tend to be unbalanced compared with their ecoregion source pools. This finding suggests that habitat filtering (or, less likely at this small scale, in situ speciation) dominates over competitive exclusion, though community phylogenetic approaches (e.g. [71,74]) would provide a more direct test. Twelve assemblages rejected the biogeographic null model, out of 215 that could be tested; seven were more balanced than expected and five more unbalanced (figure 5f).

To investigate environmental influences on imbalance signatures, we used multiple regression to predict β_dev from different variables that reflected current environmental conditions or system characteristics. The environmental variables for our spatial units were calculated using an ArcInfo macro; only assemblages with a digitized polygon were included in this analysis (215 assemblages; [76]). Variables and their sources were: mean annual actual evapotranspiration (AET, in millimetres; [78]; downloaded from http://www.grid.unep.ch); mean annual temperature (in °C; [79], downloaded from http://www.worldclim.org/); mean elevation and range in elevation (in metres; [80], downloaded from http://edc.usgs.gov); and ecosystem count as a coarse measure of habitat heterogeneity ([81], downloaded from http://edcsns17.cr.usgs.gov/glcc). Precipitation was included at first but had to be excluded because of variance inflation (it was highly collinear with AET). All models also included the area (log-transformed) and number of species within the focal unit. Because in situ diversification is expected to produce concentrations of newly formed species, we additionally included as a predictor the median terminal branch length for the species in each spatial unit on the complete mammalian phylogeny as a proxy for the recency of the species; however, because terminal polytomies in the supertree typically reflect lack of knowledge, we adjusted the branch lengths following Mooers et al. [3].

Following Lichstein et al. [82] and Dormann et al. [83], we tested for the presence of spatial autocorrelation in the regression residuals from our initial, ordinary least-squares (OLS) model with Moran's I correlograms, and accounted for the spatial autocorrelation with spatial autoregression (SAR, simultaneous autoregressive model). We used an SAR_error model, which models the autoregressive process in the error term and has been recommended as a reliable spatial method [84]. Moran's I correlograms and spatial models were generated with the R packages spdep [85] and ncf [86]. We tested standardized I values for significance with a one-tailed randomization test for positive autocorrelation (999 permutations; [82]). In the SAR models, we defined neighbours as data points closer to each other than a model-specific maximum distance, which was chosen by optimizing the model AIC value (Akaike's information criterion) following Cooper & Purvis [87]. We used a row-standardized coding scheme for the spatial weights matrix [84], calculated r² values using Nagelkerke's formula [88] and assessed the contribution of each variable to OLS and SAR model fits with likelihood-ratio tests for nested models [82].

Although β_dev was significantly negative on average at each spatial scale (meaning that the phylogeny of the species present in the spatial unit tended to be more unbalanced than the biogeographic null), the significant environmental predictors of β_dev depended on scale (table 4), perhaps reflecting the differing relative importance of top-down and bottom-up controls on imbalance (though we caution that no model has high explanatory power, and that the precision of environmental variables is often scale-dependent). At the largest scale, biorealm phylogenies were more unbalanced relative to the global phylogeny when the biorealm contained more different ecosystems and, in OLS models, was at high altitude. The altitude term distinguishes the montane biome from the remainder. Habitat filtering (a top-down process) and in situ diversification (bottom-up) are both likely to be important at this broad scale. Indeed, the latter may follow from the former—if few clades are able to persist at high altitudes, those that can are likely to radiate into a wider range of niches than they might occupy in less harsh environments.

Table 4.

Non-spatial multiple regression (OLS) and spatial autoregression (SAR) model results for β_dev at each of three spatial levels. Apart from characterizing each model, we also show each variable's slope, significance and likelihood-ratio test result (LR).

	biorealms				ecoregions				assemblages
	OLS		SAR		OLS		SAR		OLS		SAR
AIC	−35.3		−34.1		320.6		82.5		335.6		314.5
d.f.	50		48		694		692		171		169
r2	28.7		29.6		17.6		41.4		15.1		25.4
neighbourhood distance	n.a.		1970.79		n.a.		626.9		n.a.		700.6
autocorrelation parameter	n.a.		0.173		n.a.		0.614		n.a.		0.4
	slope	LR	slope	LR	slope	LR	slope	LR	slope	LR	slope	LR
AET	<0.001	<0.1	<0.001	<0.1	<0.001**	222.9	<0.001	2.7	<0.001	5.1	<0.001	0.3
temperature	−0.001	1.9	>−0.001	1.5	−0.004*	4.1	<0.001	<0.1	−0.019*	6.8	−0.016	3.2
mean elevation	>−0.001*	5.2	>−0.001	2.8	<0.001	<0.1	<0.001	0.2	<0.001	2.1	<0.001	1.6
elevation range	<0.001	0.6	<0.001	0.1	<0.001	<0.1	>−0.001	0.2	> −0.001*	4.7	> −0.001	3.0
ecosystem count	−0.008**	10.2	−0.007**	5.3	−0.006***	13.3	−0.002	1.5	−0.005	0.2	<0.001	<0.1
area	−0.016	0.8	−0.013	0.5	0.020*	4.6	0.028**	10.2	−0.010	0.1	−0.003	<0.1
species number	<0.001	0.7	<0.001	0.3	0.002***	47.0	0.001**	7.4	0.015***	12.7	0.014***	12.6
median terminal branch length	−0.197	1.0	−0.173	0.7	0.091	1.1	0.117	1.4	−0.411	3.3	−0.442	3.3

Significance levels: *** p < 0.001, ** p < 0.01, * p < 0.05.

Moving to ecoregions within biorealms, the map of β_dev (figure 5d) suggests that the most negative values are in deserts, the Northern high latitudes, and the Himalayas; the Amazonian basin fauna, by contrast, has a relatively balanced phylogeny (positive β_dev). The regression models find stronger imbalance to be associated with small ecoregions containing few species and, in OLS models, having low AET and more different ecosystems. Habitat filtering is likely to be more important at this scale than at the broader scale, and in situ diversification less so.

In situ diversification is unlikely at the scale of assemblages within ecoregions, whose patterns presumably reflect a mixture of habitat filtering and competitive exclusion. The generally negative β_dev values suggest that the former dominates, especially in warm, topographically heterogeneous areas, but the signs of the environmental predictors of β_dev are consistent with a role for competitive exclusion in assemblages that are species-rich, in cold, uniform places.

Although interpretation of our results remains tentative, the spatial decomposition of imbalance in mammalian phylogeny reveals many patterns that cannot be attributed to the biogeographic null. This shows the possible usefulness of Heard & Cox's [44] groundbreaking approach for understanding how bottom-up and top-down processes might interact to control clade diversity and hence imbalance. Their relative lack of non-null results may reflect their choice of the only large mammalian clade—Primates—that does not have an unbalanced phylogeny at a global level.

7. A descriptive model of mammalian macroevolution

What do our analyses suggest about the processes that have shaped mammalian phylogeny? The I_w and β signatures of the supertree highlight the persistence of small basal clades, and also show that closely related species often have very different chances of diversification. Our simulations indicate that the latter is more easily achieved if speciation rates decrease with time since speciation or, more plausibly, with the occupancy of adjacent areas or niches, than if they are determined by slowly evolving traits. The occupancy model is also compatible with our analysis of the spatial scale of imbalance. It suggests that diversification will show negative diversity-dependence, a pattern seen in many molecular phylogenies [58,59] and the mammalian fossil record [67]. Equilibrium diversity seems likely to depend on both the geographical area available to the clade and the amount of energy available to support populations of its species in the face of competition from other lineages.

Four main ways have been proposed by which a clade or subclade's diversity might increase deterministically beyond this initial equilibrium (e.g. [6,9,53,59,89–92]):

• — Spreading in space. A species that colonizes new geographical space, by dispersal to a disjunct region or through an expansion of suitable habitat, may diversify taxonomically without markedly expanding its ecological niche [53,91,93]. The equilibrium diversity of such a clade should depend on the size of the new area and the number of competitors present.

• — Spreading in niche space. An adaptive breakthrough to new niche space (a new adaptive zone; [9,93]) may permit a lineage to diversify more rapidly than its sister clade [53,89]; again, equilibrium diversity presumably depends on the size and occupancy of the adaptive zone [89,94].

• — Improvement. An adaptation that makes a species markedly better at occupying its niche (through, for example, increased metabolic efficiency or disease resistance) may enable the species to outcompete other species both within and at the margin of its niche [9,89,93]. How far the resulting clade is expected to spread through niche space is governed by how much of a competitive edge the improvement gives. Clades with such key innovations are always expected to be more diverse than their sister clades without them (though they may competitively wipe out their sister clades; [89]).

• — Narrower species. The first three mechanisms raise diversity by increasing the resource base; an alternative is to slice the resource base more thinly [89,95]. Sexual selection by female choice, for example, makes rapid speciation more likely, and is repeatedly associated with high diversity in sister-clade comparisons within birds [69,96]. Ecological specialization [97], behavioural and societal complexity, philopatry, changes to karyotypic architecture, or a ‘cellular’ population structure might also be relevant to mammals.

If each of these four classes of event occurs at random with respect to phylogeny (a reasonable null starting point) then, by the law of averages, they are more likely to happen within species-rich clades than in species-poor ones; any initial pattern of imbalance in the phylogeny is therefore accentuated. Adaptive improvements will, likewise by the law of averages, tend to arise in species adapted to wide rather than narrow adaptive zones and living in large rather than small regions. Individuals within these species will tend to outcompete those in related species in the same region, causing competitive extinctions as Darwin [98] envisaged; and there may be successive waves of improvement. For an innovation to spread further, however, the clade bearing it will have to either colonize new areas or break through to new niches, both of which may have long waiting times (i.e. low probabilities per unit time). ‘Unimproved’ lineages can therefore persist as relicts in isolated regions from which competitors are absent (e.g. Solenodon), or in isolated niches (e.g. myrmecophagy in Pholidota and Tubulidentata, or haematophagy in Desmodontinae) where their incumbency advantage permits them to outcompete more ‘advanced’ but less well-adapted species. If these relictual lineages have diversity-dependent dynamics, they may persist indefinitely even at low diversity; this provides a plausible mechanism for the long persistence of small basal clades suggested by the I_w signatures.

Major environmental perturbations would be expected to move the system away from this quasi-equilibrial state, changing the breadths of the adaptive zones. Some clades would then decline or go extinct whereas others, whose adaptive zones had become broader, would be able to diversify.

Under this model, phylogenies are unbalanced because regions and niches vary in the diversity they can support, because new radiations will probably originate in already-diverse clades, and because relictual lineages are hard to extirpate. Different clades radiate in different places, however, so the global phylogeny will tend to be less unbalanced than expected from the phylogeny of species found within a biorealm or ecoregion. Apparently downshifted clades arise as survivors of otherwise supplanted groups or as occupants of narrow adaptive zones: island endemics may be the ultimate evolutionary dead-ends [99]. Much of the variation in richness among clades emerges as being independent of trait variation, reflecting historical and geographical contingencies.

The model also makes predictions about the temporal pattern of nodes in phylogeny. A complex overall pattern is expected: although the overall dynamics are equilibrial, some subclades in the early phase of their radiation will be diversifying exponentially, others approaching an equilibrium diversity, and others declining deterministically. Furthermore, radiations based on niche broadening might have a different temporal pattern from those based on finer subdivision of the niche [59]. One prediction, however, is that lineages occupying biomes that have recently expanded in area and energy are expected to show rapid recent radiation; recent findings of high speciation rates in North temperate regions for birds [100], mammals [28] and an angiosperm clade (carnations; [101]) are consistent with this prediction.

Our verbal model is an attempt to develop a simple set of ecologically and evolutionarily plausible processes that could together have generated the shape of the mammalian phylogeny. Process-based simulation models are increasingly used in macroevolution (e.g. [59,102]), permitting tentative identification of parameters to which diversity patterns might be most sensitive. Although phylogenies without fossils are inevitably missing much important information about clade dynamics, large complete phylogenies are nonetheless a rich source of patterns against which model outputs can be compared, especially when combined with environmental or trait data. We anticipate that multi-scale models, incorporating local processes such as adaptation and competition as well as global processes such as global change and tectonic movement, will have much to offer in the quest for global biodiversity models, and for our understanding of why so much of the Tree of Life is so asymmetric.