Computational modeling of in vitro biological responses on polymethacrylate surfaces

Abstract

The objective of this research was to examine the capabilities of QSPR (Quantitative Structure Property Relationship) modeling to predict specific biological responses (fibrinogen adsorption, cell attachment and cell proliferation index) on thin films of different polymethacrylates. Using 33 commercially available monomers it is theoretically possible to construct a library of over 40,000 distinct polymer compositions. A subset of these polymers were synthesized and solvent cast surfaces were prepared in 96 well plates for the measurement of fibrinogen adsorption. NIH 3T3 cell attachment and proliferation index were measured on spin coated thin films of these polymers. Based on the experimental results of these polymers, separate models were built for homo-, co-, and terpolymers in the library with good correlation between experiment and predicted values. The ability to predict biological responses by simple QSPR models for large numbers of polymers has important implications in designing biomaterials for specific biological or medical applications.

1. Introduction

Following implantation of a biomaterial in the body, protein adsorption occurs within seconds around the new implanted materials [1]. Cells thus interact with these adsorbed proteins rather than the biomaterial itself [2, 3]. This initial protein adsorption plays an important role in determining the biocompatibility of the implant [4, 5]. For example, within the context of a blood-contacting implant, the level of fibrinogen adsorption is a predictor of the implant’s tendency to cause thrombosis: When fibrinogen is adsorbed strongly to an implant surface, the implant has a greater tendency to lead to thrombosis (blood clotting) than when an implant surface is designed to resist fibrinogen adsorption. Cells may then attach and grow further on implanted biomaterials. Some implant applications (for example contact lenses) require “non-fouling surfaces”, e.g., surfaces that resist protein adsorption and subsequent attachment and growth of cells. Other applications (for example tissue engineering scaffolds) require that the implant surfaces support the attachment and subsequent proliferation of cells. Therefore, the levels of protein adsorption, cellular attachment, and proliferation on implant surfaces are important design parameters in the development of new biomaterials for any type of medical implant.

The recent advances in polymer combinatorial chemistry [6, 7] have the potential to transform biomaterial development and translational use. Beginning with a small number of monomers, combinatorial parallel synthesis can generate thousands of polymers by varying the monomers and proportions of the monomers synthesized into homo-, co-, or terpolymers. These polymer libraries can now be synthesized in high throughput fashion[8] in sufficient quantity and purity that enables biological and physico-mechanical testing. Such tests could conceivably screen biomaterials with specific properties tailored for individual medical applications. However, given the large size of the polymer libraries such a screening process would be tedious, prone to experimental error, and require tremendous expense. Consequently, the capability to synthesize libraries of new polymers has now outpaced the ability to test the properties of the individual polymers for potential applications. Computational modeling may mitigate such issues by funneling the vast polymer libraries into a testable subset most likely to fit the specifications for a desired application.

The Combinatorial Computational Method (CCM) takes advantage of combinatorial synthesis, rapid screening and computational modeling as a biomaterial invention tool [9]. In this integrated approach a virtual library is formulated with a number of related monomer repeat units comprising all possible homo-, co-, and terpolymer combinations. In the place of comprehensive synthesis and testing of biological or material properties of the entire library, the semiempirical, quantitative structure property relationship (QSPR) method [10]may be able to predict particular polymer properties. This method is widely applied in the pharmaceutical industry to develop predictive models for a property of interest and ligand based design of compound libraries for virtual screening. To extend this technique to biomaterials, experimental values are obtained from representative “reference compounds” and QSPR is used to develop a predictive model that is extended to the larger library of polymers. Subsequently these predicted values are experimentally validated [11–17].

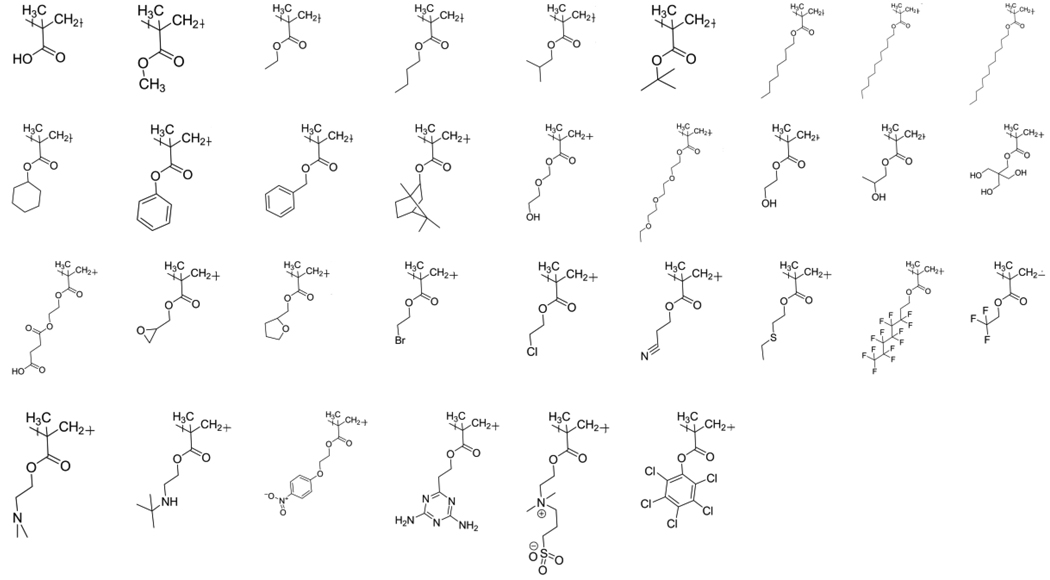
To test the validity of this method, the methacrylate family of polymers was selected as a model biomaterial system [18]. Polymethacrylates are extensively used in medicinal and industrial applications, and numerous methacrylate monomers are commercially available. For our analysis, 33 methacrylate monomers were selected as the building blocks of the polymer library (Figure I). In addition to homopolymers synthesized from the individual monomers, numerous combinations for co- and ter- polymers are possible by varying the proportions of the different monomers. For this work, co-polymers of all 33 monomers were selected in the defined ratios of 50:50, 25:75, and 75:25, leading to more than three thousand possible copolymers. Terpolymer blends of 33:33:33 were also included, leading to more than forty thousand polymer combinations in the virtual polymer library.

Figure I.

Methacrylate polymers used in the library (in homopolymer form)

A subset of 130 homo-, co- and terpolymers were chosen for synthesis and evaluation of protein adsorption and cell-material interactions. Experimental data within a certain range of cutoff value for standard deviation were considered “usable” for modeling. To build the model for the virtual polymer library an Artificial Neural Network (ANN) is constructed based on usable data collected for the 130 methacrylate polymers together with computational data of physicochemical polymer properties. The novelty in this approach is that the method makes the calculation of descriptors for any composition of co- and terpolymers easier, as the descriptors are calculated from linear combinations of the homopolymer descriptors. This process avoids the need to recalculate descriptors for each possible composition of co and terpolymers and provides enormous flexibility and extendibility of the model.

The end goal is to develop an integrated flexible computational model capable of predicting complex interactions of proteins and cells with polymer surfaces. This is accomplished by rank ordering the polymers based on their computationally calculated properties, aiming to predict values and identify trends as close as possible to the measured values obtained in validation studies. Rank ordering is achieved by dividing the experimental data for the reference polymers into different bins or classes (e.g. low, medium, high). We applied computational models to predict the properties of the same set of reference polymers. These predicted properties are then grouped into similar bins and comparisons are made whether a particular polymer is in the same bin as found from experiment or not. Rank ordering of biomaterials with respect to certain properties is important as it reduces the time and effort needed to complete costly cell and protein studies.

2. Methods

2.1. Experimental

The reference polymers (homo-, co-, and terpolymers) were synthesized using an automated parallel synthesizer (SLT 100 Accelerator, Chemspeed, Basel Switzerland) utilizing previously published methods [8, 18]. Briefly, reactors equipped with septa and reflux condensers were inertized, cooled to RT, and degassed reagents (purified monomers, chain transfer reagent, and solvent) were charged by syringe transfer using a 4-needle tool while being purged with argon. The reactions were vortexed at 600 rpm at 70 °C for 20 h under argon. The reactions were then cooled to 20 °C and precipitated manually. The polymers were dried under vacuum for ≥24 h at 60 °C. Using this robotic instrument it was possible to produce sufficient quantities of structurally related polymers with diverse pendant ester groups. Once synthesized, the polymer compositions were confirmed with proton NMR spectroscopy ( Varian 500 or 400 MHz) . Polymers were characterized for molecular weight and polydispersity using previously published methods [8] and had molecular weights of between 100 kDa and 200kDa and polydispersity index of less than 1.6 (measured in either N,N-dimethylformamide or tetrahydrofuran and calculated using PS standards). Biological properties (fibrinogen adsorption, cell attachment, cell proliferation index) were determined using characteristic techniques relevant for this computational model as described in the following sections.

2.1.1. Fibrinogen adsorption using an immunofluorescence assay

For the measurement of protein adsorption on the polymethacrylate surfaces, a rapid screening immunofluorescence assay (IFA) developed by Weber et al. [19] was applied. A brief description of this assay on solvent cast polymethacrylates is as follows.

Solvent Casting

Polymethacrylates are dissolved (5% w/v) in tetrahydrofuran (THF, EMD Chemical Inc., Gibbstown, NJ) and then filtered using a 0.45 µm PTFE filter (Whatman Inc., Clifton, NJ). A 50µl polymer solution is dispensed into the wells (n = 14) in each column of a black polypropylene 384-well plate (Nalge Nunc International, Rochester, NY). Plates are placed under a nitrogen and solvent rich atmosphere and the solvent was allowed to slowly evaporate in a hood over 16 hours. The plates are then placed in a temperature-controlled oven where the temperature was increased by 10 °C from 35 °C to 85 °C every 30 min. Then finally they are left for 96 h under vacuum at 80 °C allowing for the evaporation of any residual solvent.

Protein adsorption detected by the immunofluorescence assay

All pipetting steps are performed using multipipettes (hand pipetting). For each incubation step, the plates are centrifuged at 140G for 3 minutes followed by incubation at 37°C. All washing steps are performed using an automated micro-plate strip washer (ELx50, Biotek instruments, Winooski, VT). During washing cycles, 40 µl phosphate buffered saline (PBS, Sigma, St. Louis, MO) are dispensed in each well, followed by 20 seconds of plate shaking and aspiration. Human fibrinogen (3 mg/ml, Cat. No. 341576, Calbiochem, LaJolla, CA) is prepared in PBS for the adsorption experiments. 25 µl of this solution is pipetted into each well and incubated for 1.5 h followed by 8 rinsing steps. To block nonspecific antibody binding, wells are incubated with 40 µl 1% (w/v) Bovine Serum Albumin (BSA, Sigma, St. Louis, MO) in PBS for 0.5 h. After rinsing five times with PBS, a background measurement of the plate is performed at 485 nm (excitation) and 525 nm (emission) (Tecan, Durham, NC). The purpose of preread blanks is to correct for well-to-well variability and subtract the plate background prior to the addition of the antibody. To detect adsorbed fibrinogen, a fluorescein labeled goat IgG antibody (polyclonal) to human fibrinogen (Cat. No. 55169, MP Biomedicals, Solon, OH) diluted (1:10) in 1% BSA in PBS (w/v) (25 µl per well) is added in each well and incubated with surface-adsorbed fibrinogen for 1.5 h, followed by 6 PBS rinses. Following subtraction of the background measurement (average of 25 repetitive readings per well), the fluorescent intensity (FI), average from 14 wells per polymer are normalized to the FI of bare polypropylene wells (a control row is kept in each plate).

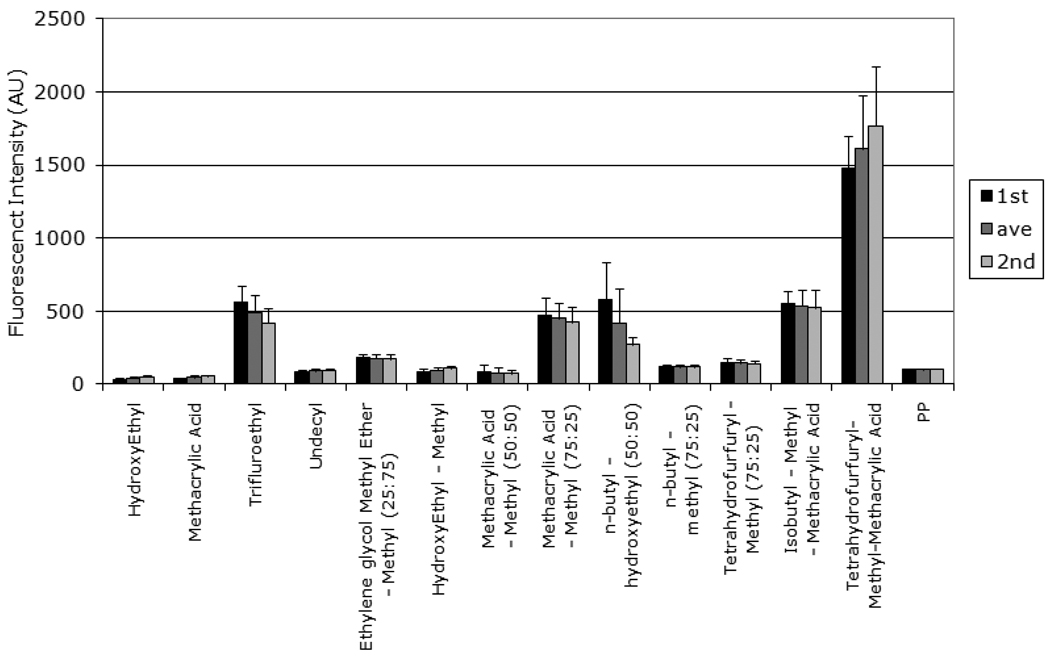
To evaluate the reproducibility of the assay, the adsorption and detection of fibrinogen is repeated. An example of data set for 13 polymers, including the polypropylene, is provided in Figure II (n =14 for each polymer per experiment). The assay is performed twice and the results obtained from the two independent experiments are compared.

Figure II.

Fibrinogen absorption reproducibility test of polymethacrylates. Two independent experiments are performed (mean ±SD; n = 14). The middle bar represents the combined average calculated from both experiments. First and third bar represent the individual plate average. The y-axis represents the fibrinogen adsorption relative to adsorption on polypropylene without polymer presented in arbitrary fluorescent intensity units.

2.1.2. Quantification of cellular response using MTS assay

To allow rapid screening, cellular response to the polymethacrylates is experimentally measured using NIH 3T3 cells seeded on spin coated glass cover slips and the MTS assay. The two parameters measured are cell attachment (short-term response; measured 4 hours after cell seeding) and cell proliferation (long-term response; measured 4 days or around 96 hours after cell seeding). This procedure is a modification of the method described previously [6] and includes a new approach to quantify cell proliferation. Briefly, the procedure includes the following:

Polymer spin coating

A 2.5% polymer solution is made in an appropriate solvent and filtered using a Whatman Puradisc PTFE, 0.45 micron filter (Whatman Inc., Piscataway, NJ, USA). Fifty microliters (50 µl) of polymer solution is placed in the center of a clean 15 mm round glass cover slip (Fisher Scientific, Pittsburgh, PA, USA) on a spin coater (Headway Research Inc., Garland, TX, USA) that is placed in a humidity-controlled environment (< 20%). Spin coating is carried out for 30 seconds at 4000 rpm and the polymer-coated cover slips are vacuum dried overnight at 50° C to remove any remaining solvent. Polymer coated cover slips are sterilized by exposure to UV for 30 minutes. These UV sterilized polymer coated slips are then placed in 24-well sterile tissue culture plates (Corning-Costar, Lowell, MA, USA) and used for cell culture experiments.

Fibroblast cell culture and cell response study

NIH/3T3 cells (ATCC No. CRL-1658; ATCC, Manassas, VA, USA) are cultured in DMEM-high Glucose medium supplemented with 10% Bovine calf Serum & Penicillin-Streptomycin antibiotics (Gibco/Invitrogen, Carlsbad, CA, USA). Sub-confluent cells of passage 6–12 are used for experiments. Cells growing in Corning® 75cm² Rectangular Cell Culture Flask (Corning Product #430641; Corning-Costar, Lowell, MA, USA) are detached using Trypsin (2.5 g/L)-EDTA.Na4 (0.38 g/L) for 2 minutes at 37° C, neutralized with 4X volume of serum containing cell culture media and then counted using the Cellometer® Auto-T4 cell counter (Nexcelom Bioscience, Lawrence, MA, USA). About 1 × 10⁴ cells are seeded/well (24-well plate containing polymer-coated cover slips, except the internal positive controls which are the original tissue-cultured plate surfaces). Two sets of identical plates (containing same polymers in similar arrangements) are used for each experiment, where one set is used for measuring cell attachment and the other for cell growth. Both plates are processed identically, except where noted. In these experiments the blank is the cell culture media and n=4 has been used for all samples.

After cell seeding, the 24-well plates (both cell attachment & cell growth) are incubated at 37° C and 5% CO₂ for 4 hours. The media is removed using a 12-channel pipette (Mettler-Toledo Inc., Columbus, OH, USA) and the cells are washed with 400 µl of 37° C pre-warmed Phosphate Buffered Saline (lacking Calcium & Magnesium). The viable cells that remained attached to the polymer surface or the tissue culture polystyrene (TCP) control are quantified using a slightly modified MTS assay [20]. 200 µl of cell culture media containing 317 µg/ml of CellTiter 96^® AQ_ueous One Solution MTS Reagent (Promega Corp., Madison, WI, USA) is added per well of the plates representing cell attachment assay and then they are incubated at 37° C/ 5% CO₂ for 1 hour. The MTS reagent is a tetrazolium compound [3-(4,5-dimethyl-2-yl)-5-(3-carboxymethoxyphenyl)-2-(4-sulfophenyl)-2H-tetrazolium, inner salt; MTS], which is bio-reduced to an aqueous (cell culture media) soluble formazan product by the dehydrogenase enzymes found in metabolically active cells. The quantity of formazan product (which is directly proportional to the number of living cells in culture) was measured from the absorbance of respective cell culture media at 490 nm using a BioTek PowerWave-x plate reader (BioTek Instruments, Winooski, VT, USA). To the plates representing cell growth assay 200 µl of cell culture media (No MTS reagent) is added per well and the plates incubated at 37° C/ 5% CO₂ for 4 days (or about 96 hours). MTS assay is carried out as described above.

Data analysis and calculation of relative proliferation index

The absorbance values (490 nm) from the MTS assay for samples containing the polymers (or TCP) were corrected for blank (media) and used for further calculations. The average absorbance value (from n=4) is used in calculations of cell attachment (expressed as a value normalized to TCP) and cell proliferation (expressed as a Relative Proliferation Index). Relative cell Proliferation Index or Relative Proliferation Index (RPI) is a more accurate measure of cellular response to a growth on polymer surfaces and enables us to compare data from independent experiments being carried over a long-time period. In the present study the synthesis and characterization of the polymers are repeated several times over a long period of time and thus an internal control surface (TCP), similar cell-growing conditions (passage, confluency) and standardized protocols to ensure data consistency and repeatability has been used. The Relative Proliferation Index (RPI) is calculated as follows:

• RPI= Δ Growth for Polymer (or TCP)/ Δ Growth for TCP

Δ Growth= Growth MTS data (Average) – Attachment MTS data (Average) Standard deviations were calculated from four cover slips per polymer. Cell attachment and proliferation were both expressed as percentage of TCP values.

2.2. Computational

The general QSPR approach consists of three steps. First the molecular descriptors are calculated using well known algorithms to represent the molecules. The molecular descriptors are the final results of logic and mathematical procedures that transform chemical information encoded within a symbolic representation of a molecule into useful numbers or the results of some standardized experiments. There are various software available [21] to calculate the descriptors and the total numbers are typically a thousand or more. The second step is reduction of the number of descriptors to identify the relevant ones for the experimental property to be modeled. Some classifying algorithms are necessary. Decision Tree (DT) [22] or Principal Component Analysis (PCA) is mostly used for this purpose. A Decision Tree is a predictive tool about observation and conclusions derived for a target value. Principal Component Analysis is a vector space transform often used to reduce multidimensional data sets to lower dimensions for analysis. In the final step the model is built using the most relevant descriptors. The descriptors are used in the Partial Least Square (PLS) regression method, the Artificial Neural Network (ANN), or the Radial Basis Function (RBF) network to model the required property, the fibrinogen adsorption or cell attachment or cell proliferation index in this case. PLS regression is an extension to multiple linear regression models. ANNs are based on attempt to mimic the neurological abilities in the brain by a set of mathematical methods, models and algorithms to process information and acquire knowledge. In mathematical terms ANN is composed of a series of non-linear sigmoid operators to find patterns among data set in input and output. Radial Basis Functions are powerful techniques for interpolation in multidimensional space and can be applied as a replacement of the sigmoid hidden layer transfer characteristic in an ANN to form the RBF network.

2.2.1. Calculation of the descriptors

Three dimensional structures were generated using the MOE (Molecular Operating Environment) [23] software package for 33 homopolymers of ten repeat units. The predictive capability of the models was found to be the same irrespective of ten or twenty repeat units. As glass transition temperature data was available for these polymers we built separate models for glass transition temperature and tested using ten and twenty repeat units. Qualitatively the models were very similar and thus a ten monomer repeat unit was used throughout this work. There was also a limitation of the total number of atoms that can be handled in the available version of DRAGON [24] software that is used to calculate the descriptors. The 3D structures generated using the MOE represent the molecular connectivity of the polymers. These molecular structures are then energy minimized in vacuum using the default force field (MMFF94x)[25] within MOE package to find the optimized structures. These optimized structures represent the equilibrium configuration of the molecules with a local minimum potential. The molecular descriptors are calculated based on these optimized structures using DRAGON version 5.4 [24] software. This version of the software is capable of calculating zero through three dimensional descriptors including constitutional, topological, WHIM, and GATEWAY descriptors.

A simple approach is followed for estimation of the descriptors for co- and terpolymers. Numerical values of the descriptors are calculated as linear combinations of homopolymer percentage composition by weight. The basic hypothesis is to build a semiempirical model of co and terpolymers from the calculated descriptors without drawing and optimizing the chemical structures, which is extremely time consuming. This method gives us the flexibility to incorporate any composition found from NMR analysis of synthesized polymers. This is a very important and simple assumption in the sense that this can be easily adapted and extended to other formulations of the co and terpolymers in future if needed. The idea is to see if there is still enough useful information from these sets of descriptors that are easily estimated.

2.2.2. Reduction of number of relevant descriptors using Decision Tree (DT)

The total number of available descriptors (1664) is large and any model based on all the descriptors would overfit the data. Highly correlated descriptors and descriptors containing identical information for over 90% of the data set are removed. Next the homopolymers are grouped into either 5 bins or 3 bins based on the experimental values using the EM (Expectation Maximization) cluster analysis algorithm from WEKA [26]. Cluster analysis can group similar items into same bins. An expectation-maximization (EM) algorithm is used in statistics for finding maximum likelihood estimates of parameters in probabilistic models. The most significant descriptors relevant for each property are found by the C4.5 Decision Tree [22] algorithm from WEKA [22]. This DT algorithm is the commercial successor of the original C4.5 program and uses a top-down induction of Decision Tree with pruning of the branches. All the experimental data for each set of polymers are used in the Decision Tree to find the most significant descriptors. The significant descriptors are capable of correctly classifying the instances for more than or equal to 90% of the cases. Either the Decision Tree algorithm is used directly or useless (constant attribute along with nominal attributes that vary too much) descriptors are removed and then CfsSubsetEval attribute selection method is used to find the best subset for each class and then the Decision Tree algorithm is applied to find the best descriptors for the clusters. CfsSubsetEval [22] function evaluates the worth of a subset of attributes by considering the individual predictive ability of each feature along with the degree of redundancy between them. Exactly similar Decision Tree approach is followed for homo-, co- and terpolymers.

2.2.3. Building Artificial Neural Network (ANN) model

These significant descriptors are then used by the back propagated Artificial Neural Network [27] with two nodes in one hidden layer to build the model. Either one random seed or 100 random seeds have been used to see the effect of the number of seeds in the model. The best model found from WEKA is also used in genetic algorithm driven [28, 29] artificial neural network with two nodes in one hidden layer to build the model and compare with the results found from WEKA.

The total number of data points for homopolymers are relatively sparse for all the properties of interest and thus the previous practice [13] of using 50% of the experimental data as training set and rest as test set is not appropriate. Instead a ten-fold cross-validation method [30] is used. For example, for cellular responses there are thirteen homopolymer data to build the model. Eleven out of thirteen data is taken to train the model and the remaining two to test the model. This is done for all possible (¹³C₂ = 78) combinations. Any data is part of the test set for 12 times and part of the training set for 66 times but no data is part of both the training and the test sets at the same time. When 100 random seeds are used to run the iteration process, the best random seed for training set to predict the test set has been taken. This exhaustive iteration is carried out to minimize the dependencies of the training on initial random weights and biases. This generally produces much better statistics than any single training run [31, 32]. Results are obtained by averaging the output values for each polymer in the test sets.

For co- and terpolymers 50% of the data is used to build the model and the rest to test the model. This is plausible as there were a fair amount of experimental data to build the model using only 50% of the data set. Randomly 100 training sets are selected from the whole data set and predicted values are found as average of those runs. All the experimental data for homo, co-, and terpolymers are combined together and used to build one uniform model for all of the polymers as well. The same procedure has been used for fibrinogen adsorption and cellular response to find different models for homo-, co-, ter- and all polymers together.

3. Results and Discussion

In this section the results of the fibrinogen adsorption model and cellular response model are presented followed by discussion of the model sensitivity to selection of the best descriptors and at the end a comparative discussion is carried out about the validity of both types of biological responses.

3.1. Fibrinogen Adsorption

The description of the best descriptors found from DT for fibrinogen adsorption for different set of polymers (homo-, co-, ter-) along with the Pearson correlation coefficients [33] are described in table I.

Table I.

Best descriptors and the Pearson correlation coefficient for different set of models for fibrinogen adsorption.

Polymer set	# of data	Best descriptors	Pearson correlation coefficient
Homopolymers	8	AMW (average weight-average molecular weight), RPCG (relative positive charge)	Training: 0.99 Test:  0.91
Copolymers	42	MAXDN (maximal electrotopological negative variation), SIC3 (structural information content – neighborhood symmetry of third order), GATS8m (Geary autocorrelation – lag 8 / weighted by atomic masses), RDF040m (radial distribution function – 4.0 / weighted by atomic masses)	Training: 0.95 Test:  0.66
Terpolymers	30	BIC4 (bond information content), HGM (geometric mean on the leverage magnitude), HATS3u (leverage-weighted autocorrelation of lag 3 / unweighted), R8v (R autocorrelation of lag 8 / weighted by atomic van der Waals volumes)	Training: 0.99 Test:  0.87
All polymers	80	RBN (number of rotatable bonds), MAXDN (maximal electrotopological negative variation), PW2 (path / walk 2 – Randic shape index), J3D (3D-Balaban index), RDF020m (radial distribution function – 2.0 / weighted by atomic masses), L1p (1st component size directional WHIM index / weighted by atomic polarisabilities), C-003 (atom centered fragments – CHR3)	Training: 0.91 Test:  0.71

Using the iteration methodology to model fibrinogen adsorption to homopolymers, the training set Pearson correlation coefficient is found to be 0.99 with a test set value of 0.91. In more than 90% of the cases the predicted fibrinogen adsorption for the homopolymers are in the right bins (low, medium, and high) as observed from experimental data (Figure III). Three bins are formed with experimental normalized fibrinogen adsorption values relative to adsorption on polypropylene without polymer i) less than 200 ii) between 200 and 400 and iii) more than 400. The numerical values of the highest two values are slightly off from the experimental values but the trend is correctly maintained.

Figure III.

Predicted fibrinogen adsorption against the experimental values for homopolymers. The legend TrainPa and TestPa stand for training and test protein adsorption respectively.

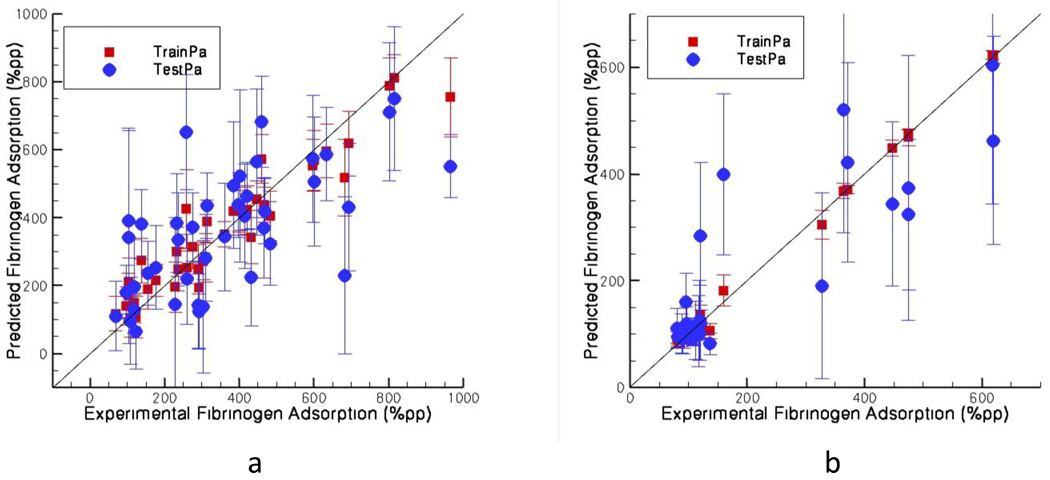
When the model is extended to copolymers and terpolymers, the numerical values of the descriptors are calculated as weighted average of the homopolymer experimental composition. It must be emphasized that although the descriptors are combined linearly, the ANN model itself is nonlinear in nature. We used 100 random training-test sets to find the average Pearson correlation coefficient as described before. The average Pearson correlation coefficients were 0.95 and 0.66 for training and test sets respectively for fibrinogen adsorption to copolymers (Figure IVa). For terpolymers these numbers are 0.99 and 0.87 respectively (Figure IVb). In both cases it is confirmed that 100 random selections of training and test sets are a reasonable number in order for the model to become statistically accurate, where all possible combinations give the same result as 100 random runs.

Figure IV.

Predicted fibrinogen adsorption against the experimental values for a) copolymers (42 data) b) terpolymers (30 data). The legend TrainPa and TestPa stand for training and test protein adsorption respectively.

Similar to what was performed for homopolymers, three bins are formed with experimental fibrinogen adsorption values on co and terpolymers relative to polypropylene control i) less than 200 ii) between 200 and 400 and iii) more than 400. In 70% of the cases the predicted fibrinogen adsorption values are in the right bins for copolymers whereas for terpolymers this number is more than 80%.

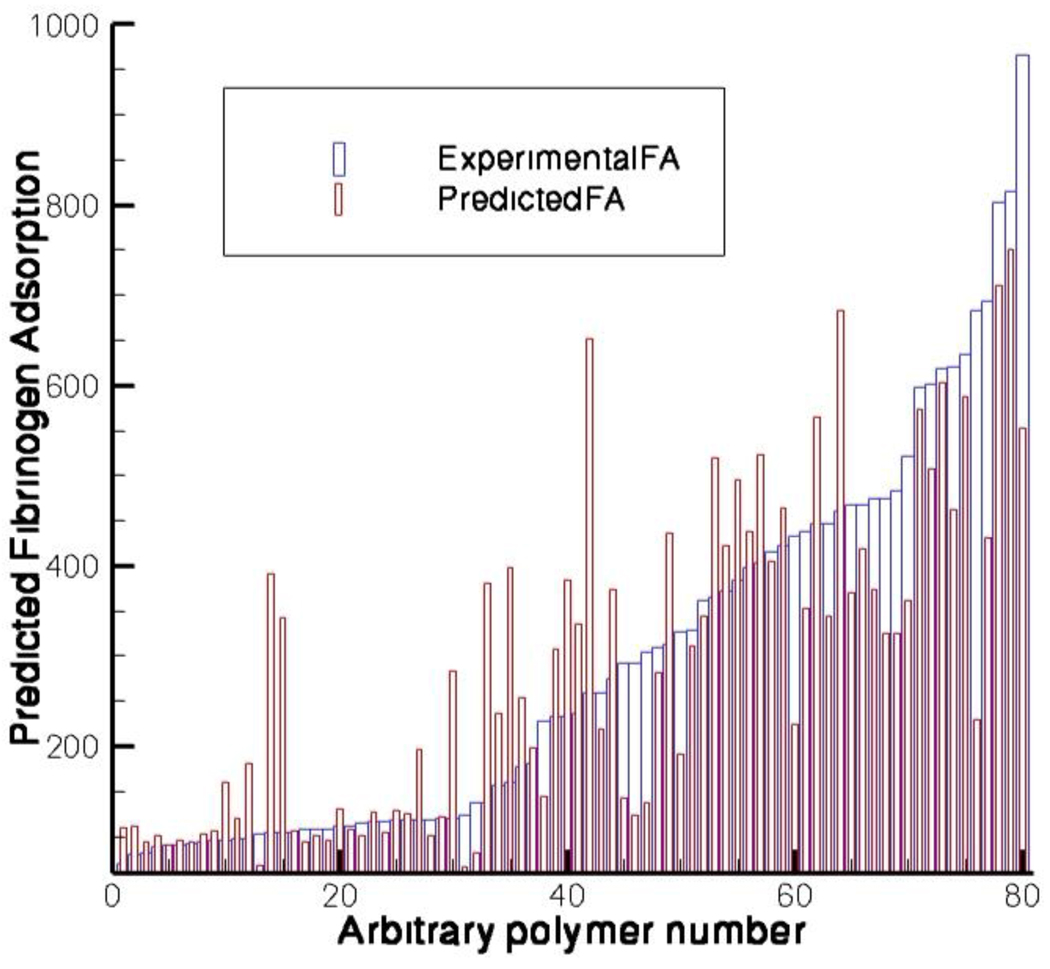
When all of the three models and the predicted values of fibrinogen adsorption are considered, more than 82% of the polymers sort into the appropriate bin. In this case the bins are formed with experimental values i) less than 200 ii) between 200 and 500 and iii) more than 500 relative to the polypropylene control. Figure V represents the experimental and predicted fibrinogen adsorption as increasing order of their experimental values. The data indicates that when all three models are combined, the overall ranking for fibrinogen adsorption to polymers is good with respect to predicted individual polymers and excellent for defining the general trends.

Figure V.

Experimental and predicted fibrinogen adsorption as increasing order of the experimental values (composition of the polymers are presented in the supplementary data sheet).

In order to consider all polymers (homo-, co-, ter-) together, a unified model was developed and a Decision Tree algorithm was used to find the top seven descriptors for fibrinogen adsorption. These descriptors were then employed to build the ANN model for the entire polymer system. 100 random training and test sets were selected and results were obtained as average over all the runs. The total data set has been split in two, with half to use as training set and the other half in the test set. The Pearson correlation coefficient of training set is 0.91 and that of test set is 0.71. These results suggest that the overall quality of the model is compromised to some extent but the prediction is very encouraging considering the wide variation of the data and the simplicity of the model.

Comparing the four models (homo-, co-, ter-, and all polymers together) reveals interesting similarities in what polymer properties could be used to best describe and predict fibrinogen adsorption. Although each set of models has a distinct set of best descriptors without much overlap, overall similar attributes were selected. As described in Table I, one of the best descriptors for homopolymers is AMW (average weight-average molecular weight), which is easy to correlate with the mass and size of the molecules. A second descriptor with good predictive value, RPCG (relative positive charge), accounts for the effects of polar intermolecular interactions or charge distribution of the molecules [21]. Among the four top descriptors for copolymers of fibrinogen adsorption, MAXDN (maximal electrotopological negative variation) represents the maximum negative intrinsic state difference in the molecule and can be related to the nucleophilicity of the molecule [34]. SIC3 (structural information content – neighborhood symmetry of third order) gives information about the third order neighborhoods of the vertices of chemical graph by applying information theory on chemical graphs [35]. GATS8m (Geary autocorrelation – lag 8 / weighted by atomic masses) is also based on molecular graph theory, describing the distribution of atomic masses along the paths connecting atom pairs of length 8 and characterizes the importance of atomic mass distribution [36]. Radial distribution function descriptors, on the other hand, are based on the distance distribution in the molecule [21]. The radial distribution functions describe how the density of surrounding matter varies as a function of the distance from a particular point and can be interpreted as the probability distribution of finding an atom in a spherical volume. Similarly the best descriptors for the terpolymers represent information about the fourth order neighborhood, bonds and multiplicity of chemical graph (BIC4) [21], the geometric mean on the leverage magnitude in study (HGM) [37] and autocorrelation coefficients. Overall the best homopolymer descriptors focus on size and electrostatics, copolymer descriptors focus on size, mass, structure, nucleophilicity, with terpolymer descriptors focusing on bonding, size and structure of the molecules. It is interesting to note that terpolymers prediction is much better than the copolymers prediction, which might be attributed to the fact that terpolymers descriptors contain more information about the polymers than the descriptors of copolymers. The seven top descriptors for the combined data set has information about the flexibility, nucleophilicity, shape, geometry, size, structure, and bulkiness of the molecules.

3.2. Cellular Response

Results for the cell attachment and proliferation for different set of polymers (homo-, co-, ter-) along with the Pearson correlation coefficients and best descriptors are detailed in Table II. The polymers encompass a variety of cell attachment characteristics, with values (relative to TCP) ranging from 0.2 to 1.0. Cell proliferation (again relative to TCP) ranged from 0 up to 2, exemplifying the diversity of the polymer library. Interestingly, the polymers having a very low proliferation index did not always match up with polymers exhibiting poor attachment of NIH3T3 cells.

Table II.

Best descriptors and the Pearson correlation coefficient for different set of models for cell attachment and cell proliferation index.

Polymer set	# of data	Cell attachment		Cell proliferation
		Best descriptors	Pearson correlation coefficient	Best descriptors	Pearson correlation coefficient
Homo-	13	EEig04r, SEigZ, G3m, R6v+	Training: 0.99 Test: 0.58	IC2, GGI5, G2p	Training: 0.99 Test: 0.51
Co-	53	D/Dr06, X4A, BELm3, BELv2, Mor25u, H8u, R4u+	Training: 0. 91 Test: 0. 44	Mor05u, Mor09v, Mor27p, HATS2p, R5m+	Training: 0.92 Test: 0.66
Ter-	26	RBF, Mor17m, Mor25p, G3e	Training: 0. 99 Test: 0. 77	BELp5, G3e, R1e+, nRCOOH	Training: 0.94 Test: 0.39
All polymers	92	ZM1v, PW5, X1A, X4A, X4Av, BIC5, BELe1, BELp5, Mor04m, Mor22e, G3e, E3e, G1S, HATS0p, HATS2p, R4u+, R6u+, R4m, R8m+, R7v+	Training: 0.98 Test: 0.51	X5A, MATS8p, JGI3, DISPm, Mor25v, P2u, G3m, P1p, HATS6p, R5m+, nRCOOH, nOHS	Training: 0.96 Test: 0.33

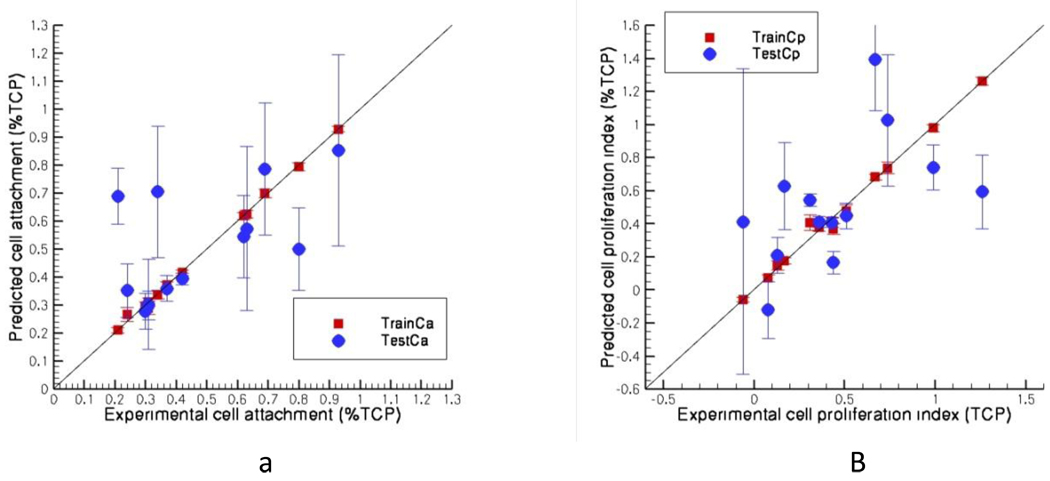
The training set Pearson correlation coefficients are found to be 0.99 for both cell attachment and cell proliferation index with test set values of 0.58 and 0.51 for attachment and proliferation respectively for homopolymers. In more than 77% of the cases the predicted cell attachment for the homopolymers are in the right bins (low, medium, and high) as found from experiments. For cell proliferation index 70% of the predicted data are within same experimental bins. In these cases the bins are formed with experimental cell attachment or proliferation index values i) less than 0.31 ii) between 0.31 and 0.61 and iii) more than 0.61. For homopolymers all possible combinations as described in the method section gives the same result as averaging 100 random training sets.

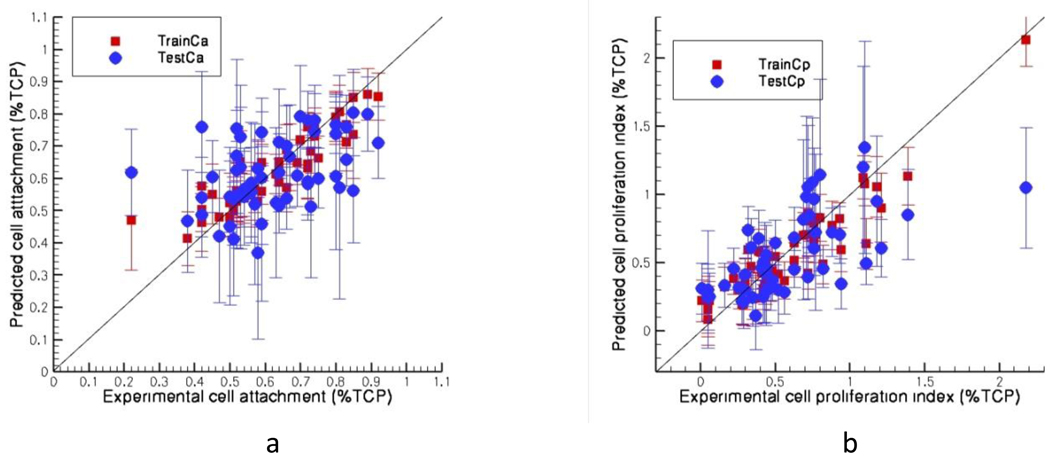
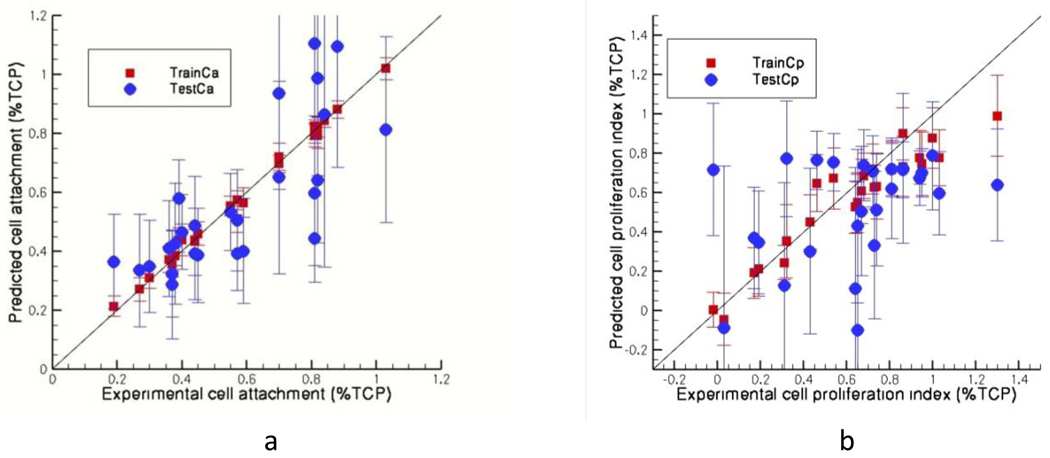
For copolymers, training sets give average Pearson correlation coefficients of 0.91 and 0.92 and those of test sets give values of 0.44 and 0.66 for the cell attachment (Figure VIIa) and cell proliferation (Figure VIIb) index respectively. For terpolymers these numbers are 0.99 and 0.95 for training sets and 0.77 and 0.40 for test sets for attachment (Figure VIIIa) and proliferation (Figure VIIIb) respectively. Three bins are formed for cell attachment values i) less than 0.31 ii) between 0.31 and 0.61 and iii) more than 0.61. In 70% of the cases the cell attachment values are in the right bins for copolymers where as for terpolymers this number is about more than 80%. For cell proliferation index these values are 64% and 38% respectively for copolymers and terpolymers with bins defined with values i) less than 0.5 ii) between 0.5 and 0.8 and iii) more than 0.8. These results show that when individual polymer models (homo, co-, ter-) are developed, a good rank ordering into bins can be achieved, with the exception of cell proliferation on terpolymers. When all of the three models and the predicted values of cell attachment and cell proliferation index are considered it was found that 75% and 56% of the polymers are in the right bins for the respective properties. These results show that overall ranking is acceptable when the 3 models are combined and used to predict the cellular responses for the entire dataset.

Figure VII.

Predicted a) cell attachment and b) cell proliferation index against the experimental values for copolymers (53 data)

Figure VIII.

Predicted a) cell attachment and b) cell proliferation index against the experimental values for terpolymers (26 data)

Two of the best descriptors for cell attachment onto homopolymers are based on the eigen values of the edge adjacency matrices whereas two other descriptors reference the three dimensional structures, atomic mass and volumes of the homopolymers. For copolymers the best descriptors represent topology, size, volume and connectivity of the molecules. Flexibility, mass, structure and polarisability of the molecules are descriptors which best predict cell attachment to terpolymers. With reference to cell proliferation, homopolymer descriptors represent information about the symmetry and electrostatics of the polymers. Three of the top five descriptors for copolymers of cell proliferation index represent three dimensional Morse descriptors and other descriptors represent the autocorrelation functions which have information about the volume, polarizability, and structure of the molecules. Topology, polarisibility, electronegativity of the molecules are main feature to depict the variation of cell proliferation index of the terpolymers within methacrylate library of polymers.

3.3. Sensitivity of the model on selection of the best descriptors

As discussed in the method section, several different strategies have been deployed to find the best descriptors. One of the strategies was to remove the useless (constant attribute along with nominal attributes that vary too much) descriptors first followed by application of CfsSubsetEval function, which evaluates the worth of a subset of attributes by considering the individual predictive capability. CfsSubsetEval function is known to improve the J48 Decision Tree algorithm from WEKA software. After these steps we applied Decision Tree algorithm on relatively smaller number of descriptors. In another strategy we used Decision Tree directly after removing the useless descriptors but used different levels of pruned tree. These different sets of best descriptors are then used to build the ANN model. The most accurate models has been discussed previously in the results section but here analysis is made on whether other sets of descriptors have any correlation with the chosen model, and consequently to the experimental data.

Table III represents the different sets of best descriptors to build the model of fibrinogen adsorption for homo-, co- and terpolymers. It is clear from the Pearson correlation coefficients of each set that it is easy to get a perfect correlation for training set but a good correlation for test set is only achieved with the proper choice of descriptors. The chosen best descriptors (AMW, RPCG) for homoplymers in this case clearly have some meaning to the variation of experimental data of homopolymer fibrinogen adsorption. Set 2, 3, and 4 are comparable as per the Pearson correlation coefficients for copolymer model but the chosen Set4 is obviously the best one with reasonable number of descriptors. Similarly if Set 1 and Set3 are compared for terpolymers it is clear that replacing the descriptor nC with two other (BIC4, HGM) gives slightly better correlation but overall different sets have overlapping best descriptors. Similar analysis on cellular models also reveals that the chosen model has relevance to the experimental variation.

Table III.

Different sets of best descriptors for model of fibrinogen adsorption. Bold represents the chosen model as described in the earlier section.

Polymers	Model	Descriptors	Pearson correlation coefficient
			Training	Test
Homopoly	Set1	Me, HATS3u	0.99	0.39
	Set2	EEig07d, R4e+	0.99	−0.23
	Set3	AMW, RPCG	0.99	0.91
	Set4	AMW, nH, RPCG	0.99	−0.36
	Set5	Me, EEig07r, HATS4u, R4e+	0.99	−0.63
	Set6	AMW, RBF, Qpos, RPCG	0.99	0.39
Copoly	Set1	MAXDN, DECC, ATS3m, GATS8m, EEig04r, BELp1, JGI6	0.97	0.51
	Set2	Xt, MSD, MAXDN, MWC02, GATS8m, EEig01x, EEig07x, EEig08r, BELe1, P1m, HATS3p, R7m+	0.98	0.63
	Set3	MAXDN, GATS8m, RDF040m	0.92	0.64
	Set4	MAXDN, SIC3, GATS8m, RDF040m	0.95	0.66
Terpoly	Set1	nC, HATS3u, R8v	0.98	0.83
	Set2	CIC0, RDF035e, R8v	0.99	0.78
	Set3	BIC4, HGM, HATS3u, R8v	0.99	0.87
	Set4	CIC0, RDF035e, Mor08u, R8u	0.99	0.70

3.4. Comparative discussion and applicability of the model

In general the cellular response models are less accurate than the fibrinogen adsorption models. This can be explained from the variability of the cellular studies. It is inherently difficult to reproduce some of the cellular response experiments, with two important issues to be considered here, chemistry and surface topography. The assumption is made that similar chemistries will generate similar topographies and that correlation can be made between cellular response and the chemistry of the polymers. This is a simple assumption to build a complicated model for a vast library of polymethacrylates with so much variation in the structures. In spite of such variation it is none the less encouraging to see correlations among the cellular response and chemistry of the polymers.

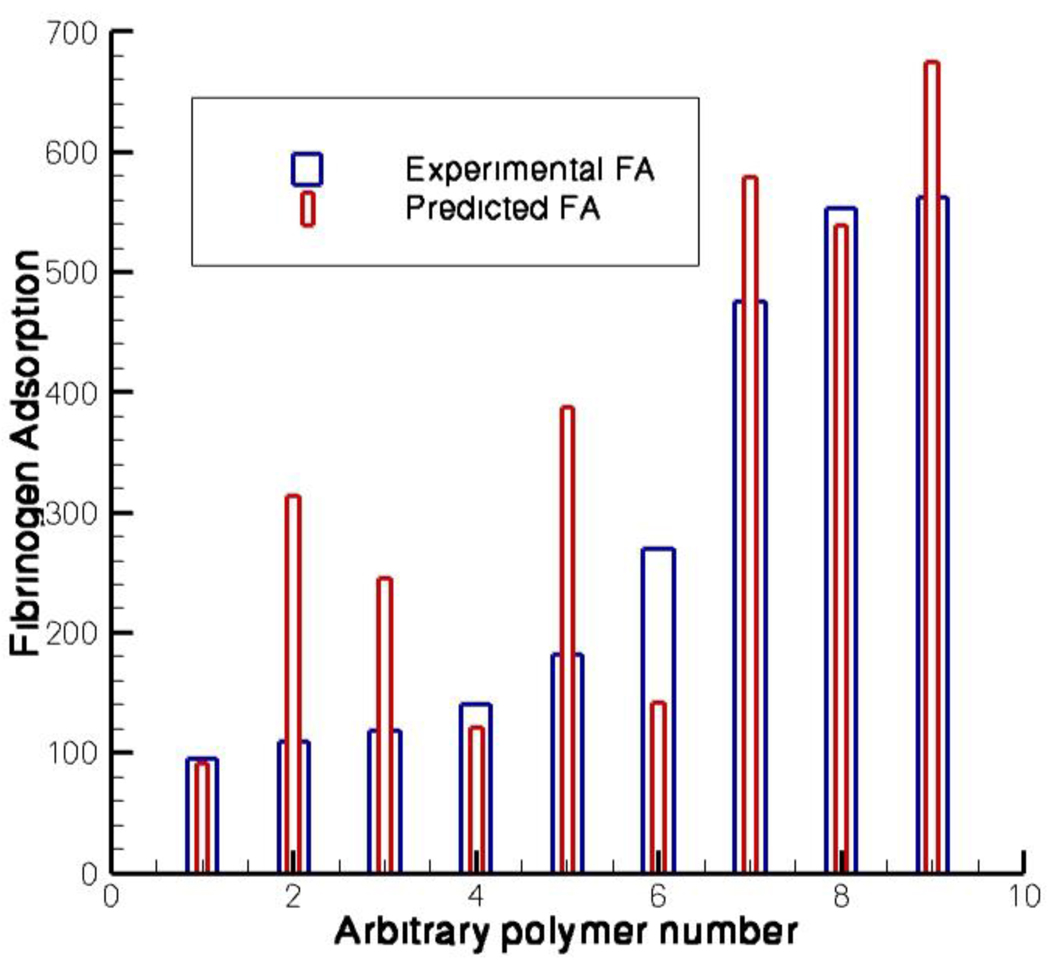
It must be noted that any QSPR model must be validated by predicting the properties (fibrinogen adsorption, cell behaviors) on polymers outside the original “reference set”. Here the external prediction of the fibrinogen adsorption is presented for polymers that were synthesized and characterized after the model was established based on the sub set of polymers. Models were constructed for each polymer sub-type in that the homopolymer model is used to predict the properties of homopolymers, and similarly for copolymers and terpolymers. Only “usable” experimental data within the range of each set of model are considered to validate the model. Data from validation experiments found that the models constructed to predict homo and terpolymers were more accurate than those constructed to predict fibrinogen adsorption to copolymers. The data shown in Figure IX exemplify the capabilities of the individual models, where predicted fibrinogen of homopolymers (#1, and #9) and a terpolymer (#8) are much closer to their actual adsorption than the predictions of the copolymers (#’s 2–7). Again it must be emphasized that we were interested in rank ordering of the polymer properties rather than predicting their exact values.

Figure IX.

External prediction for fibrinogen adsorption. Fibrinogen adsorption was most accurately predicted on homopolymers (1 and 9) and a terpolymer (8), where copolymers were much more difficult to predict with such accuracy. Polymer compositions are as follows: 1. Poly(undecyl methacrylate) 2. Poly(2-hydroxyethyl methacrylate-co-methyl methacrylate) (50:50) 3. Poly(butyl methacrylate-co-methyl methacrylate) (75:25) 4. Poly(tetrahydrofurfuryl methacrylate-co-methyl methacrylate) (75:25) 5. Poly(ethylene glycol methyl ether methacrylate-co-methyl methacrylate) (25:75), 6. Poly(butyl methacrylate-co-2-hydroxyethyl methacrylate) (50:50), 7. Poly(methacrylic acid-co-methyl methacrylate) (75:25), 8. Poly(isobutyl methacrylate-co-methyl methacrylate-co-methacrylic acid) (33:33:33) 9. Poly(2-2-2 trifluoroethyl methacrylate).

Another question is the applicability of fibrinogen adsorption model for one library of polymers to other library of polymers. In this respect particularly the applicability of the best descriptors for fibrinogen adsorption model of polyarylates to polymethacrylates is tested. J. Smith et. al [16] developed models for fibrinogen adsorption for polyarylates where they used experimental descriptors e.g. glass transition temperature, contact angle etc. and later on they improved [13] the model by replacing the experimental descriptors with the computed descriptors. Here in the context of another larger library it is interesting to see if the previously built model can be translated to other library of polymers. Three different sets [13] of J. Smith’s descriptors are used to build the ANN model for methacrylate library of polymers. Models for individual set of polymers have been tried with homo-, co-, ter-, and for all polymers together. It has been found that models for all polymers together are better than each of the other sets. Fifty percent of the data is used to build the model and rest of the data to test the model using 100 iteration cycles and taking the average from all the runs. The three sets of descriptors and the corresponding Pearson correlation coefficients (PCC) for all polymer models are represented in Table IV.

Table IV.

Different sets of descriptors from polyarylate model applied to polymethacrylate library

Set	Descriptors	PCC - training	PCC – test
Set1	number of secondary sp3 carbons, number of hydrogen atoms, hydrophilic factor, number of single bonds, sum of the van der Waals area of atoms in the molecule with negative partial charge, number of rotatable single bonds, Kier flexibility index, 2-path Kier alpha modified shape index, third – kappa shape index	0.87	0.62
Set2	molecular density, number of hydrogen atoms, log of the octanol/water partition coefficient from the liner atom type model, first kappa shape index of Kier, molecular refractivity calculated from the atomic model based on the corrected protonation state, sum of atomic van der Waals volume scaled on carbon atom, number of aliphatic ethers, log of the octanol/water partition coefficient calculated from the atomic model based on the corrected protonation state, molar refractivity from the linear atom type model	0.89	0.64
Set3	molecular density, number of hydrogen atoms, log of the octanol/water partition coefficient from the liner atom type model	0.75	0.55

The model based on the best descriptors from polyarylate library is not directly transferable to the current library. Our interpretation is that it is always best to build the model for each individual library of polymers. This result can be explained from the structural variation among polyarylates and polymethacrylates also.

4. Conclusions

In this study an Artificial Neural Network has been used to build a nonlinear QSPR model for complicated biological properties for a large library of polymers. It has been demonstrated that the quantitative structure property method can predict the complicated biological responses on polymeric substrates which include a large library of polymers comprising of homo-, co- and terpolymers. It is interesting to note that although there are three individual models having three different sets of best descriptors for homo-, co-, and terpolymers, nonetheless the best descriptors in each set contain similar information. The methodology is able to bypass the tedious calculation of all possible descriptors of co- and terpolymers for each polymer composition. It is possible that the predictive capacity of the model may be greatly improved if experimental descriptors such as reactivity ratio, direct image analysis or cell material topography, could have been obtained and utilized into the model. Despite the prospect of improving the model using further experimental data, the here described and utilized QSPR method gives very good predictions for homo-, co- and terpolymers considering the wide variation in the chemical structure and experimental data.

Using the model it is now possible to extrapolate the predicted values to other polymers in the library for which there is no experimental data yet. From the predicted rank ordering of the polymers it is easier to narrow the field of nearly countless polymer combinations to focus on a subset that are likely to give the desired outcome. This can help reduce the experimental cost to identify polymers with right order of magnitude of fibrinogen adsorption, cell attachment or cell proliferation index. Utilizing this modeling method as a complimentary technique to combinatorial chemical synthesis will greatly improve the evaluation of extensive biomaterial libraries.

Figure VI.

Predicted a) cell attachment and b) cell proliferation index against the experimental values for homopolymers (13 data)