Population-Wide Principal Component-Based Quantification of Blood-Brain-Barrier Dynamics in Multiple Sclerosis

Abstract

The processes by which new white-matter lesions in multiple sclerosis (MS) develop are only partially understood. Much of this understanding has come through magnetic resonance imaging (MRI) of the human brain. One of the hallmarks of new lesion development in MS is enhancement on T1-weighted MRI scans following the intravenous administration of a gadolinium-based contrast agent that shortens the longitudinal relaxation time of the tissue. Visible enhancement in the MRI results from the opening of the blood-brain barrier and reveals areas of active inflammation. The incidence and number of existing enhancing lesions are common outcome measures used in MS treatment clinical trials. Dynamic-contrast-enhanced MRI (DCE-MRI) can estimate the rate at which contrast agents pass from the plasma to MS lesions. In this paper, we develop a principal component-based framework for the analysis of these data that provides biologically meaningful quantification of blood-brain barrier opening in new MS lesions. To accomplish this, we use functional principal components analysis to study directions of variation in the voxel-level time series of intensities both within and across subjects. The analysis reveals and allows quantification of typical spatiotemporal enhancement patterns in acute MS lesions, providing measures of magnitude, rate, shape (ring-like vs. nodular), and dynamics (centrifugal vs. centripetal). Across 10 subjects with relapsing-remitting and primary progressive MS, we found subjects to have between 0 and 12 gadolinium-enhancing lesions, the majority of which enhanced centripetally. We quantified the spatiotemporal behavior within each of these lesion using novel measures. Further application of these techniques will determine the extent to which these lesion measures can predict or track response to therapy or long-term prognosis in this disorder.

1 Introduction

Multiple sclerosis (MS) is an inflammatory disease that causes demyelinating lesions in the central nervous system. Although gray-matter lesions are common [Calabrese et al., 2010], white-matter lesions are easiest to identify, both pathologically and radiologically, due to their loss of normal myelin and often high degree of inflammation. In the first clinical stage of MS, these lesions appear relatively frequently and can occur in unpredictable locations at unpredictable times. The disease-modifying drugs that are currently used to treat MS can reduce the incidence of these lesions [Vosoughi and Freedman, 2010].

The processes by which new lesions develop are only partially understood. Much of this understanding has come through magnetic resonance imagine (MRI) of the brain. These lesions have long been known to form around veins [Charcot, 1868, Dawson, 1916], where inflammatory cells, especially T lymphocytes, form perivenular cuffs. One of the hallmarks of newly forming lesions is enhancement on MRI following the intravenous administration of gadolinium-based contrast agents that shorten the longitudinal (T₁) relaxation time of the tissue [Grossman et al., 1988]. This visible enhancement in the MRI results from opening of the blood-brain barrier (BBB) and reveals areas of active inflammation. Lesion enhancement typically lasts 4 to 8 weeks and may be accompanied by neurological signs and symptoms, but enhancing lesions are often asymptomatic [Capra et al., 1992]. The incidence and number of enhancing lesions are common outcome measures used in MS treatment clinical trials.

The exact nature of BBB opening in new MS lesions and the selectivity of the resulting permeability remain unclear. The analysis of contrast-agent uptake can provide only limited insight into these issues. Dynamic-contrast-enhanced MRI (DCE-MRI) has been used for the past two decades to quantify the rate at which contrast agents pass from the plasma to MS lesions as a measure of BBB permeability [Kermode et al., 1990].

DCE-MRI data are typically analyzed using deterministic pharmacokinetic modeling techniques based on multi-compartment tissue models with exchange [Davidian and Giltinan, 1995]. These techniques are limited for four major reasons. The first is that the tissue composition, specifically the number of compartments in the pharmacokinetic model, is unknown, posing technical and interpretive difficulties. Second, the number of compartments may vary within and between tissue types, which makes the a-priori choice of a number of compartments for every single voxel in the brain a difficult proposition. Third, saturation of these models leads to interpolation, which in itself does not help with the quantification and dimension reduction. Finally, when fitting these models to the DCE-MRI data from our study, we have found that standard deterministic algorithms fail to converge in a majority of the voxels.

In this paper, we consider 10 subjects, 6 with relapsing-remitting MS (RRMS) and 4 with primary-progressive MS (PPMS), who were evaluated as part of a natural-history protocol. The RRMS subjects were selected for this imaging protocol because of their active disease, as evidenced by the development of contrast-enhancing lesions on monthly scans. In each subject, we observed one DCE-MRI scan recorded during a single clinical visit. The DCE-MRI consisted of short T₁-weighted scans recorded as the contrast agent flows through the brain; details concerning the acquisition of these data can be found in Section 2. Our goals were to: 1) provide a statistically principled platform for the quantification of observed lesion enhancement; 2) introduce and analyze spatiotemporal models of lesion enhancement with consistent interpretation within and between subjects; and 3) generate a set of hypotheses for the cross-sectional and longitudinal analysis of MS lesions in a large population of MS patients observed at multiple visits. To achieve these goals, in Section 3 we use functional principal components analysis (FPCA) [Ramsay and Silverman, 1998,Ramsay and Silverman, 2002] to study directions of variation in the voxel-level time series of intensities in each of the 10 subjects. In Section 4, we consider the normalization and simultaneous analysis of the data from all 10 subjects using similar techniques. We use the principal components along with their corresponding scores (loadings) to study patterns in the intensity time series, which are referred to as enhancements. We also develop a simple method for testing whether a particular voxel (or group of voxels) has enhancing properties. We finish the paper with a set of biological hypotheses that we intend to test in future studies.

2 Experimental Methods

2.1 Participants

We analyzed the MRI data of 10 people with MS (6 with RRMS and 4 with PPMS) scanned under an Institutional Review Board-approved natural-history protocol. All participants gave written consent. Demographic, diagnosis, and treatment information may be found in Table 1. The study included both treated and untreated subjects with a wide range of EDSS scores (0 to 7, where 0 corresponds to a normal neurological examination and 7 to essentially wheelchair-bound). We included both treated and untreated patients in order to capture features of lesion enhancement that are representative of a typical patient population.

Table 1.

Descriptive statistics for 10 subjects with MS, including disease subtype (RRMS/PPMS), age, sex, expanded disability status scale (EDSS) [Kurtzke, 1983], and treatment information.

Subject ID	Subtype	Age	Sex	EDSS	Treatment
1	RRMS	40	M	2.5	None
2	RRMS	41	M	2.5	None
3	PPMS	58	F	6	None
4	RRMS	26	F	1	Interferon β − 1a
5	PPMS	50	M	2	None
6	RRMS	25	F	0	None
7	RRMS	30	F	1.5	Glatiramer acetate
8	RRMS	48	M	1.5	None
9	PPMS	54	M	7	None
10	PPMS	62	M	6.5	None

2.2 MRI Protocol

As part of a comprehensive protocol, we performed whole brain DCE-MRI in a 3 tesla MRI scanner (Signa Excite HDxt, GE Healthcare, Waukeska, WI) using the body coil for transmission and an 8-channel receive coil array (Invivo Corp, Gainsville, FL) for signal detection. We acquired T₁-weighted images using a spoiled gradient echo sequence (FSPGR) with flip angle (FA)=15deg; repetition time (TR)=5.6ms; echo time (TE)=1.84ms; 8mm³ isotropic voxels; and acquisition time (TA)=35s per volume. We repeated the sequence before, during, and after a 60sec intravenous infusion of 0.1mmol/kg gadolinium-DTPA (Magnevist, Bayer HealthCare, Leverkusen, Germany) via power injector (MEDRAD, Inc., Warrendale, PA) over 58 to 155 minutes. We acquired three consecutive T₁-weighted volumes before the infusion of the contrast agent and 10 to 64 volumes during and after the infusion.

We also acquired a sagittal T₁-weighted 3D FSPGR-Brain Volume (BRAVO) before and approximately 35min after the administration of the gadolinium chelate (TR=8.8ms, inversion time (TI)=450ms, TE=3.84ms, FA=13 deg, voxel size=1mm³, TA=4.2min) as well as a sagittal 3D Fluid Attenuation Inversion Recovery (FLAIR) image approximately 40min after gadolinium administration (FA=90deg, TR=6000ms, TE=12.7ms, TI=1861ms, voxel size=1mm³, TA=8min).

2.3 Image Post-Processing

For the initial image processing, we used Medical Image Processing Analysis and Visualization (MIPAV) (http://mipav.cit.nih.gov) and Java Image Science Toolkit (JIST) (http://nitrc. We rigidly coregistered all acquired dynamic volumes to the first volume in which we detected enhancement in the arteries, resampling at 1 mm isotropic resolution. We then rigidly aligned all images to the Montreal Neurological Institute standard space and removed the extracerebral voxels using a skull-stripping procedure [Carass et al., 2007]. We used the high-resolution T₂-weighted and FLAIR images (shown for the first two subjects in Figure 1) to automatically segment the brain into separate compartments for cerebrospinal fluid, gray matter, white-matter lesions, and normal appearing white matter (NAWM) [Shiee et al., 2010].

Figure 1. FLAIR Images.

T₂-weighted FLAIR scans in the first two subjects. Black contour lines indicate the spatial extent of the lesions.

3 Single-Subject Methodology

We start by introducing some prominent characteristics of the data. As the contrast agent propagates through the areas under observation via MRI, the signal intensity on T₁-weighted images increases because the gadolinium shortens the T₁ relaxation time of the tissue. This increase in the signal is related to the concentration of the contrast agent in the tissue. However, exact calibration is not possible without careful T₁ mapping, which we explicitly avoided in order to decrease scan time, reduce variability, and limit the number of assumptions of our analysis. Without such mapping as well as knowledge of the relaxivity properties of gadolinium, units of MRI signal cannot be taken as indicative of gadolinium concentration [Tofts, 1997]. The interpretation of the recorded intensity varies with respect to the location and baseline magnetic properties of the various voxels in the brain. Quantifying the temporal and spatial behavior of the signal intensity in white matter is the primary goal of this paper.

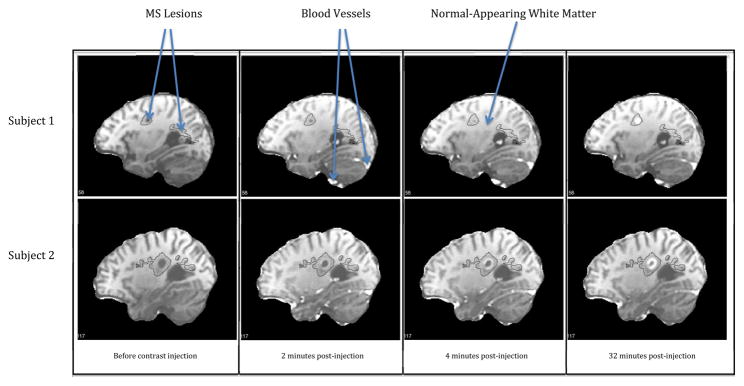
For illustration, the intensity maps for two subjects in a sagittal slice are displayed in Figure 2 at four time points: before the injection and 2, 4, and 32 minutes afterward. Although we only show four time points, many more volumes are typically observed for each subject. The 10 subjects analyzed in this paper were scanned over 58 to 155 minutes, and between 13 and 67 volumes were acquired during a single scan. The solid black contours in Figure 2 are the reconstructed in-slice boundaries of the lesions obtained using the Lesion-TOADS automatic segmentation algorithm [Shiee et al., 2010]. Most of the delineated lesions had been present on previous scans of the same subject and did not enhance with contrast.

Figure 2. DCE-MRI Scans.

DCE-MRI scans in two subjects at four time points both before and after contrast injection. Black contour lines indicate the spatial extent of the lesions as seen on T₂-weighted FLAIR scans obtained during the same session.

Several characteristics of the data are immediately apparent. First, in the time point measured 2 minutes after contrast injection, the blood vessels are bright, indicating a high concentration of the contrast agent. The rest of the brain remains essentially unchanged at this time. Second, as time progresses some of the voxels in regions of interest (ROI) within the lesions enhance. Third, lesion enhancement is also different between the two subjects: on the scan at 32 minutes, the enhancing lesion in the first subject exhibits homogeneous enhancement, whereas the enhancing lesion in the second subject shows a ring-like enhancement.

Another way of looking at the data is to plot the time series for each voxel. More specifically, the data from a single subject can be written as a T × V matrix, where T is the number of time points and V is the number of voxels. For the first subject, T=67 and V =7.2 million (corresponding to the volume of dimension 182 × 218 × 182, where each voxel is interpolated to 1mm × 1mm × 1mm cuts from an acquired resolution of 2mm³). The skull-stripping procedure [Carass et al., 2007] reduces V from 7.2 million to 1.6 million. The time series for these 1.6 million voxels are displayed in Figure 3 for the same two subjects. Unfortunately, the sheer number of voxels masks important features in the data.

Figure 3. Intensity Time Series.

Raw MR signal time series for the first subject two subjects plotted over time. Intensity is measured in arbitrary units.

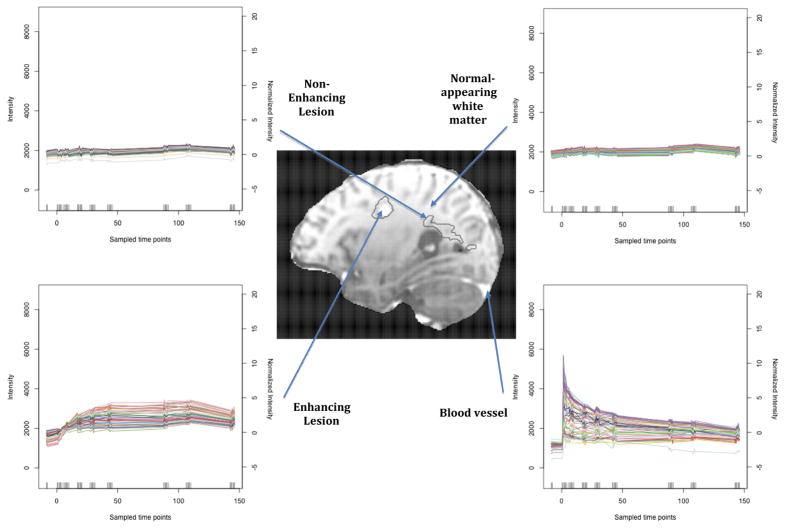
A more careful look at the data reveals hidden patterns. Figure 4 displays the time series for four different regions of the brain in the first subject: blood vessels, NAWM, a non-enhancing lesion and an enhancing lesion. The patterns are strikingly different and indicate: 1) sudden jumps in the intensity of blood vessel voxels immediately following injection as the blood enters the brain, followed by exponential decay characteristic of single-compartment pharmacokinetic modeling [Davidian and Giltinan, 1995] as the blood is evacuated; 2) time-independent trajectories in the NAWM and non-enhancing lesion voxels, indicating that perfusion is low in these regions and that the BBB is for the most part impermeable to the contrast agent; and 3) gradual increases in the intensity of enhancing lesion voxels during the first hour after injection, followed by a plateau during the second hour and small decreases in the third hour. From a physiological perspective, this indicates that the plasma seeps into these areas slowly after being delivered by the blood vessels.

Figure 4. Intensity in Different Regions.

Diagram indicating the different dynamic behaviors of anatomical sections of the brain. The black contours in the white matter depict MS lesions. The time series on the right describe the enhancement behavior of voxels in the different sections. The intensity scale on the left is the observed arbitrary scale, and the normalized scale on the right is in terms of standard deviations of NAWM intensity before contrast injection.

Given the complexity and size of the data, a natural next step in the exploratory data analysis is to find the number and shape of patterns at the subject level. Our primary goal is to quantify these patterns in the population. We start by applying FPCA to the collection of time series from each subject. For illustration, consider the data for the subject displayed in Figure 4. The first five principal components (PCs) from this analysis are depicted in Figure 5(a). The first PC (orange) is roughly a vertical shift; this corresponds to baseline discrepancies between voxels. For example, the intensity in gray matter voxels and NAWM voxels changes little over time; however, the gray matter voxel intensities tend to be shifted downward compared to the white matter due to their longer intrinsic T₁. Similarly, there is variance in the baseline intensity within each of these sections in the brain; some parts of the gray matter are darker than other parts. We conclude that the first PC captures natural differences in the magnetic properties of voxels that are independent of the contrast agent’s presence. The second PC (red) depicts a sudden increase in intensity after injection followed by an exponential decline. This behavior is identical to that seen in blood vessels in Figure 4. In terms of physiology, this is consistent with the delivery of the contrast agent in high concentrations immediately following injection, followed by its efficient clearance. The third PC (blue) is a gradual increase in intensity followed by a plateau, which is strikingly similar to the shape of the time series in the enhancing ROI. This indicates that blood is not rapidly introduced to these regions; rather, it slowly seeps in over time.

Figure 5. Subject-Level Principal Components.

First several PCs from the FPCA of the first two scans. In both plots, the color indicates the index of the PC. Most of the noticeable jumps in intensity are noise, likely related to scanner drift, onset of scanning, subject movement, and possibly other factors.

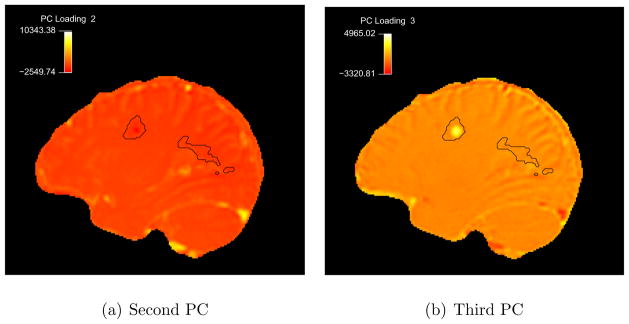
The first three PCs, which explain 99% of the variation in the data for this subject, are interpretable and apparently correspond to real features in the observed time series. To further investigate our empirical findings, we analyze the spatial patterns associated with the loadings of the voxel time series. To accomplish this, we calculate the PC loadings on each of these components for each voxel. Specifically, for a voxel v with corresponding observed time series Y^O(t, v) and a principal component φ;_j(t), we find the loading ξ(v) = < Y^O(t, v), φ_j(t) > = Σ_t Y^O(t, v)φ_j(t). We then map these scores, ξ (v), back to the three-dimensional brain volume. Figure 6 is a map of the spatial patterns of these loadings for the second and third PCs in the same sagittal slice from Figure 4 (top row). We have omitted the map for the first PC as it only shows baseline differences and is not of general interest. The second PC loads heavily only in the blood vessels (yellow spots), as expected. The third PC loads in the enhancing ROI and in residual highly vascularized extracerebral tissues (such as the meninges).

Figure 6. SLPC Loading Maps in Subject 1.

Maps indicating the second and third PCs loadings in sagittal slice 58 of the first subject. Intensity scale is arbitrary.

Similar results are shown in Figures 3(b)–5(b) for the second subject. This subject is only observed for half as long as the first subject (61 minutes versus 146). Remarkably, the first three PCs from the two subjects share similar shapes (Figure 5(a) versus 5(b)) and interpretations. The loading maps also yield similar findings (Figure 7).

Figure 7. SLPC Loading Maps in Subject 2.

Maps indicating the second and third PCs loadings in sagittal slice 117 of the second subject.

Our voxel-level FPCA methodology does not incorporate any a priori knowledge about the spatial correlation of the data. This correlation is manifested as similarities in the time series from adjacent voxels. The FPCA method incorporates information related to spatial correlation once the loading maps are drawn (Figures 6–7), when the results are interpreted with respect to their spatial trends. To validate these voxel-level methods, we conducted two simulation studies that showed our methods to be sensitive and specific to spatial trends in enhancement. The simulations also demonstrated that the principal components capture the enhancement-related patterns in the spatially-dependent time series. The simulation schemes and results are given in the Appendix.

The above subject-by-subject analysis is enlightening, but each analysis is subject-specific, and the measures defined therein are therefore only valid within the particular subject. However, our primary goal is to quantify these subject-specific patterns using measures that are meaningful across subjects. Thus, in the next sections we: 1) normalize and interpolate the data to a common grid; 2) obtain population-level PCs; 3) ensure that the features identified by the above subject-level analyses are also identified by the population-level method; and 4) generate hypotheses concerning the nature of enhancement patterns and outline appropriate statistical methods.

4 Multiple-Subject Methodology

4.1 Normalization and Interpolation

An important first step in the analysis of populations of images is to calibrate measurement units across subjects to ensure that they have the same interpretation. This process, often referred to as normalization, depends on the particular application and scientific question. We propose a subject-by-subject normalization procedure so that the construction of the normalized data from one subject will not be affected by the data from other subjects or a priori norms.

Because the focus of this research is the enhancement of MS lesions in white matter, we propose a procedure that emphasizes departures from the subject’s NAWM. Let $Y_i^O(t,v)$ be the observed intensity at time t of voxel v from subject i and normalize the data as:

$$Y_i^N(t,v)=\frac{Y_i^O(t,v)-{\mu }_{i,0}}{\sqrt{V_{i,0}}},$$ (1)

where μ_{i, 0} and V_{i, 0} denote the mean and variance of the observed intensities, $Y_i^O(t,v)$, over all time points before the injection, t, and voxels in the subject’s NAWM, v. These normalized values, $Y_i^N(t,v)$, are deviation measures from the mean baseline intensity of NAWM voxels of that particular subject expressed in standard deviation units of the baseline NAWM intensities. For example, in Figure 4, we display the raw intensities on the left side of the y-axis and the normalized values of intensity on the right side. As expected, the normalized intensity values in NAWM are very close to zero and vary from −2 to 2 (middle plot). In the enhancing ROI, the normalized time series vary between −2 (before injection) and 5 (around 100 minutes after injection). The blood vessel time series display more extreme changes, and they start as low as −5 (before injection) and peak around 15 standard deviations (immediately following injection). Note that the normalization does not change the structure of the distribution of time series and that all information is maintained as long as the μ_{i, 0} and V_{i, 0} are recorded; $Y_i^O(t,v)=\sqrt{V_{i,0}}·Y_i^N(t,v)+{\mu }_{i,0}$ can easily be recovered. Furthermore, the values μ_{i, 0} and V_{i, 0} themselves may be of interest as global predictors, but we do not present this here.

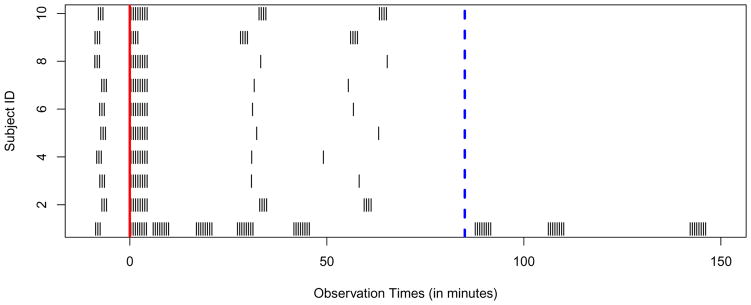
An additional complexity is that both in our study and in clinical practice, the MRI scans are not always recorded at the same times. For example, Figure 8 displays the time points at which the scans were recorded for the 10 subjects. Each subject was scanned several times before contrast injection (time 0, indicated by the red vertical line), several times immediately following the injection (in the 5 minutes following injection), and at other times scattered over the remaining scanning period. The first subject (the bottom row) was scanned for about twice as long as the other eleven. For convenience, we truncate all observations after 85 minutes (dashed blue vertical line). The other 9 subjects were scanned in only two later time regions, the first around 30 minutes and the second around 1 hour after the contrast injection. Half of the subjects (subjects 3 to 8) were scanned at only one time point in each of these regions. Although this sampling scheme may seem unusual, it allows measurement of faster enhancement (such as that in blood vessels) at times immediately following injection and slower enhancements (for example, that in enhancing ROIs) over the remaining hour. The random scatter of the remaining subjects creates technical difficulties, but it helps in the population-level inference. More specifically, having a random distribution of observation times allows us to build information across subjects about enhancement behaviors over the time frame.

Figure 8. Scanning Times.

Raster plot indicating the differing irregular time grids on which the MR scans are observed. The time of contrast agent injection is indicated by the solid red line and the dashed blue line indicates the time point 85 minutes after injection.

Because the sampling time grid across subjects is irregular, we first interpolate the time series for every brain voxel of every subject. To accomplish this, we simply use linear interpolation within the range of the data and fix values beyond the observed data to those of the nearest data points. This choice is reasonable because the time series display rather simple temporal features and the measurement error is relatively small compared to the enhancement patterns. We take these interpolated values for each subject on an equally spaced time grid, {t₁, …, t_T}, of T = 100 points from 8 minutes before the contrast injection to 83 minutes after the injection. We denote these normalized and interpolated data by f_i(t, v). To check that salient features of the data are not diluted in this process, we review the interpolated scans and confirm that the enhancement properties are still visible. Indeed, all the features (except scanner-related noise) identified in the subject-level analyses for our 10 subjects are preserved after normalization and interpolation.

4.2 Population-Level Analysis

In order to analyze the data from the 10 subjects simultaneously, we stack all time series across all of the subjects and all voxels in the brain, which creates a matrix of size (Σ_i Vi) × T, where I = 10, Σ_i V_i ≈ 16 million, and T = 100. The rows of this data matrix are voxel-specific time series with the same interpretations across subjects and measured at the same time grid. On this matrix, we perform an FPCA analysis [Ramsay and Silverman, 1998, 2002, Greven et al., 2010, Di et al., 2009]. In particular, we treat f_i(·, v) as independent observations with covariance operator Σ(s, t) = Cov[f_i(s), f_i(t)] for s ≤ t. This treats voxels from the same subject and different subjects exchangeably. A consistent estimator of the covariance operator on the time grid is:

$$\widehat{\mathrm{\sum }}(s,t)=\frac{1}{10}\sum _i\frac{1}{V_i}\sum _{v=1}^{V_i}[f_i(s,v)-\overline{f}(s)][f_i(t,v)-\overline{f}(t)]$$ (2)

where s, t ∈ {t₁,…, t_T} and $\overline{f}(t)=\frac{1}{{\sum }_i{V}_i}{\sum }_i{\sum }_{v=1}^{V_i}{f}_i(t,v)$ is the mean normalized intensity at time t across subjects. Due to the size of the data, it is not feasible to simultaneously load data from more than one subject in memory. However, the form in (1) is computable by first obtaining f̄ (t) and then cumulatively summing each subject’s contribution; thus, we may calculate (1) by sequentially loading each subject-specific data file in memory. Since Σ is a T × T (100 × 100) matrix, we can easily continue with the eigendecomposition to find the eigenvectors Φ_j(t), for j = 1, …, T. The first nine of these population-level PCs (PLPCs) are shown in Figure 9 and explain over 99.9% of the variation in time series from all voxels in the 10 brains. We now proceed with the careful study and interpretation of these PLPCs.

Figure 9. Population-Level Principal Components.

The first nine PLPCs plotted over their time grid. The first four PCs explain 99.8% of the variance in voxel time series across the 10 subjects.

4.3 Population-Level Principal Components

The first and second population-level principal components (PLPCs) in Figure 9 are similar to the subject-level principal components (SLPCs) in Figure 3. The first PLPC corresponds to baseline time-independent differences in intensity between voxels, and the second corresponds to the enhancement behavior in large blood vessels. Loadings on the third and fourth PLPCs are high in enhancing lesions. The remaining PLPCs are more difficult to interpret. However, they only explain 0.2% of the total voxel-level time-series variability and may well be due to artifacts such as subject motion.

To better understand the first four PLPCs, we proceed as in the subject-level analysis by producing maps of the loadings in the 3D brain volumes. Figure 10 provides the second through fourth PLPC maps of a sagittal slice for the first subject. Figure 10(a) confirms that the second PLPC captures the blood vessel behavior. The enhancing ROI loads primarily on the third and fourth PLPCs. This is more complex than the subject-level analysis where the enhancement was explained by one SLPC in the majority of cases. To understand this, recall that using the PLPC basis, the time series in each voxel can be expressed as:

$$f_i(t,v)=\sum _{j=1}^T{\xi }_{i,j}(v){\mathrm{\Phi }}_j(t)$$ (3)

where ξ_{i, j}(v) = < f_i(t, v), Φ_j(t) > is the j^th PLPC loading for voxel v in subject i. Thus, a linear combination of the third and fourth PLPCs explains the behavior in the enhancing ROI. The third PLPC starts below baseline and increases gradually over time. This is characteristic of the behavior of voxels in the enhancing lesions. The fourth PLPC shows a similar behavior after a dip around the injection time. The major discrepancy between the third and fourth PLPCs is a temporal shift; the fourth PLPC represents enhancement that peaks about 30 minutes after the contrast injection, whereas the third corresponds to a continual increase over the post-injection period of observation. Combinations of these two PLPCs explain mixtures of such patterns. These first four PLPCs explain more than 99.8% of the variation between all voxels in the 10 brains. As our interest in this paper centers around enhancement in white matter, we do not consider it here. Comparisons of these PLPCs to the SLPCs from the twelve subjects can be found in the Appendix.

Figure 10. PLPC Loading Maps.

Maps indicating the second through fourth PLPC loadings in sagittal slice 58 of the first subject.

We note that there are no parametric assumptions in the principal component-based framework, which is not the case in biophysical models of vascular permeability. In the next section, we use the scores from the population-level techniques described above to discriminate between enhancement patterns using flexible modeling techniques. We further suggest quantitative measures of degree of enhancement, temporal behavior, and spatial properties.

5 Quantification of Lesion Enhancement

In this section, we suggest a framework for quantitatively describing enhancements in enhancing lesion voxels. This framework is based on our 10 subjects and will require validation in larger data sets. In order to quantify the enhancements, we will use the PLPCs and the associated scores, as described in Section 3. As the third and fourth PLPCs accounted for the enhancement properties, we consider loadings of all white-matter voxels on these PLPCs. A scatterplot of these scores for the 10 subjects, indicated in differing colors by subject, can be found in Figure 11.

Figure 11. White Matter Scatterplot.

Scatterplot of the scores from white matter voxels in each of the 10 subjects. The horizontal axis is the score for the third PLPC, and the vertical axis is the score for the fourth PLPC. Each color represents voxels from a different subject.

As the loadings were estimated from the data, they are susceptible to measurement error propagating from noise in the observed intensity data. In principle, to address this problem, measurement error corrected methodologies [Carroll et al., 2006] could be applied. Here, we used a resampling procedure to estimate the reliability of the scores in an ROI from the first subject (details provided in the Appendix). The reliabilities of the first four PLPC scores were estimated to be uniformly above 99.5%. Given the high reliability of the scores in our data, we proceed treating the estimated PLPC scores as fixed.

There is a clear grouping of the scores around the origin (0, 0) for each subject. The “potato-like” shape dominating the center of the distribution is indicative of a bivariate normal distribution. There are also voxels that deviate from the central cluster in all four quadrants. After examining the voxels that deviate in the top-left, bottom-left, and bottom-right quadrants in the raw four-dimensional data, an experienced MS neuroradiologist found that these are all artifacts from patient movement and registration. We thus focus on deviations from the central part of the distribution in the top-right quadrant only.

Each point in the top-right quadrant beyond the central cluster (roughly in the region with ξ_{i, 3}(v) > 5 and ξ_{i, 4}(v) > 0) represents a voxel that enhances according to a mixture of the third and fourth PLPC behaviors. At the subject level, these deviations (visible in Figure 11) tend to be linear arms reaching outward and consisting of voxels from enhancing ROIs inside MS lesions. To locate these enhancements, we first identify the non-enhancing voxels for each subject; the scores associated with these voxels tend to be contained in the central section of the bivariate normal distribution discussed above. For this, we use quantile-based estimation of the parameters of the multivariate normal distribution of the non-enhancing white matter voxels on a subject-by subject basis. For each subject i, we:

1. Choose five points ( ${\xi }_3^{(j)},{\xi }_4^{(j)}$), for j = 1, …, 5, in the central cluster around the origin. To choose these points, we first fit a linear regression of ξ_{i, 4}(v) on ξ_{i, 3}(v) and take the 25th, 50th, and 75th quantiles of the fitted values as the first three points. We then take two more points that are on the line perpendicular to the fitted line and crossing through the median, each of which is one residual standard deviation away from the median.

2. Calculate the empirical distribution of the scores evaluated at each of these points; that is, find ${\widehat{p}}_j=\widehat{P}({\xi }_{i,3}(v)\le {\xi }_3^{(j)},{\xi }_{i,3}(v)\le {\xi }_4^{(j)})$.

3. Minimize the function

   $$\sum _j{\left[{\widehat{p}}_j-\mathrm{\Phi }\left({\xi }_3^{(j)},{\xi }_4^{(j)}\mid \mathit{\mu },\mathrm{\sum }\right)\right]}^2,$$ (4)

   in terms of the parameters μ, Σ, where Φ (· | μ, Σ) denotes the distribution function of a multivariate normal with mean μ and covariance matrix Σ.

The algorithm above gives us an approximation to the distribution of non-enhancing white matter voxels. This approximation method is especially useful in our scenario as it is not sensitive to the arm-shaped deviations in the top-right quadrant of Figure 11 that represent the enhancement behaviors of interest. Although the regression does use these points in the estimation, their influence is low as the central mass consists of many more points. The results from this fit are shown in Figure 15 in the Appendix for the first two subjects. This allows us to tackle one goal of our analysis, specifically to construct a hypothesis test to determine whether a particular white-matter voxel is enhancing.

The above method defines the distribution of the third and fourth PLPC scores in non-enhancing white matter for the individual. We then estimate the probability of observing scores as or more extreme than those observed for the voxel of interest using the fitted bivariate normal approximation. The resulting p-value for each voxel allows us to judge whether there is evidence of enhancement. In Figure 12, we show maps of transformed p-values for the first two subjects in the same sagittal slices in Figure 2. Purple areas are those with very low p-values and thus suggest the presence of enhancement.

Figure 12. P-value Maps.

Maps of transformed (negative log) p-values in sagittal slices from the two first subjects. Purple areas are those with very low p-values and thus denote candidate enhancing voxels. The light blue region indicates non-enhancing white matter.

In order to partition the white matter into voxels that are non-enhancing and those that are enhancing for each subject, we set a threshold for the p-values calculated above. For our analysis, we chose this cutoff to be 10⁻¹⁵. We then partition the enhancing voxels in each subject by grouping spatially connected voxels and refer to each connected set of enhancing voxels as an enhancing ROI.

An important note concerning our FPCA-based procedure is that it does not use prior knowledge of spatial correlations. Our approach does, however, incorporate this information in the final steps as we map our results back into the 3D brain volume, and the voxel-level results are interpreted in the context of their spatial location. Although this working assumption of independence between voxels in clearly violated as enhancing and non-enhancing regions tend to occur in clusters, it is useful as it allows for easily interpreted results that depict and quantify the rich spatial information.

In Figure 13, we show the enhancing ROIs (as determined by the above procedure) in the enhancements from the first two subjects as depicted in Figure 2. We calculate three simple summary measures to describe the enhancements in each of these subjects. First, we take the median norm (Euclidean distance from the origin in the (ξ_{i, 3}(v), ξ_{i, 4}(v)) planes) of the enhancing candidate voxels. This measures the magnitude of the enhancement, which is related to the maximum intensity of the enhancing voxels. In Figure 13, we show this as the radius of the gray circle; subjects with larger circles have more prominent enhancements. The second measure is the slope β_{3, 4} of the regression (solid red line) of ξ_{i, 4}(v) on ξ_{i, 3}(v). This measures the velocity of the enhancement since voxels that load more on the fourth PLPC peak in intensity earlier than those that load primarily on the third PLPC. Thus, enhancements with steeper (larger) slopes tend to enhance earlier (subject 1), whereas those with shallower (smaller) slopes enhance more slowly (subject 2). Third, we calculate the R² for this regression fit, which is also given in Figure 13. This measures the variance of the observed scores around the linear fit, which is a proxy for the spatiotemporal variation in intensity patterns across the ROI. Enhancements with larger values of R², as in Figure 13(a), are more homogeneous, meaning that the enhancement time course is similar across voxels. On the other hand, enhancements with smaller R², as in Figure 13(b), are more heterogeneous and for the most part appear ring-shaped. Overall, these three measures summarize the magnitude, velocity, and spatiotemporal variation of lesion enhancement.

Figure 13. Within-ROI PLPC Loading Scatterplots.

Scatterplots of the third PLPC versus fourth PLPC loadings in enhancing voxels in enhancing ROIs in the first two subjects. The color of the points indicates the distance from that voxel to the nearest boundary of the enhancing ROI. The red lines indicate the linear regressions of the fourth PLPC on the third PLPC, and the R² for these fits are indicated in the top right of each plot. The gray circles have diameters equal to the median Euclidean norms of the points in the depicted planes and measure the magnitude of the enhancements.

Based on our empirical observation that lesions tend to enhance either centripetally (from the periphery to the center) or centrifugally (from the center to the periphery), we develop a fourth measure to quantify the temporal enhancement dynamics within lesions. We first calculate the distance from each voxel to the boundary of the ROI, which we denote d(v). We then consider the relationship between d(v) and the principal component loadings ξ_{i, 3}(v) and ξ_{i, 4}(v). The values of these loadings must be interpreted with caution, however; although for the most part voxels with higher fourth PLPC loadings enhance earlier, a high fourth PLPC loading may also indicate more intense enhancement. We therefore consider the proportion of enhancement in each voxel from the third and fourth PLPCs and the relationship between these quantities and d(v), which is shown in the first column of Figure 14 for the enhancing ROI from the first two subjects. (Note that the points in these plots fall in discrete clusters due to the coarse resolution of the images relative to lesion size.) This relationship is captured in linear fits to these quantities:

$$\frac{{\xi }_{i,4}{(v)}^2}{{\xi }_{i,3}{(v)}^2+{\xi }_{i,4}{(v)}^2}={\beta }_{0,4}+{\beta }_{d4}d(v)+{\epsilon }_4(v)$$ (5)

$${\xi }_{i,3}{(v)}^2+{\xi }_{i,4}{(v)}^2={\beta }_0+{\beta }_{d}d(v)+\epsilon (v)$$ (6)

Figure 14. Distance to Boundary Scatterplots.

Scatterplots of distance to boundary versus the proportion of fourth PLPC enhancement and total enhancement magnitude in enhancing voxels in enhancing ROIs in the first two subjects. The blue lines indicate the fit of corresponding linear regressions.

Because a voxel that loads relatively more on the fourth PLPC than on the third PLPC has earlier enhancement, we interpret β_d4 > 0 as evidence for centrifugal enhancement, while β_d4 < 0 is indicative of centripetal enhancement. Using this regression framework (of Equation 5), we test the hypotheses that β_d4 > 0 or β_d4 < 0, and the p-values from these tests are also presented in Figures 14(a) and 14(c) as p_−d4 and p_d4 respectively. From these plots, we can see that there is a centripetal enhancement in both the ROIs under consideration in Figure 14.

In the second column, we present the data and fit from Equation 6, which examines spatial patterns in total enhancement magnitude. It is clear from Figure 14(b) that the center of the ROI in subject 1 is enhancing the most in magnitude. In subject 2, however, this is not the case; Figure 14(d) shows that some areas of the boundary of the ROI enhance more than the center (this is also apparent in Figure 12(b)). Indeed, the linear fit of model 6 is not ideal in this particular case, and perhaps a quantile regression-based approach would be more helpful. On average, however, there is a trend of more enhancement closer to the center of the ROI as captured by the estimated β_d of 50 (p < 0.01). The units of β_d (and similarly β_d4p) are in proportion per unit increase in distance (in our case, 1mm). This may be standardized in terms of the radius of the enhancing ROI, for example, in order to allow comparisons between lesions of different sizes captured using different resolutions. Similarly, transformations of variables and more complex models for Equations 5 and 6 may be considered, although for the goals of this analysis the above methods proved sufficient in our 10 subjects.

6 Results

We applied the above methodology to the 10 subjects in this study. We used the thresholding procedure was used to detect enhancing lesions within the white matter as segmented by the Lesion-TOADS method. Lesions smaller than 8 mm³ (the nominal volume of an acquired voxel) in volume were excluded as they were indistinguishable from noise. In each enhancing ROI, we calculated the magnitude, β_{3, 4} (the slope of the regression of loadings on PLPC 4 against loadings on PLPC 3), and the corresponding R² (Table 2). For enhancing lesions sufficiently large to have interior (non-boundary) voxels, we also calculated the distance-based spatiotemporal indices. Summaries of these measures are also presented in Table 2.

Table 2.

Results from analysis of DCE-MRI data for 10 subjects with RRMS or PPMS.

Subject ID	Number of Enhancements	Magnitude (median (IQR))	β3, 4 (median (IQR))	R2 (median (IQR))	βd4.p (median (IQR))	βd (median (IQR))/100	# Centripetal Enhancements	# Centrifugal Enhancements
1	4	5.6 (4.6,6.9)	0.29 (0.27,0.30)	0.66 (0.59,0.73)	−1.5(−1.7, −0.6)	24 (17,54)	2	0
2	2	6.5 (5.3,7.7)	0.15 (0.14,0.16)	0.16 (0.13,0.19)	0.03 (−0.2,0.3)	31 (22,41)	1	0
3	0	0	NA	NA	NA	NA	0	0
4	0	0	NA	NA	NA	NA	0	0
5	0	0	NA	NA	NA	NA	0	0
6	12	3.9 (3.4,5.1)	0.36 (0.27,0.40)	0.51 (0.32,0.66)	−0.8 (−8.2,2.4)	18 (13,38)	4	2
7	3	4.9 (4.0,5.7)	0.22 (0.21,0.33)	0.58 (0.49,0.60)	−0.07 (−0.2,2.4)	34 (20,36)	0	0
8	3	3.9 (3.3,3.9)	−0.34 (−0.42, −0.03)	0.43 (0.29,0.55)	−0.041	20	0	2
9	0	0	NA	NA	NA	NA	0	0
10	0	0	NA	NA	NA	NA	0	0

The subjects had between 0 and 12 enhancing lesions, and the median magnitude of the enhancements varied between 3.9 and 5.6 units. The median slope β_{3, 4} ranged between 0.15 and 0.36, except in subject 8 who had a negative estimated slope. In this subject, the small volume of the enhancing lesions made the estimation of this slope imprecise. The median R² ranged between 0.16 in subject 2 to 0.66 in subject 1. The estimated β_d4 and β_d are presented in Table 2. In the two rightmost columns, the number of significantly centripetally and centrifugally enhancing lesions are presented (calculated by testing β_d4 < 0 and β_d4 > 0, respectively, in each lesion with a type I error rate of 0.05).

7 Conclusion

In this paper, we have developed techniques for the analysis of DCE-MRI scans of MS patients. Using FPCA techniques, we have studied the voxel-level behaviors of MR intensities that capture permeability in new MS lesions. These techniques allow us to identify and quantify the dynamics of vascular enhancement in these lesions, which will enable a better understanding of BBB opening in this disorder.

A key step in this analysis is the normalization of the data from each subject in order for inference to be meaningful at the population level. Our simple normalization procedure is internal and does not depend on data from other subjects or external quantities. It emphasizes discrepancies in white matter, the very discrepancies that we wish to study, but it does not compress the data (that is, the structure of the data is conserved and no information is lost). Our analytical methodology, however, is general and valid after any alternate normalization scheme is applied.

Several complexities of DCE-MRI data make their statistical analysis difficult. The first is that the scans are large; although they may be stored on a hard disk in less than 1Gb each, interpreted statistical packages, without substantial novel programming, require additional memory. This makes the simultaneous analysis of many subjects difficult even with modern statistical computing facilities. In order to summarize these vast data, innovative exploratory data analysis and dimension reduction techniques are key. Our methods achieve this while remaining scalable to large studies with hundreds of patients observed at multiple visits.

Our methods are also automatic in that they do not require the manual construction of masks describing the locations where enhancement occurs. In this paper we did, however, use the TOADS white matter segmentation which suffered from some minor errors, mainly that the masks included a few voxels outside of the white matter. Erroneous ROI recognized by our methods were removed by manual inspection of the locations in the FLAIR images. One may alternatively consider analyzing all brain voxels in a similar fashion to avoid the white matter segmentation, but in that case meningeal enhancement might result in false positives.

Simple parametric models, motivated by our nonparametric principal components-based analysis, can be obtained. Specifically, we may model:

$$Y(t,v)=f(t;\mathit{\theta })+\epsilon (v)$$

where θ is low-dimensional and ε (v) is an (independent) error process. These models may be fit using, for example, nonlinear least squares estimation. They will be easy to use and will be independent of any reference population.

Our methods are not designed to supplant parametric models based on pharmacokinetics [Tofts, 1997]. Such models are very useful for understanding tissue biophysics and in particular the interaction between tissue compartments. Rather, we have built our methods to allow us to generate and address hypotheses on both voxel and lesion levels about the spatiotemporal properties of tissue enhancement, and the methods could also be applied to study enhancement outside new MS lesions. For example, in Section 4, we derive an approximation to the distribution of non-enhancing white matter voxels in each of the subjects. Although this is sufficient to enable us to identify enhancing lesions, which was the focus of this study, we could also investigate these non-enhancing voxels more closely. This could be accomplished using the techniques we have presented by considering the union of the central clusters in the (ξ_{i, 3}(v), ξ_{i, 4}(v)) plane. It also provides a natural framework for the quantification of spatial features in enhancement as described in Section 5.

This work opens several directions for future studies, including extension of the analysis to many more subjects, as well as the characterization of differences between brain regions (e.g., white vs. gray matter). The methods we have presented are computationally scalable to these situations, and based on our initial findings we expect the number of principal components that characterize enhancement to be small even in larger studies. Such studies could determine, for example, whether lesions within one subject will be more similar in enhancement patterns than those from different subjects.

The methods can also be extended to serial studies of enhancing lesions from the same subjects. Our preliminary work has shown that enhancing white-matter lesions may evolve over time, changing their spatiotemporal enhancement characteristics. This process may be modeled through the measures developed in this paper. For example, the magnitude of enhancement in a lesion ${({\xi }_3^2+{\xi }_4^2)}^{\frac{1}{2}}$ may decrease over time. In addition, we have found instances of centrifugally enhancing lesions evolving into centripetal enhancements. This may be assessed by extending the model 5 to:

$$\frac{{\xi }_{i,4}{(v,t)}^2}{{\xi }_{i,3}{(v,t)}^2+{\xi }_{i,4}{(v,t)}^2}={\beta }_{0,4}(t)+{\beta }_{d4.p}(t)d(v)+{\epsilon }_4(v,t)$$

where the t denotes the date of a study visit. Enhancement in new MS lesions tend to diminish after 4–8 weeks, while other enhancing lesions may develop. Our methods can also be extended to address this problem.

Figure 15. Bivariate Approximation Results.

Results from the bivariate fitting algorithm for the first and second subjects. The fitted central quantile ellipsoids at the median and 75th, 95th, 99th, 99.9th, and 99.9999th percentiles are indicated in darkening shades of blue. The gray dots indicate observed scores in white matter voxels.

Research Highlights.

• We study DCE-MRI scans in 10 subjects with multiple sclerosis (MS)

• We provide a statistically principled platform for the quantification of enhancement

• We introduce spatiotemporal models of lesion enhancement within and between subjects

• We generate a set of hypotheses for cross-sectional and longitudinal analysis.

Appendix

Results from Bivariate Fitting Procedure

Comparing the Subject-level and Population-level Analyses Results

Since there are obvious similarities between the SLPCs and the PLPCs, we consider their comparisons. In order to make these comparisons, we first repeat the FPCA procedure from Section 2 on the normalized and smoothed data for each subject. This gives twelve new bases for ℛ^T in addition to the PLPC basis. We now quantify discrepancy; let ${\phi }_i^{(k)}$ denote the i^th SLPC from the k^th subject and Φ_j denote the j^th PLPC. We begin by calculating the projection of ${\phi }_i^{(k)}$ on Φ_j, say ${\psi }_{i,j}^{(k)}$. Then, the norm of the difference ${\phi }_i^{(k)}-{\psi }_{i,j}^{(k)}$ measures the discrepancy between the vectors. We calculated this measure for each PLPC and each SLPC for each subject, and results are shown in Figure 16. Each rectangle corresponds to a comparison, and the brightness of the rectangle represents the discrepancy measure; darker rectangles indicate similarity between the components and brighter rectangles indicate major differences. In all of the subject-level analyses, the first SLPC is very similar to the first PLPC. The second SLPCs also tends to be very similar to the second PLPC. The third SLPCs, which generally correspond to the behavior in the enhancing ROI, are explained by the third and fourth PLPCs as noted above in Section 4. This chart helps make these comparisons more concrete and allows us to better understand the differences between enhancement behaviors at the population level.

Figure 16. SLPC versus PLPC Comparisons.

Comparison between the first several population-level and subject-level PCs for each subject. Intensity in each rectangle indicates similarity between the corresponding population-level and subject-level PCs.

Simulation Studies: One-Dimensional

To validate our methods, we performed two simulation studies; the first was a simple two-dimensional example, and the second was a more complex four-dimensional example that approximated the behavior of the DCE-MRI data. In the 2D example, we considered observations on a one-dimensional space over a temporal dimension. In each simulation we observed data on a spatial grid x₁ = 1, x₂ = 2, …, x_L = L of length L = 1000 over a time grid t₁ = 1, …, t_T = T of length T = 100. We simulated noise and stipulated spatially-correlated enhancement over time in simulated ROIs. We then used our FPCA-based methods to identify and quantify these enhancement behaviors. We simulated data, for b = 1, …, B = 50 as follows:

1. We generated white noise independently at each location and each time point:

   $${\epsilon }_b(x,t)\sim N(0,{\sigma }^2)$$
2. We sampled the number of enhancing ROI N_b randomly:

   $$N_b\sim \text{Poisson}({\lambda }_N)$$
3. We randomly assigned half of the enhancements to the temporal behavior:

   $$f_1(t)=\{\begin{array}{l}0\text{if}t<0\hfill \\ t/2\text{if}0\le t<20\hfill \\ 1\text{if}t\ge 20\hfill \end{array}$$
   and the remainder to:

   $$f_2(t)=\{\begin{array}{l}0\text{if}t<0\hfill \\ t/10\text{if}t\ge 0\hfill \end{array}$$

4. For each enhancement i = 1, …, N_b:

   1. We sampled the radii of enhancements randomly:

      $$r_{i,b}\sim \text{Poisson}({\lambda }_r)$$

   2. We sampled the center, c_i, randomly from the locations x₁, …, x_L.

   3. We assigned enhancement i one of two possible enhancement behaviors. Then, within the enhancement i, we made each voxel enhance by setting the time series to:

      $$Y_b(x,t)=\frac{1}{d(x,i)}·f^{(i)}(t)+{\epsilon }_b(x,t)$$

      where d(y, i) denotes the distance from the location x to the center of enhancement i, and f⁽ⁱ⁾ ∈ {f₁, f₂} denotes the assigned temporal behavior.

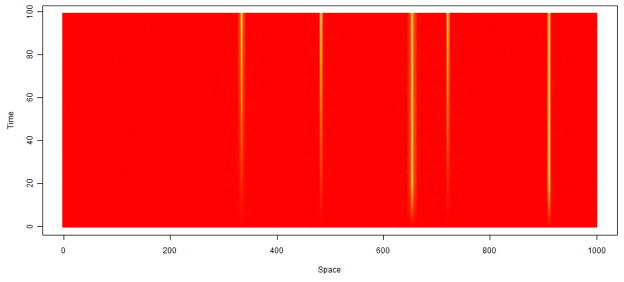
An example of the observed data is shown in Figure 17, where color indicates function value along the locations on the horizontal axis, and time is shown on the vertical axis. In this example, there are 5 enhancements which are depicted in yellow and orange in later times. Some of the enhancements are visible earlier in time than others; these correspond to the f₁ enhancement behavior.

Figure 17. 2D Simulated Data.

Example of 2D simulated data, where spatial location is shown on the horizontal axis and time on the vertical axis. Color indicates the intensity value with red denoting lower intensity and yellow higher intensity.

We applied the methodology described in Sections 3 through 5, and the observed principal components across the 50 simulations are shown in Figure 18(a) for one set of parameter choices. As some simulations had only one enhancement and thus only one enhancement pattern, these plots are difficult to read. To clarify the results, we split the simulations in Figures 18(b) and 18(c) by the number of enhancements simulated in each trial. From Figure 18(b), it is clear that the FPCA analysis revealed the true enhancement behavior f₁ or f₂ in each trial with only one simulated enhancement. In the case where both behaviors were imposed in the trial, Figure 18(c) shows the stability of the estimated PCs. Note that although these behaviors appear to differ from the simulated enhancement shapes, the FPCA methodology forces the PCs to be orthogonal. In Figure 19, we show that these are simply rotated versions of the parametric functions f₁ and f₂; the black lines indicate the true underlying enhancement behaviors and the red show the projections of the first two PCs onto these functions. To assess the spatial performance of our method, we estimated the number of enhancements that we captured using the multivariate normal fitting on the first and second principal components, using a threshold on the fitted p-value of < 10⁻⁵⁰ in more than two consecutive locations to define an enhancement. We compared these spatially with the true data-generating enhancement locations to estimate the ROI-level sensitivity of our method and the number of simulated scans with fictitious ROI estimated by our method, and the results are shown in Tables 3 and 4, respectively.

Figure 18. Estimated PCs from 2D Simulations.

The first three functional principal components for the 50 simulated datasets superimposed upon one another for the choice of noise parameter σ = 0.1, enhancement incidence rate of λ_N = 3, and enhancement radius rate parameter of λ_r = 3.

Figure 19. Comparison of Estimated PCs from 2D Simulations.

Comparison of the estimated enhancement behavior, calculated by projecting the first two PCs from Figure 18(c) onto the true enhancement functions f₁ and f₂. Black lines indicate the truth, and red lines indicate the estimated behaviors across the trials.

Table 3.

Results from two-dimensional simulations: estimated sensitivity of the method at the ROI-level. This was calculated as the number of estimated ROI that overlap a true enhancement divided by the number of true enhancements for differing values of the noise parameter σ, the enhancement incidence rate λ_N, and the radius parameter λ_r.

		λN				λN
σ = 0.1		3	5	σ = 0.5		3	5
λr	3	94%	97%	λr	3	70%	70%
	5	98%	98%		5	65%	66%

Table 4.

Results from two-dimensional simulations: estimated specificity of the method at the subject-level. This was calculated as the number of subjects without estimated ROI that do not overlap a true enhancement divided by the number of subjects for differing values of the noise parameter σ, the enhancement incidence rate λ_N, and the enhancement radius parameter λ_r.

		λN				λN
σ = 0.1		3	5	σ = 0.5		3	5
λr	3	96%	94%	λr	3	94%	90%
	5	96%	98%		5	96%	88%

Simulation Studies: Three-Dimensional

To assess the performance of our methodology in a more realistic simulation study, we first downsampled brain and white-matter masks from subject 1 from our data set to 91×109×91. Using this as our canvas, we then simulated enhancement behaviors for replicates b = 1, …, B = 50, in white matter voxels v ∈ V_WM ⊂ ℛ³ over the time grid t₁ = 1, …, t_T = 100. Specifically, for each b:

1. We generated noise in each voxel and each time point:

   $$\begin{array}{r}{\epsilon }_b^{\ast }(v,t)\sim N(I(v),{\sigma }^2)\\ {\epsilon }_b^{\ast }(v)\sim N(I(v),{\sigma }_V^2)\\ {\epsilon }_b(v,t)={\epsilon }_b^{\ast }(v,t)+{\epsilon }_b^{\ast }(v)\end{array}$$

   where I(v) is the indicator that voxel v is in the white matter.

2. We sampled the number of enhancements N_b randomly:

   $$N_b\sim \text{Poisson}({\lambda }_N)$$
3. We randomly assigned half of the enhancements to the the temporal behavior:

   $$f_1(t)=\{\begin{array}{l}0\text{if}t<0\hfill \\ t/2\text{if}0\le t<20\hfill \\ 1\text{if}t\ge 20\hfill \end{array}$$
   and the remainder to:

   $$f_2(t)=\{\begin{array}{l}0\text{if}t<0\hfill \\ t/10\text{if}t\ge 0\hfill \end{array}$$

4. For each enhancement i = 1, …, N_b:

   1. We sampled the radius of enhancements randomly:

      $$r_{i,b}\sim \text{Poisson}({\lambda }_r)$$

   2. We sampled the center, c_i, randomly from the white matter voxels v ∈ V_WM

   3. We assigned enhancement i one of two possible enhancement behaviors to all white matter voxels within the radius r_i of the center c_i. Then, we made each voxel in enhancement i enhance by setting:

      $$Y_b(v,t)=\frac{1}{d(v,i)}·f^{(i)}(t)+{\epsilon }_b(v,t)$$

      where d(y, i) denotes the distance from the voxel v to c_i, and f⁽ⁱ⁾ ∈ {f₁, f₂} denotes the assigned temporal behavior.

In this example, the simulated data have more complex features; we depict an example in Figure 20. Applying the FPCA techniques described above, the principal components for each simulated scan were calculated, and these are shown in Figure 21 for a particular choice of parameters (σ = 0.1, λ_N = 5, λ_r = 5). Other parameter choices yielded similar results. The first principal component is a vertical shift up or down in the average intensity at each voxel, attributable to both the voxel-specific noise process ${\epsilon }_b^{\ast }(v)$ and the differences stipulated between white and gray matter. The second and third principal components describe the enhancement and are very similar to those estimated in the 2D example. We thus robustly fit a bivariate normal distributions to the non-enhancing central clusters in their respective score space and thresholded the fitted voxel-level p-values at 10⁻⁵⁰. As each case in these simulations consisted of approximately 200,000 as opposed to 1.6 million voxels of the observed data, we chose the 5 points for our quantile-based procedure to be closer together, but the fitting procedure was identical. As each case in these simulations consisted of only 1000 spatial locations as opposed to 1.6 million voxels in the observed data, we chose the 5 points for our quantile-based procedure to be closer together, but the fitting procedure was identical.

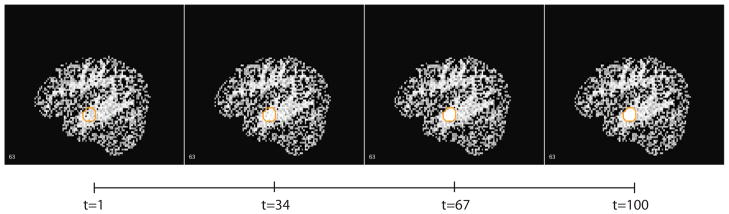
Figure 20. 4D Simulated Data.

Example of a sagittal slice from a simulation with parameter choices σ = 0.1, λ_N = 3, and λ_r = 3, shown at t=1, 34, 67, and 100. The boundaries of simulated enhancing lesions are shown in orange.

Figure 21. Estimated PCs from 4D Simulations.

First four principal components from the 50 simulated 4D trials with parameter choices σ = 0.1, λ_N = 5, and λ_r = 5 superimposed.

To assess the spatial performance of our methods, we then compared the estimated enhancing ROI to the true ROI, and the results are shown in Table 5. The left side shows shows the performance measures for the choice of noise parameter σ motivated by the observed data in our study. Under these realistic parameter choices, the method performed well. We also increased σ to 0.5 to show how our method performs when there is significantly more noise, and these results are shown to the right of the table. In these more noisy scenarios, the performance suffered but the method still yielded useful results. For all of the parameter choices, there were no fictitious enhancements detected by the method; that is, there were no false positives. Finally, we considered cases in which there was no simulated enhancement and all variation was from the noise process ε_b(v, t), and for both choices of σ = 0.1 and 0.5, our method had no false positives in the 50 simulated cases.

Table 5.

Results from four-dimensional simulations: estimated sensitivity of the method at the ROI-level. This was calculated as the number of estimated ROI that overlap a true enhancement divided by the number of true enhancements for differing values of the noise parameter σ, the enhancement incidence rate λ_N, and the radius parameter λ_r.

		λN				λN
σ = 0.1		3	5	σ = 0.5		3	5
λr	3	98%	98%	λr	3	87%	81%
	5	100%	99%		5	86%	85%

Reliability of the PLPC Scores

To investigate the reliability of the scores, we used a resampling-based procedure in a region of interest of V* = 1000 voxels from the first subject including part of the enhancing ROI shown in Figure 4. We denote the observed data in this ROI by:

$$Y_i(t,v)=Y_{i,0}(t,v)+{\epsilon }_{0,i}(t,v)$$

And the observed PLPC scores:

$${\xi }_{ij}(v)=<Y_i(t,v),{\mathrm{\Phi }}_j(t)>$$

To estimate the reliability:

1. We estimated the noise in the scan by taking a random sample of 1000 voxels from the brain in this subject. Then, we extracted the pre-contrast intensity time series at these voxels and subtracted the mean of each time series. The residuals from this procedure, which we call estimated errors, are assumed to be independent draws from a distribution that approximates the measurement error distribution of ε_{0, i}(t, v).

2. We created two new simulated datasets in the ROI:

   $$\begin{array}{l}{Y}_{i,1}(t,v)=Y_i(t,v)+{\epsilon }_{i,1}(t,v),\text{and}\\ Y_{i2}(t,v)=Y_i(t,v)+{\epsilon }_{i,2}(t,v)\end{array}$$

   Where ε_{i, 1}(t, v) and ε_{i, 2}(t, v) were sampled randomly from the estimated errors.

3. We calculated the scores ξ_{ij, 1}(v) and ξ_{ij, 2}(v) for j = 1, …, 5

4. We estimated the reliability by

   $$1-\widehat{\lambda }=1-\frac{{\sum }_v{[{\xi }_{ij,1}(v)-{\xi }_{ij,2}(v)]}^2/[2·(V^{\ast }-1)]}{\widehat{\mathit{Var}}({\xi }_{i3,1}(v))}$$

Using the above procedure for the ROI described above, we estimated the reliability of the first four PLPC scores. The results from this analysis may be found in Table 6. As all of these are above 99.5%, the measurement error is minimal and thus the estimated scores are treated as fixed in the quantifications in Section 5.

Table 6.

Estimated reliability of the scores on the first four PLPCs in an ROI from the first subject.

	PLPC 1	PLPC 2	PLPC 3	PLPC 4
Reliability (%)	100	99.5	100	99.7