Reinforcement Learning Strategies for Clinical Trials in Non-small Cell Lung Cancer

Summary

Typical regimens for advanced metastatic stage IIIB/IV non-small cell lung cancer (NSCLC) consist of multiple lines of treatment. We present an adaptive reinforcement learning approach to discover optimal individualized treatment regimens from a specially designed clinical trial (a “clinical reinforcement trial”) of an experimental treatment for patients with advanced NSCLC who have not been treated previously with systemic therapy. In addition to the complexity of the problem of selecting optimal compounds for first and second-line treatments based on prognostic factors, another primary goal is to determine the optimal time to initiate second-line therapy, either immediately or delayed after induction therapy, yielding the longest overall survival time. A reinforcement learning method called Q-learning is utilized which involves learning an optimal regimen from patient data generated from the clinical reinforcement trial. Approximating the Q-function with time-indexed parameters can be achieved by using a modification of support vector regression which can utilize censored data. Within this framework, a simulation study shows that the procedure can extract optimal regimens for two lines of treatment directly from clinical data without prior knowledge of the treatment effect mechanism. In addition, we demonstrate that the design reliably selects the best initial time for second-line therapy while taking into account the heterogeneity of NSCLC across patients.

1. Introduction

There has been significant recent research activity in developing therapies tailored to each individual. Finding such therapies in settings involving multiple decision times is a major challenge. For example, in treating advanced non-small cell lung cancer (NSCLC), patients typically experience two or more lines of treatment, and many studies demonstrate that three lines of treatment can improve survival for patients (Socinski and Stinchcombe, 2007). Discovering tailored therapies for these patients is a very complex issue since effects of covariates (such as prognostic factors or biomarkers) must be modeled within the multistage structure. In this article, we present a new kind of NSCLC clinical trial, based on reinforcement learning methods from computer science, that finds an optimal individualized regimen at each decision time as a function of available patient prognostic information. This new kind of trial extends and refines the “clinical reinforcement trial” concept developed in Zhao et al. (2009) to the NSCLC setting with right-censored survival data.

For NSCLC, first-line treatment primarily consists of doublet combinations of platinum compounds (cisplatin or carboplatin) with gemcitabine, pemetrexed, paclitaxel, or vinorelbine (Sandler et al., 2006). These drugs modestly improve the therapeutic index of therapy, but no combination appears to be clearly superior. More recently, the addition of bevacizumab, a monoclonal antibody against vascular endothelial growth factor (VEGF), to carboplatin and paclitaxel has been shown to produce higher response rate and longer progression-free survival and overall survival times (Sandler et al., 2006). However, this phase III study was only designed to investigate patients with histologic evidence of non-squamous cell lung cancer. Therefore, in first-line treatment of NSCLC, a very important clinical question is what tailored treatment to administer based on each individual’s prognostic factors (including e.g. patient histology type, smoking history, VEGF level, etc.).

All patients with advanced NSCLC who initially receive a platinum-based first-line chemotherapy inevitably experience disease progression. Approximately 50–60% of patients on recent phase III first-line trials received second-line treatment (Sandler et al., 2006). Similar to the first-line regimen, three FDA approved second-line agents (docetaxel, pemetrexed, and erlotinib) appear to have similar response and overall survival efficacy but very different toxicity profiles (Ciuleanu et al., 2008; Shepherd et al., 2005). The choice of agent should depend on a number of factors, including e.g. toxicity from previous treatments and the risk for neutropenia. A better understanding of prognostic factors in the second-line setting may allow clinicians to better select second-line therapy and lead to better designed second-line trials.

The current standard treatment paradigm is to initiate second-line therapy at the time of disease progression. Recently, two phase III trials have investigated other possible timings of initiating second-line therapy (Fidias et al., 2007; Ciuleanu et al., 2008). Both of these trials reveal a statistically significant improvement in progression-free survival and a trend towards improved survival for the earlier use of second-line therapy. However, the overall survival effect is not significant. Stinchcombe and Socinski (2008) claim that even under the best of circumstances not all patients will benefit from early initiation of second-line therapy. Hence, in addition to the difficulty of discovering individualized superior therapies in second-line treatment, another primary challenge is to determine the optimal time to initiate second-line therapy, either to receive treatment immediately after completion of platinum-based therapy, or to delay to another time prior to disease progression, whichever results in the largest overall survival probability.

Some patients who maintain a good performance status and tolerate therapy without significant toxicities will receive third-line therapy (Stinchcombe and Socinski, 2008). Since there is only one FDA approved agent (Erlotinib) available for third-line treatment, we restrict our attention hereafter to first-line and second-line only.

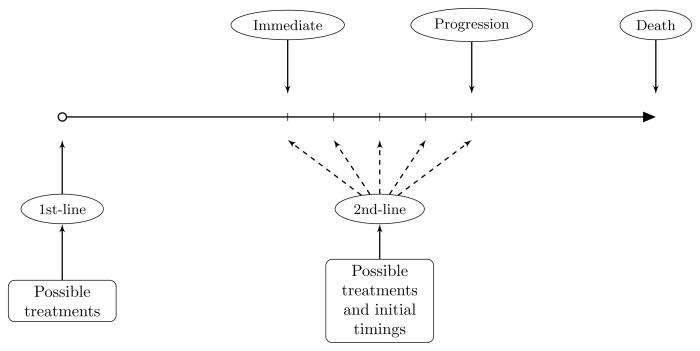
Figure 1 illustrates the treatment plan and clinically relevant patient outcomes. Given the noncurative nature of chemotherapy in advanced NSCLC, we use the overall survival time as the primary endpoint. The primary scientific goal of the trial is to select optimal compounds for first and second-line treatments as well as the optimal time to initiate second-line therapy based on prognostic factors yielding the longest average survival time. Our design proposed in this article is based on a reinforcement learning method, called Q-learning, for maximizing the average survival time of patients as a function of prognostic factors, past treatment decisions, and optimal timing. Zhao et al. (2009) introduced the clinical reinforcement trial concept based on Q-learning for discovering effective therapeutic regimens in potentially irreversible diseases such as cancer. The concept is an extension and melding of dynamic treatment regimes in counterfactual frameworks (Murphy, 2003; Robins, 2004) and sequential multiple assignment randomized trials (Murphy, 2005a) to accommodate an irreversible disease state with a possible continuum of treatment options. This treatment approach falls under the general category of personalized medicine. The generic cancer application developed in Zhao et al. (2009) takes into account a drug’s efficacy and toxicity simultaneously. The authors demonstrate that reinforcement learning methodology not only captures the optimal individualized therapies successfully, but is also able to improve longer-term outcomes by considering delayed effects of treatment. Their approach utilizes a simple reward function structure with integer values to assess the tradeoff between efficacy and toxicity. In the targeted NSCLC setting, however, this simplistic approach will not work due to the choice of overall survival time as the net reward, and new methods are required.

Figure 1.

Treatment plan and therapy options for an advanced NSCLC trial.

Our proposed clinical reinforcement trial for NSCLC involves a fair randomization of patients among the different therapies in first and second-line treatments, as well as randomization of second-line initiation time. This design enables estimation of optimal individualized treatment regimes defined in counterfactual settings (cf. Murphy, 2005a). Additionally, reinforcement learning is used to analyze the resulting data. In order to successfully handle the complex fact of heterogeneity in treatment across individuals as well as right-censored survival data, we modify the support vector regression (SVR) approach (Vapnik et al., 1997) within a Q-learning framework to fit potentially nonlinear Q-functions for each of the two decision times (before first line and before second line). In addition, a second, confirmatory trial with a phase III structure is proposed to be conducted after this first trial to validate the optimal individualized therapy in comparison to standard care and/or other valid alternatives.

The remainder of this article is organized as follows. In Section 2, we provide a detailed description of the patient outcomes and Q-learning framework, followed by the development of a new form of SVR, ε-SVR-C, for estimating Q-functions with right-censored outcomes. The NSCLC trial conduct and related computational issues are presented in Section 3. In Section 4, we present a simulation study, and we close with a discussion in Section 5.

2. Reinforcement Learning Framework

2.1 Patient Outcomes

Let t₁ and t₂ denote the decision times for the first and second treatment lines, respectively. After initiation of first-line chemotherapy, the time to disease progression is denoted by T_P. t₂ is also the time at the completion of first-line treatment, which is a fixed value usually less than T_P and determined by the number of cycles delivered in the first line of chemotherapy. We will assume for simplicity that T_P ≥ t₂ with probability 1. Denote the targeted time after t₂ of initiating second-line therapy by T_M. Thus, according to the description of the treatment plan in Section 1, the actual time to initiate the second line is (t₂ + T_M ) ∧ T_P, and the gap between the end of the first line and the beginning of the second line is T_M ∧ (T_P − t₂), where ∧ denotes minimum. At the end of first-line therapy, t₂, clinicians make a decision about the target start time T_M. We let T_D denote the time of death from the start of therapy (t₁), i.e., the overall survival time, truncated if needed at the maximum follow-up time τ.

Because of the possibility of right censoring, we denote the patient’s censoring time by C and the indicator of censoring by δ = I(T_D ≤ C). We will assume for now, however, that censoring is independent of both the death time and the patient covariates, as is often realistic when patients are approximately similar across accrual time and censoring is due primarily to administrative reasons. For convenience, we let T₁ = T_D ∧ t₂ and Y_D = I(T_D ∧ C ≥ t₂), and denote T₂ = (T_D − t₂)I(T_D ≥ t₂) = (T_D − t₂)I(T₁ = t₂) and C₂ = (C − t₂)I(C ≥ t₂). Note that T_D = T₁ + T₂, where T₁ is the years of life lived in [t₁, t₂] and T₂ is the years of live lived after t₂. We can also define the total follow-up time T⁰ = T_D ∧ C = T₁ ∧ C + Y_D(T₂ ∧ C₂).

Denote patient covariate values at the ith decision time by O_i = (O_i1, …, O_iq) for i = 1, 2. Such covariates can include prognostic variables or biomarkers thought to be related to outcome. In first-line therapy, we assume that the death time T₁ depends on the covariates O₁ and possible treatment D₁ according to a distribution [T₁ | O₁, D₁] ~ f₁(O₁, D₁; α₁), where decision D₁ only consists of a finite set of agents d₁. If the patient survives long enough to be treated by second-line therapy, we assume that the disease progression time T_P is ≥ t₂ and follows another distribution [T_P | O₁, D₁] ~ f₂(O₁, D₁; α₂). In addition, to account for the effects of initial timing of second-line therapy on survival, T₂ given T_D ≥ t₂ is then given by [T₂ | O₂, D₁, D₂, T_M] ~ f₃(O₂, D₁, D₂, T_M; α₃), where D₂ consists of a finite set of agents d₂ and T_M is a continuous initiation time. We assume also that P(T_D = t₂) = 0. Note that because of the independence of censoring, conditioning T₂ on Y_D = 1 is the same as conditioning on T_D ≥ t₂. Note that this study is designed to identify the initiation time, T_M, which is associated with the best combination of treatments d₁ and d₂, while maintaining longest survival T_D. Due to heterogeneities among patients, biomarker-treatment interactions, and the large number of possible shapes of T₂ as functions of T_M, the distributions f₁, f₂, and f₃ can be complicated and may vary between different groups of patients. Thus, incorporating O_i into models for f_i (i = 1, 2, 3) is quite challenging, and such model-based approaches can easily become intractable (Thall et al., 2007). Another important issue is accounting for delayed effects. Thall et al. (2007) claimed that conventional model-based approaches cannot handle this kind of situation very well. Based on clinical data, reinforcement learning is not only a model-free method which carries out treatment selection sequentially with time-dependent outcomes to determine optimal individualized therapy, but it can also improve longer-term outcomes by incorporating delayed effects.

2.2 Q-Learning Framework

We will utilize a Q-learning framework (Watkins, 1989), one of the most widely used reinforcement learning methods, for our approach because Q-learning directly facilitates the necessary modeling, estimation and optimization in our setting. In a multi-stage decision problem, with T decision times, if we denote each decision point by t, state S_t, action A_t, and incremental reward R_t, t = 1, …, T, are three fundamental elements of Q-learning. In the clinical setting, the meaning of state, action, and reward could be defined respectively as patient covariates and treatment history, treatment options and timing, and survival time, for example. Q-learning assigns values to action-state pairs, and it is learning, based on S_t, how best to choose A_t to maximize the expected sum R̄_t = r₁ + ··· + r_T of the incremental rewards.

The algorithm has a so-called Q function which calculates the quality of a state-action combination as follows: Q: S × A → ℝ. The motivation of Q-learning is that once the Q functions have been estimated, we only need to know the state to determine an optimal action, without the knowledge of a transition model that tells us what state we might go to next. The core of the algorithm results from the definition of the Q function and a simple value iteration update. The Q function at time t, given state S_t = s_t and action A_t = a_t, is the expectation of the sum of the incremental reward R_t = r_t and all future incremental rewards under the assumption that the optimal course of action will be taken at all decision times greater than t: t+1, …, T. This structure yields the recursive identity (Murphy, 2005b)

$$Q_t(s_t,a_t)=E\left[R_t+\underset{a_{t+1}}{max}{Q}_{t+1}(S_{t+1},a_{t+1})|S_t=s_t,A_t=a_t\right].$$ (1)

The Q-learning algorithm attempts to find a policy π (i.e., a regimen in our clinical trial setting) that maps states to actions the learner ought to take in those states. π is possibly deterministic, non-stationary, and non-Markovian. We denote the optimal policy at time t by ${\pi }_t^{\ast }(s_t)$, which satisfies: ${\pi }_t^{\ast }(s_t)={\text{argmax}}_{a_t}{Q}_t(s_t,a_t)$.

Zhao et al. (2009) performed a simulation study of a simple Q-learning approach with 6 decision time points for discovering optimal dosing for treatment of a simplistic generic cancer. While the results were encouraging, much work remained before these methods could be applied to specific, realistic cancer scenarios, such as the NSCLC setting of this paper. For example, in their study, the choice of treatments at each decision time point is taken simply among a continuum of dosing levels. However, in NSCLC treatment with two decision time points, the action variables in the second stage become two-dimensional (d₂ and T_M ). The second issue is that overall survival time, the endpoint of interest in NSCLC, cannot be utilized in the usual reward function structure in standard Q-learning, and new methodology and modeling are needed. Moreover, the presence of censoring in the reward outcome means that a fundamentally new approach for estimating the Q-function is needed.

In reinforcement learning, the state variable at a given time point could be defined as current and historical prognostic information, including both observations and actions prior to that time. In our clinical setting, we respectively denote the state and action random variables by O_i and D_i for i = 1, 2, since there are only two decision times in our setting. This is consistent with the notation used in Section 2.1. Denoting O₂ as the state variable at t₂ means we make an assumption that the next action selection only depends on patient covariate values at t₂. This is a working assumption for model building but is not in general true since the state of a patient at time t_i technically contains all historical information available up to and including time t_i. As mentioned in Section 1, we consider overall survival time T_D = T₁ + T₂ as the total reward. Specifically, by performing a treatment d₁, where d₁ ∈ D₁, the patient can transit from first line to second line treatment. This treatment associated with prognostic factors provides the patient a progression time T_P and T₁. Moreover, D₂, which consists of two dimensional action variables consisting of both a discrete action (agent) d₂ combined with a continuous action (time) T_M, provides the patient a survival time T₂ given T_D ≥ t₂. The incremental reward function for the first stage is T₁ ~ G₁(o₁, d₁). In the second stage, the incremental reward function is T₂, where T₂ satisfies T₂ ~ G₂(o₂, d₁, d₂, T_M ). Functions G₁ and G₂ are obtainable from f₁ and f₃, defined previously, and are usually not observable. Note also that both T₁ and T₂ are censored rather than directly observed. In Q-learning, because for every state there are a number of possible treatments that could be taken, each treatment within each state has a value according to how long the patient will survive due to completion of that treatment. The scientific goal of our study is to find an optimal regimen to maximize overall patient survival time T_D (in practice, we maximize restricted mean survival). Thus our reward function is T_D ∧ τ, since we cannot observe any events beyond the maximum follow-up time τ.

While learning a non-stationary non-Markovian optimal regimen from a clinical reinforcement trial data set (given T_D ∧ C ≥ t₂), where observations consist of {O₁, D₁, T₁ ∧ C, O₂, D₂, T₂ ∧ C₂}, we denote the estimate of the optimal Q-functions based on this training data by Q_t(θ̂_t), where t = 1, 2, 3. The indices 1 and 2 correspond to the decision times t₁ and t₂ while index 3 is included only for mathematical convenience. According to the recursive form of Q-learning in (1), we must estimate Q_t backwards through time, that is, use the estimate Q₃ from the last time point back to Q₁ at the beginning of the trial. For convenience we set Q₃ equal to 0. In order to estimate each Q_t, we denote Q_t(O_t, D_t; θ_t) as a function of a set of parameters θ_t, and we allow the estimator to have different parameter sets for different time points t. Once this backwards estimation process is done, we save Q₁(θ̂₁) and Q₂(θ̂₂), and we thereafter use them to respectively estimate optimal treatment policies π̂₁ = argmax_d1 Q₁(o₁, d₁; θ̂₁) and π̂₂ = argmax_d2,TM Q₂(o₂, d₂, T_M; θ̂₂), for new patients. Since the resulting estimated optimal policies are functions of patient covariates, the resulting treatment regimens are individualized. These individualized treatment regimens should also be evaluated in a follow-up confirmatory phase III trial comparing the optimal regimens with the standard care or other appropriate fixed (i.e., non-individualized) treatments.

In a counterfactual framework, optimal treatment regimes are defined via potential outcomes. In the Web Appendix A, we show that under the proposed sequential randomization design, the obtained optimal treatment policies (π̂₁, π̂₂) based on the empirical observations are actually the correct estimates of the optimal treatment regimes in the counterfactual framework.

2.3 Support Vector Regression for Censored Subjects

A strength of Q-learning is that it is able to compare the expected reward for the available treatments without requiring a model of the relationship. To achieve this, the main task is to estimate the Q functions for finding the corresponding optimal policy. However, challenges may arise due to the complexity of the structure of the true Q function, specifically, the non-smooth maximization operator in the recursive equation (1). Nonparametric statistical methods are appealing for estimating Q functions due to their robustness and flexibility. For instance, using random forest (RF) or extremely randomized trees (ERT) techniques is very effective for extracting well-fitted Q functions (Ernst, Geurts, and Wehenkel, 2005; Geurts, Ernst, and Wehenkel, 2006; Guez, Vincent, Avoli, and Pineau, 2008; Zhao et al., 2009). Besides the RF and ERT methods, other methodologies for fitting Q include, but are not limited to, neural networks, kernel-based regression (Ormoneit and Sen, 2002), and support vector machines (SVM) (Vapnik, 1995). Our experience so far indicates that both SVR and ERT work quite well and their accuracy is approximately equivalent, although ERT is more computationally intense (Zhao et al., 2009).

In the present article we apply SVR as our main method to fit Q functions and learn optimal policies using a training data set. The ideas underlying SVR are similar but slightly different from SVM within the margin-based classification scheme. To illustrate, consider the case where the rewards in the training data set are not censored. At each stage, given ${({\mathbf{x}}_i,y_i)}_{i=1}^n$, where attributes x_i ∈ ℝ^m and label index y_i ∈ ℝ, the goal in SVR is to find a function f: ℝ^m → ℝ that closely matches the target y_i for the corresponding x_i. Note that in our simulation study in Section 4, x_i may be replaced by information of states along with actions and y_i may be replaced by survival time, respectively. Instead of the hinge loss function used in SVM, one of the popular loss functions involved in SVR is known as the ε-insensitive loss function (Vapnik, 1995), which is defined as: L(f(x_i), y_i) = (|f(x_i) − y_i| − ε)₊, where ε > 0 and the subscript + denotes taking the positive part. That is, as long as the absolute difference between the actual and the predicted values is less than ε, the empirical loss is zero, otherwise there is a cost which grows linearly. Here L(f(x_i), y_i) is a loss used in estimation and bears no relation to the reward function described in previous sections. SVR is more general and flexible than least-squares regression, since it allows a predicted function that has at most ε deviation from the actually obtained targets y_i for all the training data. Unfortunately, this approach as is cannot be implemented in the presence of censoring.

In general, we denote interval censored data by ${({\mathbf{x}}_i,l_i,u_i)}_{i=1}^n$. If the patient experiences the death event and T_D is observed rather than being interval censored then we include T_D and denote such an observation by (x_i, y_i). When we observe T_D exactly (δ = 1), we let l_i = u_i = y_i. Note that by letting u_i = +∞ we can easily construct a right censored observation (x_i, l_i, +∞).

One naive way to handle censored data within Q-learning by using SVR is to consider only those samples for which the survival times T_D are known exactly. Such an approach which totally ignores censoring will both reduce and bias the sample for statistical analysis and inference. An SVR procedure that targets interval censored subjects was introduced by Shivaswamy, Chu, and Jansche (2007). The key component of their procedure is a loss function, defined as L(f(x_i), l_i, u_i) = max(l_i − f(x_i), f(x_i) − u_i)₊. However, this loss function does not have ε-insensitive properties, that is, it does not allow ε or other deviations from the predicted f(x_i), especially when l_i = u_i = y_i. In this article, we propose a modified SVR algorithm with ε-insensitive loss function (called ε-SVR-C) which can be applied to censored data.

Given the interval censored data set ${({\mathbf{x}}_i,l_i,u_i)}_{i=1}^n$, our modified loss function is defined as

$$L(f({\mathbf{x}}_i),l_i,u_i)=max{(l_i-\epsilon -f({\mathbf{x}}_i),f({\mathbf{x}}_i)-u_i-\epsilon )}_{+}.$$

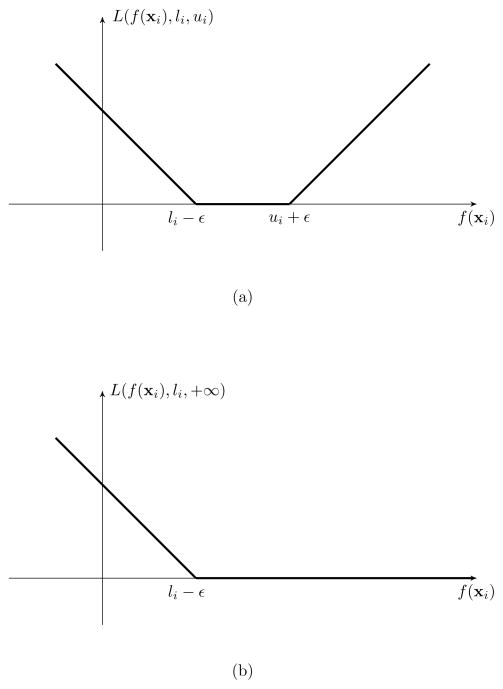
We remark that this loss function does not penalize the value of f(x_i) if it is between l_i − ε and u_i + ε. On the other hand, the cost grows linearly if this output is more than u_i + ε or less than l_i − ε. Figure 2 shows the loss function of the modified SVR. Note that when u_i = +∞, this loss function becomes one sided, which means there is no empirical error if f(x_i) ≥ l_i − ε. In addition, when the data is not censored, our modified SVR algorithm reduces to the classical SVR. Defining index sets L = {i: l_i > −∞} and U = {i: u_i < +∞}, the ε-SVR-C optimization formulation is:

$$\begin{array}{l}\underset{\mathbf{w},b,\xi ,{\xi }^{\prime }}{min}\frac{1}{2}{\left|\right|\mathbf{w}\left|\right|}^2+C_E\left(\sum _{i\in L}{\xi }_i+\sum _{i\in U}{\xi }_i^{\prime }\right),\text{subject}\text{to}\\ ({\mathbf{w}}^T\mathrm{\Phi }({\mathbf{x}}_i)+b)-u_i\le \epsilon +{\xi }_i,i\in U;l_i-({\mathbf{w}}^T\mathrm{\Phi }({\mathbf{x}}_i)+b)\le \epsilon +{\xi }_i^{\prime },i\in L;{\xi }_i\ge 0,i\in L;{\xi }_i^{\prime }\ge 0,i\in U.\end{array}$$ (2)

Figure 2.

Modified SVR loss functions for interval censored data (a) and right censored data (b).

Here, w^TΦ(x_i)+b is the separating hyperplane, where Φ is a nonlinear transformation which maps data into a feature space. ξ_i and ${\xi }_i^{\prime }$ are slack variables and C_E is the cost of error. By minimizing the regularization term $\frac{1}{2}{\left|\right|\mathbf{w}\left|\right|}^2$ as well as the training error $C_E({\sum }_{i\in L}{\xi }_i+{\sum }_{i\in U}{\xi }_i^{\prime })$, ε-SVR-C can avoid both overfitting and underfitting of the training data. A class of functions called kernels K: ℝ^m × ℝ^m → ℝ such that K(x_i, x_j) = Φ(x_i)^TΦ(x_j) (for example, the Gaussian kernel is K(x_i, x_j) = exp (−ζ||x_i − x_j||²)) are used in ε-SVR-C to guarantee that any data set becomes arbitrarily separable as the data dimension grows. Since the ε-SVR-C function is derived within this reproducing kernel Hilbert space (RKHS) context, the explicit knowledge of both Φ and w are not needed if we have information regarding K. In this case, problem (2) is equivalent to solving the following optimization dual problem:

$$\begin{array}{l}\underset{\mathbf{\lambda },{\mathbf{\lambda }}^{\prime }}{min}\frac{1}{2}{(\mathbf{\lambda }-{\mathbf{\lambda }}^{\prime })}^{T}K({\mathbf{x}}_i,{\mathbf{x}}_j)(\mathbf{\lambda }-{\mathbf{\lambda }}^{\prime })-\sum _{i\in L}(l_i-\epsilon ){\lambda }_i^{\prime }+\sum _{i\in U}(u_i+\epsilon ){\lambda }_i,\\ \text{subject}\text{to}\sum _{i\in L}{\lambda }_i^{\prime }-\sum _{i\in U}{\lambda }_i=0,0\le {\lambda }_i,{\lambda }_i^{\prime }\le C_E,i=1,\dots ,n.\end{array}$$

Both parameters ζ and C_E in ε-SVR-C are obtained by utilizing cross validation to achieve good performance. Once the above formulation is solved to get the optimal λ_i and ${\lambda }_i^{\prime }$, the approximating function at x is given by: $f(\mathbf{x})={\sum }_{i=1}^n({\lambda }_i^{\prime }-{\lambda }_i)K({\mathbf{x}}_i,\mathbf{x})+b$.

3. Trial Conduct and Computational Strategy

We will now describe a virtual clinical reinforcement trial which provides a realistic approximation to a potentially real NSCLC trial that evaluates two-line regimens for patients with NSCLC who have not been treated previously with systemic therapy. As mentioned in Section 1, while many new single agents with potential clinical efficacy currently are being produced at an increasing rate, the number of doublet combinations in the first line that can be evaluated clinically is limited. Considering the number of possible agents that may be of interest in the second line, the limitations are even greater.

Without loss of generality, suppose for simplicity that regimens are based on four FDA approved therapies (either single agents or doublets), which we denote by A_i, i = 1, …, 4. In our study we assume that the second line treatment must be different from the first. Two of the four agents A₁ and A₂ are restricted to first-line treatment, while A₃ and A₄ are restricted to second line. A total of N patients are recruited into the trial and fairly randomized at enrollment between A₁ and A₂, and each patient is followed through to completion of first-line treatment, given the patient is not dead or lost to follow-up from the study. We fix this duration t₂ − t₁ at 2.8 months, although other lengths are possible, depending on the number of cycles of treatment. At the end of first-line treatment, patients are randomized again between agents A₃ and A₄ and also randomized to treatment initiation time. This will be accomplished by randomizing to a target initiation time T_M over the interval [0, 2] (in months) and then initiating second line therapy at T_M ∧ (T_P − t₂). At the end of the trial, the patient data is collected and Q-learning is applied, in combination with SVR applied at each time point, to estimate the optimal treatment rule as a function of patient variables and biomarkers, at t₁ and t₂.

The trial described above was motivated by the desire to compare several agents as well as timing in a randomized fashion, the belief that different agents combined with different timing given consecutively may have different effects for different populations of patients, and the desire to determine a sound basis for selecting individualized optimal regimens for evaluation in a future clinical trial. Putting this all together, the entire algorithm for Q-function estimation and optimal treatment discovery can be summarized as follows:

1. Inputs: Each of n observed individual will have an initial (time t₁) set of attributes x₁ = (o₁, d₁) and index y₁ = (T₁ ∧ C, δ₁ = I{T₁ ≤ C}); and, if Y_D = 1, they will also have time t₂ observations x₂ = (o₂, d₂, T_M) and y₂ = (T₂ ∧ C₂, δ₂ = I{T₂ ≤ C₂}).

2. Initialization: Let Q₃ be a function equal to zero.

3. Q₂ is fitted with ε-SVR-C through the following equation: Q₂(o₂, d₂, T_M) = T₂ + error, where T₂ is assessed through the censored observation {T₂ ∧ C₂, δ₂}. This is possible to do since we are restricting ourselves in this step to patients for whom Y_D = 1. In other words, for those individuals with Y_D = 1, we perform right-censored regression using ε-SVR-C of (T₂ ∧ C₂, δ₂) on (o₂, d₂) to obtain Q̂₂.

4. Q₁ is fitted with ε-SVR-C through the following equation:

   $$\begin{array}{l}{Q}_1(o_1,d_1;{\mathit{\theta }}_1)=T_1+I(T_1=t_2)\underset{d_2,T_M}{max}{Q}_2(o_2,d_2,T_M;{\widehat{\mathit{\theta }}}_2)+\mathit{error}\\ =T_1+I(T_1=t_2){\widehat{T}}_2+\mathit{error},\end{array}$$

   where T₁ + I(T₁ = t₂)T̂₂ is assessed through the censored observation (X̃, δ̃), with X̃ = T₁ ∧ C + Y_DT̂₂. The reason this works can be summarized in two steps: First, we can show after some algebra that X̃ = T̂_D ∧ C̃ and δ̃ = I(T̂_D ≤ C̃), where T̂_D = T₁ + I(T₁ = t₂)T̂₂ and C̃ = CI(C < t₂) + ∞I(C ≥ t₂), and thus we have independent right censoring of the quantity T̂_D. Second, since Q₁ needs to model the expectation of T_D given the covariates (O₁, D₁) under the assumption that the optimal choice is made at the second decision time, it is appropriate that we replace T_D with the quantity T₁ + I(T₁ = t₂)T̂₂, since T̂₂ estimates E max_d2,TM E(T₂ |O₁, D₁, T_D ≥ t₂, O₂, d₂, T_M). In summary, we perform regression using ε-SVR-C of (X̂, δ̃) on (o₁, d₁) to obtain Q̂₁.

5. For the SVR computations in steps 3 and 4, we use a Gaussian kernel with a straightforward coarse grid search over C_E = 2⁻⁵, 2⁻³, …, 2¹⁵ and ζ = 2⁻¹⁵, 2⁻¹³, …, 2³, and then select the pair (C_E, ζ) that yields the highest cross-validated rate of correctly classifying the data.

6. Given Q₁(θ̂₁) and Q₂(θ̂₂), we compute the optimal polices π̂₁ and π̂₂.

4. Simulation Study

To demonstrate that the tailored therapy for NSCLC found by using the proposed clinical reinforcement trial is superior, we employ an extensive simulation study to assess the proposed approach on virtual clinical reinforcement trials of patients, and then evaluate using phase III trial-like comparisons between the estimated optimal and various possible fixed treatments.

4.1 Data Generating Models

Based on historical research, it is well known that the rate of disease progression or death for patients with advanced NSCLC is non-decreasing over time. Consequently, in order to generate simulated data, we simply consider that T₁, T_P − t₂, and T₂ conditional on T_D ≥ t₂ follow different exponential distributions. Many alternative models are also possible.

Let exp(x) denote an exponential distribution with mean e^x. Also let W_t and M_t be patient prognostic factors observable at t = 1, 2 (corresponding to times t₁ and t₂) to be defined shortly. For a patient given first-line treatment d₁, we assume that T₁ = T̃₁ ∧ t₂, where

$$[{\stackrel{\sim }{T}}_1\mid D_1,W_1,M_1]\sim exp({\alpha }_{D_1}+{\beta }_{D_1}{W}_1+{\kappa }_{D_1}{M}_1+{\tau }_{D_1}{W}_1{M}_1).$$ (3)

If T̃₁ ≥ t₂, we generate T_M from a uniform [0, 2] distribution. We now absorb T_P into T_M for modeling T₂ given T_D ≥ t₂ through an intent-to-treat structure (basically, we can ignore T_P since it depends only on D₁, M₁ and W₁ and not on T_M). In addition, for a patient given second-line treatment d₂ and initiation time T_M, we assume

$$[T_2\mid D_1,D_2,W_2,M_2]\sim exp({\alpha }_{D_{12}}+{\beta }_{D_{12}}{W}_2+{\kappa }_{D_{12}}{M}_2+h(T_M;\varphi )),$$ (4)

where h(T_M; ϕ) is a function depending on the parameter ϕ which reflects the effect of timing T_M on death. The shape of this time-related function may vary among different patients because of its dependence on patient characteristics. The total time to death is then T_D = T₁ + I(T₁ = t₂)T₂. τ is set to 25 (months). We then need to generate the right censoring time C uniformly from the interval [t₁, t₁ + u]. To find u, we estimate the unconditional survival function Ŝ(t) for the failure time T_D, where “unconditional” refers to taking expectation over the covariates D_i, W_i, M_i(i = 1, 2), and T_M of the conditional survival function T_D. Then, u is the solution to $u^{-1}{\int }_{t_1}^{t_1+u}\widehat{S}(x)dx=p$, where p is the desired probability of censoring.

Note that in our simulation study we straightforwardly use exponential pdfs (3) and (4) to replace f₁ and f₃ and we drop f₂, where (f₁, f₂, f₃) were described in Section 2.1. For the sake of simplicity, in these density functions only two state variables, quality of life (QOL) W_t and tumor size M_t, are considered as patient prognostic factors or biomarkers to be related to outcome. We consider these two factors because they are patient based, realistically easy to measure, can predict therapeutic benefit after treatment of chemotherapy, and, more importantly, they are significant prognostic factors for survival (Socinski et al., 2007). In addition, state variables for the next decision are generated by the simple dynamic models W₂ = W₁ + T_M Ẇ₁ and M₂ = M₁ + T_M Ṁ₁, where Ẇ₁ and Ṁ₁ are constants.

The parameter vector for those receiving only first-line treatment is θ₁ = (α_D1, β_D1, κ_D1, τ_D1), otherwise it is ${\mathit{\theta }}_2=({\alpha }_{D_1}^P,{\beta }_{D_1}^P,{\kappa }_{D_1}^P,{\tau }_{D_1}^P,{\alpha }_{D_{12}},{\beta }_{D_{12}},{\kappa }_{D_{12}},\mathit{\varphi })$. Note that two patients receiving different second-line treatments, say (A₁, A₃) and (A₁, A₄), both contribute data for estimating Q₁.

4.2 Clinical Scenarios

To construct a set of scenarios reflecting interaction between lines of treatment, we temporarily assume that a large portion of patients survive long enough to be treated by second-line therapy, that is, we adjust the parameters so that P(Y_D = 1) = 0.8 averaged across all patients. Other than the constraint on P(Y_D = 1), each clinical scenario under which we will evaluate the design in the simulation study is built by a unique set of fixed values of ( ${\alpha }_{D_1}^P,{\beta }_{D_1}^P,{\kappa }_{D_1}^P,{\tau }_{D_1}^P$, α_D12, β_D12, κ_D12). The remaining fixed parameter values needed for the simulations are those that determine how T₂ varies as a function of T_M. To implement this, we specified four different cases for the function h(T_M; ϕ).

The four resulting scenarios are specified and summarized in Table 1. In group 1 and 4, initial timing of second-line therapy for survival time (T₂) are functions that form an inverse-U (quadratic) shape with T_M, while initial timing in group 2 and 3 for T₂ are functions that linearly decrease and increase with T_M, respectively. Each group thus consists of a combination (A_i, A_j) as well as T_M from Table 1 (where i = 1, 2 and j = 3, 4), with the fixed values of ${\alpha }_{D_1}^P,{\beta }_{D_1}^P,{\kappa }_{D_1}^P,{\tau }_{D_1}^P$, α_D12, β_D12, κ_D12, and ϕ as described above.

Table 1.

The scenarios studied in the simulation. Sample size = 100/group.

Group	State Variables	Status	Timing (h)	Optimal Regimen
1	W1 ~ N (0.25, σ2) M1 ~ N (0.75, σ2)	W1 ↓ M1 ↑		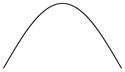A1A32
2	W1 ~ N (0.75, σ2) M1 ~ N (0.75, σ2)	W1 ↑ M1 ↑		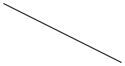A1A41
3	W1 ~ N (0.25, σ2) M1 ~ N (0.25, σ2)	W1 ↓ M1 ↓		A2A33
4	W1 ~ N (0.75, σ2) M1 ~ N (0.25, σ2)	W1 ↑ M1 ↓		A2A42

Note that whatever combination of two-line treatment (A_i, A_j) is evaluated, all patients within one group share the same trend of T₂ versus T_M. However, we assume there is only one regimen that will yield the longest survival in each group. For convenience, we denote “1, 2, 3” as the location of optimal initiation of second-line therapy, corresponding to “immediate, intermediate, and delayed”, respectively. For example, as claimed in the last column in Table 1, A₁A₃2 indicates that the two-line treatments (A₁, A₃) along with an intermediate initiation time point is the optimal regimen for group 1. The inverse-U-shaped function for T₂ versus T_M corresponds to the case where patients have relatively low QOL at enrollment but relatively large tumor size, hence, this optimal intermediate initiation of second-line therapy is recommended to delay treatment a short time for patients who may have severe symptoms and low tolerance of chemotherapy, but not to fully delay due to the need to treat the cancer. In scenario 2, due to the good QOL and large tumor size at enrollment, it is optimal for the second-line therapy to begin immediately after first-line therapy, hence, A₁A₄1 is the optimal regimen for these patients. Similarly, in scenario 3, treatment A₂A₃3 is considered the superior treatment since we believe fully that delaying the initiation of second-line therapy at the time of disease progression will improve survival and palliate symptoms. Although scenario 4 has optimal regimen A₂A₄2, due to the flat shape of T₂ versus T_M, there is no significant improvement between delaying and not delaying the initiation of second-line therapy. In this manner, many plausible effects of treatment are captured, at least to some degree, including both reversible and irreversible toxicities resulting from chemotherapy.

4.3 Simulation Methods and Results

First, according to various (W₁, M₁) as described in Table 1, a non-censored sample of N = 100 virtual patients for each of the four disease profile groups (with total sample size n = 400) is generated. Q₁(θ̂₁) and Q₂(θ̂₂) are computed via the algorithm given in Section 3 (since the method is robust to the choices of relatively small value of ε, ε is set to 0.1). The predicted optimal regimens are then computed, and an independent testing sample of size 100 per disease profile group (hence also totaling 400) is also generated. For evaluation purposes, we then assign all virtual test patients to all possible combinations of (A_i, A_j) × {immediate, intermediate, delayed} as well as the estimated optimal regimen, resulting in 13 possible treatments. Patients outcomes (overall survival) resulting from our estimated optimal regimen and the 12 different fixed regimens are all evaluated. This is similar in spirit to a virtual phase III trial with 5200 = 13 × 400 patients, except that the estimated effects will be more precise. Moreover, we repeated the simulations 10 times for the training sample trial (each trial having sample size n = 400). Then, 10 estimated optimal regimens learned from these 10 training trials were applied to the same test patients described above. All of the results for each of the 13 treatments are averaged over the 400 test patients. This is initially done with uncensored data using SVR to fit the Q-functions. We will later evaluate the effect of censoring using our proposed ε-SVR-C.

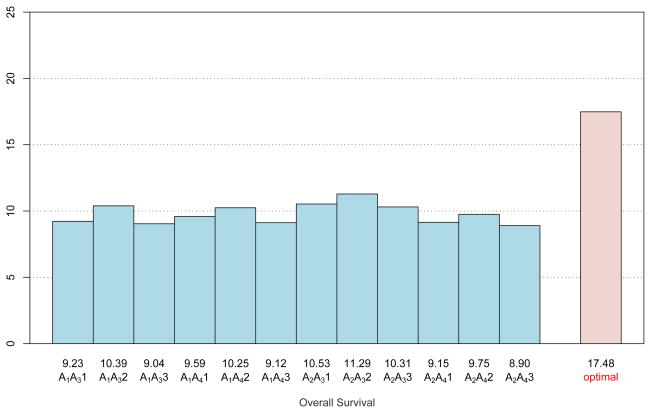
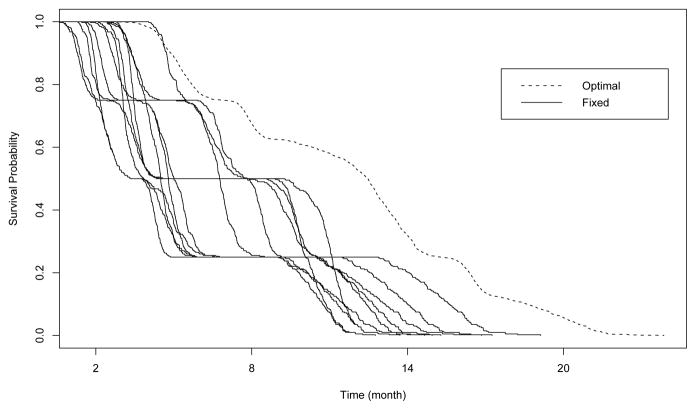
As shown in Figure 3, among regular regimens, assigning all test patients to A₂A₃2 will yield the averaged longest survival among the 12 fixed treatments at 11.29 months. It thus appears that, in terms of adaptively selecting the best regimen for each group, the optimal regimen obtained by Q-learning with SVR is superior due to its average (over 10 simulations) survival of 17.48 months. The survival curves for the groups (based on the Kaplan-Meier estimates) are shown in Figure 4, which demonstrates the effectiveness of the proposed approach for prolonging survival. Because of this encouraging result, it is worthwhile to deeply investigate whether our approximations are close to the exact solution. To carefully examine this comparison, we assign test patients from each disease profile group to the corresponding true optimal regimen described in Table 1 to obtain the “True survival” column of Table 2. The minimum, maximum, and mean values of averaged predicted survival for each group are computed based on these 10 trials, respectively. The results are summarized in Table 2. The averaged predicted survival over all groups is shown as 17.48 (which is consistent with the number shown below the “optimal” bar in Figure 3), this number along with the minimum 17.28 and the maximum 17.63 are all pretty close to the true optimal survival 17.61. In addition, the averaged selected optimal timings are shown in the fifth column of Table 2. Note that they are close to true optimal timings for each group. In terms of estimation, under each of the scenarios 1–3 our method performs very similarly and slightly underestimates the true optimal survival. In contrast, our method slightly overestimates the true optimal survival in scenario 4.

Figure 3.

Performance of optimal individualized regimen versus other 12 combinations. The numbers above the regimens (12 possible combinations and the optimal regimen) indicate the estimated average survival times for each regimen.

Figure 4.

Survival functions for testing sample treated by 13 different regimens (12 fixed treatments plus optimal regimen).

Table 2.

Comparisons between true optimal regimens and estimated optimal regimens for overall survival (months). Each training dataset is of size 100/group with 10 simulation runs. The testing dataset is of size 100/group.

Group	Optimal regimen	Optimal timing	True survival	Selected timing	Predicted survival
					Min	Mean	Max
1	A1A32	3.80	16.00	3.92	15.83	15.93	16.00
2	A1A41	2.80	15.33	2.94	14.96	15.13	15.28
3	A2A33	4.80	18.37	4.62	17.75	17.99	18.27
4	A2A42	3.80	20.75	4.11	20.60	20.86	20.97
Average			17.61		17.28	17.48	17.63

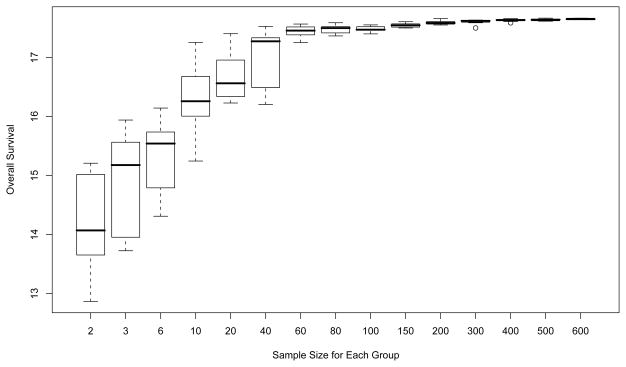
Second, although our Q-learning method with N = 100 per group using SVR leads to an apparently small bias for estimating individualized optimal regimens, an examination of performance influenced by the sample size is worthwhile. We repeated the simulations 10 times for each specified sample size while varying N from 2 to 600 per group. The results are illustrated in Figure 5, which shows that the method’s reliability is very sensitive to N when N ≤ 80, with the averaged survival for the estimated optimal regimen increasing from 14.192 when N = 2 to 17.479 when N = 80. The boxplots also show that both the variance and estimation bias of predicted survival become smaller when the sample size becomes larger. When N ≥ 100, our methods appear to do a very reliable job of selecting the best regimen. Hence, in the setting we study here, the sample sizes required to reach an excellent approximation are similar to the sizes required for typical phase III trials.

Figure 5.

Sensitivity of the predicted survival to the sample size.

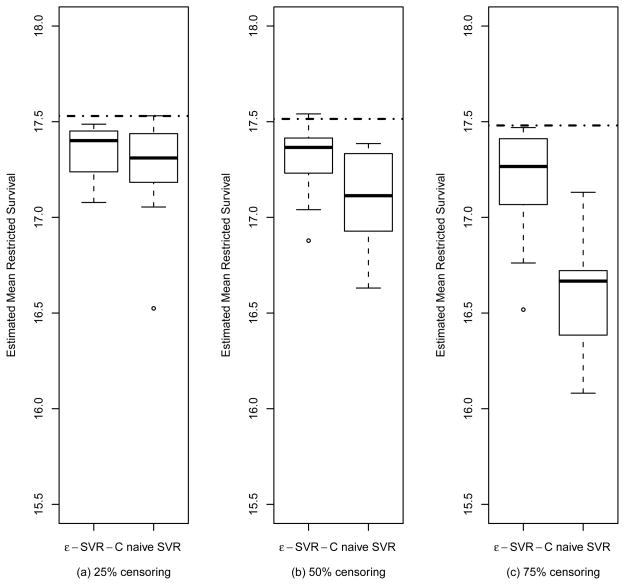
Third, in order to compare performance of ε-SVR-C for censored subjects to ignoring the censored cases and using SVR, from 400 training samples in each simulated trial, we randomly censor as described in Section 4.1 to achieve a targeted proportion of censoring p, estimate the optimal treatment regimen using ε-SVR-C, throw out the censored observations and use SVR to estimate the optimal regimen, and then apply 400 test patients to the estimated regimens to estimate the restricted mean survival. This is done for 25%, 50%, and 75% censoring proportions p, respectively. The boxplots are presented in Figure 6. For instance, in panel (a) we generate 10 training trials with 25% censoring. The dotted line going through two boxplots indicates the performance for the true optimal regimen without any censoring but with maximum possible follow-up truncation. The left boxplot indicates the performance based on ε-SVR-C applied to the 25% censored data, while, in the right boxplot, we simply delete the 25% of patients which are right-censored and apply SVR to the remaining data to estimate the optimal regimen. This basic process is repeated across the three different censoring levels. As can be observed in Figure 6, as the fraction of right-censoring increases, there is an increasing decline in performance resulting from throwing out censored observations. In contrast, our proposed approach (the left boxplot of each panel) can robustly estimate the optimal regimen under censoring, with only a minor increase in bias as censoring increases. Clearly, in terms of averaged predicted survival in all cases, the ε-SVR-C algorithm outperforms the method which totally ignores the censored data, particularly when the censoring proportion is large.

Figure 6.

Boxplots of the estimated mean restricted survival for the optimal regimen, estimated from a training sample of 400 observations. The boxplots are data summaries over 10 simulation replicates. Results are presented for ε-SVR-C and for the naive SVR analysis that discards the censored observations, with censoring levels of (a) 25%, (b) 50% and (c) 75%. The dotted line represents the true mean restricted survival for the optimal regimen.

5. Discussion

We have proposed a clinical reinforcement trial design for discovering individualized therapy for multiple lines of treatment in a group of patients with advanced NSCLC. The incorporation of Q-learning with the proposed ε-SVR-C appears to successfully identify optimal regimens tailored to appropriate subpopulations of patients. We believe in general that Q-functions in clinical applications will be too complex for parametric regression and that semiparametric and nonparametric regression approaches, such as ε-SVR-C, will be needed. While our method has been utilized for the two decision points at hand, the general concepts and algorithms of this approach could be applied to design future trials having similar goals but for possibly different diseases. Although overall survival time is considered among many clinicians to be the appropriate primary endpoint in late stage NSCLC, a potentially important alternative outcome to consider is quality-of-life-adjusted survival (Gelber et al., 1995). This may require some modification of the proposed ε-SVR-C methodology.

An important point to make is that the primary goal of the proposed Q-learning approach is to obtain optimal treatments that are reproducible. Thus our first goals is to ensure that our operating characteristics are such that optimal, or nearly-optimal, treatments can be consistently and reproducibly identified with our proposed method. We believe that we have demonstrated this in this paper. An important next step in the research process is to obtain more refined statistical inference for our proposed approach, including confidence sets for the resulting treatment regimens and associated Q-functions. This is an area of active, ongoing work, which we are pursuing. In this article, we studied the prediction accuracy of our method with varying sample sizes. The simulation studies show that with sample size N ≥ 100 our method can yield a small estimation bias. Thus, another important and challenging question is: how do we determine an appropriate sample size for a clinical reinforcement trial to reliably obtain a treatment regimen that is very close to the true optimal regimen? This sample size calculation is related to the statistical learning error problem. Recently, there has been considerable interest in studying the generalization error for Q-learning. Murphy (2005b) derived finite sample upper bounds in a closely related setting which depends on the number of observations in the training set, the number of decision points, the performance of the approximation on the training set, and the complexity of the approximation space. We believe further development of this theory is needed to better understand how performance of Q-learning with SVR is related to sample size of the training data in clinical reinforcement trials. We hope that this article will serve to stimulate interest in these issues.