Abstract
Thanks to its proven utility in both clinical and research applications, diffusion tensor tractography (DTT) is regularly employed as a means of delineating white matter tracts. While successful efforts have been made to validate tractographic predictions, comparative methods which would permit the validation of such predictions at microscopic resolutions in complex biological tissues have remained elusive. In a previous study, we attempted to validate for the first time such predictions at microscopic resolutions in spinal cords of the rat and pig using a semi-quantitative analysis method. In the current study, we report improved quantitative analysis methods that can be used to determine the accuracy of DTT through comparative histology and apply theses techniques for the first time to human tissue (spinal cord) samples. Histological images are downsampled to resolutions equivalent to our magnetic resonance microscopy (MRM) and converted to binary maps using an automated thresholding tool. These maps (n = 3) are coregistered to the MRM allowing us to quantify the agreement based on the number of pixels which contain tracts common to both imaging datasets. In our experiments we find that—on average—89% of imaging pixels predicted by DTT to contain in-plane white matter tract structure correspond to physical tracts identified by histology. In addition, angular analysis comparing the orientation of fiber tracts measured in histology to their corresponding in-plane primary eigenvector components is presented. Thus, as well as demonstrating feasibility in human tissue, we report a robust agreement between imaging datasets taken at microscopic resolution and confirm the primary eigenvector’s role as a fundamental parameter with clear physical correlates in the microscopic regime.
Introduction
One of the most pivotal developments in the application of diffusion-weighted MR imaging involves using diffusion tensor imaging (DTI) (Basser et al., 1994a) in conjunction with diffusion tensor tractography (DTT) (Mori et al., 1999) to delineate white matter tracts in the brain. This technique relies on the structural characteristics of axons which, due to their continuity and—to some degree—their myelination (Song et al., 2002; Tyszka et al., 2006), render water diffusion parallel to the axon fibers highly favorable compared to diffusion perpendicular to them. Such anisotropic diffusion can be described by the self-diffusion tensor which represents the overall orientational preference to diffusion within the MRI voxel and serves as the most accurate model for the first-order approximation of water diffusion in brain tissue (Mori, 2007). The primary eigenvector of the diffusion tensor represents the overall preferred direction of diffusion in the voxel, and is therefore assumed to be co-linear with the dominant fiber direction in the voxel. As such, the tensor model forms the basis for estimation of neuroanatomical features from DTI data. Subsequent DTT analysis is then used to generate synthetic fiber maps by determining the likelihood of intervoxel connectivity based on various selection criteria: angles between primary eigenvectors in adjacent voxels, degree of anisotropy, etc. Because the integrity of white matter structures is essential to neural connectivity and thus function, such techniques are currently being employed in the clinic as a tool for planning minimally traumatic surgical interventions (Yu et al., 2005). DTT has also been used to detect structural abnormalities in the white-matter of patients suffering from various diseases including schizophrenia (Voineskos et al., 2010; Phillips et al., 2009), multiple sclerosis (Werring et al., 1999; Lin et al., 2007), amyotrophic lateral sclerosis (Ellis et al., 1999; Ciccarelli et al., 2006), as well as a host of other cognitive disorders (Catani, 2006) demonstrating great potential for future applications in differential diagnosis.
Despite the demonstrable utility of DTT, questions still remain regarding the accuracy of these methods as they relate to delineation of fiber structures. Resolution limitations of contemporary MRI scanners preclude tracking of individual axons, thus the synthetic tractography maps provide structural accuracy limited by factors such as attainable imaging resolution, the number of diffusion encoding directions, and the sophistication of the DTT algorithm employed. Such factors become even more important as the complexity of intersecting fiber structures within the imaging voxel increases because the diffusion tensor model is insufficient to describe the signal behaviour when multiple fiber orientations are present in a voxel (see e.g. Alexander et al., 2001; Alexander et al., 2002; and Frank et al., 2002 for reports on early experiments or Seunarine and Alexander 2009 for review of this topic). Previous attempts have been made to validate the accuracy of DTT maps using physical phantoms (Lin et al., 2003; Perrin et al., 2005), software phantoms (Lori et al., 2002; Tournier et al., 2002) or biological samples of uniform construction (Van Doorn et al., 1996; Van Donkelaar et al., 1999; Lin et al., 2001). Some studies have compared fractional anisotropy values from DTI data to measures of fiber orientation derived from histology in humans (Simonyan et al., 2008) and animal models (Kim et al., 2007; Kim et al., 2006; Leergaard et al., 2010). Others have employed both histological and MR-visible tracers as a means to validate tractography (Dyrby et al. 2007). For a comprehensive overview of studies focusing on DTT validation, we refer the reader to the review by Hubbard and Parker (2009). Recently, we presented a new method for validating the accuracy of DTT predictions in complex biological systems at microscopic image resolutions (Flint et al., 2010). In our previous study, we reported the results of diffusion tensor microscopy experiments with subsequent tractographic analysis and correlative histology taken in spinal cord samples of the rat and pig. While such studies were useful as proof-of-principle experiments demonstrating our ability to perform structurally relevant tractographic analysis at resolutions necessary to observe cellular structure using MR, such data will not be as useful in modeling or validation studies applicable to human tissue structures encountered during clinical imaging. Thus, in order to obtain such data, we must begin by demonstrating that equivalent structural information can be attained from human tissue. To this end, we have performed diffusion tensor microscopy experiments followed by tractographic analysis in the ventral horn of fixed, human spinal cord. By comparing imaging datasets, it is possible to see if the synthetic maps from our DTT analysis compare favorably with the tract positions observed in the histology. Our data also allow us to quantify the agreement between structural components observable by light microscopy in the samples used in our DTI experiments and the structural information—i.e., the in-plane component of the primary eigenvector—derived from the DTI data.
Given the resolutions obtained in our MRM experiments, we assume that a single tensor is sufficient to faithfully describe the diffusion in each voxel. At the gray/white matter (GM/WM) boundary of the spinal cords’ ventral horns, we expect a portion (70%–80%) of the in-plane fiber components to be myelinated and nearly all of the through-plane fibers to be myelinated (Coggeshall et al., 1975; Ko et al., 2009). We therefore chose a myelin-specific stain for the quantitative portion of our study. This direct histological comparison with emphasis on fibrous content enables us to determine the fraction of MR image pixels predicted by the primary eigenvector to have in-plane fibrous content that are supported by the histological evidence. Taken together, the two imaging modalities employed in our study allow us to investigate the accuracy of DTI methods and shed light on the fundamental assumption that the orientation of maximal diffusion given by the primary eigenvector in each voxel is co-linear with the dominant fiber direction in the voxel. Since all diffusion tractography techniques rely on the assumption that diffusion is less hindered along fibers than across them (Behrens and Jbabdi, 2009) we believe this study to be relevant to most if not all current tractographic techniques because it provides quantitative information about the amount of overlap between fibers in histology and the structural information in the tensor field as well as providing direct visual demonstration of the accuracy of the fiber maps produced by tractography based on the same tensor fields.
Validation efforts in the current study are similar in some respects to methods in studies mentioned above; however, important differences distinguish this work. First, we believe that our study will include DTT validation methods performed at the highest reported resolution to date. This is significant in relation to our chosen analysis method which relies solely on a single diffusion tensor to determine the characteristics of water diffusion within the MR imaging voxel. While this method may seem antiquated compared to some of the most modern techniques for describing intravoxel water diffusion in complex tissues, the fact remains that increasing complexity of tissue structure is the characteristic which necessitates either model-based methods e.g. multi-tensor analysis (see Seunarine and Alexander 2009 for review) or non-parametric methods such as Diffusion Spectrum Imaging (DSI) (Wedeen et al. 1999; Tuch, 2002), QBall (Tuch 2004, Tuch et al. 2003), Spherical Deconvolution (SD) (Anderson and Ding 2002; Tournier et al. 2004) or Persistent Angular Structure (PAS) MRI (Jansons and Alexander, 2003). As imaging voxels become larger, they contain more tissue and are more likely to contain complex, meso-scale structures such as crossing, kissing or intersecting fiber bundles. Interpreting data of this nature correctly requires higher order analysis which demands high image SNR as well as increased numbers of data points: i.e. multiple measurements of diffusion along different axes. Data in the current study will be collected at resolutions high enough to ensure relative uniformity of intravoxel tissue structure such that diffusion within the voxel can reasonably be assumed to be accurately described using a single diffusion tensor. Perhaps more important than the ultimately attainable resolution, comparisons made between optical and MR imaging datasets for the purposes of validation will be performed on images of equivalent resolution. We believe this to be a nontrivial distinction as it permits direct spatial comparisons of imaged tissue on a voxel by voxel basis and is limited only by the accuracy of our image registration. Also particular to our method is the use of a high-contrast histological dye for the purpose of distinguishing in-plane and through-plane white matter tracts. This particular step in our protocol allows for the automated segregation of pixels in binary maps based on underlying tissue structure and eliminates the need to perform such selections manually. This particular feature helps reduce subjectivity from the analysis used in our validation method and stands as a marked improvement over methods employed in our previous work (Flint et al., 2010). Lastly, other methods of DTT validation achieved through comparison of DTI datasets to different imaging modalities have traditionally required the use of MR contrast agents such as manganese (e.g. Dyrby et al., 2007), or potentially confounding post-MR tissue processing (Leergaard et al., 2010). Such methods allow for the retrograde tracing of tracts and the gross comparison of anatomical features in tissue. Unfortunately, these protocols call for the addition of agents which affect relaxivity or contain processing steps which result in physical differences between tissue samples used in comparative imaging datasets. In the case of post-MR tissue sectioning, it is impossible to ensure that a slide preparation consists of the same tissue segment imaged in a particular slice of the MR dataset. Our method relies only on native MR contrast present in the tissue samples and includes pre-MR histological sectioning and post-MR histological processing (staining, mounting and photography) to ensure that the tissue specimen’s physical characteristics are not altered between experiments and are thus exactly the same in both imaging datasets. We believe our stated protocols represent a more direct method of comparing imaging modalities for the purpose of validating DTT methods.
Methods
Tissue Prep & Imaging
Immersion fixed (4% formaldehyde) samples from both the cervical and lumbar enlargements of two human spinal cords were excised by gross dissection, affixed to a cutting chuck, and placed in an ice-cold bath of phosphate-buffered saline (PBS) (137mM NaCl, 2.7mM KCl, 10mM Na2HPO4, and 1.8mM KH2PO4: pH 7.3 to 7.4 at 300mOsm). Serial cross sections (50µm) of spinal cord were cut from the samples using a Lancer vibratome (Ted Pella, series 1000) and placed in a PBS bath overnight to reduce formaldehyde levels in the tissue. Next, an area of tissue (approximately 3mm by 4mm) including the white-gray matter boundary in the cord’s ventral horn was cut from one of the slices and placed inside the tissue well (5mm diameter) of a micro surface-coil (500µm diameter) (Bruker Biospin, B6370). Each slice was positioned so that the tissue boundary between white and gray matter passed along the coil’s diameter and was held in place using a mesh insert and retention ring as described in detail previously (Flint et al., 2009). Hand cutting and tissue placement were performed with the assistance of a dissecting microscope (Zeiss, OPMI 1-FC). Finally, additional PBS was placed inside the tissue well before sealing it closed using a square section (1cm by 1cm) cut from a sheet of PCR film (ABgene, AB-0558). The coil was placed in a vertical bore, 600MHz imaging spectrometer (Oxford) interfaced to a Bruker console and 21-direction diffusion tensor imaging datasets (n = 3) were collected (TR = 2000ms, TE = 17.5ms, b = 2000s/mm2, Δ = 8.36ms, δ = 2.0 ms, resolution = 15.6µm in-plane, Avg = 15/scan, Total Scan Time = 23h28m). For the purpose of generating correlative structural data following MR imaging, slices were removed from the coil and subjected to histological analysis using either the neuronal marker Nissl (0.5% cresyl violet acetate, 0.3% glacial acetic acid, 99.2% ddH2O) or the myelin stain Black-Gold II (Histo-Chem Inc., 1BGII). Briefly, slices stained with Nissl were submerged for 2 min and subsequently rinsed in a destaining bath (0.3% glacial acetic acid, 99.7% ddH2O) prior to mounting with Histomount medium (National Diagnostics, HS-103). Slices stained with Black-Gold II were incubated at 60°C in a 1X working solution (0.3% dye, 0.9% NaCl, 98.8% ddH2O) for 12min followed by immersion in a sodium thiosulfate stop-bath solution (1% Na2S2O3, 99%, ddH2O) at ambient temperature for 3min prior to slide mounting as described above. Histological specimens were then photographed using a digital camera (QImaging, Retiga 4000R Fast 1394 Color) interfaced with a Zeiss microscope (Zeiss, Axioplan 2). Light microscopy image capture was performed using commercial software from QImaging (QCapture Pro 6.0).
MRI Analysis
Following a uniform scaling step to achieve noise regularization, the diagonalized diffusion tensor and primary eigenvector describing the preferred axis of diffusion was determined with Matlab (R2009b, The MathWorks Inc.) using non-linear least squares regression. The presented examples of diffusion tensor tractography based on our DTI data were performed using the FACT algorithm (Mori et al., 1999) as implemented in the Matlab-based DTI tools software package (DTI Tools, Freiburg University Hospital, Germany). All co-registrations of MR data and histology were based on directly identifiable landmarks—primarily large-diameter fiber bundles (tracts) and the GM/WM boundary—present in both MR and histological imaging datasets. Image registration involved combinations of rotation, translation and uniform scaling only. For one of the samples stained with Nissl and all three samples stained with Black-Gold II, we also investigated the relation between the component of the primary eigenvector orthogonal to the image plane (related to the preference for diffusion through the image plane) and the GM/WM boundary. For the three tissue samples in which Black-Gold II stain was employed, we used the tensor field to construct a map of MR pixels in which the primary eigenvector’s projection length in the image plane was greater than that orthogonal to the image plane. For the quantitative analysis, the co-registered histology images of these samples were processed using the GNU Image Manipulation Program (GIMP ver. 2.6.8) to distinguish between in-plane and through-plane fibrous structure in a binary fashion. Processing (color inversion, leveling, pixelization and thresholding) was applied evenly across the entire image field. Individual steps involved in this segmentation process are subsequently described. After inversion, the co-registered histology images were converted to gray scale and adjusted for optimal contrast between stained and non-stained areas. The images were then down-sampled to match MR image resolution thus averaging the pixel’s stain content in the procedural equivalent to how the preferred diffusion direction in each image pixel is a volume average of structural detail across the entire image voxel. GIMP’s auto-thresholding tool (threshold between 0 and 255 based on image histogram) was then used on the down-sampled image thus producing a binary map of structural components in the histology at a resolution matching that of the MR data. The map was exported to Matlab allowing for the comparison of equivalently scaled imaging data (processed histology and MR based tensor maps). These images were analyzed on a pixel-by-pixel basis allowing the direct comparison of image pixels predicted by DTI to contain fiber material to the actual histology. Performing such analysis yielded the fraction of MR-based fiber predictions supported by the histology: i.e., the degree of correspondence (DC)
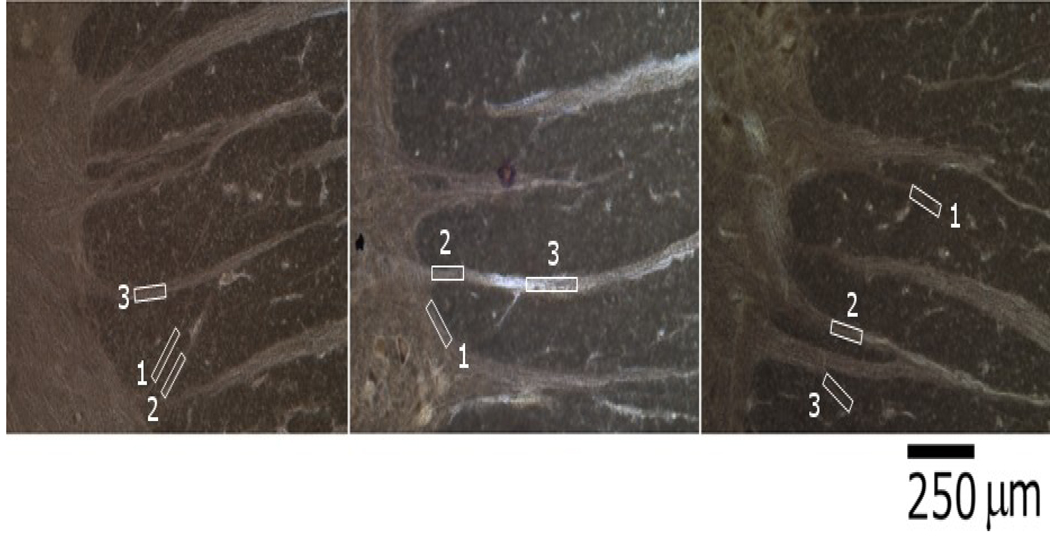
where M is the set of pixels predicted by DW MRI to contain tracts, H is the set of pixels predicted by the down-sampled histology to contain tracts, M∩H is the intersection of sets M and H, and n(M) and n(M∩H) denote number of elements in set M and M∩H respectively. This measure is mathematically identical to the volume overlap fraction used as a similarity measure in (Anbeek et al., 2004). The individual steps of this analysis are illustrated in figure 1. In order to compare directions of the in-plane components of the primary eigenvector to fiber directions measured in the histology, three regions of interest (ROIs) of varying sizes were placed in each of the three samples stained with Black-Gold II. The positions of the ROIs were chosen such that the areas could be identified with certainty in both tensor fields and histology. From the vector field of in-plane components of the primary eigenvector, the average direction ± std (in degrees) across pixels was determined in each ROI. The fiber direction in each ROI was measured in the coregistered histology using the GIMP's angle measurement tool.
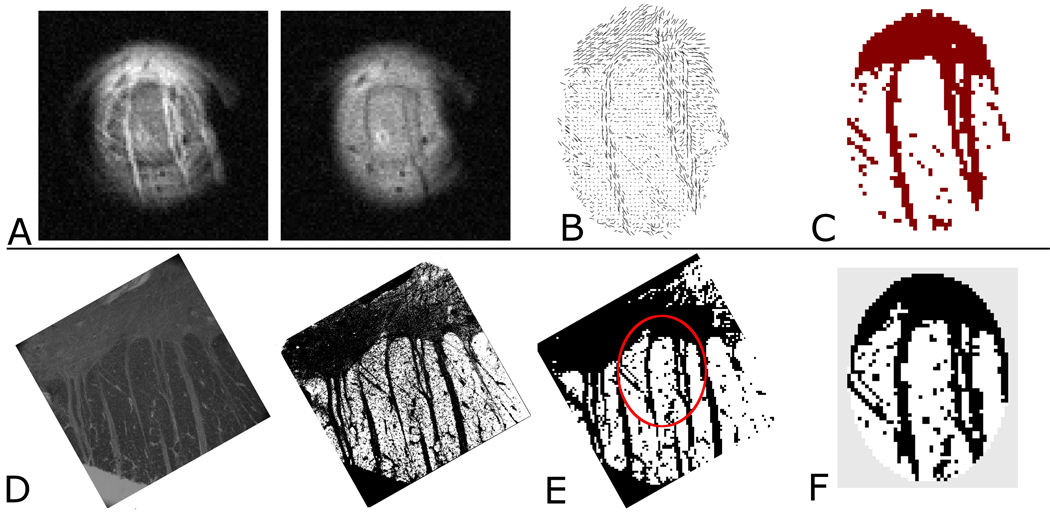
Figure 1.
Top row, left (A–C) shows (A) representative DWIs from the 21-direction MR data. The difference in contrast between the two images is the result of the differing diffusion gradient directions employed. From these data, the tensor map (B) is obtained and the image pixels with predominantly in-plane structure (dark red) are mapped (C). Bottom row, left (D–F) shows (D) left: the coregistered Black Gold II stained histology (otherwise unprocessed), right: the histology after color inversion (E) the binary map of structural components visible in the histology after processing and down sampling to a resolution matching the MRM. The micro surface-coil’s approximate FOV is indicated (red oval) (F) The portion of the histological binary map which corresponds to the coil’s FOV. The two coregistered maps thus obtained (C and F) form the basis for calculation of the fraction of tensor map pixels supported by the histology. The gray area around the histology map in (F) is to illustrate the masking employed so that only histology within the coil FOV is included in the final steps of the analysis. In this particular experiment which corresponds to the tissue sample from figure 4 (far left column, rotated 90 degrees), the degree of correspondence is 0.82 which was the lowest of the three values calculated in the current study.
Results
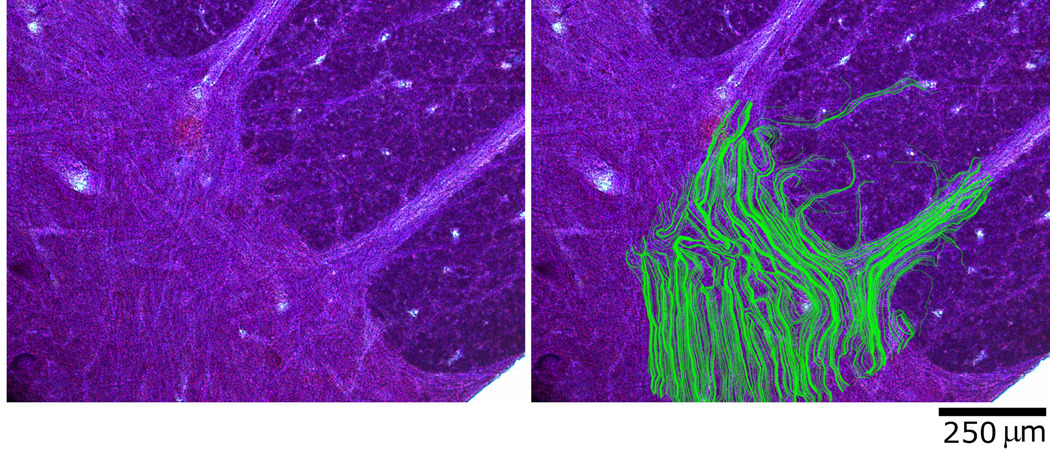
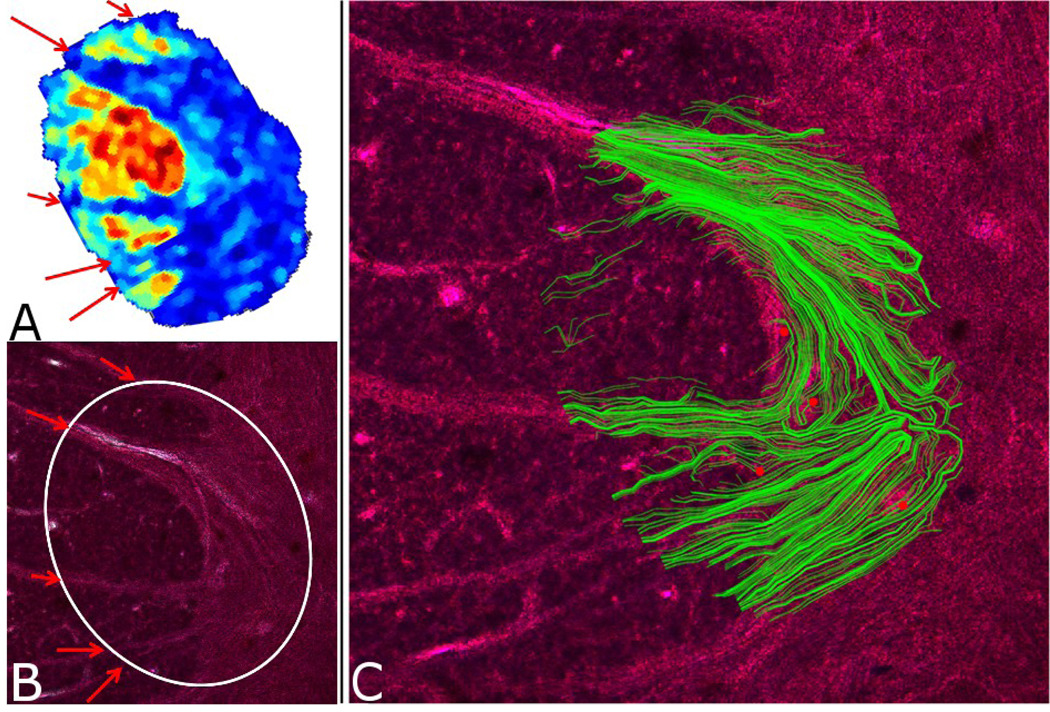
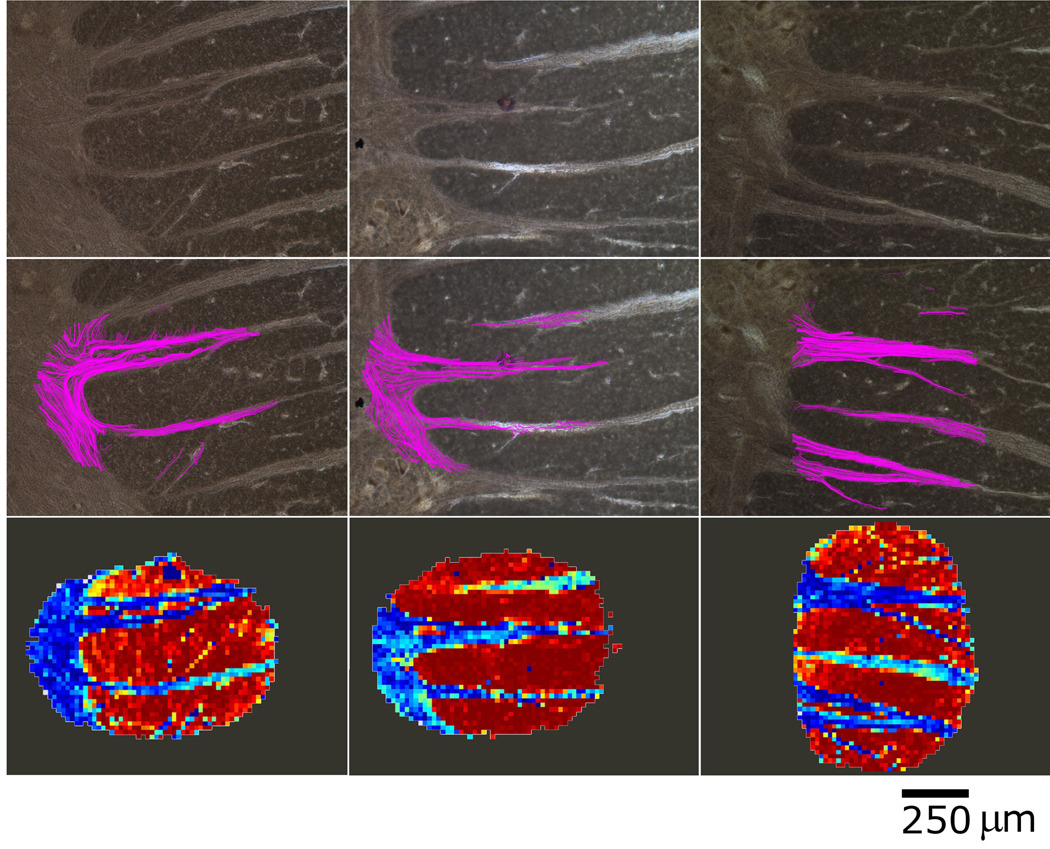
Figure 2 shows a set of coregistered images—light microscopy and MRM—depicting the tracts predicted by the DTT algorithm superimposed on the Nissl-stained histology image. Spatial characteristics of the in-plane white matter tracts—i.e., those remaining contiguous over many voxels across the histology slice—are clearly visible. While the synthetic tracts do not offer an error-free illustration of the motor efferents’ locations in the spinal cord sample, the correlation between actual and predicted tracts is robust and evident upon viewing the histology and overlay. Analysis from a second sample is presented in figure 3 where it is shown that the spatial variation in the primary eigenvector component orthogonal to the image plane (figure 3A) corresponds well to the GM/WM boundary in the sample visualized in the histology (figure 3B). The results of the tractographic analysis for this data set are seen in figure 3C. Figure 4 illustrates the results from three additional DTI experiments correlated with histology images stained using the Black-Gold II compound. Histological results are displayed in the top row and the predicted tracts from our DTT analysis are shown overlaid on the same light microscopy images in the middle row. The location of fibers predicted by the tractography is seen to be quite precise when compared to the locations of actual fiber bundles present in the histology. The degree of correspondence is quantified using the processes outlined in figure 1. It should be noted that similar binary maps generated using FA values were found to be insufficient for describing the microstructural architecture within the slice (data not shown). We find that the agreement between the maps of pixels with predominantly in-plane fiber orientation and the histology is high (from left to right in fig 4: 0.82, 0.95, 0.89) for all three Black-Gold II stained tissue samples, with a mean degree of correspondence (DC) equal to 0.89 ± 0.06. The bottom row of panels consists of maps representing the orthogonal component of the primary eigenvector which can be seen to reflect tissue structure quite closely. Figure 5 shows the selected ROIs used in the angular analysis described above. The results from the angular analysis are provided in Table 1 where mean direction (measured in degrees) of the in-plane components of the primary eigenvector in each ROI is provided along with the fiber direction (also measured in degrees) measured in the corresponding areas of the correlative histology. Our results indicate that there is agreement between the angles derived from DTI and those selected from histology in all nine cases.
Figure 2.
A) Nissl-stained histology image of human spinal cord section (50µm tissue thickness) B) The same sample overlaid with predicted fiber trajectories obtained by FACT tractography.
Figure 3.
A) A map of human S.C. tissue showing WM/GM boundary as reflected in the size of the primary eigenvector component that is orthogonal to the tissue plane (map was interpolated to higher resolution than the MR data). Blue regions correspond to areas with a smaller component in the direction orthogonal to the image plane while warmer colors represent larger components. The variation is seen to compare favorably to the gray/white matter separation seen in the histology (B). The white circle in B represents the area of the slice in the excitation profile of the surface coil while the red arrows indicate locations of the largest diameter tracts. C) The tractography overlay (green) superimposed on the image of Nissl-stained histology. Red dots indicate histological landmarks that were used in the coregistration.
Figure 4.
Three example datasets of Black-Gold II stained histology (top row) and their corresponding superimposed tractography overlays (middle row). Note the different structural contrast obtained with the Black Gold II stain which exhibits specific binding to myelin structures compared to the Nissl stain used for neuronal labeling employed in figures 2 and 3. The bottom row shows the variation in the component of the primary eigenvector orthogonal to the image plane (through-plane). Blue colors represent the smaller components while warmer colors represent the larger. This component of the primary eigenvector is seen to reflect tissue structure closely. In this manner, all three components of the primary eigenvector (two in-plane used in the DTT, and the through-plane component in the bottom row) are shown graphically to contain precise structural information matching the histology. The DC values for these sets are from left to right: 0.82, 0.95, 0.89.
Figure 5.
The ROIs selected for use in our angular analysis. Areas of varying sizes were chosen to ensure that each could be precisely identified in both DTI data and histology and to avoid possible bias which could result from having only large or only small ROIs.
Table 1.
Results from the angular analysis of three ROIs selected in each of the three Black-Gold II stained samples. No uncertainty is stated for the histological measures as these are numbers are based on one measurement along the entire length of the chosen ROI.
| Sample 1 | Sample 2 | Sample 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ROI1 (8 pixels) |
ROI2 (4 pixels) |
ROI3 (10 pixels) |
ROI1 (5 pixels) |
ROI2 (15 pixels) |
ROI3 (9 pixels) |
ROI1 (9 pixels) |
ROI2 (18 pixels) |
ROI3 (6 pixels) |
|
| Mean DTI angle ± std (degrees) | 42.7±5.2 | 44.6±4.9 | 85.1±5.7 | 41.2±6.9 | 90.8±6.7 | 92.6±12.7 | 23.9±7.7 | 9.4±4.3 | 29.0±6.9 |
| Fiber angle measured in histology (degrees) | 41.5 | 41.9 | 87.3 | 42.5 | 87.8 | 89.4 | 28.9 | 13.0 | 32.4 |
Discussion
Spinal cord tissue is ideally suited for the current study due to it being well ordered with fiber trajectories running through-plane in the case of the spinal cords’ exterior white matter and running in-plane in the case of tracts projecting from the gray matter into the orthogonally oriented white matter. This order is reproduced faithfully in figure 3A–B where only the through-plane component of the primary eigenvector is needed to outline this tissue structure.
The obvious orientational agreement between the DTT analysis and the actual tissue fibers seen in figures 2–4 and the angular analysis summarized in Table 1 all support the assumption that the direction of the primary eigenvector corresponds to actual fiber orientation. This is no doubt due to the high image resolution achievable with the micro surface-coils employed where we are far less likely to encounter voxels containing kissing, crossing or curving fiber bundles compared to data collected at lower resolutions. Having demonstrated this orientational agreement, our further quantitative analysis focused exclusively on the in-plane component of the primary eigenvector of the diffusion tensor as indicative of fibrous structure. Our analysis shows that—on average—89% of the pixels predicted to contain in-plane fiber structure correlate with fibrous structure in the histology. Taken together with the faithful reproduction of the GM/WM boundary (figure 3A–B and figure 4 top and bottom rows) by the remaining (orthogonal) component of the primary eigenvector, we have demonstrated that all three components of the primary eigenvector (two in-plane components used in the tractography, and the out-of-plane component compared to GM/WM boundary) reflect tissue structure in a very direct manner. Potential causes for failure in the remaining 11% of voxels may be attributed to multiple sources, including uneven uptake of stain, stain contrast lost in image processing (downsampling and thresholding), registration errors, low SNR, and possibly small signal distortions due to susceptibility artifacts at these high field strengths. A thorough investigation of these issues is needed prior to commenting on the specific contributions of each and will be addressed whenever possible as the presented techniques are refined.
While myelin is not solely responsible for the anisotropy of diffusion in white matter, it is nonetheless an effective target for identifying white matter tracts in the central nervous system; however, because only a portion of axons in the spinal cords’ ventral roots are myelinated, not all axonal material will be labeled when employing a myelin-specific stain. While this technical limitation may seem to confound our ability to successfully delineate axonal structure in our histology, it is important to consider the methodology being employed in the DTT analysis. For example, despite the high–resolution nature of our DTI data, we are not as of yet able to regularly visualize individual axons. Due to volume-averaging effects and the tendency of axons to be organized into bundles which form tracts, the data generated in each MR voxel containing said tracts is—in the majority of cases—still comprised of multiple axonal elements. As such, the histology’s ability to report the spatial characteristics of each individual axon is less important than its ability to distinguish between groups of axons traveling across the tissue plane and axons passing orthogonally to these: i.e. through the tissue plane. Owing to the increased myelin content in white-matter portions of the spinal cord—consisting primarily of through-plane axonal tracts—this was indeed the case as evidenced by the contrast generated in our histology. With these considerations in mind, we assert that a myelin-specific stain is relevant for assessing DTT accuracy using the MR microscopy methods presented here. An alternative measure of correlation was introduced in (Flint et al., 2010), but with the larger fiber bundles present in samples used in the current study, we believe the chosen method based on a myelin-specific stain is the most suitable. Also, generation of the binary maps allowing for our quantitative analysis would not have been possible using the Nissl staining methods employed in our previous study.
Dyrby et al. (2007) also use the overlap fraction introduced in (Anbeek et al. 2004) as a measure of the spatial agreement between projections they detect by manganese labeling and probabilistic tractography. It is interesting to note that the best agreements reported in that study (range = 0.59–0.98; overall average ± std = 0.77 ± 0.13) resemble ours although with more variation. This may be due to the fact that their results were obtained in three different regions of cortex and using methods that differ fundamentally from our approach.
The study by Leergaard et al. (2010) contained an analysis of the angular agreement between fiber orientation distributions obtained from both MRI (QSI – q-space imaging) and histology. They reported an average orientation error of 5–7 degrees even in regions with complex architectures of crossing fibers. As studies such as this demonstrate, experiments employing higher imaging resolution report improved angular agreement between DTI and histology even when using less advanced analytical methods. This phenomenon is also demonstrated in the present study and is attributable to the high intravoxel tissue homogeneity exhibited by MRM.
An alternative approach could have been to compare the performance of different tractography algorithms or analytical strategies: i.e. deterministic compared to probabilistic methods; however, such studies geared at comparing differences between algorithms run the risk of reporting differences that could be implementation-specific rather than method specific in nature. Such issues have recently been reported in a study comparing tractography results compiled from the same DW MRI data set but analyzed with four different tractography toolboxes (Bürgel et al., 2009). Here, the authors showed that comparable tracking results were not obtained despite having used similar or identical tracking algorithms in their analysis.
Because DTI and tractography are used regularly in both the laboratory and the clinic, their precision and relation to tissue structure are important for improving existing methods as well as developing new investigative and diagnostic tools. What’s more, strategies for detailed investigation of tissue microstructure with DWMR—be they aimed at direct visualization of structure as in the present study or at model-based derivation of microstructural parameters as in e.g. (Jespersen et al., 2007 and Jespersen et al. 2010)—are important milestones in developing tools for disease-specific, non-invasive MR-based diagnostics.
In summary, we have presented the first DTI in human spinal cord tissue with direct histological correlation. Our results show that the agreement between orientations of maximal diffusion and fiber orientation in the tissue is strong and thus lends support to the assumptions behind commonly employed DTT methods by which connectivity maps of the brain are obtained.
Research Highlights.
First instance of diffusion tensor microscopy with direct histological correlation in human tissue
Quantitative methods for assessing the accuracy of DTT predictions
Examination of the primary eigenvector’s role in compiling maps of tissue microstructure
Acknowledgements
Funding provided by the NIH (1R01EB012874), the NSF through the National High Magnetic Field Laboratory, the KTI (Switzerland, CTI project 6364.1 KTS-NM), the Danish National Research Foundation (95093538- 2458, project 100297), and the Augustinus Foundation. BH thanks Jesper R. Frandsen (CFIN) for discussions. We would like to thank the AMRIS facility at the University of Florida McKnight Brain Institute for institutional support. We would also like to thank Science Care, Inc. for providing the human tissue specimens employed in the current study.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Author contributions:
JF, BH, PVP and SJB designed research; JF and BH performed research; BH analyzed data; MAK and CHL assisted with histology; MF and DS designed and fabricated the microcoils; JF and BH wrote the paper; JF, BH, PVP and SJB edited the paper.
The authors declare no conflict of interest.
None of the authors have any competing financial interests.
References
- Alexander AL, Hasan KM, Lazar M, Tsuruda JS, Parker DL. Analysis of partial volume effects in diffusion-tensor MRI. Magn Reson Med. 2001;45(5):770–780. doi: 10.1002/mrm.1105. [DOI] [PubMed] [Google Scholar]
- Alexander DC, Barker GJ, Arridge SR. Detection and modeling of non-Gaussian apparent diffusion coefficient profiles in human brain data. Magn Reson Med. 2002;48(2):331–340. doi: 10.1002/mrm.10209. [DOI] [PubMed] [Google Scholar]
- Anderson A, Ding Z. Sub-voxel measurement of fiber orientation using high angular resolution diffusion tensor imaging; Proc. 10th annual meeting of the ISMRM Honolulu; Berkeley, USA: ISMRM; 2002. p. 440. [Google Scholar]
- Anbeek P, Vincken KL, van Osch MJP, Bisschops RHC, van der Grond J. Probabilistic segmentation of white matter lesions in MR imaging. Neuroimage. 2004;21:1037–1044. doi: 10.1016/j.neuroimage.2003.10.012. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys J. 1994;66(1):259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens TEJ, Jbabdi S. MR Diffusion Tractography. In: Johansen-Berg H, Behrens TEJ, editors. Diffusion MRI – From quantitative measurement to in vivo neuroanatomy. Academic Press; 2009. pp. 333–351. Chapter 15 in ISBN: 978-0-12-374709-9. [Google Scholar]
- Bürgel U, Mädler B, Honey CR, Thron A, Gilsbach J, Coenen VA. Fiber tracking with distinct software tools results in a clear diversity in anatomical fiber tract portrayal. Cen Eur Neurosurg. 2009;70(1):27–35. doi: 10.1055/s-0028-1087212. [DOI] [PubMed] [Google Scholar]
- Catani M. Diffusion tensor magnetic resonance imaging tractography in cognitive disorders. Curr. Opin. Neurol. 2006;19(6):599–606. doi: 10.1097/01.wco.0000247610.44106.3f. [DOI] [PubMed] [Google Scholar]
- Ciccarelli O, Behrens TE, Altmann DR, Orrell RW, Howard RS, Johansen-Berg H, Miller DH, Matthews PM, Thompson AJ. Probabilistic diffusion tractography: a potential tool to assess the rate of disease progression in amyotrophic lateral sclerosis. Brain. 2006;129:1859–1871. doi: 10.1093/brain/awl100. [DOI] [PubMed] [Google Scholar]
- Coggeshall RE, Applebaum ML, Fazen M, Stubbs TB, III, Sykes MT. Unmyelinated axons in the human ventral roots, a possible explanation for the failure of dorsal rhizotomy to relieve pain. Brain. 1975;98:157–166. doi: 10.1093/brain/98.1.157. [DOI] [PubMed] [Google Scholar]
- Dyrby TB, Søgaard LV, Parker GJ, Alexander DC, Lind NM, Baaré WF, Hay-Schmidt A, Eriksen N, Pakkenberg B, Paulson OB, Jelsing J. Validation of in vitro probabilistic tractography. Neuroimage. 2007;37(4):1267–1277. doi: 10.1016/j.neuroimage.2007.06.022. [DOI] [PubMed] [Google Scholar]
- Ellis CM, Simmons A, Jones DK, Bland J, Dawson JM, Horsfield MA, Williams SC, Leigh PN. Diffusion tensor MRI assesses corticospinal tract damage in ALS. Neurology. 1999;53(5):1051–1058. doi: 10.1212/wnl.53.5.1051. [DOI] [PubMed] [Google Scholar]
- Flint JJ, Lee C-H, Hansen B, Fey M, Schmidig D, Bui JD, King MA, Vestergaard-Poulsen P, Blackband SJ. Magnetic resonance microscopy of mammalian neurons. Neuroimage. 2009;46(4):1037–1040. doi: 10.1016/j.neuroimage.2009.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flint JJ, Hansen B, Fey M, Schmidig D, King MA, Vestergaard-Poulsen P, Blackband SJ. Cellular-level diffusion tensor microscopy and fiber tracking in mammalian nervous tissue with direct histological correlation. Neuroimage. 2010;52(2):556–561. doi: 10.1016/j.neuroimage.2010.04.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank LR. Characterization of anisotropy in high angular resolution diffusion-weighted MRI. Magn Reson Med. 2002;47(6):1083–1099. doi: 10.1002/mrm.10156. [DOI] [PubMed] [Google Scholar]
- Hubbard PL, Parker GJM. Diffusion MRI – From quantitative measurement to in vivo neuroanatomy. Chapter 17. Academic Press; 2009. Validation of Tractography. 2009. [Google Scholar]
- Jansons KM, Alexander DC. Persistent angular structure: New insights from diffusion MRI data. Inverse Problems. 2003;19:1031–1046. doi: 10.1007/978-3-540-45087-0_56. [DOI] [PubMed] [Google Scholar]
- Jespersen SN, Kroenke CD, Østergaard L, Ackerman JJ, Yablonskiy DA. Modeling dendrite density from magnetic resonance diffusion measurements. Neuroimage. 2007;34(4):1473–1486. doi: 10.1016/j.neuroimage.2006.10.037. [DOI] [PubMed] [Google Scholar]
- Jespersen SN, Bjarkam CR, Nyengaard JR, Chakravarty MM, Hansen B, Vosegaard T, Østergaard L, Yablonskiy D, Nielsen NC, Vestergaard-Poulsen P. Neurite density from magnetic resonance diffusion measurements at ultrahigh field: comparison with light microscopy and electron microscopy. Neuroimage. 2010;49(1):205–216. doi: 10.1016/j.neuroimage.2009.08.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim JH, Budde MD, Liang HF, Klein RS, Russell JH, Cross AH, Song SK. Detecting axon damage in spinal cord from a mouse model of multiple sclerosis. Neurobiol. Dis. 2006;21(3):626–632. doi: 10.1016/j.nbd.2005.09.009. [DOI] [PubMed] [Google Scholar]
- Kim JH, Loy DN, Liang HF, Trinkaus K, Schmidt RE, Song SK. Noninvasive diffusion tensor imaging of evolving white matter pathology in a mouse model of acute spinal cord injury. Magn. Reson. Med. 2007;58(2):253–260. doi: 10.1002/mrm.21316. [DOI] [PubMed] [Google Scholar]
- Ko H-Y, Shin YB, Sohn HJ, Chang HJ, Ahn YH, Ha YH. Unmyelinated fibers in human spinal ventral roots : C4 to S2. Spinal Cord. 2009;47:286–289. doi: 10.1038/sc.2008.97. [DOI] [PubMed] [Google Scholar]
- Leergaard TB, White NS, de Crespigny A, Bolstad I, D'Arceuil H, Bjaalie JG, Dale AM. Quantitative histological validation of diffusion MRI fiber orientation distributions in the rat brain. PLoS One. 2010;5(1) doi: 10.1371/journal.pone.0008595. e8595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin CP, Tseng WY, Cheng HC, Chen JH. Validation of diffusion tensor magnetic resonance axonal fiber imaging with registered manganese-enhanced optic tracts. Neuroimage. 2001;14(5):1035–1047. doi: 10.1006/nimg.2001.0882. [DOI] [PubMed] [Google Scholar]
- Lin CP, Wedeen VJ, Chen JH, Yao C, Tseng WY. Validation of diffusion spectrum magnetic resonance imaging with manganese-enhanced rat optic tracts and ex vivo phantoms. Neuroimage. 2003;19(3):482–495. doi: 10.1016/s1053-8119(03)00154-x. [DOI] [PubMed] [Google Scholar]
- Lin F, Yu C, Jiang T, Li K, Chan P. Diffusion tensor tractography-based group mapping of the pyramidal tract in relapsing-remitting multiple sclerosis patients. AJNR Am. J. Neuroradiol. 2007;28(2):278–282. [PMC free article] [PubMed] [Google Scholar]
- Lori NF, Akbudak E, Shimony JS, Cull TS, Snyder AZ, Guillory RK, Conturo TE. Diffusion tensor fiber tracking of human brain connectivity: aquisition methods, reliability analysis and biological results. NMR Biomed. 2002;15(7–8):494–515. doi: 10.1002/nbm.779. [DOI] [PubMed] [Google Scholar]
- Mori S, Crain BJ, Chacko VP, Van Zijl PCM. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann. Neurol. 1999;45:265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Mori S. Introduction to Diffusion Tensor Imaging. Elsevier, Amsterdam. 2007 ISBN: 978-0-444-52828-5. [Google Scholar]
- Perrin M, Poupon C, Rieul B, Leroux P, Constantinesco A, Mangin JF, Lebihan D. Validation of q-ball imaging with a diffusion fibre-crossing phantom on a clinical scanner. Philos Trans R Soc Lond B Biol Sci. 2005;360(1457):881–891. doi: 10.1098/rstb.2005.1650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips OR, Nuechterlein KH, Clark KA, Hamilton LS, Asarnow RF, Hageman NS, Toga AW, Narr KL. Schizophr. Res. 2009;107(1):30–38. doi: 10.1016/j.schres.2008.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seunarine KK, Alexander DC. Diffusion MRI – From quantitative measurement to in vivo neuroanatomy. Chapter 4. Academic Press; 2009. Multiple fibers: beyond the diffusion tensor. 2009. [Google Scholar]
- Simonyan K, Tovar-Moll F, Ostuni J, Hallett M, Kalasinsky VF, Lewin-Smith MR, Rushing EJ, Vortmeyer AO, Ludlow CL. Focal white matter changes in spasmodic dysphonia: a combined diffusion tensor imaging and neuropathological study. Brain. 2008;131(Pt 2):447–459. doi: 10.1093/brain/awm303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song SK, Sun SW, Ramsbottom MJ, Chang C, Russell J, Cross AH. Dysmyelination revealed through MRI as increased radial (but unchanged axial) diffusion of water. Neuroimage. 2002;17(3):1429–1436. doi: 10.1006/nimg.2002.1267. [DOI] [PubMed] [Google Scholar]
- Tournier JD, Calamante F, King MD, Gadian DG, Connelly A. Limitations and requirements of diffusion tensor fiber tracking: an assessment using simulations. Magn Reson Med. 2002;47(4):701–708. doi: 10.1002/mrm.10116. [DOI] [PubMed] [Google Scholar]
- Tournier JD, Calamante F, Gadian DG, Connelly A. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. Neuroimage. 2004;23(3):1176–1185. doi: 10.1016/j.neuroimage.2004.07.037. [DOI] [PubMed] [Google Scholar]
- Tuch DS. PhD thesis. 2002. Diffusion MRI of complex tissue structure. available online at http://noodle.med.yale.edu/~mjack/papers/tuch-thesis.pdf. [Google Scholar]
- Tuch DS, Reese TG, Wiegell MR, Wedeen VJ. Diffusion MRI of complex neural architecture. Neuron. 2003;40(5):885–895. doi: 10.1016/s0896-6273(03)00758-x. [DOI] [PubMed] [Google Scholar]
- Tuch DS. Q-ball imaging. Magn. Reson. Med. 2004;52:1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
- Tyszka JM, Readhead C, Bearer EL, Pautler RG, Jacobs RE. Statistical diffusion tensor histology reveals regional dysmyelination effects in the shiverer mouse mutant. Neuroimage. 2006;29(4):1058–1065. doi: 10.1016/j.neuroimage.2005.08.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Donkelaar CC, Kretzers LJ, Bovendeerd PH, Lataster LM, Nicolay K, Janssen JD, Drost MR. Diffusion tensor imaging in biomechanical studies of skeletal muscle function. J Anat. 1999;194(Pt 1):79–88. doi: 10.1046/j.1469-7580.1999.19410079.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Doorn A, Bovendeerd PH, Nicolay K, Drost MR, Janssen JD. Determination of muscle fibre orientation using Diffusion-Weighted MRI. Eur J Morphol. 1996;34(1):5–10. doi: 10.1076/ejom.34.1.5.13156. [DOI] [PubMed] [Google Scholar]
- Voineskos AN, Lobaugh NJ, Bouix S, Rajji TK, Miranda D, Kennedy JL, Mulsant BH, Pollock BG, Shenton ME. Diffusion tensor tractography findings in schizophrenia across the adult lifespan. Brain. 2010;133:1494–1504. doi: 10.1093/brain/awq040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedeen VJ, Reese TG, Tuch DS, Dou J-G, Weiskoff RM, Chessler D. Mapping fiber orientation spectra in cerebral white matter with Fourier-transform diffusion MRI; Proc. 7th Annual meeting of the ISMRM; Philadelphia, Berkeley, USA: ISMRM; 1999. p. 321. [Google Scholar]
- Werring DJ, Clark CA, Barker GJ, Thompson AJ, Miller DH. Diffusion tensor imaging of lesions and normal-appearing white matter in multiple sclerosis. Neurology. 1999;52(8):1626–1632. doi: 10.1212/wnl.52.8.1626. [DOI] [PubMed] [Google Scholar]
- Yu CS, Li KC, Xuan Y, Ji XM, Qin W. Diffusion tensor tractography in patients with cerebellar tumors: a helpful technique for neurosurgical planning and postoperative assessment. Eur. J. Radiol. 2005;56(2):197–204. doi: 10.1016/j.ejrad.2005.04.010. [DOI] [PubMed] [Google Scholar]