Three-dimensional Elastic Image Registration Based on Strain Energy Minimization: Application to Prostate Magnetic Resonance Imaging

Abstract

The use of magnetic resonance (MR) imaging in conjunction with an endorectal coil is currently the clinical standard for the diagnosis of prostate cancer because of the increased sensitivity and specificity of this approach. However, imaging in this manner provides images and spectra of the prostate in the deformed state because of the insertion of the endorectal coil. Such deformation may lead to uncertainties in the localization of prostate cancer during therapy. We propose a novel 3-D elastic registration procedure that is based on the minimization of a physically motivated strain energy function that requires the identification of similar features (points, curves, or surfaces) in the source and target images. The Gauss–Seidel method was used in the numerical implementation of the registration algorithm. The registration procedure was validated on synthetic digital images, MR images from prostate phantom, and MR images obtained on patients. The registration error, assessed by averaging the displacement of a fiducial landmark in the target to its corresponding point in the registered image, was 0.2 ± 0.1 pixels on synthetic images. On the prostate phantom and patient data, the registration errors were 1.0 ± 0.6 pixels (0.6 ± 0.4 mm) and 1.8 ± 0.7 pixels (1.1 ± 0.4 mm), respectively. Registration also improved image similarity (normalized cross-correlation) from 0.72 ± 0.10 to 0.96 ± 0.03 on patient data. Registration results on digital images, phantom, and prostate data in vivo demonstrate that the registration procedure can be used to significantly improve both the accuracy of localized therapies such as brachytherapy or external beam therapy and can be valuable in the longitudinal follow-up of patients after therapy.

Introduction

The use of magnetic resonance imaging (MRI) in the staging and follow-up of patients with prostate cancer has been steadily increasing, and MRI has been used for preoperative evaluation, cancer staging, and image guidance for prostate interventions.^1–4 Magnetic resonance imaging in conjunction with endorectal coil and MR spectroscopy (MRS) has been shown to further improve the sensitivity and specificity of cancer detection, providing high-quality images with nearly a tenfold signal-to-noise improvement over body phased-array coils.^5–7 Although rigid endorectal probes are available, the most popular endorectal probe uses a balloon. This device involves the insertion of the endorectal coil in the rectum followed by inflation of the balloon that covers the coil to about 40∼60 cc of air while ensuring that the coil face is against the posterior portion of the prostate gland. This procedure secures the prostate gland between the coil and pubic bone and ensures that the gland itself does not move during the imaging procedure. However, this technique results in images with significant distortion. For image-guided interventions such as external beam therapy or brachytherapy, such distortions must be taken into account before an effective treatment plan can be generated.

Several investigators have proposed both rigid and nonrigid registration to correct for prostate image distortion introduced by the endorectal coil. Rigid body registration deals with the translation and rotation of images.^8,9 The underlying global transformation is expressed in terms of a finite number of parameters (i.e., three parameters each for translation, rotation, scaling, and shear). Under certain circumstances, however, these global transformations are inadequate to describe the transformation, especially in the case of highly localized deformation. This has led to the development of nonrigid registration techniques. The two general transformation functions employed in nonrigid registration that delineate the local distortion are polynomials¹⁰ and thin-plate splines (TPS).^11–13 The coefficients of the polynomial and the TPS functions are obtained by maximizing the cost functions using normalized cross-correlation or mutual information.¹³

Other nonrigid registration methods provide transformations that are solutions to the governing equations based on the physical model used. These methods include elastic registration,^14–17 fluid registration,¹⁸ diffusion-based registration,¹⁹ and optical flow-based registration.²⁰ Among these registration methods, elastic registration is of particular interest in prostate imaging because it appropriately models the prostate as a 3D, incompressible elastic object.

Here, we present a novel elastic registration algorithm that is based on strain energy minimization. Rather than computing the forces and solving the force–balance equations for deformation as demonstrated by many investigators, the proposed registration algorithm derives the deformation using the strain energy minimization technique. Results from this algorithm are presented on simulated digital images, prostate phantom images, and images obtained from patients who underwent prostate MR imaging using the endorectal coil.

Materials and Methods

Theory of Strain Energy Minimization

According to the principles of dynamics, the potential energy function has a stationary value if the system is conservative and is in equilibrium. This implies that when the system is stable, the potential energy function is at a minimum.²¹ This theorem has broad applications in engineering in determining the deformation, stress, and strain distributions of a static system. This theorem forms the basis in deriving the transformation matrix to align endorectal coil based images before and after distortion.

Treating the prostate as an elastic body, the potential energy of the system at static equilibrium is purely the strain energy U, as defined in the following expression:²²

1

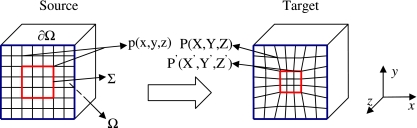
where, λ and μ are two Lame constants characterizing material constitutive properties, μ is the shear modulus of the material characterizing the rigidity, λ is an engineering constant that describes the effects of dilatation based on tensile stress, ε_p (p = x, y, or z) is the normal strain in p direction, γ_pq (pq = xy, yz, or zx) is the shear strain in the p plane pointing toward q, e is the unit volume change, and Ω is the prostate volume (Fig. 1).

Fig 1.

Schematic of the registration model. Voxels in the source image are denoted p(x,y,z). Under deformation they evolve into P(X,Y,Z) or P’(X’,Y’,Z’) if the source voxel belongs to the set Σ. In this figure, Σ is a voxel set of interest as denoted by the red square. Also, Ω denotes the image volume, and ∂Ω denotes the surfaces of volume Ω.

Krouskop et al.²³ determined the Poisson’s ratio of prostate tissue to be 0.495, this was also confirmed by Read’s study.²⁴ Given this, the first term λe² in Eq. 1 can be ignored since it is two orders of magnitude lower than the other two terms (see Appendix 1). Thus the above equation is simplified to:

2

Based on the strain–displacement relationship,²² this equation can be rewritten in terms of displacement (position change of a point) in the Cartesian coordinate system as:

3

where, u, v, and w are the displacements in x, y, and z directions, respectively.

The strain energy minimization requires that

4

and when this is subjected to the Dirichlet boundary conditions:

5

where, ∂Ω denotes the boundary of volume Ω (see Fig. 1).

Equation 4 is also constrained by the correspondences of image features (such as contours in 2D or surfaces in 3D) between the source and target images. Please note that the source image is the non-deformed image, the target image, or the reference image is the one obtained in the deformed state, and the registered image is the source image that has been transformed to the reference image. Suppose that we have a point p(x, y, z) in the source image, and as a result of distortion correction it moves to point P(X, Y, Z) (P is to be determined through registration). If point p(x, y, z) belongs to Σ (the set of voxels of those features in the source image that have corresponding features in the target; Fig. 1), it will move to its corresponding point P^’(X^’,Y’,Z’) in the target image for which a position is measured manually or automatically. Then the constraint can be expressed in the form of the energy function:

6

The transformation between the source and target images can be obtained by solving Eqs. 4–6. The obtained transformation, that is, the strain energy minimization transformation (SEMT), forms the basis of the novel elastic registration on prostate endorectal coil MR imaging (erMRI).

Discretization

Suppose we have 2 images I_s and I_t, where I_s is the source image and I_t is the target image. The voxel p_ijk(x_ijk, y_ijk,z_ijk) in I_s evolves into the voxel P_ijk(X_ijk, Y_ijk,Z_ijk) in I_t. Here i, j, and k are in the range of [1,L], [1,M], and [1,N], respectively, and (L,M,N) are the dimensions of the image volume. The displacement vector (u, v, w) of voxel p_ijk is:

7

Plugging in Eqs. 3 and 7 to Eq. 4 and using forward difference formula, Eq. 4 can be discretized to a set of linear equations. The new positions P_ijk(X_ijk, Y_ijk, Z _ijk) are the solutions of the linear equation system:

8

for 2 ≤ i ≤ L – 1, 2 ≤ j ≤ M – 1, 2 ≤ k ≤ N–1, and (i, j, k) ∉ Σ.

The boundary conditions as described by Eq. 5 and the constraints as expressed in Eq. 6, leads us to the following:

9

10

The final registered image volume can be computed from Eqs. 8–10.

Note that there are no constitutive parameters such as λ and μ in Eqs. 8–10, which makes this algorithm essentially parameter free. The new voxel position P_ijk(X_ijk, Y_ijk, Z_ijk) is expressed as an explicit function of the positions of its closest neighbors.

Numerical Implementation

The Gauss–Seidel method was used to iteratively compute the solutions of the linear equation system (Eqs. 8–10). Convergence for the numerical implementation was set such that the position difference (or displacement) of any voxel between two consecutive iterations was less than ε (0.01 pixels in our case) or when the number of iteration reached s₀. Figure 2 illustrates the procedure of this novel registration algorithm and the numerical implementation of SEMT. This algorithm was implemented in the MATLAB environment (Mathworks, Inc., Natick, MA, USA).

Fig 2.

Flowchart of the registration procedure and the SEMT algorithm using Gauss–Seidel method.

To estimate the number of iterations required for convergence, the above algorithm was applied to a pair of digital images consisting of a rectangular grid of correspondence points with a deformation similar to the one depicted in Figure 1. After each iteration, the maximum difference between the source and target correspondence points (in voxels) was found Figure 3 shows a typical relationship between the difference of two consecutive iterations and the iteration number. As can be seen, a difference of 0.01 is approached when the number of iterations reaches 300. For the purpose of our study we set the maximum number of iterations, s₀, to 300. The computation time needed for 300 iterations is about 20 s for a 2D registration and 15∼30 min for 3D registration on a 3.4-GHz personal computer.

Fig 3.

Semi-log plot depicting the number of iterations required for a given maximum difference.

Validation

Validation of the algorithm was accomplished on digital phantoms, a prostate phantom designed in house, and actual prostate MR images acquired using an endorectal coil. To assess the accuracy of the strain energy minimization transformation (SEMT) algorithm, the intensity difference, normalized cross-correlation coefficient (NCC), and displacement of known landmarks were computed.

Digital Phantom

A digital phantom was generated that consisted of a sphere (radius 10, arbitrary units) centered in a 30 × 30 × 30 (arbitrary units) volume. A 3D character ‘F’ was embedded in the sphere as shown in Figure 4. For simplicity, the sphere was assumed to be elastic, isotropic, and homogeneous. A known deformation was applied to this digital phantom to test the efficacy of the algorithm in registering the sphere to the ellipsoid. In our study the sphere was elastically deformed to an ellipsoid (three semiaxes: a = 9, b = 12, and c = 10 in x, y, and z directions, respectively) along with the embedded 3D character ‘F’. In this case, the sphere is the source image, which is deformed to the ellipsoid, the target or reference image. A total of 186 predefined matching landmarks on the surfaces of the sphere and the ellipsoid were used to derive the transformation matrix using the SEMT algorithm.

Fig 4.

The 3D open look of a the source sphere, b the target ellipsoid, and c the registered volume with a character ’F’ inside. The Cartesian coordinate system is shown for later reference in Figure 6.

Prostate Phantom

The prostate phantom as shown in Figure 5 was built in-house and incorporates all the necessary elements of a prostate gland, including tissue consistency and the biochemicals contained within a normal prostate tissue.²⁵ The gland was constructed from 0.5% agarose (Type I Low EEO 9012-36-6, Sigma Chemical Co., St. Louis, MO, USA) and was made in the shape of an ellipsoid with dimensions of 50 × 40 × 30 mm³ in the x, y, and z directions. The gland was doped with 0.1 mM gadolinium diethyltriaminepentaacetic acid, producing visible contrast between the gland and the background gel. The biochemicals choline (10 mM), creatine (30 mM), citrate (100 mM), and lactate (35 mM), which are predominantly seen in prostate MRS imaging, were also added. A thin layer of lard was added surrounding the gland to mimic periprostatic fat. A piece of polycarbonate bar was placed above the gland to constrain deformation, much as the pubic bone would do in the actual prostate. At the bottom of the phantom, a tunnel allowed insertion of the endorectal coil. Sesame seeds were randomly embedded within the prostate phantom, and their displacement was used in assessing the accuracy of the registration. Images of this prostate phantom were first obtained with the endorectal inserted but with no balloon inflation (source images). As in normal prostate erMRI, the balloon was then inflated with 100 cc of air, which allowed the prostate phantom to distort in a manner similar to that of a real prostate gland during an in vivo erMRI procedure. MR images were obtained in this distorted position (target images).

Fig 5.

Prostate phantom: a picture of the prostate phantom, and b representative MR image. Sesame seeds are shown as dark dots in the gland.

Forty matching landmark points along each of the semi-automatically drawn contours were used to correct for deformation. In total, there were 400 landmark points for the entire prostate that were used in determining the transformation matrix.

In vivo Data

The registration algorithm was also applied on ten sets of human prostate data, each with two typical deformation states (one with 0 cc of air and the other with 40–60 cc of air inflated in the endorectal coil balloon). Once again, the source images are obtained with deflated coil and the target images are obtained with the balloon inflated. The matching landmarks along the prostate surface were selected in the same fashion as stated in the section above. There were a total of 200∼400 landmarks used to derive the transformation depending on the size of each prostate. Approval from the University of Maryland Institutional Review Board was obtained for this study.

Registration Evaluation

The performance of the registration algorithm was assessed using normalized NCC between the target and the registered images using the following relationship:

where, I_1ijk and I_2ijk are the image intensities at point (i,j,k) in image I₁ and I₂, respectively, and and are the average intensities of I₁ and I₂, respectively. If NCC = 1, then I₁ and I₂ are identical, which means a perfect registration.

Registration error was assessed by averaging the displacement of a fiducial landmark in the target image to its corresponding point in the registered image. These fiducial landmarks were either geometric or anatomic, both of which were identified in the target image and have correspondences in the registered image. A typical dataset usually used two to six fiducial landmarks per slice depending on the visible features inside the prostate. In the case of the prostate phantom, the embedded sesame seeds allowed us to measure the displacement of a point resulting from the inflation of the coil balloon and then to assess the accuracy of the registration algorithm.

Comparison to Other Registration Techniques

We compared the results of our SEMT registration with established affine and B-spline registration techniques. Both these techniques are available on MIPAV (Ver 3.1.1, 2007, Center for Information Technology, National Institute of Health, Rockville, MD, USA). We performed 12-parameter affine registration, which includes three translations, three rotations, three scaling, and three shearing. For the B-spline registration, the degree of the basic functions was set to three, which guarantees a smooth displacement field. Tri-linear interpolation for performing registration operations and correlation ratio as the cost function was used for both methods.

MRI Data Acquisitions

The prostate phantom and patient data were acquired on a Philips Eclipse 1.5-T system (Philips Medical System, Cleveland, OH, USA). An endorectal coil (Medrad, Inc., Indianola, PA, USA) was used to acquire the T2-weighted axial images using a fast spin echo sequence.

The T2-weighted images of the prostate phantom were acquired while the inserted endorectal coil was fully deflated or was inflated with about 100 cc of air. The acquisition parameters were: TR/TE = 3412/91 ms, , field of view (FOV) = 16.0 cm, slice thickness = 3.0 mm, and number of slices = 29.

Ten patients (ages, 61 ± 9 years) with biopsy-confirmed prostate malignancy underwent erMRI. T2-weighted axial images of the prostate gland were obtained from patients with the inserted endorectal coil in its inflated state (40–60 cc air inflation) and completely deflated state (TE = 91 ms, TR varied from 3,500 to 4,500 ms depending on the patients, , FOV = 16 cm, and slice thickness = 3.0 mm). The slice number varied from 25 to 38, depending on the size of the prostate.

Results

Simulated Phantom Data

Figure 6 displays the registration results in three orthogonal central planes of the object shown in Figure 4. The first row shows results in the xy plane; the second row, the yz plane; and the third row, the xz plane, respectively. Each column in Figure 6 shows the target, source, registered images, the intensity difference images between the source and target images, and the intensity difference images between the target and registered images in all three orthogonal planes. Also shown in Figure 6 is the displacement distribution along the three planes, which is superimposed on the source images in the second column. The blue arrows represent the displacement vectors with the length of the arrows representing their magnitude. To facilitate visual comparison of the intensity difference between the pre- and post-registration images (Fig. 6, column 4 and column 5), the same grayscale was adopted between the two sets of images. As shown in Figure 6, the registration reduced the intensity difference in the subtracted images between the target and the registered images. The NCC improved from 0.91 to 1.0 after SEMT registration.

Fig 6.

Registration results on the synthesized digital phantom. Each row shows images in each of the orthogonal planes. Columns represent image type. The source image column is overlaid by the displacement vectors in three orthogonal planes. Also shown in target image (xy plane) are the landmarks (marked by red crosses) used to measure the accuracy of registration. NCC improved from 0.91 to 1.0.

To assess the registration error, ten corners of the character “F” (Fig. 6, xy plane and column 1) on the central slice were selected to serve as fiducial landmarks. Table 1 summarizes the displacement of these landmarks between the source and target images and the registration error. The average displacement of the landmarks between the source and target images was 1.0 ± 0.5 pixels. The algorithm attained an average registration error of 0.2 ± 0.1 pixels.

Table 1.

Position, Displacement, and Registration Error of Ten Corners of Character F in a Digital Phantom

Corner	Position (x,y) (pixel)			Displacement (pixel)	Error (pixel)
	Source	Target	Registered
C1	9.0, 7.0	10.0, 6.4	10.0, 6.1	1.3	0.3
C2	18.3, 7.0	17.2, 6.4	17.4, 6.2	1.4	0.3
C3	11.7, 9.9	11.8, 9.1	11.7, 9.1	0.9	0.1
C4	18.3, 9.9	17.2, 9.1	17.3, 9.0	1.5	0.2
C5	11.7, 12.0	11.8, 11.9	11.7, 11.9	0.2	0.1
C6	17.4, 12.0	16.2, 11.9	16.5, 12.0	1.3	0.3
C7	11.7, 14.7	11.8, 14.7	11.7, 14.7	0.1	0.1
C8	17.4, 14.7	16.2, 14.7	16.5, 14.8	1.3	0.3
C9	9.0, 20.4	10.0, 21.1	10.0, 21.3	1.3	0.2
C10	11.7, 20.4	11.8, 21.1	11.7, 21.1	0.8	0.1

Prostate Phantom Data

Figure 7 shows the registration results from one of the axial MR images taken through the center of the prostate phantom shown in Figure 5. A comparison of the intensity difference between the target and source (Fig. 7d) and the target and registered images (Fig. 7e) qualitatively demonstrates the registration accuracy obtained using the SEMT algorithm. The NCC improved from 0.84 to 0.99 after registration. Twelve sesame seeds were used as features that were matched between the target and registered information to assess the registration error. Table 2 provides a list of measurements made using these 12 seeds. The average displacement of the sesame seeds was 4.8 ± 0.4 pixels (3.0 ± 0.3 mm). The registration error was found to be 1.0 ± 0.6 pixels (0.6 ± 0.4 mm).

Fig 7.

Registration results of the prostate phantom in the xy plane: a target image, b source image overlaid with the displacement, c registered image, d intensity difference image (a–b), and e intensity difference image (a–c). NCC improved from 0.84 to 0.99.

Table 2.

Position, Displacement, and Registration Error of 12 Sesame Seeds in the Prostate Phantom

Sesame seed	Position (pixel)			Displacement (pixel)	Error (pixel)
	Source	Target	Registered
S1	130, 170	130, 174	130, 175	4.0	1.0
S2	126, 157	126, 162	125, 161	5.0	1.4
S3	119, 160	119, 165	120, 165	5.0	1.0
S4	117, 161	115, 165	116, 165	4.5	1.0
S5	140, 150	140, 155	140, 154	5.0	1.0
S6	135, 139	135, 144	135, 144	5.0	0.0
S7	130, 138	130, 143	130, 142	5.0	1.0
S8	107, 141	107, 146	106, 146	5.0	1.0
S9	141, 131	141, 136	139, 135	5.0	2.2
S10	134, 127	133, 132	133, 132	5.1	0.0
S11	125, 126	124, 131	123, 131	5.1	1.0
S12	121, 128	120, 132	120, 133	4.1	1.0

In vivo Prostate Data

Figure 8 shows an example registration from in vivo prostate images. The blue arrows shown in Figure 8b show the direction and magnitude of displacement. The comparison of intensity difference images in Figure 8d, e before and after registration, qualitatively demonstrates the registration accuracy as determined by the SEMT algorithm. Five feature landmarks (see Fig. 8a) depicting benign prostatic hyperplasia nodules of the prostate was chosen to evaluate the registration error for the slice shown. The average displacement of these five landmarks was 6.7 ± 1.5 pixels (4.2 ± 0.9 mm). The registration error was 1.7 ± 1.3 pixels (1.1 ± 0.8 mm).

Fig 8.

Representative registration results for a prostate patient: a target image with five feature landmarks marked by red crosses, b source image overlaid with the displacement, c registered image, d intensity difference image (a–b), and e intensity difference image (a–c). NCC improved from 0.69 to 0.97.

The NCC was computed over the segmented volume of the prostate and was found to improve from 0.69 to 0.97 for this particular case.

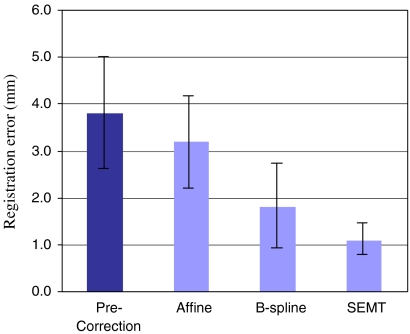
The results on all ten sets of patient images were summarized in Table 3. The NCC was improved on average from 0.72 ± 0.10 to 0.96 ± 0.03 for the whole group after SEMT registration (P < 0.0001). The average displacement of fiducial landmarks inside the prostate gland from all the subjects was found to be 6.1 ± 1.9 pixels (3.8 ± 1.2 mm) before registration, which was reduced to 1.8 ± 0.7 pixels (1.1 ± 0.4 mm) after registration. Also shown in Table 3 are the registration errors made by the 12-parameter affine registration and B-spline registration programs. The registration errors were 5.2 ± 1.6 pixels (3.2 ± 1.0 mm) when using the affine registration method and 2.9 ± 1.4 pixels (1.8 ± 0.9 mm) when using the B-spline method.

Table 3.

Normalized Correlation Coefficient, Maximum Pixel Displacement Before and After Registration Using the SEMT, Affine, and B-Spline Algorithms on In vivo Prostate Images

Patient	NCCa		Original displacement (Pixel)	Registration error (Pixel)
	Before	After		SEMT	Affine	B-spline
P1	0.71	0.98	6.0	1.3	2.2	2.1
P2	0.50	0.92	6.1	1.1	(fail)	4.8
P3	0.75	0.99	6.7	1.6	6.5	2.7
P4	0.73	0.90	6.4	3.1	5.0	1.9
P5	0.72	0.98	8.5	1.5	7.4	4.6
P6	0.74	0.98	3.0	1.4	4.6	3.6
P7	0.74	0.98	5.6	2.9	5.3	1.8
P8	0.69	0.97	6.7	2.0	6.3	1.9
P9	0.75	0.96	3.0	1.7	3.9	0.9
P10	0.62	0.98	8.8	1.2	5.6	4.8
Mean ± std	0.72 ± 0.10	0.96 ± 0.03	6.1 ± 1.9	1.8 ± 0.7	5.2 ± 1.6	2.9 ± 1.4

^aNCC was computed after manual segmentation of prostate

Discussion

MR images of the prostate are typically obtained when the prostate is in its distorted position. Advanced imaging techniques, such as diffusion-weighted imaging, perfusion-weighted imaging, and MRS, have been shown to increase specificity in the detection of cancer. However, all the information provided from these techniques is obtained with the prostate in its deformed state. For techniques such as external beam therapy and brachytherapy to be effective, prostate images obtained in the distorted state must be registered back to their original state. For example, in the case of external beam brachytherapy, the images and the spectroscopic information obtained from the prostate with the endorectal coil (deformed images) can be registered to the MR images obtained without the use of endorectal coil (non-deformed images). These images and spectra can then be co-registered with the CT images for treatment planning. This will ensure accurate localization of the tumor in its undistorted state and will allow for accurate treatment planning.

We have developed a novel SEMT algorithm to perform prostate image registration that registers images to single-pixel accuracy. The algorithm requires that the object undergoing deformation be elastic, incompressible, and in equilibrium while scanning. Incompressible tissue, such as the breast and prostate, are suitable candidates for such elastic registration.^8,13 In a physically conservative system, the potential energy has a stationary value if the system is in equilibrium. In the case of our registration problem, in which image volumes are treated as elastic bodies, the potential energy is purely the strain energy. The minimization of this strain energy allows for the transformation of the deformed elastic, incompressible objects to be registered.

In most in vivo situations it is difficult to quantitatively evaluate the performance of a registration algorithm because of the lack of ‘ground truth’. Our initial results on the simulated digital phantom and the development of a prostate phantom were essential in evaluating the robustness of the SEMT algorithm.²⁵ This multipurpose phantom mimicked the tissue property of the prostate and provided us a scenario that was as close as possible to that routinely experienced in the clinical setting. Because it has all the necessary tissue properties and biochemicals normally seen in a prostate gland, the phantom can be used to test the robustness of new imaging and spectroscopic techniques. The periprostatic fat also allows us to mimic the difficulty associated with saturating outer-volume chemical species that may alias into the volume of interest, especially when performing MRS. The sesame seeds also may be used for practicing image-guided biopsies. However, here, we used the seeds to determine the registration error of the SEMT algorithm.

The transformation matrix obtained by SEMT relies on feature correspondences between the source and target images. Any mismatch of the correspondences may result in registration errors. We have chosen well populated, uniformly distributed points along the whole surface of the prostate to derive the transformation between the source and target images. We have shown that our algorithm is accurate up to 1.1 mm based on the measurements made at corresponding feature points of the prostate. Other methods, such as active contour²⁶ and/or active surface models,²⁷ may be adopted to generate the correspondences automatically to further reduce the resolution to a subpixel level.

We compared our SEMT algorithm to two other well-established methods of registration namely the 12-parameter affine registration and B-spline registration. Figure 9 shows the performance of these two techniques in comparison to our SEMT algorithm. Given the range of displacements seen in ten prostate images as shown by the first metric in Figure 9, the SEMT algorithm outperformed the other two techniques by demonstrating nearly 38% reduction in registration errors over B-spline, and over 60% reduction in errors in comparison to the affine registration technique, respectively.

Fig 9.

Graph depicting the performance of SEMT, affine, and B-spline registration algorithms on prostate images. Minimum registration errors are realized with the SEMT algorithm.

In the last decade, many applications of image registration for prostate images have been reported. Dubois et al.⁸ implemented a rigid registration on a prostate phantom and obtained a registration error of 1.6 ± 0.7 mm. Because of anatomical variability in the prostate and because of the fairly nonrigid characteristics of transformation, rigid registration may not yield accurate results for registration of prostate images. Wu et al.¹⁰ adopted a polynomial transformation to register prostate MRSI with an error of 2 mm or less. Fei et al.¹³ applied TPS to prostate image registration, reducing the prostate centroid displacement from 3.4 to 0.6 mm. Wang et al.²⁸ implemented a ‘demons’ algorithm (a grayscale-based deformable image registration algorithm) on a phantom prostate and achieved a tracking accuracy of better than 1.5 mm. The results from our method are either comparable or better than these reported methods. A notable difference between our study and those mentioned here is that our approach is based on the use of correspondence points coupled with physical constraints, whereas the cited studies used voxel-intensity based approaches for registration.

The proposed SEMT approach is similar to those reported in the literature in that they all identify the feature correspondences (points, contours, or surfaces) in the source and target images and then use these correspondences as input to derive the underlying deformation transformation. The principal difference between our method and these others is that our transformation is derived from strain energy minimization using elastic theory. Broit¹⁴ was the first to use a model derived from elasticity theory to match 2D and 3D images. He defined a cross-correlation coefficient between local regions in two images to derive forces that deform the source image to the target. The transformation is obtained by solving the Navier–Lame equations. Instead of using the local similarity as the measure of external driving forces, Davatzikos et al.¹⁵ proposed a spring model in which the external force is obtained from mapping the contours of structures in the source and target images. They obtained their transformation by empirically choosing the two Lame constants in the equilibrium equations. Peckar et al.¹⁷ incorporated the known displacements of some boundary structures in the source and target images as hard constraints to the registration to compute the transformation. In that study, λ was intentionally set to zero and the other constant μ was eliminated. This makes the registration model completely parameter free. Unlike traditional elastic registration methods, which solve the equilibrium equations for the transformation, the SEMT method obtains the transformation by minimizing the strain energy of the registered image volume. Making a reasonable assumption of incompressibility (Krouskop et al.²³), the registration model is parameter free. The advantages of the proposed approach include the need for only a scalar energy function instead of a set of equilibrium equations; the reasonable assumption of incompressibility, which makes the algorithm parameter free; and the ability to handle both rigid and nonrigid deformation equally well.

It should be noted that we performed the registration on the entire prostate image with a subtle assumption that the image volume has the same mechanical property throughout. As we know, many different structures and tissues are inside and outside the prostate gland. So this assumption may lead to some systematic registration error. For more accurate registration, it would be necessary to take these structures into consideration. Some differences in the mechanical property of the tissue are expected, but when dealing with tissues that have significantly different mechanical properties, it should be noted that the SEMT algorithm no longer remains parameter free. Hence, a modification to Eq. 8 is required that takes into consideration the surrounding tissue characteristics. Our future studies will characterize tissues from different regions of and surrounding the prostate for an accurate assessment of displacement and strain during compression of the prostate.

Conclusion

We have implemented a novel registration algorithm based on strain energy minimization and demonstrated its effectiveness on phantom and prostate images. Results from our study show registration error of approximately 1 mm over the entire volume of the prostate. Accurate registration of prostate images obtained in the deformed state can be useful in treatment planning and also for longitudinal evaluation of progression/regression in patients with prostate cancer. In addition, although we have demonstrated the utility of our algorithm on MR images, we believe that this method can also be applied to images from any two different imaging modalities provided that corresponding features are available in both.

Appendix 1

The relationship between the two constants λ and μ is:

A. 1

And the relationship between the unit volume change e and normal strain ε_x is:

A. 2

So the first term λe² of Eq. 1 can be rewritten as:

A. 3

Given Poisson’s ratio v = 0.495,²³ the above expression is approximately

A. 4

which makes it negligible as compared to the other two terms in Eq. 1.