Abstract
Electrophoretic separation of a mixture of chemical species is a fundamental technique of great usefulness in biology, health care and forensics. In capillary electrophoresis the sample migrates in a microcapillary in the presence of a background electrolyte. When the ionic concentration of the sample is sufficiently high, the signal is known to exhibit features reminiscent of nonlinear waves including sharp concentration ‘shocks’. In this paper we consider a simplified model consisting of a single sample ion and a background electrolyte consisting of a single co-ion and a counterion in the absence of any processes that might change the ionization states of the constituents. If the ionic diffusivities are assumed to be the same for all constituents the concentration of sample ion is shown to obey a one dimensional advection diffusion equation with a concentration dependent advection velocity. If the analyte concentration is sufficiently low in a suitable non-dimensional sense, Burgers’ equation is recovered, and thus, the time dependent problem is exactly solvable with arbitrary initial conditions. In the case of small diffusivity either a leading edge or trailing edge shock is formed depending on the electrophoretic mobility of the sample ion relative to the background ions. Analytical formulas are presented for the shape, width and migration velocity of the sample peak and it is shown that axial dispersion at long times may be characterized by an effective diffusivity that is exactly calculated. These results are consistent with known observations from physical and numerical simulation experiments.
Keywords: capillary electrophoresis, Burger’s equation
1 Introduction
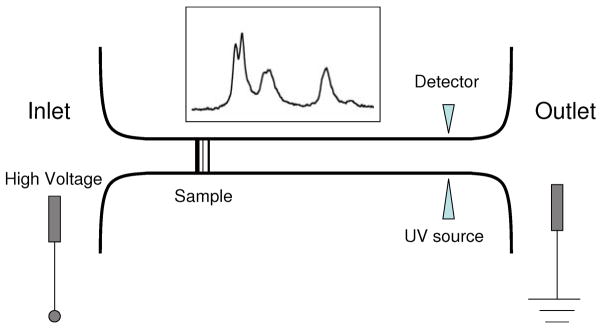
Slab gel electrophoresis has long been a familiar technique in molecular biology for sorting biomolecules according to their size and charge. For example, the Sanger method of sequencing DNA and RNA uses gel electrophoresis for sorting the products of the chain termination reaction. The SDS-PAGE technique used for sorting proteins by size uses electrophoresis in a polyacrylamide gel to separate the surfactant coated amino acid chains resulting from the denaturing of the proteins. The technique of Capillary Electrophoresis (CE) was introduced about thirty years ago and has largely replaced gel electrophoresis in many modern applications. In CE, the sample migrates through a microcapillary (about 50 μm in diameter and tens of centimeters long) instead of a slab of porous gel. The microcapillary is connected at the inlet and at the outlet to reservoirs, as shown in the schematic sketch in Figure 1 and the entire system is filled with an electrolytic buffer [1]. A large electrical voltage (tens of kilovolts) is applied with electrodes between the inlet and outlet reservoirs. The sample separates into distinct zones based on the migration speeds of individual components in the applied electric field. A detector placed near the outlet records a series of peaks (an electropherogram) that may be used for analyzing the sample. Often (but not always) there is an electroosmotic flow [2] present in the capillary that causes both positive and negative ions to be swept past a single detector placed near the outlet. For linear polyelectrolytes (e.g. DNA) the mobility is insensitive to the polymer length. In such cases a sieving medium such as a polyacrylamide gel may be loaded into the microcapillary.
Fig. 1.
A schematic sketch showing the CE setup and the electropherogram (inset) recorded by the detector. The diagram is not to scale.
CE has many advantages over the traditional slab gel electrophoresis method, one of the most important ones being ease of parallelization. Since many CE channels can be etched on a single substrate, multiple separations can be run simultaneously. Such scalability is critical to applications such as genome sequencing, and indeed CE is the method of choice in most such applications. Though CE is generally considered superior to the more traditional gel electrophoresis methods one of its limitations is the high demands placed on the sensitivity of the photo detector. The detector, which consists of a UV or laser source coupled to a photo cell must be sensitive to light attenuation over very short optical path lengths (the capillary diameter). Therefore, in order to maximize the likelihood of detection, it is preferable to use high sample concentrations. This requirement however conflicts with the other requirement of CE which is to minimize peak broadening or dispersion in order to improve resolution and signal strength [3]. The conflict is caused by a phenomenon known as “electromigration dispersion” or the “sample overloading effect”. The underlying physical mechanism is well understood and may be roughly explained as follows: when the concentration of sample ions is non-negligible compared to that of the background electrolytes the local electrical conductivity (σ) is altered in the vicinity of the peak. On the other hand, since the current (J) is constant, the electric field (E) must change locally since by Ohm’s law J = σE. This varying electric field alters the effective migration speed of the sample (or analyte) ion which in turn alters its concentration distribution thereby giving rise to a nonlinear transport problem that must be solved in a self consistent manner. Electromigration dispersion causes highly asymmetric concentration profiles, high rates of dispersion and shock like structures that are reminiscent of nonlinear waves seen in many other physical systems. These effects have been widely reported in the literature on electrophoresis (see e.g. [4]).
Simple one dimensional mathematical models of electromigration dispersion have been constructed [5–8] by invoking the assumption of vanishing diffusivity of all species and the requirement of local charge neutrality, which for a three ion system yields a single nonlinear hyperbolic equation. Solutions describe the observed steepening of an intitially smooth profile leading to subsequent shock formation. Two recent reviews [9, 10] provide more extensive references to one dimensional models and the behavior of their solutions as evident from numerical simulations. These models assume that only strong electrolytes are involved so that the valence states of the constituent ions are fixed. This assumption is inadequate when ampholytes (such as proteins) are present. The separation of ampholytes is usually performed by exploiting two other modes of electrophoresis: Isotachophoresis and Isoelectric focusing. The mode of electrophoresis described in the introduction and discussed in this paper by contrast is called “Zone electrophoresis”. From a mathematical perspective the various modes of electrophoresis correspond to different kinds of initial and boundary conditions of the same governing equations. An excellent discussion of the mathematical problem involved in the various modes of electrophoresis may be found in Chapter 3 of the book by Fife [11] and the practical aspects are discussed in a number of text books [1,12]. The essential technique for reducing the complexity of the transport equations in the presence of ampholytes was developed by Saville and Palusinski [13] using the well founded assumption that the time scale associated with ionization phenomena is very short compared to the time scale of diffusive or electrophoretic transport. Thus, local equilibrium may be assumed to exist between the ampholyte and its dissociation products so that the concentrations of the various charged states can be algebraically related to the concentration of the ampholyte in the neutral state. A historically contentious issue and an area of some mathematical interest concerns the assumption of local charge neutrality mentioned earlier. Local charge neutrality results when the small parameter (in some appropriate dimensionless formulation) multiplying the Laplacian of the potential in Poisson’s equation vanishes. This assumption, first invoked by Planck [14], results in a singular perturbation problem leading to boundary layers and associated interesting physics in various areas including semiconductor junctions and in selectively permeable membranes [15]. In the context of electrophoresis, the singular nature of the local charge neutrality assumption is manifested at the sharp boundaries of isotachophoretic shocks where the shock is regularized by finiteness of the small parameter. This aspect has been studied by Fife [16] who also presented some results relating to the regularity of solutions. A proof of the global existence of solutions for the coupled species and electric field equations in one dimension in the absence of ampholytes have been presented by Avrin [17]. In the present paper, we consider the one dimensional model of electromigration dispersion in the absence of ampholytes, however, we replace the assumption of zero ionic diffusivities with one of equal diffusivity of the ionic constituents. We show that this simple modification leads to a nonlinear advection-diffusion equation which reduces to Burgers’ equation for the analyte concentration if this concentration is not too large. The wealth of information that is available about the Burgers’ equation can thereby be exploited for understanding electromigration dispersion.
2 Fundamental equations of transport
We consider a system of N ionic species and denote by ci(x, t) the number of ions of species i (i = 1, 2, …, N) present per unit volume. Here x is the direction along the capillary and t is time. The system is presumed one dimensional, that is, the dependent variables are assumed not to vary over the cross-section of the capillary. In particular, this implies, electroosmotic flow, if present, is of the “plug flow” type. Cross stream variations can and do arise in CE and have been widely studied but it is not central to the present discussion. The concentrations obey the equations
| (1) |
where qi is the flux (amount passing per unit area of cross section per unit time) of species i. In writing Eq. (1) we have presumed that there are no sources or sinks for the ions. In particular, ionization and recombination phenomena are ignored, which is justified if only strong electrolytes are involved. The fluxes qi are related to the concentration fields through the Nerst-Planck model
| (2) |
where E(x, t) is the electric field (directed along the capillary), μi is the electrophoretic mobility and Di is the diffusivity of the ‘ith’ species. In addition to the electrophoretic mobility, which is the velocity acquired by the ion per unit of applied electric field, we would also refer to the mobility (ui) which is the velocity per unit applied force. The two are related1 to each other as μi = zieui and related to the diffusivity through the Stokes-Einstein relation [18] Di/ui = kBT, where kB is Boltzmann’s constant, T is the absolute temperature, e denotes the proton charge and zi is the signed valence of the ith species which can be positive, negative or zero. When fluid flow with velocity V is present, a term V ci is added to the right hand side of Eq. (2). However, if the flow is an electroosmotic plug flow, this term may be absorbed in the second term by simply redefining μi as the “total” instead of the “electrophoretic” mobility. If the capillary is filled with a polymer network then the mobility and diffusivity introduced above should be interpreted as the “effective” values of these quantities in the porous medium and the dependent variables must be regarded as averages of the corresponding physical quantity over the cross-section of the capillary.
The system of equations Eq. (1) – (2) is closed by Poisson’s equation of electrostatics, which in SI units is written as
| (3) |
Here ρe(x, t) is the charge density and ε is the permittivity of the medium. Time variations in electrophoresis are sufficiently slow that any errors resulting from replacement of the complete Maxwell’s equations of electromagnetism by Poisson’s equation, Eq. (3), is negligible. Eq. (1) – (3) provide a closed system of equations for calculation of the time evolution of the functions ci(x, t) if the initial conditions are known and if appropriate boundary conditions are specified.
3 Electroneutrality and the Kohlrausch function
If ‘a’ denotes a characteristic length scale over which the concentrations may be considered to vary (this may be taken, for example, as the peak width), then it may be shown that the ratio of the term on the left hand side of Eq. (3) to that on the right is of the order of (λD/a)2, where λD is the Debye length in the buffer. Since in CE, a is of the order of microns while λD is in the nanometer range, (λD/a)2 is extremely small. As a result, Eq. (3) may be replaced by the electroneutrality condition:
| (4) |
first invoked by Planck [14] in the context of the problem of the liquid junction potential. This condition caused some confusion in the early history of the subject, since it appeared that in the absence of the charge density, no electric field, or in our problem, perturbation to the applied field is possible. The controversy was resolved [19] when it was realized that Eq. (4) should be interpreted in an asymptotic rather than in an exact sense.
The disappearance of the left hand side of Eq. (3) may at first sight appear to be problematic because we have now lost our equation for determining E. This is not in fact a difficulty as E can be determined directly from Ohm’s law and the condition of the constancy of current:
| (5) |
where the electrical conductivity is2
| (6) |
and J0 is a constant. The first of the two equalities in Eq (5) is a consequence of charge neutrality but the second requires certain additional assumptions. To see this, substitute qi from Eq. (2) in the expression for the current
| (7) |
If the diffusive contributions are now neglected, then the second part of Eq. (5), J = σE or Ohm’s law follows.
The constraints imposed by Eq. (4) and (5) have the effect of replacing two of the differential equations governing the transport by algebraic relations. It was pointed out by Kohlrausch [21] that a further reduction of the governing equations is possible if the diffusion terms are neglected in the ion transport equations. To see this we define the Kohlrausch function:
| (8) |
If we now take the derivative of both sides of this relation with respect to time and use Eq. (1), (2) and (4) we get
| (9) |
If the right hand side is neglected we get
| (10) |
and this provides an algebraic relation to replace one more differential equation for transport.
In contrast to the electro-neutrality condition which is respected to high accuracy, the neglect of the diffusion terms in arriving at either Ohm’s law or the Kohlrausch relation is questionable in applications related to CE. The ratio of the diffusive term to the other terms is measured by the inverse of the Peclet number, Pe = va/D in terms of the characteristic peak width a and velocity v. While it is true that the Peclet number is generally large in the applications we are concerned with here, the transit times L/v across the length (L) of the capillary is also very long. Thus, the ratio of the diffusive broadening ( ) to a characteristic peak width (a) is measured by the square root of (L/a)Pe−1 which is generally not small even though Pe ~ 10 – 100. Furthermore, when the profile steepens, as it does in electromigration dispersion, the second derivative term multiplying Di in the transport equations can become very large so that the diffusive term once again has a finite effect no matter how small the diffusivity is. Nevertheless, the Kohlrausch relations have been fruitfully applied for certain special situations such as in calculating fluxes across interfaces separating two homogeneous regions. In the next section we show how the ideas of Kohlrausch and Ohm’s law can be generalized to treat the case of nonzero diffusivities.
4 Reduction to a one equation model
Let us now consider an idealized model of electrophoresis where only three species are involved: a sample or analyte ion, a positive ion and a negative ion. In place of the suffix i we will from now on use a suffix ‘p’ to denote the positive ion, ‘n’ to denote the negative ion and no suffix at all to indicate the sample. Thus, zp is the signed valence of the positive ion, zn that of the negative ion and z that of the sample. Clearly zp is positive, zn is negative and z could be of either sign (but not zero, since a neutral species does not electromigrate). We will further assume that all the species have the same mobility (u), and therefore the same diffusivity D = ukBT, though their electrophoretric mobilities μi = eziu could be widely different. Many analytes of importance in electrophoresis are linear polyelectrolytes, and for these molecules the charge scales linearly with the mass M while the diffusivity scales roughly as M−1/3. It might therefore be argued that diffusivities of ions vary over a relatively small range when compared to their electrophoretic mobilities, though it must be acknowledged that our primary motivation for introducing this assumption is the pragmatic one of wanting to reduce the mathematical complexity of the problem.
It is readily seen that by virtue of our assumption Di = D and the electroneutrality condition Eq. (4), the first term of Eq. (7) vanishes so that Ohm’s law, Eq (5) is recovered. Further, in view of our assumption of equal diffusivities, Eq. (9) reduces to the diffusion equation
| (11) |
which admits an analytical solution:
| (12) |
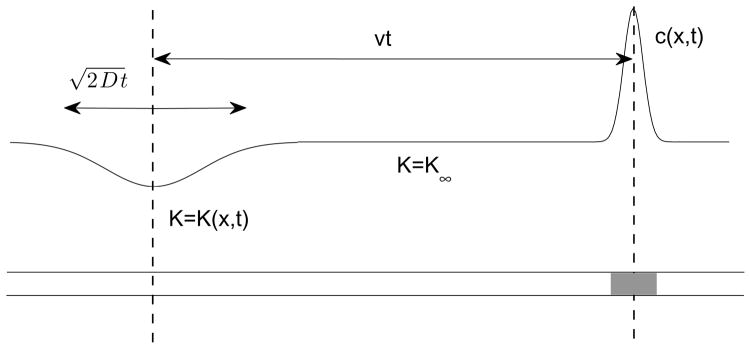
If K∞ denotes the unperturbed value of K, then the perturbation in K, δK = K − K∞ spreads diffusively from the injection region so that its width, , where w0 is the width of the peak at injection. The essential observation that allows us to extend Kohlrausch’s ideas to the diffusive case is illustrated in Figure 2 and it is the following: even though K(x, t) is in general a time dependent quantity, in the vicinity of the analyte peak we may assume it to be a constant equal to its unperturbed value K = K∞. This is because the distance between the analyte peak and the injection zone (X) increases linearly with time X ~ μE0t where E0 is the applied field so that at long times, X ≫ w. The minimum length of time that needs to pass for this to happen is max [w0/v, D/v2] where v = μE0 is the velocity of an isolated analyte ion in the back ground electrolyte and max [ ] indicates the larger of the two numbers within the brackets. It is instructive to express this in terms of the diffusion time τd = a2/D the time it takes the analyte to diffuse over a characteristic distance. If we identify this characteristic distance with w0, that is, a = w0, then the condition may be written as t/τd ≫ max[ Pe−1, Pe−2 ] where Pe = va/D is the Peclet number introduced earlier. If we use the estimates v ~ 1 mm/s, a = w0 ~ 10 μm, D ~ 10−5 cm2/s which are fairly typical, we have Pe ~ 10 and τd ~ 0.1 s. Thus, the condition K = K∞ in the vicinity of the analyte peak may be used with confidence for times t ≫ 10−2 s. This is indeed very small in comparison to the time interval between injection and detection which is tens of minutes. In simple terms, δK spreads so slowly that the analyte peak leaves it behind essentially in the time it takes to traverse a distance of the order of its own width.
Fig. 2.
Sketch illustrating the basis of the assumption that the Kohlrausch function may be assumed constant in the sample zone shortly after sample injection.
Setting the right hand side of Eq. (8) to the constant value K∞ immediately yields a third algebraic relation in addition to Eq. (4) and Eq. (5) between the set of four dependent variables: cp, cn, c and E. If we use these to express all of the remaining variables in terms of c and substitute in the transport equation for c, we obtain, after some algebra that we omit, a single nonlinear partial differential equation describing the evolution of the analyte concentration c. This equation may be conveniently expressed in terms of the dimensionless quantity where is the concentration of the negative ions in the background electrolyte:
| (13) |
The dimensionless parameter α is defined as
| (14) |
Since μp > 0 and μn < 0, α is positive if μ is in the interval (μn, μp) and is negative otherwise. The parameter α is essentially a dimensionless form of the “velocity slope parameter” that has been used [22] to characterize electromigration dispersion, since αv = V′(0) where V (φ) = v/(1 − αφ) is the local value of the migrational velocity of an analyte ion within the sample zone.
The concentrations of the negative and positive ions may be readily expressed in terms of φ using the charge neutrality condition, Eq (4) and the defining relation for K(x, t), Eq (8):
| (15) |
| (16) |
It is seen from the above equations that once the analyte has moved out of the injection zone (φ → 0) the background ions do not immediately return to their equilibrium concentrations. A fluctuation is created in the concentration of the background ions which does not propagate, but decays in place on a diffusive time scale. If the capillary carries an electroosmotic flow and if the sensor is sensitive to the background ions (e.g. a UV absorbance detector) these fluctuations may be detected with the analyte peaks complicating the interpretation of the signal. The existence of these anomalous peaks are well known [23–25] and are variously referred to as “water peaks”, “system peaks” or “vacancy peaks”.
When α is positive, the evolution equation for φ, Eq (13) has a singularity at φ = 1/α which needs to be understood. Clearly, this singularity arises because of the vanishing of the conductivity σ in Ohm’s law Eq (5). Since μi = eziu, the vanishing of the conductivity when φ → 1/α implies that one or both of the background ion concentrations must have become negative. This, of course is physically impossible and would imply that at least one of our two assumptions, namely charge neutrality or constancy of the Kohlrausch function would have to be violated before this singularity is reached. In fact, the highest analyte concentration to which Eq (13) may still be used can be calculated by requiring that both the conditions cn > 0 and cp > 0 be respected where cn and cp are given by Eq. (15) and Eq. (16) with δK = 0. These inequalities may be reduced after some algebra to the requirement φ < φc where φc = (zp − zn)/(zp − z) when z < 0 and φc = −[zn(zp − zn)/[zp(z − zn)] when z > 0. As a practical example, if z = ±2zp and zn = −zp we get φc = 2/3 which would correspond to conditions of extremely high sample loading. If initial conditions are used such that φ > φc in some regions, there will be an initial transient period that is not described by Eq (13), but once diffusion causes the analyte concentration to drop below the critical value, the subsequent evolution should follow Eq. (13).
5 Analysis of the one equation model
Eq. (13) in general describes a one dimensional nonlinear wave [26]. The nonlinearity arises because the local wave speed V (φ) = v/(1 − αφ) changes with φ. In particular, if α > 0, larger values of φ correspond to higher speeds, so that if φ has a maximum at some point, then analyte ions near the maximum out runs the slower ions ahead of it causing the distribution of φ to lean forward and develop a sharp gradient at its leading edge (a shock wave). An analogous situation arises if α < 0 except in this case the distribution of φ leans backwards as seen in Panels C and D of Figure 3. The diffusive term on the right hand side of Eq. (13) works to counter the sharpening of the wave due to the nonlinearity. When it is dominant the wave approaches a Gaussian shape in time with small departures from this limiting shape due to the nonlinearity. In case of small diffusivity the diffusive term is small everywhere except in the vicinity of the shock; its presence prevents the sharp change in φ at the shock from evolving into a true mathematical discontinuity. In the remainder of this section we attempt to rationalize some of the observed facts about electromigration dispersion by exploiting some well known results from the mathematical theory of nonlinear waves.
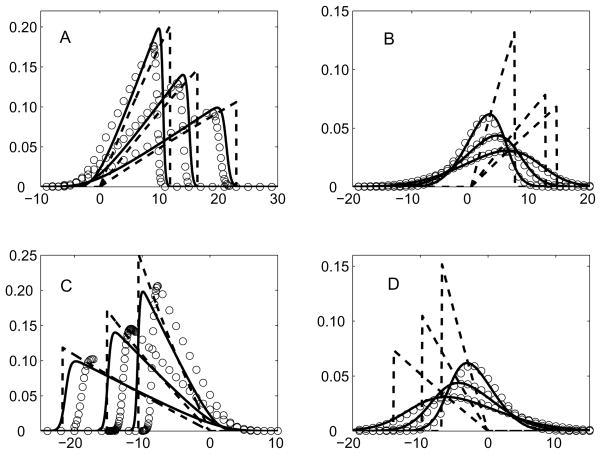
Fig. 3.
Comparison of the normalized concentration φ (y-axis) as a function of (x − vt)/σ 0 (x-axis) obtained from the full solution, Eq. (13) (open circles), Eq. (22) (solid lines) and Eq. (42) or Eq. (51) (dashed lines) at fixed instants of time vt/σ0 = 50, 100 and 200. The parameters are: P = 62.7: α = 0.5 (Panel A), α = −0.5 (Panel C) and P = 5.0: α = 0.5 (Panel B), α = −0.5 (Panel D).
5.1 The weakly nonlinear case
Let us suppose that |αφ| ≪ 1 for all x and t. Since φ is the ratio of analyte ion to that of the background ions, typically |φ| ≪ 1. The above condition can also be satisfied even when |φ| is not small compared to unity, provided |α| is small, that is, if the electrophoretic mobility of the analyte ion closely matches that of one of the background electrolytes. In either case, one may wish to neglect the term αφ in the denominator of Eq. (13), which would then describe waves that propagate with constant velocity v while simultaneously undergoing diffusive spreading. This of course describes the usual “linear” electrophoresis. To see the effect of electromigration dispersion we must treat the term αφ as small, but not zero. This is achieved by making the approximation (1 − αφ)−1 ≈ 1 + αφ in Eq. (13), which then becomes:
| (17) |
Eq. (17) takes a more familiar form if we describe it in a reference frame translating with velocity v, that is, we transform variables from (x, t) to (ξ, t) where ξ = x − vt. Eq. (17) then becomes the one dimensional Burgers’ equation3
| (18) |
Eq. (18) is well known in fluid mechanics and is studied as a model for breaking water waves, one dimensional shocks in gas dynamics and the like. It can be reduced [26] to the one dimensional diffusion equation through a nonlinear transformation of variables and thus solved exactly. The solution is:
| (19) |
where
| (20) |
Given any initial profile for φ its subsequent time evolution may be calculated simply by evaluating the integrals in Eq. (19). A special case of interest is
| (21) |
where (a conserved quantity) and δ(x) is the Dirac delta function. This may be an appropriate model for t ≫ τd when the peak width is much larger than its initial value so that the detailed shape of the initial concentration distribution may be disregarded. We will use the quantity Γ to characterize the degree of sample loading. It has dimensions of length and may be attributed the following simple meaning: it is the length along the capillary that contains the same number of negative ions as there are analyte ions in the injected peak. Substitution of Eq. (21) in Eq. (19) yields
| (22) |
where
| (23) |
with denoting the complementary error function. The constant A is given by A = eαP − 1 where P = Γv/D is a Peclet number based on the characteristic length scale Γ. If αP is small, A ≈ 0 and in this case the denominator in Eq. (23) may be approximated by one. In this limit Eq. (22) reduces to a spreading Gaussian profile as expected. If αP is significant, A is non-negligible and it has the same sign as α. In this case the denominator in Eq. (23) creates an asymmetry in the profile, Eq. (22), causing it to steepen in the direction of peak propagation or create a steep trailing edge depending on the sign of α. This behavior of course is well known from experimental and numerical studies of electromigration dispersion and is often referred to as “fronting” or “tailing”. It may be of interest to note that Eq. (23) is similar to a certain empirical function that has historically been used to fit experimental data on asymmetric peaks [27,28]. However, unlike this so called “Haarhoff-Van der Linde (HVL) function” Eq. (23) is not an empirical fit but a mathematical consequence of the governing equations. The quantity |α|P that determines the strength of this effect may be expressed in terms of several relevant time scales: where τa = a/v is an advective time, τd is the diffusive time scale introduced earlier and τe = |α|Γ/v is a new time scale associated with sample loading. The importance of the scale τe will become apparent later, but here we provide some numerical estimates. If we assume that the analyte peak is a Gaussian with a 10 μm width and a peak concentration that is 2 percent of the background, then τe ~ 0.5 ms, if v ~ 1 mm/s and |α| ~ 1. The other two timescales using the estimates provided earlier are τa ~ 10 ms and τd ~ 100 ms. Thus, in this example, P ~ 0.5 and therefore A ~ 1 which would correspond to “high” sample loading and on the basis of Eq. (23) strong deviations from Gaussianity may be expected. Thus, the quantity |α|P may be regarded as a suitable measure of sample loading in the context of peak distortion.
Another useful quantity that may be calculated [26] from the theory of nonlinear waves is the time needed to develop a shock:
| (24) |
where the suffix ‘min’ indicates the minimum value of the function (which is clearly negative for a unimodal distribution). If the initial profile is a Gaussian of standard deviation w0 then the minimum is easily evaluated and we get
| (25) |
If we substitute our numerical estimates, we get tshock ~ 0.2 s which is very short compared to the total transit time across the capillary, typically tens of minutes.
Shock like solution profiles may be obtained [26] from Eq. (22) on taking the asymptotic limit of D → 0. If α > 0 we have leading edge shocks:
| (26) |
| (27) |
| (28) |
and if α < 0, we have trailing edge shocks:
| (29) |
| (30) |
| (31) |
Here xf and xb are the locations of the “front” and “back” of the distribution φ(x, t) which vanishes outside the interval [xb, xf ].
The profile, Eq. (22), may be used to calculate some useful quantities such as the location of the centroid:
| (32) |
and the variance:
| (33) |
The evaluation of the integrals is facilitated on transforming to the new variable . The second moment about the centroid (xc), Eq (33), is related in a simple way to which is defined as in Eq (33) but with xc replaced by x0 = vt. This relation (sometimes referred to as the “parallel axis theorem” in mechanics): easily follows from Eq (33). Its use simplifies the calculation of the second moment, and we get after some algebra:
| (34) |
and
| (35) |
where is the k th moment of the function F(η) defined by Eq. (23). In general the Fk need to be determined numerically except for k = 0, in which case which is merely a statement of the fact that the solution, Eq (22), satisfies the normalization implied by Eq (21). The speed of the centroid Vc = dxc/dt readily follows from Eq (34):
| (36) |
with the + or − sign depending on whether α is positive or negative. If the effective diffusivity is defined by then
| (37) |
The asymptotic forms for large P following the symbol ~ in Eq. (36) and Eq. (37) are easily obtained on calculating the moments Fk using the profiles Eq. (26) and Eq. (29). Thus, we see that the centroid velocity approaches v asymptotically for times that are large compared to τe, however the spread of the peak is diffusive at all times and may be described by the effective diffusivity indicated by Eq (37). The phrase “all times” here refers to times that are nevertheless large compared to τd since otherwise Eq (22) may not be applied and the solution in this regime depends on the detailed features of the initial profile.
5.2 The strongly nonlinear case
The assumption |αφ| ≪ 1 may not be a good one especially during the early part of the evolution in the case of high sample loading. The replacement of Eq. (13) by Burgers’ equation, Eq. (18), is not a good approximation in that case and we refer to this as the strongly nonlinear regime. However, an analytical solution is still possible if Pe ≫ 1. In this case, the diffusion term in Eq. (13) may be neglected except in the immediate vicinity of a shock. Since Pe is usually large in electrophoresis it is reasonable to treat the problem as one of propagation of a shock front for times t > tshock, which formally corresponds to setting the right hand side of Eq. (13) to zero while admitting discontinuous functions within the class of solutions. It should be pointed out that Eq. (13), with D = 0, and its solution Eq. (42) had been noted earlier by others [6, 8], though its consequences for electromigration dispersion had not been adequately worked out. We do so here.
A solution to Eq. (13) with D = 0 may be sought4 in similarity form in terms of the variable X = x/vt, that is, we look for solutions of the type φ (x, t) = Φ(X) where Φ(X) is an unknown function. Substitution of this form in Eq. (13) with D set to zero results in the following requirement that Φ(X) needs to satisfy:
| (38) |
which may be easily rearranged as
| (39) |
Thus, Φ must either satisfy the differential equation dΦ/dX = 0 and therefore must be a constant or an algebraic equation that is easily solved:
| (40) |
It is clear that neither of these functions by itself can represent the solution for all X but rather each describes a piece of it. The branch Φ is constant must describe the solution outside the analyte zone and because of the requirement Φ(±∞) = 0 the constant must be zero. The solution within the analyte zone is best discussed by considering the cases corresponding to the two signs of α separately.
5.2.1 Leading edge shocks (α > 0)
The solution branch Eq. (40) can be matched at one of its boundaries to the branch Φ(X) = 0 only if we accept the negative sign. This boundary then corresponds to X = 1 which must be identified with the trailing edge. The leading edge is at some unknown position X = Xf > 1. We can determine Xf by exploiting the condition that the integral of φ is a conserved quantity, which immediately follows on integrating Eq. (13):
| (41) |
It is best to present the solution in terms of our original variables:
| (42) |
| (43) |
| (44) |
and φ(x, t) = 0 outside the interval [xb, xf ]. Here τe = |α|Γ/v is the time scale introduced earlier. Two quantities of particular importance in electrophoresis are the maximum value of φ, φm(t) = φ(xf, t) and the peak width w = xf − xb. These may be easily calculated from Eq. (42) – (44):
| (45) |
| (46) |
The propagation speed of the peak is
| (47) |
It is easy to verify by direct substitution that Eq. (45) and Eq. (47) satisfy the Rankine-Hugoniot condition for shock waves [26].
It is clear from these formulas that in the asymptotic limit of long times (t ≫ τe) the wave propagates unchanged in shape with its width increasing in proportion to the square root of time and its amplitude decreasing in inverse proportion to the square root of time while its integral is conserved. This is classical diffusive behavior, and therefore an effective diffusivity (Deff) can be introduced through the asymptotic relation σ2 ~ 2Deff t for the increase of variance with time. To determine Deff one needs to calculate the variance of the distribution represented by Eq. (42) and then determine the leading order term in its asymptotic expansion in the small parameter τe/t. This may be done and leads after some algebra to the rather simple final result
| (48) |
We write |α| in place of α in anticipation of the fact that this expression is equally valid for a trailing edge shock (α < 0). This is seen to be identical to the large Peclet number (P) limit of the effective diffusivity obtained from the solution of Burgers’ equation indicated in Eq. (37).
5.2.2 Trailing edge shocks (α < 0)
The requirement that Φ must be non-negative implies that only the negative sign in Eq. (40) corresponds to physically realizable solutions. Thus,
| (49) |
where X ≤ 1. Therefore in this case, X = 1 actually corresponds to the leading edge and X = Xb < 1 is the trailing edge which is where the shock is located. To determine Xb we once again use the constancy of the integral of φ:
| (50) |
The relations analogous to Eq. (42) – (44) are
| (51) |
| (52) |
| (53) |
The amplitude, width and speed of the peak may be calculated as before, they are
| (54) |
| (55) |
| (56) |
The effective diffusivity Deff is once again given by Eq. (48).
Since Burgers’ equation follows from Eq. (13) if φ is small, one might expect that Eq. (51) – (53) should reduce to Eq. (29) – (31) at asymptotically large times. This is indeed true. To show this, first observe that from Eq. (52)
| (57) |
at large times. Secondly, if we put x = xf − ξ and regard ξ/xf as small (since while xf ~ t), then
| (58) |
Thus, Eq. (29) – (31) are recovered. Similarly, if α > 0, Eq. (42) – (44) go over to Eq. (26) – (28) at large times.
6 Numerical simulations
In order to test the accuracy of some of the results presented in the previous section, they were compared to solutions of Eq. (13) computed numerically using a second order (central) finite difference algorithm for spatial derivatives coupled with a fourth order Runge-Kutta time stepping scheme with fixed grid and step size. We will refer to this numerical calculation as “the full solution”.
As a test problem, an initial profile was specified and φm was varied keeping σ0 fixed. This involves no loss of generality because if Eq. (13) is rewritten in terms of dimensionless space and time variables: x* = x/σ0 and t* = vt/σ0, then it is easily seen that the only parameters that enter into the problem are: α, P = vΓ/D and . Comparisons were made over a wide range of parameter values, but for brevity, we present here only a few cases that are illustrative of the general trend.
In Figure 3 we compare the analyte concentration profiles obtained by numerically evolving Eq (13) with the analytical formulas Eq. (22) and Eq. (42) or Eq. (51). It is seen that for large values of P all of the profiles are very close. For smaller value of P, the full solution is in good agreement with the analytical solution of the Burgers’ equation, Eq. (22), but does not agree with the shock profiles Eq. (42) or Eq. (51). This is because the dynamics is dominated by diffusion.
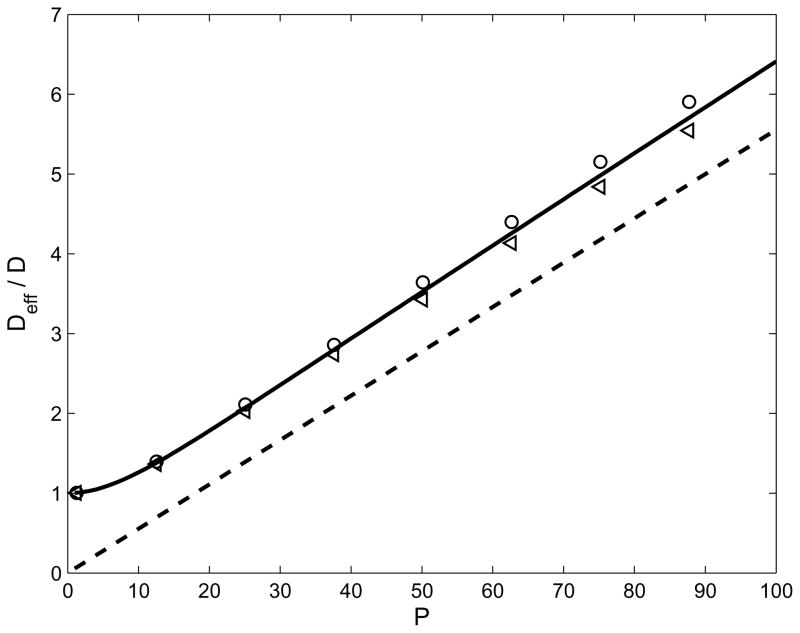
The formulas given by Eq. (37) and Eq. (48) could be of some practical value so we compared them with the corresponding results from the full solution in Figure 4. To do this, the variance σ2 was calculated from the concentration profile in the full solution and the rate of change of variance d(σ2)/dt was plotted as a function of time t. In all cases, this quantity was found to asymptote to a constant value, and equating this value to 2Deff gave an effective value of the diffusivity. These are shown in Figure 4 by the symbols for a range of values of the Peclet number P, for α = ±0.5. It should be observed that Deff is independent of the sign of α as predicted by the theoretical results. The small difference in the value of Deff for positive and negative α is due to the fact that the peak width approaches its asymptotic value from above or from below depending on the sign of α as is suggested by Eq. (46) and Eq. (55) for the peak width. Thus, the numerical determination based on the full solution results in a slight over estimate of the asymptotic value in one case and a slight under estimate in the other. The numerical calculation is seen to be in good agreement with Eq. (37). However, the dashed line has a constant offset with respect to the solid line because when P is large, , and the limit represented by Eq. (48) is obtained by neglecting the first term in relation to the second. It is therefore a valid approximation and has a low relative error when P is much larger than unity, but if this is not the case then one must use Eq. (37).
Fig. 4.
The normalized effective diffusivity as a function of the Peclet number P. The solid line is from Eq. (37) and the dashed line is from Eq. (48). The symbols indicate values calculated from the numerical solution of Eq. (13). Two cases are shown, α = +0.5 (circles) and α = −0.5 (triangles).
7 Concluding remarks
In this paper a simple model is constructed and rigorously solved with the objective of providing a physical understanding of the essential features observed in the CE signal at high sample loading. The model leaves out many features that are undoubtedly present in any real experiment, such as, the presence of many more than three ionic species, shifts in ionic equilibria, differential diffusion between species and the like. On the other hand, the fact that the principal qualitative features of the signal may be reproduced in this highly simplified model indicates that the neglected effects, though present, are not causative but only incidental to the problem.
The main results that follow from this analysis that might have some validity in a broader context are:
Leading edge shocks are to be expected when the analyte ion has an electrophoretic mobility that is intermediate to that of the co and counter ions and a trailing edge shock should be seen otherwise.
A peak showing a leading edge shock will elute earlier and a peak showing a trailing edge shock will elute later compared to the arrival times in an otherwise identical experiment where sample loading is kept low.
The quantity |α|P, where P = Γv/D is a Peclet number based on the length scale Γ, completely determines the nature of the wave. If |α|P ≪ 1 the peak would evolve into a Gaussian with a small amount of asymmetry and if |α|P ≫ 1 a shock like structure is formed. It is the single controlling parameter that must be kept low in order to mitigate the effects of electromigration dispersion.
At long times the peak spreads diffusively with an effective diffusivity Deff. The ratio Deff/D depends on the Peclet number P; it is proportional to P when P is large.
The peak asymmetry that is characterized by the quantity A has an exponential dependence on the Peclet number, P: A = eαP − 1, as a result, the transition from a “weak asymmetry” to a “strong shock” as one increases the sample loading is very sharp.
If the analyte electrophoretic mobility is closely matched to the electrophoretic mobility of one of the background species (this makes |α| small) peak distortion and dispersion can be minimized.
These observations appear to be consistent with laboratory experiments [4,29] and results from numerical simulations [7]. The analytical formulas presented in this paper can be checked quantitatively through carefully designed experiments that closely mimic the simplifying assumptions made in this study. It is hoped that this paper will motivate efforts in that direction.
Acknowledgments
supported by the NIH under grant R01EB007596.
This manuscript was prepared when the first author was on sabbatical at the Institute for Mathematics and its Applications (IMA) at the University of Minnesota and thanks the IMA for their kind hospitality. We also thank Professor Joseph B. Keller for reading and commenting on a draft of the manuscript.
Footnotes
this relation is not valid for macro-ions or colloidal particles owing to Debye layer effects. The relation is valid provided the ionic size is much smaller than the Debye length
the dependance of conductivity on concentrations is actually nonlinear at high concentrations [20]. However we ignore this effect as it does not fundamentally alter our analysis except in replacing one nonlinear dependence of ion velocity on concentration by another
in contrast to Eq. (13), the solutions of Burgers’ equation are well behaved for all φ, though the solution would correspond to physical reality only if 0 < φ < φc
the existence of such similarity solutions is suggested by the invariance of the equations under a scale transformation: x → x/ρ and t → t/ρ for any nonzero constant ρ
Contributor Information
Sandip Ghosal, Email: s-ghosal@northwestern.edu, Northwestern University, Dept. Mech. Eng., 2145 Sheridan Road, Evanston, IL 60208, Tel.: +1 847 467 5990, Fax: +1 847 491 3915.
Zhen Chen, Email: zhenchen2011@u.northwestern.edu, Northwestern University, Dept. Mech. Eng., 2145 Sheridan Road, Evanston, IL 60208, Tel.: +1 847 491 3663, Fax: +1 847 491 3915.
References
- 1.Landers J, editor. Introduction to Capillary Electrophoresis. CRC Press; Boca Raton, U.S.A: 1996. [Google Scholar]
- 2.Probstein R. Physicochemical Hydrodynamics. John Wiley and Sons, Inc; New York, U.S.A: 1994. [Google Scholar]
- 3.Ghosal S. Electrokinetic flow and dispersion in capillary electrophoresis. Annu Rev Fluid Mech. 2006;38:309–338. [Google Scholar]
- 4.Boušková E, Presutti C, Gebauer P, Fanali S, Beckers J, Boček P. Experimental assessment of electromigration properties of background electrolytes in capillary zone electrophoresis. Electrophoresis. 2004;25:355–359. doi: 10.1002/elps.200305539. [DOI] [PubMed] [Google Scholar]
- 5.Weber H, Riemann B. Die partiellen Differential-gleichungen der mathematischen Physik. F. Vieweg und Sohn; 1910. [Google Scholar]
- 6.Mikkers F, Everaerts F, Verheggen TP. Concentration distributions in free zone electrophoresis. J Chromatogr. 1979;169:1–10. [Google Scholar]
- 7.Mikkers F. Concentration distributions in capillary electrophoresis: Cze in a spreadsheet. Anal Chem. 1999;71:522–533. [Google Scholar]
- 8.Babskii V, Zhukov M, Yudovich V. Mathematical Theory of Electrophoresis. Consultants Bureau, Plenum Publishing; New York, U.S.A: 1989. [Google Scholar]
- 9.Gaš B. Theory of electrophoresis: Fate of one equation. Electrophoresis. 2009;30:S7–S15. doi: 10.1002/elps.200900133. [DOI] [PubMed] [Google Scholar]
- 10.Thormann W, Caslavska J, Breadmore M, Mosher R. Dynamic computer simulations of electrophoresis: Three decades of active research. Electrophoresis. 2009;30:S16–S26. doi: 10.1002/elps.200900058. [DOI] [PubMed] [Google Scholar]
- 11.Fife PC. Dynamics of internal layers and diffusive interfaces. SIAM; Philadelphia, U.S.A: 1988. [Google Scholar]
- 12.Camilleri P, editor. Capillary Electrophoresis, Theory & Practice. CRC Press; Boca Raton, U.S.A: 1998. [Google Scholar]
- 13.Saville DA, Palusinski OA. Theory of electrophoretic separations. part i: Formulation of a mathematical model. AIChE Journal. 1986;32(2):207–214. [Google Scholar]
- 14.Planck M. Ueber die erregung von electricität und wärme in electrolyten. Ann phys Chem. 1890;39:161–186. [Google Scholar]
- 15.Rubinstein I. Electro-Diffusion of Ions. SIAM; Philadelphia, U.S.A: 1990. [Google Scholar]
- 16.Fife PC, Palusinski OA, Su Y. Electrophoretic traveling waves. Transactions of the American Mathematical Society. 1988;310(2):759–780. [Google Scholar]
- 17.Avrin JD. Global existence for a model of electrophoretic separation. SIAM Journal on Mathematical Analysis. 1988;19(3):520–527. [Google Scholar]
- 18.Russel W, Saville D, Schowalter W. Colloidal Dispersions. Cambridge University Press; Cambridge, UK: 1989. [Google Scholar]
- 19.Hickman H. The liquid junction potential – the free diffusion junction. Chem Eng Sci. 1970;25:381–398. [Google Scholar]
- 20.Robinson R, Stokes R. Electrolyte Solutions. Dover; Mineola, U.S.A: 2002. [Google Scholar]
- 21.Kohlrausch F. Ueber concentrations-verschiebungen durch electrolyse im inneren von lösungen und lösungsgemischen. Ann Phys. 1897;62:209–239. [Google Scholar]
- 22.Gebauer P, Boček P. System peaks in capillary zone electrophoresis i. simple model of vacancy electrophoresis. J Chromatogr A. 1997;772:73–79. [Google Scholar]
- 23.Desiderio C, Fanali S, Gebauer P, Boček P. System peaks in capillary zone electrophoresis ii. experimental study of vacancy peaks. J Chromatogr A. 1997;772:81–89. [Google Scholar]
- 24.Bullock J, Strasters J, Snider J. Effect of multiple electrolyte buffers on peak symmetry, resolution, and sensitivity in capillary electrophoresis. Anal Chem. 1995;67:3246–3252. [Google Scholar]
- 25.Poppe H. System peaks and non-linearity in capillary electrophoresis and high-performance liquid chromatography. J Chromatogr A. 1999;831:105–121. [Google Scholar]
- 26.Whitham G. Linear and Nonlinear Waves. Wiley-Interscience; New York, U.S.A: 1974. [Google Scholar]
- 27.Erny G, Bergstrŏm E, Goodall D. Predicting peak shape in capillary electrophoresis: a generic approach to parametrizing peaks using the haarhoff-van der linde (hvl) function. Anal Chem. 2001;73:4862–4872. doi: 10.1021/ac010758g. [DOI] [PubMed] [Google Scholar]
- 28.Erny G, Bergstrŏm E, Goodall D. Electromigration dispersion in capillary zone electrophoresis experimental validation of use of the haarhoff-van der linde function. J Chromatogr A. 2002;959:229–239. doi: 10.1016/s0021-9673(02)00454-5. [DOI] [PubMed] [Google Scholar]
- 29.Horká M, Šlais K. Low-conductivity background electrolytes in capillary zone electrophoresis – myth or reality? Electrophoresis. 2000;21:2814–2827. doi: 10.1002/1522-2683(20000801)21:14<2814::AID-ELPS2814>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]