Non-technical summary
Navigation by mammals relies on neurons in the brain that encode location, but the mechanisms involved are not understood. Some theories propose critical roles for oscillations generated intrinsically by location-encoding neurons. Correlations between the frequency of intrinsic activity and the resolution of location encoding support this idea. However, other evidence suggests that cellular mechanisms thought to set the frequency of intrinsic activity may instead primarily function to tune neuronal responses to synaptic input. This study provides evidence that activity intrinsic to location-encoding neurons is explained by random opening and closing of neuronal ion channels and is not consistent with oscillator theories. The correlation between intrinsic frequency fluctuations and resolution of spatial encoding is explained by differences in the density of ion channels that account for tuning of synaptic responses. These results point towards the importance of synaptic response tuning for encoding of spatial location.
Abstract
Abstract
The membrane potential dynamics of stellate neurons in layer II of the medial entorhinal cortex are important for neural encoding of location. Previous studies suggest that these neurons generate intrinsic theta-frequency membrane potential oscillations, with a period that depends on neuronal location on the dorsal–ventral axis of the medial entorhinal cortex, and which in behaving animals could support generation of grid-like spatial firing fields. To address the nature and organization of this theta-like activity, we adopt the Lomb method of least-squares spectral analysis. We demonstrate that peaks in frequency spectra that differ significantly from Gaussian noise do not necessarily imply the existence of a periodic oscillator, but can instead arise from filtered stochastic noise or a stochastic random walk. We show that theta-like membrane potential activity recorded from stellate neurons in mature brain slices is consistent with stochastic mechanisms, but not with generation by a periodic oscillator. The dorsal–ventral organization of intrinsic theta-like membrane potential activity, and the modification of this activity during block of HCN channels, both reflect altered frequency distributions of stochastic spectral peaks, rather than tuning of a periodic oscillator. Our results demonstrate the importance of distinguishing periodic oscillations from stochastic processes. We suggest that dorsal–ventral tuning of theta-like membrane potential activity is due to differences in stochastic current fluctuations resulting from organization of ion channels that also control synaptic integration.
Introduction
The trajectory of a neuron's membrane potential is critical to its role in information processing (Llinas, 1988; Koch, 1999; Fricker & Miles, 2000). When the membrane potential of stellate neurons in layer II of the medial entorhinal cortex (MEC) is close to the threshold for initiation of action potentials, it fluctuates at frequencies in the theta (4–12 Hz) range (Alonso & Llinas, 1989). As layer II neurons encode location through grid-like firing fields (Fyhn et al. 2002), because the intrinsic theta-like activity resembles periodic oscillations, and as periodic oscillations are a useful substrate for computation (Hopfield, 1995), this observation has stimulated influential theoretical models for how animals compute their location (Burgess et al. 2007; Giocomo et al. 2007; Giocomo & Hasselmo, 2008a). In assuming that perithreshold membrane potential activity is periodic, these models are supported by biophysical simulations demonstrating that ion channels expressed by stellate neurons can be configured to generate periodic oscillations (Dickson et al. 2000; Fransen et al. 2004). Importantly, these models for generation of grid fields correctly predict that the frequency of intrinsic membrane potential activity recorded from stellate neurons at different positions along the dorsal–ventral axis of the MEC correlates with the resolution of spatial firing fields of neurons at the same location (Giocomo et al. 2007; Giocomo & Hasselmo, 2009; Boehlen et al. 2010). However, several observations suggest that stellate neurons might configure their ion channels primarily to tune computations that rely on synaptic integration, rather than to control the period of subthreshold oscillations (O'Donnell & Nolan, 2010). First, integration of synaptic responses by stellate neurons follows a dorsal–ventral organization similar to perithreshold membrane potential activity and to grid field spacing (Garden et al. 2008). Second, some biophysical simulations suggest that perithreshold theta-like activity might at least in part be stochastic (White et al. 1998; Dudman & Nolan, 2009). Third, ion channels important for perithreshold theta-like activity also influence synaptic integration (Nolan et al. 2007; Garden et al. 2008). Reconciling these different perspectives is important for understanding the cellular mechanisms responsible for spatial encoding and navigation.
To address these issues, we used a quantitative method for analysis of activity recorded from stellate neurons at different locations along the dorsal–ventral axis of the MEC. We show how discrete frequency peaks identified using power spectral density and autocorrelation methods do not necessarily reflect the existence of a periodic oscillatory process, but can also be caused by stochastic mechanisms. We demonstrate that in MEC stellate neurons the perithreshold theta-like activity is described by multiple spectral peaks, with frequency distribution that varies according to the position of a neuron along the dorsal–ventral axis of the MEC. Dorsal neurons have more relatively high-frequency spectral peaks than neurons found at more ventral locations. Higher frequency peaks are promoted by the presence of the hyperpolarization-activated current (Ih). The dorsal–ventral organization of theta-like activity is accounted for by tuning a stochastic model of a stellate neuron (Dudman & Nolan, 2009) with Ih and leak K+ currents adjusted according to previous descriptions of their dorsal–ventral organization (Garden et al. 2008). Our results establish new approaches to distinguishing periodic from stochastic membrane potential activity, demonstrate how the dynamics of theta-like membrane potential activity results from filtering of stochastic membrane currents, and explain previous observations of dorsal–ventral organization of the membrane potential dynamics of stellate neurons in the MEC.
Methods
Electrophysiology
Parasagittal brain slices (400 μm thick) containing the medial entorhinal cortex were prepared using previously described procedures (Garden et al. 2008). Mice were killed by cervical dislocation, the brain carefully removed and cut using a vibrating-blade microtome (Vibratome 3000, Intracel, Royston, Herts, UK), in chilled (4°C) modified artificial cerebrospinal fluid of the following composition (mm): 86 NaCl, 1.2 NaH2PO4, 2.5 KCl, 25 NaHCO3, 25 glucose, 0.5 CaCl2, 7 MgCl2 and 75 sucrose, bubbled with 95% O2–5% CO2. Slices were incubated at 35°C for 15 min in standard artificial cerebrospinal fluid of the following composition (mm): 124 NaCl, 1.2 NaH2PO4, 2.5KCl, 25 NaHCO3, 20 glucose, 2 CaCl2 and 1 MgCl2 and then maintained at room temperature. For recording, slices were transferred to a submerged chamber and stellate neurons were visually identified under infrared illumination. Whole-cell recordings were obtained at 35–37°C from the soma of stellate neurons in MEC layer II using 2–5 MΩ resistance electrodes filled with intracellular solution comprising (mm): 130 potassium methylsulfate, 10 KCl, 10 Hepes, 2 MgCl2, 0.1 EGTA, 4 Na2ATP, 0.3 Na2GTP and 10 phosphocreatine. Series resistances were <35 MΩ, and appropriate bridge and electrode capacitance compensation were applied. Data, sampled at 20 kHz and filtered at 10 kHz, were acquired with a Multiclamp 700B amplifier (Molecular Devices, Sunnyvale, CA, USA) connected to an Instrutech ITC-18 interface (HEKA Elektronik, Lambrecht, Germany) using Axograph X acquisition software (http://axographx.com/). An experimentally measured liquid junction potential of +8.1 mV (bath potential relative to the patch pipette) for the standard artificial cerebrospinal fluid was not corrected for. All experiments were performed in the presence of 5 μm 2,3-dihydroxy-6-nitro-7-sulfamoyl-benzene(f)quinoxaline (NBQX), 50 μm d-aminophosphonovalerate (D-APV) and 50 μm picrotoxin to block AMPA/kainate, NMDA and GABAA receptors, respectively. A total of sixteen mice were used. All experiments were carried out according to the guidelines laid down by the University of Edinburgh's animal welfare committee and in accordance with the UK Animals (Scientific Procedures) Act 1986. The authors have read, and the experiments comply with, the policies and regulations of The Journal of Physiology given by Drummond (2009).
To induce theta-like membrane potential activity in stellate neurons, a series of 20 s duration current injections were applied to depolarize cells to potentials close to threshold as described previously (Nolan et al. 2007). Unless indicated otherwise, analysis was performed on the final 15 s of data from the most depolarized subthreshold response using custom-written IGOR routines. For some analyses, each trace was further divided into five consecutive, non-overlapping, 3 s segments and measurements carried out on each segment.
Stellate neuron simulations
A single-compartment model previously constructed to account for key physiological properties of MEC stellate neurons (Dudman & Nolan, 2009) was used with the following minor modifications. In order that the membrane time constant and membrane potential fluctuations correspond more closely to experimentally measured values (Nolan et al. 2007; Garden et al. 2008), the membrane capacitance was modified to 4 μF cm−2 and the single-channel conductance of the leak K+ current reduced to 20 pS. The model was implemented in versions with resting membrane properties that correspond to typical stellate neurons from the dorsal and ventral parts of the MEC (Garden et al. 2008). In the dorsal configuration, the densities of hyperpolarization-activated, cyclic nucleotide gated (HCN) and leak K+ channels were 5 and 0.12 μm−2, respectively, while in the ventral configuration their respective densities were 1 and 0.02 μm−2. The dorsal model had a resting membrane potential of −67.0 mV, input resistance of 18.1 MΩ and membrane time constant of 8.3 ms. The ventral model had a resting membrane potential of −67.8 mV, input resistance of 76.1 MΩ and membrane time constant of 32.6 ms. To evaluate perithreshold membrane potential activity, direct current of amplitude 465 or 90 pA was injected into the dorsal and ventral models, respectively. In both cases, action potential firing was reliably triggered by increasing the amplitude of the current by 5 pA. All other properties of the dorsal and ventral stellate neuron models were identical. The model was simulated using PSICS (Cannon et al. 2010). For all simulations, the model was run in the stochastic mode with a time step of 0.05 ms.
General data analysis
Electrophysiological and simulation data were analysed in IGOR pro (Wavemetrics, Lake Oswego, OR, USA) or MATLAB (The MathWorks, Natick, MA, USA) using custom-written routines. Input resistance was calculated from the steady-state voltage response to injected hyperpolarizing current steps (<−100 pA). The median age of mice used in the study was 41 days (range 35–65 days). Statistical analysis was carried out using R (http://www.r-project.org/). Differences between groups were assessed using Student's paired or unpaired t test, ANOVA or ANCOVA as appropriate. Relationships between dorsal–ventral location and neuronal properties were evaluated with linear regression and are reported as adjusted R2 values (Garden et al. 2008). Mean values are ± SEM.
Methods for analysis of intrinsic theta-like membrane potential activity
Theta-like membrane potential activity was analysed with power spectra and autocorrelation methods used in previous studies (e.g. Alonso & Llinas, 1989; Giocomo et al. 2007; Nolan et al. 2007; Boehlen et al. 2010) and with the Lomb method of least-squares frequency analysis (Lomb, 1976; Press et al. 1992). The Lomb method has the advantage that it provides a measure of the statistical significance of peaks in the power spectra compared with the null hypothesis that the data points arise from an exponential distribution.
To determine whether these methods can distinguish between oscillatory and stochastic processes, we evaluated them with the following artificial data: broad-band Gaussian noise (Fig. 1A); a 10 Hz sinusoidal oscillation summed with broad-band Gaussian noise (Fig. 1B); a 10 Hz sinusoid containing phase noise (Fig. 1C); Gaussian noise low-pass filtered with a cut off of 10 Hz (Fig. 1D); and a random walk generated by incremental addition of low-variance Gaussian noise with a 25 ms decay time constant (Fig. 1E). While oscillators are generally defined as periodic processes, they may be subject to noise that modifies their period. In general, an oscillating signal [V(t)] can be defined as V(t) =A(t)cos[ωot+ϕ(t)], where ωo is the frequency of the oscillation, A(t) is the amplitude and ϕ(t) a phase reference. Noise can be introduced into the oscillation through time-dependent changes in A(t) or ϕ(t). Phase noise is of most concern for an oscillator that must provide a reference signal for computation. In the example shown in Fig. 1B, A(t) and ϕ(t) are constant and a separate Gaussian noise term is added to the oscillation. In the example shown in Fig. 1C, A(t) is constant and phase noise is introduced by varying ϕ(t).
Figure 1. Comparison of methods for analysis of oscillatory activity.
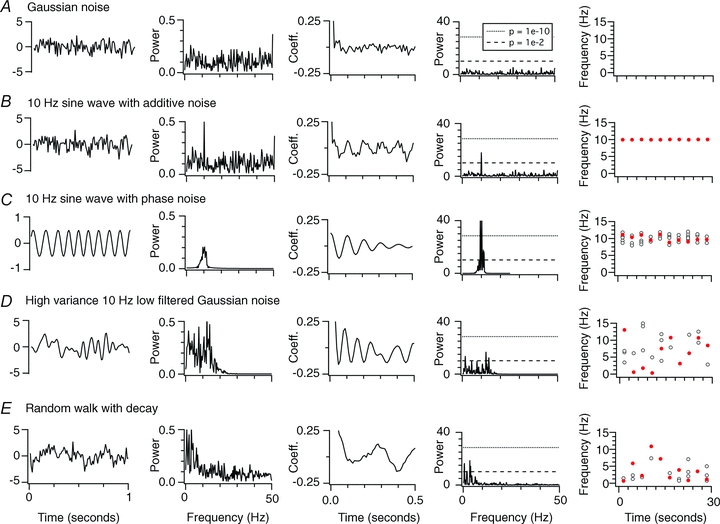
A–E, examples of analysis of unit variance Gaussian noise (A), a 10 Hz sine wave with added unit variance Gaussian noise (B), a 10 Hz sine wave with amplitude 0.5 units containing phase noise with maximum period shift of ± 0.5 units (C), high (2 unit) variance Gaussian noise filtered with a cut off of 10 Hz (D) and a random walk generated by incremental addition of low (1 unit) variance Gaussian noise with a 25 ms decay time constant (E). The first column shows 1 s of example data, the second to fourth columns shows the power spectral density, the autocorrelation function and the Lomb spectra generated from 3 s waveforms generated by each process, while the fifth column plots the frequency of the largest amplitude significant peak in the Lomb spectra (red filled circles) and the frequencies of all other significant peaks (open circles) for 10 consecutive simulation epochs each of duration 3 s.
For calculation of spectra, data were first filtered (0.5–50 Hz), then resampled at 1 kHz for power spectra and at 100 Hz for Lomb analysis. Power spectral densities were computed using Hanning windowing, a 2048 ms window and frequency bin width of 0.0666667 Hz. Lomb periodograms were calculated following previous implementations (Press et al. 1992), with the oversampling parameter equal to 4 and highest frequency equal to the Nyquist frequency. Similar analysis parameters were used for experimental and simulation data.
As expected, Gaussian noise was characterized by a flat power spectrum and autocorrelogram, and a Lomb periodogram that did not contain any significant (P < 0.05) peaks (Fig. 1A), while the signal containing 10 Hz oscillations was characterized by a power spectral peak at 10 Hz, an autocorrelogram with period of 100 ms, and a significant (P < 1e–10) 10 Hz peak in the Lomb periodogram (Fig. 1B). The frequency of the spectral peak generated by the oscillator was similar on repeated trials (Fig. 1B). The oscillator with phase noise also generated a signal characterized by a peak in the power spectral density and a periodic autocorrelogram, but in this case the spectral peak was ‘smeared’ and the autocorrelation function decayed rapidly (Fig. 1C). For the oscillator with phase noise, the largest Lomb peak has a similar frequency from trial to trial, while smaller nearby side-peaks cluster around the largest peak. The stability and the smearing of the spectral peak are consistent with theoretical predictions (Hajimiri & Lee, 1998; Demir et al. 2000). With noise introduced into the amplitude coefficient [A(t)], the spectral peak also remained stable from trial to trial, and was also accompanied by adjacent, smaller side-peaks (not shown).
While filtered Gaussian noise and the random walk are both generated by stochastic processes, they nevertheless also produced power spectra containing clear peaks and Lomb spectra with significant (P < 0.01) peaks (Fig. 1D and E). However, in contrast to spectral peaks generated by oscillators, the stochastic processes generate spectra with multiple peaks distributed across a broad frequency range. The frequency of the largest amplitude spectral peak varied substantially between trials (Fig. 1D and E). Thus, while spectral peaks may reflect genuine oscillatory processes (Fig. 1B and C), they may also result from random processes that are filtered (Fig. 1D) or arise from processes with history dependence (Fig. 1E). We show below that the latter two properties may apply to neuronal membrane potential.
Construction and testing of filters
To derive filters corresponding to the dorsal and ventral models, we recorded the membrane potential and the total membrane ionic current during simulation of 100 s duration periods of perithreshold activity. The current and voltage signals were Fourier transformed to frequency domain representations. Filters were obtained by dividing the Fourier-transformed voltage signal by the corresponding Fourier-transformed current signal. To predict membrane potential changes caused by filtering of membrane currents from a particular model, a new simulated total membrane ionic current was Fourier transformed, multiplied with a previously derived filter, and then converted back to the time domain using an inverse Fourier transform.
Results
Perithreshold membrane potential activity is consistent with stochastic and not periodic processes
We initially focus on distinguishing two distinct types of process that can underlie intrinsic subthreshold changes in membrane potential (Fig. 1). We consider oscillatory processes to generate changes in membrane potential that vary around a mean value with a periodic cycle. Interactions between voltage-dependent ion channels expressed by stellate neurons can in principle establish periodic subthreshold oscillations (Dickson et al. 2000; Fransen et al. 2004). In contrast, changes in membrane potential that vary around a mean value could instead be generated by stochastic processes, but in this case will have a trajectory that is not periodic. While stochastic gating of ion channels influences the membrane potential of stellate neurons (White et al. 1998; Dorval & White, 2005), it is not clear whether stochastic fluctuations are superimposed on a periodic oscillation (as in Fig. 1B), contribute noise to an oscillator (as in Fig. 1C) or are the sole cause of intrinsic membrane potential fluctuations (as in Fig. 1D and E). Distinguishing between these possibilities is critical to understanding the integrative roles of stellate neurons. Moreover, because methods previously used to analyse theta-like intrinsic activity of stellate neurons do not distinguish periodic oscillations from stochastic processes, it is not clear whether the dorsal–ventral organization of theta-like activity reflects tuning of a periodic oscillator, as previously suggested (Giocomo et al. 2007; Giocomo & Hasselmo, 2009; Boehlen et al. 2010), or if it is due to some other mechanism that has not previously been considered. To distinguish these possibilities, we compared the properties of different processes that generate spectral peaks (Fig. 1) with properties of perithreshold membrane potential activity recorded from stellate neurons (Figs 2–4).
Figure 2. Dorsal–ventral organization of the autocorrelation of perithreshold membrane potential activity and of resting membrane properties.
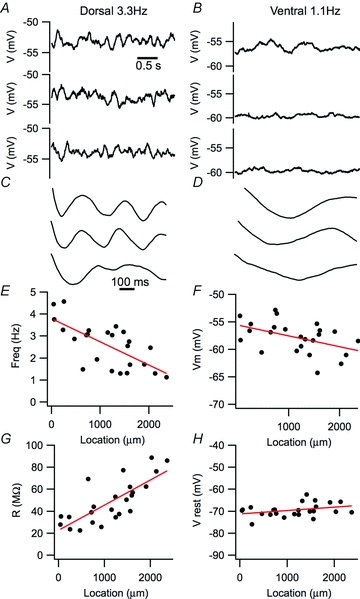
A and B, examples of the 3 s segments of perithreshold membrane potential recordings containing the largest amplitude peaks in their autocorrelogram obtained from dorsal (A) and ventral MEC stellate neurons (B). Selection of the segments is as in Giocomo et al. (2007). C and D, autocorrelograms corresponding to the membrane potential segments shown in A and B. E–H, frequency of the first peak in the autocorrelogram, R2= 0.45, P = 0.00019 (E), perithreshold membrane potential, R2= 0.18, P = 0.022 (F), resting input resistance, R2= 0.56, P = 1.4e–5 (G) and resting membrane potential, R2= 0.077, P = 0.10 (H), plotted as a function of neuronal location along the dorsal–ventral axis of the MEC.
Figure 4. Modulation of relatively high-frequency spectral peaks causes dorsal–ventral organization of perithreshold membrane potential activity.
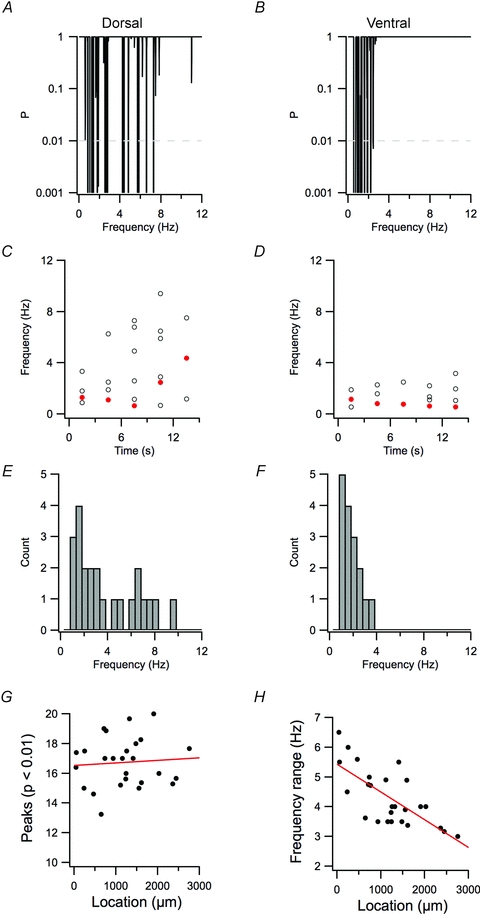
A and B, examples of periodograms of 15 s of perithreshold membrane potential activity from dorsal (A) and ventral stellate neurons (B). C and D, frequencies of significant peaks (P < 0.01) for contiguous 3 s segments of data from A and B, respectively. The frequencies of the peak with the highest significance in each epoch are indicated in red. E and F, distribution of frequencies for the significant peaks in A–D. G and H, the mean number of peaks in each 15 s epoch (G) and the range of frequencies spanned by the significant peaks (H) are plotted as a function of the dorsal–ventral position of each recorded neuron. For number of peaks, R2= 0.036, P = 0.71. For frequency range, R2= 0.49, P = 4.4e–5.
We first established whether dorsal–ventral organization of oscillatory activity of stellate neurons in layer II of the MEC is found in recording conditions that previously revealed dorsal–ventral organization of synaptic integration (Garden et al. 2008). To evaluate perithreshold theta-like activity, we injected current to depolarize the membrane potential to just below spike threshold and recorded the resulting membrane potential fluctuations (e.g. Figs 2A and B and 3A and B). To prevent spontaneous synaptic events influencing the membrane potential, all recordings were made in the presence of blockers of ionotropic glutamate and GABAA receptors. Similar to previous descriptions of stellate neurons (Alonso & Llinas, 1989; Alonso & Klink, 1993; White et al. 1998; Dickson et al. 2000; Erchova et al. 2004; Giocomo et al. 2007; Nolan et al. 2007; Burton et al. 2008; Boehlen et al. 2010), perithreshold activity was characterized by power spectral peaks at frequencies below 10 Hz and by corresponding peaks in autocorrelograms of the activity (Figs 2C and D and 3C and D). We followed a previously reported procedure of calculating autocorrelation functions for 3 s epochs of data and selecting the three epochs with the largest peaks for calculation of a characteristic frequency for each neuron (Giocomo et al. 2007). Using this procedure, we also found a dorsal–ventral organization of the frequency of perithreshold oscillatory activity. Thus, for neurons at more dorsal locations, the largest autocorrelogram peaks had higher frequencies than for neurons at more ventral locations (cf. Fig. 2A and C with B and D). This organization of theta-like activity is reflected in a significant correlation between the frequency of autocorrelogram peaks and the location of each recorded neuron along the dorsal–ventral axis of the MEC (P = 1.9e–4; Fig. 2E). We also found that the most depolarized membrane potential that could be maintained without triggering action potentials, which is the membrane potential at which perithreshold oscillations were recorded, followed a similar dorsal–ventral organization (P = 0.022; Fig. 2F). In addition, the population of neurons used to evaluate oscillatory activity demonstrated a dorsal–ventral organization of their resting membrane resistance (P = 1.4e–5; Fig. 2G), but not their resting membrane potential (P = 0.1; Fig. 2H). The latter two observations are consistent with previous analysis of dorsal–ventral organization of resting membrane properties that are important for synaptic integration by stellate neurons (Boehlen et al. 2010; Garden et al. 2008). Together, these data establish that the population of neurons we recorded from demonstrate a dorsal–ventral organization of perithreshold theta-like activity measured according to previous criteria (Giocomo et al. 2007), and a similar organization of their resting membrane properties, also as described previously (Garden et al. 2008).
Figure 3. Perithreshold membrane potential activity contains multiple frequency components.
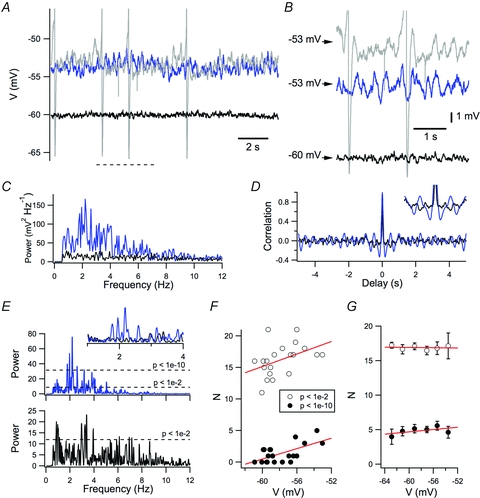
A, example of perithreshold membrane potential activity (blue trace), threshold membrane potential activity (grey trace) and activity of the membrane potential when it is more than 5 mV hyperpolarized to threshold (black trace). B, membrane potentials in A, shown on expanded time and voltage scales. C–E, power spectral density (C), autocorrelogram (D) and Lomb periodogram (E) of the perithreshold membrane potential activity (blue trace) and activity of the membrane potential when it is more than 5 mV hyperpolarized to threshold (black trace) from A. F and G, number of Lomb peaks with significance < 0.01 (open circles) or < 1e–10 (filled circles) plotted as a function of membrane potential for the neuron in A–E (F) and on average for all neurons (G). While in the example neuron the number of peaks with significance < 1e–10 appeared to correlate slightly with membrane potential (peak threshold at 0.01, R2= 0.14, P = 0.060; peak threshold at 1e–10, R2= 0.035, P = 0.0036), in the population data the number of peaks at either significance threshold did not vary as a function of membrane potential (peak threshold at 0.01, R2=−0.019, P = 0.79; peak threshold at 1e–10, R2=−0.020, P = 0.90).
Is the perithreshold membrane potential activity due to a periodic oscillation, as in Fig. 1B and C, or is it instead consistent with stochastic processes that also cause spectral peaks, as in Fig. 1D and E? To quantify the membrane potential fluctuations, we use the Lomb method of least-squares spectral analysis (Lomb, 1976). In common with the power spectral density, the Lomb periodogram identifies the frequency of fluctuating components of a signal, but also quantifies the statistical significance of changes at particular frequencies compared with the null hypothesis that they arise from an exponential process. As the significance estimate is normalized to the mean variance of fluctuations, we adopt this value for comparison of activity between neurons. We find that Lomb spectra generated from the perithreshold membrane potential activity of stellate neurons have multiple significant peaks with frequency <10 Hz (Fig. 3). Even within a single 15 s epoch, the multiple peaks have widely differing frequencies, with a mean range of 3.9 ± 0.2 Hz when detected using a significance threshold of P < 0.01 and a range of 2.5 ± 0.2 Hz when detected with a more stringent cut off of P < 1e–10. When epochs are binned according to their modal membrane potential, the number of significant oscillatory components is relatively independent of the membrane potential during the epoch in individual neurons (Fig. 3F) and across the population as whole (Fig. 3G). During the most depolarized epoch, the number of peaks quantified with either significance threshold was also independent of the membrane potential during this epoch and of the resting membrane potential prior to depolarization (R2 < 0.05 and P > 0.4 for both comparisons). These data suggest that perithreshold theta-like activity recorded from stellate neurons does not arise from a mechanism that generates oscillations (cf. Fig. 1B and C). Instead, even in a single neuron, theta-like activity occurs with a broad range of frequencies. This is consistent with properties of filtered noise source or a random walk (cf. Fig. 1D and E).
Dorsal–ventral organization of perithreshold activity reflects tuning of stochastic spectral peaks
How is the dorsal–ventral organization of theta-like activity, suggested by the analysis used in previous studies (Giocomo et al. 2007; Giocomo & Hasselmo, 2009; Boehlen et al. 2010) and in Fig. 2, related to the multiple frequency peaks identified in Fig. 3? We found multiple significant frequency peaks in periodograms generated from the perithreshold activity of neurons at all dorsal–ventral locations (Fig. 3). However, while dorsal neurons typically demonstrated peaks with frequency in the range of 1–10 Hz (Fig. 4A and E), for more ventral neurons the maximal peak frequency was typically less than 5 Hz (Fig. 4B and F). When activity was broken up into 3 s segments, the most significant peak was not stable, but from segment to segment had a coefficient of variation of 0.50 ± 0.03 (Fig. 4C and D). The range of frequencies with significant peaks (Fig. 4H) varied significantly as a function of neuronal location (R2= 0.49, P = 4.4e–5). In contrast, the number of oscillatory components did not depend significantly on location (R2= 0.036, P = 0.71; Fig. 4G). These properties provide further evidence that changes in the perithreshold membrane potential are not driven by a periodic oscillator, because an oscillatory process, even containing phase noise, would have a dominant frequency that differs very little between trials (cf. Fig. 1B and C). These data are consistent with the viewpoint that dorsal–ventral organization of the frequency of intrinsic activity reflects differences in stochastic membrane potential fluctuations. According to this interpretation, previous suggestions of increased frequency of oscillations in more dorsal neurons are instead explained by more relatively high-frequency stochastic fluctuations.
Since Ih, which is mediated by HCN channels, influences the stability of the perithreshold membrane potential (Nolan et al. 2007; Dudman & Nolan, 2009), has an amplitude that follows a dorsal–ventral organization (Garden et al. 2008) and, in some models, is required for perithreshold theta-like activity (Dickson et al. 2000; Fransen et al. 2004, but see White et al. 1998; Dudman & Nolan, 2009), we asked whether block of Ih with ZD7288 affected the dorsal–ventral organization of perithreshold activity. As expected, block of Ih with ZD7288 hyperpolarized the resting membrane potential of stellate neurons and increased their input resistance (Fig. 5A–C). Consistent with the effects of deletion of HCN1 (Nolan et al. 2007), the main HCN subunit expressed by stellate neurons, we found that block of Ih with ZD7288 reduced the most stable perithreshold membrane potential that could be maintained without triggering action potentials (P = 0.047; Fig. 5F). The dominant frequency calculated from autocorrelation functions depended on the dorsal–ventral location of the recorded neuron (P = 0.003) and, consistent with previous studies (Giocomo & Hasselmo, 2009), appeared to be reduced in ZD7288, although this difference was not statistically significant (P = 0.14; Fig. 5G–I). In contrast, the maximum frequency of spectral peaks measured with Lomb analysis was significantly reduced by ZD7288 (P = 0.0047; Fig. 5J–L). Thus, HCN channels appear to modulate, but are not required for, theta-frequency activity, and appear to contribute to the dorsal–ventral organization of higher frequency spectral peaks.
Figure 5. Block of Ih reduces the maximal frequency of perithreshold oscillatory activity.
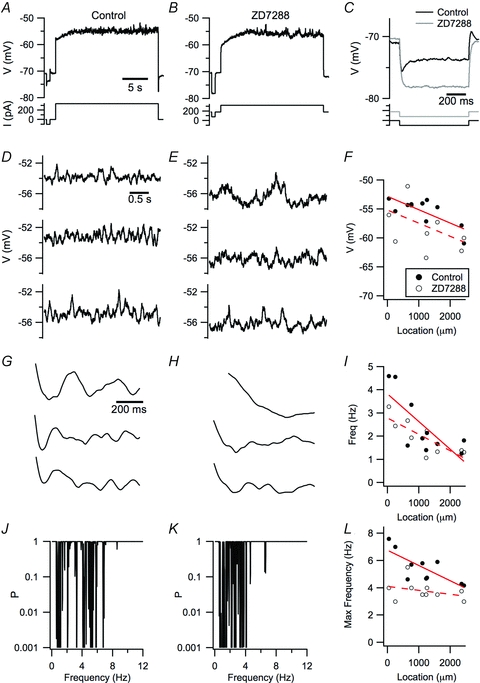
A and B, examples of perithreshold membrane potential responses of a stellate neuron to current steps before (A) and during perfusion of 10 μm ZD7288 (B). C, the amplitude of voltage responses to negative current steps is increased and the membrane potential sag is abolished by ZD7288. To compensate for the hyperpolarization of the membrane potential induced by ZD7288, a constant positive offset current is injected into the neuron. D and E, the three 3 s segments of activity with the largest autocorrelation scores obtained from the responses in A and B. Selection of the segments is as in Giocomo et al. (2007). G and H, autocorrelation functions for the data in D and E. J and K, Lomb periodograms obtained from the data in A and B. F, I and L, perithreshold membrane potential (F), frequency of autocorrelation peaks (I) and frequency range (L) of the significant peaks in the Lomb periodogram before (filled circles) and during perfusion of ZD7288 (open circles) is plotted as a function of dorsal–ventral location of the recorded neuron. The most depolarized membrane potential was reduced by ZD7288 (P = 0.047, Student's paired t test; P = 0.063, ANCOVA), while the dependence on location (P = 0.0498, ANCOVA) was not significantly altered (P = 0.98, ANCOVA). The autocorrelogram peak frequency was not significantly affected by ZD7288 (P = 0.14, Student's paired t test; P = 0.13, ANCOVA), while the peak frequency depended on location (P = 0.0030, ANCOVA). The Lomb frequency range depended on location (P = 0.00014) and was affected by ZD7288 (P = 0.0047), while the number of Lomb peaks did not depend on location (P = 0.54) and was not affected by ZD7288 (P = 0.43).
Is the dorsal–ventral organization of spectral peaks in the perithreshold membrane potential activity of stellate neurons consistent with stochastic models for generation of membrane potential fluctuations (White et al. 1998)? To address this question, we used a model of a stellate neuron in which all ion channels gate stochastically (Dudman & Nolan, 2009). We previously showed that this model accounts for key resting and active properties of stellate neurons and for the consequences of deletion of HCN1 channels (Dudman & Nolan, 2009). We configured dorsal (Fig. 6A) and ventral (Fig. 6C) versions of the model by adjusting the density of HCN channels and leak K+ channels according to our previous measurements (Garden et al. 2008). Power spectra and Lomb periodograms generated from simulations of the models that recapitulate experiments in Fig. 3 had multiple peaks at frequencies below 10 Hz. Periodograms from the dorsal model had slightly more significant peaks compared with the ventral model (P = 0.002; Fig. 6E) and, importantly, the peaks occurred at a wider range of frequencies (P < 1e–16; Fig. 6F). The small difference in the number of significant peaks is within the cell-to-cell variation of our recordings and so is unlikely to be detected experimentally (cf. Fig. 4G), while the difference in the frequency range of the significant peaks corresponds well to the experimental data (cf. Fig. 4H). Comparison of averaged power spectral densities (Fig. 6G) and mean Lomb spectra (Fig. 6H) indicated less activity at frequencies below 3 Hz and more at frequencies above 5 Hz in the dorsal compared with the ventral model. Together, these simulations suggest that dorsal–ventral organization of the density of conductances mediated by HCN and leak K+ channels is sufficient to explain the dorsal–ventral organization of perithreshold membrane potential activity described in Figs 2–4 and in previous studies (Giocomo et al. 2007; Giocomo & Hasselmo, 2009; Boehlen et al. 2010).
Figure 6. Tuning of HCN and leak K+ channels in a stochastic stellate neuron model accounts for dorsal–ventral organization of perithreshold activity.
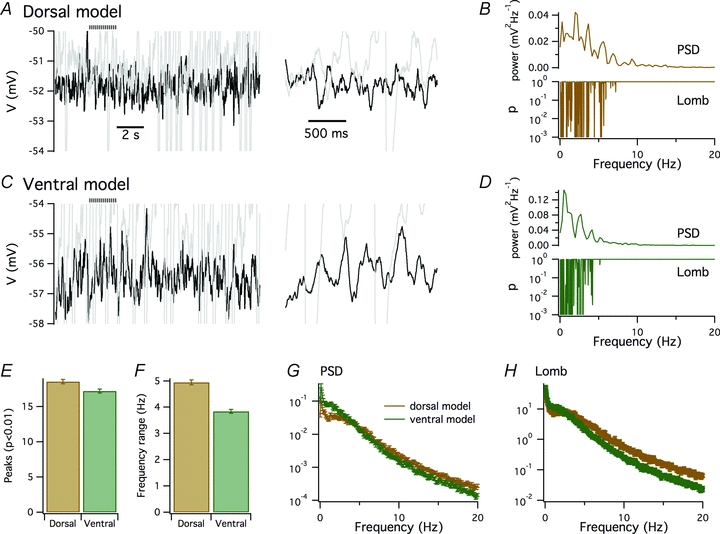
A–D, examples of perithreshold membrane potential (A and C) and corresponding plots of power spectral density and significance of peaks in the Lomb periodogram as a function of frequency (B and D) obtained from dorsal (A and B) and ventral configurations (C and D) of a stochastic model of an MEC stellate neuron. Perithreshold membrane potential responses are to injection of 465 (A and B) and 90 pA current steps (C and D). Traces in grey are the just suprathreshold responses to 470 (A and B) and 95 pA current steps (C and D). The horizontal striped bar indicates the regions shown on an expanded time scale to the right. E–H, the mean number of significant (P < 0.01) peaks in the Lomb periodogram (E), the mean range of frequencies at which significant peaks occurred (F), the mean power spectral density (G) and the mean Lomb periodogram (H) obtained from 100 simulations of the dorsal (brown) and ventral configurations (green) of the stellate neuron model. The dorsal neurons had on average more significant peaks (P = 0.002, Student's unpaired t test) and a wider range of peak frequencies (P = 0.7e–17, Student's unpaired t test) compared with the simulated ventral neurons. Comparison of power spectral density and Lomb periodogram data points at 0.5 Hz intervals indicated that perithreshold membrane potential fluctuations generated by the dorsal model had less power (P < 0.05, Student's unpaired t test comparison of individual data points) at frequencies below 3 Hz and more power (P < 0.05) at frequencies >5 Hz compared with the ventral model.
Tuning of stochastic spectral peaks is accounted for by differences in stochastic current fluctuations
How is theta-frequency activity modulated by dorsal–ventral organization of HCN and leak K+ channels? Our results are inconsistent with the notion that HCN and leak K+ channels control the periodicity of an intrinsic oscillator, but support the viewpoint that these channels modulate voltage fluctuations driven by stochastic ion channel gating. In principle, this could be achieved either through differences in stochastic fluctuations in the total membrane current, or through differential filtering of the stochastic currents as they charge and discharge the membrane capacitance (Cannon et al. 2010). Consistent with the former possibility, we found that the larger total ionic current in the dorsal (Fig. 7A) compared with the ventral model (Fig. 7B) contains more power at frequencies above approximately 10 Hz (Fig. 7C). Nevertheless, from these data alone it is unclear whether it is the difference in the ionic current or differences in filtering of the current that account for the apparent dorsal–ventral tuning of intrinsic theta-like activity.
Figure 7. Dorsal–ventral organization of oscillatory activity is accounted for by differences in stochastic membrane currents.
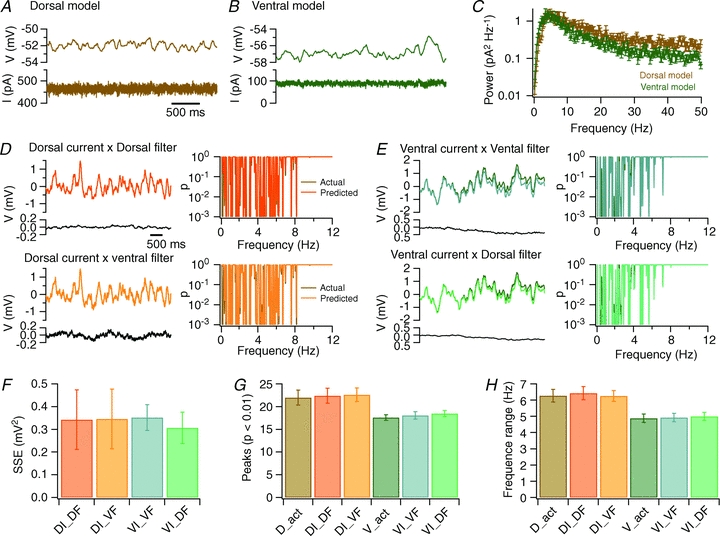
A and B, examples of membrane potential (upper traces) and total membrane current (lower traces) obtained from simulation of perithreshold membrane potential activity of a stellate neuron model in dorsal (A) and ventral configurations (B). C, average power spectral density of perithreshold membrane current fluctuations from dorsal and ventral configurations of the stellate neuron model. Each spectrum is the mean of 10 spectra calculated from the total ionic current as in (A and B). D and E, comparison of the membrane potential predicted by multiplying current input with a filter, with the actual membrane potential (upper traces). The difference voltage is calculated by subtracting the predicted from the actual membrane potential (lower traces). Corresponding Lomb periodograms are shown to the right. The membrane potential and corresponding Lomb periodograms from the dorsal model (D) and the ventral model (E) are well predicted by multiplying currents generated by the dorsal model with filters generated from either the dorsal or the ventral model as indicated. Scale bars and labelling of traces in D and E are identical. In several panels, the simulation result is obscured because it is almost identical to the result predicted by convolving the filter with the current input. F, the sum of the squared errors (SSE) between the actual voltage and the voltage predicted by multiplying the perithreshold ionic current generated by the dorsal (DI) or ventral model (VI) with a filter obtained from previous simulations with a dorsal (DF) or a ventral neuron (VF). G and H, the number of significant peaks (G) and the range of significant frequencies (H) generated by simulation of the dorsal (D_act) or ventral (V_act) models, or calculated as in D and E (symbols as in F). ANOVA indicated that the number of significant peaks and the range of significant peaks were independent of the identity of the filter (P = 0.95 and P = 0.97, respectively), but depended on the origin of the input current (P = 9.0e–6 and P = 1.9e–6). Subsequent Student's paired t tests also indicated significant differences between membrane potential fluctuations driven by currents from dorsal and ventral models (P < 0.05 in all cases) and absence of a significant difference (P > 0.3) between potential fluctuations driven by the same currents and different filters.
To address this issue further, we reasoned that if differences in filtering account for dorsal–ventral tuning of theta-like activity, then filters constructed from either a dorsal or a ventral model should produce dorsal-like and ventral-like membrane potential fluctuations when applied to ionic currents recorded from either dorsal or ventral models. Conversely, if differences in stochastic current fluctuations account for dorsal–ventral organization of theta-like activity, then membrane potential fluctuations predicted by filtering ionic currents should depend only on the identity of the model used to generate the currents, but not on the identity of the filter. To distinguish these possibilities, we first derived, for both dorsal and ventral models, a corresponding filter based on the membrane potential and membrane current during simulation of a total of 100 s of perithreshold activity (see Methods). With each model, we then carried out a further 10 simulations of 10 s of perithreshold activity, and compared the membrane potential from these simulations with the predicted membrane potential generated by applying the previously generated filters to the membrane current during each new simulation (Fig. 7D and E). Membrane potential fluctuations produced by the dorsal model were recapitulated by combining the dorsal ionic current with either dorsal or ventral filters (Fig. 7D). In both cases, the peaks in the corresponding Lomb periodograms were at similar frequencies to the peaks obtained from the original simulation results. Likewise, membrane potential fluctuations and peaks in the Lomb periodogram produced by the ventral model were recapitulated by combining the ventral ionic current with either dorsal or ventral filters (Fig. 7E). The difference between the predicted and actual membrane potential was independent of the filter used (Fig. 7F), while the number (Fig. 7G) and frequency range (Fig. 7H) of peaks in the Lomb periodogram depended on the origin of the ionic current (P = 9.0e–6 and P = 1.9e–6, respectively), but not on the identity of the filter (P = 0.95 and P = 0.97, respectively). Together, these results suggest that dorsal–ventral tuning of theta-like activity is accounted for by differences in stochastic fluctuations in the membrane current driving perithreshold activity and not by differences in filtering of the current.
Discussion
The mechanisms that configure the membrane potential dynamics of neurons in layer II of the MEC are likely to be critical for neural encoding of location. To assess the organization of theta-like activity recorded from these neurons, we adopted the Lomb method for frequency analysis. We show that perithreshold activity differs significantly from Gaussian noise and has properties consistent with a stochastic rather than a periodic process. The dorsal–ventral organization of this activity is accounted for by a difference in fluctuations in the membrane current resulting from stochastic ion channel gating. Our results are inconsistent with models for spatial encoding that require intrinsic oscillations in the membrane potential of stellate neurons, but support the idea that dorsal–ventral organization of stellate neuron ion channels that tune subthreshold synaptic integration also leads to differences in perithreshold membrane potential dynamics.
Dorsal–ventral organization of theta-like membrane potential activity results from differences in filtered stochastic current fluctuations
Our results suggest a novel cellular mechanism for the dorsal–ventral organization of perithreshold theta-like membrane potential activity intrinsic to stellate neurons in layer II of the MEC. Previously, organization of perithreshold activity was interpreted using a deterministic framework, in which theta-like activity is assumed to be periodic, with a single dominant frequency that might in principle be used by models for spatial encoding (Burgess et al. 2007; Giocomo & Hasselmo, 2008a; Zilli et al. 2009). In this framework, theta-like activity emerges through deterministic interactions between a persistent Na+ current and a hyperpolarization-activated current (Ih) mediated by HCN channels (Dickson et al. 2000; Fransen et al. 2004). The period of this type of activity is determined by the gating kinetics of membrane ion channels, with noise causing variation of the period (Fransen et al. 2004; Zilli et al. 2009). While our results reproduce previous observations of dorsal–ventral organization of autocorrelogram peaks (Fig. 2), our more detailed analysis suggests that the properties and organization of theta-like activity are inconsistent with this deterministic model (Fig. 3). In particular, when perithreshold activity is evaluated over relatively long durations a dominant spectral peak at a single frequency, which would be expected for an oscillator with period that varies about a mean value (cf. Fig. 1B and C), is not present. Instead, peaks are distributed evenly across a relatively wide range of frequencies.
The new analysis we introduce here supports an alternative mechanism whereby the dorsal–ventral organization of theta-like activity recorded from stellate neurons results from differences in the fluctuation of the membrane current resulting from stochastic gating of ion channels. Several observations support this viewpoint. First, while multiple significant spectral peaks are inconsistent with perithreshold activity arising from broad-band Gaussian noise or from a periodic process (Fig. 1A–C), they are consistent with a filtered noise source (cf. Figs 1D and E and 3). Previous studies, using 3 s duration epochs for calculation of power spectra, are less likely to reveal multiple peaks, and may also suffer bias in characterization of neurons because only epochs with the most power were considered. Second, dorsal–ventral organization of the frequency of theta-like activity does not reflect tuning of a dominant oscillatory peak (cf. Fig. 1B and C), but rather reflects redistribution of spectral peaks so that ventral neurons have fewer high-frequency peaks than more dorsal neurons (cf. Fig. 4 with Fig. 1D and E). Third, tuning of a stochastic model that accounts for key membrane properties of stellate neurons can explain the dorsal–ventral organization of the frequency of perithreshold activity (Fig. 6). Fourth, filtered stochastic currents generated by the model account for the corresponding membrane potential activity and predict that differences between theta-like activity in dorsal and ventral neurons result from different stochastic membrane currents rather than modified filtering of the currents (Fig. 7). While we demonstrate that the experimental conditions we use are able to reproduce previous reports of dorsal–ventral organization of perithreshold activity (Fig. 2), we cannot rule out that in experimental conditions used in other studies periodic subthreshold processes may be present. However, if this is the case then application of the analysis we use here should enable periodicity to be clearly demonstrated.
A critical difference between models for theta-like activity based on generation of periodic oscillations compared with activity driven by stochastic ion channel gating is the proposed role for the large hyperpolarization-activated current (Ih) found in stellate neurons (Dickson et al. 2000; Richter et al. 2000; Nolan et al. 2007). In deterministic models, delayed deactivation of Ih during depolarization drives the hyperpolarizing phase of periodic oscillations (Dickson et al. 2000; Fransen et al. 2004). According to this viewpoint, dorsal–ventral organization of perithreshold theta-like activity can be achieved by changing the kinetics of Ih (Giocomo et al. 2007; Hasselmo et al. 2007; Giocomo & Hasselmo, 2009). Measurements of Ih have been suggested to support this idea (Giocomo & Hasselmo, 2008b), although in our experimental conditions the kinetics of Ih activation are independent of neuronal location along the dorsal–ventral axis of the MEC (Garden et al. 2008). In contrast to the oscillatory function proposed for Ih, our analysis of theta-like perithreshold activity supports a very different role. This is to act, together with leak K+ currents, to facilitate membrane potential fluctuations arising from stochastic gating of ion channels open at potentials close to spike threshold (Fig. 7). Stochastic gating of HCN and leak K+ channels may contribute directly to fluctuations in the total membrane current. In addition, by enabling the membrane potential to reach more depolarized values without triggering action potentials, HCN channels can increase the contribution of persistent Na+ currents to the membrane potential fluctuations (Nolan et al. 2007; Dudman & Nolan, 2009). This role of Ih is distinct from its contribution to membrane resonance, which relies on voltage-dependent gating to oppose membrane potential fluctuations with frequency below approximately 5 Hz (Hu et al. 2002; Nolan et al. 2007; Narayanan & Johnston, 2008).
Consequences of stochastic perithreshold theta-like activity for organization of information processing in the medial entorhinal cortex
The discovery that the spatial firing fields of neurons in layer II of the MEC follow a dorsal–ventral organization suggests the possibility of establishing cellular mechanisms that map directly onto computations that cognitive circuits carry out during behaviour (Hafting et al. 2005; Fyhn et al. 2008). Two different aspects of the intrinsic membrane properties of stellate neurons have been shown to correlate with position along the dorsal–ventral axis of the MEC. On the one hand, perithreshold activity and membrane resonance are organized such that higher frequency activity predominates in dorsal compared with ventral neurons (Giocomo et al. 2007; Giocomo & Hasselmo, 2008b, 2009; Boehlen et al. 2010). On the other hand, integration of synaptic responses is organized so that more dorsal neurons demonstrate less temporal summation of gamma-, but not theta-frequency inputs, and a narrower time window for detection of coincident synaptic inputs (Garden et al. 2008). The results we describe here suggest that organization of the density of HCN and leak K+ currents can explain the organization of perithreshold activity (Fig. 6) as well as the organization of synaptic integration (Garden et al. 2008). Perithreshold activity produced by this mechanism is unstable, with spectral peaks that have multiple frequencies and therefore are unlikely to be consistent with models for spatial firing that rely on oscillations (Welinder et al. 2008). Thus, not only are stellate neurons unable to support interactions between intrinsic oscillations required for some versions of interference theories of grid cell firing (Remme et al. 2010) or stable periodic oscillations (Welinder et al. 2008; Zilli et al. 2009), but their intrinsic properties may not support generation of oscillations of any kind.
Is dorsal–ventral organization of stochastic perithreshold activity or synaptic integration important for encoding of location by neurons within the entorhinal cortex? In principle, stochastic perithreshold activity could influence responses of stellate neurons to physiological patterns of synaptic input (Haas & White, 2002; Haas et al. 2007; Dudman & Nolan, 2009). This might reduce correlations between output from different stellate neurons to downstream neurons in the dentate gyrus. In this scenario, the dependence of the frequency spectra of perithreshold activity on dorsal–ventral location may reflect different requirements for de-correlation of stellate neuron output. Alternatively, the dorsal–ventral organization of perithreshold activity may itself have no function for computations carried out by stellate neurons, but might instead be an indirect consequence of organization of synaptic integration (Garden et al. 2008). This scenario is consistent with reduction of intrinsic perithreshold theta-like activity by artificial synaptic conductances designed to replicate in vivo activity (Fernandez & White, 2008) and with intracellular recordings of stellate neurons in anaesthetized animals (Quilichini et al. 2010). In this case, dorsal–ventral tuning of HCN and leak K+ channels might be important to control integration of synaptic responses. This could tune cellular computations such as synaptic coincidence detection, temporal summation and spike timing (O'Donnell & Nolan, 2010). Experimental tests that distinguish between these and other possible computational roles for stellate neurons will be important for establishing cellular mechanisms responsible for the neural representation of location.
Acknowledgments
This work was supported by the Biotechnology and Biological Sciences Research Council (M.F.N.), a Marie Curie Excellence grant (M.F.N.) and the Commonwealth Scholarships Commission (H.P.).
Glossary
Abbreviations
- Ih
hyperpolarization-activated current
- MEC
medial entorhinal cortex
Author contributions
M.F.N. conceived the study and wrote the manuscript. P.D.D. and M.F.N. designed and analysed electrophysiology experiments. H.P. and M.F.N. designed and analysed computational experiments. P.D.D., H.P. and M.F.N. interpreted the data and revised the manuscript. Experiments were carried out in the Centre for Integrative Physiology at the University of Edinburgh.
References
- Alonso A, Klink R. Differential electroresponsiveness of stellate and pyramidal-like cells of medial entorhinal cortex layer II. J Neurophysiol. 1993;70:128–143. doi: 10.1152/jn.1993.70.1.128. [DOI] [PubMed] [Google Scholar]
- Alonso A, Llinas RR. Subthreshold Na+-dependent theta-like rhythmicity in stellate cells of entorhinal cortex layer II. Nature. 1989;342:175–177. doi: 10.1038/342175a0. [DOI] [PubMed] [Google Scholar]
- Boehlen A, Heinemann U, Erchova I. The range of intrinsic frequencies represented by medial entorhinal cortex stellate cells extends with age. J Neurosci. 2010;30:4585–4589. doi: 10.1523/JNEUROSCI.4939-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess N, Barry C, O'Keefe J. An oscillatory interference model of grid cell firing. Hippocampus. 2007;17:801–812. doi: 10.1002/hipo.20327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burton BG, Economo MN, Lee GJ, White JA. Development of theta rhythmicity in entorhinal stellate cells of the juvenile rat. J Neurophysiol. 2008;100:3144–3157. doi: 10.1152/jn.90424.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cannon RC, O'Donnell C, Nolan MF. Stochastic ion channel gating in dendritic neurons: morphology dependence and probabilistic synaptic activation of dendritic spikes. PLoS Comput Biol. 2010;6:e1000886. doi: 10.1371/journal.pcbi.1000886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demir A, Mehrotra A, Roychowdhury J. Phase noise in oscillators: a unifying theory and numerical methods for characterization. Circuits and systems I: fundamental theory and applications. IEEE Transactions. 2000;47:655–674. [Google Scholar]
- Dickson CT, Magistretti J, Shalinsky MH, Fransén E, Hasselmo ME, Alonso A. Properties and role of Ih in the pacing of subthreshold oscillations in entorhinal cortex layer II neurons. J Neurophysiol. 2000;83:2562–2579. doi: 10.1152/jn.2000.83.5.2562. [DOI] [PubMed] [Google Scholar]
- Dorval AD, Jr, White JA. Channel noise is essential for perithreshold oscillations in entorhinal stellate neurons. J Neurosci. 2005;25:10,025–10,028. doi: 10.1523/JNEUROSCI.3557-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond GB. Reporting ethical matters in The Journal of Physiology: standards and advice. J Physiol. 2009;587:713–719. doi: 10.1113/jphysiol.2008.167387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudman JT, Nolan MF. Stochastically gating ion channels enable patterned spike firing through activity-dependent modulation of spike probability. PLoS Comput Biol. 2009;5:e1000290. doi: 10.1371/journal.pcbi.1000290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erchova I, Kreck G, Heinemann U, Herz AV. Dynamics of rat entorhinal cortex layer II and III cells: characteristics of membrane potential resonance at rest predict oscillation properties near threshold. J Physiol. 2004;560:89–110. doi: 10.1113/jphysiol.2004.069930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandez FR, White JA. Artificial synaptic conductances reduce subthreshold oscillations and periodic firing in stellate cells of the entorhinal cortex. J Neurosci. 2008;28:3790–3803. doi: 10.1523/JNEUROSCI.5658-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fransen E, Alonso AA, Dickson CT, Magistretti J, Hasselmo ME. Ionic mechanisms in the generation of subthreshold oscillations and action potential clustering in entorhinal layer II stellate neurons. Hippocampus. 2004;14:368–384. doi: 10.1002/hipo.10198. [DOI] [PubMed] [Google Scholar]
- Fricker D, Miles R. EPSP amplification and the precision of spike timing in hippocampal neurons. Neuron. 2000;28:559–569. doi: 10.1016/s0896-6273(00)00133-1. [DOI] [PubMed] [Google Scholar]
- Fyhn M, Hafting T, Witter MP, Moser EI, Moser MB. Grid cells in mice. Hippocampus. 2008;18:1230–1238. doi: 10.1002/hipo.20472. [DOI] [PubMed] [Google Scholar]
- Fyhn M, Molden S, Hollup S, Moser MB, Moser E. Hippocampal neurons responding to first-time dislocation of a target object. Neuron. 2002;35:555–566. doi: 10.1016/s0896-6273(02)00784-5. [DOI] [PubMed] [Google Scholar]
- Garden DL, Dodson PD, O'Donnell C, White MD, Nolan MF. Tuning of synaptic integration in the medial entorhinal cortex to the organization of grid cell firing fields. Neuron. 2008;60:875–889. doi: 10.1016/j.neuron.2008.10.044. [DOI] [PubMed] [Google Scholar]
- Giocomo LM, Hasselmo ME. Computation by oscillations: implications of experimental data for theoretical models of grid cells. Hippocampus. 2008a;18:1186–1199. doi: 10.1002/hipo.20501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giocomo LM, Hasselmo ME. Time constants of h current in layer II stellate cells differ along the dorsal to ventral axis of medial entorhinal cortex. J Neurosci. 2008b;28:9414–9425. doi: 10.1523/JNEUROSCI.3196-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giocomo LM, Hasselmo ME. Knock-out of HCN1 subunit flattens dorsal–ventral frequency gradient of medial entorhinal neurons in adult mice. J Neurosci. 2009;29:7625–7630. doi: 10.1523/JNEUROSCI.0609-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giocomo LM, Zilli EA, Fransen E, Hasselmo ME. Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science. 2007;315:1719–1722. doi: 10.1126/science.1139207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haas JS, Dorval AD, 2nd, White JA. Contributions of Ih to feature selectivity in layer II stellate cells of the entorhinal cortex. J Comput Neurosci. 2007;22:161–171. doi: 10.1007/s10827-006-0005-7. [DOI] [PubMed] [Google Scholar]
- Haas JS, White JA. Frequency selectivity of layer II stellate cells in the medial entorhinal cortex. J Neurophysiol. 2002;88:2422–2429. doi: 10.1152/jn.00598.2002. [DOI] [PubMed] [Google Scholar]
- Hafting T, Fyhn M, Molden S, Moser MB, Moser EI. Microstructure of a spatial map in the entorhinal cortex. Nature. 2005;436:801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]
- Hajimiri A, Lee TH. A general theory of phase noise in electrical oscillators. Solid-state circuits. IEEE Journal. 1998;33:179–194. [Google Scholar]
- Hasselmo ME, Giocomo LM, Zilli EA. Grid cell firing may arise from interference of theta frequency membrane potential oscillations in single neurons. Hippocampus. 2007;17:1252–1271. doi: 10.1002/hipo.20374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hopfield JJ. Pattern recognition computation using action potential timing for stimulus representation. Nature. 1995;376:33–36. doi: 10.1038/376033a0. [DOI] [PubMed] [Google Scholar]
- Hu H, Vervaeke K, Storm JF. Two forms of electrical resonance at theta frequencies, generated by M-current, h-current and persistent Na+ current in rat hippocampal pyramidal cells. J Physiol. 2002;545:783–805. doi: 10.1113/jphysiol.2002.029249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch C. Biophysics of Computation: Information Processing in Single Neurons. New York: Oxford University Press; 1999. [Google Scholar]
- Llinas RR. The intrinsic electrophysiological properties of mammalian neurons: insights into central nervous system function. Science. 1988;242:1654–1664. doi: 10.1126/science.3059497. [DOI] [PubMed] [Google Scholar]
- Lomb NR. Least-squares frequency analysis of unequally spaced data. Astrophysics and Space Science. 1976;39:447–462. [Google Scholar]
- Narayanan R, Johnston D. The h channel mediates location dependence and plasticity of intrinsic phase response in rat hippocampal neurons. J Neurosci. 2008;28:5846–5860. doi: 10.1523/JNEUROSCI.0835-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nolan MF, Dudman JT, Dodson PD, Santoro B. HCN1 channels control resting and active integrative properties of stellate cells from layer II of the entorhinal cortex. J Neurosci. 2007;27:12,440–12,451. doi: 10.1523/JNEUROSCI.2358-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Donnell C, Nolan MF. Tuning of synaptic responses: an organizing principle for optimization of neural circuits. Trends Neurosci. 2010;34:51–60. doi: 10.1016/j.tins.2010.10.003. [DOI] [PubMed] [Google Scholar]
- Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical Recipes in C: The Art of Scientific Computing. Cambridge, UK: Cambridge University Press; 1992. Spectral analysis of unevenly sampled data. [Google Scholar]
- Quilichini P, Sirota A, Buzsaki G. Intrinsic circuit organization and theta–gamma oscillation dynamics in the entorhinal cortex of the rat. J Neurosci. 2010;30:11,128–11,142. doi: 10.1523/JNEUROSCI.1327-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remme MW, Lengyel M, Gutkin BS. Democracy-independence trade-off in oscillating dendrites and its implications for grid cells. Neuron. 2010;66:429–437. doi: 10.1016/j.neuron.2010.04.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richter H, Heinemann U, Eder C. Hyperpolarization-activated cation currents in stellate and pyramidal neurons of rat entorhinal cortex. Neurosci Lett. 2000;281:33–36. doi: 10.1016/s0304-3940(00)00794-1. [DOI] [PubMed] [Google Scholar]
- Welinder PE, Burak Y, Fiete IR. Grid cells: the position code, neural network models of activity and the problem of learning. Hippocampus. 2008;18:1283–1300. doi: 10.1002/hipo.20519. [DOI] [PubMed] [Google Scholar]
- White JA, Klink R, Alonso A, Kay AR. Noise from voltage-gated ion channels may influence neuronal dynamics in the entorhinal cortex. J Neurophysiol. 1998;80:262–269. doi: 10.1152/jn.1998.80.1.262. [DOI] [PubMed] [Google Scholar]
- Zilli EA, Yoshida M, Tahvildari B, Giocomo LM, Hasselmo ME. Evaluation of the oscillatory interference model of grid cell firing through analysis and measured period variance of some biological oscillators. PLoS Comput Biol. 2009;5:e1000573. doi: 10.1371/journal.pcbi.1000573. [DOI] [PMC free article] [PubMed] [Google Scholar]


