Real-time Optical Motion Correction for Diffusion Tensor Imaging

Abstract

Head motion is a fundamental problem in brain MRI. The problem is further compounded in diffusion tensor imaging (DTI) because of long acquisition times, and the sensitivity of the tensor computation to even small misregistration. To combat motion artifacts in DTI, a novel real-time prospective motion correction method was introduced using an in-bore monovision system. The system consists of a camera mounted on the head coil and a self-encoded checkerboard marker that is attached to the patient’s forehead. Our experiments showed that optical prospective motion correction is more effective at removing motion artifacts compared to image-based retrospective motion correction. Statistical analysis revealed a significant improvement in similarity between diffusion data acquired at different time points when prospective correction was used compared to retrospective correction (p<0.001).

Introduction

Diffusion tensor imaging (DTI) has notoriously long acquisition times and, thus, successfully correcting for rigid head motion artifacts is key for both clinical exams and neuroscience studies, which is often overlooked. Particularly, with the more complex variants of DTI, scan times increase excessively, which in turn leads to a higher likelihood of involuntary patient motion, even in subjects who comply and try to remain still. Additional complications arise when imaging children or patients with severe medical conditions (e.g. stroke or Parkinson’s disease) that prevent them from staying stationary for even short times.

Gross patient motion during MRI exams results in spatial misregistration, which may cause blurring or complete loss of anatomical structures. With DTI, pixel misregistration also affects the shape of the diffusion tensor or orientation distribution functions (ODF). To mitigate misregistration artifacts, image-based retrospective methods have been suggested (1). These remedies are rather straightforward to apply for single-shot sequences and mostly involve retrospective volume-to-volume registration. However, retrospective volume-to-volume registration does not account for the influences of through-plane motion on local spin-history. In addition, a whole motion-free volume must be acquired to perform reliable volume-to-volume registration because motion within the acquisition of a single volume (i.e. intra-volume motion) will render the volume inconsistent. This can be particularly problematic for DTI where repetition times may approach 10 seconds.

Apart from retrospective volume-to-volume registration methods, retrospective slice-to-volume registration is also used for motion correction in DTI (2). The performance of slice-to-volume registration is not degraded by intra-volume motion. Nevertheless, this method is also susceptible to spin history effects. Slice-to-volume registration also restricts the minimum image resolution in the slice-select direction to guarantee sufficient sampling of the volume after motion correction.

With image-based retrospective methods, an adjustment of the b-matrix for each rotated image is applied to correct for the directional encoding error (1). While changes in the b-matrix can be corrected retrospectively, the distribution of diffusion-encoding directions that are effectively applied is sub-optimal and can cause errors in the estimation of diffusion tensors or ODFs (3). Matters become ever more challenging for multi-shot sequences, such as PROPELLER (4) or SNAILS (5), where each profile/interleave can experience different motion. In fact, there is a great chance that each interleave is encoded with a different b-matrix than originally prescribed. Therefore, it becomes impossible to reconstruct a diffusion-weighted image, which has a single defined diffusion-weighting direction (6).

In contrast, prospective correction techniques directly adapt scan geometry in (quasi) real-time to compensate for patient motion during data acquisition (7–10). A prospective approach would greatly overcome the aforementioned limitations of retrospective methods. One such method, PACE (Prospective Acquisition Correction) (9), registers each newly acquired volume to a template volume in real-time from which it determines pose changes, and feeds back the updated pose information to the sequencer so that the scanned plane follows patient motion. Although PACE addresses some of the challenges with retrospective volume-to-volume registration, it is still susceptible to intra-volume motion and has a latency of one TR. Ultimately, all image-based registration methods have in general a degraded performance if the image signal level is low, which might happen for high b-value scans.

Computer-vision based pose tracking is an effective variant to measure head movement that is compatible with prospective motion correction (10–12). This approach is particularly promising as it does not require any additional MR data acquisition (i.e. navigators) and is entirely independent from the regular MR imaging procedure. It also eliminates certain disadvantages related to retrospective or prospective image-based methods. Even for single-shot methods, it has been shown previously that prospective motion correction based on optical tracking (7) or active markers (8,13) perform superiorly to image-based retrospective or prospective correction, predominantly due to the considerably reduced spin history effects. Do note that, compared to conventional structural imaging, motion-correction for diffusion-weighted MRI is considerably more challenging. For exact tensor estimation, motion-induced phase-errors (14) and signal drop-outs (caused by motion in the presence of the strong diffusion-encoding gradient field) must also be considered.

In this study, our aims were: 1) to show the application of a prospective monovision-based optical tracking system (15) to perform rigid head motion correction, and 2) to compare the effectiveness of retrospective and prospective motion correction for DTI.

Theory and Methods

A) Prospective Motion Correction System Setup

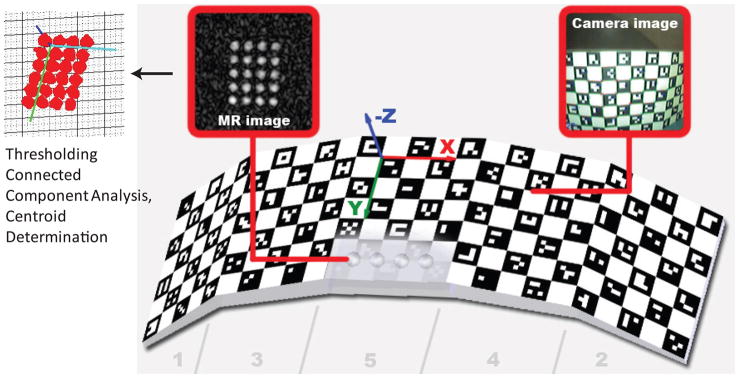
The optical motion correction system is shown in Fig. 1. A single MR compatible camera (Fig. 1b) was mounted on an 8-channel phased-array head coil (InVivo Corp., Gainesville, FL) (15). The camera acquired images of a self-encoded checker-board marker with MR-visible features (Fig. 1c,d, Fig. 2) that was fixed to the patient’s head. The images taken by the camera were then sent to an external processing laptop (IBM Lenovo, Inter Core 2 Duo CPU @ 2.80 GHz, 4GM RAM, 32-bit Windows Vista operating system), which was connected to the Gigabit Ethernet backbone of the MRI scanner. For every camera frame, each square on the checkerboard was segmented out and identified by a unique ID imprinted on it (16). This step was followed by the determination of the intersection points of the checkerboard squares. The detected grid point coordinates were then used as input to the 3D pose estimation algorithm (17). Here, the estimated pose of the marker allows one to get a geometry (i.e. slice position, orientation) update to be fed back to the scanner gradient and RF hardware controller in real-time. At the beginning of each patient study, a scanner-camera cross-calibration was performed in order to relate the camera-frame-of-reference to the scanner-frame-of-reference. A more detailed description of these steps is provided below.

Figure 1.

System setup. An MR-compatible camera was mounted on the head coil inside the scanner bore (b). The camera took images of a self-encoded marker that was attached to the patient’s forehead (c,d). These images were processed by an external laptop where 1) the marker was segmented out, 2) its pose was estimated and 3) the 6 parameters (i.e. 3 rotations and 3 translations) to update the scanner geometry were sent to the scanner RF and gradient hardware controller. This allowed the slice being scanned to follow the subject’s head in real-time.

Figure 2.

The 3D self-encoded marker used for pose tracking. Each black square on the marker included a unique 2D barcode that represented the position of that square on the marker geometry. In order to perform cross calibration, we also put MR-detectable agar droplets at the back of the marker. By measuring the poses of the MR detectable agar filled holes and the self-encoded checkerboard pattern simultaneously by the scanner and the camera, it was possible to find the relation between the scanner and the camera frame of references.

Camera

Figure 1 shows the camera and rig used to mount the camera onto the coil. An off-the-shelf, small CMOS (380 TV lines, 1/3″ sensor) spy camera (Swann Communications USA Inc., CA) was optimized for MR-compatibility. Customized infrared light-emitting diodes (IR-LEDs) were added on the front panel of the camera to illuminate the checkerboard inside the scanner and operated at an intensity level safe to the human eye.

Self-Encoded Marker

In order to determine pose changes of the patient’s head, the camera needs to track some feature points that are rigidly connected to the head. Due to the proximity between the marker and camera (5–7 cm), part of the marker can go outside of the camera’s field-of-view if large head motion occurs. If part of the marker is not visible to the camera, the positioning of the feature points with respect to each other cannot be determined. Occlusions of the marker can also occur due to the small gaps between rungs of the birdcage head-coil.

A self-encoded marker was used to address these issues, as shown in Fig. 2. This marker was conceived and developed in-house, and was built in the machine shop of our institution. A detailed description of this marker can be found in (16). The basis of this marker is a checkerboard pattern. Our custom-modification consists of a rotationally-invariant 2D-barcode inside each square of the checkerboard. Each barcode identifies the relative position of a given square within the checkerboard. This allows for accurate and robust pose tracking even with a partial view of the marker, thus allowing even larger head rotations than field-of-view supported by the camera to be detected. Moreover, the non-planar marker geometry increased the pose detection accuracy over planar markers (specifically when marker plane is parallel to and directly facing the camera image plane, which is otherwise a challenge for other 2D markers (18)). Previous studies performed to measure the reproducibility (i.e. precision) of motion tracking have shown that, using this marker, the noise on the motion tracking data is on the order of 0.05 mm and 0.1° (16).

Scanner-Camera Cross-Calibration

A cross-calibration procedure is necessary to determine the coordinate transform between camera-space where the checkerboard is tracked, and scanner-space where the scan-plane is prescribed. A fast calibration technique was developed, where a small-FOV 3D-SPGR (TR/TE = 8.4/2.9 ms, 128×128×48 resolution, FOV = 12cm, slice thickness = 1mm, NEX=2, scan time=52 seconds) was used to map the agar-filled holes embedded underneath the checkerboard, while the camera simultaneously observed the checkerboard surface (Fig. 2). The information collected from the scanner and the camera was then used to calculate the cross-calibration transformation matrices, which is described in the next section. The pose estimation error (i.e. the accuracy) of the combination of motion tracking and cross-calibration was below 1mm and 1° in a range of ~20° motion (16).

Mathematical Description

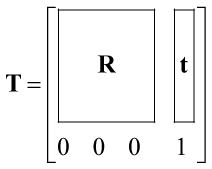
The mathematical description of optical prospective motion correction was presented previously (10), and is briefly reviewed here. Let c denote the camera frame of reference, m₀ the initial marker position, m_i the marker position at time i, s₀ denote the initial scan plane position, s_i the scan plane position at time i. Let T be a 4×4 transformation matrix that consists of a 3×3 rotation matrix R and 3×1 translation vector t:

[1]

The purpose of prospective motion correction is to make sure that the rotation and translation between the scanned volume and the marker stays constant for each point (i) in time. This is described mathematically as:

$${\mathbf{T}}_{m_0\to s_0}={\mathbf{T}}_{m_i\to s_i}$$ [2]

With straightforward matrix manipulations, the following can be obtained:

$$\begin{array}{l}{\mathbf{T}}_{m_0\to s_0}={\mathbf{T}}_{m_i\to s_i}\\ {\mathbf{T}}_{c\to s_0}{\mathbf{T}}_{m_0\to c}={\mathbf{T}}_{s_0\to s_i}{\mathbf{T}}_{c\to s_0}{\mathbf{T}}_{m_i\to c}\\ {\mathbf{T}}_{s_0\to s_i}={\mathbf{T}}_{c\to s_0}{\mathbf{T}}_{m_0\to c}{\mathbf{T}}_{c\to m_i}{\mathbf{T}}_{s_0\to c}\end{array}$$ [3]

T_s0→si represents the geometry update that needs to be applied to the scanned volume in real-time for motion correction. T_c→s0 is the scanner-camera cross-calibration matrix and is obtained using the method described in the previous section. T_m0→c and T_mi→c are the marker position with respect to the camera at time 0 and time i. These marker positions are obtained using the principles of computer vision and a perspective camera model as described above and in (16,17).

B) Experiments

All in-vivo experiments were carried out using a 1.5T GE Signa scanner (GE Healthcare, Software Release 15.0 M4, with a maximum gradient strength of 40mT/m and a slew rate of 150 T/m/sec). All human subjects experiments were approved by the institutional review board at our university (Protocol ID: 10774). With written informed consent, three male volunteers (age 27–30) were scanned for this study. Before each session, all subjects practiced for the motion experiments to guarantee reproducibility of motion patterns.

In-vivo DTI Experiments, 96×96 Resolution, Single-Shot EPI Readout

A single-shot DTI sequence with EPI readout with the following parameters was used: TR/TE=10,000msec/75msec, FOV=24cm, 96×96 acquisition resolution, half-Fourier readout with 20 overscans, 36 slices, slice thickness=3mm, 1mm gap, b=1000 sec/mm², number of diffusion-encoding directions = 25 (+3 b=0 acquisitions), total scan time = 4:40min. For this experiment, the volunteer was asked to perform mixed shaking (predominantly in-plane) and nodding (predominantly through-plane) motion throughout the scan once every ~15 seconds. This was repeated with the prospective motion correction system turned off and on. The shaking and nodding datasets with no prospective motion correction active were also reconstructed after volume-to-volume realignment using Statistical Parametric Mapping (SPM, version 5.0) software. To get reference data and to observe the effects of prospective motion correction on motion-free data, two additional scans were performed where the volunteer was asked to lie still while prospective motion correction system was again either turned off or on. Thus, a total of 5 datasets were obtained: 1) (reference dataset) no motion - no correction; 2) no motion -prospective correction; 3) shaking and nodding motion - no correction; 4) shaking and nodding motion - retrospective correction (i.e. volume-to-volume realignment); 5) shaking and nodding motion - prospective correction. The slices with low average signal levels were removed from DTI analysis prior to reconstruction of tensors. For each dataset, fiber tractography was performed using a custom built software (19). Seed regions were placed and saved for the corpus callosum and both cortico-spinal tracts so that they could be applied reliably each of the 5 data sets. Euler’s method was used for tracking with FA threshold = 0.15, curvature threshold = 40°.

In-vivo DTI Experiments, 128×128 Resolution, Multi-Shot Spiral Readout

Here, a constant-density multi-shot spiral-in & variable-density spiral-out pulse sequence was used (6). Specifically, the variable-density spiral-out part contributed one spiral arm of the final high-resolution diffusion-weighted image, while corresponding to each spiral-out arm the constant-density spiral-in part provided a low-resolution navigator image that was sampled at Nyquist rate. These spiral-in navigators were used for two purposes: 1) correction of the nonlinear phase variation caused by motion during diffusion-encoding (14), as described by Liu et al. (20), and 2) estimation of (in-plane) 2D pose changes between spiral-out interleaves for retrospective 2D motion correction. To estimate the pose changes between interleaved acquisitions, individual low-resolution navigators were (rigidly) co-registered to a template by minimizing the Pearson cross-correlation coefficient between the template navigator image and the navigator image to be registered. The robustness of this approach has been demonstrated in a recent study (21). The following acquisition parameters were used: TR/TE=3,000msec/55msec, FOV=24cm, 128×128 acquisition resolution, variable-density spiral-out readout with a pitch factor α=3.0 (22), 8 spiral interleaves, 13 slices, slice thickness=5mm, 1mm gap, b=800 sec/mm², number of diffusion-encoding directions = 6 (+1 b=0 acquisition), NEX=2, spiral-in navigator acquisition resolution: 32×32. Total scan time was 5:36 min. The acquisition matrix was comparable to regular single-shot scanning but with a roughly 8-fold reduction in image distortion due to the interleaved spiral acquisition.

Similar to the previous case, seven datasets were obtained with this study: 1) (reference dataset) no motion – no correction; 2) shaking motion - no correction; 3) shaking motion – retrospective 2D correction (as described above); 4) shaking motion – prospective correction; 5) nodding motion - no correction; 6) nodding motion - retrospective 2D correction; 7) nodding motion - prospective correction;

All reconstructions were performed using augmented SENSE reconstruction and non-linear phase correction (20). To compare the performance of retrospective and prospective methods, the following analyses were performed. Each method was applied separately to datasets 2–7 separately:

Angular deviation maps

As a metric for consistency of directional diffusion-encoding, the pixel wise angular deviation of the reconstructed primary eigenvectors relative to the eigenvectors of the reference data set (i.e. no motion, no correction) was obtained for each reconstructed dataset (6). The angular deviation was measured by taking the scalar product between the test and reference eigenvector for each voxel. On these deviation maps, ROI analyses were performed for the splenium of corpus callosum. Since uncorrected motion will also affect the accuracy of the directional information in the tensor, a lower angular deviation will be an indicator of a more successful motion correction. In order to facilitate better interpretation of these maps, we also obtained two reference angular deviation maps between 1) no motion & no correction - no-motion & no correction; and 2) no motion & no correction - no motion & prospective correction scans.

Distribution of correlation coefficients between navigators

The low-resolution spiral-in navigator images were obtained for each interleave (112 images = 8 interleaves × 14 directions) and a template image was formed by coregistering and averaging all navigators. Thereafter, the Pearson correlation coefficient between each individual navigator and this template was calculated for each of the three groups (no correction, retrospective correction, and prospective correction). A Mann-Whitney-U test was performed to investigate whether the correlation coefficients between the retrospectively corrected and prospectively corrected groups differed significantly using the hypothesis that prospective motion correction allowed for greater data consistency (as indicated by a higher correlation coefficient). To visualize the distribution of the correlation coefficients of the navigators, box and whisker plots were used. Specifically, for each box plot, the center of the box represented the median and the edges were the 25 and 75 percentiles. The whiskers indicated range of correlation values that were not considered to be outliers. This test was repeated for the shaking and nodding motion experiment.

Variance maps

To eliminate the effect caused by contrast differences between navigator images that were acquired with diffusion-weighting applied along different-encoding directions, only navigator images obtained with b=0 were analyzed. Specifically, from 16 b=0 navigator images (8 interleaves, NEX=2) the signal variance was computed across all 16 time points for each pixel.

In-vivo DWI Experiments, 256×256 high-resolution, Multi-Shot Spiral Readout

A high-resolution spiral DWI scan was performed using the following parameters: TR/TE=4,000msec/55msec, FOV=24cm, 256×256 acquisition resolution, variable-density spiral-out readout with a pitch factor α=3.0, 24 spiral interleaves, 13 slices, slice thickness=5mm, 1mm gap, b=800 sec/mm², diffusion-encoding directions = 3, NEX=1, spiral-in navigator acquisition resolution: 32×32. Without loss of generality and in the interest how much time the subjects spent in total in the magnet, only diffusion-weighted scans were performed along the three principal axes. Reconstruction and retrospective 2D correction were done using the methods described for the 128×128 experiment. The volunteer was asked to perform mixed shaking and nodding motion throughout the scan. A total of five datasets were obtained: 1) (reference dataset) no motion -no correction; 2) no motion - prospective correction; 3) shaking and nodding motion – no correction; 4) shaking and nodding motion – restrospective 2D correction; 5) shaking and nodding motion - prospective correction.

As a quality metric to measure the amount of motion artifacts, we used the signal energy in the high frequency power spectrum of k-space (8). This was calculated by taking the sum-of-squares of k-space points above a cut-off frequency (cut-off = 2.6 rad/cm). For objects containing sharp edges and small structures (i.e., human brain), motion is expected to cause blurring and loss of edge structures in image space, which is reflected in a decrease in energy at high spatial frequencies in k-space (since high spatial frequencies mostly contain edge information). Thus, higher energy at high spatial frequencies is an indication of less motion artifacts. To eliminate the energy differences between different scans that may arise due to different prescan values, the images were first normalized by the mean image intensity of the middle slice for all 5 datasets. The high frequency energy of each slice was then represented as a percentage relative to the reference volume.

Results

In-vivo DTI Experiments, 96×96 Resolution, Single-Shot EPI Readout

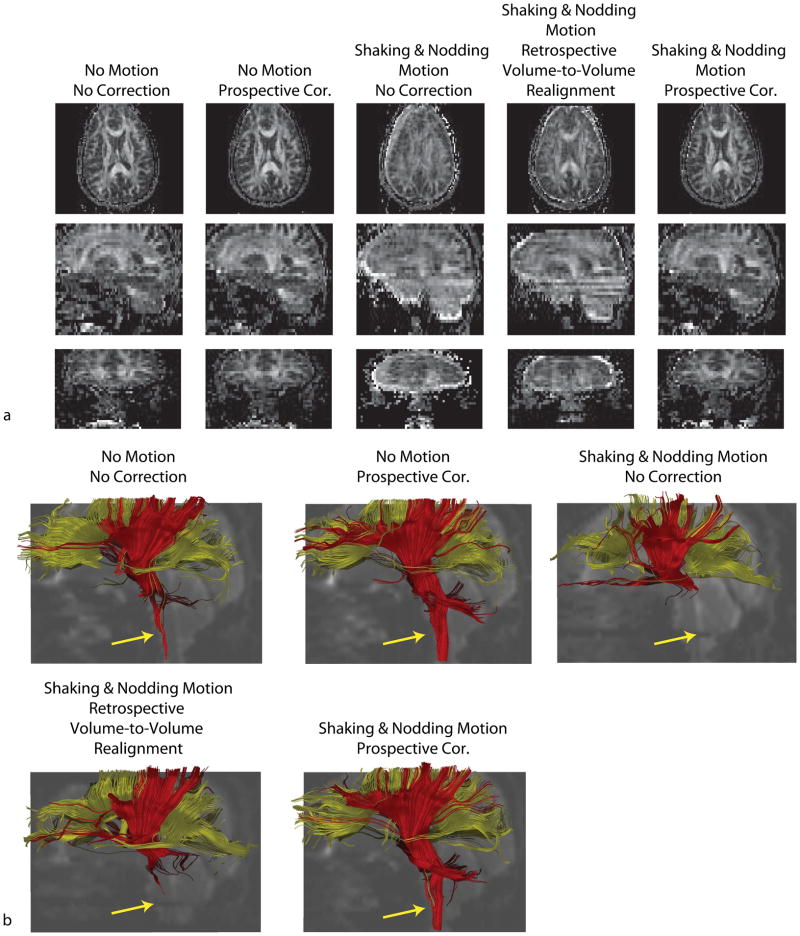
Figure 3a shows the axial, sagittal and coronal FA maps and Fig. 3b shows the fiber tracts obtained for 5 different datasets. The range of motion detected by the optical system was 6° and 6mm, and the occurrence of motion was once per ~15 seconds. The non-corrected FA maps show detrimental motion artifacts. Retrospective correcting using volume-to-volume realignment improved the image quality, but artifacts still remain mainly due to intra-volume motion and spin history effects. The dataset with prospective motion correction shows the highest degree of similarity with the data with no motion. The reconstructed fiber pathways also reveal that prospective motion correction provides better visualization of cortico-spinal tracts compared to retrospective correction (Fig. 3b, yellow arrow). For the two scans where the subject was instructed to stay still, visualization of cortico-spinal tracts was also better for prospectively corrected data compared to non-corrected data. This was due to the fact that, despite the subject was to remain still for the non-motion dataset, a small amount of motion was still detected (~1.5° and ~1mm drift throughout the scan). Thus, running prospective motion correction on the non-corrupted dataset still improved the data quality.

Figure 3.

Results of in-vivo DTI experiments with 96×96 single-shot EPI readout. Reconstructed FA maps show that, even with retrospective volume-to-volume realignment, motion-related image artifacts remain because of intra-volume motion and spin history effects. Prospectively corrected FA maps show the most similarity with the reference dataset. The visualization of cortico-spinal tracts was also more successful when prospective correction was used compared to retrospectively corrected dataset.

In-vivo DTI Experiments, 128×128 Resolution, Multi-Shot

FA and Mean Diffusion Images

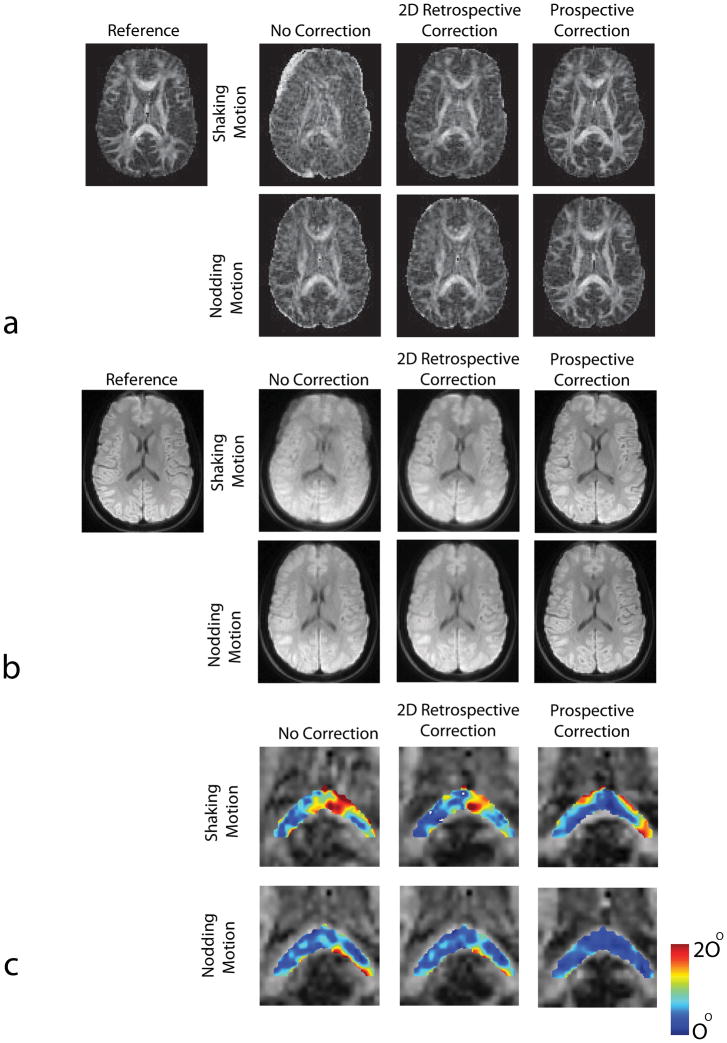
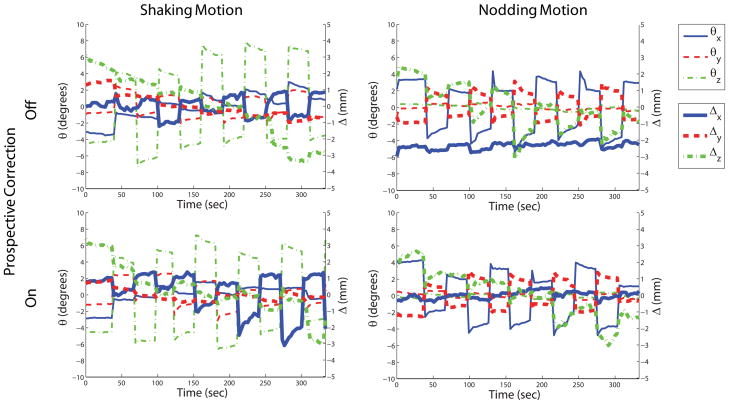
Figure 4a,b,c shows the in-vivo experiments in which the subjects were asked to perform either shaking or nodding motion during the course of the diffusion tensor imaging exam. Figure 5 shows the volunteer motion as measured by the optical system. As anticipated, without any motion correction, there were significant motion artifacts on both iso-DWI images and the FA maps that severely degraded image interpretation (Fig. 4a,b).

Figure 4.

Results of in-vivo DTI experiments with 128×128 resolution. Reconstructed FA maps (a) and isotropic DWI images (b) with and without 2D retrospective and prospective correction in the presence of shaking and nodding motion are shown. It can be seen that in the presence of random head motion the resulting images show significant motion related artifacts if optical motion tracking was turned off. These artifacts were largely removed after motion tracking was turned on. Superiority of prospective correction over retrospective method is better demonstrated in the presence of nodding motion. In this case, retrospective correction did not improve image quality because of the inability of this method to correct for through-plane motion, whereas prospectively corrected image looks very similar to the reference. The differences in structure between the reference FA map and the motion corrected maps are due to the fact that the subject did not return to the original position between “no motion” and “motion” scans. The angular deviation maps of the major eigenvectors from true orientations are shown in (c). True orientations are given by the dataset with no motion. Prospective correction provided eigenvectors with lower deviation compared to retrospective correction for both cases.

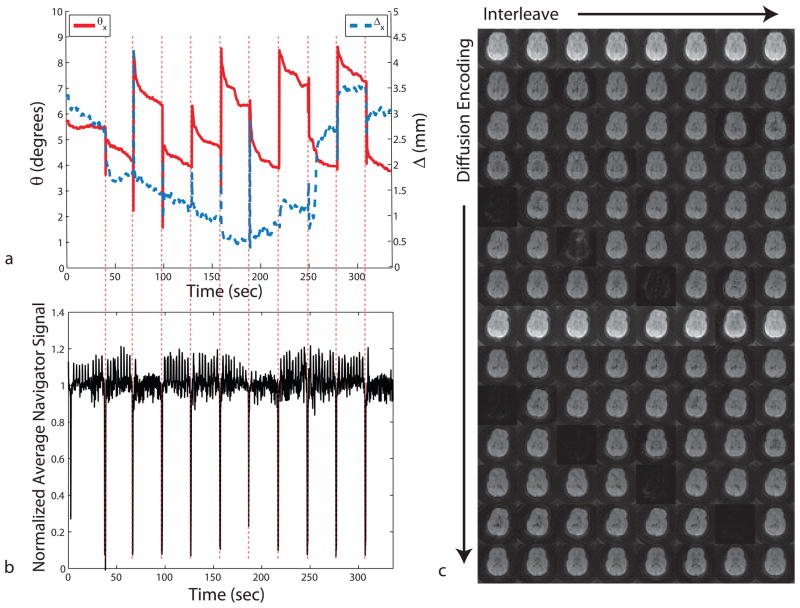
Figure 5.

Motion plots corresponding to the shaking and nodding motion experiments in Fig. 4. The motion performed by the patient was similar for both scans when the motion tracking was turned off and on.

For the experiment with left-right head rotation, retrospective correction cleared out some of the artifacts. However, for head rotation the volunteers typically also performed some involuntary through-plane motion (see Fig. 5). Since our retrospective 2D-correction algorithm only corrects for in-plane motion, residual artifacts remained due to unaccounted through-plane motion components. Conversely, the images reconstructed with prospective motion correction appeared visually of higher quality compared to images reconstructed with retrospective correction.

For the DTI experiment with the subject nodding, no significant improvement in image quality was observed after the application of retrospective in-plane motion correction (Fig. 4a,b). Again, this is due to the inability of 2D-retrospective motion correction to correct through-plane motion and demonstrates the limitations of 2D acquisition methods that rely solely on in-plane motion correction (4–6,23). The application of prospective motion correction provided a significant improvement in image quality.

Angular deviation maps

Figure 4c and Table 1 show the deviation of the major eigenvectors from their true orientations inside an ROI containing the splenium of the corpus callosum. The true orientations were given by the non-motion corrupted dataset. The error in the orientation of the major eigenvectors is the largest when motion was not corrected (Fig. 4c). The angular error inside the ROI was 10.14±6.32° for in-plane motion and 6.02±3.83° for nodding motion. For the experiment including in-plane rotation, prospective correction performed similar (7.38±4.99 vs. 7.02±4.81 degrees mean deviation). The difference between prospective and retrospective correction was more pronounced in the presence of nodding motion (5.3±2.99 vs 3.29±1.63 degrees deviation). The residual angular deviation after motion correction was significantly larger for the in-plane versus through-plane case since the possible range of shaking motion (±15°) was more than the range of nodding motion (±10°) (Fig. 4d) because of the restricted area in the head coil. Thus, the secondary effects of motion (e.g. susceptibility effects, gradient non-linearities, etc.) were more pronounced in the shaking motion images. In addition, independent of the range of motion possible, the change in effective coil sensitivity was also greater for shaking versus nodding motion due to the coil geometry (that is, the coil sensitivity variation is more pronounced in the R/L direction compared to S/I direction.)

Table 1.

Mean angular deviation of major eigenvectors from true orientations inside an ROI enclosing the splenium of the corpus callosum containing 89 pixels (shown in Fig. 4c). The true orientations were defined by the no motion & no correction scan

	No correction	Retrospective	Prospective
Shaking Motion	10.14 ± 6.32	7.38 ±4.99	7.02± 4.81
Nodding Motion	6.02±3.83	5.30±2.99	3.29±1.63

To provide reference values for Table 1, scans with the volunteer lying still were acquired. The mean angular deviation between two “no motion” scans with “no correction” was 2.55 ± 1.47 degrees. The mean angular deviation between the “no motion, no correction” and “no motion, prospective correction” scan was 2.39 ± 1.43 degrees. Note that the high standard deviation of the angular deviations shown in Table 1 is due to the inherent sensitivity of the reconstructed eigenvectors to small signal fluctuations which might be caused by off-resonance effects or coil sensitivity changes. Thus, the values in Table 1 should be evaluated in connection with the angular deviation maps given in Fig. 4c.

Distribution of correlation coefficients between navigators

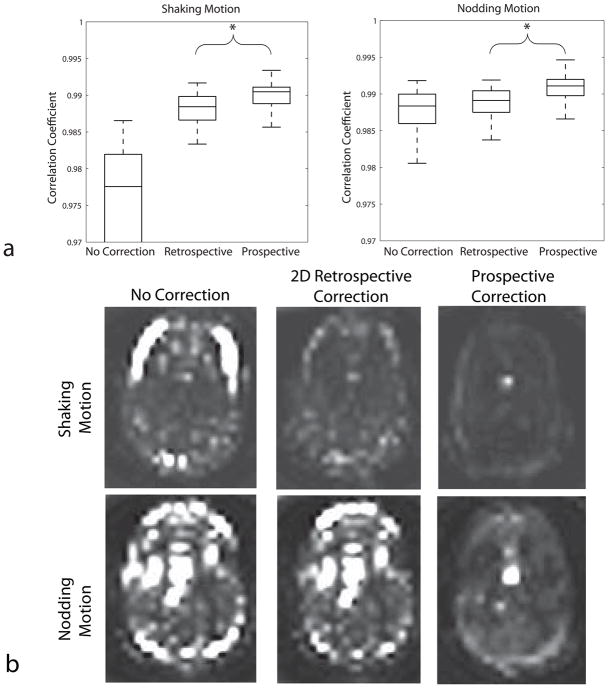
The Mann-Whitney-U test revealed statistically significant differences between retrospectively and prospectively corrected groups (p<0.001). Figure 6a shows the box-and-whisker plots of the correlation coefficients for navigator images that were obtained with each interleave. For both in-plane and nodding motion, the performance of prospective correction was better than retrospective correction, as given by the higher correlation coefficient between the navigators.

Figure 6.

(a) Correlation coefficients of each navigator with the template for the three different methods. The higher correlation coefficient obtained while using prospective motion correction compared to retrospective correction implies that the navigator images are more “similar” to each other when prospective correction was used. (b) Pixel-by-pixel variance maps throughout the b=0 images (16 images). In the nodding motion case, prospective correction was much successful in reducing the variation between navigators. The bright spot visible in the lower 3 images is due to pulsation of the lateral ventricle.

Variance maps

Figure 6b shows the pixel-by-pixel variance of signal intensity throughout the 16 b=0 images. Without motion correction a large pixel variance was seen, especially at the edges of the brain. Pixel variance was lowest when prospective motion correction was applied.

Due to the high sensitivity of the diffusion-weighting to motion, any motion during the diffusion-weighting period results in irrecoverable signal loss and presents a limitation for any motion correction technique. This is shown in Fig. 7. The presence of patient motion (Fig. 7a) results in a decrease in average signal intensity in the corresponding navigator data (Fig. 7b). This motion-related signal loss can be attributed to signal dephasing (Fig. 7b), and is also evident when looking at the corresponding navigator images (Fig. 7c). To account for data corruption caused by motion during the diffusion preparation period, a rescanning strategy was employed wherein, if motion detected by the optical system was larger than a set threshold (1mm and 1° for this study), a number of recently acquired k-space segments were reacquired. To reflect the true scenario for retrospective motion correction, no rescanning data were used for the tensor reconstruction from measurements performed with either no motion correction or retrospective correction.

Figure 7.

Navigator signal loss due to motion. Due to the motion sensitivity of the diffusion weighting gradients, patient motion during the diffusion preparation period causes irrecoverable signal dropouts. This is clearly visible from the navigator signal that was obtained from the spiral-in readout. It can be seen that whenever there is patient motion (a), the navigator signal was significantly reduced. Only the dominant motion axes (i.e., θ_x and Δx) are shown to simplify the graph. Example navigator images from one slice are shown at the right (c).

In-vivo DWI Experiments, 256×256 Resolution, Multi-Shot

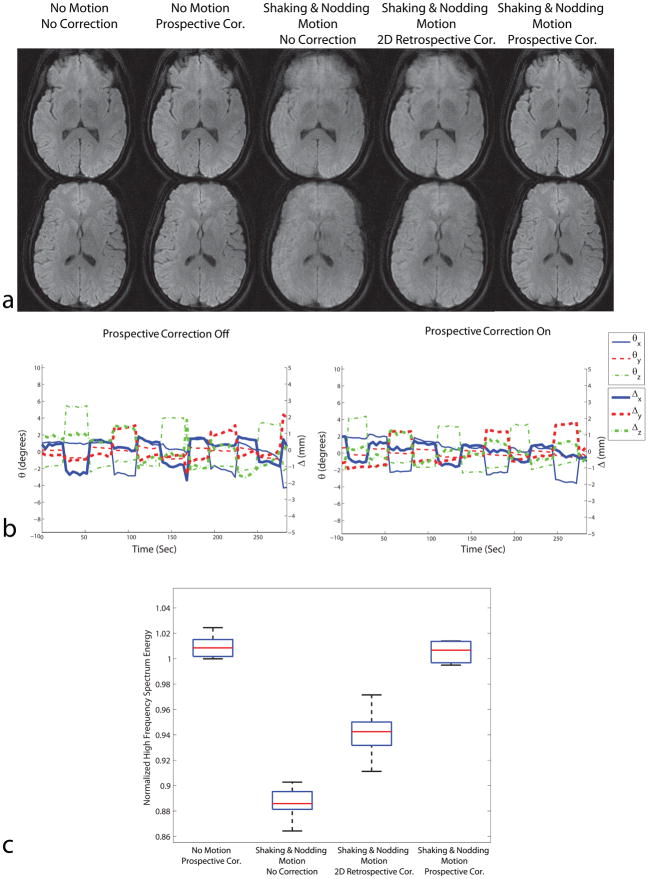
Figure 8a shows high-resolution isotropic diffusion-weighted images acquired without and with subject motion. Figure 8b shows the motion plots detected by the optical system. The image quality metric based on high frequency spectrum energy is shown in Fig. 8c, where greater high frequency power implies less motion artifacts (8). Similar to the previous in-vivo experiment, the dataset with motion and without motion correction showed detrimental motion artifacts. 2D retrospective correction was successful in removing some of the artifacts; however, some artifacts remained due to the existence of through-plane motion. The best image quality in the presence of motion was obtained with prospective correction. Also, the total high frequency power for no motion & prospective correction was close to 1 for all slices (Fig. 8c), which demonstrates that the image quality of the resting scan was not degraded by prospective motion correction.

Figure 8.

Results of high resolution DWI experiments with resolution 256×256. Similar to the in-vivo experiments with 128×128 resolution, prospective motion correction performed better compared to retrospective correction due to the existence of through-plane motion. The motion plots are shown in (b). The distribution of high frequency spectrum energy for 7 slices in the acquisition is shown in (c). For all slices shown, the images with prospective correction had higher energy at high frequencies compared to uncorrected or retrospectively corrected images, implying less motion artifacts.

Discussion

The ever-increasing complexity of DTI studies leads to very long scan times and an increased chance of patient motion. Head motion correction is therefore very important for DTI. Although the chances of head motion is higher for certain patient populations (e.g. stroke or Parkinson’s disease patients), head motion can be observed even for highly cooperative subjects (3) due to the excessively long acquisition times seen with DTI.

The vast majority of motion correction methods used for single and multi-shot DTI apply retrospective processing techniques (1,2,5,6,24–27). There are considerable shortcomings associated with retrospective approaches, which were addressed in this work by a monovision-based optical tracking system and an adaptive prospective motion correction approach. Unlike other in-bore optical tracking systems that have been introduced previously (12), the system presented here uses a single camera, which eliminates the necessity to perform extrinsic stereo calibration. The novel marker design used in this study allowed for accurate tracking of large head motions, with minimum latency between the instance of motion in the camera and the scan-plane update in response to the pose changes.

In general, prospective methods that use external tracking devices have been proposed to perform 6 degree-of-freedom head motion correction with little or no change in the pulse sequence. Zaitsev et al. used a stereovision system that had been placed outside the scanner bore to track and correct for rigid head motion (10). Despite compelling results, the aforementioned method also faced some challenges: 1) due to the distance between the cameras and the marker, the system required very high accuracy, which in turn required careful and tedious scanner-camera cross-calibration; 2) the line-of-sight between the cameras and the self-reflecting marker can be obstructed due to longer bore size (e.g. 7T) or a patient’s larger girth. To alleviate these difficulties, stereovision systems were placed inside the scanner bore (11,12,15). The advantage of an in-bore system compared to an out-of-bore set-up is that there are no obstructions between the camera and the object being tracked. Due to the proximity of the camera, several aspects still need to be considered: 1) replacing magnetic parts of the video imager with non-magnetic components; 2) preventing RF noise of the video imager from leaking into the RF chain; 3) preventing the imager itself from perturbing the B₁ field; and 4) preventing the RF transmit from affecting the video signal. A major benefit of the approach used in this study was that no extrinsic stereo calibration was needed since there was a single camera, and the cross-calibration between MR scanner and the camera coordinate system was fast (~60sec) and could be carried out with the patient inside the scanner. A potential challenge could be the accuracy of position detection of agar droplets (used for cross-calibration) due to off-resonance. One of the strengths of the calibration approach used for this study is the fitting of a spatial grid pattern to the measured MR-visible droplet tessellation. Similar to registration, accuracy and precision can be improved by using a large number of pixels and droplets and, thus, cross-calibration errors due to local field inhomogeneities can be reduced to an insignificant level (Fig. 2).

It has been shown that depending on the desired image resolution and SNR, tracking precision must be better than a voxel size (28). High precision is important in order to guarantee that the image quality is not degraded when the subject is staying still. In our experiments, we observed that prospective motion correction of “non-motion” data did not degrade the image quality of single-shot DTI (Fig. 3) and high-resolution in-vivo DWI scans (Fig. 8a,c). In terms of accuracy and precision requirements, an advantage of using external tracking systems is that the performance can be improved independent of the MR scanning process by choosing better hardware (e.g., better optics to give sharper images). Alternatively, it is possible to improve precision by averaging the motion signal or using Kalman filtering (29).

The mounting of the marker on the patient is also an important consideration in order to guarantee both patient comfort and adequate tracking accuracy. In this study, the marker was mounted on the forehead using Velcro straps. The forehead is a good location to place the marker since the rigidity assumption between the marker and the brain becomes invalid only for frowning motions. Even in the presence of frowning motion, the marker will go back to its original position after the frowning motion is complete and is usually not a persistent state. Thus, we do not expect the rigidity between the marker and the head to become invalid except for rare cases.

In this study, it has been shown that the performance of prospective optical motion correction was better compared to retrospective 3D volume-to-volume realignment or retrospective navigator-based 2D correction. Advantages of using prospective optical motion correction can be summarized as follows:

Through-plane Motion

A profound shortcoming of retrospective motion correction methods is its inability to correct for through-plane motion. The prospective approach maintained slice position with respect to the patient-frame-of-reference and assured data consistency. This approach eliminated issues resulting from through-plane motion. The benefits of prospective motion correction over retrospective methods have been shown in in-vivo experiments of this study. Specifically, it was observed that in the presence of through-plane motion (e.g. predominantly nodding motion), retrospective motion correction was ineffective at removing motion artifacts, whereas most of the artifacts were removed with prospective correction (Figs. 3,4,6,8).

k-space undersampling due to rotational motion

Retrospective correction of rotational motion can also leave gaps in k-space, which causes undersampling artifacts (21). If prospective methods are used, the scanner geometry is updated before data readout takes place. Thus, aliasing artifacts from local k-space undersampling are not an issue.

Signal loss due to motion during diffusion-preparation period

Due to the sensitivity of diffusion-weighting gradients to small motion, gross head motion during the diffusion-preparation period results in irrecoverable signal loss (Fig. 7) (14). Retrospective compensation methods are limited to identifying and discarding this potentially corrupted data. However, data elimination may result in undersampling of k-space, which, in turn, may impair the quality of the diffusion-weighted images. Eliminating corrupted data is also a common policy for single-shot scans, which can go unnoticed if there are an excessive number of diffusion directions or signal averages. However, for a borderline number of directions, such as for higher resolution scans, data elimination might severely impair the estimation of the tensor. Another possible challenge with retrospectively discarding data is that the detection of corrupted slices using image-based metrics (mean signal intensity or entropy) becomes unreliable if the image signal-to-noise ratio (SNR) is low. This was the case for inferior slices in the single-shot EPI DTI scan; due to their low SNR, some of these corrupted slices were mistakenly included in the DTI analysis. This caused significant artifacts in FA maps, and missing visualization of the cortico-spinal tracts (Fig. 3a,b). With our prospective approach, a rescanning strategy was implemented whereby data was reacquired if the detected motion exceeded a certain threshold, which eliminated the problems with retrospectively discarding data. However, for the high resolution scans, subject movement was not frequent enough to cause significant undersampling in k-space (Figs. 5,8b). Thus, the artifacts seen in the retrospectively corrected images of Fig. 4a,b and Fig. 8a were mainly due to misregistration.

Change in effective diffusion-encoding direction

As described in the introduction section, rotational head motion causes the effective diffusion-encoding direction to change (1). Correcting the b-matrix is therefore necessary to get accurate fiber tracts (3). In the current system, the scanner geometry was updated in real-time before the diffusion-preparation period. Thus, the diffusion-encoding directions played out were always the same with respect to the patient frame of reference. This eliminated entirely the aforementioned difficulties that might result from b-matrix alterations and varying diffusion-encoding directions throughout successive interleaves.

Partial volume artifacts

For the high-resolution scans used in this study, the slice thickness was rather large (5mm) in order to obtain adequate SNR. With thicker slices, the ability of retrospective image-based methods to resolve partial volume artifacts decreases. This can impact the performance of slice-to-volume registration methods where the slice thickness must be lower than a certain threshold in order to provide sufficient sampling coverage in 3D space (2). Image-based methods are expected to work better with thinner slices, but the low SNR due to decreased slice thickness can be a challenge. The performance of optical prospective motion correction to resolve partial volume artifacts is independent of the slice thickness.

In general, another advantage of using an external optical tracking system is that it eliminates the necessity to obtain MR navigator data for motion correction, thus providing more sequence design flexibility. However, for the high-resolution scans performed in this study, 2D spiral-in navigators were used for both phase and motion-correction. In this context, it must be noted that, for high-resolution DWI and DTI, the primary purpose of optical tracking is not eliminating the need to use navigator data. Even if 2D navigator data is available, it is better to use the optical tracking system due to the reasons described above; the most important of which is through-plane motion. Non-linear phase correction could have been done also by using the central part of a variable density spiral (5), but would not have provided the navigator data for our study to simultaneously compare the optical approach against retrospective/navigator based methods.

Despite prospective motion correction, a challenge that remains is the variation of receiver coil sensitivity relative to the patient frame of reference. This becomes increasingly important for larger motion or smaller coil elements (30,31) and needs to be considered for parallel imaging. A remedy has been described in (21) and may be incorporated into a non-linear phase correction parallel imaging algorithm (20), but its validation together with prospective motion correction was beyond the scope of this study.

Conclusion

An optical tracking system was presented to correct for rigid head motion for DTI. The system uses a single camera mounted on the head coil and a self-encoded marker. The setup and cross-calibration of the system was fast (<1min), which is important for clinical applicability of such systems. Initial in vivo results showed that the proposed system performed superior to retrospective motion correction, especially when through-plane motion was present.