Computerized Prediction of Risk for Developing Breast Cancer Based on Bilateral Mammographic Breast Tissue Asymmetry

Abstract

This study developed and assessed a computerized scheme to detect breast abnormalities and predict the risk of developing cancer based on bilateral mammographic tissue asymmetry. A digital mammography database of 100 randomly selected negative cases and 100 positive cases for having high-risk of developing breast cancer was established. Each case includes four images of craniocaudal (CC) and mediolateral oblique (MLO) views of the left and right breast. To detect bilateral mammographic tissue asymmetry, a pool of 20 computed features was assembled. A genetic algorithm was applied to select optimal features and build an artificial neural network based classifier to predict the likelihood of a test case being positive. The leave-one-case-out validation method was used to evaluate the classifier performance. Several approaches were investigated to improve the classification performance including extracting asymmetrical tissue features from either selected regions of interests or the entire segmented breast area depicted on bilateral images in one view, and the fusion of classification results from two views. The results showed that (1) using the features computed from the entire breast area, the classifier yielded the higher performance than using ROIs, and (2) using a weighted average fusion method, the classifier achieved the highest performance with the area under ROC curve of 0.781±0.023. At 90% specificity, the scheme detected 58.3% of high-risk cases in which cancers developed and verified 6 to 18 months later. The study demonstrated the feasibility of applying a computerized scheme to detect cases with high risk of developing breast cancer based on computer-detected bilateral mammographic tissue asymmetry.

1. INTRODUCTION

Although periodic mammographic screening results in earlier detection of breast cancers and reduces patient’s mortality rate [1], visually interpreting mammograms and detecting cancer is quite difficult, due to a large variability of breast abnormalities, dense fibro-glandular tissue overlapping, and low cancer prevalence of 3 to 5 cancers detected per every 1,000 examinations in the population-based screening environment [2]. As a result, the efficacy of mammography screening remains a very controversial issue to date [3]. To improve the efficacy of breast cancer prevention and/or screening programs, such as detecting more early cancer cases without increasing false-positive rates, accurately classifying women into two groups of high and low risk of developing breast cancer is one important approach. Such risk stratification approach can also help to optimally allocate cancer prevention and diagnostic resources to the high-risk women and potentially reduce the overall medical cost of the society. In cancer epidemiology field, many breast cancer risk models have been proposed and tested for this purpose, but most of these models did not include breast density as a risk factor [4]. Recent studies have shown that after age, breast density was the strongest breast cancer risk factor discovered to date [5] and among many different methods to assess breast density, mammographic tissue density measured by the percentage or ratio between the fibro-glandular tissue area and the entire segmented breast area depicted on the mammogram was a much stronger risk predictor than the others including the popular Wolfe model that classifies mammographic parenchymal patterns into four categories based on radiographic appearance of prominent ducts and dysplasia [6]. The mammographic tissue density has also been proved to be associated with some of genetic risk factors including BRCA1 and BRCA2 gene mutation [7]. As a result, researchers have suggested that the mammographic density should be included into the breast cancer risk models to improve their discriminatory power on individual women [8]. Meanwhile, assessing mammographic tissue density is routinely performed by radiologists in the clinical practice. Currently, the most widely used standard for assessing breast tissue density is using the Breast Imaging Reporting and Data System (BIRADS) established by the American College of Radiology [9]. Fig. 1 displays an example of four digital mammograms depicting breast tissue density in four BIRADS categories.

Fig. 1.

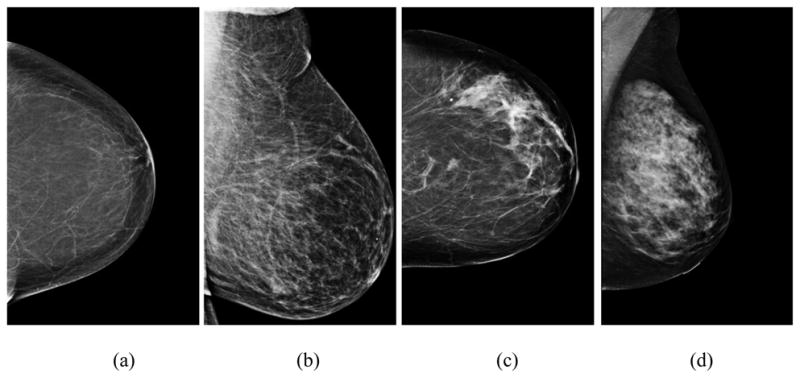
Four example images showing mammographic breast tissue density rated by radiologists in four BIRADS categories including (a) BIRADS 1 - almost entire fatty, (b) BIRADS 2 - scattered fibro-glandular density, (c) BIRADS 3 - heterogeneously dense, and (d) BIRADS 4 - extremely dense.

Since visual assessment of mammographic density into four BIRADS categories is difficult and often inaccurate due to the large inter-observer variability [10], a number of research groups have developed computerized algorithms and schemes to detect and quantify breast tissue density based on a variety of features including the image statistic features of the pixel values, such as mean, standard deviation, skewness, kurtosis, entropy, and the other higher order momentum based measures, computed from the original and/or processed images, the mathematical morphology and texture based features, such as power spectrum and fractal dimension [11–18]. For example, Zhou et al. reported developing an automated method to segment fibro-glandular breast tissue based on an adaptively determined histogram-based threshold. The study reported that the correlation between the automated and radiologists’ visual segmentation of the fibro-glandular tissue ratios was 0.94 and 0.91 for CC and MLO view images, respectively [13]. Oliver et al. also reported a correlation of 0.81 between an automated scheme and radiologists’ assessment on mammographic tissue density [19]. By computing eight texture-based features and deriving a computerized index to mimic radiologists’ BIRADS rating, Chang et al. reported that the correlation between the computerized index and the average rating of three radiologists in assessing mammographic tissue density was 0.87, which was also comparable to the correlation levels between radiologists [14]. Recently, several groups have developed and tested support vector machine (SVM) based feature classifiers to detect and classify images that depict fatty, glandular and dense tissue. The reported SVM classification accuracy ranged from 93.7% to 95.4% [20, 21]. In addition, previous studies have investigated whether using the computed mammographic tissue density and texture features was able to classify women into two groups with and without carrying BRCA1/BRCA2 gene mutation [22, 23]. Using a database of 172 cases that include 30 women carrying BRCA1/BRCA2 gene mutation and the power spectral analysis based on the manually selected regions of interest (ROIs) depicted on CC view images, the classification performance measured with the area under receiver operating characteristic (ROC) curve of AUC = 0.9 was reported [23].

Although a large number of studies have been conducted in the breast cancer research field to develop and assess breast cancer risk prediction models or schemes based on many known risk factors including mammographic tissue density, one important fact is that more than 60% of breast cancers actually arise or diagnosed in the women without any known risk factors [4, 24]. Thus, the currently available breast cancer risk prediction models have very limited discriminatory power or positive predictive value to correctly identify which individual women are highly likely to develop breast cancer in the period of interests [8]. To increase the positive predictive value of cancer risk prediction, we investigated and tested a new approach based on a number of well-known facts including that (1) humans naturally show bilateral symmetry in paired morphological traits including two breasts [25], (2) breast asymmetry is one of very few radiographic image phenotypes that relates to the biology process [26], (3) radiologists routinely examine bilateral mammographic tissue asymmetry to detect early suspicious lesions, and (4) using computerized schemes can achieve more reliable and/or consistent results in assessing mammographic tissue density or patterns by avoiding the inter-observer variability. Despite these well-known facts and the other related studies (i.e., predicting the risk of developing breast cancer based on the asymmetry of bilateral breast sizes measured from mammograms [25] and detecting the subtle malignant masses based on analysis of bilateral breast asymmetry using MRI images [27]), the bilateral mammographic tissue asymmetry has not been investigated in any of previously developed breast cancer risk assessment models [4]. Therefore, the hypothesis of our approach is that using a computerized scheme, one can more accurately and consistently detect and assess bilateral mammographic tissue asymmetry, and hence be able to increase the positive predictive value in identifying women with high-risk of developing breast cancer. Flagging these high-risk cases may ultimately help radiologists detect more breast cancers at an early stage. To test this hypothesis, we have developed and preliminarily tested a unique computerized scheme based on the bilateral mammographic tissue density asymmetry [28]. In our previous study, we only used bilateral mammographic tissue asymmetrical features computed from the entire breast areas of two cranio-caudal (CC) view images [28]. In this study, we first investigated and compared the scheme classification performance using the optimally selected mirror-matched regions of interest (ROIs) and the entire segmented breast areas depicted on two bilateral CC view images. We then investigated and assessed whether adding bilateral breast tissue asymmetry computed from medio-lateral oblique (MLO) view images into the scheme and fusing classification results from both CC and MLO view images can significantly improve the classification performance of the scheme.

2. MATERIALS AND METHODS

2.1. An image dataset

A total of 200 cases were selected from an ascertained full-field digital mammography (FFDM) image database pre-established in our research laboratory [29]. In brief, the FFDM database includes a total of 6478 FFDM images acquired from 1120 women who underwent regular mammography screening examinations in our medical center between 2006 and 2008. Some of the women had multiple sequential FFDM examinations during this period of time. All examinations were acquired using Hologic Selenia (Hologic Inc., Bedford, MA) FFDM systems. From this database, we randomly selected 200 cases, each of which contains four FFDM images representing both CC and MLO views obtained from the left and right breast of a woman. Thus, a total of 800 FFDM images were included in the dataset. Of these 200 cases, 100 were randomly selected from the negative cases that were not-recalled during the screening mammography, and 100 were positive cases for high risk of developing breast cancer. Among these 100 positive cases, 39 were prior examinations of verified cancer cases and 21 were prior examinations of the detected interval cancers. All these prior examinations were interpreted as negative during the original screening mammography and no dominant masses and/or micro-calcifications were considered visually detectable by radiologists during the retrospective review. However, the cancers were detected and verified either during the next annual screening examination that were 12 to 18 months later for the 39 cancer cases or between two periodic screening examinations that were 6 to 9 months later for 21 interval cancer cases. The other 40 cases were recalled due to suspicious findings on the images, in which 8 were determined as high-risk pre-cancer cases with surgical excision of the lesions and 32 were eventually biopsy-proved benign cases. The majority of cases, namely 28.5% (57/200) and 61% (122/200), were rated by radiologists as heterogeneously dense (BIRADS II) and extremely dense (BIRADS III), respectively (Table 1).

Table 1.

The distribution of BIRADs rating in 100 negative and 100 positive cases of the testing dataset

	BIRADS I	BIRADS II	BIRADS III	BIRADS IV
Negative	4	31	59	6
Positive	4	26	63	7

2.2. Feature extraction and normalization

The first step of our computerized scheme is to automatically segment the breast tissue area depicted on each image and detect two landmarks including nipples and the chest wall. The detailed description of this step has been reported in our previous study [30]. In brief, the scheme first detects the orientation of an image of the left or right breast and automatically flips the image of right breast. Thus, the chest walls of the breasts always align on the left side (edge) of the image. Second, based on the grey level histogram of the image, the scheme applies an iterative searching method to detect the smoothest curvature between breast tissue and the air background as representing the skin line that is the interface between breast tissue and air background. All air-background related pixels depicted on the image are removed from the segmented breast area. Third, the scheme detects the chest wall. Since the chest wall is often outside the depicted field of view on the CC images, for the purpose of this work, our scheme is only applied to detect the chest wall depicted on each MLO view image. The scheme horizontally scans the breast image from left to right and searches for the pixel with the maximum gradient. Then, the chest wall is detected by employing linear regression to fit all identified pixels with the maximum gradient on each scan. After detecting the chest wall, all pixels located inside the chest wall (the pectoral muscle region) are also excluded from the segmented breast area. Finally, the scheme detects the nipple by searching either a small protruding area or a relatively low density smooth area along the detected skin line. In this study, the results of automated breast area segmentation and landmark detection on each of 800 images selected in our testing dataset were visually examined and manually corrected if errors were detected. In this experiment, we manually corrected approximately 10% and 15% of computerized detected nipple locations depicted on CC and MLO view images, respectively, as well as 21.5% of detected chest wall locations and/or orientations.

From a large number of image features that have been previously investigated and used to quantify or classify mammographic tissue density or patterns by several research groups [11–18], we initially selected 20 features in our studies. The detailed descriptions of these 20 selected features are presented in the appendix of this article. These features include image statistics based features computed from the original FFDM image and the local pixel value fluctuation mapping images (i.e., mean, standard deviation, skewness, and kurtosis), the texture-based features of fractal dimension, and the features related to the simulated BIRADS density ratings. In this study, we computed the same 20 features from the selected regions of interest (ROIs) in the bilateral CC view images and the entire segmented breast areas from the bilateral MLO view images. Two values of the same feature computed from two matched regions depicted on the bilateral images were subtracted and the absolute difference between these two values is used to represent bilateral mammographic tissue asymmetry.

Unlike some of the previous studies that manually selected ROIs with 256 × 256 pixels located in the central region behind the nipple [16, 23] to compute mammographic tissue related features, our scheme automatically selected the ROIs with sizes adaptively adjusted based on the imaged breast size. Thus, the selected ROIs can cover the approximately similar proportion of breast tissue regions that are independent to the variation of breast sizes. Specifically, the size of each ROI is defined as d × d, where d equals to half of the distance between the nipple and the edge of imaged breast area (close to the chest wall). Using the mirror-matched concept, two ROIs will be defined and extracted from two bilateral CC view images. If the sizes of the segmented breast areas vary between two bilateral mammograms, the sizes of two extracted ROIs also vary. Fig. 2 shows an example of two ROIs automatically extracted from two breasts with different sizes in CC view images. From a pair of two matched ROIs, 20 features were independently computed and two values of the same feature were subtracted to represent the region-based bilateral mammographic tissue asymmetry. For each testing case, 20 image features were also separately computed from the entirely segmented breast areas depicted on two bilateral MLO view images and subtracted. In summary, to assess bilateral mammographic breast tissue asymmetry, each feature used in this study is represented by the absolute difference (subtraction) of two feature values computed from the two bilateral images.

Fig. 2.

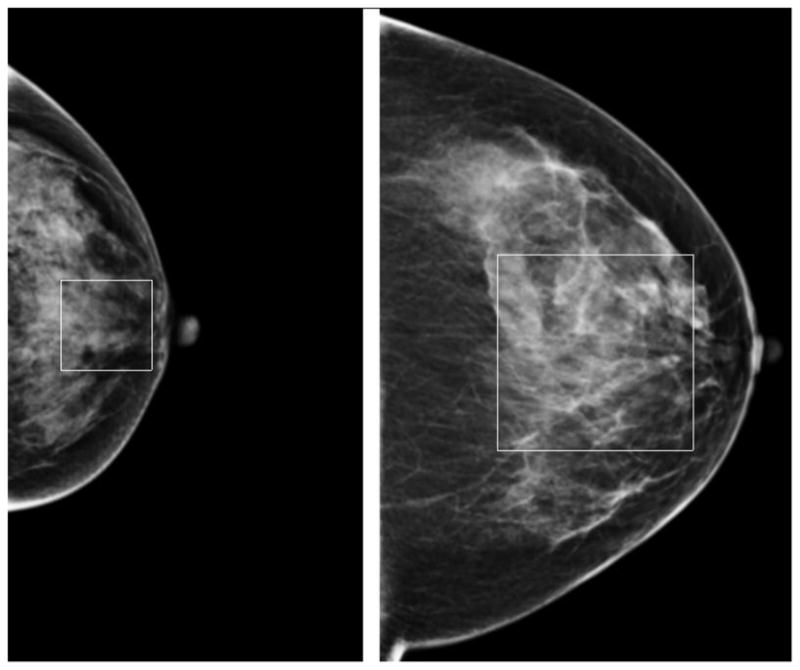
Two regions of interest adaptively selected and extracted from two breasts with different sizes in CC view.

Since the mean and standard deviation of feature values can vary widely among these 20 features, a feature normalization process was applied for each of 20 features F_i, i = 1,…,20. The mean (μ_i) and standard deviation (σ_i) of each feature vector (F_i) from all of 200 testing cases were computed. The values of each feature were normalized within the range between [μ_i −2σ_i] and [μ_i + 2σ_i]. For each feature value, if F_ij < μ_i − 2σ_i, it is assigned to μ_i − 2σ_i, if F_ij > μ_i + 2σ_i, it is assigned to μ_i + 2σ_i. Then normalized feature value $F_{ij}^{\prime }$ is computed by

$$F_{ij}^{\prime }=(F_{ij}-F_{jmin})/(F_{jmax}-F_{jmin})$$ (1)

Where F_{j min} and F_{j max} is the minimum and maximum value for each input feature F_j. As a result, all feature values are normalized and distributed in the range from 0 to 1. Thus, in building a multi-feature based machine learning classifier, all selected features have the same weights in the classifier. Thus, two new initial feature pools were built in this study, one containing 20 bilateral mammographic tissue asymmetric features computed from the selected ROIs of CC view images and one including the same 20 features computed from the entire breast areas depicted on bilateral MLO view images.

2.3. Feature selection and optimization of an artificial neural network

Based on the computed features described above, we built a multi-feature based artificial neural network (ANN) to detect the level of bilateral mammographic breast tissue asymmetry and used it to predict the likelihood of the cases being positive for having high-risk of developing breast cancer later. An ANN is designed to simulate a biological learning system with a densely interconnected set of simple units (neurons), where each neuron takes a number of real-valued inputs and produces a single real-valued output [31]. Each ANN built in this study has a simple three-layer feed-forward topology, which includes N input neurons connecting to N selected features in the first layer, M hidden neurons in the second layer, and one output neuron in the third layer. The relationship between the input neurons (x_i) and the output neuron (y) is determined by

$$y=f[\sum _{j=1}^m{w}_{j}f(\sum _{i=1}^n{w}_{ji}{x}_i+{\theta }_{in})+{\theta }_{\mathit{hid}}]$$ (2)

where w_j is the weight from the jth hidden neuron to the output neuron, w_ji is the weight from ith input neuron to the jth hidden neuron, θ_in and θ_hid are two bias neurons in the input and hidden layer of the ANN, respectively. A nonlinear sigmoid function

$$f=O_{pj}=\frac{1}{1+e^{-({\displaystyle \sum _i}{w}_{ji}{o}_{pi}+{\theta }_j)}}$$ (3)

is used as the activation function for each process neuron, where O_pj is the jth element of the output pattern produced by the input pattern O_pi. Using a back-propagation training concept, the weights that link between the neurons are iteratively adjusted and computed as follows:

$$\mathrm{\Delta }{w}_{ji}(k+1)=\eta {\delta }_{pj}{O}_{pi}+\alpha \mathrm{\Delta }{w}_{ji}(k)$$ (4)

Where is the η learning rate, α is momentum that determines the effect of past weight changes on the current changes, k is the number of iterations, and δ_pj is the mean squared error (MSE) between the desired and actual ANN output value. Using a set of training data - feature vectors, the ANN is iteratively trained to reduce the error and minimize the difference between the desired and actual ANN output values. The decision neuron generates a likelihood score ranging from zero to one [32]. The greater score, the higher risk the case has to develop breast cancer.

Since selecting an optimal feature set through the process of discarding redundant features is an important step in developing any data-driven computerized schemes, we applied a genetic algorithm (GA) in this study to build an optimal ANN by selecting a set of optimal features from the initial pool of 20 features and determine the appropriate number of hidden neurons. GA is a machine learning method to simulate biological evolution process in which GA generates successor chromosomes by repeatedly mutation and recombining parts of the best currently known chromosomes [31]. Once the GA chromosomes are specifically coded to represent a machine learning classifier and the GA iteration process is guided by an application-based fitness function or criterion, GA can generate a classifier that achieves the optimal performance. A publicly available GA software package [33] was modified and used in this study. During the GA optimization process, a binary coding method was applied to create GA chromosome strings that represent which features are either selected or discarded and the number of selected hidden neurons. Specifically, each GA chromosome includes 24 genes. Among these, the first 20 genes represent 20 features related to the bilateral mammographic tissue asymmetry. In these 20 genes, the code of 1 indicates that the feature represented by this gene is selected and implemented in ANN and 0 means that the feature is discarded. The last four genes indicate the number of neurons. For example, the code of 0101 represents 5 hidden neurons. In the first generation, 100 GA chromosomes were randomly generated by the GA program. Once a GA chromosome was selected, the corresponding ANN structure was also determined. During the ANN training, a limited number of training iterations (500) and a larger ratio between the training momentum (0.9) and learning rate (0.01) was used to minimize over-fitting and maintain robustness of ANN performance. Due to the size limitation of our dataset and reduction of training bias, a leave-one-case-out training and testing method [34] was implemented to train and assess performance of the ANN built by the specific GA chromosome. During the process of training and assessing each ANN, 199 cases were used to train the ANN and one remaining case was used to test the ANN. This process was repeated 200 times, so that each case in the dataset was used once to test the classifier. The ANN-generated detection (classification) scores of all 200 cases were read and analyzed by a ROC curve fitting program (ROCKIT [35]). The computed area under the ROC curve (AUC) was used as a summary index to assess ANN performance. If the ANN yielded higher performance, the corresponding GA chromosome has the higher probability to be selected by the GA program to generate the new chromosome in the next generation using the crossover and mutation process. The GA optimization is terminated when no significant performance improvement can be achieved or the number of iterations reaches the predefined maximum iteration generations. In this study, the maximum iteration generation was 100.

In summary, using this GA optimization process, we independently optimized two ANNs using two initial feature pools including the bilateral mammographic tissue asymmetrical features computed from (1) the ROIs with adaptive size extracted from the central regions of two bilateral CC view images and (2) the entire segmented breast areas depicted on two bilateral MLO view images.

2.4. Performance assessment

After GA optimization, the classification performance levels of two ANNs measured by the areas under ROC curves (AUC) were separately computed using ROCKIT program. By including another previously optimized ANN using the bilateral mammographic tissue asymmetric features computed from the entire segmented breast areas depicted in two bilateral CC view images [28], we compared the performance levels of three ANNs using the features computed from either the selected ROIs or the entire segmented breast area depicted on a single view (CC or MLO) images. To test whether the risk assessment performance can be further increased by combining the results acquired from bilateral images of different views, we also tested several ANN scoring fusion methods as reported in the previous study for the similar fusion purpose [36] to select or combine the classification results (detection scores) acquired from CC and MLO views of the same test cases. We generated several sets of new detection scores (S_new) from the ANN-generated detection scores in CC (S_CC) and MLO (S_MLO) view, which includes selecting the maximum score S_new = MAX (S_CC, S_MLO), the minimum score S_new = MIN (S_CC, S_MLO), and computing a set of weighted average detection scores S_new = (W₁ × S_CC + W₂ × S_MLO)/2, in which W₁ and W₂ are different weights ranging from 0.5 to 1.5 in this study. Each set of 200 detection scores for 100 positive and 100 negative cases were reprocessed by ROCKIT program to generate a new performance index (AUC). The results of different fusion methods are analyzed and compared. In addition, we analyzed and reported changes in the actual sensitivity levels for detecting different types of cases including verified cancer cases, high-risk pre-cancer cases recommended for surgery excision based on current clinical guidelines, and other recalled cases with biopsy, as well as the relationships between classification results and several clinical features at a set of specificity levels from 80% to 95%.

3. RESULTS

From the initial 20 features, GA independently generated three optimal ANNs with different features and structures as shown in Table 2. Among these 20 features, 12 were selected either once (6) or twice (6) used in three ANNs. No single feature was selected and used in all three ANNs. The number of input neurons was 6, 5, 7 and the number of hidden neurons was 8, 5, and 8 for these three ANNs, respectively. Table 3 shows and compares the classification performance levels of applying each of three ANNs to each of three feature datasets extracted from the entire segmented breast areas depicted on either CC or MLO view images as well as from the adaptively selected ROIs from CC images. The results indicated that due to the difference among the three methods to extract the bilateral mammographic tissue asymmetry, GA was able to adaptively select a small set of effective features (ranging from 5 to 7) and discard the majority of others based on the specific training feature datasets. As a result, the GA-optimized ANN for each feature extraction method or dataset has its own unique structure including the selected input features and the number of hidden neurons.

Table 2.

Summary of three GA-optimized ANNs using bilateral mammographic tissue asymmetry related features computed from the entire segmented breast areas depicted on either CC or MLO view images as well as from the selected ROIs from CC images

ANN	Input neurons	Hidden neurons	Output neurons	Selected input features
Entire breast areas in CC view	6	8	1	1,4,8,11,12,13
Entire breast areas in MLO view	5	5	1	3, 8, 10, 14,20
Selected ROIs in CC view	7	8	1	1,4,11,12,13,15,17

Table 3.

Comparison of AUC for using the same ANN structure and input features extracted from the entire segmented breast areas depicted on either CC or MLO view images as well as from the selected ROIs from CC images

Input– hidden– output neuron	AUC
	6-8-1	5-5-1	7-8-1
Entire breast areas in CC view	0.754	0.653	0.721
Entire breast areas in MLO view	0.558	0.688	0.549
Selected ROIs in CC view	0.681	0.569	0.690

Fig. 3 shows and compares three ROC performance curves generated by three GA-optimized ANNs. The areas under ROC curves (AUC) ranged from 0.688 ± 0.027 to 0.754 ± 0.024. Although the ANN optimized using the features extracted from the entire breast areas depicted on CC view images yields the highest performance, the ANOVA (analysis of variance) test shows that the performance levels of three ANNs is not significantly different from each other with three p-values ranging from 0.12 (using the entire breast areas and ROIs depicted on CC view images) to 0.76 (using the entire breast areas depicted on MLO view images and ROIs depicted on CC view images).

Fig. 3.

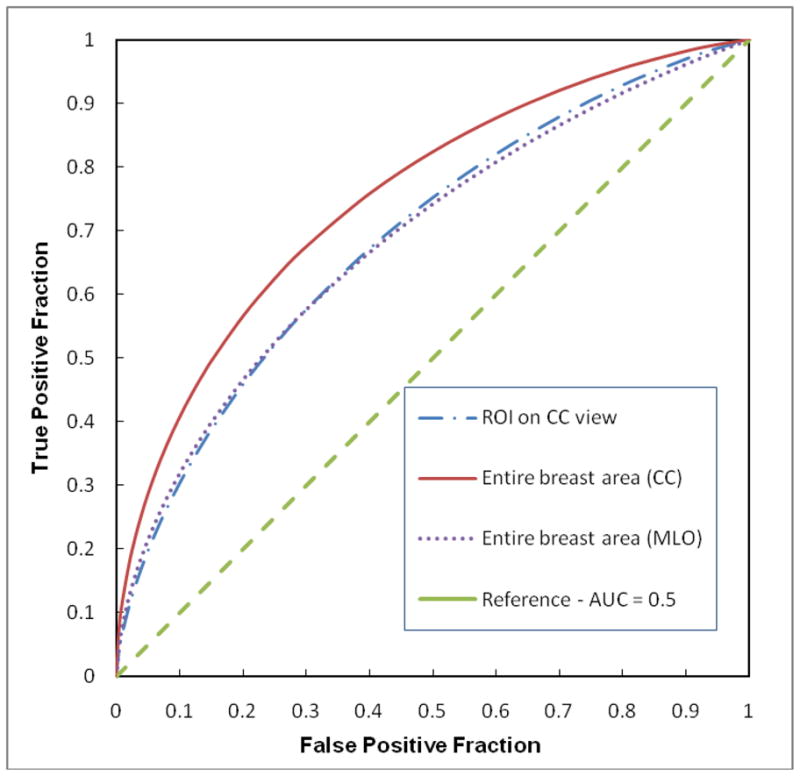
Comparison of three ROC curves generated by three ANNs trained using the features computed from the selected ROIs, the entire segmented breast areas depicted on either MLO view or CC view images. The areas under these three ROC curves are 0.690± 0.026, 0.688± 0.027, and 0.754± 0.024, respectively.

Table 4 summarizes and compares the classification performance levels of two ANNs optimized using features computed from the entire segmented breast areas depicted on CC and MLO views as well as the performance levels yielded using three basic scoring fusion methods namely, the average, the minimum, and the maximum of detection scores generated by these two ANNs. The correlation coefficients of two sets of ANN-generated detection scores between using two bilateral CC and MLO view images are 0.486 (for positive cases) and −0.201 (for negative cases), respectively. Comparing three scoring fusion methods, using both maximum and minimum scores the classifier yielded the lower performance levels than using the scores generated from the ANN using features computed from the entirely segmented breast area depicted on CC view images only, while using average scores, the classifier yielded comparable performance with AUC = 0.754±0.024 versus AUC = 0.756±0.026. Table 5 summarizes and compares the performance levels of applying the weighted average scoring fusion method in which the weights varied from 0.5 to 1.5 on the detection scores generated by two ANNs that use the features computed from the entire breast areas depicted on either CC or MLO view images. The best classification performance was AUC = 0.781±0.023 achieved using the weight of 1.25 on the CC view and 0.75 on the MLO view images, which is significantly higher than using features computed only from CC or MLO view (p < 0.05).

Table 4.

Comparison of classification performance measured by the area under ROC curve (AUC) and its standard deviation (STD) using features computed from CC and MLO view images, as well as three scoring fusion methods using the minimum, the maximum, and the average scores generated from two ANNs using the features computed from CC and MLO view images.

	CC	MLO	Minimum	Maximum	Average
AUC	0.754	0.688	0.728	0.740	0.756
STD	0.024	0.027	0.023	0.025	0.026

Table 5.

Comparison of the ROC performance levels measured by the area under ROC curve (AUC) and its standard deviation (STD) using a series of weighted average of detection scores generated by two ANNs using the features computed from CC and MLO view images.

Weight between CC and MLO view	0.5: 1.5	0.75: 1.25	1.0: 1.0	1.25: 0.75	1.5: 0.5
AUC	0.722	0.742	0.756	0.781	0.750
STD	0.024	0.026	0.026	0.023	0.025

Table 6 summarizes the actual number of positive cases correctly detected and classified by our scheme when using the weighted average scoring method to combine detection results of two ANNs at four specificity levels (from 80% to 95%). The sensitivity levels applying to this testing dataset with 100 positive cases are 49% and 59% at specificity levels of 90% and 80%, respectively. Specifically, our scheme detected 59 and 79 “positive” cases at these two specificity levels. Among the 59 detected cases at 90% specificity, 49 are true-positive (TP) cases and 10 are false-positive (FP) cases, while among the 79 detected cases at 80% specificity, 59 are TP and 20 are FP cases, Thus, the positive predictive values (PPV) are 0.83 (49/59) and 0.75 (59/79) at these two specificity levels, respectively. By analyzing the sensitivity levels for four different high-risk sub-groups namely, the prior examinations of the cancer cases and the interval cancer cases, as well as the high-risk cases with surgery excision of the lesions and the recalled suspicious cases with biopsy-proved benign lesions, we found that although the classifier was not specifically trained with cancer cases only rather trained using a mix group of positive high-risk cases, it yielded a higher classification sensitivity on actual cancer cases than the other suspected benign cases. For example, at 90% specificity, 58.3% (35/60) cancer cases were detected at 6 to 18 month early, while 34.4% (11/32) recalled benign cases were detected as the positive for high-risk of developing breast cancer. The classification results also showed that the performance of our scheme was not affected by breast density levels. At 90% specificity, our scheme detected 50% (2/4), 50% (13/26), 50% (32/64), and 33% (2/6) positive (“high-risk”) cases at each of four BIRADS categories (1 to 4), respectively.

Table 6.

The actual number of positive cases correctly identified (sensitivity levels) at four specificity levels when using the optimal weighted average scoring method to combine the detection results of two ANNs using the features computed from CC and MLO view images.

Specificity	95%	90%	85%	80%
All positive cases	44 (44.0%)	49 (49.0%)	54 (54.0%)	59 (59.0%)
39 cancer cases	18 (46.2%)	21 (53.8%)	23 (59.0%)	26 (66.7%)
21 interval cancer cases	13 (61.9%)	14 (66.7%)	14 (66.7%)	14 (66.7%)
8 high-risk cases	2 (25.0%)	3 (37.5%)	4 (50.0%)	5 (62.5%)
32 recalled benign cases	11 (34.4%)	11 (34.4%)	13 (40.6%)	14 (43.8%)

4. DISCUSSION

This study supported no matter whether the features were computed from the mirror-matched ROIs or the whole segmented breast areas depicted on the bilateral CC or MLO view images, using bilateral mammographic tissue asymmetry related features was able to classify women into two groups of high and low risk of developing breast cancer with relatively higher positive predictive value (PPV) than the currently available breast cancer risk models [4]. For example, PPV = 0.90 (44/49) for all positive high-risk cases or PPV = 0.63 (31/49) for cancer cases only at 95% specificity (Table 6). The results demonstrated that after one baseline mammography examination, a new computerized scheme using a set of bilateral mammographic tissue asymmetry related features was able to detect or flag a higher fraction of high-risk cases for developing breast cancer six to 18 months later.

Although using the local-based bilateral mammographic breast tissue asymmetry has been tested to detect suspicious breast masses by several groups in developing computer-aided detection (CAD) schemes [37–39], this approach has not been implemented in any commercialized CAD schemes to date due to the difficulty of bilateral mammogram registration. Our approach to compute bilateral mammographic tissue asymmetry is different. Unlike the commercialized CAD schemes that focus on detecting subtle but visually detectable masses and micro-calcification clusters depicted on single digitized or digital mammograms [40], our scheme does not target and detect any specific lesions. We detected bilateral mammographic tissue asymmetry without performing automated image registration to avoid the potential registration error between two bilateral images. Hence, our computerized risk assessment scheme does not directly compete with the conventional CAD schemes due to the different application purposes. All images in our database were interpreted as negative or benign by the radiologists during the original mammographic screening. Without the dominant and visually detectable masses or micro-calcifications depicted on the images of these examinations, applying the conventional CAD schemes to process these images can only generate false-positive detections (marks) that cannot help radiologists in their interpretation of these images. However, our scheme is able to flag warning signs for the cases with high-risk of developing breast cancer based on the detection and analysis of the bilateral mammographic tissue asymmetry. The results may attract radiologists more attention to analyze or monitor (follow-up) these cases and eventually help them to detect a large fraction of cancers early.

Although the results are encouraging, we recognized that this was a very preliminary study using a small dataset which cannot be adequately cover or represent the actual population base in the clinical practice. Thus, the actual performance level and the robustness of this scheme needs to be further tested in future studies. In addition, due to the limitation of dataset size, we used the leave-one-case-out training and testing method in which features were normalized based on the entire dataset of 200 cases. This is different from the traditional feature normalization method only based on the training dataset. However, based on our experiments, we found that the difference of the feature normalization between using the entire 200 cases and adaptively using 199 training cases was negligible. Hence, the reported testing results are valid when using our dataset and the leave-one-case-out testing method.

At our current research stage, we only selected and computed mammographic density or texture based features that have been investigated by other researchers in previously reported studies and proved to be effective in quantifying the breast tissue density or patterns depicted on single mammogram [12–18, 22, 23]. However, the difference of our study is that we investigated the effectiveness of these features in correlating with bilateral mammographic tissue asymmetry. Thus, all features used in this study were represented as the absolute differences or subtraction of the same features computed from two bilateral mammograms. The study results demonstrated that a genetic algorithm was able to select a set of optimal features to detect bilateral mammographic tissue asymmetry and build an optimal machine learning classifier (e.g., an ANN) to predict a fraction of cases with high-risk of developing breast cancer. In addition, we also investigated and compared our scheme performance levels using the features extracted or computed from either adaptively selected ROIs or the entire segmented breast areas of mammography images in both CC and MLO view images. Although using the global features computed from two bilateral CC view images our scheme yielded the relatively higher performance than using the features computed from MLO view images (as shown in Fig. 3), the correlation coefficients of the ANN-generated detection scores between using features extracted from CC and MLO view images are relatively lower. Thus, applying the scoring fusion method to select or combine two sets of detection scores is able to further improve the classifier performance. Due to the higher classification performance generated by the ANN using global features computed from CC view images than that using MLO view images, higher weights needs to be added in the classification scores generated from the ANN using CC view images than using MLO view images. In this study, when using the weight ratio of 1.25 on CC view to 0.75 on MLO view, the scheme yielded the best classification performance (Table 5). Hence, the bilateral mammographic breast tissue asymmetrical features computed from both CC and MLO views can make contribution to improve the final classification performance of our scheme.

In summary, we investigated and assessed several issues to optimize a unique computerized scheme that is able to flag or classify a fraction of women with high-risk of developing breast cancer within the period of interest namely (i.e., 6 to 18 months in this preliminary study). The robustness of the scheme performance needs to be further tested using large and diverse image databases in the future studies. If it succeeds, this computerized scheme with high positive predictive value may eventually provide a new and reliable breast cancer risk stratification tool to identify a group of women with high-risk of developing breast cancer at an early stage.

APPENDIX: Summary of 20 bilateral mammographic tissue asymmetric features

The selected 20 features are divided into five groups. Each is computed by the subtraction (the absolute difference) of two same feature values computed from two bilateral images.

Group 1

This group includes 5 features computed from the gray level histogram of the segmented breast area.

• 1 $F_1=\frac{N_M}{N}$, where N_M is the number of pixels within the bin of the maximum value inside the histogram, and N is the total pixel number of the segmented breast area.
• 2 $F_2=\frac{N_H}{N}$, where N_H is the number of pixels with gray value larger than the average value of the histogram.
• 3 $F_3=\frac{1}{m-1}{\displaystyle \sum _{i=1}^{m-1}}\mid H_i-H_{i+1}\mid$, where m is the total number of histogram bins, H_i and H_i+1 are two histogram values in two adjacent histogram bins (i and i+1) representing the average local value fluctuation of the histogram.
• 4 $F_4=\frac{1}{m}{\displaystyle \sum _{i=1}^m}{H}_i$, the mean of histogram values.
• 5 $F_5=\sqrt{\frac{1}{m-1}{\displaystyle \sum _{i=1}^m}{(H_i-F_4)}^2}$, the standard deviation of histogram values.

Group 2

We converted the original image of the segmented breast area into a local pixel value fluctuation map by applying a 5×5 square convolution kernel to scan the original image. The absolute pixel value differences between the center pixel (i) and each of the other pixels (j) inside the kernel were computed. The maximum difference value (PF_i) computed inside the kernel was used to replace the original pixel (i) value in the map. This group includes 3 features computed from this converted map.

• 6 $F_6=\frac{1}{N}{\displaystyle \sum _{i=1}^N}({PF}_i)$, mean of the pixel value in the map.
• 7 $F_7=\sqrt{\frac{1}{N-1}{\displaystyle \sum _{i=1}^N}{({PF}_i-F_6)}^2}$, the standard deviation of the pixel values in the map.
• 8 $F_8=\frac{1}{N-1}{\displaystyle \sum _{i=1}^N}{(\frac{{PF}_i-F_6}{F_7})}^3$, the skewness of the pixel values in the map.

Group 3

This group includes 2 fractal dimension based features reported by Chang et al [14].

• 9F₉ is a slope of a log scale fitted regression line between a kernel (k), k = 4×n + 1, n = 1,2,3,4,5. and the F (k) by Gaussian functions: $F(k)=I_k^H(x,y)=I-{\displaystyle \sum _{(x,y)\in R}}{I}_k^L(x,y)$, Where $I_k^L(x,y)$ is a low-pass filtered image by Gaussian functions.
• 10F₁₀ is a slope of a log scale fitted regression line between the distance (t) of the pixels and the gradient $g(t)={\displaystyle \sum _{(x,y)\in R}}(\mid I-I_{x+t}\mid +\mid I-I_{x-t}\mid +\mid I-I_{y+t}\mid +\mid I-I_{y-t}\mid )$ within the region (R).

Group 4

This group includes 4 conventional statistical data analysis features computed from the pixel value distributions of the segmented breast areas.

• 11 $F_{11}=\overline{I}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{I}_i$, the mean of all pixel values (I_i, i = 1,2,…, N).
• 12 $F_{12}=\sigma =\sqrt{\frac{1}{N-1}{\displaystyle \sum _{i=1}^N}{(I_l-\overline{I})}^2}$, the standard deviation of all pixel values.
• 13 $F_{13}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{(\frac{I_i-\overline{I}}{\sigma })}^3$, the skewness of all pixel values.
• 14 $F_{14}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{(\frac{I_i-\overline{I}}{\sigma })}^4$, the kurtosis of all pixel values.

Group 5

This group includes 6 features that mimic the BIRADS rating method to divide the segmented breast area into four regions based on the pixel value.

• 15 – 17

  $F_{15}=\frac{{\overline{I}}_{25\%}}{\overline{I}},F_{16}=\frac{{\overline{I}}_{50\%}}{\overline{I}},F_{17}=\frac{{\overline{I}}_{75\%}}{\overline{I}}$, where Ī_25%, Ī_50%, Ī_75% are the average gray value of the pixels under three thresholds of 25%, 50%, 75% of the maximum pixel value, respectively.

• 18 – 20

  $F_{18}=\frac{N_{25\%}}{N},F_{19}=\frac{N_{50\%}}{N},F_{20}=\frac{N_{75\%}}{N}$, where N_25%, N_50%, N_75% are the number of the pixels with pixel values smaller than three thresholds representing 25%, 50%, and 75% of the maximum pixel value inside the segmented breast area.