Evaluation of Specific Metabolic Rates of Major Organs and Tissues: Comparison Between Men and Women

Abstract

Objectives

The specific resting metabolic rates (Ki, in kcal/kg per day) of major organs and tissues in the Reference Man were suggested in 1992 by Elia: 200 for liver, 240 for brain, 440 for heart and kidneys, 13 for skeletal muscle, 4.5 for adipose tissue and 12 for the residual mass. However, it is unknown whether gender influences the Ki values. The aim of the present study was to compare the Ki values observed in non-elderly non-obese men to the corresponding values in women.

Methods

Elia’s Ki values were evaluated based on a mechanistic model: REE = Σ(Ki × Ti), where REE is whole-body resting energy expenditure measured by indirect calorimetry and Ti is the mass of major organs and tissues measured by magnetic resonance imaging. Marginal 95% confidence intervals (CIs) for the model-estimated Ki values were calculated by stepwise univariate regression analysis. Subjects were non-elderly (age 20 - 49 yrs) non-obese (BMI 18.5 - 29.9 kg/m²) men (n = 49) and women (n = 57).

Results

The measured REE (REEm) and the mass of major organs and skeletal muscle were all greater in the men than in women. The predicted REE by Elia’s Ki values were correlated with REEm in men (r = 0.87) and women (r = 0.86, both P <0.001). Elia’s Ki values were within the range of 95% CIs for both men and women groups, revealing that gender adjustment is not necessary.

Conclusions

Elia’s proposed adult Ki values are valid in both non-elderly non-obese men and women. Further studies are needed to explore the potential influences of age and obesity on Ki values in humans.

INTRODUCTION

Exploring specific resting metabolic rate (Ki value) for individual organs and tissues is one of the primary aims of human energy metabolism research (Wang et al., 2001). Based on reported experimental results in humans and other mammals, Elia (1992) presented a review on the Ki values for major organs and tissues in the Reference Man (Snyder et al., 1975), including liver (200), brain (240), heart (440), kidneys (440), skeletal muscle (13), adipose tissue (4.5) and residual mass (12, all units are in kcal/kg per day). Residual mass includes skeleton, blood, skin, gastrointestinal tract, lung, spleen and other tissues and organs present in small amounts.

Although the Ki values of individual organs and tissues were assumed stable, published studies suggested that some biological factors influence Ki values, including growth, development, aging and adiposity (Bosy-Westphal et al., 2004; Gallagher et al., 2000; Hsu et al., 2003; Wang et al., 2005, 2010).

Gender is a major source of variation in body composition and physiological functions. Biological differences between men and women may influence body composition per se, such as percentage of body weight as fat, and physiological functions such as daily resting energy expenditure (REE). However, it remains unknown whether the Ki values suggested by Elia are applicable in both adult men and women.

The aim of the present study was to evaluate the applicability of Elia’s Ki values for major organs and tissues across non-elderly non-obese men and women. An approach was applied to evaluate Elia’s Ki values by combining a mechanistic REE model with stepwise univariate regression analysis.

METHODS

Model Establishment

A mechanistic REE model was applied that represents REE as the sum of the products of individual organ/tissue mass and corresponding specific resting metabolic rates (Gallagher et al., 1998; Wang et al., 2001),

$$\mathrm{REE}=\Sigma (K_{\mathrm{i}}\times {\mathrm{T}}_{\mathrm{i}})$$ (1)

where Ti is the individual organ and tissue mass, i the organ/tissue number (i = 1, 2, …, n), and Ki is the specific resting metabolic rate of the individual organs and tissues.

Because liver, brain, heart and kidneys have large Ki values and skeletal muscle and adipose tissue are the largest components at the organ-tissue level, the following body composition model was applied,

$$\mathrm{BM}=\mathrm{T}\text{liver}+\mathrm{T}\text{brain}+\mathrm{T}\text{heart}+\mathrm{T}\text{kidneys}+{\mathrm{T}}_{\mathrm{SM}}+{\mathrm{T}}_{\mathrm{AT}}+\mathrm{T}\text{residual}$$ (2)

where BM is body mass, and SM and AT are skeletal muscle and adipose tissue, respectively. Residual mass in this study was calculated as BM minus the sum of liver, brain, heart, kidneys, skeletal muscle and adipose tissue.

Based on the Ki values suggested by Elia, a working REE model can be expressed as,

$$\begin{array}{cc}\hfill \mathrm{REE}=& 200\mathrm{T}\text{liver}+200\mathrm{T}\text{brain}+400\mathrm{T}\text{heart}+400\mathrm{T}\text{kidneys}+13{\mathrm{T}}_{\mathrm{SM}}+4.5{\mathrm{T}}_{\mathrm{AT}}\hfill \\ \hfill & 12\mathrm{T}\text{residual}\hfill \end{array}$$ (3)

Our strategy to evaluating Elia’s Ki values was to examine each organ and tissue separately for the men and women groups. We constructed marginal 95% confidence intervals (CIs) for each of the seven Ki values via univariate linear regression analysis within the men and women groups, respectively (Weisberg, 2005).

First, we evaluated the Ki value of liver (Kliver) with the statistical hypothesis Kliver = 200 kcal/kg per day suggested by Elia (1992) via the following regression model,

$$\begin{array}{cc}\hfill K\text{liver}\times & \mathrm{T}\text{liver}=\mathrm{REE}-(240\mathrm{T}\text{brain}+440\mathrm{T}\text{heart}+440\mathrm{T}\text{kidneys}+13{\mathrm{T}}_{\mathrm{SM}}\hfill \\ \hfill & +4.5{\mathrm{T}}_{\mathrm{AT}}+12\mathrm{T}\text{residual})\hfill \end{array}$$ (4)

An estimate with standard error (95% CI) for Kliver was obtained by fitting equation 4 with least square method. The 95% CIs were then compared with the hypothesized value of K1iver suggested by Elia (1992) for both men and women groups. Testing the statistical hypothesis K1iver = 200 kcal/kg per day at a significance level of 0.05 was tantamount to checking whether K1iver = 200 kcal/kg per day falls inside the 95% CI.

Second, we evaluated the Ki value of brain (Kbrain) and fitted a linear regression model by using equation 3,

$$\begin{array}{cc}\hfill K\text{brain}\times & \mathrm{T}\text{brain}=\mathrm{REE}-(200\mathrm{T}\text{liver}+440\mathrm{T}\text{heart}+440\mathrm{T}\text{kidneys}+13{\mathrm{T}}_{\mathrm{SM}}\hfill \\ \hfill & +4.5{\mathrm{T}}_{\mathrm{AT}}+12\mathrm{T}\text{residual})\hfill \end{array}$$ (5)

The value of Kbrain and its SE (95% CI) were estimated by using the least squares analysis for both men and women groups. Then the 95% CIs were compared with the hypothesized value Kbrain = 240 kcal/kg per day suggested by Elia (1992).

The same process was repeated for each of the remaining Ki values in the men and women groups, including Kheart, Kkidney, K_SM, K_AT and Kresidual.

To further evaluate the applicability of Elia’s Ki values, we assess the necessity of adjusting gender effect for Elia’s Ki values in the men and women, respectively. A gender-stratified mechanistic model of resting energy expenditure can be formulated as

$$\mathrm{REE}=\Sigma \left(G\mathrm{i}\right)\times \text{Elia}\prime \mathrm{s}K\mathrm{i}\times \mathrm{T}\mathrm{i})$$ (6)

where Gi is the gender-adjusted coefficient for Elia’s Ki values of individual organs and tissues. In the present study, we assumed that the Gi values are the same across all organs and tissues for each gender group, or Gi = G. Thereby, a simplified gender-stratified REE model was as follows,

$$\begin{array}{cc}\hfill \mathrm{REE}=& G\times (200\mathrm{T}\text{liver}+240\mathrm{T}\text{brain}+440\mathrm{T}\text{heart}+440\mathrm{T}\text{kidneys}+13{\mathrm{T}}_{\mathrm{SM}}\hfill \\ \hfill & +4.5{\mathrm{T}}_{\mathrm{AT}}+12\mathrm{T}\text{residual})\hfill \end{array}$$ (7)

The G value with SE (95% CIs) of major organs and tissues was estimated in the men and women, separately. By testing the significance of the difference between G value and one, we can be decided whether gender-adjustment is necessary for the men and women.

Subjects

Existing REE, organs and tissues data were collected at the Institute of Human Nutrition and Food Science, Christian-Alberchts University, Kiel, Germany. The subjects in the present study had participated in other studies (Bosy-Westphal et al., 2003, 2004; Later et al., 2008). IRB approvals were obtained and subjects signed an informed consent. In order to exclude the potential influences of aging, race, adiposity and diseases on Ki values, subjects with age ≥50 yrs and/or BMI ≥30 kg/m² were excluded from this study. Only non-elderly (20 - 49 yrs old) and non-obese (BMI 18.5 - 29.9 kg/m²) healthy Caucasian subjects were included (n = 106, 49 men and 57 women).

Body Composition

Body mass was measured to the nearest 0.1 kg following a 12 h fast with the subjects wearing minimal clothing. Height was measured with a wall-mounted stadiometer to the nearest 0.1 cm.

Organ volumes were obtained by summing pixels from images obtained with a 1.5-T Magnetom Vision scanner (Siemens, Erlangen, Germany). The MRI protocol details were described in elsewhere (Bosy-Westphal et al., 2003, 2004).

In brief, for brain, a T1-weighted fast low-angle shot (FLASH) breath-hold sequence was performed with repetition time 174.9 ms, echo time 4.1 ms and flip angle 80°. For heart, ultrashort scans were made by electrocardiogram (ECG)-triggered, T2-weightted half-single-shot turbo spin-echo (HASTE) sequences (breath hold, repetition time 800 ms, echo time 43.0 ms and acquisition time 20 ms). Liver and kidney images were produced using an axial T1-weighted spin echo sequence. Approximately 40 slices were acquired from the diaphragm to the base of the kidneys. Total body SM and AT volumes were derived from the acquisition of ~40 axial images across the whole body.

All MRI images were segmented manually (TomoVision 4.3 Software; Slice-O-Matic, Montreal, Canada). Each organ and tissue was analyzed by the same observer. Visible AT areas within organ/tissue cross-sectional scans were removed from the cross-sectional area, including the small amount of visible AT within skeletal muscle bundles, so as to obtain an AT-free organ/tissue mass. The intra-observer CVs based on comparison of repeated segmentations were 0.07% for liver, 1.8% for brain, 1.7% for heart and 1.0% for kidneys. The technical errors for measurement of the same scan on two separate days by the same observer of MRI-derived ST and AT volumes are 0.7 ± 0.1% and 1.1 ± 1.2% (mean ± SD), respectively.

The sum of all areas multiplied by the slice thickness and the gaps between slices were used to calculate organ and tissue masses as,

$$\text{organ}∕\text{tissue mass}=d\times (t+g)\times \Sigma \left[\right({\mathrm{S}}_{\mathrm{i}}+{\mathrm{S}}_{\mathrm{i}+1})∕2]$$ (8)

where S is the cross-sectional area of individual organ and tissue; i is the image number; t is the thickness of each image; g is the gap (i.e., distance) between consecutive images; and d is the assumed stable density of individual organ and tissue.

Body composition was measured with a dual-energy X-ray absorptiometry (DXA) scanner (Hologic QDR 4500A, Whaltham, MA, USA, software version V8.26a:3). The between-measurement technical error for fat in the same person is 1.2%. In some subjects adipose tissue and skeletal muscle masses were calculated from DXA-estimation, as previously described (Bosy-Westphal et al., 2004). Adipose tissue mass was predicted from fat mass, assuming a stable fat content of 80% (Snyder et al., 1975). Skeletal muscle mass (in kg) was predicted from appendicular lean-soft tissue (ALST, in kg), SM = 1.13 × ALST − 0.02 × age + 0.61 × sex + 0.97; sex = 0 for women and = 1 for men; R² = 0.96, SEE = 1.58 kg (Kim et al., 2002). In the present project, DXA-predicted SM were significantly correlated with MRI-measured SM in those subjects in whom both DXA and MRI techniques were applied: SM (by MRI) = 1.03 × SM (by DXA) − 2.21; R² = 0.92, SEE = 1.74 kg, n = 54.

Resting Energy Expenditure

The REE measurement protocol details were described in elsewhere (Bosy-Westphal et al., 2003, 2004). In brief, REE was measured by indirect calorimetry with participants in a post-absorptive state. No food or calorie containing beverages were consumed after 7 p.m. until the REE and all body composition tests were completed. REE was measured between 7 a.m. and 9 a.m. in the next morning with subjects resting comfortably on a bed with a plastic transparent ventilated hood placed over their heads for 30 min. Continuous gas exchange measurements (Vmax Spectra 29n, SensorMedics, Bilthoven, Netherlands) were made to analyze the rates of O₂ consumption and CO₂ production. All gas exchange data were collected in a resting awake state at least 8 hrs after physical activity and an environmental temperature of ~25 °C (FAO/WHO/UNU, 2004).

Statistical Methods

Descriptive statistics from the database were expressed as the group mean ± standard deviation (SD). Statistical significance was set at P <0.05. The significance of body composition differences between the men and women was evaluated by Student’s t test. Elia’s Ki values for the 7 organs and tissues were applied to predict REE and to examine the associations between measured REE (REEm) and predicted REE (REEp) with the use of simple linear regression analysis. We explored for bias in the relation between REEm and REEp using the method reported by Bland and Altman (1985). The marginal 95% confidence intervals (CIs) for the seven Ki values were separately predicted in the men and women using simple univariate linear regression analysis (Weisberg, 2005). Data were analyzed by programming in R, version 2.10.0, initially written by Robert Gentleman and Ross Ihaka of Statistics Department, University of Auckland.

RESULTS

Body Composition and Energy Expenditure

The subjects were 106 non-elderly non-obese adults, 49 men and 57 women (Table 1). Body fat mass and %fat were greater in the women than in the men (both P <0.001). In contrast, body mass, height, body mass index (BMI), fat-free mass (FFM) and bone mineral content (BMC) were greater in the men than in the women (all P <0.001).

Table 1.

Subject characteristics and body composition

	Men	Women	P
n	49	57
Age (yrs)	38.6 ± 11.0	33.9 ± 9.3	0.02
Body mass (kg)	81.6 ± 10.6	66.6 ± 9.2	<0.001
Height (m)	1.80 ± 0.06	1.69 ± 0.06	<0.001
BMI (kg/m2)	25.1 ± 2.6	23.2 ± 2.8	<0.001
Fat (kg)	15.3 ± 6.5	20.3 ± 5.9	<0.001
%Fat	19.2 ± 6.2	30.5 ± 6.3	<0.001
Fat-free mass (kg)	66.3 ± 6.5	46.3 ± 5.6	<0.001
BMC (kg)	2.90 ± 0.36	2.31 ± 0.31	<0.001

All values are mean ± SD. P value, t test for significant difference between the men and women.

Abbreviations: %fat, percentage of body mass as fat mass; BMC, bone mineral content; BMI, body mass index.

The masses of four high metabolic rate organs (i.e., liver, brain, heart and kidneys) and three low metabolic rate tissues (i.e., skeletal muscle, adipose tissue and residual mass) for the two genders are presented in Table 2. Adipose tissue mass was greater in the women than in the men (P <0.001). In contrast, the masses of rest six organs and tissues were greater in the men than in the women (all P <0.001).

Table 2.

Major organ/tissue masses and whole-body resting energy expenditure

	Men	Women	P
Liver (kg)	1.54 ± 0.26	1.27 ± 0.18	<0.001
Brain (kg)	1.40 ± 0.08	1.26 ± 0.09	<0.001
Heart (kg)	0.37 ± 0.07	0.26 ± 0.06	<0.001
Kidneys (kg)	0.32 ± 0.05	0.26 ± 0.05	<0.001
Skeletal muscle (kg)	32.4 ± 3.7	21.5 ± 3.2	<0.001
Adipose tissue (kg)	17.1 ± 6.2	21.4 ± 5.7	<0.001
Residual mass (kg)	28.5 ± 4.3	20.7 ± 3.0	<0.001
REEm (kcal/day)	1780 ± 188	1407 ± 137	<0.001
REEp (kcal/day)	1789 ± 157	1409 ± 137	<0.001
REEm – REEp (kcal/day)	−9 ± 91	−2 ± 74	0.66
REE/BM (kcal/kg per day)	21.9 ± 1.7	21.3 ± 2.1	0.10

All values are mean ± SD. P value, t test for significant difference between the men and women. There were no significant differences between REEm and REEp (paired Student’s t test, P = 0.49 for the men and P = 0.86 for the women).

Abbreviations: REE/BM, mass-specific basal metabolic rate; REEm, resting energy expenditure measured by indirect calorimetry; REEp, resting energy expenditure predicted by equation 3.

The measured REE for the men and women are presented in Table 2. There were significant differences in REEm between the two groups (mean ± SD; men 1780 ± 188 kcal/day vs. women 1407 ± 137 kcal/day; P <0.001).

Mass-specific basal metabolic rates (i.e., the ratio of REE to body mass, REE/BM) are presented in Table 2. There were no significant differences in REE/BM between the men and women (21.9 ± 1.7 vs. 21.3 ± 2.1 kcal/kg per day, P = 0.10).

Evaluation of Ki Values

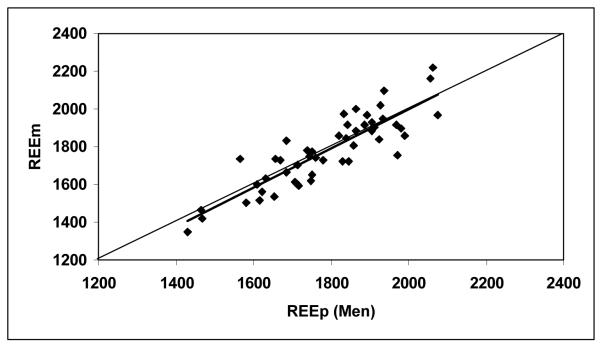
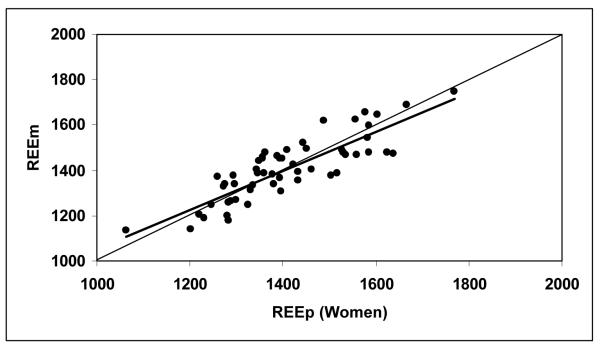
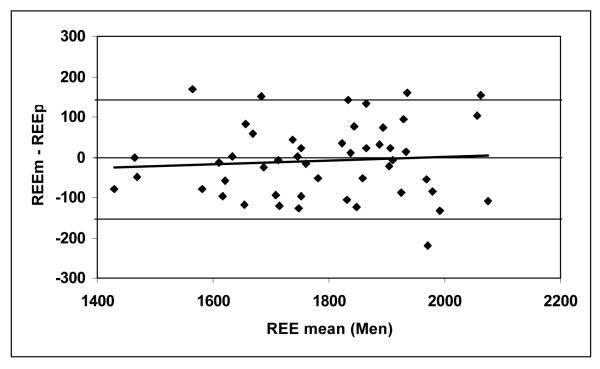
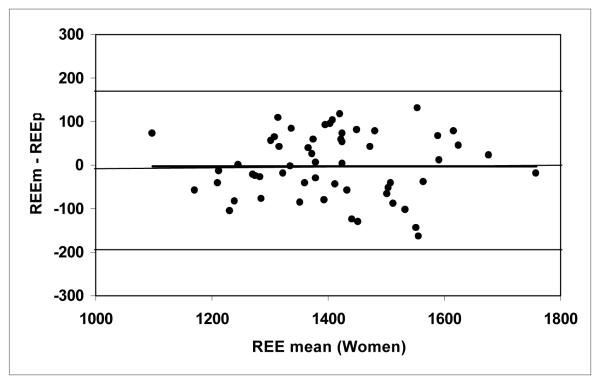
According to equation 3, the predicted REE were calculated as 1789 ± 157 kcal/day for the men and 1409 ± 137 kcal/day for the women (Table 2). Figures 1a and 1b show correlations between REEm and REEp in the men (r = 0.874) and women (r = 0.855, both P <0.001). There were no significant differences between REEm and REEp (paired Student’s t test, P = 0.49 for the men and P = 0.86 for the women). The mean differences between REEm and REEp (i.e., REEm – REEp) were −9 ± 91 kcal/day for the men and −2 ± 74 kcal/day for the women, respectively. Bland-Altman plots (Figures 2a and 2b) show that there are no significant trends between the measured and predicted REE differences versus the average of REEm and REEp for the men (r = 0.075) and for the women (r = 0.001, both P >0.50), respectively.

Figure 1a.

Measured resting energy expenditure (REEm, in kcal/day) versus predicted REE (REEp, in kcal/day) for the men (Figure 1a) and women (Figure 1b). REEp were calculated from the Ki values suggested by Elia (1992), according to equation 3. The lines of identity are shown.

REEm = 1.044 × REEp − 87.1, r = 0.874, P <0.001, n = 49 men.

Figure 1b.

Measured resting energy expenditure (REEm, in kcal/day) versus predicted REE (REEp, in kcal/day) for the men (Figure 1a) and women (Figure 1b). REEp were calculated from the Ki values suggested by Elia (1992), according to equation 3. The lines of identity are shown.

REEm = 0.855 × REEp + 201.7, r = 0.855, P <0.001, n = 57 women.

Figure 2a.

The difference between measured and predicted resting energy expenditure (REEm – REEp, in kcal/day) versus the mean of REEm and REEp for the men (Figure 2a) and women (Figure 2b). REEp was calculated from the Ki values suggested by Elia (1992), according to equation 3. The zero difference lines are shown.

(REEm – REEp) = 0.044 × REE mean − 87.1; r = 0.075, P >0.50; n = 49 men. The lines representing 2SDs for the REE differences (−149, 146 kcal/day) are shown.

Figure 2b.

The difference between measured and predicted resting energy expenditure (REEm – REEp, in kcal/day) versus the mean of REEm and REEp for the men (Figure 2a) and women (Figure 2b). REEp was calculated from the Ki values suggested by Elia (1992), according to equation 3. The zero difference lines are shown.

(REEm – REEp) = 0.0007 × REE mean − 2.7; r = 0.001, P >0.50; n = 57 women. The lines representing 2SDs for the REE differences (−192, 174 kcal/day) are shown.

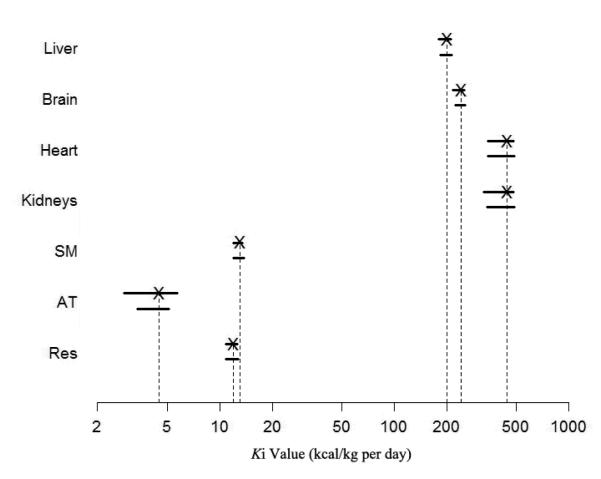
The 95% CIs of each Ki value are presented in Table 3. Elia’s Ki values are located within the 95% CIs for all of the seven organs and tissues for both men and women (Figure 3). The gender-adjusted coefficients of Elia’s Ki values were G = 0.995 (P = 0.52) for the men and G = 0.997 (P = 0.71) for the women. Both of the coefficients were not significantly different from 1.

Table 3.

Specific metabolic rates and 95% confidence intervals for major organs and tissues

Organ/Tissue	Elia’s Ki value	95% Confidence Intervals of Ki and P values
		Men	Women
Liver	200	(179, 213) P = 0.61	(183, 214) P = 0.82
Brain	240	(216, 253) P = 0.56	(223, 254) P = 0.85
Heart	440	(342, 481) P = 0.41	(342, 488) P = 0.49
Kidneys	440	(325, 484) P = 0.38	(339, 491) P = 0.51
Skeletal muscle	13	(11.9, 13.5) P = 0.48	(12.0, 13.8) P = 0.74
Adipose tissue	4.5	(2.83, 5.71) P = 0.75	(3.82, 5.14) P = 0.59
Residual mass	12	(10.8, 12.6) P = 0.54	(10.9, 12.8) P = 0.70

All units of Ki values are in kcal/kg per day. P, P-value of testing H0: Ki equals to the coefficient suggested by Elia.

Figure 3.

The 95% confidence intervals (CIs) for the Ki values of seven organs and tissues, fitted by stepwise univariate analysis are shown on a logarithmic scale. The upper line is for the men, and the lower line is for the women. The Xs represent the Ki values suggested by Elia (1992). Abbreviations: AT, adipose tissue; Res, residual mass; SM, skeletal muscle.

DISCUSSION

Body composition and physiological functions, including organ/tissue masses and REE, differ significantly between men and women (FAO/WHO/UNU, 2004). However, it is unknown whether gender influences the specific resting metabolic rates of individual organs and tissues. To our knowledge, the present study is the first exploration of potential gender difference in Ki values.

There are several possible approaches that could be used to compare Ki value differences between men and women. The Ki value of an organ can be estimated in vivo by measuring the arteriovenous difference in O₂ concentration across the organ combined with the assessment of blood flow perfusing the organ and the organ mass. Positron emission tomography (PET) with ¹⁵O or ¹¹C markers may allow for in vivo quantification of organ/tissue energy expenditure (Gallagher, 2005). However, this approach is usually impractical in humans as it requires invasive procedures such as arterial and venous catheterization.

In theory, another approach might be applied. According to the mechanistic REE model (i.e., equation 1), there are three inter-related model variables, REE, Ki and Ti. With REE as the dependent variable and Ti as predictors, the Ki values might be predicted using multiple linear regression analysis. However, due to the high collinearity among some organs and tissues (e.g., the collinearity between heart and kidneys), multiple linear regression analysis produced unstable results when applied in the present database. Specifically, the standard errors for the resulting estimators of Ki values were exceptionally large, so that the resulting 95% CIs provided little information on the true Ki values.

Based on the reported experimental results in humans and other mammals, Elia presented an excellent review on the Ki values for seven organs and tissues in the Reference Man (Elia, 1992; Snyder et al., 1975). According to the mechanistic organ-tissue level model, REE = Σ (K_i × T_i), REE can be predicted from the measured organ/tissue masses and Elia’s Ki values. A REEm – REEp approach was then applied to compare the applicability of Elia’s Ki values. If the REEm – REEp difference is close to zero, one may consider that Elia’s Ki values are applicable in this group. According to the existing database of the current study, the REEm – REEp differences (men, −9 ± 91 kcal/day; women, −2 ± 74 kcal/day) were not significant different from zero. In addition, there were significant correlations between REEm and REEp in both men and women (Figures 1a and 1b). Moreover, Bland-Altman plots showed that there were no significant trends between REEm – REEp vs. the average of REEm and REEp for the two gender groups (Figures 2a and 2b). These observations suggest that Elia’s Ki values, as a whole, are applicable in both non-elderly non-obese men and women.

In order to further evaluate the applicability of Elia’s Ki values in men and women, a new approach was applied in the present study that combines a mechanistic REE model with stepwise univariate analysis. Our results showed that each Elia’s Ki value of the seven organs and tissues was located within the 95% CIs for both the men and women (Figure 3). In addition, there is no need to adjust Elia’s Ki values because the gender-adjusted coefficients were not significantly different from 1 for both men (G = 0.995; P = 0.52) and women (G = 0.997; P = 0.71).

All of the above observations validated the applicability of Elia’s Ki values in non-elderly non-obese men and women. The question thus arises: whether or not the Ki values suggested by Elia are applicable in children, adolescents, elderly adults with normal-weight or overweight? We are now exploring the potential influence of age and adiposity on the Ki values of individual organs and tissues.

In conclusion, although there are significant gender differences in REE and organ/tissue masses, the differences in the Ki values are negligible between non-elderly non-obese men and women.