QUANTITATIVE CEREBRAL BLOOD FLOW IN DYNAMIC SUSCEPTIBILITY CONTRAST MRI USING TOTAL CEREBRAL FLOW FROM PHASE-CONTRAST MRA

Abstract

Dynamic susceptibility contrast magnetic resonance imaging (DSC-MRI) during bolus injection of gadolinium (Gd) contrast agent is commonly used to investigate cerebral hemodynamics. The large majority of clinical applications of DSC-MRI to date have reported relative CBF values due to dependence of the result on the accuracy of determining the arterial input function (AIF), the robustness of the singular value decomposition (SVD) algorithm, and others. We propose a calibration approach that directly measures the total (i.e. whole brain) cerebral blood flow (tCBF) in individual subjects using phase-contrast (PC) magnetic resonance angiography (MRA). The method was applied to data from 11 patients with intracranial pathology. The sum of squares variance about the mean (uncorrected: white matter =105.6, gray matter=472.2; corrected: white matter=34.1, gray matter=99.8) after correction was significantly lower for white matter (p=0.045) and for gray matter (p= 0.011). The mean gray and white matter CBF in the contralateral hemisphere were not significantly altered by the correction, however. The proposed PC-MRA calibration technique appears to be one of the most direct correction schemes available for DSC-MRI CBF values and can be performed rapidly, requiring only a few minutes additional scan time.

INTRODUCTION

Dynamic susceptibility contrast magnetic resonance imaging (DSC-MRI) during bolus injection of gadolinium (Gd) contrast agent is commonly used to investigate cerebral hemodynamics in diseases such as stroke, brain tumors and other disorders (1). Ideally, for patients with cerebrovascular disease, DSC-MRI data should be analyzed to produce quantitative maps of cerebral blood flow (CBF) (2,3). However, the calculation of ‘absolute’ CBF using DSC-MRI is difficult because of numerous factors that may cause bias or error. The most commonly used approach uses singular value decomposition (SVD) to estimate CBF by deconvolution of the arterial input function (AIF), which is typically measured from pixels selected in the vicinity of the middle cerebral artery (MCA) (2,3). The reliability of the resulting CBF depends critically on the accuracy of determining the AIF, and the robustness of the SVD algorithm. The AIF can vary because of partial volume effects with surrounding tissue due to the limited spatial resolution of DSC-MRI, and there may also be errors due to variations in individual microvascular hematocrit (4). In addition, there may be other errors associated with potential non-linear relationships between the contrast agent concentration and changes in measured relaxation times (R₂ or R₂*), arterial signal saturation at high concentrations, and local geometric image distortions during the bolus passage (5,6). Finally, CBF estimates may also be sensitive to bolus arrival delay and dispersion between the location where the AIF is measured and the brain, although optimized SVD algorithms have been developed to mitigate the delay problem (7).

For these reasons, the large majority of clinical applications of DSC-MRI to date have reported either relative CBF values, or other hemodynamic indices such as mean transit time (MTT), relative cerebral blood volume (CBV) or time-to-peak (TTP). Typically, relative CBF values are referenced relative to normal-appearing white matter or cerebellum, or post-hoc corrections are applied to scale the relative CBF maps such that the flow measurements obtained are in the known physiological range from studies of normal volunteers using PET and MRI techniques (8). However, even after correction based on normal population average CBF values, both over- and under-estimation of CBF may still occur. Assumption of a “normal” white matter flow value will most likely lead to systematic errors, since white matter CBF may vary from individual to individual, and as a function of age. There is increasing interest in the literature in obtaining quantitative CBF measurements (qCBF), for example after three-point estimation technique on a Look-Locker EPI scan using the bookend method (9). In general, it is difficult to validate these new qCBF methods to the reference standard, [¹⁵O]-H₂ positron emission tomography (PET); and existing literature commonly uses consistency of obtained qCBF measurements with historical reference values and clinical reproducibility as alternatives for validation (9,10). A major impediment to the dissemination of existing qCBF techniques is the use of non-standard MR imaging protocols, the often complex postprocessing and need of specialized software (9–12).

This manuscript proposes a calibration approach that directly measures the total (i.e. whole brain) cerebral blood flow (tCBF) in individual subjects using phase-contrast (PC) magnetic resonance angiography (MRA). The tCBF value from PC-MRA is used to calibrate the DSC-MRI CBF maps. The method, which measures tCBF from the internal carotid and vertebral arteries (which provide 100% of the blood supply to the brain), was applied to 11 patients with intracranial pathology. The PC-MRA calibration technique appears to be one of the most direct correction schemes available for DSC-MRI CBF values and can be performed rapidly, requiring only a few minutes additional scan time.

METHODS

Outline of the calibration procedure

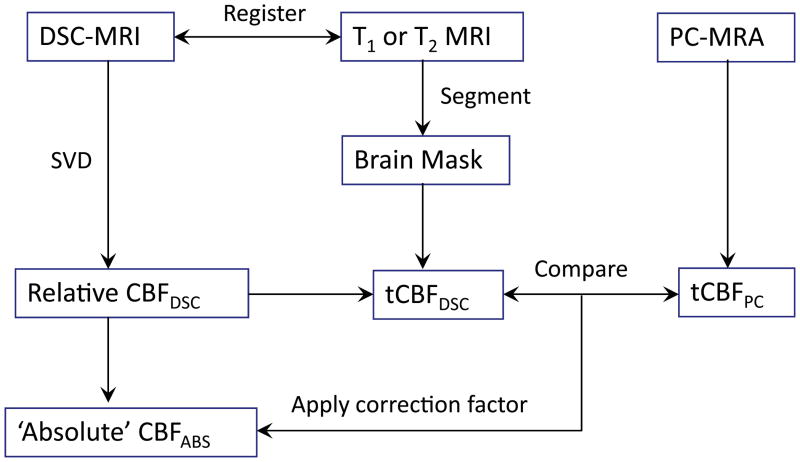
The data processing algorithm for the proposed method is schematically illustrated in Figure 1. In addition to the regular DSC-MRI acquisition, an additional cardiac-gated phase-contrast MRA of the internal carotid and vertebral arteries is required, as well as a suitable sequence (in this case T₂-weighted, but other sequences (e.g. T₁-weighted) could be used) in order to segment the images into brain (‘brain mask’) and non-brain pixels. The DSC-MRI source images themselves could also be used for this purpose, although they are not optimal in terms of contrast or resolution.

Figure 1.

Schematic diagram of the data processing scheme for calibration of CBF_DSC maps to produce ‘absolute’ cerebral blood flow.

Initial processing steps include registration of DSC-MRI images to the series used for segmentation. After the AIF is determined (see below), maps of relative CBF (CBF_DSC) are then produced using SVD, which are then summed over all brain pixels (determined from the brain mask) to determine tCBF_DSC. The PC-MRA data are processed to measure tCBF_PC, based on the sum of flow through left and right vertebral and internal carotid arteries. In each patient, a calibration factor (C) is then determined from

$$C=\frac{{\mathit{tCBF}}_{PC}}{{\mathit{tCBF}}_{\mathit{DSC}}}$$ [1]

which can be applied to the relative CBF_DSC maps in order to produce maps of ‘absolute’ CBF_ABS.

MRI protocol

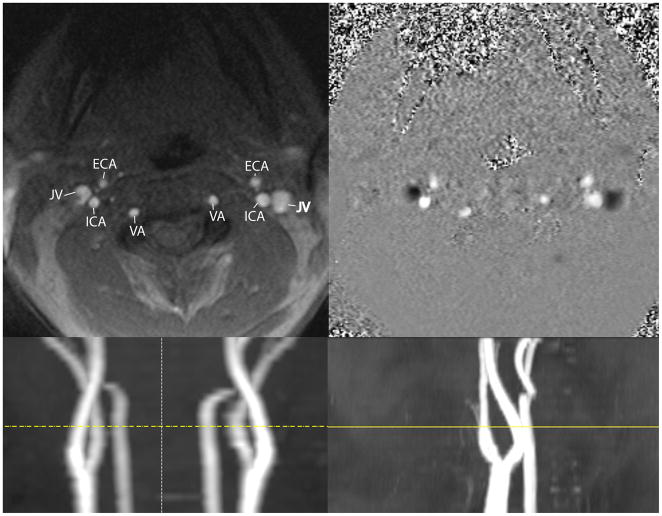
MRI scanning was performed on a Siemens Trio scanner (Siemens, Erlangen, Germany) at 3 Tesla using the standard head coil. All patients underwent axial T₂ weighted MRI, DSC-MRI using single-shot gradient-echo echo-planar imaging (EPI) during bolus injection of 0.1 mmol/kg gadolinium based contrast agent (‘Multihance’, Bracco) into the antecubital vein, and a retrospective cardiac-gated 2D PC-MRA of the upper neck with a velocity encoding (v_enc) gradient of 70 cm/sec (other sequence details are given in Table 1). Rapid vascular scout images of the neck were also acquired, in order to help plan the slice location of the 2D PC-MRA, which was placed above the carotid bulb and angulated in order to be perpendicular to both left and right vertebral and internal carotid arteries (Figure 2).

Table 1.

MRI Pulse sequence Parameters.

	Sequence
	Turbo spin echo T2	Gradient echo EPI DSC	2D FLASH PC-MRA
TR (msec)	8850	1614	49
TE (msec)	99	45	7.7
Flip Angle	90	90	15
Number of Slices	89	18	1
Number of Phases	-	50	32
Slice thickness/gap	89/0	5/2.5	5
FOV	224 × 178	230 × 230	138 × 138
Matrix	448 × 355	128 × 128	256 × 256
Pixel Size (mm)	0.5 × 0.5 × 2.0	1.8 × 1.8 × 5.0	0.5 × 0.5 × 5.0
Approx Scan Time	2 min 30 sec	1 min 20 sec	~ 1 min 15 sec*

Notes:

^*Cardiac gated, venc = 70 cm/sec, exact scan time depends on heart rate and retrospective gating efficiency.

Figure 2.

Upper: Left panel: Magnitude PC-MRA axial single slice (5 mm thickness) demonstrating a typical phase MRA contrast examination. Major vessels are labeled: ECA=external carotid artery, JV=jugular vein, ICA=internal carotid artery, VA=vertebral artery. Image position is above the carotid bulb at the level of the transverse foraminal vertebral artery. Right panel: phase data displayed in gray scale, velocity encoding was 70 cm/sec. Slice location is the same as in the left panel. The jugular veins demonstrate caudal flow, which is encoded as negative values (dark), while the cranial flow is encoded with positive values. Lower: The slice location (yellow line) is depicted on coronal (left) and sagittal (right) vascular scout images.

Image processing – DSC-MRI

Post-processing of the DSC-MRI data was performed using ‘Penguin’ software (Aarhus University Hospital) which provides an implementation of the standard singular value decomposition (sSVD) method (2,3,13–16) to calculate the regional cerebral blood flow maps from the DSC-MRI raw data. A semiautomatic approach for the selection of the arterial input function was used, in which the slice at the level of the proximal middle cerebral artery (MCA) was chosen. An automated algorithm detected candidate voxels based on the signal curve shape and maximum signal decrease. Voxels compatible with the MCA location were then selected manually in the hemisphere contralateral to the pathology and the average of the concentration-time curves used as the global AIF (17).

Non-brain voxels in the sSVD output maps were extracted using a brain mask derived from the high-resolution T₂ weighted axial data, which were co-registered to the DSC-MRI raw data using Statistical Parametric Mapping software (‘SPM’, Wellcome Trust Centre for Neuroimaging). We used 12-parameter affine coregistration between the high resolution T₂ weighted image and the unenhanced initial volume of the perfusion dataset which was upsampled to match the higher resolution T2W image using trilinear interpolation. The coregistered T2W image was then segmented into gray and white matter probabilistic maps. A total brain mask was generated from the gray and white matter probabilistic maps by summation of all voxels. The total cerebral blood flow (tCBF), in units of ml/min, was calculated from

$${\mathit{tCBF}}_{\mathit{DSC}}={\rho }_B·V_{\mathit{voxel}}\sum _{z=1}^{mz}\sum _{y=1}^{my}\sum _{x=1}^{mx}{\mathit{CBF}}_{\mathit{DSC}}(x,y,z)$$ [2]

where ρ_B is the density of brain tissue in g/ml, V_voxel is the voxel volume (ml) defined as the in-place resolution times the inter-slice spacing; mx, my and mz are the matrix dimensions and CBF_DSC(x,y,z) is the CBF measurement in pixel (x,y,z) in units of ml/g/min.

Image processing – PC-MRA

PC-MRA data were analyzed using ‘Qflow’ software (MEDIS, Leiden, Netherlands) (18,19) to determine the total cerebral blood flow as the sum of the blood volumetric flow rate of the 4 neck vessels (tCBF_PC). Center points in the four vessels comprising both internal carotid arteries and both vertebral arteries were selected manually. A contour detection algorithm then automatically detected the vessel boundaries in the frame in which the points where selected and automatically propagated the contours to adjacent time frames, adjusting the contours according to dynamic changes of the vessel positions, shapes and luminal diameters. The reproducibility of this method has been previously assessed to be excellent, with intra- and inter-observer reproducibility having coefficients of variation of less than 2% in the aorta and 7.1% in the evaluation of CBF with cardiac triggering (19–21). Total CBF was calculated using the summation

$${\mathit{tCBF}}_{PC}=\frac{60}{RR}\sum _i^{\mathit{vessels}}\sum _k^{\mathit{phases}}\mathrm{\Delta }t·\nu (i,k)·A(i,k)$$ [3]

where RR is the duration of one heart cycle, i is the index of the vessel, k is the index of the phase in the heart cycle, Δt is the time interval between two phases, ν(i,k) is the velocity measured in vessel i during phase k, and A(i,k) is the cross-sectional area of vessel i during phase k. In fact, the numerical integration represented by the above formula was carried out using the trapezoid rule approximation for numerical integration.

Calculation of ‘absolute’ CBF maps

The correction factor C for calibration of the CBF_DSC maps was calculated in each subject using equation [1], and the ‘absolute’ CBF maps were then calculated from

$${\mathit{CBF}}_{\mathit{abs}}(x,y,z)=C\times {\mathit{CBF}}_{\mathit{DSC}}(x,y,z)$$ [4]

Determination Of Contralateral Hemispheric Gray And White Matter CBF

For the purpose of assessment of the data quality after correction, it was hypothesized that the gray and white matter in the hemisphere contralateral to the lesion would be unaffected by the pathological process, and is therefore expected that their CBF values be close to the normal values in the literature.

The gray and white matter probabilistic maps which were calculated for the calibration contain voxelwise probabilities for the respective voxels containing the respective tissue. The voxelwise values from the gray and white matter probabilistic maps add to 100% in brain tissue. To determine an estimate for CBF in “pure” gray and white matter, only contralateral voxels which had a probability of 95% or greater to belong to either gray or white matter were included. To avoid contribution of the higher flow from basal ganglia and interfaces between gray and white matter on the average white matter CBF measurement, the white matter mask was eroded using a binary edge removal algorithm with a 3×3 neighborhood. The cerebellum and regions near air interfaces, such as portions of the temporal lobes and the inferior temporal lobes which contained EPI artifacts were avoided. As a result, the obtained “pure” segmented CBF measurements contained only data distant enough from gray-white matter interfaces, brain-cerebrospinal fluid (CSF) interfaces or air-tissue interfaces to be unaffected by partial volume artifact, and we did not include tumor tissue. The use of a subset of the segmented gray and white matter probabilistic maps is valid because an average measurement is sought, and not, as in the case of the calibration, an absolute measurement, the latter of which necessitates the inclusion of the entire volume.

The accuracy of the segmentation based on T₂ weighted axial images was compared to the more commonly used approach of T₁ weighted image segmentation. Sagittal T₁ weighted images acquired during the study were segmented using SPM and postprocessed similarly to the T₂ weighted data. Finally, the estimated total brain volume after segmentation using T₁ and T₂ weighted data were compared.

Subjects

The study was approved by the local institutional internal review board. In order to avoid giving gadolinium contrast agent to normal control subjects, instead the PC-MRA sequence was added on to examinations of patients who were already receiving a DSC-MRI study as part of their routine clinical evaluation. Fifteen consecutive patients underwent MR imaging including DSC-MRI perfusion imaging during their clinical evaluation for brain pathology. Four patients were excluded from the subsequent analysis due to either incorrect placement or angulation of the PC-MRA slice location, or due to exclusion of portions of the rostral brain on DSC-MRI (i.e. lack of whole brain coverage). Eleven patients between the ages of 21 and 76 years (median 50 years, 45.4±17.7 mean ± standard deviation) were included in the study. 10 patients were diagnosed with brain tumors, while one patient had an aneurysm of the right internal carotid artery (Table 2).

Table 2.

Patient characteristics.

Patient	Gender	Age	Pathology
1	m	29	Anaplastic astrocytoma (WHO grade III)
2	m	27	Metastatic embryonal carcinoma (primary: testicular cancer)
3	f	23	Oligodendroglioma (WHO grade II)
4	f	54	Glioblastoma multiforme (WHO grade IV)
5	m	57	Meningioma (WHO grade I)
6	f	59	Right para-ophthalmic ICA aneurysm, no brain parenchymal abnormality
7	f	50	Anaplastic oligodendroglioma (WHO grade III)
8	f	21	Astrocytoma (WHO grade II)
9	f	76	Glioblastoma multiforme (WHO grade IV)
10	f	53	Diffuse astrocytoma (WHO grade II)
11	m	50	Oligodendroglioma (WHO grade II)

Abbreviations: WHO: World Health Organization; m: male; f: female

The area under the AIF curve (AUC) was determined in all cases, and the hematocrit (hct) measurement closest to the MRI examination (median 38 days between hct measurement and MRI examination) obtained, to examine for any possible dependency of the correction factor on these measurements.

The brain mask used to calculate tCBF_DSC was inspected, and manually edited if necessary. Editing was rarely necessary in cases where few voxels in the location of an intra-axial tumor that had not segmented as gray or white matter needed to be manually included. Only in one case was significant editing performed, namely, in an extra-axial meningioma, the tumor was deliberately excluded from the mask since it was located in the middle cranial fossa and along the sphenoid wing. From the neuroangiographic literature it is known that meningiomas in this location are predominantly supplied by branches of the middle meningeal artery (MMA) which is a branch of the external carotid artery (ECA), and therefore do not share a common blood supply with the brain. This meningioma was subsequently resected and found to have been completely devascularized after surgical intraoperative extradural devascularization procedure, excluding the possibility of pial supply, which is seen in some meningiomas. The exclusion of the meningioma from the brain mask and tCBF calculation in this case therefore is highly justified. All other tumors were completely included in the tCBF calculation.

Statistical Analysis

It was hypothesized that uncorrected CBF_DSC values in normal appearing brain (i.e. brain contralateral to the lesions) would be both over- and under-estimated due to the factors mentioned in the introduction, and that applying the correction factor would reduce the standard deviation of gray- and white-matter contralateral CBF values between subjects. Implicit in this hypothesis is that CBF contralateral to the lesion is relatively unaffected by the presence of the lesion, so that only small patient-to-patient differences are expected.

Results of corrected and uncorrected gray and white matter CBF values were compared with literature values (8,22). An F-test was used to determine if the variance in contralateral hemispheric gray and white matter CBF was significantly reduced after correction. Paired Student’s t-test was used to determine if the mean CBF was different between gray and white matter before and after correction.

Reproducibility Analysis

To investigate the reproducibility of the post-processing analysis procedures, steps which required manual operator intervention (choice of AIF for SVD, and determination of tCBF_PC from the PC-MRA data) were repeated 4 times, and coefficients of variation (CV) calculated.

RESULTS

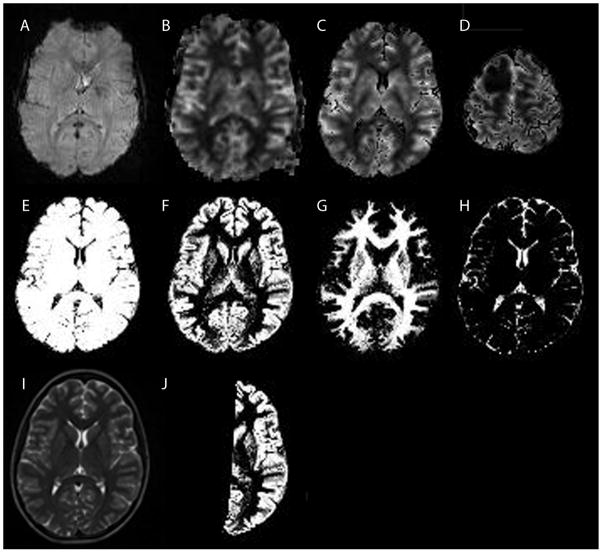
An example of the PC-MRA data is given in Figure 2, showing the locations of the vertebral arteries (VA) and internal carotid arteries (ICA) used to determine tCBF_PC. Figure 3 demonstrates DSC-MRI data from one patient with a right frontal astrocytoma (WHO grade II) (3D). DSC-MRI raw data (3A) were used to generate the output CBF_DSC map (3B). The T₂ weighted sequence (I) was used to generate gray (3F) and white matter (3G) probabilistic maps (as well as a CSF map (3H)), from which the brain mask (3E) was generated as described above and used to generate CBF_DSC maps after removal of non-brain voxels (3C). Figure 3J shows an example of a contralateral hemispheric gray matter probabilistic map that was used to generate the average gray matter CBF value. A similar mask (not shown) was used to calculate average contralateral white matter CBF.

Figure 3.

Example DSC-MRI and segmentation data in a patient with a grade II right frontal astrocytoma. A: A raw data GRE-EPI image acquired at t=0 before contrast administration. B: Cerebral blood flow map generated from the raw data using standard singular value decomposition. The image was thresholded to exclude extracerebral tissues, while avoiding to exclude cerebral tissue. Some extracerebral tissue could not be removed with this simple threshold approach. C: Cerebral blood flow map after the brain mask (E) was applied. Extracerebral tissues are no longer included. This dataset was used to calculate total cerebral blood flow from the DSC-MRI data. D: Same as C, but more superior slice location showing the right frontal lesion. E: Brain mask generated from the brain segmentation, used to improve the removal of extracerebral tissues (C and D). F: Gray matter segmented image. G: White matter segmented image. H: CSF segmented image. I: T2 weighted image used as input to the segmentation algorithm. J: Gray matter brain mask of the hemisphere contralateral to the brain tumor. A similar mask was generated for the white matter (not shown). Hemispheric masks were used to calculate the regional tissue perfusion in normal appearing gray and white matter.

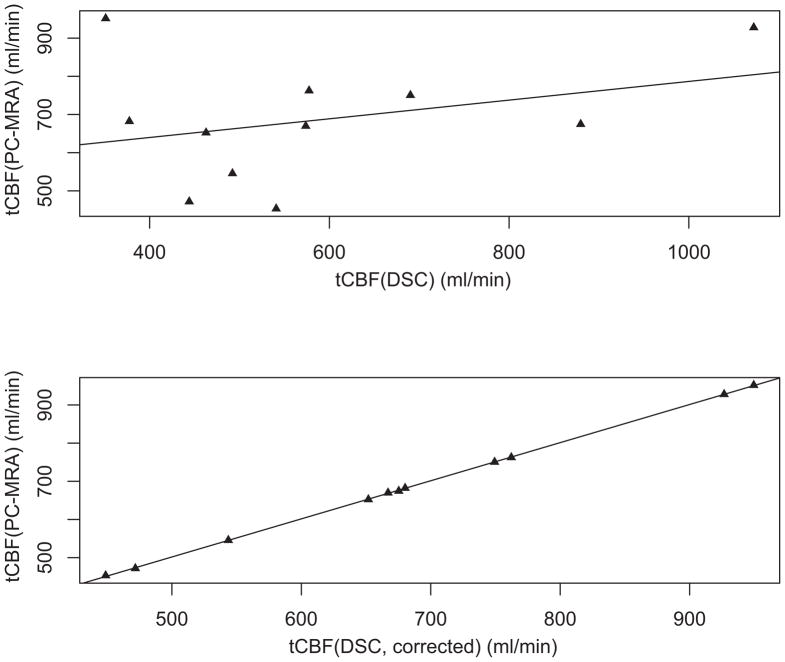
Figure 4 shows a plot of tCBF determined by (uncorrected) DSC-MRI and PC-MRA. It can be seen that there is little correlation between uncorrected tCBF_DSC and tCBF_PC (r² = 0.110), suggesting both over- and under-estimation of tCBF using DSC-MRI. The correction factors (C) determined from equation 1 for each patient are given in Table 3.

Figure 4.

Scatterplots of the total cerebral blood flow (tCBF) measured by DSC-MRI (abscissa) before (upper panel) and after (lower panel) calibration versus tCBF determined from PC-MRA (ordinate). There is poor correlation between tCBF measured by DSC-MRI and PC-MRA before calibration (Pearson’s r²=0.110). After calibration, the tCBF represented in the three-dimensional CBF images is identical to the PC-MRA measurements.

Table 3.

Cerebral Blood Flow Measurements And Related Variables.

Pt	C, mean± SD (CV%)	AUCAIF	#p	Hct	tCBFPC, mean± SD (CV%)	tCBFDSC, mean± SD (CV%)
						Uncorrected	Corrected
1	1.416±0.120 (8.4%)	0.628	7	49.4	652.4±1.5 (0.2%)	462.8±41.1 (8.9%)	651.8±1.5 (0.2%)
2	1.105±0.032 (2.9%)	0.623	3	36.3	545.6±4.9 (0.9%)	492.1±13.6 (2.8%)	543.6±4.9 (0.9%)
3	1.805±0.089 (4.9%)	0.628	7	42.1	682.2±4.5(0.7%)	377.4±17.9 (4.7%)	680.2±4.5 (0.7%)
4	1.064±0.046 (4.4%)	0.575	7	34.8	471.8±0.8 (0.2%)	444.0±19.5 (4.4%)	471.8±0.8 (0.2%)
5	0.768±0.024 (3.2%)	0.601	6	31.5	674.6±2.7 (0.4%)	879.7±27.2 (3.1%)	675.3±2.7 (0.4%)
6	2.706±0.054 (2.0%)	0.538	7	42.2	951.7±4.7 (0.5%)	351.0±6.8 (1.9%)	949.6±4.6 (0.5%)
7	0.830±0.026 (3.1%)	0.623	7	32.4	453.2±13.1 (2.9%)	540.8±6.4 (1.2%)	448.8±13.0 (2.9%)
8	1.164±0.043 (3.7%)	0.620	3	33.6	669.8±8.3 (1.2%)	573.7±19.3 (3.4%)	667.0±8.2 (1.2%)
9	1.320±0.014 (1.1%)	0.638	6	39.7	762.5±4.0 (0.5%)	577.4±5.5 (1.0%)	762.2±4.0 (0.5%)
10	0.866±0.055 (6.4%)	0.563	7	42.9	927.9±16.8 (1.8%)	1,072.2±66.3 (6.2%)	926.7±16.8 (1.8%)
11	1.086±0.030 (2.8%)	0.558	4	40.8	750.5±2.5 (0.3%)	690.2±19.0 (2.8%)	749.3±2.5 (0.3%)

Abbreviations: Pt, Patient; C, Correction Factor; AIF, arterial input function; AUC_AIF, area under the AIF curve (arbitrary units); #p, number of pixel samples to generate AIF; Hct, Hematocrit measurement closest to MR examination; tCBF, total cerebral blood flow; tCBF_PC, tCBF determined with phase-contrast MRA; tCBF_DSC, tCBF determined with dynamic susceptibility contrast MRI; SD, standard deviation; CV%, coefficient of variation (SD/mean).

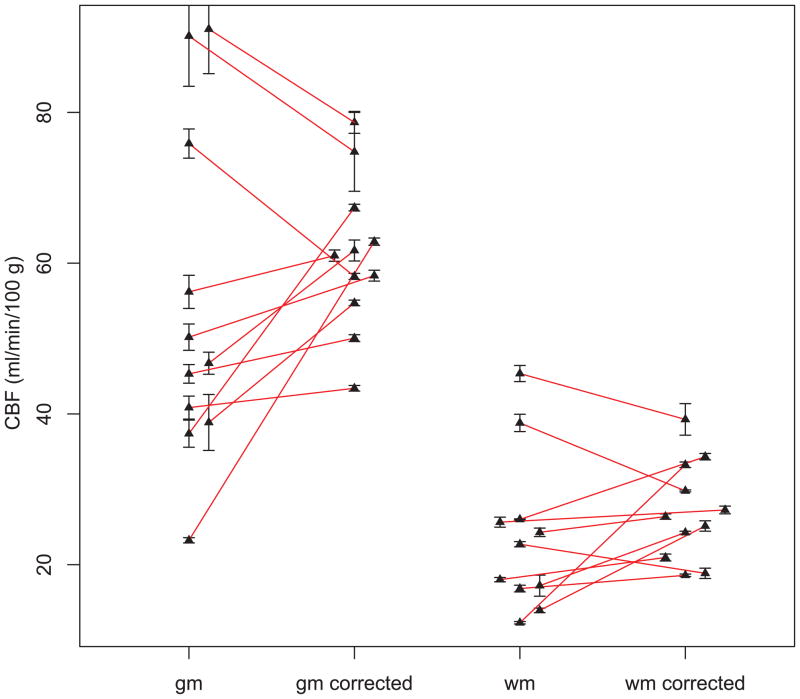
Figure 5 shows CBF_DSC maps after correction in the patient with a right frontal meningioma. Uncorrected CBF_DSC maps (not shown) showed slightly elevated average CBF values (76.4 mL/100gm/min for gray matter, and 38.5 mL/100gm/min for white matter) over accepted literature values (8,22). After calibration using the PC-MRA derived correction factor, the figure demonstrates white matter and gray matter CBF in a range consistent with the literature (average of 57.8 mL/100gm/min in gray matter and 29.2 mL/100gm/min in white matter) (8,22,23). Contralateral hemisphere CBF_DSC values for gray and white matter before and after correction for all eleven patients are shown in Figure 6. The spread of the data around the mean is considerably decreased (more than a factor of 2 for gray matter) after correction (Table 4). Statistical analysis reveals that the sum of squares variance about the mean (uncorrected: white matter =105.6, gray matter=472.2; corrected: white matter=34.1, gray matter=99.8) after correction was significantly lower (p=0.045) for white matter, and significantly lower (p= 0.011) for gray matter (F-test, Table 4). The mean gray and white matter CBF in the contralateral hemisphere were not significantly changed by the correction (paired T-tests were not significant, Table 4).

Figure 5.

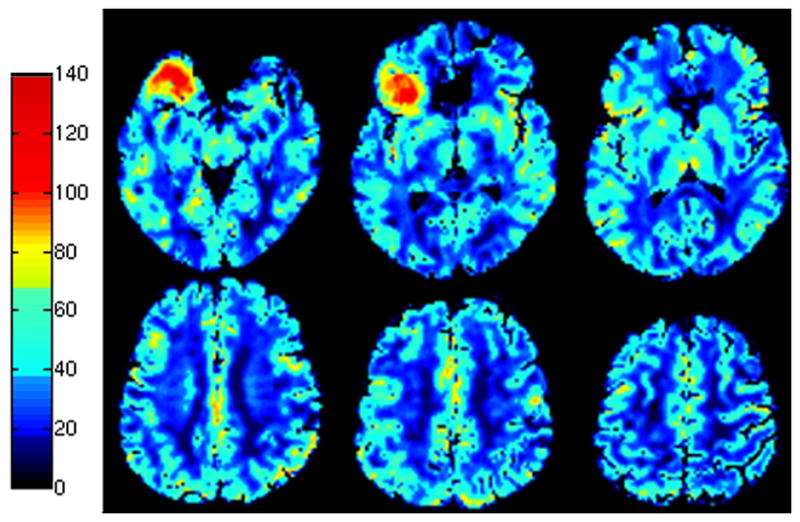
Selected corrected DSC-MRI CBF maps in a patient with a right frontal meningioma. Images are depicted in pseudocolor according to the colorscale on the left. Measurements are in ml/100 g/min. CBF maps demonstrate that after correction gray and white matter perfusion are in accordance with literature values. The highly vascular meningioma is seen in the right frontal lobe. This extra-axial tumor is supplied by external carotid artery branches and therefore was manually excluded from the voxel-based tCBF calculation.

Figure 6.

Uncorrected and corrected gray (gm) and white (wm) matter average CBF values measured with DSC-MRI. The spread of the data points is larger before correction for both gray matter and white matter. Error bars indicate the standard deviation of the data between individual measurements in the reproducibility analysis.

Table 4.

Average whole brain CBF, and gray and white matter CBF in the contralateral hemisphere before and after calibration

Contralateral Hemisphere	Measurement (mean±SD)
	GM CBF	WM CBF
Uncorrected	54.0 ± 21.7	23.7 ± 10.3
Corrected	64.0 ± 10.0*†	28.3 ± 5.8*‡
Whole Brain	Measurement (mean±SD)
	tCBF
Uncorrected	587.4 ± 218.0
Corrected	684.2 ± 161.6

Abbreviations and annotations:

WM, white matter, GM, gray matter; CBF,: regional cerebral blood flow (mL/100gm/min); tCBF, total cerebral blood flow (mL/min); SD,: standard deviation;

^*significant reduction of the sum of squares variance by means of the proposed correction method;

^†one-sided F-test, p=0.011;

^‡one-sided F-test, p=0.045; Paired T-test demonstrated no statistically significant difference between the mean CBF measurements in gray (p=0.100) or white matter (p=0.113) before and after correction.

As can be seen in Table 3, the AUC under the AIF and the patients’ hematocrit showed no covariation with the correction factors. Regression analysis found no relationship between either the area under the curve or the patient hematocrit.

Comparison of the segmentation results using T2 and T1 weighted images showed that after masking of gray (white) matter data, more than 98% (98%) of the gray matter voxels selected with either approach were inside of the boundary of the T1-based gray (white) matter segmentation. There was a 0.6% volume difference between total brain volumes determined using T1 weighted as compared to T2 weighted images.

For the reproducibility analysis, repeating the determination of tCBF_DSC 4 times resulted in an average coefficient of variation (CV) of 3.66%. For the PC-MRA analysis, the average CV was 0.88%.

Finally, corrected and uncorrected tumor CBF measurements are given in Table 5.

Table 5.

Corrected and un-corrected Tumor CBF Values (mL/100gm/min)

Pt	Tumor CBFDSC
	Uncorrected	Corrected
1	38.7	54.0
2	16.2	18.9
3	19.9	52.5
4	122.0	114.5
5	197.0	150.7
6	N/A	N/A
7	124.8	114.1
8	12.1	14.0
9	96.8	121.2
10	69.2	53.2
11	57.5	62.4

N/A – not applicable, patient had non-neoplastic disease (right para-opthalmic ICA aneurysm)

DISCUSSION

The current study demonstrates that a rapid PC-MRA scan which produces a measure of tCBF can be used to reduce variance in brain CBF_DSC values by up to slightly more than 2-fold, and is therefore a promising calibration method for DSC-MRI. Additional scan time is relatively minor (< 5 minutes) including both the PC-MRA itself as well as a vascular scout image, although postprocessing time is longer than that required to create uncalibrated CBF maps from DSC-MRI data. Reducing the variance of the brain CBF_DSC values in this subject group does not prove that the method is accurate, however it seems likely that the physiological variations in contralateral CBF should be smaller than the variations observed in the uncorrected CBF_DSC values. However, the current study is in no way a validation of the accuracy of the method, and a full validation of the proposed technique with comparison to other, gold standard, CBF methods such as H₂¹⁵O positron emission tomography (PET) will require future studies in more homogeneous subject groups. It is certainly possible that CBF may vary quite widely in the current study population of brain tumor patients with a wide range of ages.

Previous attempts to calibrate CBF_DSC values using other modalities have included comparisons to H₂¹⁵O PET using a population average correction factor (24,25) with a common conversion factor Φ_Gd=0.87 (24) that was applied to the spin-echo EPI-derived CBF data. In another study (in pigs), it was found that gradient-echo EPI technique resulted in approximately threefold overestimation of absolute CBF compared to the spin-echo technique (26). Other CBF calibration schemes include a correction factor based on the venous outflow derived from the superior sagittal sinus (a large vessel which may have less partial volume effects than the MCA)(27), or subject-to-subject corrections based on steady-state cerebral blood volume (CBV) measurements (11). However, all of these approaches have drawbacks: population average correction factors cannot correct for individual variations, while single-vessel venous-outflow and/or CBV-based correction factors may not correlate with CBF under all conditions.

Many of the potential sources of error in calculating CBF_DSC are mentioned in the introduction, and are too numerous to be discussed in detail here. However, it should be recognized that only those errors, which cause a global and linear deviation of the voxelwise CBF values are amenable to correction by the proposed tCBF calibration method. For instance, regional CBF_DSC errors (for instance due to regional variations in the AIF) cannot be corrected using a global correction factor. Likewise, a single, linear correction factor will not provide ‘true’ CBF values if the (non-corrected) CBF_DSC maps are non-linear with respect to (true) CBF. However, our data suggest that a large component of the between subject variation in CBF_DSC is related to linear scaling over the entire brain volume. Multiple factors can be considered as causes for such a global scaling problem. Many considerations will entail the determination of the AIF, which is critical for the determination of tCBF. The exact determination of the nature of effects that lead to the variation of tCBF_DSC measurements is beyond the design of this study. Due to the complicated interplay of multiple factors, exact prediction of the final amount of scaling is difficult.

The accuracy of the tCBF calibration approach will also depend on the accuracy and reproducibility of the tCBF_PC determination. Generally, tCBF values determined by cardiac-gated PC-MRA of the vertebral and internal carotid arteries have been found to be reproducible (20,21) with a coefficient of variation of less than 10%, and about 5% difference between calculated and absolute flows in a phantom. However, there is certainly potential for error in the PC-MRA measurement, including incorrect slice positioning (e.g. non-perpendicular to the arteries to be measured) or the effects of turbulent flow. It is also important that optimized analysis techniques are used to automatically detect the edges of the vessels throughout the cardiac cycle, and that precise and reproducible software is used to define the vessel wall. In the current study, the commercial ‘MEDIS’ software package was used to perform this function; it was found that tCBF estimates varied as a function of the ‘pressure’ parameter used to define the vessel contours. By adjustment of this pressure parameter, tCBF_PC values could be found that were in excellent agreement with those reported in the literature (21,28). Clearly any future studies using this analysis technique should use optimal and consistent algorithms for vessel wall definition. With consistent use of automated vascular selection parameters, excellent reproducibility of PC-MRA derived tCBF measurements was achieved with coefficients of variation in the range of 0.2% to 2.9% (average 0.88%). These measurements, however pertain to the variability of postprocessing only, and do not include physiologic variation, inter-scan variation or influence of slice positioning. They do, however suggest that our data are comparable with the accuracy reported in the literature (21,28). For completeness we provide quantification of lesion CBF, although lesion quantification was not the main purpose of this study. Many of the examined lesions enhanced strongly, and it is therefore expected that blood-brain barrier breakdown will have a significant effect on CBF_DSC estimates of the tumors (28). A variety of methods have previously been proposed to correct the effects of BBB leakage, including post-processing methods (29) or ‘preloading’ the patient with a low-dose of Gd contrast agent before the DSC-MRI acquisition (30). Either or both of these methods could be used in conjunction with the PC-MRA calibration method, and will be subject to further research employing this method in the evaluation of brain tumors. The effect of the enhancing lesion on the tCBF_DSC determination will be small, however, since the lesion volume in all cases studied here was small in comparison to the total brain volume, and therefore should have minimal impact on the correction factor used to determine contralateral hemisphere CBF_DSC values. Since the calibration procedure requires whole-brain DSC-MRI coverage, it is also important that inter-slice gap be not too large to avoid systematic errors. We have implemented computer simulations on a digital CBF phantom and found the effect of the slice gap negligible on global measurements like those used in this study. This issue can also be eliminated in the future by the use of 3D (or no gap 2D) DSC perfusion sequences.

This study is not without limitations. For example, although the results suggest improvement of CBF quantification, a direct comparison with an established standard of reference for CBF measurements was not performed. Currently, ¹⁵O PET is regarded as a “gold standard” to measure quantitative cerebral perfusion parameters in humans. Unfortunately, the research subjects in this study did not have access to concurrent ¹⁵O PET, as indeed has been the case in the assessment of other qCBF and qCBV techniques in the literature (9,10). Our analysis of the reproducibility of the postprocessing demonstrated an average coefficient of variation of 3.66%, however there are limitations to completely assessing test and re-test reproducibility of this methodology, due to the difficulty of administering a second dose of contrast agent for research purposes, which was avoided due to the risk of nephrogenic systemic fibrosis. For full confidence in the technique, future validation studies are required in a homogeneous group of normal volunteers, in comparison to other techniques such as ¹⁵O PET.

Other approaches to calibrate DSC-MRI have been proposed (31). Such calibration techniques have been developed using steady-state T₁ changes in the brain parenchyma and blood pool (11), for example using a “bookend” technique, and have been used for cross-sectional studies (12). The initial drawback of lengthy acquisition (11) due to inversion-recovery (IR) fast imaging with steady precession (FISP) has been partially overcome using IR Look-Locker EPI (LL-EPI) (12). These sequences are not currently commercially available, however, unlike the currently proposed PC-MRA methodology, The PC-MRA method is also faster, and allows direct, independent assessment of tCBF.

The segmentation into gray and white matter probabilistic maps used affine registration of T₂ weighted images to the EPI data, since T₂ weighted images were available in all cases as part of the clinical MR protocol. A non-linear registration to correct for distortions in the EPI data was not used for simplicity. The volume fraction of mismatch was estimated to be up to 5% as a result, and it is expected that the use of non-linear coregistration in the future may decrease this error. Alternatively, brain segmentation (for whole brain volume) might be performed directly on the EPI images themselves, which would remove any co-registration errors.

In our assessment, T₂ weighted image-derived total brain volume was in very good agreement with the total brain volume derived from T₁ weighted data. We also found that although the T₁ and T₂ based segmentation result in slightly different gray and white matter segmentation, the use of a restrictive masking to select “pure” tissue resulted in selection of gray and white matter voxels by the T₂ method, 98% of which would have been selected by the T₁ method. We conclude from this that the T₂ weighted image segmentation did not introduce error of a magnitude that would have significantly affected our data.

The meningioma included in this study highlights several interesting possible confounding factors of the analysis. Meningiomas are the most common extra-axial tumors and the most common non-glial intracranial tumors, accounting for approximately 15% of primary intracranial tumors in the general population. It is therefore highly likely that meningiomas will be frequently examined during more widespread clinical use of DCE-MRI. Meningiomas arise from the dura and derive their primary arterial blood supply from meningeal artery branches, most commonly the MMA, but dependent on location also from ICA and vertebral artery meningeal branches. For more detail, we refer to the extensive neuroangiographic literature on this topic. Due to their high vascularity, inclusion or exclusion of the meningioma will have a notable effect on the derived correction factor and tCBF estimate, but will also affect DSC-MRI techniques which rely on calibration to population standards or which derive a calibration from a segmentation which cannot classify the meningioma accurately as an extra-axial lesion. In our case, the meningioma was subsequently resected and it is therefore certain that vascular supply was from the ECA, allowing us to assess the performance of our approach. The slight deviation from physiological values in the DSC-MRI output was successfully corrected into a more physiological range. In addition, the exclusion of meningioma voxels avoided additional overestimation of tCBF. Thus, in an interesting fashion, the meningioma case underlines the importance of consideration of anatomical and neuroangiographic knowledge into the analysis, which otherwise will cause bias which may be erroneously attributed to other parameters in the analysis.

In summary, a technique is presented that provides a straightforward calibration of CBF_DSC data using PC-MRA. The method considerably reduces the variance of the data compared to non-corrected CBF estimates in this group of patients. In future applications, PC-MRA tCBF could be used to calibrate other MRI methods or brain imaging modalities that determine relative CBF, such as for example arterial spin-labeling (ASL) MRI (32).