Actin Filament Segmentation Using Dynamic Programming

Abstract

We introduce a novel algorithm for actin filament segmentation in 2D TIRFM image sequences. This problem is difficult because actin filaments dynamically change shapes during their growth, and the TIRFM images are usually noisy. We ask a user to specify the two tips of a filament of interest in the first frame. We then model the segmentation problem in an image sequence as a temporal chain, where its states are tip locations; given candidate tip locations, actin filaments' body points are inferred by a dynamic programming method, which adaptively generates candidate solutions. Combining candidate tip locations and their inferred body points, the temporal chain model is efficiently optimized using another dynamic programming method. Evaluation on noisy TIRFM image sequences demonstrates the accuracy and robustness of this approach.

1 Introduction

Actin is one of the most abundant proteins in cells. It has the ability to polymerize into long filaments out of monomers (single proteins). These filaments form a fibrous network within cells called the “cytoskeleton”, which provides cells with mechanical integrity and shape. Through the fast assembly and disassembly of the cytoskeleton fibers, cells can change shape, move and divide. One way to study the cytoskeleton is to analyze actin filaments' polymerization in vitro using Total Internal Reflection Fluorescence Microscopy (TIRFM) [1], [2] (see Fig. 1.(a–b)). Biologists are interested in measuring actin filaments' elongation rates (by measuring their length differences between frames) and rigidity (by measuring the curvature along them). Therefore, actin filaments need to be segmented before the analysis.

Fig. 1.

(a–b) Two frames in a TIRFM sequence. (c–d) It is difficult to judge which points at time i + 1 should be the temporal correspondences of the red point at time i.

There has been related work on tracking or segmentation of filamentous and microtubule (MT) structures in biological images. Hadjidemetriou et al. [3] developed a method to automatically track microtubules which are characterized locally using consecutive level sets segments. In [4], after MT tips are detected in the first frame, they are tracked by looking for the closest ones in the subsequent frames. Active contours are then used to extract MT bodies based on obtained tip locations. In [5], MT tips are located using second order derivative of Gaussian filtering. Geodesic paths are then iteratively calculated to segment MT bodies. In [6], Stretching Open Active Contour (SOAC) is used to segment and track actin filaments in TIRFM images frame by frame. In the above methods, movements of the structures are assumed small, which is not always valid in our TIRFM images.

More complex movement models can be taken into consideration in Baysian tracking frameworks. In [7] and [8], Particle Filters (PF) are used to track the locations of tip parts of MT. The MT bodies can then be segmented in a subsequent step using obtained tip locations [7]. Li et al. [9] combined the SOAC and PF to simplify the modeling of PF in a one-dimensional state space while integrating filament body constraints into tip estimation. However, biological sequences are usually taken prior to data analysis and therefore do not need real time performance. The above methods only consider temporal information up to the current frame and thus ignore all available information after it. In [10], a 2D time-lapse image sequence is treated as a 3D image volume, and a spatiotemporal active surface model is proposed to segment an actin filament in all frames simultaneously. The assumption of this method is that an actin filament's body remains static across time. However, this assumption does not apply to general actin filament data, where an actin filament may grow, drift, and change shape at the same time (see Fig. 1).

In this paper, we propose a novel method to segment actin filaments in the general data while fully utilizing all available temporal information. We treat the segmentation of an actin filament across time as a 1D temporal chain model. Tip locations are used as the state of each temporal node because tips are usually blurry in the images, and their localization is most difficult. The temporal chain can be globally optimized using dynamic programming. Filament bodies are inferred in the same process using another dynamic programming method, which adaptively generates candidate solutions. Dynamic programming has been used to optimize tree models in [11] or chain models in [12]. Compared with existing methods [9],[10], which have some strong assumptions and constraints, our proposed method is more flexible. Every constraint in the framework can be freely modified or deleted, and new constraints can be easily added in.

2 Methodology

2.1 Problem Formulation

The problem of actin filament segmentation in a single image can be viewed as optimizing a 1D spatial chain model as shown in Fig. 2.(a), where each node's state represents the position of a point on the actin filament [6]. Compared with other pixel-wise segmentation methods, one major advantage of the 1D chain model is that it has clear topology. Its results are ready for further biological analysis, while other methods need post-processing to reconstruct the topology.

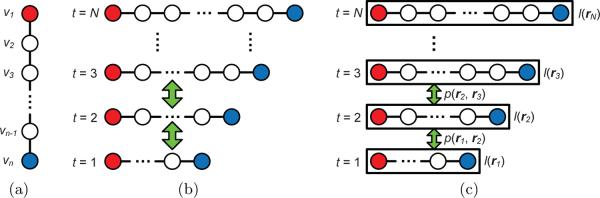
Fig. 2.

(a) Illustration of the 1D spatial chain in a single frame. (b) Illustration of a series of spatial chains. (c) Illustration of the temporal chain model. Tip nodes of spatial chains are marked in red and blue. Spatial relations are shown as solid lines. Temporal relations are shown as green arrows.

If segmenting an actin filament in a time-lapse sequence, temporal information would be helpful, for example, to recover information on an intermediate frame that is unclear. The problem of actin filament segmentation in a time-lapse sequence can then be defined as optimizing a series of 1D spatial chain models while considering their temporal relations between each other. Fig. 2.(b) illustrates the segmentation model for a time-lapse sequence. However, formulating this model is challenging on three aspects. (i) The number of nodes in each 1D chain is different. To represent different actin filaments with the same resolution, the number of points on a chain should be proportional to its length. (ii) Each node's temporal correspondences are difficult to define because an actin filament may move its entire body during its growing process (see Fig. 1.(c–d)). (iii) The desired energy functions measuring how well a 1D spatial chain represents an actin filament (likelihood terms) or how well two chains are temporally constrained (pairwise terms) may have very complex forms.

To address the difficulties, we partially bypass the second difficulty because there is no convincing way to establish temporal correspondences between nodes at two chains (see Fig. 1(c–d)). By focusing on addressing the first and third difficulties, we are able to propose a simplified model aiming at jointly recovering the best tip points in all time frames while considering inferred filament body points' temporal relations. The entire segmentation problem is modeled as a 1D temporal chain as shown in Fig. 2.(c), where the ith node's state represents the starting (red) and ending (blue) points of the actin filament in the ith frame. Jointly using image information in all time frames and temporal information between every two frames, we locate the best tip points, $\{{\widehat{\mathbf{r}}}_1,{\widehat{\mathbf{r}}}_2,\cdots ,{\widehat{\mathbf{r}}}_N\}$, in the image domain Ω by minimizing the following energy function:

$$f({\mathbf{r}}_1,{\mathbf{r}}_2,\cdots ,{\mathbf{r}}_N)=\left(\sum _{i=2}^{N}l\left({\mathbf{r}}_i\right)+\sum _{i=1}^{N-1}p({\mathbf{r}}_i,{\mathbf{r}}_{i+1})\right),$$ (1)

where N is the number of frames in the input sequence, r_i = [r_i,1, r_i,2]^T ε Ω × Ω is the state of the ith node (i.e., the locations of the two tip points, r_i,1 and r_i,2, in the ith frame). For instance, if r_i,1 has two candidate locations {v₁, v₂}, and r_i,2 has two candidate locations {v₃, v₄}, r_i's candidate states would then include [v₁, v₃]^T, [v₁, v₄]^T, [v₂, v₃]^T, and [v₂, v₄]^T. l(r_i) is the likelihood term measuring how well the 1D spatial chain inferred by the two tip points, r_i, represents an actin filament, and p(r_i, r_i+1) is the pairwise term measuring how well the ith and i + 1th spatial chains inferred by the tip points, r_i and r_i+1, follow the given temporal constraints. The objective function does not calculate the likelihood cost in the 1st frame, l(r₁), because the user was asked to specify the correct tip locations of the actin filament of interest in the 1st frame. The choices of l(·) and p(·) are very flexible. We introduce our implementation in Section 3. However, they can be freely modified and deleted to fit any new constraints.

2.2 Efficient Optimization of the Temporal Chain Using Dynamic Programming

Taking advantages of the 1D structure of the temporal chain, the objective function (1) can be efficiently optimized using dynamic programming if the solution set is discrete. We restrict tip points to only be on image pixel locations. The dynamic programming algorithm involves generating a sequence of “optimal-value” functions of one discrete variable, ${\left\{s_i\right\}}_{i=1}^{N-1}$. To obtain each s_i, a minimization is performed over a single variable. (1) can then be iteratively optimized as follows:

$$s_1\left({\mathbf{r}}_2\right)=p({\mathbf{r}}_1,{\mathbf{r}}_2)+l\left({\mathbf{r}}_2\right),$$ (2)

$$s_2\left({\mathbf{r}}_3\right)=\underset{{\mathbf{r}}_2}{\overset{\min }{}}[s_1\left({\mathbf{r}}_2\right)+p({\mathbf{r}}_2,{\mathbf{r}}_3)]+l\left({\mathbf{r}}_3\right),$$ (3)

$$s_{N-1}\left({\mathbf{r}}_N\right)=\underset{{\mathbf{r}}_{N-1}}{\overset{\min }{}}[s_{N-2}\left({\mathbf{r}}_{N-1}\right)+p({\mathbf{r}}_{N-1},{\mathbf{r}}_N)]+l\left({\mathbf{r}}_N\right),$$ (4)

$$\underset{{\mathbf{r}}_1,{\mathbf{r}}_2,\cdots ,{\mathbf{r}}_N}{\overset{\min }{}}f({\mathbf{r}}_1,{\mathbf{r}}_2,\cdots ,{\mathbf{r}}_N)=\underset{{\mathbf{r}}_N}{\overset{\min }{}}{s}_{N-1}\left({\mathbf{r}}_N\right).$$ (5)

In the 1st iteration, for every possible r₂, the algorithm calculates p(r₁, r₂)+l(r₂) and assign this value to the function s₁(r₂). No minimization is performed in this iteration since r₁ is fixed. In the 2nd iteration, for every possible r₃, the algorithm searches for a r₂ that minimizes s₁(r₂) + p(r₂, r₃). Then all such (r₃, r₂) pairs are stored in a table, and the function values of (3) are assigned to s₂(r₃); The remaining iterations are performed similarly. As shown in (5), the minimum of f(r₁, r₂, ⋯, r_N) can be obtained as the minimal element in the table s_N−1(r_N). The optimal tip locations in all frames are then recovered by back-tracking the minimization-correspondence tables from the last one to the first.

If there are m possible pairs of starting and ending points in each frame, the overall time complexity of the above dynamic programming algorithm is O(Nm²) (see Section 3.5 for actual computation time).

2.3 Inference of Actin Filament Body Points

The calculation of both the likelihood terms, ${\left\{l\left({\mathbf{r}}_i\right)\right\}}_{i=2}^N$, and the pairwise terms, ${\left\{p({\mathbf{r}}_i,{\mathbf{r}}_{i+1}\}\right)}_{i=1}^{N-1}$, requires body points to be efficiently and accurately inferred by given tip points ${\left\{{\mathbf{r}}_i\right\}}_{i=1}^N$, i.e., optimizing the 1D spatial chain model in Fig. 2.(a). The problem can be viewed as a shortest path problem with given starting and ending points. We propose a novel algorithm to e ciently solve for the shortest path, $\{{\widehat{v}}_1,{\widehat{v}}_2,\cdots ,{\widehat{v}}_n\}$, by minimizing an active contour model energy function:

$$E(v_1,v_2,\cdots ,v_n)=\alpha \sum _{j=1}^{n-1}{\mid v_{j+1}-v_j\mid }^2+\beta \sum _{j=2}^{n-1}{\mid v_{j+1}-2v_j+v_{j-1}\mid }^2+\sum _{j=1}^n{E}_{\mathit{ext}}\left(v_j\right),$$ (6)

where v_j ε Ω denotes the location of the jth point's on the path, n is the number of points on the path, α and β are the weights of the first-order and second-order smoothness terms. The first two internal energy terms keep the path smooth. The last external energy term, E_ext(·), makes the path fit the bright ridges in the image. The smaller E_ext(v_j) is, the better v_j represents a point on bright ridges. If n is given and ${\left\{v_j\right\}}_{j=1}^n$ are constrained to only be on pixel locations, (6) can be efficiently minimized by dynamic programming [12]:

$$\begin{array}{cc}\hfill e_1(v_2,v_3)& =\alpha {\mid v_2-v_1\mid }^2+\beta {\mid v_3-2v_2+v_1\mid }^2+E_{\mathit{ext}}\left(v_2\right),\hfill \\ \hfill e_2(v_3,v_4)& =\underset{v_2}{\overset{\min }{}}[e_1(v_2,v_3)+\alpha {\mid v_3-v_2\mid }^2+\beta {\mid v_4-2v_3+v_2\mid }^2]+E_{\mathit{ext}}\left(v_3\right),⋮\hfill \\ \hfill e_{n-2}(v_{n-1},v_n)& =\underset{v_{n-2}}{\overset{\min }{}}[e_{n-3}(v_{n-2},v_{n-1})+\alpha {\mid v_{n-1}-v_{n-2}\mid }^2+\beta {\mid v_n-2v_{n-1}+v_{n-2}\mid }^2]+E_{\mathit{ext}}\left(v_{n-1}\right),\hfill \\ \hfill e_{n-1}\left(v_n\right)& =\underset{v_{n-1}}{\overset{\min }{}}[e_{n-2}(v_{n-1},v_n)+\alpha {\mid v_n-v_{n-1}\mid }^2],\underset{v_1,v_2,\cdots ,v_n}{\overset{\min }{}}E(v_1,v_2,\cdots ,v_n)=e_{n-1}\left(v_n\right),\hfill \end{array}$$ (7)

The above equations have similar meanings as those of (2)–(5) except that the optimal-value functions ${\left\{e_j\right\}}_{j=1}^{n-1}$ now have two discrete variables. This is because the calculation of second-order smoothness terms involves three neighboring spatial nodes. Minimizations in the first and last iterations are not needed because the starting and ending points are given. The time complexity of this algorithm is O(nk⁴) if every point can take k different locations. We further improve the above algorithm by proposing a scheme to adaptively generate candidate locations, and by decreasing minimization-search range for each candidate point.

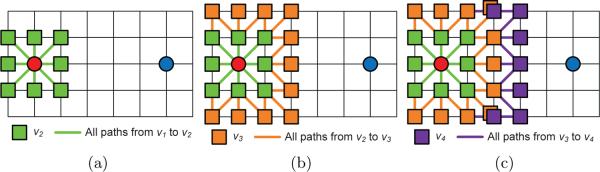
In the first iteration, our method generates candidate locations of v₂ as 8 neighbors of the starting point on the image grid. Candidate locations of v₃ are generated as neighbors of v₂ with some path constraints (see the next paragraph). Similarly, candidate locations of v_j are generated as the 8-connection neighbors of v_j−1 on the image grid. 3 iterations of our method are illustrated in Fig. 3.

Fig. 3.

(a) Generating candidate locations of v₂. (b) Generating candidate locations of v₃. (c) Generating candidate locations of v₄. Red and blue dots represent the starting point (v₁) and the ending point (v_n) of a path. Colored lines represent possible paths.

To decrease the number of candidate locations in every iteration, we do not allow any consecutive path segments to have turning angles greater than 90 degrees. In Fig. 3, all possible paths are shown as colored lines. When calculating e_j(v_j+1, v_j+2), our method only searches for v_j that does not generate sharp turns on any path v_j → v_j+1 → v_j+2. Obviously, for any e_j(v_j+1, v_j+2) entry, the algorithm searches for at most three locations of v_j. In this way, we are able to decrease the time complexity of each iteration from O(k⁴) to O(k²).

To prevent too many loops on a path, we let any grid location can only be used as a candidate location for at most n_v times. To exclude oblivious short-cuts and wrong paths, our method stops continuing a path if a consecutive n_thres of points on the path have intensity below I_thres. This operation explicitly excludes possible short-cuts and further improves the efficiency of our method. The algorithm terminates the iterations if (i) the ending point is visited for more than 10n_v times or (ii) the maximum iteration number, n_max is reached. We empirically set n_max = 200 in our application, since no actin filament is longer than 200 pixel-long in our dataset. During the iterations, all paths ended with the given ending point are recorded. After the iterations terminate, the path with the smallest energy value per node is chosen as the best one. In other words, the proposed method does not penalize length and therefore would not favor “short-cuts”.

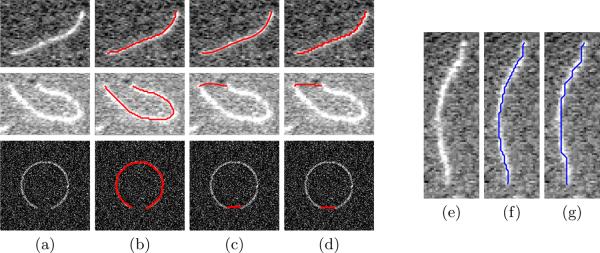
Compared with other shortest path methods, such as the global minimal path method [13] and the graph-based method, our method has three advantages. (i) It avoids the common short-cut problems. Two operations, excluding paths with too many consecutive points with low intensity and choosing the path with minimal unit energy value, contribute to this advantage. Fig. 4 shows comparison results with other methods using real TIRFM images and a synthetic image. (ii) This method is efficient. Our MATLAB MEX implementation takes less than 0.02s to optimize a 200 pixel-long path with a complex external energy term (9) on an Intel E6850 3.0GHz CPU. (iii) Our method is able to take the second-order smoothness terms into consideration and therefore is more versatile to different applications, while other methods only consider first-order smoothness terms. Fig. 4 illustrates paths with different β settings.

Fig. 4.

(Left) Comparison between our proposed method, the global minimal path method [13], and the shortest-path-on-the-graph method. (a) Original images. (b) Results of our proposed method with α = 1, β = 0.1. (c) Results of the global minimal path method with weight equaling 1. (d) Results of the shortest-path-on-the-graph method. (Right) The influence of the second-order smoothness term. (e) The original image. (f) α = 1, β = 0.1. (g) α = 1, β = 0.5.

3 Implementation

3.1 Image Preprocessing

The input TIRFM images are usually noisy and sometimes have biased intensity fields. We use the Frangi vessel enhancement filter [14] to enhance filamentous structures and to suppress noises. Let I_F and I_F,i represent the vessel-enhanced results of a general image and the ith frame of a sequence, respectively. I(v) represents the intensity value of image I at position v ε Ω. If v falls between pixel grid locations, its intensity is obtained by bilinear interpolation.

3.2 Implementation of The External Energy E_ext in (6)

The smaller E_ext(v_j) is, the better v_j represents a point on an actin filament. In [14], the Gaussian-second-order-derivative kernel shows its effectiveness in detecting vessel-like structures. The 1D kernel with scale σ, $G_{\sigma }^{″}\left(x\right)$, measures the contrast between the regions inside and outside the range (−σ, σ) in the direction of the derivative:

$$G_{\sigma }^{″}\left(x\right)=\frac{(x^2-{\sigma }^2)}{\sqrt{2\pi }{\sigma }^5}{e}^{-\frac{x^2}{2{\sigma }^2}}$$ (8)

We adopt this 1D kernel and calculate E_ext(v_j) as its correlation with the image at location v_j. This 1D correlation has the lowest response if the filter's direction is perpendicular to the path's direction at location v_j. To calculate the path's direction at v_j, the external energy term needs three neighboring points, v_j−1, v_j, and v_j+1, we re-define the external energy term as

$$\begin{array}{cc}\hfill & {\tilde{E}}_{\mathit{ext}}(v_{j-1},v_j,v_{j+1})=\sum _{x=-4\tilde{\sigma }}^{4\tilde{\sigma }}{I}_F(v_j+x\mathbf{d})\cdot G_{\tilde{\sigma }}^{″}\left(x\right)\hfill \\ \hfill & \mathrm{where}\mathbf{d}\perp (\frac{v_{j+1}-v_j}{2{\parallel v_{j+1}-v_j\parallel }_2}+\frac{v_j-v_{j-1}}{2{\parallel v_j-v_{j-1}\parallel }_2}),{\parallel \mathbf{d}\parallel }_2=1.\hfill \end{array}$$ (9)

⊥ denotes that the unit vector d is perpendicular to the path's direction at v_j, and $\tilde{\sigma }=1.5$, which is half of the width of actin filaments. Consequently, the optimal-value functions ${\left\{e_j\right\}}_{j=2}^{n-1}$ in (7) should be re-defined as

$$e_j(v_{j+1},v_{j+2})=\underset{v_j}{\text{min}}[e_{j-1}(v_j,v_{j+1})+\alpha \mid v_{j+1}-v_j{\mid }^2+\beta \mid v_{j+2}-2v_{j+1}+v_j{\mid }^2+{\tilde{E}}_{\mathit{ext}}(v_j,v_{j+1},v_{j+2})],$$ (10)

3.3 Implementation of The Likelihood Term l(r_i) in (1)

Given a pair of starting and ending points, r_i, in the ith frame, a spatial chain {v_i,1, ⋯, v_i,ni} is optimized to represent the best location of the actin filament with r_i as its tip points. The likelihood of this spatial chain representing an actual actin filament, l(r_i), is defined as a summation of a tip likelihood term, l_t(r_i), and a body likelihood term, l_b(r_i):

$$l\left({\mathbf{r}}_i\right)={\lambda }_t{l}_t\left({\mathbf{r}}_i\right)+{\lambda }_b{l}_b\left({\mathbf{r}}_i\right),$$ (11)

where λ_t and λ_b are the weights of the two likelihood terms. The tip likelihood term is calculated as correlations between a 9 × 9 template tip patch I_t with the rotated enhanced image I_F,i at tip locations v_i,1 and v_i,ni. The template tip patch is the mean of 50 manually labeled actin filament tip patches. The rotation directions are the two directions d_i,1 and d_i,ni pointing outward the resulting spatial chain from the two tip points, v_i,1 and v_i,ni, respectively:

$${\mathbf{d}}_{i,1}=\frac{v_{i,1}-v_{i,5}}{{\parallel v_{i,1}-v_{i,5}\parallel }_2},{\mathbf{d}}_{i,n_i}=\frac{v_{i,n_i}-v_{i,n_{i-4}}}{{\parallel v_{i,n_i}-v_{i,n_{i-4}}\parallel }_2}.$$ (12)

The tip likelihood term is defined as

$$l_t\left({\mathbf{r}}_i\right)=\frac{1}{81}\sum _{s=-4}^4\sum _{t=-4}^4{I}_t(s,t)\cdot \left[1∕2I_{F,i}(v_{i,1}+s{\mathbf{d}}_{i,1}+t{\mathbf{d}}_{i,1}^{\perp })+1∕2I_{F,i}(v_{i,n_i}+s{\mathbf{d}}_{i,n_i}+t{\mathbf{d}}_{i,n_i}^{\perp })\right],$$ (13)

where ${\mathbf{d}}_{i,1}^{\perp }$ and ${\mathbf{d}}_{i,n_i}^{\perp }$ are unit vectors perpendicular to d_i,1 and d_i,ni, respectively. The body likelihood term is calculated as the average intensity value on the path:

$$l_b\left({\mathbf{r}}_i\right)=\frac{1}{n_i}\sum _{j=1}^{n_i}{I}_{F,i}\left(v_{i,j}\right).$$ (14)

3.4 Implementation of the Pairwise Term p(r_i, r_i+1) in (1)

We consider the pairwise relation of two adjacent spatial chains, {v_i,1, ⋯, v_i,ni} and v_i+1,1, ⋯, v_i+1,ni+1}, which are inferred by r_i and r_i+1 respectively. The relation is constrained by the desired growing speed and differences of tip directions, i.e.,

$$p({\mathbf{r}}_i,{\mathbf{r}}_{i+1})={\lambda }_g{p}_g({\mathbf{r}}_i,{\mathbf{r}}_{i+1})+{\lambda }_d{p}_d({\mathbf{r}}_i,{\mathbf{r}}_{i+1}),$$ (15)

where λ_g and λ_d weight the growing speed term p_g(·) and the tip direction difference term p_d(·). The growing speed term is defined as

$$p_g({\mathbf{r}}_i,{\mathbf{r}}_{i+1})=\{\begin{array}{cc}\hfill 0\hfill & \hfill \mid L\left({\mathbf{r}}_{i+1}\right)-L\left({\mathbf{r}}_i\right)-5\mid <3,\hfill \\ \hfill \parallel L\left({\mathbf{r}}_{i+1}\right)-L\left({\mathbf{r}}_i\right)-5\mid -3{\mid }^2\hfill & \hfill \text{otherwise},\hfill \end{array}\phantom{\}}$$ (16)

where $L\left({\mathbf{r}}_i\right)={\sum }_{j=2}^{n_i}{\parallel v_{i,j}-v_{i,j-1}\parallel }_2$ is length of the spatial chain inferred by r_i· p_g(·) does not penalize growing length in the range [2, 8] pixel-long (around [0.24, 1.36] μm). Note that this range is set according to our data at hand and can be changed for data with other growing speed priors. p_d(·) is calculated as the differences between the pair of spatial chains' tip directions at the two tips:

$$p_d({\mathbf{r}}_i,{\mathbf{r}}_{i+1})=1∕2{\parallel {\mathbf{d}}_{i+1,1}-{\mathbf{d}}_{i,1}\parallel }_2+1∕2{\parallel {\mathbf{d}}_{i+1,n_{i+1}}-{\mathbf{d}}_{i,n_i}\parallel }_2.$$ (17)

3.5 Generating the Solution Set of r_i and Body Points Inference from r_i

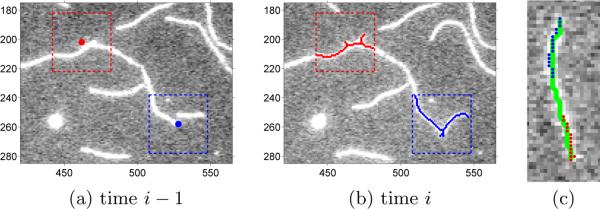
The dynamic programming algorithm (2)–(5) guarantees a global minimum on a discrete solution set. If the starting and ending points in the ith frame, r_i, can be set to any grid location in that image, the size of solution set for each r_i would be tremendous but also unnecessary. We threshold the vessel-enhanced image I_F,i and perform the skeleton morphological operation to obtain the candidate locations for r_i. In our application, we set the threshold to 0.2. We further constrain r_i within the domain $[{\tilde{r}}_{i-1,1}-D,{\tilde{r}}_{i-1,1}+D]\times [{\tilde{r}}_{i-1,2}-D,{\tilde{r}}_{i-1,2}+D]$, where $[{\tilde{r}}_{i-1,1},{\tilde{r}}_{i-1,2}]={\tilde{\mathbf{r}}}_{i-1}=\text{arg}{\text{min}}_{{\mathbf{r}}_{i-1}}{s}_{i-2}\left({\mathbf{r}}_{i-1}\right)$. ${\tilde{\mathbf{r}}}_{i-1}$ represents the best tip locations on the i − 1th frame based on the information of only the first i − 1 frames (see Fig. 5.(a) and 5.(b)). Note that it may not equal the final optimized result ${\widehat{\mathbf{r}}}_{i-1}$. In this way, we usually obtain no more than 30 candidate points for each tip point with D = 20. Therefore, the size of the solution set for r_i is usually no more than 30 × 30 = 900.

Fig. 5.

(a) The best tip locations (red and blue) calculated on the i−1th frame based on the first i−1th frames, ${\tilde{\mathbf{r}}}_{i-1}=\text{arg}{\text{min}}_{{\mathbf{r}}_{i-1}}{s}_{i-2}\left({\mathbf{r}}_{i-1}\right)$. The dashed-line boxes represent the range specified by D = 20 for the ith frame. (b) The solution set of r_i. Red and blue points represent the candidate locations of the two tip points. (c) One snake calculated for all starting (red) and ending (blue) points.

Each iteration of (2)–(5) takes most time on inferring body points given m pairs of different r_i. Although an exhaustive calculation usually takes no longer than 0.02s × 900 = 18s, it can be further shortened by calculating only several paths. Given candidate tip points, inferred bodies usually coincide each other. Therefore, we calculate the path inferred by the tip pair with farthest distance first, and pairs with smaller distance later. In details, given two tip points v₁ and v_n, let {v₁, ⋯, v_i, ⋯, v_j ⋯, v_n} represent its inferred body points. If [v_i, v_j]^T is or close to a possible solution of r_i, we use the path {v_i, ⋯, v_j} as the inferred body points of that possible solution. In this way, we usually calculate no more than 40 paths for each r_i. An example is shown in Fig. 5.(c), where only one path is calculated for all possible tip locations.

4 Experiments

We used 7 TIRFM image sequences from [2]. In these experiments, polymerization of muscle Mg-ADP-actin was monitored in the presence of varying concentrations of inorganic phosphate (Pi) and actin monomers. 30% of the actin was labeled on lysine side chains with Alexa green. Methylcellulose was used to suppress lateral Brownian movements of the actin filaments. Images were captured with 500 ms exposure time using a 488-nm laser on an Olympus IX71 microscope. Photobleaching is minimal in these sequences. The resolution was 0.17 μm/pixel. There were 15–25 frames in each sequence. The time interval between frames was 10 sec or 30 sec.

For the spatial chains, we set α= 1, β= 0.1, n_v = 10, n_thres = 5, I_thres =0.15. For the temporal chain, we set λ_t = 1, λ_b = 0.5, λ_g = 0.5, D = 20 for all sequences and empirically chose λ_d from {0.1, 0.5, 1.5 for each sequence. These parameters are empirically set according to experiments on a small set of 10 randomly sampled filaments. The errors of our segmentation method are among two types: (i) tips being inaccurately located, and (ii) body points being wrongly inferred to include several actin filaments. A biologist selected 62 actin filaments of interest in the 7 sequences (which consist of 1104 individual 2D segmentation cases), and marked the actin filaments' correct tip locations in each frame as ground truth. We evaluated our algorithm's performance by calculating the L₂ distances between the ground truth and our method's results, and by counting how many times several actin filaments are mis-segmented as one. The statistics of our method is recorded in Table 1. The two previous methods [6] and [9] assumes a filament's body mostly remains static across time. However, in the general actin filament data that we tested, the actin filaments drift, grow, and change shapes at the same time. The previous methods failed in at least 1/3 of the cases because they require a part of the filament remain static over time for successful initialization.

Table 1.

Tip tracking error statistics of successful segmentation cases and the number of mis-segmentation cases. (Unit: pixel)

Sequence	# of Selected Filaments	Mean	Maximum	Standard Deviation	# of Mis-segmentation
I	8	1.2845	3.3642	0.8968	6 out of 135
II	7	1.0931	3.8613	1.0961	0 out of 108
III	14	1.0273	4.4414	0.8194	4 out of 212
IV	6	1.1092	5.7203	1.0658	12 out of 108
V	13	1.5557	3.4653	0.6634	4 out of 321
VI	5	1.7516	6.4418	1.3195	2 out of 100
VII	9	0.7515	1.8070	0.5781	9 out of 120

We analyzed the proposed method's segmentation results and found two factors contribute most to large errors: (i) the Frangi filter enhances filaments' bodies robustly but may generate large artifacts around tip locations if the image has heavy noises. Such artifacts degenerate the performance of the tip likelihood term and result in most inaccurate tip localizations. To alleviate this factor, preprocessing filter need to be re-designed to generate less artifacts around tip parts. A more robust likelihood term also need to be considered. (ii) Our shortest-path method may infer a path across several actin filaments' bodies mostly if several filaments are tangled together in the image. This problem may be solved by jointly segmenting all actin filaments of interest in a sequence simultaneously. In this way, a temporal chain can exchange information from others and thus has better knowledge to avoid segmenting several actin filaments together.

5 Conclusion

In this paper, we proposed a novel algorithm to segment actin filaments in time-lapse sequences. The overall problem is modeled as a 1D temporal chain model which is efficiently optimized using dynamic programming. All available temporal information is integrated in this model. The body points are inferred in the process using another dynamic programming method which adaptively generates candidate solutions. Each likelihood term or pairwise term can be freely modified or deleted, and new terms representing new constraints can easily be added into this framework. Therefore, the proposed method is very flexible. Extensive experiments demonstrated the effectiveness and robustness of our proposed method.

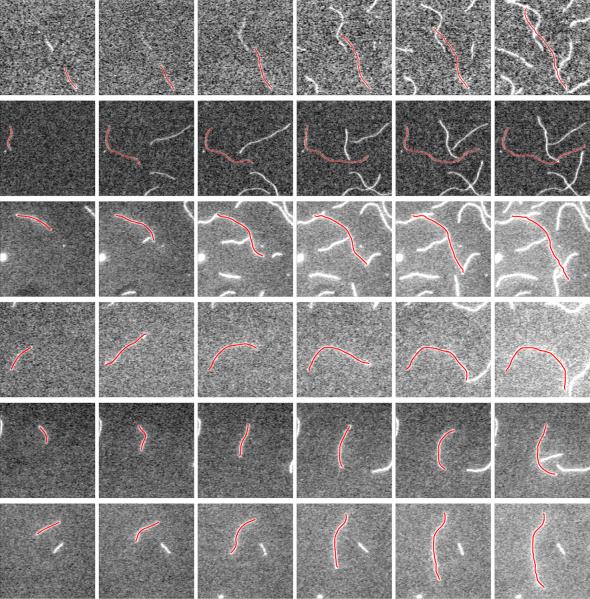
Fig. 6.

Six example results of our proposed method. Each row shows segmentation results of one actin filament polymerizing in a period of time.