3D Symmetry Measure Invariant to Subject Pose During Image Acquisition

Abstract

In this study we evaluate the influence of subject pose during image acquisition on quantitative analysis of breast morphology. Three (3D) and two-dimensional (2D) images of the torso of 12 female subjects in two different poses; (1) hands-on-hip (HH) and (2) hands-down (HD) were obtained. In order to quantify the effect of pose, we introduce a new measure; the 3D pBRA (Percentage Breast Retraction Assessment) index, and validate its use against the 2D pBRA index. Our data suggests that the 3D pBRA index is linearly correlated with the 2D counterpart for both of the poses, and is independent of the localization of fiducial points within a tolerance limit of 7 mm. The quantitative assessment of 3D asymmetry was found to be invariant of subject pose. This study further corroborates the advantages of 3D stereophotogrammetry over 2D photography. Problems with pose that are inherent in 2D photographs are avoided and fiducial point identification is made easier by being able to panoramically rotate the 3D surface enabling views from any desired angle.

Introduction

An important component of the treatment process for many women undergoing breast cancer surgery is reconstruction, wherein surgical procedures are used to rebuild the breast after partial or total mastectomy. Breast reconstruction is integral to improving the cancer survivor’s quality of life, as it can provide psychological benefits related to improvements in body image, self-esteem and depression. The primary aim of reconstruction is to optimize the physical appearance (morphology) of the surgically altered breasts. Breast morphology is described in terms of physical characteristics such as shape, position and appearance, symmetry, and ptosis.¹ Standards for breast reconstruction have evolved, and patients and surgeons alike strive to achieve the most optimal cosmetic outcome particularly in terms of symmetry and natural appearance of the breasts. Although, the conventional practice is to qualitatively evaluate breast appearance following reconstructive surgery, there is growing interest in developing new methods for providing an objective quantitative assessment of outcome (i.e., breast morphology in terms of quantitative measures). Reconstructive outcomes can be evaluated using direct anthropometry,^2,3 photogrammetry,^4–7 and measurements using three-dimensional (3D) data (or stereophotogrammetry).^8–10

Stereophotogrammetry, a practice of determining the geometric properties of an object by measuring defined fiducial (landmark) points on a 3D image of the object, has gained considerable interest in plastic surgery. Because this form of imaging is non-invasive and images can be obtained and processed quickly,¹¹ it has made possible the evaluation of various quantitative measures describing breast shape, symmetry and volume.^11–16 Typically, distances between fiducial points, or the ratios of such distances have been proposed as measurements for estimating the structural characteristics of the breast, such as symmetry, projection, proportion and ptosis. Methods of this type have been successfully implemented in the field of breast conservation therapy.^6,7,11–16 The ultimate goal of these studies is to objectively quantify the correlation of various patient demographics and treatment parameters with outcome (i.e., the morphology of the reconstructed breast).⁷

The effectiveness of 3D assessments in terms of the quantitative distances computed depends on the measurement technique. Key methodological factors include the influences of imaging equipment (scanner alignment and calibration, etc.), and subject factors (movement, regaining a certain position, skin properties, etc.). Most equipment manufacturers include stringent calibration and alignment protocols to minimize equipment related artifacts. However, factors influenced due to human interactions need to be addressed both at the user’s (i.e., operator in the clinic), and the subject’s end. Due to the geometry of the breast region, quantitative analyses of characteristics such as symmetry may be of limited usefulness in evaluating factors related to morphological outcome if the measurements are compromised due to human influences. The key subject influence is movement and is typically addressed by requesting the subject to remain still during image acquisition or via simple image based adjustments retrospectively. Furthermore, improved high resolution 3D imaging systems are now available (3dMDTorso^™, 3Q Technologies, Atlanta, GA) that enable high speed (∼1.5 ms) image capture which eliminates most artifacts related to subject movement. Similarly, user (operator) related errors are eliminated by the implementation of user-friendly single “click and capture” operation. Thus, the only remaining human influence is related to the differences in breast shape and sizes among women, which imposes a need to establish appropriate acquisition protocols in terms of pose. Previous studies have considered the influence of subject movement on imaging and quantitative measurements, but the impact of pose on quantitative assessment of breast appearance has been less studied and standards for subject positioning have not been defined. In some of the previous studies involving volume measurements,^12,16 the arms raised pose is suggested to be preferred; but no data are presented to corroborate the claim.

In this study, we evaluate the influence of subject pose during image acquisition on some objective measures used for quantitative assessment of breast appearance. At present, the most widely used measure for assessing breast symmetry is the Breast Retraction Assessment (BRA) index, introduced by Pezner et al.,¹⁷ and refined by Van Limberger et al.,¹⁸ as the Percentage Breast Retraction Assessment (pBRA) index. The pBRA measure is normalized to account for images acquired at different magnifications. In this study, we introduce an extension of the pBRA index to three-dimensions; namely the 3D pBRA for stereophotogrammetry and employ it to evaluate the effect of pose on quantification of breast morphology. First, we present data to validate the newly introduced 3D pBRA index, and second, apply 3D pBRA to study the impact of pose on quantitative assessment of symmetry. In order to address these questions, we used both 3D and 2D images of the subject’s torso. Photographs (2D images) were included in this study for calculation of 2D pBRA, which provided the reference for validation of 3D pBRA. Multiple observers annotated fiducial points on both 3D and 2D images to compute: 1) the contoured distance between the fiducial points marked on the surface of the 3D images and 2) the line-of-sight (Euclidean) distance between the fiducial points marked on clinical photographs. The contoured distances were used to compute the 3D pBRA index, whereas the Euclidean distances were used to compute the 2D pBRA index. Statistical analyses were performed to validate the 3D pBRA index and to quantify the influence of pose on the same.

Methods and Materials

Study population

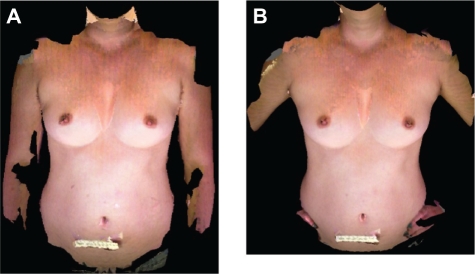
Female patients who underwent or were scheduled for breast reconstruction surgery at The University of Texas MD Anderson Cancer Center were recruited for this study under a protocol approved by the institutional review board. In addition, four healthy female volunteers were commissioned under contract to participate in the study. We used images acquired in two different poses, hands-on-hips (HH) and hands-down (HD) (shown in Fig. 1). 3D and 2D images were obtained of eight patients who had not yet undergone breast reconstruction surgery (both breasts and nipples intact) and of the four commissioned volunteers. The subjects (patients and volunteers) ranged in age from 30 to 64; 9 were white and 3 were Hispanic/Latino. The patients ranged in weight and height from 51.7 to 61.7 kg (57 ± 3.3 kg) and 1.49 to 1.78 m (1.64 ± 0.1 m) respectively with body mass index (BMI) in the range of 20 to 25 kg/m² (21.2 ± 1.8 kg/m²). BMI information was not available for the healthy female volunteers.

Figure 1.

Poses used in this study. A) Hands-down pose and B) Handson-hips pose.

Imaging systems

The 3D surface images were obtained using a commercially available system (DSP 800, 3Q Technologies, Atlanta, GA, http://www.3dmd.com) consisting of an array of multiple digital cameras that are integrated by a computer to yield a single 3D surface image of the subject’s torso. Each reconstructed surface image consists of 3D positions (x, y, and z coordinates) and their corresponding color and texture. The 2D images were taken with a Nikon Coolpix 8400 (Nikon, USA). Images were analyzed using custom programs written by our research team.¹¹

Study design and data collection

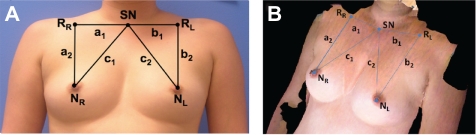
The aim of the study was to determine the effect of pose (HH vs. HD) on the evaluation of symmetry measures (such as pBRA). Images of subjects having both the breasts and nipples intact were considered for this comparison. Six naïve observers annotated the location of three fiducial points, sternal notch (SN) and left and right nipples (N_L and N_R), on the 2D and 3D images of the subjects in each of the two poses (Figs. 2A and 2B).

Figure 2.

pBRA measurements on (A) 2D clinical photographs (B) 3D torso scans. For both 2D and 3D pBRA calculations, same fiducial points are considered. For 2D pBRA euclidean distances and for 3D pBRA contoured distances are evaluated.

The location of a reference point was determined from these annotated points. For locating the right reference point (R_R) and left reference point (R_L), we used the x-coordinate of N_R and N_L, respectively, and y-coordinate of the SN. That is, right nipple’s x-coordinate was assigned as the R_R x-coordinate and its y-coordinate was equal to the SN y-coordinate, and then using the intersection of these x and y values with the 3D surface, we found the corresponding z-coordinate. Two trials of measurements were performed at an interval of 2 weeks to include analyses of intra- and inter-observer variability. Using customized software developed by our research team,¹¹ the contoured and Euclidean distances between the fiducial points were computed. The contoured distance is the shortest path along the contoured surface of the subject’s torso between two points, whereas the Euclidean distance is the straight-line measure between the same two points. The 2D pBRA value was computed to be equal to the BRA value divided by the distance from sternal notch to the nipple that is farthest from the sternal notch. We introduced a 3D version of the 2D pBRA for 3D images. Instead of using the Euclidean distance, we used the contoured distance between the fiducial points and defined 3D pBRA (see Fig. 2) as follows:

$$\mathit{BRA}\hspace{0.17em}=\hspace{0.17em}\sqrt{{(a_1\hspace{0.17em}-\hspace{0.17em}{b}_1)}^2\hspace{0.17em}+\hspace{0.17em}{(a_2\hspace{0.17em}-\hspace{0.17em}{b}_2)}^2}$$ (1)

$$\mathit{pBRA}\hspace{0.17em}=\hspace{0.17em}\frac{\mathit{BRA}}{\mathit{max}(c_1,\hspace{0.17em}{c}_2)}$$ (2)

where, a₁ is the contoured distance between R_R and SN, b₁ is the contoured distance between R_L and SN, a₂ is the contoured distance between R_R and N_R, b₂ is the contoured distance between R_L and N_L, c₁ is the contoured distance between the N_R and SN, and c₂ is the contoured distance between N_L and SN.

We calculated 3D pBRA for each of the two poses for each subject. As the distances used for the calculation of 3D pBRA depend on the identification of fiducial points, we initially determined inter- and intra-observer variability in the annotation of fiducial points on the 3D images. Next, the newly introduced 3D pBRA was validated against the 2D pBRA index, and finally we employed the 3D pBRA to study the effect of pose on measurement of breast symmetry.

Variation in annotation of fiducial points

The value for 3D pBRA is computed using contoured distances between the fiducial points. As a result, one possible source of variation in the value of 3D pBRA could arise from variation in the localization of fiducial points. Thus, the inter- and intra-observer variability for annotating fiducial points was evaluated for both poses. Each observer marked three fiducial points (right nipple, left nipple and the sternal notch) on 3D surface images of twelve subjects. The trial was repeated after an interval of two weeks to minimize the likelihood of the observer’s recollection of his/her previous markings. The inter- and intra-observer variability was assessed by comparing 1) the spatial location, i.e., (x, y, z) coordinates for each of the fiducial points, and 2) the 3D pBRA measurement computed from the manually annotated points. The inter- and intra-observer variability was assessed using the Intraclass Correlation Coefficient.

Agreement between 2D pBRA and 3D pBRA

The newly introduced 3D pBRA was validated against the previously established 2D pBRA index of symmetry. Each observer marked the fiducial points on both the 2D and 3D images, and the 2D and 3D pBRA indexes were computed as described in equation 1 and 2. The agreement between 2D and 3D pBRA was determined using Pearson’s Correlation coefficient.

Effect of pose on 3D pBRA

The effect of subject pose on symmetry was evaluated using the 3D pBRA index. Two different subject poses, HD and HH were compared to determine if pose influenced the computation of the symmetry index. The significance of the analysis was assessed using the Analysis of Variance (ANOVA) statistical test.

Statistical analyses

Intraclass Correlation Coefficient (ICC) is a measure used for assessing the consistency or reproducibility of quantitative measurements made on the same subject. ¹⁹ The interpretation of intraclass correlation coefficient used for this study is as follows; ICC < 0.4 indicates poor reproducibility, 0.4 ≤ ICC < 0.75 indicates fair to good reproducibility, and ICC ≥ 0.75 indicates excellent reproducibility.²⁰ ICC was used to determine the inter- and intra-observer variability in the calculation of the symmetry assessment measure, 3D pBRA index.

Pearson Correlation Coefficient (denoted by “ρ”) measures the degree of association between two quantities.¹⁹ The value of ρ always lies between −1 and 1 inclusive. It is given by ρ_x,y =cov(x,y)σ_xσ_y, where cov(x, y) is covariance between x and y, σ_x and σ_y are standard deviations of x and y respectively. The correlation between 2D pBRA and 3D pBRA was assessed using two quantities, 1) linear correlation coefficient, ρ and 2) P-value to test the hypothesis of no correlation. If the P-value is small (P < 0.05), it indicates that the corresponding correlation ρ is significantly different from zero, and it is safe to reject the idea that the correlation is a coincidence. If the P-value is large, the data do not give reason to conclude that the correlation is real. Pearson correlation coefficient was used to statistically validate the newly introduced 3D pBRA measure against the 2D pBRA index.

Analysis of variance (ANOVA) is a hypothesis test, which helps to determine if two or more samples have the same “mean” or average.¹⁹ The variance between sample means provides an idea whether the sample means are “close enough” or not. If the variance between the groups is small then we can conclude that the sample means are equal otherwise, if the variance is large, then we can conclude that the sample means are not equal. The null hypothesis in ANOVA is that the means of the groups are equal. If the null hypothesis is true, then the “between group variance” is equal to “within group variance”. The test statistic, F is defined as the ratio of variance between items to variance within items. For the ANOVA test if F_critical > F_calculated, then we fail to reject the null hypothesis, i.e., the data suggest that there is no difference between the sample means. We used the one-way ANOVA test to assess the 3D pBRA values calculated for the two poses.

Results

Inter- and intra-observer variability in localization of fiducial points

Six observers annotated three fiducial points (sternal notch, left nipple, and right nipple) for a total of twelve images in two trials. To evaluate the inter-observer variability, the spatial locations of the points were compared, e.g., the location of the right nipple marked by Observer 1 and that marked by Observer 2 for a given single trial. The variability between the six observers was determined by considering all 15 combinations of two observers for each trial. For calculation of intra-observer variability, the spatial locations of the fiducial points marked by the same observer in two different trials performed two-weeks apart were considered, e.g., the location of the right nipple marked by Observer 1 in trial 1 and that marked by the same observer in trial 2.

The comparison of the spatial locations of the fiducial points was performed by computing the distance between the two points under consideration. That is, in the case of intra-observer variability, the distance between the location of a fiducial point identified by an observer in the first trial and the location marked by the same observer in the second trial. Similarly, for inter-observer variability the distance between the coordinates of the same fiducial point located by two different observers in the same trial was computed. In this study, the following criterion was used to determine variation in the annotation of fiducial points. Tolerance thresholds were used in the classification of precision for marking points.²¹ If the average distance (D_avg) between two points met the condition 0 ≤ D_avg ≤ 7 mm, the variability between the two points was low (negligible), whereas if D_avg > 7 mm, the variability in the annotation of the points was deemed to be high. This criterion was based on anthropometric measurements of the diameter of the nipple, which is estimated to be in the range of 1.00–2.75 cm with a mean value of 1.53 (± 0.37) cm.^22,23 These data suggest that any point that falls within the average radial distance of approximately 7.65 mm could be annotated as a nipple. Thus, we chose a conservative estimate of 0 ≤ D_avg ≤ 7 mm as the criterion for low variability. Since the sternal notch is a subtle landmark that is more difficult to locate and typically has a larger diameter than the nipple, the criterion chosen also provides an appropriate, albeit stringent, criterion for assessment.

Tables 1A and 1B present the inter-observer variability in the annotation of the three fiducial points for the 15 different combinations of the six observers taken in pairs at a time, for the HD and the HH poses, respectively. For all 15 comparisons, the lowest variability (i.e., D_avg << 7 mm) was found to be in the annotation of the nipples. The average distance for both the right and left nipples (i.e., 24 points from 12 subjects) was found to be D_avg = 4.5 ± 1.1 mm for the HD pose. A similar trend was observed for the HH pose, with one exception, where the spatial location of right nipple between Observer 3 and Observer 4 was an outlier with a value of 7.3 mm. Higher inter-observer variability was observed for both the HD and HH pose in the annotation of the sternal notch with values of D_avg > 7 mm (D_avg = 7.8 ± 1.5 mm for HD and D_avg = 9.4 ± 2.9 mm for HH).

Table 1A.

Inter-observer variability in localization of fiducial points. For most images the average distance (MEAN_HD ± STD_HD) between annotations of fiducial points by two different observers is less than 1 cm. Although for few cases we get higher variation, on inspection of the two annotations visually, they seem to represent the same fiducial point (see Fig. 3B).

Inter-observer variability for HD pose (mm)
MEAN_HD	Obs.1-Obs.2	Obs.1-Obs.3	Obs.2-Obs.3	Obs.2-Obs.4	Obs.1-Obs.4
Nipple left	4.42	3.36	5.03	4.51	3.19
Nipple right	3.36	5.61	4.89	3.54	3.89
Sternal notch	7.01	7.45	6.42	6.75	9.40
STD_HD
Nipple left	2.88	3.90	3.55	3.51	3.96
Nipple right	2.65	6.06	5.22	2.24	3.02
Sternal notch	3.35	4.44	5.46	4.09	3.85
MEAN_HD	Obs.1-Obs.5	Obs.3-Obs.5	Obs.2-Obs.5	Obs.4-Obs.5	Obs.3-Obs.4
Nipple left	3.26	4.81	4.14	4.85	4.67
Nipple right	3.69	6.24	3.34	4.06	6.94
Sternal notch	8.09	7.45	6.77	8.98	11.28‡
STD_HD
Nipple left	2.77	3.83	3.90	4.03	5.05
Nipple right	2.54	5.92	2.72	2.42	5.21
Sternal notch	4.47	3.83	3.81	5.89	7.62
MEAN_HD	Obs.6-Obs.1	Obs.6-Obs.2	Obs.6-Obs.3	Obs.6-Obs.5	Obs.6-Obs.4
Nipple left	3.60	5.19	6.50	3.92	4.91
Nipple right	3.70	4.65	5.62	5.20	5.36
Sternal notch	8.06	4.73	8.50	8.40	8.32
STD_HD
Nipple left	3.49	5.38	3.72	3.06	3.84
Nipple right	4.63	4.62	6.18	3.82	4.26
Sternal notch	4.64	3.75	5.23	4.49	4.49

Note:

^‡Measurements where the difference between two observers is more than 1 cm.

The intra-observer variability in the repeated annotation of the three fiducial points for a given observer across two different trials is presented in Tables 2A and 2B, for the HD and HH poses, respectively.

Table 2.

The intra-observer results are better than inter-observer variability results. For few points the mean distance is greater than 5 mm but when inspected visually, these points represent the same fiducial points.

A. Intra-observer variability in localization of fiducial points for HH pose (mm)
MEAN_HD	Obs.1	Obs.2	Obs.3	Obs.4	Obs.5	Obs.6
Nipple left	2.28	4.68	4.90	3.37	3.83	4.91
Nipple right	5.39	2.86	6.13	4.31	3.74	4.51
Sternal notch	4.92	3.90	7.53	8.39	5.41	6.15
STD_HD
Nipple left	2.23	3.44	4.09	2.46	3.00	4.49
Nipple right	3.99	3.34	5.21	2.85	2.46	5.08
Sternal notch	3.71	4.17	4.26	5.16	4.00	5.44
B. Intra-observer variability in localization of fiducial points for HH pose (mm)
MEAN_HH	Obs.1	Obs.2	Obs.3	Obs.4	Obs.5	Obs.6
Nipple left	3.72	4.22	3.05	4.56	4.80	3.18
Nipple right	4.51	3.14	4.50	4.69	3.67	4.95
Sternal notch	4.67	5.56	5.72	5.54	6.41	5.18
STD_HH
Nipple left	2.74	2.26	2.97	2.74	1.29	2.85
Nipple right	3.76	2.42	4.49	3.76	4.11	3.83
Sternal notch	4.87	3.24	5.27	4.87	2.48	3.46

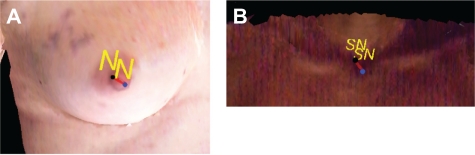
Low variability (D_avg = 4.2 ± 1.08 mm for HD and D_avg = 4.1 ± 0.69 mm for HH) was observed in the identification of nipples, whereas localization of the sternal notch showed slightly higher variability (D_avg = 6.05 ± 1.6 mm for HD and D_avg = 5.5 ± 0.57 mm for HH). Overall, the observers were found to be more consistent over time in marking all of the fiducial points for both poses as indicated by lower intra-observer variability when compared to the inter-observer variability. It should be noted that although we have quantitatively defined D_avg > 7 mm as an indication of high variability in the annotation of fiducial points, a qualitative visualization of fiducial points identified at distances greater than 1 cm (10 mm) apart appears to be in close proximity and within the local area of the landmark. For example, as seen in Figure 3A and 3B, fiducial points at a distance of 1 cm are found to be located within the local neighborhood of the landmark and, thus, can be qualitatively visualized to be the appropriate representations of the same fiducial point.

Figure 3.

Inter- and intra-observer variability in localization of fiducial points. A) The black and blue points are marked by the same user in two different trials. Although 1 cm apart from each other, they represent the same fiducial point i.e., Nipple. B) Similarly, the black and blue points are the points marked by two different observers. These points are greater than 1 cm apart but when observed on the image, they represent the SN. This indicates despite the variability (∼10 mm) in localizations of fiducial points, the calculation of 3D pBRA is reliable as long as these points represent the same fiducial point.

Inter- and intra-observer variability in 3D pBRA

Next, we assessed if there was any bias in the computation of the 3D pBRA index that was determined based on the distances measured between the manually annotated fiducial points. ICC was used to assess inter- and intra-observer variability in the 3D pBRA index. As shown in Table 3, for the intra-observer case, there is excellent agreement (ICC ≥ 0.75) between the two trials. Similarly, for inter-observer variability (Table 4), we found good agreement between the 3D pBRA index values for both poses. In spite of the slightly higher variability in localization of the sternal notch, the 3D pBRA index showed low variability. A probable explanation is that the slight variations (≤1 cm) in the annotation of fiducial points are negligible in the computation of the 3D pBRA index since the distances used for the calculation of pBRA are significantly larger (range of 10–25 cm). These data suggest that the computation of the 3D pBRA index is invariant to inter- and intra-observer variability in the annotation of fiducial points with a tolerance limit of at least 1 cm.

Table 3.

ICC for intra-observer variability of 3D pBRA. There was excellent agreement for both the poses.

Pose	Obs.1	Obs.2	Obs.3	Obs.4	Obs.5	Obs.6
HD	0.85	0.87	0.84	0.83	0.82	0.75
HH	0.81	0.77	0.76	0.68	0.80	0.77

Table 4.

ICC for inter-observer variability of 3D pBRA. There was good agreement for both the poses.

Trials	HD	HH
1	0.6755	0.6935
2	0.7421	0.6622

Agreement between 2D pBRA and 3D pBRA

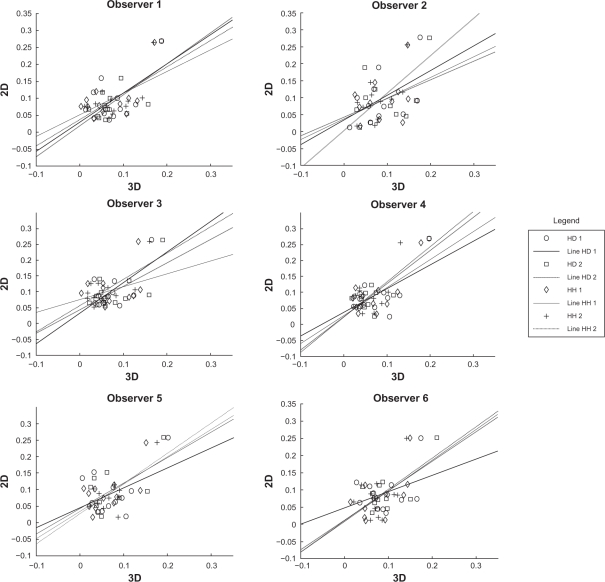
For each subject we computed two symmetry measures for each pose, first the 3D pBRA index, and second the 2D pBRA index. Table 5 shows the results of Pearson correlation coefficient analysis between 2D pBRA and 3D pBRA for each observer and for each pose. Though we have results for two trials, we performed the 2D measurements only once since the aim of 2D measurements was to provide a reference for validation of 3D pBRA. Thus, the same 2D pBRA index was used for estimating the agreement between trial one as well as trial two measurements of the 3D pBRA index. Although for a few cases (highlighted with ‡ in Table 5), the test failed to show statistical significance (results having P-value > 0.05), for all the observers the correlation plots shown in Figure 4, clearly show linear correlation between 2D and 3D pBRA index. The positive correlation between 2D and 3D pBRA implies that the 3D pBRA index is a valid symmetry measure for stereophotogrammetry.

Table 5.

Assessment of the correlation between 2D and 3D pBRA index. Overall the results show a high association between 2D and 3D pBRA. Correlation coefficient (ρ), P-value to test the hypothesis of no correlation (P-val), Hands-down pose (HD), Hands-on-hip pose (HH), Trial number (T#).

Observers	Obs.1	Obs.2	Obs.3	Obs.4	Obs.5	Obs.6
ρ_HD_T1	0.621	0.521*	0.658	0.634	0.470*	0.385*
P-val_HD_T1	0.031	0.082‡	0.020	0.027	0.123‡	0.216‡
ρ_HH_T1	0.686	0.405*	0.666	0.811	0.646	0.679
P-val_HH_T1	0.014	0.192‡	0.018	0.001	0.023	0.015
ρ_HD_T2	0.593	0.429*	0.338*	0.700	0.639	0.609
P-val_HD_T2	0.042	0.164‡	0.283‡	0.011	0.025	0.035
ρ_HH_T2	0.637	0.610	0.685	0.624	0.683	0.482*
P-val_HH_T2	0.026	0.035	0.014	0.030	0.014	0.113‡

Notes:

^‡P-value > 0.05;

^*ρ < 0.05.

Figure 4.

Graphs showing linear correlation between 2D and 3D pBRA. Despite few outliers in Table 3, the data suggests high association between the 2D and 3D pBRA measures. This validates the newly introduced 3D pBRA index.

Comparison of 3D pBRA index for the hands-down and hands-on-hip poses

ANOVA was used to determine the effect of pose on the symmetry measure 3D pBRA. We defined our null hypothesis as; Ho:3D pBRA index for HD and HH poses are equivalent. The 3D pBRA index for the two different poses was compared for each observer, i.e., we had 6 comparisons per trial and the results of these comparisons for both the trials are as shown in Table 6. If P-value < 0.05, it implies that there is a significant difference between the sample means and the null hypothesis is rejected. As shown in Table 6, F_calculated < F_critical and P-value > 0.05 for the 3D pBRA index computed for all the observers in both the trials. Thus, we fail to reject the null hypothesis. These data suggest that we cannot statistically conclude that the 3D pBRA is different for the HH and HD pose, which implies that the subject’s pose may not influence the computation of the 3D pBRA index.

Table 6.

Results for ANOVA test for comparison of HD and HH pose. F_calculated < F_critical, thus we fail to reject the null hypothesis, that the 3D pBRA for both the poses are same; in other words, they are equivalent at a 95% confidence level.

Statistics	Obs.1	Obs.2	Obs.3	Obs.4	Obs.5	Obs.6
ANOVA test for Trial 1
Fcalculated	0.062	0.008	0.001	0.160	0.513	0.218
P-value	0.805	0.929	0.975	0.693	0.481	0.645
Fcritical	4.300	4.301	4.300	4.301	4.301	4.301
ANOVA test for Trial 2
Fcalculated	0.093	0.791	1.120	0.292	0.0004	0.218
P-value	0.763	0.383	0.301	0.594	0.983	0.645
Fcritical	4.301	4.301	4.301	4.301	4.301	4.301

Discussion

Over the past few years, engineering quantification is finding an increasing role in clinical medicine. Likewise, in the field of reconstructive surgery, stereophotogrammetry is currently under scrutiny to allow pre- and post-operative objective assessment of breast morphology. Most quantitative measures are based on distance calculations between fiducial points on the torso. There have been anecdotal suggestions that annotations of fiducial points as well as measurements of distances between these points may be affected by the subject’s pose during image acquisition. An invalidated notion is that pose can affect not only the viewer’s perception about the image, but it can also affect the quantitative measurements performed on the image. To this end, studies have preferentially selected a particular pose (e.g., arms raised pose),^12,16 without justifying or validating this choice. The standardization of the subject’s pose for anthropometry and photogrammetry has been a matter of debate since the 1950’s when photogrammetry was first introduced for anthropometric measurements.²⁴ Typically, any effects introduced due to inappropriate pose are difficult to mitigate and hence the emphasis has been to determine the most appropriate pose prior to image acquisition. A recent study evaluated the effect of pose on the reliability of stereophotogrammetric measurements for quantitative assessment of facial geometry for the diagnosis of fetal alcohol syndrome. ²⁵ They found that for facial imaging it was not only important to obtain images while the subject was in the correct pose but it was critical that all cameras in the stereophotogrammetric system capture images at the same instant. However, there are no studies to date that have addressed this issue for 3D imaging of the human torso. In this study, we evaluate the effect of pose on the 3D assessment of breast morphology. Symmetry of breasts plays an important role in breast reconstructive surgery. Accordingly, objective measures developed for breast symmetry such as the BRA and pBRA index have been used for both anthropometric and photogrammetric evaluation of surgical outcomes.^17,18 In this study, we introduced a 3D extension to the conventional 2D pBRA index—3D pBRA for stereophotogrammetry using the contoured distances measured on 3D surfaces. We validated the 3D pBRA using its 2D counterpart, i.e., 2D pBRA for each observer. We used Pearson’s Correlation Coefficient to show the association between the two measures and thereby validate the use of the 3D pBRA index for assessment of symmetry in 3D images. Furthermore, we also determined the inter- and intra- observer variability in the calculation of the 3D pBRA index from manually annotated fiducial points. For the manual annotation of points, we found that the position of nipples was identified more reliably than that of the sternal notch. Higher variability in the annotation of the sternal notch is expected, since 1) the sternal notch defines a larger area compared to the area defined by each nipple, and 2) there are often no prominent physical characteristics for the sternal notch and typical manual identification involves palpation of the soft tissue to feel underlying bony landmarks, which is not feasible in images and this problem is particularly difficult in subjects with high body mass index (BMI). However, on the other hand when two annotations for sternal notch are visually inspected on the image, they appear to represent the same local neighborhood for sternal notch identification (as shown in Fig. 3B), and would have been reliably identified if a larger tolerance threshold were applied. Also, it should be noted that the 3D images used in this study were acquired using an older version, the DSP 800 imaging station which allows acquisition of a 3D point cloud consisting of ∼15,000 points. In contrast, the current model employs high resolution cameras and supports acquisition of a 3D point cloud of ∼75,000 points. Thus, it is likely that low precision in the identification of fiducial points is due to the low resolution of the imaging system. An increased resolution would minimize the variation and increase the precision in the annotation of fiducial points. Even with the low precision in marking fiducial points, the measurement of 3D pBRA was found to be robust, since the contoured distances between fiducial points used for calculation of 3D pBRA index, are relatively much larger in dimensions than the discrepancy found in localization of fiducial points.

Finally, we evaluated the effect of the subject’s pose on the calculation of the 3D pBRA index. From our analysis of intra- and inter-observer variation in computing the 3D pBRA index, we found that there is no significant difference in the measurements for both poses. We also observed that the pose does not affect the measurement of 3D pBRA. Results of a single factor ANOVA test for all the observers resulted in failure to reject the null hypothesis that the 3D pBRA for both the poses are same; in other words, they are equivalent at a 95% confidence level. This study not only introduced and validated a 3D symmetry measure but also showed that the pose has negligible effect on its measurements. Moreover, this study further corroborates the advantages of 3D stereophotogrammetry over 2D photography. Problems with pose that are inherent in 2D photographs are avoided and fiducial point identification is made easier by being able to panoramically rotate the 3D surface enabling views from any desired angle.

Table 1B.

Inter-observer variability in localization of fiducial points for subjects in HH pose. The results for HH pose are similar to those in HD pose. When the annotations are viewed on 3D images, they appear to represent the same fiducial point.

Inter-observer variability for HH pose (mm)
MEAN_HH	Obs.1-Obs.2	Obs.1-Obs.3	Obs.2-Obs.3	Obs.2-Obs.4	Obs.1-Obs.4
Nipple left	2.52	3.84	3.75	4.35	5.11
Nipple right	2.64	5.76	5.71	4.28	5.26
Sternal notch	7.49	13.35‡	7.43	8.25	7.00
STD_HH
Nipple left	3.30	2.23	2.19	3.27	3.57
Nipple right	3.22	3.75	4.81	6.96	6.94
Sternal notch	3.89	4.81	5.40	5.97	4.23
MEAN_HH	Obs.1-Obs.5	Obs.3-Obs.5	Obs.2-Obs.5	Obs.4-Obs.5	Obs.3-Obs.4
Nipple left	3.81	4.64	3.91	5.83	5.00
Nipple right	3.24	6.73	4.48	4.66	7.28
Sternal notch	12.91‡	6.98	5.58	13.15‡	14.88‡
STD_HH
Nipple left	2.01	2.49	2.04	3.81	4.89
Nipple right	4.43	4.90	4.11	3.08	6.39
Sternal notch	6.63	4.61	4.99	7.44	8.87
MEAN_HH	Obs.6-Obs.1	Obs.6-Obs.2	Obs.6-Obs.3	Obs.6-Obs.5	Obs.6-Obs.4
Nipple left	3.05	3.32	4.40	3.49	4.93
Nipple right	3.84	4.96	5.44	3.38	5.43
Sternal notch	9.41	5.83	11.31‡	9.67	8.07
STD_HH
Nipple left	2.49	2.68	2.33	3.12	3.59
Nipple right	4.52	3.94	5.53	2.09	2.78
Sternal notch	4.24	3.55	7.02	4.88	4.05

Note:

^‡Measurements where the difference between two observers is more than 1 cm.