Quantitative Assessment of Macromolecular Concentration during Direct Infusion into an Agarose Hydrogel Phantom using Contrast-Enhanced MRI

Abstract

Convection-enhanced delivery (CED), i.e., direct tissue infusion, has emerged as a promising local drug delivery method for treating diseases of the nervous system. Determination of the spatial distribution of therapeutic agents after infusion is important in evaluating the efficacy of treatment, optimizing infusion protocols, and improving the understanding of drug pharmacokinetics. In this study, we provide a methodology to determine the concentration distribution of Gd-labeled tracers during infusion using contrast-enhanced MR imaging. To the best of our knowledge, MR studies that quantify concentration profiles for CED have not been previously reported. The methodology utilizes intrinsic material properties (T₁ and R₁) and reduces the effect of instrumental factors (e.g., inhomogeneity of MR detection field). As a methodology investigation, this study used an agarose hydrogel phantom as a tissue substitute for infusion. An 11.1 T magnet system was used to image infusion of Gd-DTPA labeled albumin (Gd-albumin) into the hydrogel. By using data from preliminary scans, Gd-albumin distribution was determined from the signal intensity of the MR images. As a validation test, MR-derived concentration profiles were found comparable to both results measured directly using quantitative optical imaging and results from a computational transport model in porous media. In future studies, the developed methodology will be used to quantitatively monitor the distribution of Gd-tracer following infusion directly into tissues.

INTRODUCTION

Recently, direct infusion of therapeutic agents, i.e., convection-enhanced delivery (CED), into the parenchyma of nervous tissues has emerged as a promising drug delivery method for treating diseases of the nervous system. CED circumvents vascular barriers and enhances the interstitial (extracellular) transport by introducing convective flow. Previous nervous tissue infusion studies have shown CED to be reproducible and clinically safe [1-4].

Concentration distribution of therapeutic agents after infusion is significantly related to the CED protocol (e.g., selection of infusion site, infusate concentration, and infusion rate). Concentration distribution also plays an important role in the efficacy of treatment [5-7]. Real-time monitoring of agents transported within nervous tissues will not only provide information on the drug-affected region, but also improve the understanding of drug pharmacokinetics and aid clinical protocol design. Due to its noninvasive nature, experimental contrast-enhanced MRI methods have been developed to monitor agents distribution during infusion [1, 3, 8]. For example, Krauze et al. [8] used real-time imaging of Gd-labeled liposomes to quantify distribution volumes after infusion into the primate brain. These previous CED studies have not investigated the relationship between signal intensity and tissue concentration of Gd-labeled tracers. Also, only distribution volumes rather than spatial concentration profiles were quantified. Recently, Kim et al. [9] used a signal-concentration reference table to determine the spatial concentration profile of a drug released from an implant into vitreous of rabbit eyes. The table was obtained by imaging calibration vials with varying concentrations of Gd-DTPA in gels, which mimic vitreous. Such a method may be difficult to implement in vivo where calibration samples may not capture the heterogeneity of tissues. Accuracy of a reference table may also decrease if the MR excitation or detection field is inhomogeneous. Further examination of the mechanism of signal intensity enhancement by contrast agents may improve and simplify the determination of spatial concentration distribution during direct infusion.

More fundamental MR imaging studies [10-13] have investigated the mechanism of signal enhancement by contrast agent in tissues or solutions. Early studies [10, 11, 14] have examined the effect of a contrast agent on water relaxation rates, i.e., 1/T₁ and 1/T₂, in tissue. These studies found that changes in water relaxation rates are proportional to the agent concentration through the contrast agent relaxivities, R₁ and R₂. Recent studies [12, 15, 16] have investigated the sensitivity of relaxivities to environmental factors, such as magnetic field strength and solvent media. Analysis methods and imaging procedures based on relaxivities have been investigated to map signal intensity to agent concentration [17-19]. These studies generally used fluid media as a solvent, since the concentration is uniform and easier to verify than in structured media. Hittmair et al. [17] determined the relative Gd-DTPA concentration in distilled water defined as a relative change of MR signal before and after the addition of a contrast agent. More recently, Morkenborg et al. [18] investigated the capacity of different pulse sequences to quantify Gd-DTPA concentrations in human plasma. Concentration was determined by numerically solving a nonlinear equation that related the concentration with the ratio of signal intensity before and after doping the plasma with contrast agents. These studies suggest that the absolute spatial concentration profile of a drug may be quantified during direct infusion using contrast-enhanced MRI.

The purpose of this study was to develop and validate a methodology for contrast-enhanced MR imaging to quantify the evolving spatial concentration distribution in a porous media during CED. To the best of our knowledge, MR studies that quantify concentration profiles for CED have not been previously reported. We present a data acquisition and analysis method to relate the signal intensity to the infusate concentration. The method utilizes intrinsic material properties (T₁ and R₁) and reduces the effect of instrumental factors (e.g., inhomogeneity of MR detection field). As a methodology study, this study used an agarose hydrogel phantom as a tissue substitute. Agarose hydrogels have been previously used as phantoms for nervous tissue studies [20, 21] and are well-characterized. An 11.1 T magnet system was used to obtain preliminary scans and image the infusion of Gd-DTPA labeled albumin (Gd-albumin), which has a molecular size similar to a therapeutic drug, into the hydrogel phantom. Calibration solutions were used to measure the relaxivities of Gd-albumin. Analysis of MR signal dependence on infusate concentration was conducted to optimize the dynamic range of MR signal. By using T₁-weighted scans of the hydrogel before and during infusion, signal enhancement was calculated and radial concentration profiles along the infusion site were derived. As a validation test, MR-derived concentration profiles were compared with results measured directly using quantitative optical imaging and with results from a computational transport model for porous media.

THEORY

Relationship between Concentration and Signal Intensity

Signal intensity from conventional spin-echo (SE) MR imaging is expressed as [22]

$$S=S_0(1-e^{-TR∕T_1})e^{-TE∕T_2}$$ (1)

where TR is the time for recovery, TE is the time of echo, and S₀ is the maximum signal intensity determined by proton density and instrument factors, such as the resonance frequency, and the receiving coil geometry. The effects of contrast agent on relaxation times are governed by [10, 13, 23]

$$1∕T_1=1∕T_{10}+R_1\cdot c$$ (2)

$$1∕T_2=1∕T_{20}+R_2\cdot c$$ (3)

where T₁₀ and T₂₀ are the relaxation times without contrast agent, T₁ and T₂ are the relaxation times with contrast agent at a concentration c, and R₁ and R₂ are the longitudinal and transverse relaxivities of the contrast agent on water, respectively. Substituting Eqs. (2) and (3) into (1) results in the relation

$$S\left(c\right)=S_0[1-e^{-TR(1∕T_{10}+R_1\cdot c)}]\cdot e^{-TE(1∕T_{20}+R_2\cdot c)}$$ (4)

which is the enhanced signal after addition of a contrast agent. The signal enhancement is defined as

$$\frac{S\left(c\right)}{S\left(0\right)}=\frac{[1-e^{-TR(1∕T_{10}+R_1\cdot c)}]\cdot e^{-TE(1∕T_{20}+R_2\cdot c)}}{[1-e^{-TR∕T_{10}}]\cdot e^{-TE∕T_{20}}}$$ (5)

where S(c) and S(0) are the signal intensities at concentrations c and zero, respectively. For T₁-weighted imaging, the infusion concentration was selected such that exp(TE · R₂ · c) ≈ 1. Thus

$$c=\frac{1}{R_1}[\frac{1}{TR}\ln \frac{S\left(0\right)}{S\left(0\right)-S\left(c\right)\cdot (1-e^{-TR∕T_{10}})}-\frac{1}{T_{10}}]$$ (6)

Equation (6) relates the signal intensity to the contrast agent concentration for known values of R₁, S(0), and T₁₀.

Signal in the Presence of Noise

A low signal-to-noise ratio (SNR) may significantly affect the accuracy of estimated concentrations. Zero-mean Gaussian noise was assumed and the confounding effect of noise on the measured signal was removed by using [24, 25]

$$\langle S\rangle =\sqrt{\langle M^2\rangle -2{\sigma }^2}$$ (7)

where 〈S〉 is the average signal intensity within a region of interest (ROI) (for simplicity, the bracket is dropped when referring to 〈S〉 thereafter), 〈M²〉 is the average of the square measured-image-intensity, and σ is the standard deviation of observed noise.

The level of SNR also determines the minimum detectable concentration. The relative signal enhancement (RSE) was defined as

$$RSE=\frac{S\left(c\right)-S\left(0\right)}{S\left(0\right)}$$ (8)

For a given SNR value, we assumed that the enhancement is not detectable if $RSE<\epsilon \frac{\sigma }{S\left(0\right)}$, where ε is a factor to increase or decrease the stringency of criteria (ε = 1 was used). That is, if the signal increment, S(c) – S(0), is less than the noise level, σ, the concentration is not detectable. The minimum detectable concentration, c_min, can be found using Eq. (6) where S(c) is defined by

$$S\left(c_{\min }\right)=\sigma +S\left(0\right)$$ (9)

Porous Media Model of Direct Infusion

Infusion into hydrogels can be modeled as an infusion into rigid porous media [26]. Fluid flow in rigid porous media, without source and sink terms, satisfies the continuity equation

$$\nabla \cdot {\mathbf{v}}^f=0$$ (10)

and Darcy's law

$$\varphi {\mathbf{v}}^f=-k\nabla p$$ (11)

where ϕ is the porosity, i.e., fractional volume of fluid in the porous media, k is the hydraulic permeability, v^f is the fluid velocity in the porous media, and p is the pore pressure.

Transport of a non-binding, non-reacting agent, such as albumin, is described by the convection-diffusion equation

$$\frac{\partial c}{\partial t}+\nabla \cdot (c{\mathbf{v}}^f-{\mathbf{D}}_{eff}\cdot \nabla c)=0$$ (12)

where c is the solute concentration in the hydrogel, and D_eff is the effective diffusivity of solute in the hydrogel.

MATERIALS AND METHODS

Materials

A stock solution of 25 mg/mL Gd-albumin (Galbumin, BioPAL Inc., Worcester, MA) was used, which has 10-15 Gd-DTPA per albumin molecule and a molecular weight of 70 kDa. This solution was diluted with deionized water into ~100 μL calibration vials at concentrations of 2, 4, 6, 8, 10, 11, 12, 13, 14, 15 mg/mL. Calibration vials based on this series were used for T₁ and T₂ measurements to obtain R₁ and R₂ values. Hydrogel calibration vials were not used due to the extremely slow diffusion of albumin in the hydrogel. A diluted concentration of 10 mg/mL was used for hydrogel infusion studies. In addition, Gd-albumin was mixed with Evans blue for visualization purposes and direct optical measurement of the concentration. The concentration of Evans blue (1 mg Evans blue per 2 mL stock solution of Gd-albumin) was low enough that Evans blue was completely bound to the albumin.

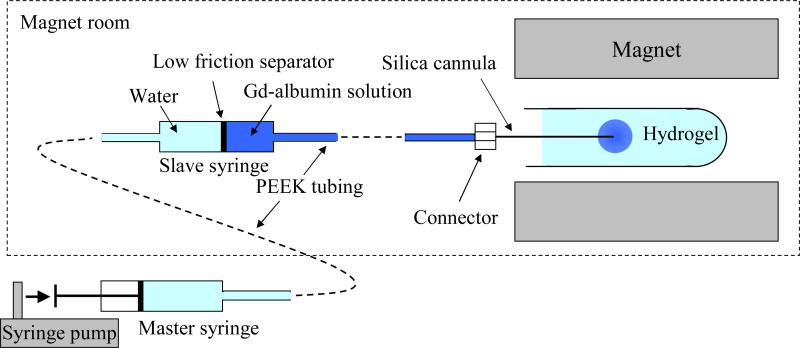
For infusion studies, ~15 mL of 1% (w/w) agarose-based hydrogel (TreviGel 5000, Trevigen, Inc., Gaithersburg, MD) was prepared in 15 mL plastic test tubes. A custom MR-compatible infusion system was designed and built (shown in Fig. 1). A silica cannula (ID = 50 μm, OD = 147 μm) was inserted ~2 cm into the hydrogel. This cannula was coupled to a non-metallic hydraulic drive which consisted of modified gas-tight syringes (100 μL luer-tip syringe, Hamilton, Reno, NV) and PEEK tubing (Upchurch Scientific, Oak Harbor, WA). The hydraulic drive allowed placement of the syringe pump remote from the high magnetic field. The infusion was delivered at a constant rate of 0.29 μL/min over 91 min (total 26 μL).

Figure 1.

Schematic of the infusion system setup.

MR Imaging

MR imaging procedures were conducted at room temperature (~25 °C) using a Bruker Avance 11.1 T magnet system (Bruker NMR Instruments, Billeria, MA) with a custom quadrature birdcage MR coil used for excitation and detection. To excite the ROI homogeneously (e.g., to reduce the flip angle variation within the ROI), samples were placed at the center of the cylindrical birdcage coil where a homogeneous excitation field was expected. T₁ and T₂ values were measured in calibration vials with various Gd-albumin concentrations. For T₁ measurements, a SE sequence was used with TR = 250, 500, 1000, 2000, 4000 ms, TE = 15 ms, and 2 averages. For T₂ measurements, a SE sequence was used with TE = 15, 30, 45, 60, 75, 100, 125 ms, TR = 2000 ms, and 3 averages. The T₁ and T₂ values of agarose hydrogel were also measured by using the same method. Multi-slice T₁-weighted MR imaging of infused region before and during infusion were performed with TR = 330 ms, TE = 9.4 ms, and 6 averages. For all sequences, the image resolution was 0.229 mm × 0.229 mm × 1.0 mm per voxel.

MRI Data Processing

T₁ and T₂ values were obtained by fitting mono-exponential curves to signal values of the variable TR and TE experiments using a least square error method. Using the calculated values of T₁ and T₂, relaxivity values of R₁ and R₂ were calculated using Eqs. (2) and (3). T₁₀ and T₂₀ of the hydrogel were also calculated and used together with R₁ and R₂ values to estimate a range of infusate concentrations, which provides distinct signal contrast at different concentrations of contrast agent. Following pre-infusion MR scans to measure S(0), infusion and simultaneous MR scanning were performed to measure S(c) at different times. Spatial concentration profiles were then obtained using Eq. (6).

Quantitative Optical Measurement of Concentration

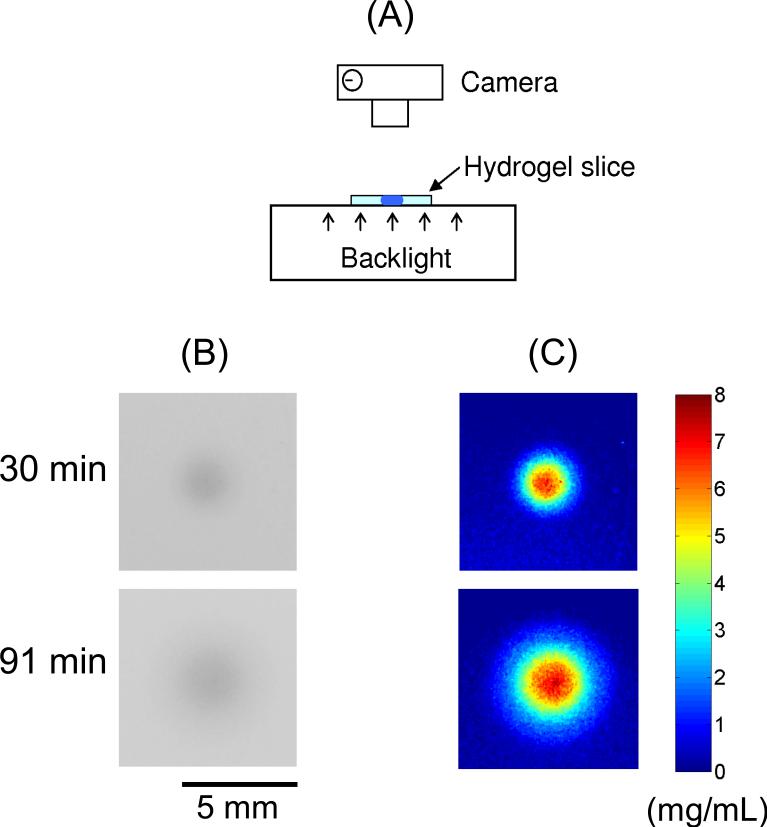
With the same infusion configuration that was used in MRI experiments, Evans-blue-bound Gd-albumin concentration was also measured directly using optical imaging. After infusing 30 and 91 min, hydrogels were cut into slices with ~ 1 mm thickness. The slice with the maximum distribution radius at each time point was used for concentration measurement and the slice thickness was also measured. A fluorescent light box was used to backlight the transparent hydrogel slices and images were recorded using a digital SLR camera (Nikon D50) fixed on a tripod. Pixel intensity from each image was converted to dye concentration by using Beer's law[27], which is log₁₀(I₀/I₁) = αhc, where I₀ and I₁ are the light intensity entering and leaving the hydrogel slice, respectively; α is the absorption coefficient of the dye; h is the slice thickness, and c is the dye concentration. A calibration solution, with a known concentration of Evans-blue-bound Gd-albumin (10 mg /mL), was used to measure α, so that the Evans-blue-bound Gd-albumin concentration in the hydrogel could be quantified. Figure 2 shows the optical imaging method used in this study and typical recorded optical images and calculated concentration maps at two time points.

Figure 2.

Schematic of the optical imaging method used to measure the concentration of Evans blue labeled Gd-Albumin in the hydrogel slice is shown in (A). Part (B) shows recorded grayscale optical images and part (C) shows the calculated concentration maps. The conversion from the pixel intensity to the dye concentration was based on Beer's law [27].

Simulation of Infusion into Porous Media

A finite element model for the infusion into porous media was implemented using COMSOL (v.3.0, COMSOL, Burlington, MA). We modeled infusion into a spherical isotropic porous media (radius = 7.5 mm) from a spherical infusion cavity ( radius = 75 μm, corresponding to the OD of infusion cannula) at the center. Constant concentration and constant flow rate of 0.29 μL/min were applied to the embedded infusion cavity. Zero pore pressure was applied at the outer surface of the spherical porous media since it is large enough that the pore pressure decayed to approximately zero.

Fluid velocity, v^f, was first obtained by solving Eqs. (10) and (11). A hydraulic permeability, k = 1.427 × 10^-12 m⁴N^-1s^-1 was used. This value was measured using a custom permeameter system [28], which measured the pressure drop (0.8-7.8 kPa) across a hydrogel membrane for a given flow (5-50μL/hr). It should be noted that, for a constant flow rate infusion, v^f is not sensitive to changes of k value and only pore pressure magnitude changes. By using the obtained v^f, spatial and temporal concentration profiles for Gd-albumin was solved using Eq. (12). The transport model was executed using different values of albumin diffusivities, D_eff = 1.0 – 9.0 (10^-11m²/s). This range is based on a previous study [29] where D_eff = 5.0 and 7.12 (10^-11m²/s) at temperatures of 25°C and 37°C, respectively, were directly measured for bovine serum albumin in 1% (w/w) agarose hydrogel. Also, curve fitting between MRI and simulation results was conducted to find an optimal diffusivity by comparing values of R², which measures the goodness-of-fit for nonlinear regression. Considering that the signal intensity in an MR image is an average over each voxel, concentrations obtained from porous media simulations were adjusted accordingly by averaging the concentration along the thickness of slice (1.0 mm) in the slice direction. Porosity of the hydrogel was estimated by the ratio of V_i to V_d. V_d is the distribution volume calculated by using the measured distribution diameter after infusion, and V_i is the volume infused. The measured ratio of V_i to V_d was ~0.6.

RESULTS

Measurement of T₁₀, T₂₀, R₁, and R₂ for the Hydrogel

Relaxation times, T₁₀ = 3.52 ± 0.323 s and T₂₀ = 0.117 ± 0.00141 s, were measured directly in the hydrogel. Relaxivities, R₁ = 22.3 ± 0.557 L/mmol-s and R₂ = 42.3 ± 2.53 L/mmol-s, were measured in water. The R₁ and R₂ values of the 1% agarose-based hydrogel were assumed to be equivalent to those measured in water because of the high water content ~ 99% (w/w) in the hydrogel.

Infusion Concentration Analysis

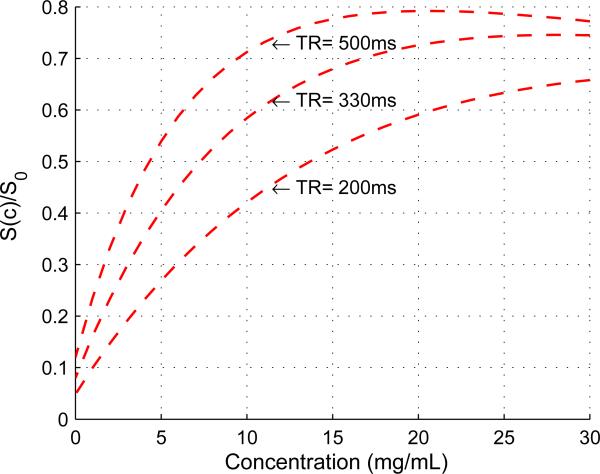
By using Eq. (4) and the measured parameter values, the signal intensity versus concentration relationship for T₁-weighted imaging was quantified. As shown in Fig. 3, signal intensity was found to increase with concentration for low concentration ranges and decrease at concentrations higher than a threshold value, at which the maximum signal intensity is reached. This threshold value changed for different TR values, e.g., 20 mg/mL for TR = 500 ms, and 29 mg/mL for TR = 330 ms.

Figure 3.

Plot of the theoretical relationship between concentration and signal intensity used to determine optimal infusate concentration (T₁-weighted imaging; Eq. (6)). Parameter values were based on our measurements (see Results).

To map the signal intensity change with changing agent concentrations, the range of low concentrations is desired due to the one-to-one relationship between signal intensity and concentration. In addition, a larger slope value of dS/dc (i.e., the sensitivity of signal intensity to the change of concentration) is desired since it gives a higher dynamic range, i.e., a broader range of signal intensity for a given range of concentrations. Longer TR values give higher dynamic ranges but increase the imaging time. For this study, TR = 330 ms and an infusate concentration of 10 mg/mL were selected to provide a relatively high dynamic range and a short imaging time.

MRI Results

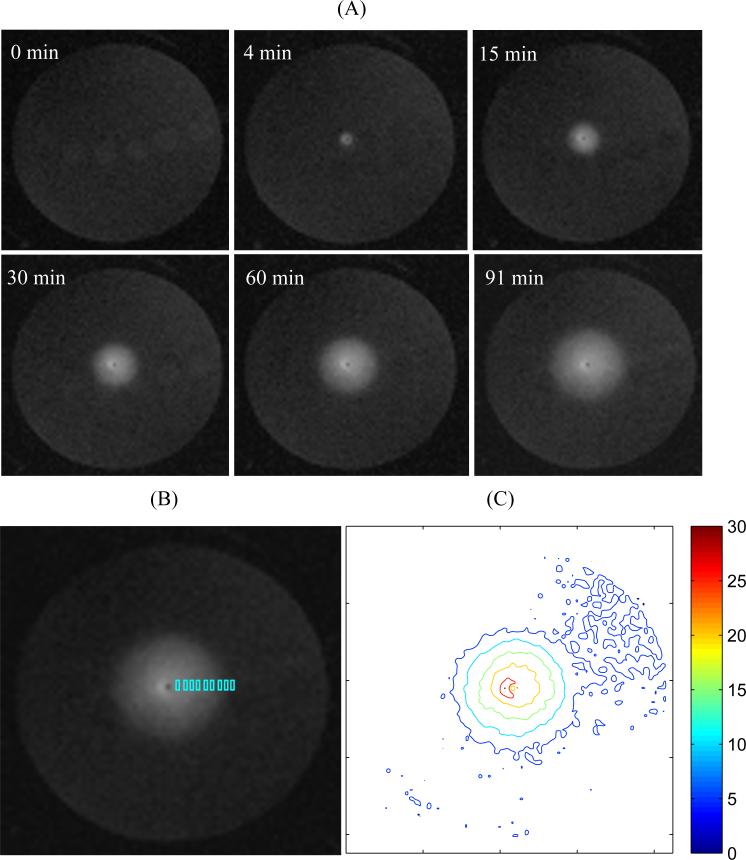
Figure 4 shows the evolution of the MR signal during infusion of Gd-albumin. The location of the silica cannula and infusion site was identified as a black dot in the image center (axial view across the test tube). MR images show a spherical distribution of Gd-albumin symmetric around the infusion site in the agarose hydrogel. Contours of MR signal show approximately concentric circles in the infusate-distributed region (Fig. 4C). The signal profile along the radial direction was obtained by sampling in small rectangular ROIs aligned in the radial direction (Fig. 4B). Small rectangular ROIs instead of individual pixels were used to calculate the local concentration because the contribution of noise can be reduced by using Eq. (7).

Figure 4.

(A) Evolution of T₁-weighted MR signal during infusion of Gd-Albumin into 1% agarose hydrogel at a rate of 0.29 μL/min (transverse image at approximate center of infusion site; the cannula is perpendicular to the transverse plane; slice thickness = 1 mm). (B) The signal profile in radial direction was obtained by sampling in the small rectangular regions of interest (ROIs) (~20 pixels in each rectangle). The final signal profile was obtained by sampling in the orthogonal directions symmetric around the infusion site. This figure only shows the sampling in the positive horizontal direction. The infusion cannula/site was identified by a black dot in the image center. (C) Contours of MR signal intensity at time = 91 min.

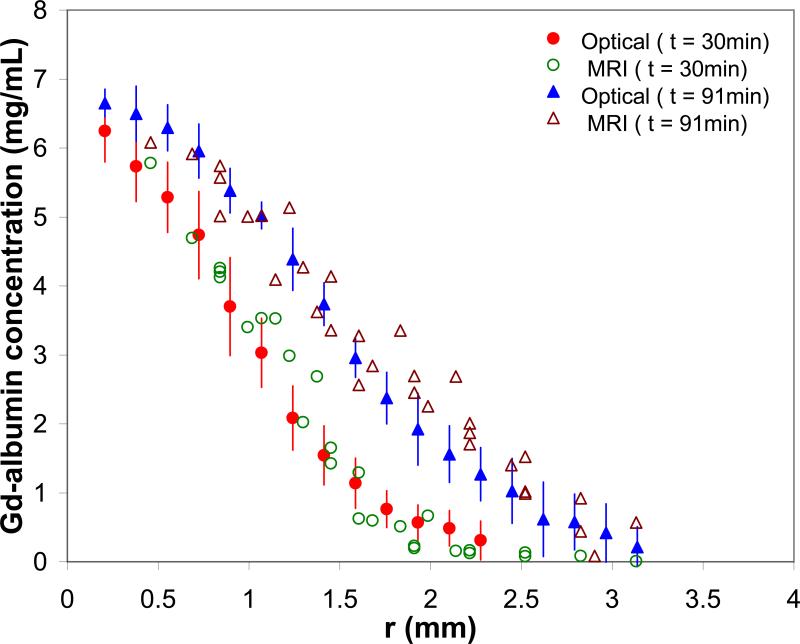
Figure 5 compares MRI-derived Gd-albumin concentration profiles with results measured using quantitative optical imaging at two different time points. The MR-derived concentration was obtained by converting the signal intensity to Gd-albumin concentration using Eq. (6). A maximum MR-derived concentration of 6.4 mg/mL was determined near the infusion site. This value is consistent with the estimated porosity, ~0.6, and the infusate concentration of 10 mg/mL since the dilution effect in porous media is described by, average concentration = porosity × infusate concentration. The MR-derived results correspond well with concentration profiles measured directly using optical imaging (R² = 0.94 and 0.92 at time = 30 and 91 min, respectively).

Figure 5.

MR-derived concentration of Evans blue labeled Gd-Albumin compared with profiles measured directly using quantitative optical imaging in a 1 mm thick hydrogel slice. R² = 0.94 and 0.92 at time = 30 and 91 min, respectively. Error bars are the standard deviation (n = 12) of the optical measures.

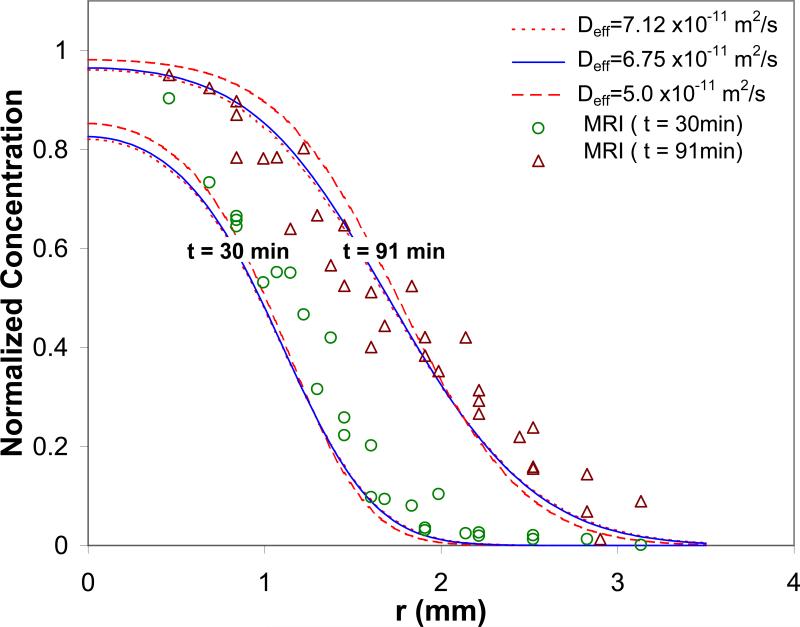
Figure 6 compares Gd-Albumin concentration profiles obtained by porous media transport simulations and MRI experiments. MR-derived concentration data corresponds well with the simulation profiles at higher values of reported diffusivity, e.g., D_eff = 7.12 × 10^-11 m²/s (R² = 0.91 at time = 30 and 91 min). By fitting MRI and simulation profiles, an optimal diffusivity was found to be D_eff = ~6.75 × 10^-11 m²/s (R² = 0.92 and 0.91 at time = 30 and 91 min, respectively; room temperature). This value is well within the measured range of 5.0 – 7.12 (10^-11 m²/s) for temperatures 25 – 37°C [29]. For the longer time infusion of 91 min, a good match was found in high concentration regions. MR-derived concentrations were slightly higher than those predicted by simulation within the low concentration region of the advancing front. For the shorter time infusion of 30 min, MR-derived concentrations were higher than those predicted by simulation.

Figure 6.

MR-derived concentration of Gd-Albumin compared with predicted porous media transport profiles at time = 30 and 91 min. Concentration was normalized by dividing by the maximum MR-derived concentration, 6.4 mg/mL. D_eff = 7.12 and 5.0 (10^-11 m²/s) were experimentally measured at temperatures 37 and 25°C, respectively, by Liang et al. [29]. D_eff = 6.75 (10^-11 m²/s) was the optimal diffusivity obtained in this study. For D_eff = 7.12, 6.75, and 5.0 (10^-11 m²/s), R² = 0.91, 0.91, and 0.84 for t = 91 min, and 0.91, 0.92, and 0.92 for t = 30 min, respectively.

DISCUSSION

In this study, we presented a methodology to quantify the concentration profiles of Gd-albumin following direct infusion into an agarose hydrogel. Measurements of relaxation times and relaxivities were first conducted using calibration samples. Analysis of MR signal dependence on infusate concentration was then conducted to optimize the dynamic range of MR signal intensity. T₁-weighted SE imaging was used to obtain the spatial-temporal signal evolution during infusion. Signal intensity was converted to Gd-albumin concentration using Eq. (6), using the measured R₁, S(0), and T₁₀ values. The MR-derived concentration profiles were found comparable to both results measured directly using quantitative optical imaging and results from a computational transport model.

Theoretical infusate concentration analysis showed that infusate concentration and imaging parameters, such as TR and TE, should be carefully chosen to obtain a broader dynamic range of MR signal and a one-to-one signal-concentration relationship. Choosing proper agent infusion concentration is important since concentrations that are too low may lead to a poor SNR and may not be detectable, and concentrations that are too high yield T₂ effects that diminish signal intensity and skew data. According to the analysis of minimum detectable concentration (Eq. (9)), Gd-albumin concentrations less than 0.1 mg/mL cannot be separated from noisy signal intensity for this experimental protocol. At high concentrations, the relaxivities will change. But Tweedle et al. [10] have found that relaxivities were invariant for Gd concentrations from 0 to 2 mmol/L in agar and blood solutions, respectively.

The signal-concentration relation (Eq. (6)) is based on T₁-weighted imaging, and it assumes that exp(TE · R₂ · c) ≈ 1. This assumption is reasonable since for the parameters in this study, exp(TE · R₂ · c) = 1.01 ~ 1.03 (R₂ ≈ 42.3 L/mmol-s, TE = 9.4 ms, MW = 70 kDa, and c = 1-6 mg/mL). Also, this term is not sensitive to changes of the R₂ value for the range of parameters in this study. The signal-concentration relationship may also be obtained by directly using Eq. (4), which necessitates quantifying the unknown S₀ (which may be obtained during T₁ or T₂ measurements). Hittmair et al. [17] used a modified form of Eq. (4) to define an enhancement factor, which required calculating [S₀ – S(0)]/[S₀ – S(c)] . They used a very low flip angle sequence to obtain S₀. However, S₀ is environment-dependent, e.g., depending on the receiving coil, and may be different for each MR measurement. Our method uses the relative signal change, S(c) / S(0), and avoids the need of measuring S₀. Using the ratio, S(c) / S(0), implies that the concentration calculation is minimally affected by the inhomogeneity of detection field, e.g., surface coils, where the non-uniform field will affect both S(c) and S(0) equally. Also, adiabatic pulses [30] can be used for MR excitation so that the SE sequence can be used with MR coils that have inhomogeneous fields. In addition, this study used a SE sequence and each scan took ~3 min. This time resolution is acceptable given the relatively slow velocities of albumin transport in the hydrogel (average radial velocity of 0.022 mm/min over the 91 min with a maximum of ~0.060 mm/min at the beginning of infusion).

R₁ and R₂ values measured in water solutions were used as an approximation for the relaxivities of water in agarose hydrogel. Previous studies [12, 15, 16, 31] show that R₁ values may be media-dependent, and the difference may be determined by the nature of different media, e.g., the macromolecular content. Stanisz et al. [12] and Rohrer et al. [16] measured different R₁ values for Gd-DTPA in water, powdered milk, egg white and plasma. In contrast, Donahue et al. [15] measured similar R₁ values in saline, plasma, uncompressed and compressed cartilage. However, the approximation in this study is reasonable given the high water content and fibrous structure (polysaccharide chain network) in the hydrogel. Stanisz et al. [12] have shown that at low macromolecular content, the variation of R₁ in water is negligible. In addition, since Gd-DTPA relaxivity is also affected by magnetic field strength, temperature, and the macromolecule to which it is attached, direct comparison of our results with other studies is difficult. Schmiedl et al. [32] reported a R₁ value for Gd-DTPA-Albumin (9 Gd-DTPA per albumin) to be 110 L/mmol-s measured at 0.25 T, 37 °C. Brasch [14] reported a R₁ value of 14.4 L/mmol-s per Gd for Albumin-Gd-DTPA at 0.25 T, 25 °C. Accurate determination of R₁ value is necessary for applying this method to biological tissue. R₁ may be measured using phantoms which can properly mimic the biological tissue. Alternatively, it may be determined by injecting different concentrations of tracer directly into tissue.

The validity of this methodology was first confirmed by comparing the MRI results with quantitative optical measurement. It should be noted that the accuracy of optical measurements may be affected by several factors, such as, background noise and the homogeneity of the hydrogel slice thickness. Comparison of concentration profiles obtained by porous media simulation and MRI experiments also show good agreement. It was found that MR-derived concentrations were slightly higher than those predicted by simulation within the low concentration region of the advancing front. At low concentrations, noise becomes dominant and we cannot accurately separate the low concentration from the noisy MRI signal according to our minimum detectable concentration analysis. It was also found that during short time infusion, e.g., 30 min, MR-derived concentrations were higher than those predicted by simulation. Several factors may contribute to the discrepancy between MRI experiments and simulations. (1) A spherical infusion cavity assumption was used in the computational model. In experiments, the infusion cavity may expand preferentially along the track of the cannula to form a tear-drop shape [33]. In our measurements, an asymmetric distribution in the cannula direction was observed at early infusion times. However, we did not model this expanding non-spherical source since modeling such a moving boundary problem is technically difficult. (2) The tip of the infusion cannula was assumed to be in the middle of an MR slice (along the slice or z-direction) within the computational model. This may not match the MR data since exact z-position of the tip within the slice is unknown and as a result, the MRI concentration profiles may be shifted slightly. In addition, by comparing the ratio of infusion volume and distribution volume, a porosity of 0.6 was estimated for the 1% (w/w) agarose hydrogel. This value is different from those reported by others [34, 35], where volume fraction of water was reported, and the difference may result from the space occupied by bounded water which is not accessible to macromolecules.

Accuracy of the methodology will also be affected by several factors, including the signal-noise ratio and the measurement stability during DCE-MRI. In this study, we account for noise in our measurements using the assumption that measured noise has a zero-mean and is Gaussian distributed. This assumption can be validated by measuring the ratio of the noise magnitude to the standard deviation of the noise, which should have a value of ~1.913 in an ideal case [36, 37]. We measured a value of 1.83 ± 0.07, which is very similar to the ideal case and justifies our assumption. Our DCE-MRI measurements were very stable during infusion. For example, the MR signal from a fixed ROI in the pure hydrogel, measured at different times during DCE-MRI, were quite consistent with a value of 3.93 ± 0.07. Yet, the noise standard deviation in these measurements was only 0.02 so the variation is at the level of the noise. In a typical hydrogel infusion measurement, the SNR was high with a maximum in the infused region of ~19.8 and a minimum in the pure hydrogel of ~7.2. Therefore, our measurements were both accurate and stable over the time course of studies.

Although a high field magnet system was used for MR imaging, the proposed methodology may also be applicable to clinical field strengths. However, the accuracy will be limited by the SNR available at lower field strengths and will require the use of an optimal infusate concentration. At clinical field strengths, data is generally acquired at a lower resolution than at high field strengths to overcome the decreased SNR. The SNR can be improved by increasing the number of averages, which results in a longer total acquisition time. Typically, this has an undesirable effect in MR tracer experiments since transport phenomena may not be accurately assessed at a lower temporal resolution. However for CED into nervous tissue, the convective and diffusive transport may be slow enough to allow a decrease in temporal resolution (increased number of averages) using a clinical magnet system, which will allow image resolution to be increased. The minimal detectable concentration analysis, outlined in this study, can be used to evaluate the sensitivity of the experiment as a function of SNR. The optimal infusate concentration will change with field strength since the optimal concentration is a function of background T₁ and T₂, as well as relaxivity properties of the contrast agent. As field strength is lowered, de Graaf et al. [38] have shown that T₁ decreases and T₂ increases in both rat brain white matter and gray matter. Rinck et al. [39] have shown increasing relaxivities, R₁ and R₂ (decreased relaxation times T₁ and T₂), of gadolinium-based contrast agents with decreases in field strength. For different contrast agents, Rohrer et al. [16] have also shown variations of relaxivities with decreases in field strength. Therefore, the infusate concentration should be optimized for the properties of the tissue and the contrast agent at a particular magnetic field strength in order to provide the greatest sensitivity to changes in contrast agent concentration to improve the accuracy of the method.

Noninvasive visualization and quantification of drug distribution in tissues using MR imaging are important. Real-time and quantitative monitoring may provide physiological insights to drug transport in tissues, help in understanding the efficacy of treatment, and aid in optimization of infusion protocols. As a methodology investigation, this study used an agarose hydrogel phantom to mimic a biological tissue and provide a validation test which demonstrated that this method can quantify properly the spatial concentration profiles during CED. To the best of our knowledge, MR studies that quantify concentration contours for CED have not been previously reported. In future studies, the presented methodology will be applied to direct infusion into biological tissue, e.g., nervous tissue.