Optically based-indentation technique for acute rat brain tissue slices and thin biomaterials

Abstract

Currently, micro-indentation testing of soft biological materials is limited in its capability to test over long time scales due to accumulated instrumental drift errors. As a result, there is a paucity of measures for mechanical properties such as the equilibrium modulus. In this study, indentation combined with optical coherence tomography (OCT) was used for mechanical testing of thin tissue slices. OCT was used to measure the surface deformation profiles by placing spherical beads onto submerged test samples. Agarose-based hydrogels at low-concentrations (w/v, 0.3–0.6 %) and acute rat brain tissue slices were tested using this technique over a 30 min time window. To establish that tissue slices maintained cell viability, allowable testing times were determined by measuring neuronal death or degeneration as a function of incubation time with Fluor-Jade C (FJC) staining. Since large deformations at equilibrium were measured, displacements of surface beads were compared with finite element elastic contact simulations to predict the equilibrium modulus, μ_∞. Values of μ_∞ for the low- concentration hydrogels ranged from 0.07–1.8 kPa, and μ_∞ for acute rat brain tissue slices was 0.13 ± 0.04 kPa for the cortex and 0.09 ± 0.015 kPa for the hippocampus (for Poisson ratio=0.35). This indentation technique offers a localized, real-time, and high resolution method for long-time scale mechanical testing of very soft materials. This test method may also be adapted for viscoelasticity, for testing of different tissues and biomaterials, and for analyzing changes in internal structures with loading.

1. Introduction

The biomechanics of the brain in reaction to injury, surgery, or disease is dependent on bulk mechanical properties of central nervous tissues. Mechanical properties can be used to predict structural changes and determine internal stresses within brain tissues subjected to various environmental forces. A bulk property such as the equilibrium modulus, which is a measure of tissue stiffness over a long time scale, is necessary to understand deformation under continuous loading conditions that occur in disease states such as hydrocephalus or during tissue swelling ^1–3. Force-displacement relationships needed to measure this property can be determined by indentation testing of tissue samples. An advantage of this technique compared to the other testing methods is the ability to home in on localized regions of interest in anatomically complex regions ^4–6. In this study, an indentation and optical coherence tomography (OCT) technique is presented to measure the equilibrium shear modulus (μ_∞) of soft nervous tissues. The developed testing technique provides high-resolution images of local tissue deformations over long testing periods.

Mechanical properties of brain tissues have been measured in previous studies and have been found to vary depending on the choice of testing method, testing condition, sample preparation, and animal species. In unconfined compression relaxation tests, the equilibrium Young’s moduli (E_∞) of excised calf and rat brain tissues have been estimated to be in the range of 0.35 to 0.66 kPa with relaxation times of 360–3500 s ^7,8. In other unconfined compression tests, μ_∞ of excised porcine brain tissues have been measured to range between 0.075 to 0.32 kPa under stress relaxation (relaxation time = 60 s) and small strain rate testing (0.64 × 10⁻⁵ s⁻¹) ^9,10. Other shear testing studies which also used excised porcine and rat brain tissues have estimated the shear modulus (μ) to range from 0.075 to 1.2 kPa for large and small strain regimes (2.5 – 50% total strain) ^10–12. Less invasive studies have also been conducted using magnetic resonance elastography which measures the response of tissue to an introduced shear wave ^13–15. These studies measured the viscoelastic behavior of human brain tissues in vivo (μ ranged from 1.7 to 13.5 kPa). These previous compression and shear tests were limited in their ability to measure mechanical properties of local or specific anatomical regions within the brain. For localized measurements, indentation has been used to determine the force- displacement response of porcine, embryonic chicken and rat brain tissues ^16–20 and μ measures ranged between 0.2 to 1.2 kPa. Atomic force microscopy (AFM) indentation has also been used on rat hippocampal slices to measure local micron-level displacements in hippocampal subregions, and measurements of E at the tissue surface ranged between 0.14 to 0.31 kPa ⁸. While this study showed heterogeneous and homogeneous patterns of tissue integrity of hippocampal slices using Nissl staining and electron microscope scanning, like most previous studies, cell viability in the test tissue was not determined. However, known requirements of cellular structural components (cytoskeleton) for critical membrane ionic gradients and metabolic processes predict that mechanical properties of nervous tissue depend upon cellular viability. Another important consideration is that the testing durations for these previous studies were short (on the order of seconds to minutes). To determine mechanical behavior on a temporal scale relevant to actual neuropathological states, longer testing times are required to measure such properties as the equilibrium modulus.

Indentation measurement of bulk tissue properties relevant to tissue-level mechanical behavior is challenging for very soft tissues. Although AFM provides a testing system capable of measuring the mechanical properties at high displacement and force resolutions, indentation depths and contact areas are limited to cellular-level (< 5 µm) testing from which it is difficult to extrapolate tissue-level behavior. For larger displacement tests, a current limitation of piezoelectric-based indentation systems is that they can only be used to measure over short time spans since instrument drift errors accumulate over time. This is a problem for transient testing of soft materials since this can result in significant indenter displacement error. As a result of this, there is a paucity of measures of equilibrium moduli for soft tissues such as nervous tissues and soft biomaterials since these tests require long testing times. Another limitation of many indentation devices is that the initial point of contact between the indenter tip and the surface of a soft material is hard to detect correctly. To detect surface contact, most systems rely on small changes in the measured reaction force, and even small threshold trigger forces can result in large tissue deformations within soft tissues. These deformations must be corrected for when determining exact contact positions (indenter penetration depths) and sample heights.

OCT uses low coherence interferometry to measure the reflection and scattering of near-infrared light from localized positions and obtain cross sectional images through samples ²¹ It can provide real-time and non-invasive imaging of biological tissues at a micrometer-level resolution sufficient to detect deformations of tissue on a cellular scale. Clinical applications of OCT in neuroscience or neural imaging include brain tumor imaging, image-guided surgery and imaging of developmental neurobiology ^22–25. Mechanical testing applications of OCT are less prevalent. In a previous study, Schmitt has shown the potential use of OCT for determining the mechanical properties of soft tissues by using images of compressed muscle tissues to obtain microscopic deformation and strain fields ²⁶. An OCT- based micro-indentation system has been previously developed by Yang et al., for hydrogel testing ²⁷. The gravitational weight of beads was used to apply a constant indentation force on the surface of hydrogel slices. OCT was used to capture bead displacements and provide direct optical measurements of indenter penetration depths. Elastic modulus was estimated by applying Hertz’s contact theory to relate indentation force and hydrogel deformation with the Young’s modulus. This theory is applicable for small deformations. This simple approach does not introduce instrumental drift error and allows for prolonged testing. Such an OCT-based indentation system has not been yet been used to measure mechanical properties of tissues.

In this study, an OCT-based indentation approach similar to Yang et al. was used to measure the mechanical properties of very soft hydrogels and rat brain tissue. OCT was used to scan the through-thickness deformation profiles of thin hydrogel and tissue slices loaded with spherical metal beads. Since large deformations at equilibrium were measured, equilibrium displacement profiles were compared with computational solutions of indenter contact for large deformations and hyperelastic material properties to predict μ_∞. The system was initially tested using low concentration agarose hydrogels since this material has similar mechanical properties to biological tissues. Then, μ_∞ in two different regions (cortex and hippocampus) of acute rat brain tissue slices were measured. An important goal of this study was to use an ex vivo model and maintain cell viability of the tissue samples. Allowable testing times were determined by measuring neuronal death or degeneration within slices as a function of incubation time.

2. Experimental Methods

2.1 Sample preparation

Hydrogel formulation

In the first series of tests, five concentrations of an agarose-based hydrogel were tested: 0.25, 0.3, 0.4, 0.5 and 0.6% (w/v). To prepare samples, hydrogel powder (Trevigel 5000, Trevigen, Gaithersburg, MD) was completely dissolved in deionized water. Then, gel solutions were poured into Petri-dishes to a 4 mm thickness, and allowed to solidify at room temperature. Before and during testing hydrogels were submerged in deionized water to prevent dehydration.

Animal use and rat brain tissue slicing

Adult female Sprague Dawley rats (~ 250 g) were used for all brain tissue slice tests. Five rats were used for indentation tests and five rats were used for cell viability tests. Rat surgery was conducted in accordance with the NIH guidelines on the use of animals in research and the regulations of the Animal Care and Use Committee of the University of Florida. Rats were anesthetized by isoflurane inhalation and checked for absence of toe-pinch, righting, and corneal reflexes prior to euthanization. After euthanasia, standard protocols for tissue retrieval, brain tissue slicing, and tissue maintenance were implemented ²⁸. Medial sections from excised rat brains were sliced using a vibratome (Leica VT 1000A, Leica Microsystems Inc., Germany) to obtain coronal sections of 300 and 400 µm initial thickness. To ensure uniform slicing, rat brain tissues were supported on three free sides by 1% hydrogel blocks. Brain tissues were also submerged in O₂ saturated artificial cerebrospinal fluid (aCSF, Neurobasal™ Media, GIBCO, Invitrogen Co., CA) and maintained between approximately 5 – 7 °C during slicing. Brain tissue slices were then placed in a temperature controlled (35–36°C) perfusion chamber. 95% O₂ and 5% CO₂ gases were continuously supplied and 0.5 mM L-Glutamine (Invitrogen Co., CA) and 1% penicillin-streptomycin (Invitrogen Co., CA) were supplemented to the aCSF. pH of aCSF measured before testing was 7.4.

2.2 Brain slice viability in the perfusion chamber

To determine a suitable time window for indentation tests, tissue viability tests were conducted. Brain tissue slices were perfused in the chamber for up to 10 hours and neuronal viability was measured by Fluoro-Jade C (FJC) staining which detects degenerating and dead neurons ^29–31. For FJC tests, tissue slices were taken from the chamber after 2, 4, 6, 8, 10 hours and fixed in 4% buffered formaldehyde solution overnight. To prepare for frozen sectioning, slices were immersed in a 30% sucrose phosphate-buffered saline for another night. Frozen brain slices then were cut into 50 µm sections on a sliding microtome and mounted onto microscopy slides. Slides were then dried overnight at room temperature. Standard protocols for Fluoro-Jade C (FJC) staining were followed similar to previous studies. However, the protocol was modified to improve fluorescent images. Tissue sections were first immersed in a basic alcohol solution consisting of 1% sodium hydroxide in 80% ethanol for 5 min. They were then rinsed for 20 min in 70% ethanol, rinsed for 2 min in distilled water, and then incubated in 0.02% potassium permanganate solution for 3 min. Sections were then rinsed for 2 min in distilled water and then transferred for 15 min to a 0.0002% solution of Fluoro-Jade C (Histo-Chem Inc., Jefferson, AR) dissolved in a 0.1% acetic acid vehicle.

To label nuclear DNA 4′, 6-diamidino-2-phenylindole (DAPI; Sigma, St. Louis MO) was added in the FJC solution (0.0001%). Finally, the sections were rinsed through three changes of distilled water for 1–2 min per change. Sections were air dried overnight in a dark room and then cleared in xylene for 5 min and coverslipped. The FJC and DAPI stained sections were examined with an epifluorescence microscope using a filter system suitable for visualizing fluorescein. FJC stains neuron cell bodies, dendrites and axons. To differentiate neuron cell bodies in the FJC images, DAPI stained images were taken on the same field and overlaid on FJC images.

2.3 OCT system and slice imaging

OCT system

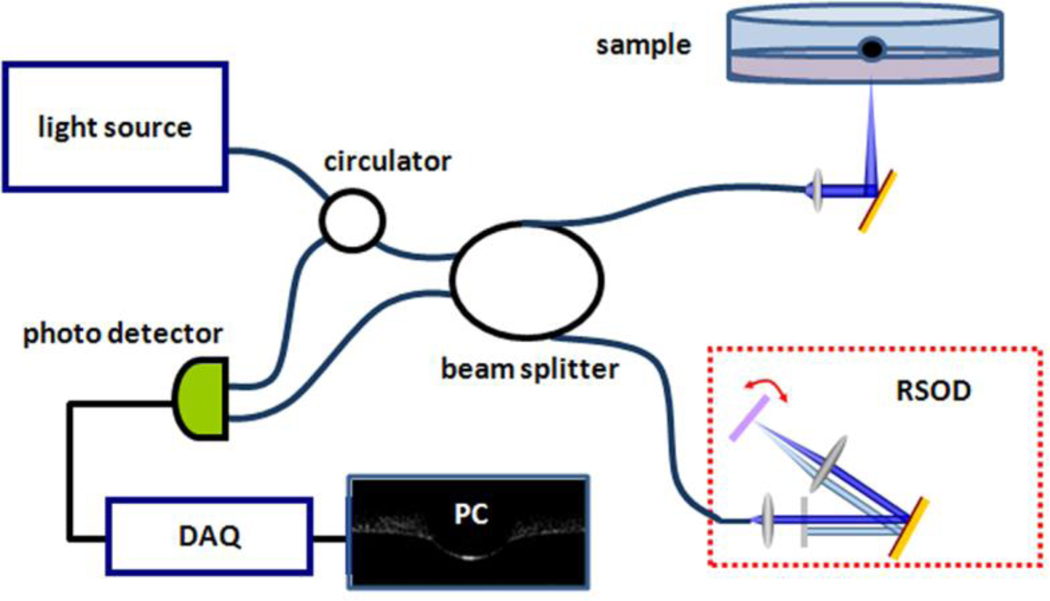
The OCT system used in this study is based on a Michelson interferometer, and a schematic of the OCT system is shown in Fig. 1. Two interference arms were used as a reference arm and sample arm, respectively. Depth information was obtained by scanning the rapid scanning optical delay line (RSOD) in the reference arm, and the transverse scanning was realized by moving the tissue sample on a motor stage. A broadband light source (DenseLight, DL-BX9-CS3159A, Singapore) which has a center wavelength of 1310 nm and a full width at half maximum (FWHM) of 75 nm was used to scan samples from bottom to top with a 10 µm resolution in air. Light was channeled through a circulator and divided by a 2×2 beam splitter into two arms. The RSOD in the reference arm scanned with a frequency of 0.5 KHz. A fixed reflective mirror was used in the sample arm. The transverse scanning was performed by a 1D linear motor stage moving with a velocity of 1 mm/sec. The interference signal was received by a heterodyne photo detector, captured by a data card (NI PCI 5122, Austin, TX), and then processed by a computer.

Figure 1.

Schematic of the OCT -based indentation system.

OCT slice imaging

For OCT imaging of hydrogels, slice samples were submerged in Petri dishes and scanned from below, as illustrated in Fig. 1. For tissue testing, rat brain tissue slices were removed from the perfusion chamber and similarly placed in Petri-dishes filled with oxygenated aCSF for scans. OCT provided cross-sectional images of hydrogels and brain tissue slices with fields of view of 2.3 mm × 1.6 mm. Scanned images were based on differences in refractive indices in tissue, hydrogel, covering fluid layers, and air. Since the refractive index of rat brain tissues and hydrogels are not accurately known, images were modified based on the known radial dimensions of beads used for indentation. The horizontal dimensions were stretched uniformly within the image field until the bead became spherical.

Preliminary OCT tests were conducted to determine if significant changes in tissue slices thickness (tissue swelling) occurred over the course of testing. Since thinner tissue slices provided improved OCT visualization of the tissue surface, 300 µm thick rat brain tissue slices (n=2) were scanned. After approximately one hour in the perfusion chamber, slices were removed and scanned every 10 min over a 90 min testing period in oxygen-saturated aCSF at room temperature, Fig. 2. The top and bottom surfaces of slices were clearly observed by OCT and increases of thickness in the cerebral cortex region were measured to be less than 2% of the total thickness. While some tissue initial tissue expansion may occur after initial slicing, tissue expansion over the time course of our testing period was considered to be negligible.

Figure 2.

OCT images of the cerebral cortex (CC) region in rat brain tissue slices at varying perfusion times used to measure changes in tissue thickness. A 300 µm thick slice of the cerebral cortex at (a) 0 min, (b) 30 min, (c) 60 min and (d) 90 min.

2.4 OCT indentation testing

For the indentation tests, spherical balls were placed on submerged samples and allowed to sink in over 30 min, and the average deformation depth, d, at the bead center was measured. 1.17 mm diameter tungsten carbide (WC) beads were placed on hydrogels and 1 mm diameter stainless steel (SS) bead were placed on brain tissue slices. (Heavier WC beads were used on hydrogels for detectable deformations, and SS beads were used on tissues due to their biocompatibility and non-toxicity.) The applied indentation force for submerged beads was calculated by subtracting the buoyancy force from the gravitational force (F_WC = 119 µN, F_SS = 37 µN).

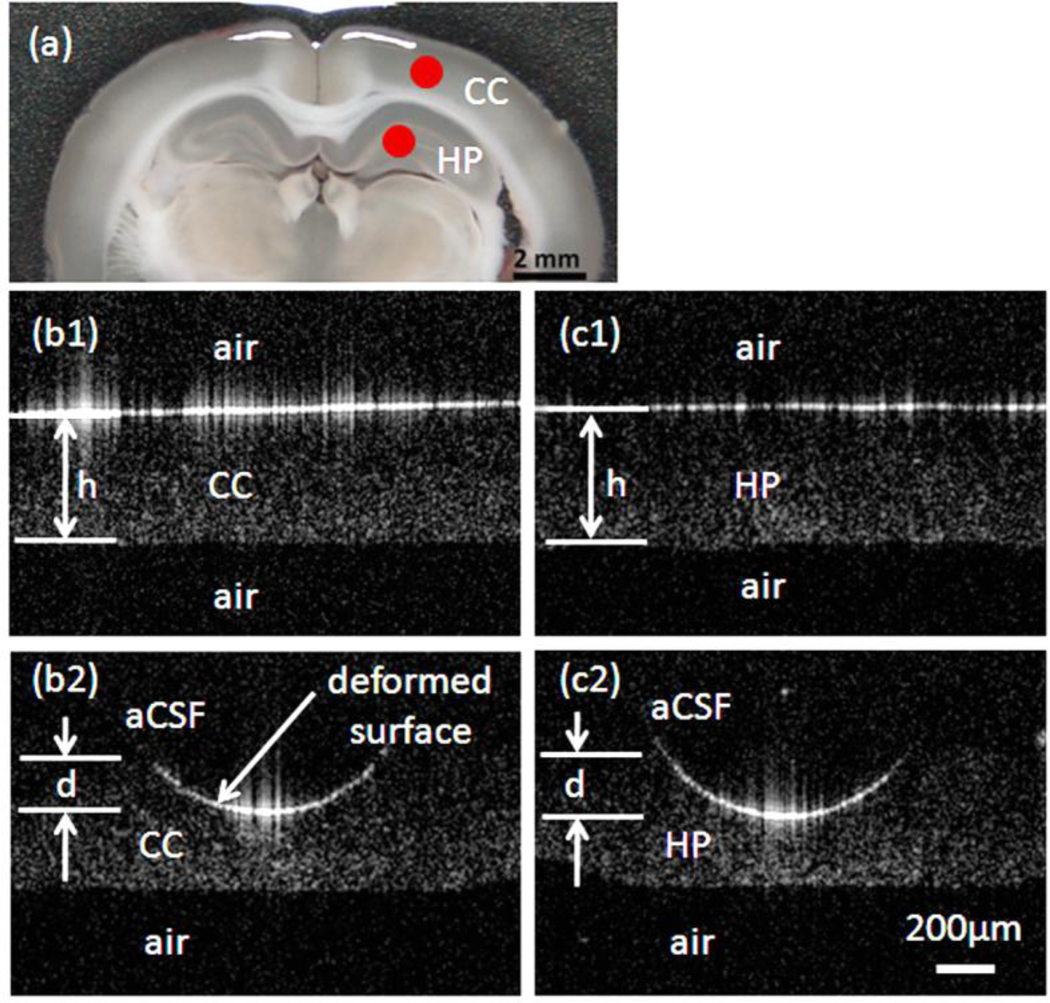
For hydrogel testing, d was measured from OCT images for five samples at each concentration. Due to similar refractive indexes between the low-concentration hydrogel and the adjacent water layer, a small amount of visible protein marker (i.e. two drops of milk) was added just before taking OCT images, Fig. 3. For tissue slice tests, measure of the initial tissue slice thickness, h, was also necessary. These were obtained for each slice by removing aCSF until only a thin film of aCSF remained over slices, see Fig 4. This step took less than 2 min. The slices were then submerged and gently covered by a polymer mesh to prevent floating. Two anatomical regions, the cerebral cortex and hippocampus, were indented, Fig. 4. Indentation tests were completed within 3 hrs after tissue slicing.

Figure 3.

OCT images of bead indentation of (a) 0.25%, (b) 0.3%, (c) 0.4% and (d) 0.5% (w/v) concentration agarose hydrogels. Hydrogels were indented using spherical tungsten carbide beads (OD=1.17 mm). d is the deformation depth.

Figure 4.

Representative rat brain tissue slice images used for indentation analysis: (a) acute rat brain tissue slice. Red dots indicate points of indentation; OCT cross-sectional images taken before indentation testing for cerebral cortex (b1) and hippocampus (c1). During indentation testing (t = 30 min) of the cerebral cortex region (b2) and hippocampus (c2) with a spherical (OD= 1 mm) stainless steel bead. Slices were submerged in oxygenated aCSF. h is the initial tissue thickness; d is deformation depth; and CC and HP correspond to the cerebral cortex and hippocampus label, respectively.

2.5 Finite element indentation model

In this study, thin brain tissue slices were used to overcome optical length limitations. Correspondingly, large deformations were induced during indentation, and finite element (FE) models were used to account for boundary effects associated with thin sample deformation. The indenter contact problem was solved using the FE software package Abacus (v.6.2) and indentation was modeled as a 2-D, axi-symmetric problem with a spherical indenter contacting the slice at varying penetration depths, see Fig. 5. Since the modulus of the bottom substrate and indenter were orders of magnitude greater than test samples, the substrate and indenter were modeled as a non-porous rigid body. Negligible friction, adhesion, and surface tensions were assumed to act on these surfaces. The slice was modeled as a uniformly thick (agarose hydrogel = 4 mm, rat brain tissue = 400 µm), isotropic, and Neo-Hookean (which assumes a large elastic deformation and small strain) material. While large strains are expected near the bead, hyperelastic finite strain models were not used since only one deformation point was measured. The isotropic Neo-Hookean strain energy density function is given by

$$W=\frac{1}{2}\mu (I_1{J}_e^{-2/3}-3)+\frac{k}{2}{(J_e-1)}^2$$ (1)

where μ and k are the shear and bulk modulus, I₁ is the first invariant of the right Cauchy-Green deformation tensor (= F^TF where F is the elastic deformation gradient tensor) and J_e (= det F) is the elastic volume ratio. The Cauchy stress tensor is given by the constitutive relation,

$$\mathbf{\sigma }=J_e^{-1}\mathbf{F}·\partial W/\partial {\mathbf{F}}^{\mathbf{T}}.$$ (2)

Figure 5.

Axially symmetric FE mesh of spherical indentation. l = 4 mm, h=4 mm and R=0.585 mm for the hydrogel study, l= 1.5 mm, h= 0.4 mm and R= 0.5 mm for rat brain tissue slices.

The compressibility of a material is given by the ratio of k and μ. This ratio can also be expressed in terms of the Poisson's ratio,

$$\nu =\frac{3k/\mu -2}{6k/\mu +2}.$$ (3)

which is the ratio of lateral to axial strain.

For the contact problem, target elements were generated on the indenter surface and 50 contact elements were generated on the top of the sample surface. The FE mesh consisted of 2240 4-node quadrilateral elements. Indenter displacement, d, was calculated for constant applied indenter forces, F. Force- displacement responses were predicted for a range of μ_∞ from 0.03 to 3 kPa in increments of 0.02 kPa. A range of ν from 0.35 to 0.499 corresponding to compressible and nearly incompressible materials, respectively, were investigated based on previous studies of brain tissues ^7,32 and hydrogels ³³. Minimization of the mean square error of predicted and measured d values provided estimates of μ in agarose hydrogels and brain tissue slices.

3. Results

3.1 Determination of indentation testing time

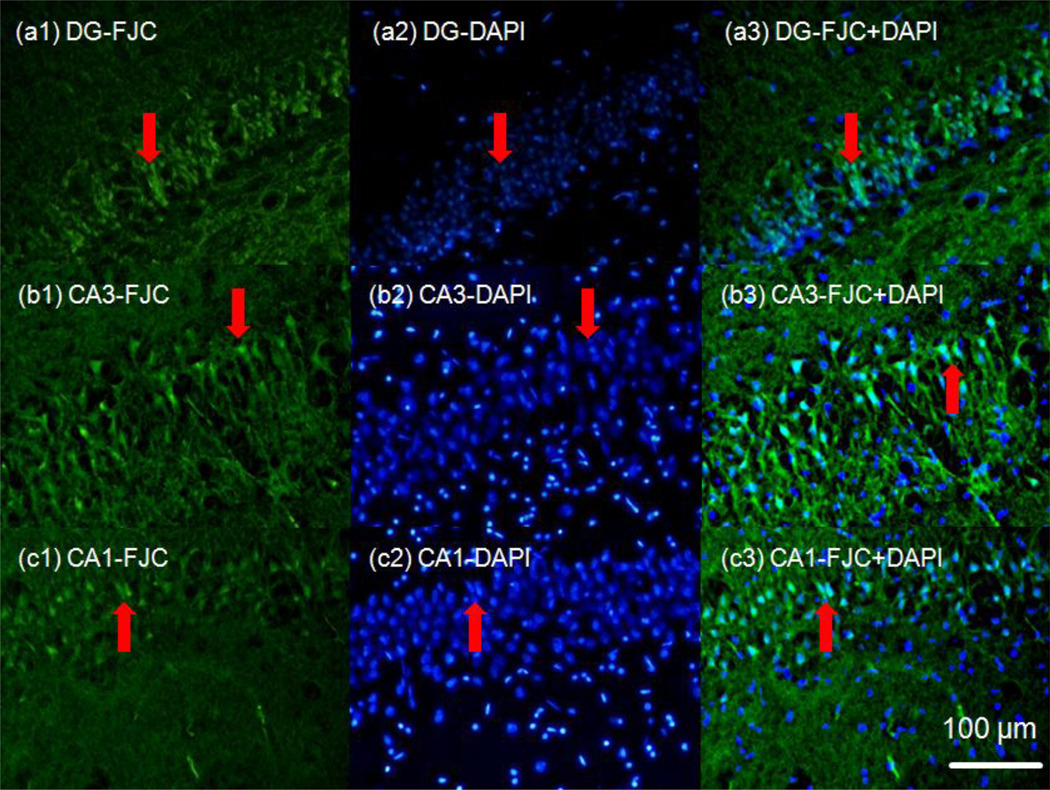
To maintain ex-vivo conditions, viability tests were conducted to determine an acceptable range of incubation times for brain slices. Figure 6 shows FJC staining within the rat hippocampus region over 10 hours of incubation in the perfusion chamber. For incubation times less than 4 hours the fluorescent signal did not significantly differ from time 0 controls. Neural degeneration in the hippocampus was detected by FJC (increased fluorescence intensity) after 4 hours of incubation and significant increases in fluorescence intensity were detected between 6 to 8 hrs hours of incubation, see Fig. 6. Superimposed DAPI staining in Fig. 7 shows degeneration by neurons (bright green triangular shapes) at this time point. The fluorescence intensity of degenerating cells at 6 hours was found to be 2 to 3 times higher than for intensities measured after 2 and 4 hours of incubation. It should be noted that there may be a delay between when a cell dies and when it becomes FJC-positive; this delay may take on the order of 2–4 hours based on preliminary studies. Based on this, indentation experiments were conducted within 4 hours after rat brain removal to ensure that viability conditions were maintained.

Figure 6.

Viability testing of acute rat brain tissue slices. Hippocampal regions (DG: dentate gyrus, CA3 and CA1) were tested over 2 hour intervals (a- 0 hour, b- 2 hours, c- 4 hours, d- 6 hours and e-10 hours incubation time). Fluorescent images show bright green regions (red arrows) corresponding to degenerating neurons (FJC-positive). Extensive degeneration throughout the hippocampus was observed after 6 hours incubation.

Figure 7.

Superimposed images of DAPI (blue) and FJC (green) fluorescent staining taken after a 6 hour incubation period. DAPI and FJC images were overlaid to confirm that FJC staining coincided spatially with neuronal cell bodies. DAPI binds to DNA and stains the nuclei inside cell bodies blue.

3.2 OCT- based indentation tests

Agarose hydrogel indentation

OCT indentation images for varying agarose hydrogel concentrations are presented in Fig. 2. Contact surfaces between the hydrogel and bead and fluid were clearly detected, as well as, changes in bead deformation depths for small changes in hydrogel concentration. Measured d at equilibrium was found to decay non-linearly for small increases in hydrogel concentration, Fig. 8. As a result, μ_∞ was estimated to increase non-linearly with changes in hydrogel concentration and this relation was fit to a power law relation, Fig. 9. Statistical analysis revealed significantly different shear moduli among the sample groups tested (0.25, 0.3, 0.35, 0.4, 0.5 and 0.6 % hydrogel samples). A Tukey-Kramer test was used with significance set at p<0.05, and significant differences between indentation depths were shown for all hydrogel samples except for between 0.5 and 0.6 % hydrogels. However, a statistical difference between 0.5 and 0.6 % hydrogel samples was found using the one-tailed t-test, and p was found to be less than 0.0102. μ_∞ for hydrogel was determined to range from 0.07 to 0.08 kPa for 0.25% (w/v) and to range from 0.95 to 1.2 kPa for 0.5% hydrogel for the range of Poisson’s ratio considered (0.35 to 0.5).

Figure 8.

Indentation depths for various low-concentration agarose hydrogels. Depths of submerged spherical tungsten carbide beads were measured after 30 min (OD = 1.17 mm, FSS = 119 µN). Box plots show the upper and lower 25th percentile of indentation depths, mean value (+), and median (red line). Error bars show ± 1.5 interquartile from upper and lower hinges. Slice thickness = 4 mm; sample size n=5 at each concentration. (***) Significant difference in indentation depths between concentrations was tested by Tukey-Kramer test for p<0.05. 0.25, 0.3, 0.35, 0.4, and 0.5% hydrogel samples show significant differences in indentation depths from each other (p<0.0004). (*) 0.5 and 0.6 % hydrogels show a statistical difference using t-test (p<0.020).

Figure 9.

Estimated μ_∞ in low-concentration agarose hydrogels for varying Poisson’s ratios. Indentation depths from constant force indentation were compared to FE model simulations to estimate μ_∞ (a–d). Modulus was fit to the power law (μ_∞= a(Cw)ⁿ, a and n are fitting parameters) with concentration (e). for n =0.35, a=12937 and n=3.49, for n =0.40, a=12024 and n=3.49, for n =0.45, a=10999 and n=3.47, and for n =0.499, a=10395 and n=3.50. Indentation depths were averaged from 5 samples. Bars correspond to differences in μ_∞ calculated from ±1SD in depth.

Indentation of rat brain tissue slices

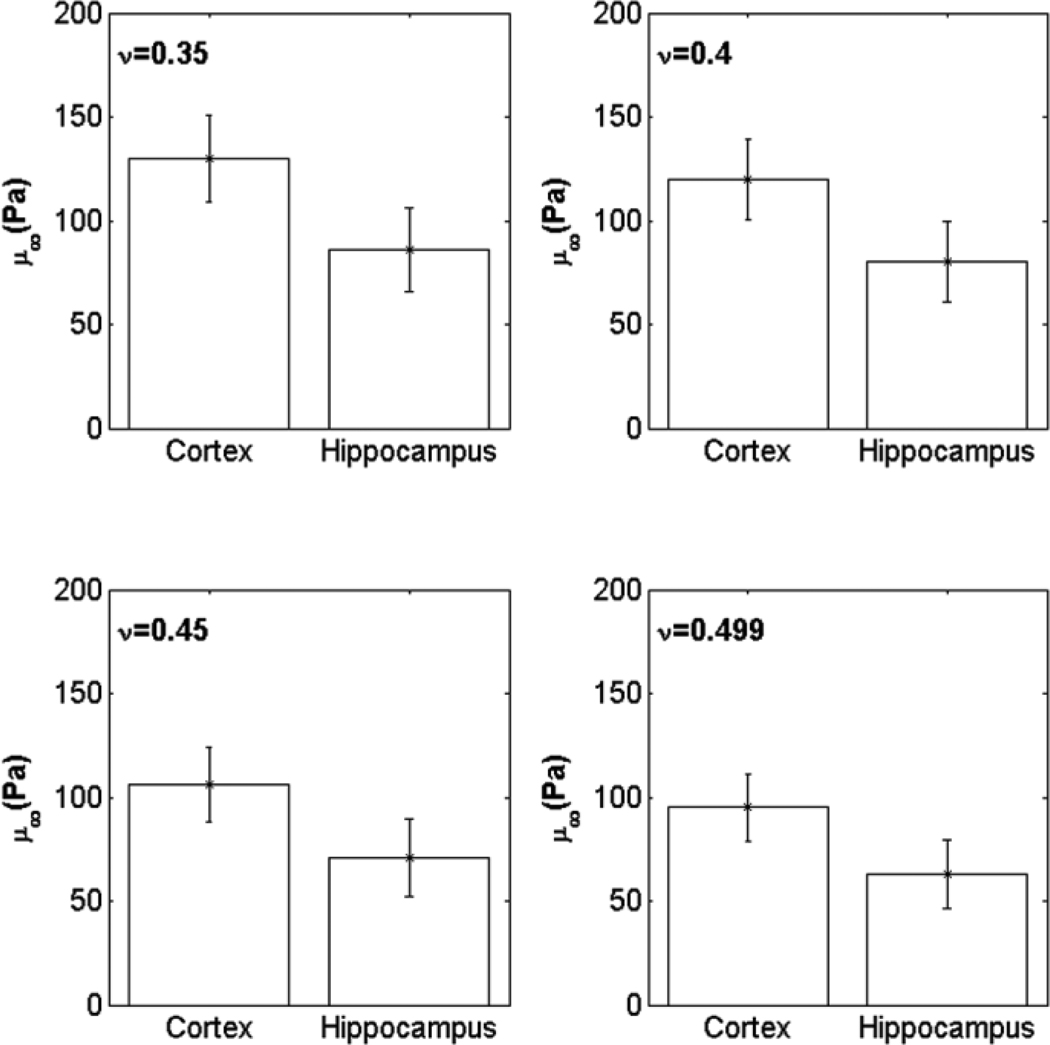
The average cross sectional thickness of brain tissue slices before indentation testing was measured to be 420 ± 25µm from OCT images. Cerebral cortex and hippocampus regions within brain slices were tested and no significant changes in h were observed after 30 min (less than a 3% decrease in h was observed at 50 min). OCT cross-sectional images of a brain tissue slice undergoing indentation are shown in Fig. 4, and average indentation depths are graphed in Fig. 10. Indentation depths in the hippocampus were 20% greater than in the cerebral cortex. A statistically significant difference in indentation depths between locations was found by using the two-tailed t-test (p < 0.0084). The cerebral cortex was estimated to have a ~ 30% greater shear modulus than the hippocampus based on average measured values. The estimated μ_∞ of cerebral cortex and hippocampus regions are plotted for varying Poisson ratio in Fig. 11. By varying Poisson’s ratio between 0.35 to 0.499, μ_∞ changed by up to 25% in both brain regions.

Figure 10.

Measured indentation depths within the cerebral cortex and hippocampus. Five rats were tested with three slices taken from each brain. Submerged slices were indented using stainless steel beads (t = 30 min, OD = 1 mm, F_SS = 37 µN). The box plot shows the upper and lower 25th percentile of indentation depths, mean value (+), and median (red line). Error bars show minimum and maximum depths. Slice sample thickness = 400 µm; sample size n=5. A significant difference in indentation depths between the cortex and hippocampus was measured (p<0.0084).

Figure 11.

Estimated μ_∞ in the cerebral cortex and hippocampus for varying Poisson’s ratio (ν). μ_∞ was estimated by comparing with FE simulations. The standard deviation (SD) of μ_∞ was calculated based on the upper and the lower SD values for measures of d. Bars show ±1SD.

4. Discussion and Conclusions

In this study, an OCT-based indentation technique was developed for thin tissue slices and used to estimate the equilibrium shear modulus of low-concentration agarose hydrogels and ex vivo rat brain tissue slices. The system was designed to combine advantages of both indentation and optical coherence tomography techniques. Indentation provides small sample capacity and the ability to measure localized mechanical properties. OCT provides rapid imaging and direct visualization of deforming tissues under applied loads. Such an image-based indentation system eliminates any errors generated by instrumental drift and provides a direct measure of the point of contact between the sample and indenter tip. Thus, this technique is ideal for measuring very soft tissue responses over long times.

The OCT based-indentation system was first tested using low-concentration agarose hydrogels which have been previously used as tissue phantoms and have similar mechanical properties to brain tissues. Lower concentrations than generally reported were tested (0.25 to 0.6 %) and measured μ_∞ were over a lower range (0.07 to 1.8 kPa for ν=0.35 – 0.499) than previously reported. For the 0.5 % agarose hydrogel, the estimated value of μ_∞ (1.1 ± 0.33 kPa for ν= 0.499) was similar to that found previously by Fernandez et al. (μ_∞ ~ 1.3 kPa) under low frequency (1 Hz) tensional shear testing ³⁴ and by Normand et al. (μ_∞ ~ 1.8 kPa) under compression testing of low viscous agarose gels ³⁵ (we compared values for ν=0.499 since previous mechanical testing studies assumed material incompressibility). Our estimated value was also similar to the modulus moduli measured by Yang et al. using a similar OCT-indentation system (μ_∞ ~ 0.8 kPa estimated from their displacement curve using our Abacus model) ²⁷. Furthermore, estimated μ_∞ at lower agarose concentrations were found to increase non-linearly with small changes in concentration. This non-linear behavior may be due to a non-linear increase in polymer cross-linking density in the hydrogels.

Within brain tissue slices, estimated μ_∞ corresponded to very soft tissues (0.06 – 0.09 kPa in the hippocampus and 0.09 – 0.13 kPa in the cortex for ν= 0.35 – 0.499). These values are based on equilibrium conditions, and they likely represent the shear modulus of the solid matrix component of brain tissues. This consists of the solid and non-communicating fluid spaces which includes primarily cells and some extracellular matrix (ECM). These estimated μ_∞ values were similar but lower than previously measured brain tissue values for long time-scale or low strain rate testing. Cheng and Bilston and Elkin et al. conducted unconfined compression tests on excised brain tissues over long times (3000 and 360 s, respectively) and found E=0.350 to 0.66 kPa (equivalent μ_∞ of 0.13 to 0.25 kPa based on ν= 0.35) ^7,8 which are higher than the values we measured. Low strain-rate compression tests have also been conducted by Miller and they found μ_∞ of ~ 0.32kPa at a low strain-rate of 0.64 ×10⁻⁵/s ⁹. Our measured values are more similar to those measured by low velocity indentation tests using AFM (11.5 µm/sec) and micropipette indenters (46 µm/sec) by Elkin et al. (E= 0.14 to 0.4 kPa) and Xu et al. (μ = 0.2 to 0.3kPa), respectively, in which equivalent μ ranged between 0.05 to 0.3 kPa in brain tissues ^8,20 (based on ν=0.499).

In terms of localized measures, Elkin et al. indented excised rat brain tissue slices within hippocampal regions and our moduli measurements are comparable to those measured in their study. However, our measured values were an order of magnitude lower than values measured at high strain rates or over short time periods. High strain-rate shear tests (2– 40 s⁻¹) and high strain-rate compression tests (0.64 s⁻¹) found equivalent μ of 1.1 to 3.3 kPa ^9,12. Indentation relaxation tests conducted over short time periods (relax times < 160 s) by Dommelen et al. and Gefen et al. found μ_∞ of 0.6–1.2 kPa ^16,17,19. Higher shear modulus values in these previous studies may be due to viscoelastic effects or the fact that there was not sufficient time for fluid redistribution and pressurized fluid spaces may have contributed to a more rigid response. Also, it should be noted that most of these previous studies measured equilibrium mechanical properties over time periods < 100 s. Overall, these measured mechanical properties are difficult to compare due to differences in testing conditions and test samples. It is likely that the lower moduli measured in our study are due to the combination of longer time periods of tests, low strain-rates, ex-vivo slice conditions, and differences in testing live tissues versus freshly excised samples.

In most previous studies, the shear modulus of brain tissue has been calculated assuming tissue to be nearly incompressible (v ~ 0.5). This assumption is valid in soft hydrated tissues when interstitial (extracellular) fluids are confined within the tissues during testing or when testing over short enough time periods for which fluids cannot redistribute. Over longer time periods of testing this assumption may not hold since fluids can redistribute and the underlying solid matrix behavior may govern the mechanical behavior. The Poisson’s ratio in foam-like, porous solids is known to be lower than 0.5. For example, Cheng and Bilston performed long-time scale stress relaxation tests (~ 1 hour) on brain tissues, and they determined ν = 0.35 through parameter analysis of a poroviscoelastic model which assumes an underlying solid matrix ⁸. In this study, μ_∞ was estimated over a range of ν = 0.35 to 0.499. It is appropriate to select μ_∞ based on ν=0.35 for which higher moduli values are predicted than for ν=0.499. Therefore, μ_∞ is 1.23 ± 0.3 kPa for 0.5% agarose hydrogel, μ_∞ is 0.13 ± 0.4 kPa for the cortex, and μ_∞ is 0.9 ± 0.15 kPa for the hippocampus. In hydrogels, μ_∞ increased by ~ 10% and ~ 3% with ν= 0.35 and 0.45, respectively, compared with the value at ν=0.499. In tissues, μ_∞ was increased ~ 26% and ~ 15% with ν= 0.35 and 0.45, respectively, compared with the value at ν=0.499. Both values of ν and μ_∞ may also be simultaneously fit to the FE model using indentation depth in addition to surface deformation profile data. However there were a couple problems applying this approach to this study. (1) In the FE model, the shape of the hydrogel/tissue surface profile under indentation loading is not very sensitive to changes in ν for the free edge boundary condition used. (2) Also in OCT tissue images, resolution of the surface interface between aCSF and deformed brain tissue was not sufficient for curve fitting (resolution of the indenter and brain tissue interface was clearer).

In this study, the intent was to measure tissue-level mechanical properties. Thus, relatively large penetration depths and a large contact radius that was at least approximately 10 cell layers deep and 10 cell diameters across was targeted. Also cells on the top and the bottom surfaces of tissue slices were likely damaged by slicing, and this damaged layer is expected to extend approximately 5 cell layers. As a result, indentation penetration depths also should extend beyond damaged cell layers. Measured displacements at equilibrium ranged between 120 to 150 µm and the radius of contact was approximately 350 µm, which is well within our target goals. Few similar studies have been conducted at this length scale. In the previous AFM study by Elkin et al., indentation depths (3 µm) and contact areas (OD=25 µm spherical probe tip) were over a smaller length scale and provided more cellular-level properties ⁸. The similarity in measured mechanical properties between our study and theirs may be due to the fact that both methods measure the solid matrix response which is governed by the composition of the solid matrix which is composed primarily of cells. Tissue-level measures may be different at higher strain rates if extracellular fluid flow is induced. Another consequence of large deformation is the need to fit indentation data to FE models to account for boundary effects. However, in studies with smaller indenter deformations or that use thicker slices simpler analytical solutions can be used ^27,36.

Mechanical properties of tissue may also be dependent on a cell viability and tissue integrity. For example, lack of transport oxygen and nutrients induces hypoxic neuronal injury and increases cell membrane permeability resulting in cell swelling ^37,38. With increasing time post-mortem, cell membranes and matrix components will also lose their structural and mechanical integrity. These physical changes may have an effect on mechanical properties. In most previous mechanical testing studies, the viability of tissue was not usually maintained since it is difficult to supply oxygen over large sample thicknesses. The resulting modulus could be different due to tissue changes with time. An objective of this study was to see if these physical changes have an effect on mechanical properties. In previous studies looking at changes in mechanical properties in brain tissue post-mortem, Metz et al., found 30–70% decreases in Young’s modulus after 45 min³⁹. In contrast, Garo et al. found a 20% increase in shear modulus of brain tissue after 10 hrs post-mortem⁴⁰. In this study, we found that measured properties using living tissues did not differ significantly from other studies in which cell viability was not specifically maintained. However, changes in the mechanical properties of brain slices based on tissue viability remain inconclusive over long time periods post-mortem. Experiments to directly compare differences in mechanical properties between viable and non-viable tissues for our test conditions will be conducted in future studies.

Limitations of this technique are associated with the limited optical penetration depth of near-infrared light which is approximately 1 to 2 mm in most tissues. Thus, the technique is ideal for thin tissue slices or near surface measurements. For the indentation tests, only one bead size was used to determine indentation depths. It should be noted that the bead size and weight should not affect predicted modulus results if the material behaves ideally. However, effects related to extent of tissue deformation (e.g., strain hardening), tissue heterogeneity and surface adhesion may change modulus results with changes in bead size. In our FE models, material behavior was governed by an neo-Hookean model which assumes large deformation with small strains. While large strains were predicted in the vicinity of the indenter tip, it is difficult to account for non-linear material behavior since only equilibrium measures were taken. Other hyperelastic or viscoelastic constitutive models may be used in FE models with collection of transient deformation or using different sized beads. For transient responses, it should be noted that initial deformation would need to be able to be captured by the OCT system sampling rate.

Overall, this OCT-based indentation technique is relatively simple to implement and provides improved characterization of the mechanical behavior of acute rat brain tissue slices and hydrogels over long testing periods. The mechanical properties estimated in this study provide a structural measure of the mechanical response of tissues over a long time scale (~ 30 min). Mechanical properties can be used in models of surgical loading and tissue swelling, as well as, to understand deformation or injury patterns in specific brain structures such as the hippocampus. This technique may be used to characterize mechanical behavior of other thin tissue slices and biomaterials with appropriate optical properties. Changes in internal structures with loading also may be analyzed with sufficient OCT image resolution.