Control of Action Potential Duration Alternans in Canine Cardiac Ventricular Tissue

Abstract

Cardiac electrical alternans, characterized by a beat-to-beat alternation in action potential waveform, is a naturally occurring phenomenon, which can occur at sufficiently fast pacing rates. Its presence has been putatively linked to the onset of cardiac reentry, which is a precursor to ventricular fibrillation. Previous studies have shown that closed-loop alternans control techniques that apply a succession of externally-administered cycle perturbations at a single site provide limited spatially-extended alternans elimination in sufficiently large cardiac substrates. However, detailed experimental investigations into the spatial dynamics of alternans control have been restricted to Purkinje fiber studies. A complete understanding of alternans control in the more clinically relevant ventricular tissue is needed. In this paper, we study the spatial dynamics of alternans and alternans control in arterially perfused canine right ventricular preparations using an optical mapping system capable of high-resolution fluorescence imaging. Specifically, we quantify the spatial efficacy of alternans control along 2.5 cm of tissue, focusing on differences in spatial control between different subregions of tissue. We demonstrate effective control of spatially-extended alternans up to 2.0 cm, with control efficacy attenuating as a function of distance. Our results provide a basis for future investigations into electrode-based control interventions of alternans in cardiac tissue.

I. Introduction

Cardiac repolarization alternans, sometimes referred to as action potential duration (APD) alternans, is an electrical phenomenon corresponding to alternating changes in action potential duration. Clinically, alternans has been closely associated with sudden cardiac death (SCD) and ventricular fibrillation (VF), in particular [1]–[5]. More importantly, mediated by the spatial dispersion of repolarization, alternans has been shown to be mechanistically linked to the pathogenesis of reentrant wave activity [6]. Spatial manifestations of alternans can be either concordant, during which the beat-to-beat alternations in APD are in-phase at all points in space, or discordant, during which two distinct regions exhibiting relative out-of-phase behavior are present. Spatial differences in APD phase can lead to gradients of repolarization (dispersion) within the myocardium, which if steep enough, can facilitate local conduction block of normal wave propagation [7]–[11]. Electrical disruptions of this kind can turn a normally planar wave into a spiral wave [12], and furthermore can break a single spiral wave into multiple wavelets of electrical activity [13], which are thought to underlie ventricular fibrillation.

Because of the putative link between APD alternans and the onset of ventricular fibrillation, it may be beneficial to develop means to terminate and/or prevent alternans in cardiac tissue. Closed-loop feedback mechanisms aimed at controlling a dynamically stable period-2 rhythm (alternans) to an unstable period-1 rhythm (no alternans) using single-site intervention from an external source may be one such option.

Previous studies demonstrating successful alternans control include the elimination of atrio-ventricular alternans – a type of alternans that shares similar characteristics with APD alternans – in rabbit heart preparations [14], [15] the suppression of APD alternans in small isolated frog heart preparations [16], and control in single myocytes [17]. Despite these successes, however, complete alternans control has so far been limited to these small-scale systems (i.e., single-cell or sufficiently small tissue preparations) that do not allow for spatiotemporal variations in wave-propagation or repolarization dynamics – single-site control of physically larger systems has proven to be more difficult.

Investigations of alternans control in larger systems have been limited chiefly to cardiac Purkinje fibers. In all studies – including in silico modeling and analytical theory [18], and in vitro experimentation [19] – it was demonstrated that spatiotemporal control of alternans is limited to small distances (≈1 cm, depending on the pacing rate) from the site of electrode intervention. This failure of spatially-extended control stems from the complex spatial and temporal interactions that arise between APD and conduction-velocity restitution dynamics that occur during the rapid pacing of sufficiently large regions of tissue [18].

Still missing, however, is a better understanding of alternans and alternans control dynamics in the more clinically relevant ventricular tissue. In particular, the spatial extent of alternans control in ventricular tissue is needed if more complex methods of alternans suppression (e.g., multisite control) are to be developed for clinical use. Given the results yielded by linear stability analysis of general alternans behavior, which suggests that spatial controllability of alternans is dependent on conduction velocity (CV), one would expect that alternans control would behave differently in ventricular tissue (CV <100 cm/s [20]–[22]) as compared with Purkinje fibers (CV ≈200 cm/s [23]).

More generally, in order to fully characterize spatial controllability within real tissue, detailed quantification and analysis of electrophysiological and/or dynamically-induced properties – including conduction velocity restitution, repolarization heterogeneities, and spatial APD variations – are needed at very fine temporal and spatial resolutions.

Aiming to fill this knowledge void, in this study we investigated alternans and alternans control dynamics in arterially perfused canine right ventricular preparations using a previously developed optical mapping system capable of simultaneous real-time control application and high-resolution voltage data imaging [24].

Utilizing the high-resolution capability of the optical mapping system while subjecting the tissue sample to either static or control-perturbed pacing, we were able to observe and quantify the spatial efficacy of alternans control in our preparations. In addition, we were able to observe and analyze spatial changes in APD and repolarization dynamics resulting from the application of control, adding further insight to our understanding of this problem.

Our quantitative results, derived from six different preparations, paced at varying basic cycle length (BCL) values, show that single-site alternans control, although unable to completely eliminate alternans at each point in the field-of-view (2.5 cm), was able to substantially reduce the spatially averaged alternans magnitude (A_M,S) within the proximal (0–1 cm) and middle (1–2 cm) regions of tissue in 15/17 and 12/17 control trials, respectively. Although the relative success of control was greater at regions more proximal to the control site – in agreement with previous alternans control experiments [18], [19] – the extent to which control reduced alternans at distances up to 2.0 cm from the control site warrants optimism in the development of more advanced electrode-based intervention techniques for the management of cardiac alternans.

II. Methodology

A. Isolated Arterially Perfused Right Ventricular Preparation

All experimental procedures were approved by the Institutional Animal Care and Use Committee (IACUC) of the Center for Animal Resources and Education of Cornell University. Hearts used in the experiments were extracted from adult beagle dogs of either sex weighing between 10–30 kg. The dogs were anesthetized using Fatal-Plus (Vortex Pharmaceuticals; 390 mg/mL pentobarbital sodium; 86 mg/kg IV), and their hearts were excised rapidly. The right coronary artery was cannulated using polyethylene tubing and the right atrial and ventricular myocardium were extracted and suspended, endocardial surface facing the camera, in a heated (@ 30°C, in order to more easily induce large-scale alternans) and transparent custom-built tissue chamber. The preparation was superfused and arterially perfused with normal Tyrode’s solution for the duration of each experiment. After 15 to 30 minutes of equilibration, the preparation was stained with the voltage-sensitive fluorescent dye 4{β-[2-(di-n-butylamino)-6-napathy]vinyl} pyridinium, a.k.a. di-4-ANEPPS, (Molecular Probes; 10 μmol/L bolus; 10μM) and immediately following, blebbistatin [25] (Enzo Life Sciences; 10 μmol/L constant infusion over 20 to 30 minutes) was administered to prevent motion artifacts.

B. Imaging Hardware

In order to properly characterize alternans and alternans control behavior in our tissue preparations, high spatial resolution signals were needed. Commonly used microelectrode techniques, though capable of providing high quality temporal voltage measurements, are spatially limited due to the difficulty in placing multiple electrodes in close proximity with one another, and their inherent fragility further complicates usage in tissue preparations. In contrast, optical mapping systems used in conjunction with voltage-sensitive fluorescent dyes are capable of providing very high spatial resolution measurements while maintaining adequate temporal resolution at each spatial location. For this reason, we opted to use a previously developed optical mapping system [24] for our experiments.

Technical limitations arise when attempting to simultaneously record from many spatial locations and further consideration was needed because of the real-time requirements of alternans control. Because imaging from too large an area would have caused an insurmountable data transfer bottleneck, we opted to use a line scan CCD camera capable of detection along a single dimension only, which greatly reduced the size of each frame.

The main hardware components of the optical mapping system included a line scan CCD camera, a custom-developed tandem-lens assembly, and an LED-based light source [24]. The CCD camera consisted of a 1-D array of 2,048 pixels, each 14 μm² in dimension. Use of the tandem lens assembly enabled ×0.47 magnification at a working distance of 40 mm, while six 5-W high-powered LEDs, positioned no more than 20 mm from the tissue, provided the dye excitation. The imaging array was situated transverse to the long axis of the endocardial muscle fibers for all experiments.

Recordings were performed at a frame rate of 1–2 KHz. In general, alternans frequencies were 1–3 Hz. Spurious signals at frequencies needed to adversely affect alternans measurements (aliasing) given the typical CCD integration times were not detected. A National Instruments PCI-6254 analog-to-digital board provided the link between the controlling software (RTXI; described in the next section) and the electrode stimulator. The short working distance of the tandem lens (allowing for high fluorescence signal detection) posed strict physical constraints, which prevented easy microelectrode access to points along the imaging line (including the control site). Thus, no microelectrode recordings were obtained.

C. Signal Processing and Software

Real-time signal processing was needed for signal-to-noise (S/N) improvement and the removal of signal base line drift (attributable to voltage dye photo-bleaching and light-source instability). Use of a mean spatial filter (16-pixel width) improved S/N while effectively reducing the spatial resolution to 480 μm (1 recording channel = 16 pixels = 480 μm) and a nonlinear recursive high-pass filter [24] acted to detrend the signal in an effective and robust manner. In this way, 2,048 pixels were spatially averaged into 128 channels, each corresponding to 480 μm in length, which were used for all subsequent analyses.

Real-time data acquisition and control functionality was managed by the Real-Time experiment Interface (RTXI; www.rtxi.org), a software system developed specifically for real-time closed-loop feedback tasks of this type and successfully employed in several previously performed cardiac tissue control studies [17], [24]. The optical signal measured at the control site (see Section II.D. for details on control channel selection) was fed into RTXI, and the system calculated the APD and determined any pacing rate modifications (according to the prescribed alternans control algorithm – see Section II.D. for details).

During post-acquisition processing, a 2-D spatiotemporal boxcar filter (5 pixels²) was used to further smooth the data for analysis. APD threshold values at 80% of repolarization (APD₈₀) were used for post-processing analysis of alternans magnitude and dynamical behavior.

D. Experiment Protocol

Tissue pacing was administered via a bipolar electrode in firm contact with the surface of the tissue preparation. Pacing occurred at cycle lengths sufficiently fast so as to induce steady-state alternans at the pacing site (BCL range: 290–500 ms) and at each BCL tested, a pair of optical mapping images was acquired for each trial, the first half during static pacing (no-control) and the second during the application of alternans control at the pacing site. Each “image” consisted of 10–20 seconds of exposure time along the field-of-view.

The alternans control algorithm implemented by the system was similar to those used in previous cardiac control experiments [17]–[19]. The basic principle of alternans control is to force the underlying dynamical system to its unstable period-1 fixed point – having been made unstable by the dynamically induced period-doubling bifurcation (i.e., parameter-sensitive change to initial condition instability behavior [26]) that naturally occurs at sufficiently fast pacing rates [27]. By exploiting the APD restitution relationship [28], whereby smaller diastolic intervals (the “rest” period before an action potential) correspond to smaller subsequent APDs, alternans control uses the APD information from consecutive action potentials to calculate the necessary adjustment to the cycle length in a manner that will decrease the alternans magnitude over time. The cycle length interval adjustment (ΔT) and the resulting control-perturbed cycle length (T_n) are determined by the following equations [19]:

$$T_n=\{\begin{array}{ll}{T}^{\ast }+\mathrm{\Delta }{T}_n\hfill & \text{if}\mathrm{\Delta }{T}_n<0,\hfill \\ T^{\ast }\hfill & \text{if}\mathrm{\Delta }{T}_n\ge 0,\hfill \end{array}$$ (1)

where

$$\mathrm{\Delta }{T}_n=(\lambda /2)({\mathit{APD}}_n-{\mathit{APD}}_{n-1}),$$ (2)

T* is the target BCL (i.e., cycle length applied when control is turned off), λ is the feedback gain, and n is the beat number. In other words, given a sequence of alternating APDs (L-S-L-S), instances of APD_n−1>APD_n, which immediately follow relatively “short” (S) APDs and precede “long” (L) APDs, elicits a premature pulse (T*+ΔT_n) that effectively reduces the diastolic interval (DI) of the would-be “long” APD. This reduction in DI temporarily disrupts the steady-state alternating pattern by shortening the “long” APD and lengthening the subsequent “short” APD according to electrophysiological properties reflected in the APD restitution relationship. These situations require the repeated application of control, however, to maintain a relatively constant beat-to-beat APD pattern because of the system’s dynamically-induced tendency towards an alternans rhythm [29].

Within this manuscript, references to “BCL” in the context of static pacing imply stimulation at a steady pacing rate, whereas in the context of alternans control, “BCL” refers to the target BCL (T*). Given the relatively poor S/N inherent to optical mapping techniques and the increased likelihood that an errant APD measurement would disrupt the controlling process, a relatively high feedback gain of 2.0 was chosen to achieve control quickly. Included in (1) is a condition that allows for only premature stimulation. Allowing only cycle length shortening more accurately reflects what would happen in a clinical setting during which the native excitation of the heart, corresponding to cycle length = T*, cannot be delayed. Interestingly, algorithms using only negative perturbations have been shown analytically to have a larger successful control regime than those that apply both positive and negative perturbations [30].

All stimuli, whether statically-timed or control-perturbed, were administered using the same bipolar stimulating electrode at twice diastolic threshold (obtained @ BCL = 500 ms). The APD values measured by RTXI, and thus those used in the control algorithm, were those measured at the recording channel closest to the stimulating electrode. This channel, herein referred to as the control channel, was ≤2 mm from the stimulating electrode for all experiment trials. The APD thresholds used during real-time acquisition were chosen manually; post-acquisition analysis revealed that all threshold values were within the APD₉₀ to APD₆₀ range.

E. Data Selection

Alternans and alternans-control dynamics obtained from long recording durations were difficult to analyze because even the relatively small (given the temporal quality expectations of optical mapping recordings) amounts of noise associated with our recordings resulted in occasional misestimates of the true underlying APD and ill-timed perturbations during the application of control. As a result, we used APD values derived from a single sequence of six successive action potentials (six-AP) to calculate the resulting alternans magnitudes, on a channel-by-channel basis (the same six for each channel), for each imaging record.

The APD alternans fluctuation coefficient, F (computed in (3)], was used to identify regions of stable alternans during control-off conditions. For each post-processed control-off image, the six-AP sequence corresponding to the largest alternans magnitude, A_M [computed in (4)], with F < 0.5 was selected for analysis. For each post-processed control-on image, the sequence with the smallest alternans magnitude (A_M) was used. The selection of all sequences was determined by the APD measurements derived from the control channel only.

Control pairs in which the control-off and control-on results at the control channel yielded sequences of robust, steady-state alternans (A_M > 10 ms; F < 0.5) and successful alternans control (A_M ≤ 10 ms), respectively, were selected for final analysis. This resulted in 17 pairs of control-off/control-on images, derived from six preparations, being chosen. For each BCL that yielded multiple pairs of useable data for a particular preparation, the pair consisting of the best control-off results was selected. It should be noted that the trial selection criteria were constructed in an effort to analyze and quantify the spatial efficacy of control – analysis of the overall control success rate was not an objective of this study.

F. Equations

Alternans Fluctuation Coefficient

The APD alternans fluctuation coefficient, F, was used as a measure of the variation in beat-to-beat alternans within a given series of action potentials. The fluctuation coefficient was calculated according to the following:

Given a sequence of APD Δ values, D:

$$D=\left(\mid A_2-A_1\mid ,\mid A_3-A_2\mid ,\dots ,\mid A_n-A_{n-1}\mid \right),$$

where A is a sequence of n positive real APD values:

$$A=\left(A_1,A_2,\dots ,A_n\right),$$

the alternans fluctuation coefficient, F, is defined as:

$$F=[max(D)-min(D)]/\text{mean}(D).$$ (3)

Alternans Magnitude Calculation

The APD alternans magnitude for a given series of action potentials was calculated according to the following:

Given a sequence of n positive real APD values, A:

$$A=\left(A_1,A_2,\dots ,A_n\right),$$

alternans magnitude, A_M, is defined as:

$$A_M=\left(\sum _{i=1}^{n-1}\mid A_{i+1}-A_i\mid \right)/(n-1)$$ (4)

and phase - specific alternans magnitude, a.k.a. alternans difference, A_D, is defined as:

$$A_D=\left(\sum _{i=1}^{n-1}(A_{i+1}-A_i){(-1)}^i\right)/(n-1).$$ (5)

The different alternans equations enabled the quantification of both alternans magnitude (4) – useful when analyzing spatially averaged alternans reduction – and phase-specific alternans magnitude (5) – necessary in the analysis of alternans spatial dynamics (i.e., concordance vs. discordance). Calculations of |A_D|, as opposed to A_M (technically, a measurement of absolute variability), are sensitive to alternans phase reversals with respect to time, which often occurred during the application of control, resulting in misleadingly small alternans values. Thus, A_M was used where appropriate. (It should be noted that |A_D| quantification led to almost identical hypothesis testing results).

G. Statistical Analysis

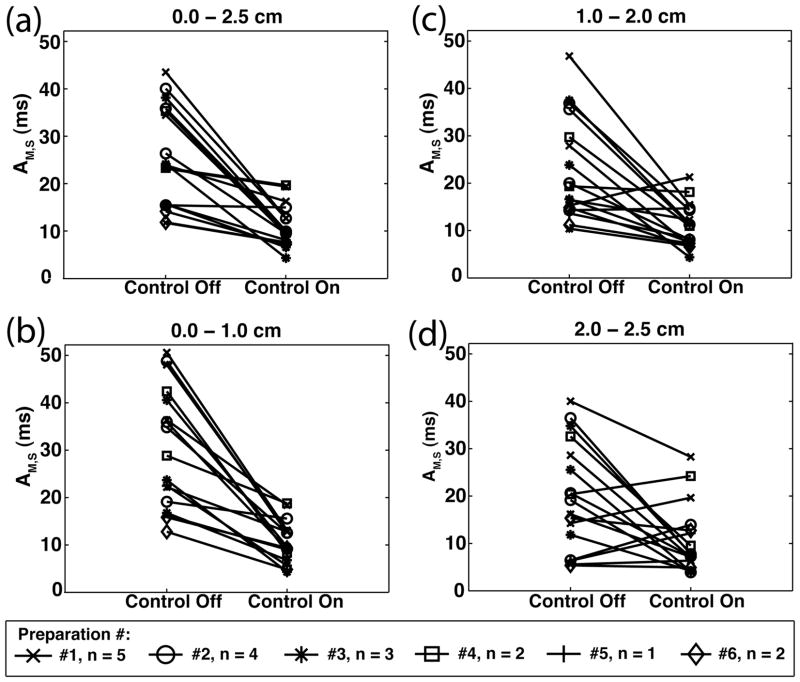
Statistical comparisons between control-off and control-on spatially averaged A_M values (A_M,S – Table I) were achieved using paired student t-tests. For each experiment trial, channel-indexed pairs resulted in comparisons between control-off and control-on A_M,S values. Comparisons within specific regions of tissue (0.0–2.5 cm, 0.0–1.0 cm, 1.0–2.0 cm, and 2.0–2.5 cm) resulted in p-values associated for each (Table I).

Table I.

Spatially Averaged Alternans Results For All Experiment Trials

		0 – 2.5 cm control-off control-on				0 – 1 cm control-off control-on				1 – 2 cm control-off control-on				2 – 2.5 cm control-off control-on
	BCL	AM,S	AM,S	Δ	P	AM,S	AM,S	Δ	P	AM,S	AM,S	Δ	P	AM,S	AM,S	Δ	p
Preparation #1	500	23.9	16.2	7.7	<0.01	36.4	18.4	18.0	<0.01	16.5	12.3	4.2	>0.05	14.3	19.6	−5.4	<0.05
	450	23.2	19.4	3.8	>0.05	22.2	12.8	9.4	>0.05	15.3	21.3	−6.0	>0.05	40.0	28.3	11.7	<0.01
	400	11.7	7.6	4.1	<0.01	16.2	9.0	7.2	<0.01	10.4	6.8	3.6	<0.01	5.6	6.4	−0.8	>0.05
	375	43.5	12.7	30.8	<0.01	48.0	12.9	35.1	<0.01	46.8	15.4	31.4	<0.01	28.6	7.1	21.5	<0.01
	350	34.5	9.4	25.1	<0.01	50.6	13.1	37.5	<0.01	27.9	6.8	21.1	<0.01	16.2	7.2	9.0	<0.01
Preparation #2	460	35.9	9.9	26.0	<0.01	36.0	9.2	26.8	<0.01	35.6	11.3	24.3	<0.01	36.5	7.7	28.7	<0.05
	420	40.1	12.7	27.4	<0.01	48.8	12.5	36.3	<0.01	36.9	14.3	22.5	<0.01	20.6	7.3	13.3	>0.05
	415	26.4	15.0	11.4	<0.01	34.8	12.1	22.7	<0.01	20.0	12.5	7.5	>0.05	19.1	33.6	−14.5	<0.05
	400	15.4	15.0	0.5	>0.05	19.1	15.6	3.6	>0.05	14.3	14.7	−0.4	>0.05	6.4	13.9	−7.5	<0.05
Preparation #3	430	15.7	6.6	9.1	<0.01	16.7	6.8	10.0	<0.01	16.6	7.6	9.1	<0.01	11.8	4.2	7.6	<0.01
	420	24.1	4.3	19.9	<0.01	23.7	4.3	19.4	<0.01	23.8	4.4	19.5	<0.01	25.5	4.1	21.5	<0.01
	410	38.2	10.0	28.2	<0.01	40.6	9.6	31.0	<0.01	37.5	11.5	26.0	<0.01	34.8	7.9	26.9	<0.01
Preparation #4	300	23.3	19.7	3.7	<0.05	28.8	18.8	10.1	<0.01	19.4	18.1	1.2	>0.05	20.4	24.2	−3.8	>0.05
	290	35.4	9.7	25.7	<0.01	42.4	8.4	34.0	<0.01	29.7	11.0	18.7	<0.01	32.6	9.5	23.0	<0.01
Preparation #5	400	15.6	8.1	7.6	<0.01	22.5	5.6	16.9	<0.01	13.6	8.4	5.2	<0.01	6.3	12.2	−5.8	<0.05
Preparation #6	400	11.8	7.6	42	<0.01	15.8	9.3	6.5	<0.01	11.2	7.3	3.9	<0.01	5.4	4.9	0.5	>0.05
	390	14.1	7.16	7.0	<0.01	12.8	4.8	8.0	<0.01	14.9	6.6	8.3	<0.01	15.3	12.7	2.6	>0.05

Trial-by-trial comparisons of spatially averaged alternans magnitude (A_M,S) during control-off and control-on conditions for different subregions of tissue (0.0–2.5 cm; 0.0–1.0 cm; 1.0–2.0 cm; 2.0–2.5 cm). “Δ” denotes difference between control-off and control-on A_M,S value; p-value indicates significance level of the paired student t-test result for the associated trial and tissue subregion. Pairing was according to spatial location (i.e., channel-specific paired t-test). Elements shaded denote a statistically significant decrease in A_M,S was observed during the application of control.

Statistical comparisons of control efficacy between different regions of tissue were achieved using paired student t-tests. In this case, pairs indexed by individual trial, comparing A_M,S reduction (Δ) with respect to specific regions of tissue, resulted in spatial comparisons of control efficacy (Fig. 6).

Repolarization dispersion values (σ²) were calculated, for each action potential in a given six-AP sequence, by computing the variance in repolarization times with respect to control channel activity. Grouping action potentials from every-other beat resulted in two sets (AP_n and AP_n+1) of three action potentials [AP_n = (AP₁, AP₃, AP₅); AP_n+1 = (AP₂, AP₄, AP₆)]. Mean σ² values ( $\overline{{\sigma }^2}$) were computed for each set and the greater of the two was used in the analysis of the three concordant/control-off: discordant/control-on cases [Fig. 4(e)] and that of the four discordant/control-off: discordant/control-on cases (see Discussion).

All error bars shown denote standard error.

III. Results

A. Control Channel Results (Preparation #1)

Examples of APD alternans behavior (and signal quality) induced at the control site under static and control-adjusted pacing are illustrated in Fig. 1. An optical mapping recording during static pacing is shown in Fig. 1(a), and the resulting APD values, as were measured by the system, are denoted by the gray X’s superimposed on the trace. Beat-to-beat alternations were fairly constant for the duration of the recording, reflective of steady-state dynamical behavior.

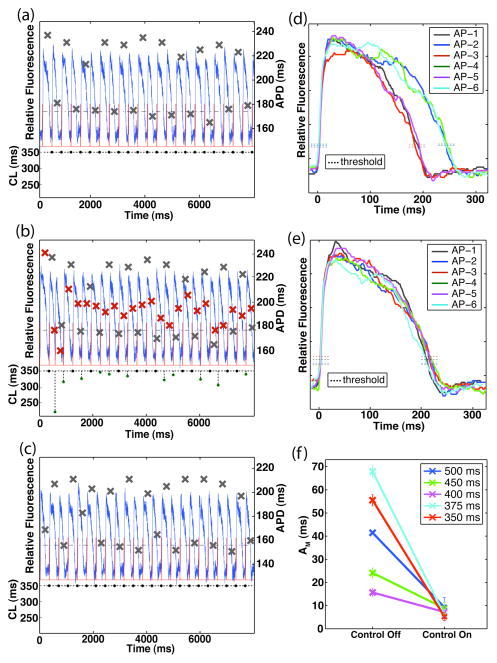
Fig. 1.

Optical signal recordings and APD alternans results derived from the control channel during statically-timed and control-perturbed pacing (preparation #1). (a) Pre-processed optical recording during static pacing (top – left axis; BCL = 350 ms); superimposed X’s denote APD values (right axis). Bottom-axis shows the preceding pacing cycle length (CL) for the corresponding action potential. APD threshold values and stimuli are shown as the dashed black line and the red trace, respectively. (b) Pre-processed optical recording during the application of control (BCL = 350 ms); immediately followed that shown in (a). Superimposed red (gray) X’s denote APD values for control-on (control-off). Note change in cycle lengths as a function of preceding APD values. (c) Subsequent control-off optical recording resulted in the re-emergence of robust alternans at the control site (post-processed six-AP A_M = 55 +/− 1.8 ms). (d)–(e) Action potential waveforms of post-processed six-AP sequences during control-off (d; six-AP A_M = 56 +/− 2.4 ms) and control-on (e; six-AP A_M = 5 +/− 1.7 ms) conditions; sequence selected according to the methods described in Section II.E. (f) Control-off and control-on six-AP A_M values calculated at the control channel derived from all experiment trials performed on preparation #1 (BCL = 500, 450, 400, 375, and 350 ms).

Immediately following the acquisition of the control-off image, control was applied at the control site; the resulting optical signal is shown in Fig. 1(b). This panel demonstrates the system’s ability to acquire optical data, calculate the necessary changes in cycle length, and deliver the controlling electrical stimulus (notice changes in cycle length as a function of preceding APD values) – all in real-time. Directly comparing the APD values from the control-off (gray X’s) and control-on (red X’s) halves of the trial illustrates more clearly the high degree of control the system was able to achieve. Reverting back to static pacing allowed for the return of large and stable alternans at the control site [Fig. 1(c)].

Comparing the post-processed six-AP sequences associated with this particular control-off/control-on trial (selected according to the methods explained in Section II.E.) exemplifies the effect that control had on the entire action potential waveform. Static pacing yielded clear alternations in the beat-to-beat waveform [Fig. 1(d)], whereas the application of control resulted in consistently similar waveforms and the near elimination of APD alternans [Fig. 1(e)].

A total of five trials, each at a different BCL, were performed on this particular preparation. A summary of the control channel results is shown in Fig. 1(f). As shown in the figure, at each of the five BCLs tested, control greatly reduced A_M at the control site.

B. Spatial Results

The optical mapping system enabled the observation and post-hoc analysis of action potential dynamics at points distal to the control site with high spatial and temporal resolution. Fig. 2(a) shows an example optical signal, as a function of distance and time, acquired during the application of control. The spatial location of the stimulating electrode and the timings of the applied stimulus current are denoted on the distance-time plot by the vertical-dashed red line and the horizontal-dashed white lines, respectively. Propagation of the wave front, which starts at the point of stimulation on the left-hand side, is smooth and linear, and from its inverse slope the CV of the wave front can be calculated. For any given experiment trial, the conduction velocity along the entire field-of-view was measured to be constant (CV range across trials: 84–115 cm/s).

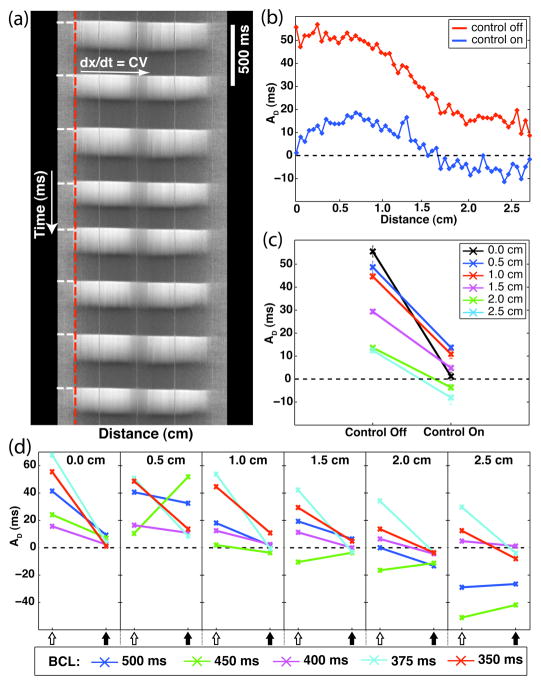
Fig. 2.

Examples of spatial alternans dynamics. (a) Example distance-time plot of relative fluorescence data. Shown is the propagation of eight action potentials along the length of the tissue (BCL = 420 ms; CV = 92 cm/s). Color-coding: white – depolarized fluorescence; gray – resting fluorescence. The vertical-dashed red line and the horizontal-dashed white lines on the left-hand side of the plot correspond to the spatial location of the stimulating electrode and the timings of the applied stimulus current, respectively. The three equally spaced wavy vertical lines are from the calibration coverslip, which was placed over the sample preparation (1 cm spacing). This signal was detrended and smoothed according to the methods described in Section II.C. (b)–(d): Phase-specific alternans magnitudes, A_D, measured during control-off and control-on conditions (preparation #1). (b) Measurements from each channel within the field-of-view (BCL = 350 ms). Control-off – red; Control-on – blue. (c) Measurements from equally spaced locations from the control channel (distances = 0.0, 0.5, 1.0, 1.5, 2.0, and 2.5 cm; BCL = 350 ms). (d) Spatial measurements derived from all experiment trials performed on preparation #1 (BCL = 500, 450, 400, 375, and 350 ms). Open-arrows: control-off; closed-arrows: control-on.

Optical mapping signals from a continuous region of tissue consisting of 53 channels (≈2.5 cm; as described in Section II.C., each channel was comprised of 16 pixels, each pixel corresponding to 30 μm) were used for the spatial analysis. Fig. 2(b) is a plot of the calculated A_D values for each of the 53 channels, beginning with the control channel, during one alternans control trial (preparation #1 – BCL = 350 ms). As reflected in the control-off spatial profile, static pacing resulted in concordant alternans with large A_D values along the entire field-of-view. The noted decrease in A_D magnitude at points distal to the site of stimulation is similar in profile to that seen in Purkinje fiber studies [19]. In contrast, the application of control resulted in spatially discordant alternans along the imaging line, characterized by the presence of two distinct regions of out-of-phase alternans behavior. Two nodes of no-alternans resulted – one separating the two out-of-phase regions and another, reflecting the successful application of control, at the control site. Along with a change in spatial dynamics, alternans control resulted in a marked decrease in A_D magnitude across the entire length of the imaged tissue.

Selecting equally spaced locations (distances = 0.0, 0.5, 1.0, 1.5, 2.0, and 2.5 cm from the control channel) allowed for easier visualization of multiple data sets while still retaining pertinent spatial dynamical information. The control-off and control-on alternans values of Fig. 2(b) are displayed in this manner within Fig. 2(c). Comparing the before and after conditions, both the reduction in A_D magnitude at points along the imaging line and the induction of discordant alternans during the application of control are evident.

The control-off and control-on spatial dynamics at each of the five BCLs tested on this particular preparation (#1) are shown in Fig. 2(d). In the absence of control, concordant alternans was observed at three of the five BCLs tested (400, 375, and 350 ms), whereas discordant alternans was clearly discernable during the other two (500 and 450 ms). Some of the results during control-on were ambiguous (likely due to the localized viewing region) but in each of the three cases exhibiting concordant control-off behavior, control reduced the A_D at each representative spatial location to values below 10 ms in magnitude.

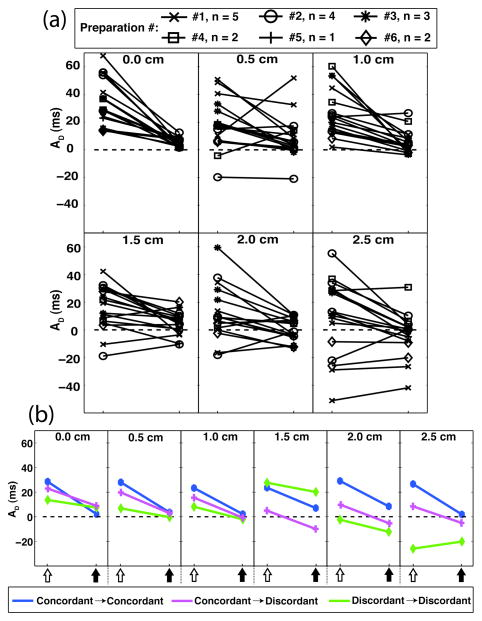
Experimental results compiled from all trials across all preparations are summarized in Fig. 3. As determined by the selection criteria described in Section II.E., robust steady-state alternans was observed at the control channel for each trial during static pacing (A_D range: 14 –68 ms, mean: 35 ms) and control reduced the A_D to values ≤10 ms (range: 2–10 ms, mean: 5 ms) in all cases [Fig. 3(a), first panel]. In addition, three different control-off:control-on pairings of spatial dynamics were observed – concordant:concordant, concordant:discordant, and discordant:discordant [Fig. 3(b)]. (The spatial dynamics were indeterminate for several of the trials).

Fig. 3.

Phase-specific alternans magnitudes, A_D, measured during control-off and control-on conditions. Measurements are from equally spaced locations from the control channel (distances = 0.0, 0.5, 1.0, 1.5, 2.0, and 2.5 cm). (a) Results from all experiment trials (# of preparations = 6, n = 17 total trials). (b) Representative spatial dynamics results demonstrating effect of control. Control-off:control-on pairings – concordant:concordant (preparation #3: BCL = 420 ms); concordant:discordant (preparation #5: BCL = 400 ms); discordant:discordant (preparation #6: BCL = 390 ms). Open-arrows: control-off; closed-arrows: control-on.

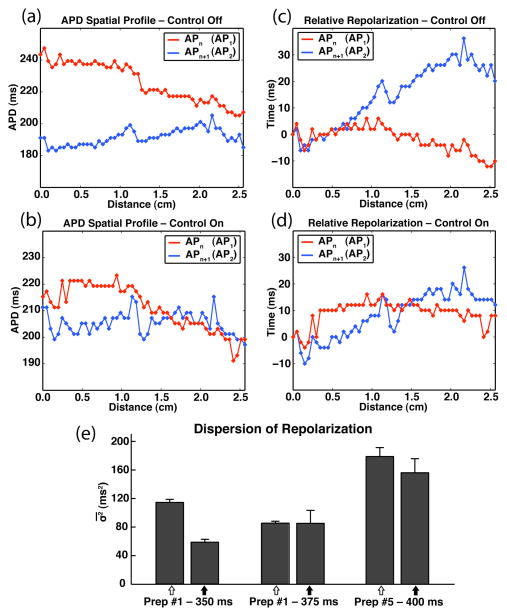
Cases of concordant:discordant behavior [preparation #1: 350, 375 ms – Fig. 2(d); preparation #5: 400 ms – Fig. 3(b)] are of particular importance given the recent attention concerning the genesis, dynamics, and general characteristics of discordant alternans [6]–[11]. Instances of discordant alternans are usually associated with an increase in repolarization gradients (dispersion), which can be quantified by calculating the variance in the times to repolarization (σ²) within a chosen region of space. Fig. 4 shows the APD and repolarization time profiles for AP₁ and AP₂ (representative AP_n/AP_n+1 pair) during the absence [Fig. 4(a),(c)] and presence [Fig. 4(b),(d)] of control (preparation #1 – BCL = 350 ms). The observed differences in the APD profiles [Fig. 4(a),(b)] reflect the control-induced transition from concordance to discordance that occurred within the imaging region, whereas the differences in the relative repolarization time profiles [Fig. 4(c),(d)] simply reflect the dynamics associated with each representative action potential. $\overline{{\sigma }^2}$ values calculated from the repolarization times of the AP_n and AP_n+1 action potential sets derived from this trial (see Section II.G. for selection specifics) show a decrease in repolarization dispersion after the application of control despite the transition from concordance to discordance [Fig. 4(e), first column pair]. This observation can be attributed to the overall reduction in alternans magnitude (quantified next) that accompanied the successful application of control, which effectively outweighed the positive effect that a phase reversal has on dispersion. Fig. 4(e) also shows the effect that alternans control had on $\overline{{\sigma }^2}$ for the other two observed instances of clear concordant:discordant behavior. In all, the calculated dispersion ( $\overline{{\sigma }^2}$) either decreased or remained constant with the application of control.

Fig. 4.

Control-induced transition from concordance (control-off) to discordance (control-on). (a)–(b) Representative APD spatial profiles for AP_n and AP_n+1 (first two action potentials of six-AP sequence) during control-off (a) and control-on (b). (c)–(d) Representative relative repolarization times for AP_n and AP_n+1 during control-off (c; AP₁-σ²: 22.4 ms², AP₂-σ²: 122.2 ms²) and control-on (d; AP₁-σ²: 13.5 ms², AP₂-σ²: 59.9 ms²) conditions. (a–d: Preparation #1 – BCL = 350 ms.) (e) Control-off:control-on (open-arrows and closed-arrows, respectively) repolarization dispersion values ( $\overline{{\sigma }^2}$) derived from cases of concordant:discordant behavior (preparation #1 – BCL = 350, 375 ms; preparation #5 – BCL = 400 ms). Shown is the greater of the two σ²-mean ( $\overline{{\sigma }^2}$) values calculated for each six-AP sequence: ${\text{AP}}_{\text{n}}-\overline{{\sigma }^2}(\text{n}=3)$ or AP_n+1-σ² (n=3).

The spatial efficacy of alternans control was quantified by averaging the A_M values across regions of space. Comparing the results from statically-paced and control-perturbed conditions, control reduced the spatially averaged alternans magnitude, A_M,S, as calculated for the entire 2.5 cm length for each trial [Fig. 5(a)]. Table I includes the before and after A_M,S values and the control induced reduction (Δ) for each trial. A channel-specific paired t-test calculated for channels spanning the entire 0.0–2.5 cm region of tissue reveals significant (p < 0.05) reductions in alternans for 15/17 of the trials.

Fig 5.

Spatially averaged alternans magnitudes (A_M,S) under control-off and control-on conditions; compiled from all trials (# of preparations = 6, n = 17 total trials). (a) 0.0–2.5 cm; (b) 0.0–1.0 cm; (c) 1.0–2.0 cm; (d) 2.0–2.5 cm.

To determine more precisely the spatial effect that control had on the tissue, we compared the extent to which control reduced A_M,S at the proximal (0–1 cm), middle (1–2 cm), and distal (2–2.5 cm) regions of tissue. Focusing first on each individual subregion of tissue, Fig. 5(b)–(d) shows the A_M,S values for each, calculated across all trials. Control reduced A_M,S by a significant amount in 15/17, 12/17, and 8/17 cases with respect to the proximal (b), middle (c), and distal (d) regions of tissue (p < 0.05, Table I).

A trial-specific paired t-test, comparing the control-induced reductions (Δ) of one tissue segment with that of another across all trials reveals that a significantly greater reduction in A_M,S occurred at the proximal end of the tissue as compared with both the middle and distal regions, both in absolute and proportional amounts, suggesting a decrease in control efficacy as a function of distance (p < 0.05; Fig. 6).

Fig. 6.

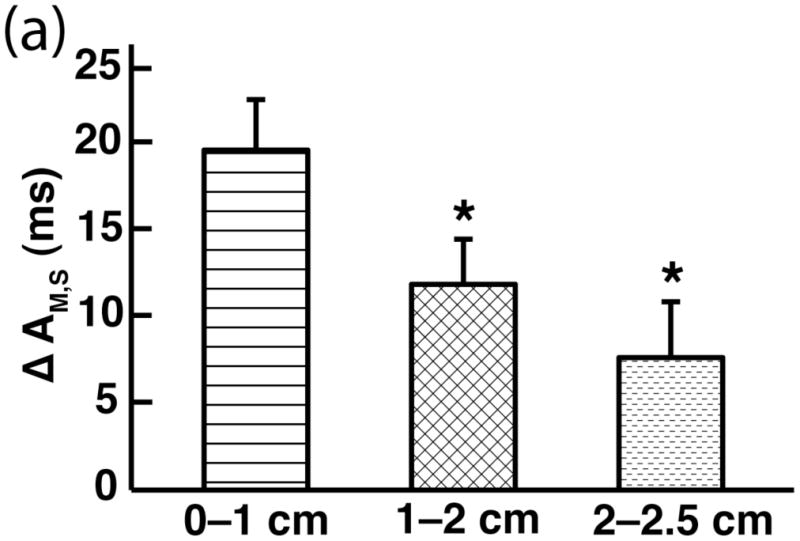
Reduction in spatially averaged alternans magnitude (A_M,S) across different subregions of tissue. Both absolute (Δ) and percentage [Δ (%)] reductions were computed [%ΔA_M,S: 0.0–1.0 cm (60%), 1.0–2.0 cm (40%), 2.0–2.5 cm (20%)]. “*” indicates a statistically significant difference (p < 0.05) in reduction was observed when comparing the reduction for the proximal (0.0–1.0 cm) region with that of either the middle (1.0–2.0 cm) or distal (2.0–2.5 cm) region of tissue. Similar statistical significance results for %ΔA_M,S regional comparisons were observed (data not shown).

IV. Discussion and conclusion

Previous studies of alternans control have been limited to Purkinje fibers [18], [19], and though informative, a better understanding of alternans control dynamics in the more clinically relevant ventricular tissue is needed. In this study, we investigated the effects of static pacing and single-site control applied to arterially perfused canine right ventricular preparations using an optical mapping system capable of high-resolution transmembrane voltage imaging. We were able to demonstrate that compared with static pacing, the application of alternans control significantly reduced the spatially averaged alternans magnitude (A_M,S) across 2.5 cm of tissue [Fig. 5(a)] – a result which was observed across several different preparations and at varying BCLs. Furthermore, we showed that control-induced reduction was greatest for regions of the tissue that were most proximal to the control site, indicating an attenuation of control efficacy as a function of distance (Fig. 6) – in agreement with previous Purkinje fiber study results [18], [19].

In our experiments, we observed the two spatial manifestations of alternans – concordant and discordant – and though we were unable to draw any statistically significant results linking spatial efficacy of control with alternans type, important observations can still be made.

The likely mechanism by which alternans promotes conduction block and subsequent VF formation involves the creation of steep repolarization gradients within the tissue. Thus, substantial reductions in gradient magnitude are potentially anti-arrhythmic. Previous studies have quantified relative gradient steepness using dispersion calculations [6], [8], [31]. Examples illustrating the direct causal relationship between dispersion (both APD and repolarization specific) and wave-break abound [6–8], [10].

Given the successful application of control, a decrease in the overall alternans magnitude will tend to reduce the gradients of repolarization within regions sufficiently close to the control site. Successful control would likely reduce the gradients of repolarization when comparing discordant/control-off and discordant/control-on cases (discordant:discordant) and certainly when comparing discordant/control-off and concordant/control-on cases (no observations of the latter off/on pairing were made in our experiments). Analysis of the discordant:discordant cases observed in our experiments (preparation #1 – BCL = 500, 450 ms; preparation #6 – BCL = 400, 390 ms) suggest that this was the case ( $\%\mathrm{\Delta }\overline{{\sigma }^2}$, percentage reduction after control application = 30%, 11%, 27%, and 38%, respectively – data not shown). Even in cases when large-amplitude concordant alternans was transformed into small-amplitude discordant alternans (Fig. 4), one can argue that such a result would be desirable given the tendency for large-scale concordant alternans to transform into large-scale discordant alternans with either a slight decrease in pacing cycle length or a properly timed ectopic beat [8], [9]. Moreover, σ² calculations derived from our experiments suggest that the dispersion remained the same or decreased during the control portion of these concordant:discordant trials [Fig. 4(e)]. That a concordant:discordant reduction in dispersion is possible implies a positive σ² (relative to the natural dispersion resulting from forward AP propagation) existed during control-off concordant alternans behavior. This could result from spatial heterogeneities that naturally exist in cardiac physiology [31]–[33]. Reducing alternans magnitude in such systems could be of particular benefit. More precise repolarization measurements made possible by better imaging techniques will further address these issues, while allowing for generally better analysis and understanding of action potential propagation dynamics in cardiac tissue.

Although recent studies have proposed several possible mechanisms for discordant alternans initiation, this process is still not completely understood. Sudden changes in pacing cycle length [8], ectopic beat activity [9], and CV/APD restitution interactions [11] may all play a role. A significant limitation in our experiments was the inability to capture long duration (>1 min) noise-free action potential sequences. To fully understand the time-dependent phenomena associated with discordant alternans dynamics (e.g., initiation, node movement, etc.), both with and without respect to alternans control, an imaging system capable of longer acquisition times is necessary.

The whole tissue dynamics of wave propagation and alternans across the surface of any particular preparation were missed by our imaging system, which was capable of imaging from a 1-D line segment only. However, in all cases there was close proximity between the control channel and the stimulating electrode (≤2 mm), and forward wave propagation originating from the control channel was observed along the imaging line in all of the analyzed trials. Because of this, both the dynamical manifestations of alternans and the induced changes as observed within the field-of-view were likely the direct result of pacing by the stimulating electrode. That being said, cases of ambiguity would be expected given the noise inherent to the system. This also does not preclude the existence of other dynamics along other propagation axes and at distances beyond the scope of the 2.5 cm viewing region. Qualitative differences in the observed alternans control behavior with respect to viewing orientation would certainly be expected, in part due to the differences in propagation velocity parallel and transverse to fiber orientation [20]-[22]. Doubtless, high-fidelity observations of whole tissue dynamics are a next step that would yield useful information.

The benefits of using fluorescent dyes like di-4-ANEPPS for cardiac electrodynamical experiments (linearly changing fluorescence behavior in response to changes in transmembrane potential, the ability to track voltage changes on a time scale of microseconds [34], etc.) are tempered by the S/N issues that are commonly associated [34], [35]. The largest source of noise in our optical mapping system was due to the light detection limits of the CCD camera, and given the operational range of our experiments, shot noise represented the predominant CCD-related noise present [24]. Noise level increases over the time-course of 1/2 hour could be expected [24], but limiting analysis to six-AP sequences largely controlled for this.

In choosing to use the optical mapping system, a trade-off between spatial and temporal resolution was implicitly made. On the one hand, by using the optical system we were able to clearly observe both concordant and discordant alternans dynamics, and our ability to quantify the spatial effects of alternans control was enhanced. On the other, the inherently more noisy system (as compared with microelectrode recordings) made experiment execution and downstream analysis more difficult. To compensate for these limitations, we aimed to uncover the true behavior of alternans behavior during static pacing and control intervention by selecting a six action potential sequence according to the methods described in Section II.E. Whereas the use of the fluctuation coefficient selected for stable alternans dynamics during control-off conditions, selection for representative “successful control” sequences was based only on the control site alternans magnitude. This type of selection would bias our results if we were interested in the overall success rate of alternans control, but our primary concern was the spatial efficacy of control given effective control at the control site. In choosing the six-AP sequence, only the alternans magnitude at the control channel was used and the aim was to focus on periods during which control was successful; subsequent spatial analysis followed accordingly.

The inability to completely eliminate alternans at the site of intervention is not at all surprising given the noise inherent to the system. Additionally, despite placing the stimulating electrode at distances ≤2 mm from the control channel, small location disparities could have further destabilized the control mechanism – the straightforward result of wave propagation and the time delays associated. But even in the absence of noise and location disparities, the failure of complete control would be expected, nonetheless, because of the effects of electrical coupling between neighboring cells, as predicted by previously published analytical work [18].

In order to promote large-scale alternans, our experiments were conducted at a reduced temperature [6], [36] rather than body temperature. Changes to cell function kinetics, specifically Ca²⁺ handling dynamics, at lower temperatures have been well documented [37]. That notwithstanding, the same underlying mechanisms for concordant and discordant alternans should apply at slightly reduced temperatures as it does for physiological temperatures and any differences in control would likely be quantitative but not qualitative. Precise measurements of physiological controllable distances, however, will necessitate further experiments conducted at near-physiological conditions.

The spatial reduction in alternans magnitude is an average across regions of tissue, and as such, a reduction across 2.5 cm of tissue does not necessarily constitute equal control efficacy as a function of space. The comparisons of alternans control between the proximal, middle, and distal regions were intended to uncover these differences. Spatially averaging across regions spanning less than 1.0 cm were avoided when possible due to the loss in statistical power associated with quantifying alternans dynamics across too few channels (unfortunately, the image quality was inadequate beyond 2.5 cm for many of the trials, hence the inclusion and analysis of the 2.0–2.5 cm region). Given that previous control experiments have suggested ≈1 cm as the controllable “unit” for single-site control [18], [19], use of this sub-division length-scale seemed both adequate and appropriate. Ideally, statistical analysis of control efficacy would have been done on a preparation-by-preparation basis, but the individual sample sizes were not large enough. More rigorous statistical testing will accompany larger data sets in the future.

Although control decreased alternans to a greater extent in the regions more proximal to the control site, it should be noted that even in the middle (1–2 cm) tissue region, control reduced A_M,S by a statistically significant amount in 12/17 experiment trials. As well as decreasing the magnitude (mean reduction across all trials = 12 ms), the resulting A_M,S after the application of control was ≤ 10 ms in 7/17 cases (mean control-on A_M,S = 11 ms – Table I). Fully understanding the reasons for failed spatially-extended alternans control (including the role of CV, APD, and repolarization dynamics interactions) in real tissue will require more advanced imaging techniques.

Nonetheless, more complex methods of alternans suppression that rely on multiple electrodes are likely needed if electrode-based alternans therapy is to succeed at the whole heart level. Though demonstrating reasonable control success at distances up to 2.0 cm represents only a slight increase in effective controllability as compared with previous Purkinje fiber results, an increase in the minimum spacing required would lessen the technical challenges associated with the clinical implementation of multisite control. Studies such as this, which help to illuminate the degree to which single-site control can reduce spatial alternans, will aid in the development of such therapies.

Currently, the predominant ventricular fibrillation therapy consists of applying large voltages across the heart using internally implanted electrical leads [38]–[40]. The implantable cardioverter defibrillator (ICD) is the primary delivery mechanism for treatments of this type, and though reasonably effective in the termination of VF [41], repeated use can cause physical damage to the cardiac tissue, which can act as an arrhythmogenic substrate for future VF initiation [42], [43]. Also, psychological factors that are often times associated with ICD use, such as persistent stress and anxiety, are not to be dismissed [44], [45]. Thus, there is a real need to develop improved strategies that can terminate and/or prevent VF.

Given the supporting evidence suggesting that alternans may be a precursor to VF initiation, alternans management warrants further investigation. Because of the relatively straightforward implementation requirements, model-independent alternans control mechanisms like the one used in this study represent a potentially viable option. Alternans control capability could be added to current ICD modalities, and technologies such as multipole leads or the CorCap cardiac support device [46], [47] could provide a means for the clinical realization of multisite control.

Biographies

Uche B. Kanu received the B.S. degree in biomedical engineering from Columbia University, New York, NY, in 2005 and the M.S. degree in biomedical engineering from Cornell University, Ithaca, NY, in 2007. He is currently a Graduate Student in biomedical engineering at Cornell University, Ithaca, NY. His primary research interests are in cardiac electrophysiology, with an emphasis on alternans and alternans control.

Shahriar Iravanian received the M.D. from Tehran University of Medical Sciences, Tehran, Iran, in 1996 and the M.S. degree in computer science from the Johns Hopkins University, Baltimore, MD, in 2000.

He was a postdoctoral fellow in the Cardiac Bioelectric System Laboratory of the Johns Hopkins University, Baltimore, MD. He finished his residency in internal medicine in 2004, at the St. Luke’s-Roosevelt Hospital Center, New York, NY. He was a postdoctoral fellow in the Cardiac Electrodynamics Laboratory, Weill Cornell Medical College, New York, NY. In 2009, he finished his fellowship in basic science and clinical cardiology at Emory University, Atlanta, GA, where he is currently a fellow in clinical cardiac electrophysiology. His research interests include theoretical and experimental work on cardiac electrophysiology, especially dynamics of reentrant arrhythmias in heart and cardiac signal processing.

Robert F. Gilmour, Jr. received the A.B. degree in english and biology from Bowdoin College, Brunswick, ME, in 1973, and the Ph.D. degree in pharmacology from the State University of New York (SUNY) Upstate Medical Center, Syracuse, NY, in 1977.

He was an Associate Professor of pharmacology and medicine at the Indiana University School of Medicine. He was also a Research Associate at Krannert Institute of Cardiology. He is currently a Professor of physiology in the Department of Biomedical Sciences, Cornell University College of Veterinary Medicine, Ithaca, NY, where he is also an Associate Dean for Research and Graduate Education. His current research interests include the identification of underlying cellular mechanisms for lethal heart rhythm disorders.

David J. Christini (S’96–M’97) received the B.S. degree in electrical engineering from the Pennsylvania State University, University Park, in 1991 and the M.S. and Ph.D. degrees in biomedical engineering from Boston University, Boston, MA, in 1993 and 1997, respectively. He did postdoctoral training in cardiac electrophysiology at Cornell University Medical College, New York, NY.

He is currently a Professor in the Departments of Medicine and Physiology and Biophysics at the Weill Cornell Medical College, New York, NY. His primary research interests are in cellular- to organ-level cardiac electrophysiological dynamics, with an emphasis on understanding the mechanisms underlying arrhythmia initiation and in developing new arrhythmia therapies.