Direct perception of action-scaled affordances: The shrinking gap problem

Abstract

The aim of this study was to investigate the perception of possibilities for action (i.e., affordances) that depend on one’s movement capabilities, and more specifically, the passability of a shrinking gap between converging obstacles. We introduce a new optical invariant that specifies in intrinsic units the minimum locomotor speed needed to safely pass through a shrinking gap. Detecting this information during self-motion requires recovering a component of the obstacles’ local optical expansion due to obstacle motion, independent of self-motion. In principle, recovering the obstacle motion component could involve either visual or non-visual self-motion information. We investigated the visual and non-visual contributions in two experiments in which subjects walked through a virtual environment and made judgments about whether it was possible to pass through a shrinking gap. On a small percentage of trials, visual and non-visual self-motion information were independently manipulated by varying the speed with which subjects moved through the virtual environment. Comparisons of judgments on such catch trials with judgments on normal trials revealed both visual and non-visual contributions to the detection of information about minimum walking speed.

To safely and efficiently navigate through complex, dynamic environments, people must choose actions and control their movements in a way that takes their movement capabilities into account. For example, when stepping off a curb, a pedestrian may need to decide whether to go now ahead of an approaching vehicle or wait until it passes. Similarly, a child playing a game of tag may need to decide whether to go to the left or right around a stationary obstacle to intercept another player. In both cases, the possible actions (i.e., the affordances) are partly determined by the person’s locomotor capabilities. If people were unable to perceive affordances in a way that takes their locomotor capabilities into account, they would sometimes choose actions that are beyond their capabilities and therefore have no chance of succeeding, and other times fail to choose beneficial actions that are within their capabilities. Such decisions lead to energetically inefficient behavior and increase the risk of injury (e.g., see Plumert, Kearney, & Cremer, 2004). Thus, the ability to take one’s movement capabilities into account is essential for safe and efficient locomotor control.

The aim of this study is to explore how people perceive affordances in a way that takes their locomotor capabilities into account. Locomotor capabilities constrain affordances in a variety of tasks, but will be investigated in the present study within the context of perceiving whether it is possible to walk through a shrinking gap between a pair of converging obstacles. We begin this paper by summarizing previous research on the visual guidance of locomotion through gaps. We then introduce a new optical invariant that specifies the passability of a shrinking gap, and present the results of two experiments designed to investigate the detection of this information.

Perceiving the size and passability of an aperture

Narrow openings between stationary and moving obstacles are among the most commonly encountered potential impediments to forward locomotion. In some situations, dealing with narrow openings is a matter of rotating the hips and shoulders to decrease body width enough to fit through the gap (Higuchi, Cinelli, Greig, & Patla, 2006). However, when an alternative route is available, it is sometimes preferable to avoid the gap entirely. In such situations, knowing whether a narrow gap is passable in advance allows one to select alternative routes if necessary.

The size of fixed-width apertures, such as doorways, is optically specified in intrinsic, body-scaled units by eyeheight-scaled information (Sedgwick, 1980;W. H. Warren & Whang, 1987), allowing for the direct perception of passability. The hypothesis that aperture size is perceived in intrinsic units is supported by the finding that both small and large individuals perceive gaps as passable when the width of the gap is 15–20% greater than shoulder width, and by the fact that manipulations of eyeheight affect the perception of passability in a direction that is consistent with the use of eyeheight-scaled information (W. H. Warren & Whang, 1987).

In addition to stationary apertures, individuals also frequently encounter dynamically changing openings created by moving objects such as vehicles, other people, and sliding doorways. The few studies to investigate dynamically changing gaps have focused on the visual control strategies used to guide locomotion through fixed-width, moving apertures (Cinelli, Patla, & Allard, 2008), and oscillating doorways (Montagne, Buekers, Camachon, De Rugy, & Laurent, 2003). Rather than focus on visual control strategies, our aim in the present study is to understand how people perceive whether such gaps are passable in the first place. We explore this issue within the context of shrinking gaps formed by pairs of converging obstacles. Because the passability of such gaps depends in part on the person’s body dimensions and locomotor capabilities, passability must be perceived in a way that takes these properties into account.

Visual information about the passability of a shrinking gap

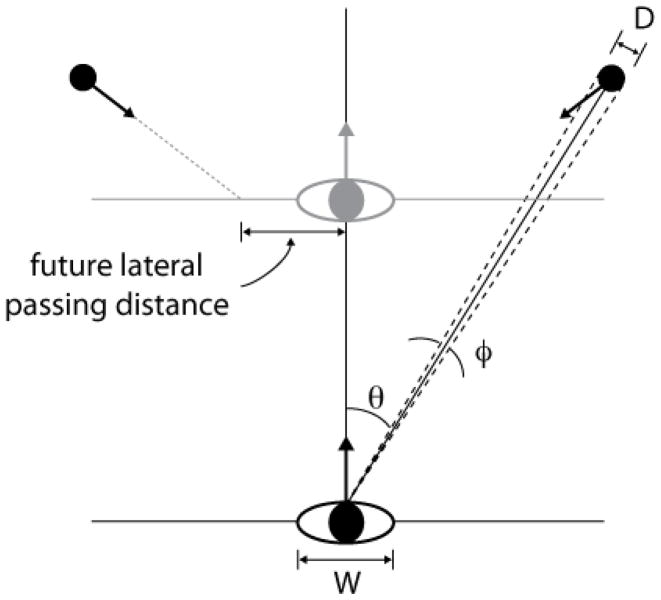
One hypothesis is that the passability of shrinking gaps is perceived on the basis of information that is available only while the observer is moving. Figure 1 depicts an observer moving along a linear path toward a pair of moving objects converging to a point on the observer’s future path. Under such condition, the future lateral passing distance of both objects assuming that the person continues moving at his or her current speed is optically specified in units of object diameter (D) byθ̇/φ̇, where θ̇ and φ̇ are the first temporal derivatives of the object’s azimuth (θ) and optical angle (φ), respectively (Bootsma & Peper, 1992; Michaels, Jacobs, & Bongers, 2006; Regan & Kaushal, 1994).¹ If a person is approaching the gap and θ̇/φ̇ specifies that the future lateral passing distance is greater than one-half of the sum of the person’s body width (W) and the diameter of the object (D), that is [½(W+D)], the person’s current locomotor speed is sufficient for safe passage. As long as current locomotor speed can be maintained, the gap is passable. Conversely, if the person is moving at his or her maximum locomotor speed, and θ̇/φ̇ specifies that the obstacles will pass within [½(W+D)], the person’s maximum speed is not sufficient and the gap is not passable. In this sense, θ̇/φ̇ also specifies the passability of the gap, but only under these two conditions.

Figure 1.

Top down view of an observer (width W) moving along a straight path, with two obstacles (diameter D) converging on a point along the observer’s future path. θ is the visual direction of the obstacle relative to the direction of locomotion and φ is the visual angle subtended by the obstacle. The distance along the frontal plane from the observer to the obstacles at the moment that the obstacles pass by the observer is the future lateral passing distance. In this example, the future lateral passing distance is greater than [½(W+D)], indicating that the observer will safely pass through the gap if current speed is maintained.

The advantage of this solution is that it offers a way in which the passability of a gap can be perceived entirely on the basis of currently available visual information without appealing to knowledge of locomotor capabilities (see Oudejans, Michaels, Bakker, & Dolne, 1996 for a similar solution to the problem of how outfielders perceive the catchableness of fly balls). However, because future lateral passing distance is specified in units of D, using θ̇/φ̇ to perceive passability requires knowledge of the size of D relative to W. In addition, θ̇/φ̇ specifies passability only under the two conditions mentioned above. In all other cases, θ̇/φ̇ by itself is ambiguous about passability. To illustrate this point, it is helpful to consider the distinction between what will happen if current walking speed is maintained, and what is possible given the person’s locomotor capabilities. Suppose, for example, that the person at the origin in Figure 1 has not yet started to move. If current walking speed (which is assumed to be zero) is maintained, the gap will close before the person reaches it. However, this is not the same as whether it is within the person’s locomotor capabilities to pass through the gap if he or she was to begin moving at that instant. θ̇/φ̇ specifies the former, but is ambiguous about the latter. In other words, for the person in Figure 1 who has not yet started to move, θ̇/φ̇ can be used to perceive that it is necessary to move to pass through the gap, but cannot be used to perceive whether the gap is passable.

Because θ̇/φ̇ specifies passability only when the observer is moving, a prediction of this hypothesis is that movement is necessary to perceive passability. That is, people should be unable to perceive the passability of a shrinking gap while they are stationary. Evidence from a recent study by Fajen, Diaz, and Cramer (in press) does not support this prediction. In that study, subjects were instructed to judge whether a shrinking gap was passable under two conditions. In one condition, subjects remained stationary and viewed a pair of converging cylinders for 1 s before judging whether they could safely pass through the gap before it closed. In the other condition, subjects walked for 1 s while viewing the converging cylinders, and then made the judgment. The accuracy of judgments in both conditions was measured by comparing judgments to trials in which subjects attempted to walk through the gap before it closed. The main finding was that the passability of a shrinking gap was perceived equally well regardless of whether subjects were stationary or allowed to move for a brief period. The implication is that the range of conditions across which people can accurately perceive passability is broader than one would expect based on the use of θ̇/φ̇ alone.

The second hypothesis that we consider better accounts for the wider range of conditions across which passability can be perceived and does not require knowledge of the relation between body width and obstacle size. According to this hypothesis, the perception of passability is based on information about the minimum locomotor speed required to safely pass through the gap (v_min), which is equal to the distance that the observer must travel to pass through the gap divided by the amount of time remaining until the gap reaches a size at which it is no longer passable. In terms of spatial variables, v_min is given by:

$$v_{min}(t)=\lceil z_g\left(T_{g=W}\right)-z_o(t)\rceil /\left(T_{g=W}-t\right)$$ (1)

where z_o(t) is the position of the observer along the z-axis (the locomotor axis) at time t, T_g=W is the time at which the size of the gap is equal to the observer’s body width, and z_g(T_g=W) is the z-coordinate of the obstacles at T_g=W (see Figure 2). The numerator in Equation 1, [z_g(T_g=W) − z_o(t)], is the distance from the position of the observer at time t to the position of the gap at the moment its size is equal to W (i.e., T_g=W). As shown on the right side of Figure 2, [z_g(T_g=W) − z_o(t)] is equal to the current distance from the observer to the gap minus the distance that the gap moves between t and T_g=W; that is:

$$z_g\left(T_{g=W}\right)-z_o(t)=\left[z_g(t)-z_o(t)\right]-\left[z_g(t)-z_g\left(T_{g=W}\right)\right]$$ (2)

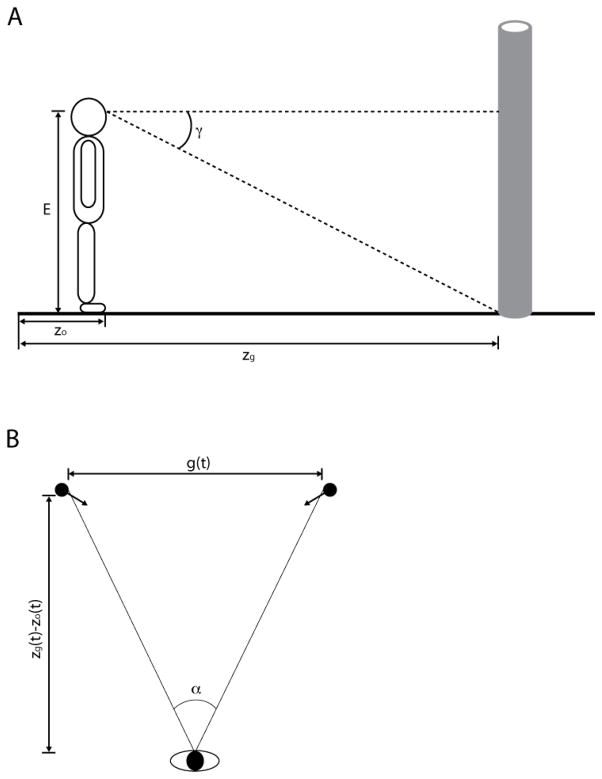
Figure 2.

Top down view of observer and a pair of converging obstacles at time t (black circles) and time T_g=w (gray circles). T_g=W is the time at which the size of the gap between the obstacles is equal to the observer’s body width (W). g is the size of the gap, z_o is the position of the observer, and z_g is the position of the gap.

The distance that the gap moves from t to T_g=W is:

$$z_g(t)-z_g\left(T_{g=W}\right)=V_g\times \mathit{TTC}\times [1-W/g(t)]$$ (3)

where V_g is the z-component of the obstacles’ velocity in world coordinates and TTC (time-to-closure) is the amount of time remaining until the size of the gap is equal to zero. V_g × TTC is the distance that the gap moves from t until gap size is equal to zero. To get the distance that the gap moves from t to T_g=W, we multiply V_g × TTC by [1−W/g(t)]. Substituting Equation 3 into Equation 2, and Equation 2 into Equation 1, and multiplying both sides by (T_g=W−t)/E yields:

$$\frac{v_{min}(t)}{E/\left(T_{g=W}-t\right)}=\frac{[z_g(t)-z_o(t)]}{E}-\frac{V_g}{E}\times \mathit{TTC}\times [1-W/g(t)]$$ (4)

The final step is to substitute k_E->W × E for W, where k_E->W is the constant that relates eyeheight to body width:

$$\frac{v_{min}(t)}{E/\left(T_{g=W}-t\right)}=\frac{[z_g(t)-z_o(t)]}{E}-\frac{V_g}{E}\times \mathit{TTC}\times \left[1-k_{E\to W}\left(\frac{E}{g(t)}\right)\right]$$ (5)

This allows gap size to be expressed in units of E, which is important in one of the steps below (see Equation 9).

Next, we show that each of the components on the right side of Equation 5 is optically specified. Our derivation of the optical specification of v_min(t) is restricted to situations in which the following assumptions are valid. First, the observer and the obstacles must be resting on a flat ground plane, and the obstacles must be moving at a constant velocity. Second, the two obstacles must be at equal distances along the observer’s locomotor axis (i.e., the z-axis). Third, the relation between the observer’s eyeheight (E) and body width (W) must be fixed.² We begin by showing that each component is optically specified when the observer is stationary, and then generalize to the situation in which the observer is moving.

The first component is the distance from the observer to the gap (z_g − z_o), which is optically specified in units of E by

$$\left[z_g(t)-z_o(t)\right]/E=1/tan\gamma$$ (6)

where γ is the visual angle between eye level and the base of the object (see Figure 3A).

Figure 3.

(A) Side view of observer and cylindrical obstacle, showing angular declination of base of obstacle (γ), and eyeheight (E). (B) Top down view of observer and a pair of converging obstacles, showing visual angle of gap (α), gap size (g), and gap distance (z_g − z_o).

The second component is the speed at which the gap is approaching or receding (V_g), which is equivalent to the z-component of the obstacles’ velocity. When the observer is stationary, V_g is optically specified in units of E by

$$V_g/E=\stackrel{.}{\gamma }/{sin}^2\gamma$$ (7)

(adapted from Lee, 1980).

The third component is the amount of time remaining until the gap is completely closed (TTC), which is optically specified by

$$\mathit{TTC}={\left(\frac{\stackrel{.}{\phi }}{sin\phi }-\frac{\stackrel{.}{\alpha }/2}{tan(\alpha /2)}\right)}^{-1}$$ (8)

where φ is the local visual angle subtended by the inside and outside edges of either obstacle (see Figure 1), and α is the visual angle between the inside edges of the two obstacles (Bootsma & Craig, 2002; see Figure 3B).

The fourth component is the size of the gap (g); that is, the distance between the inside edges of the two obstacles. g(t) is optically specified in units of E by

$$g(t)/E=[2tan(\alpha /2)]/tan\gamma$$ (9)

(Sedgwick, 1980;W. H. Warren & Whang, 1987). Because body width is, by assumption, a fixed proportion of eyeheight, the fact that g(t)/E is optically specified means that g(t)/W is also optically specified.

Equations 6, 7, 8, and 9 show that each of the components in Equation 5 is optically specified, and therefore by extension, that v_min is also optically specified. The units in which v_min is optically specified are E/(T_g=W−t), which is the number of eyeheights that must be covered in the amount of time remaining until the size of the gap equals the width of the observer’s body. Therefore, by detecting the information captured by Equation 5, the observer can directly perceive the minimum locomotor speed needed to safely pass through the gap. Because v_min is specified in intrinsic units, it can be calibrated to allow for the direct perception of the passability of a shrinking gap, in the same way that eyeheight scaled information about gap size can be calibrated to allow for the direct perception of the passability of static gaps (W. H. Warren & Whang, 1987). Thus, detecting and calibrating the information in Equation 5 is sufficient to allow for the direct perception of the passability of a shrinking gap, taking into account both the width of the observer’s body and his or her locomotor capabilities (see Warren, 2007, for an excellent discussion of the importance of body-scaled and action-scaled information for the visual control of locomotion).

In the derivation presented above, it was assumed that the observer was stationary. Obviously, it must also be possible to perceive the passability of a shrinking gap while one is moving. Equations 6, 8, and 9 invariantly specify z_g, TTC, and g, respectively, regardless of whether the observer is stationary or moving. Equation 7, however, specifies V_g only when the observer is stationary. When the observer is moving, the rate of change of the visual angle between eye level and the base of the object (γ̇) is influenced by the movement of both the observer and the gap. Specifically, γ̇ is the sum of the rate of change of γ due to the observer’s self-motion (γ̇_o) and the rate of change of γ due to the motion of the gap (γ̇_g). Therefore, the property that is specified byγ̇/sin²γ is the relative speed between the observer and the gap, not the absolute speed of the gap. If people rely on γ̇/sin²γ while moving, they would misperceive the gap as approaching faster than it actually is and therefore underestimate v_min, resulting in a bias to perceive the gap as passable. If, however, the visual system could recover γ̇_g, and use γ̇_g/sin²γ rather than γ̇/sin²γ, V_g/E could be accurately perceived, and the information about v_min captured by Equation 5 could be detected even during self-motion.

Visual and non-visual contributions to the recovery of γ̇_g

The problem of recovering γ̇_g is a specific example of the more general problem of perceiving object motion during self-motion. Formally, the component of optic flow due to object motion is that which remains after the component due to self-motion is subtracted from the optic flow field. Regardless of whether the visual system actually estimates and subtracts the component due to self-motion, or recovers γ̇_g directly, questions arise about whether visual information (i.e., optic flow) alone is sufficient to recover object motion, or whether non-visual self-motion information (e.g., proprioception, kinesthesis, vestibular system stimulation, and/or motor efference) is also involved.

The purely visual solution relies on the radially expanding pattern of optic flow that accompanies forward self-motion. The component of the optic flow that remains after vector subtraction of the optic flow due to self-motion can be attributed to object motion. Because the visual solution relies entirely on optic flow, it accounts for the accuracy with which object motion is perceived even when self-motion is not accompanied by reliable non-visual self-motion information. In cycling, for example, a cyclist moving at a given speed may be pedaling as hard as possible, pedaling lightly, or not pedaling at all. Because the relation between non-visual self-motion information (e.g., proprioception, kinesthesis, motor efference), and self-motion is variable, non-visual self-motion information is unreliable. Being passively transported in an automobile is another situation in which non-visual self-motion information is unreliable.

The sufficiency of visual information has been investigated by presenting stationary observers with stimuli depicting moving objects, accompanied by optic flow simulating forward self-motion. Although self-motion results in a complex pattern of optic flow across the entire visual field, moving objects “pop out” in the sense of being easily and quickly detected even in a scene filled with many other identical objects that are not moving relative to the scene (Rushton, Bradshaw, & Warren, 2007). Furthermore, the perceived trajectory of moving objects is influenced by optic flow (Matsumiya & Ando, 2009; Rushton & Warren, 2005;P. A. Warren & Rushton, 2007, 2009). This occurs even when the optic flow and moving object are located in different parts of the visual field (P. A. Warren & Rushton, 2009), implicating global motion processing and not just local motion contrast.

Although visual self-motion information is sufficient to allow observers to perceive object motion during simulated self-motion, non-visual information may also contribute when self-motion is real rather than simulated. Indeed, the influence of non-visual information on the perception of self-motion is well established (e.g., see Gu, Angelaki, & Deangelis, 2008). An influence of non-visual self-motion information arising from head movements on the perception of object motion was reported by Wexler and colleagues (see Wexler & van Boxtel, 2005 for a review). The stimuli in these studies were ambiguous in the sense that they could be interpreted as a plane rotating about a vertical axis or a plane simultaneously rotating about a horizontal axis and translating relative to the observer. Depending on whether head movements were actively or passively generated, subjects reported radically different combinations of 3D structure and motion. Because the visual information was the same in both conditions, the findings were attributed to the influence of non-visual self-motion information that accompanies actively generated movements.

An influence of non-visual self-motion information is also consistent with the finding that walking leads to a reduction in the perceived rate of optic flow – that is, optic flow viewed while walking appears to be slower than the same rate of optic flow viewed while stationary (Durgin, Gigone, & Scott, 2005). Such effects are thought to reflect the suppression of visual motion to facilitate the perception of a stable world (Wallach, 1987) (but see Durgin, 2009; Durgin & Gigone, 2007 for an alternative account). Either way, the findings suggest that the availability of non-visual self-motion information affects the amount of optic flow that is attributed to self-motion.

To summarize, the availability of information about v_min (Equation 5) offers a solution to the problem of perceiving the passability of a shrinking gap, an affordance that depends on both the body dimensions and locomotor capabilities of the observer. When passability is perceived while moving, detecting the relevant information requires recovering the component of γ̇ due to the motion of the gap (i.e., γ̇_g). Previous research on the perception of object motion during self-motion suggests that visual information is sufficient, but that non-visual information may also play a role. In this study, we present the results of two experiments designed to explore the contributions of visual and non-visual information to the detection of information about v_min.

Experiment 1

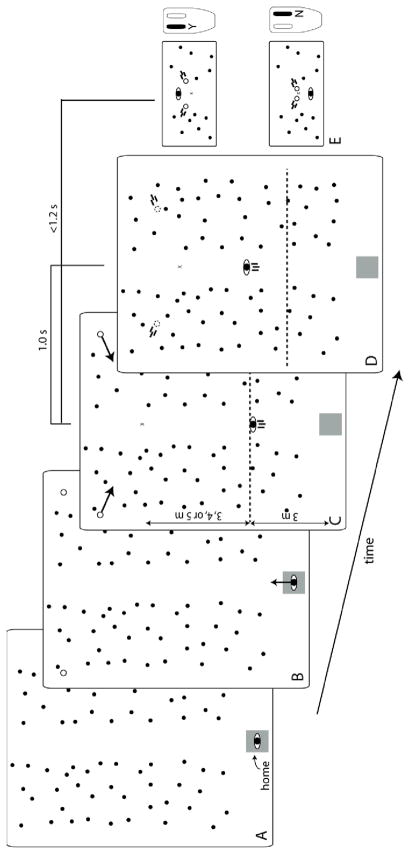
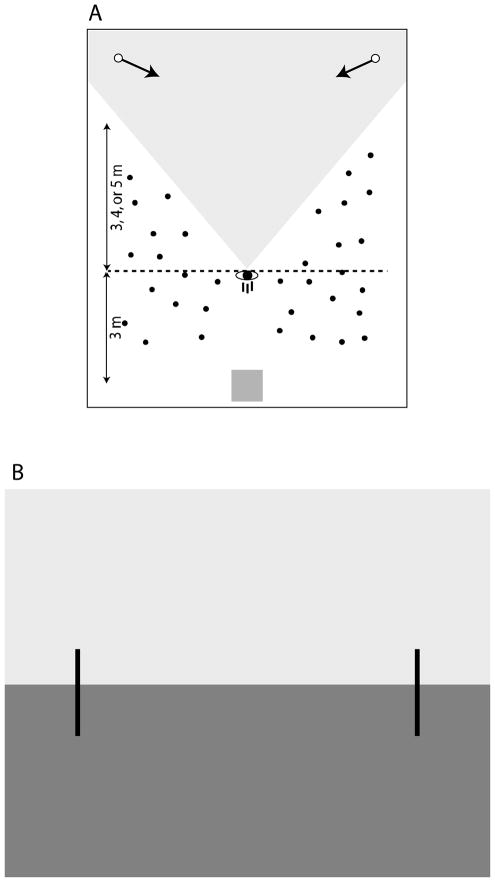
The task used in both experiments required subjects to judge whether they could safely pass through a gap between a pair of converging obstacles in a fully immersive virtual environment viewed through a head-mounted display. Subjects began each trial by standing at a designated home location and looking down a path lined by narrow posts (Figure 4A). When they pressed a button on a handheld remote mouse, two stationary yellow cylinders appeared off in the distance (one on each side), cueing subjects to begin moving down the path (Figure 4B). After walking 3 m, the pair of obstacles began to converge toward an intersection point lying on the subjects’ future path (Figure 4C). The initial distance to the point of intersection and the time-to-closure of the gap were manipulated such that the speed at which subjects would have to move to safely pass through the gap ranged from slower-than-normal walking speed to faster-than-maximum walking speed. The obstacles disappeared 1 s after they began moving (Figure 4D). Within 1.2 s of the onset of obstacle movement (i.e., 0.2 s after the obstacles disappeared), subjects had to judge whether or not they could have safely passed through the gap by pressing one of two buttons on the remote mouse (Figure 4E).

Figure 4.

Sequence of events in task used in Experiment 1.

Each experimental session consisted of a combination of 120 normal trials and 24 randomly interspersed catch trials. Normal trials and catch trials differed in terms of the rate at which subjects moved through the virtual environment relative to the physical world, which we refer to as visual gain; e.g., when visual gain was 1.5×, subjects moved 50% faster through the virtual environment relative to the physical world. Visual gain was set to 1.0× on normal trials and 1.5× on catch trials. Thus, on 83% of the trials, subjects moved through the virtual environment as if their locomotor capabilities were the same as they are in the real world. On the remaining 17% of trials, subjects moved as if they were 50% faster than they are in the real world.

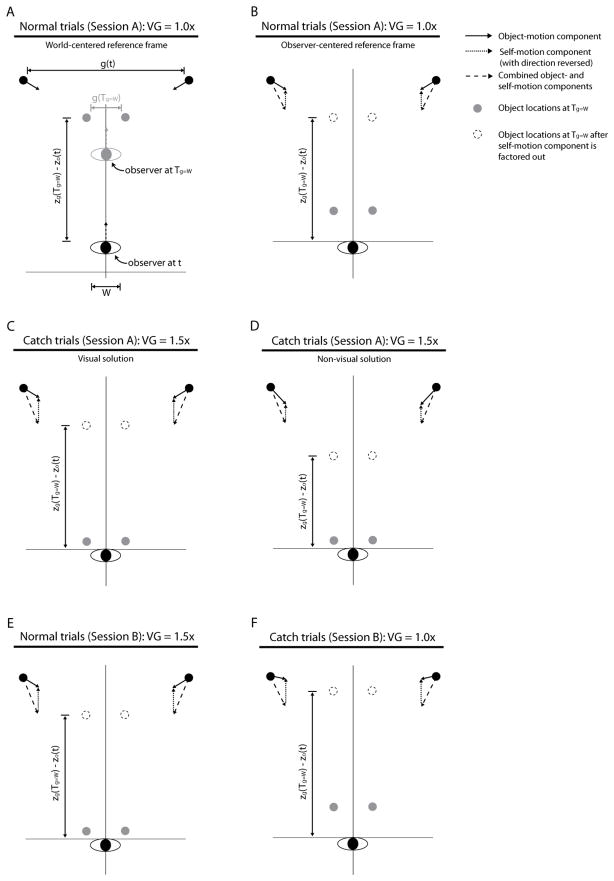
The predictions of the purely visual solution, according to which γ̇_g is recovered using visual self-motion information, and the purely non-visual solution, according to which γ̇_g is recovered using non-visual self-motion information, are illustrated in Figure 5. Figure 5A depicts the situation on normal trials in a world-centered reference frame. The black objects represent the positions of the observer and cylinders at time t. As the observer moves from z_o(t) along a linear path, the cylinders converge toward a point along the observer’s future path. The positions of the observer and cylinders at T_g=W are represented by the gray objects. z_g(T_g=W) − z_o(t) is the distance from the observer at time t to the position of the cylinders along the z-axis at time T_g=W. Figure 5B depicts the same situation in an observer-centered reference frame. The dashed line indicates the relative motion (combined self-motion and object motion), the dotted line indicates the component of relative motion attributed to self-motion, and the solid line indicates the component attributed to object motion. Because visual and non-visual information is both reliable and consistent on normal trials, it is assumed that subjects will be able to recover γ̇_g and perceive v_min. This assumption is supported by findings reported in Fajen et al. (in press). Subjects in that study made judgments of passability that closely matched their ability to actually pass through gaps, which was measured on separate trials. The accuracy of judgments can be interpreted as evidence that subjects can recover γ̇_g and perceive v_min when visual and non-visual information is reliable and consistent, as it was on normal trials in the present study.

Figure 5.

Predictions for normal and catch trials in Experiment 1.

Figures 5C–D depict the situation encountered on catch trials. Note that the vector with the dashed line indicating the relative motion of the cylinder is pointed farther down the z-axis, reflecting the faster speed with which subjects moved through the virtual environment on catch trials. According to the visual hypothesis (Figure 5C), the amount of relative motion attributed to self-motion is proportional to the rate of self-motion specified by visual information from the stationary background. Because the manipulation of visual gain affected both the stationary background and the moving obstacles, the amount attributed to self-motion and subtracted from the optic flow of the cylinder should be equal to the actual magnitude of self-motion in the virtual environment. The remaining component attributed to object motion would be equal to the component attributed to object motion on normal trials (compare arrows with solid lines in B and C). Therefore, the purely visual hypothesis predicts that passability judgments on normal trials and catch trials should be the same. According to the non-visual hypothesis (Figure 5D), the magnitude of optic flow attributed to self-motion is based on non-visual information. Because the manipulation of visual gain did not affect non-visual self-motion information, the amount attributed to self-motion and subtracted from the optic flow of the cylinder should be equal to the amount attributed to self-motion on normal trials. The component that remains after vector subtraction points farther down the z-axis, as if the point to which the cylinders converge is closer to the observer and the minimum speed required to pass through the gap is slower. Therefore, the non-visual hypothesis predicts that subjects should be more likely to perceive the gap as passable on catch trials.

The experiment also included a second session (Session B) wherein the visual gains on normal trials and catch trials were reversed. That is, visual gain was set to 1.5× on normal trials and 1.0× on catch trials. The two sessions were completed on different days, and the order of sessions was counterbalanced across subjects. The second session allowed us to further test the non-visual hypothesis by taking advantage of the fact that non-visual self-motion information must be calibrated. As properties of the environment and the body change, the relation between non-visual self-motion information and the amount of optic flow due to self-motion also changes. For example, when the support surface changes from concrete to sand or when load increases by wearing a backpack, the amount of effort needed to bring about a particular rate of optic flow increases. In order to use non-visual self-motion information to recover γ̇_g, it must be possible to update the relation between non-visual self-motion information and the amount of optic flow attributed to self-motion. That is, it must be possible to recalibrate non-visual self-motion information. In Session B, visual gain was set to 1.5× on the majority of trials. If subjects recalibrate to the change, the component of γ̇ that is attributed to self-motion should be 50% greater. The remaining component, which is the component attributed to motion of the gap, should be the same as that in Session A (compare Figures 5E and 5B). Therefore, if the non-visual hypothesis is correct and if subjects recalibrate to the faster-than-normal optic flow, perceived v_min should be unaffected by the manipulation of visual gain. In other words, judgments on normal trials in Session B should be similar to judgments on normal trials in Session A. This prediction is counterintuitive because subjects moved through the virtual environment 50% faster on normal trials in Session B, and therefore would have been able to pass through gaps that were impassable in Session A. Nonetheless, such results would be consistent with the use of non-visual self-motion information to recoverγ̇_g.

Methods

Participants

Ten students participated in the experiment. They were recruited from psychology courses and received extra credit for participating. All participants reported that they had normal or corrected-to-normal vision and no visual or motor impairments.

Equipment

The experiment was conducted in a 6.5 m × 9 m virtual environment laboratory. Participants wore an nVis nVisor SX stereoscopic, head mounted display (HMD). The HMD weighed 1000 g, the resolution was 1280 pixels × 1024 pixels per eye, and the diagonal field-of-view was 60°. Participants’ head position and orientation were tracked using an Intersense IS-900 motion tracking system. Data from the head tracker were used to update the position and orientation of the simulated viewpoint. Participants also wore a glove to which an Intersense hand tracker was attached to track hand position and orientation during the practice session (see below). The cables from the HMD and tracking system were bundled together and held by the experimenter, who walked alongside the participant as he or she moved to ensure that the cables did not interfere with the subject’s movement. The virtual environment was created using Sense 8 World Tool Kit software running on a Dell Workstation 650 with a Wildcat 7110 dual-head graphics card.

Virtual environment and procedure

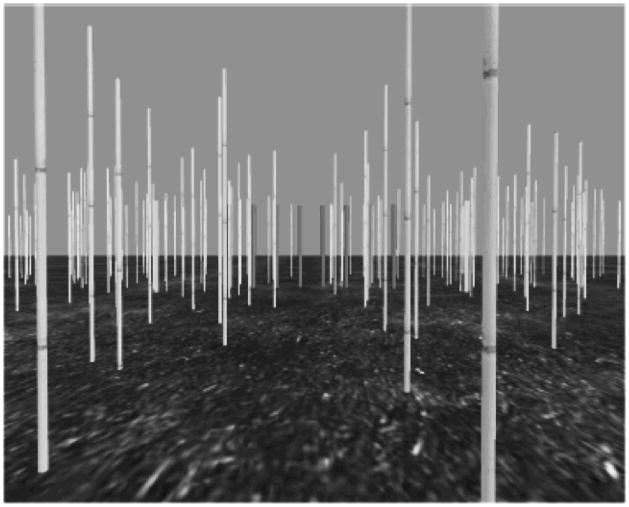
The virtual environment consisted of a grass textured ground plane, a solid blue sky, and an array of randomly distributed posts that lined a walkway extending out in front of the home location (Figure 6). Subjects began each trial by standing at the home location and pressing a button on a remote mouse. As soon as the button was pressed, two stationary yellow cylinders (2.0 m tall × .05 m in radius) appeared in front and off to the side of the home location, with one cylinder on the left and the other on the right. The initial positions varied randomly on each trial between 8 and 11 m in depth and between 2.5 and 3.5 m to the side, but the cylinders were always positioned symmetrically about the midline. Subjects were instructed to begin walking as soon as the cylinders appeared. They walked a distance of 3 m from the center of the home location before the cylinders began moving at a constant speed toward their respective final positions. The distance between the inside edges of the cylinders when they were at their final positions was equal to the subject’s shoulder width, which was measured prior to the beginning of the experiment. The initial distance in depth from the subject’s position at the moment that the cylinders began moving to the position of the cylinders when the gap size was equal to W was manipulated as an independent variable with three levels (3.0, 4.0, and 5.0 m). Cylinder velocity was determined by the initial and final positions of the cylinder, as well as the time-to-closure of the gap, which was manipulated as an independent variable with five levels (1.2, 1.4, 1.6, 1.8, and 2.0 s). There were eight repetitions per condition for a total of 120 trials.

Figure 6.

Grayscale version of screenshot of virtual environment used in Experiment 1.

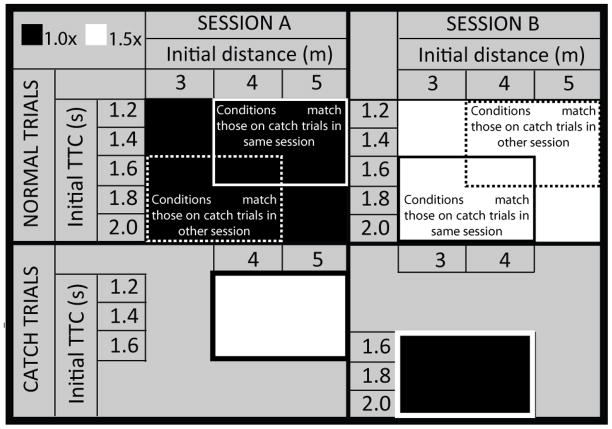
In addition, there were also 24 randomly interspersed catch trials per session, comprised of two initial distances, three time-to-closures, and four repetitions per condition. On catch trials in Session A, initial distance was 4.0 or 5.0, and initial time-to-closure was 1.2, 1.4, or 1.6 s. In Session B, initial distance was 3.0 or 4.0 m, and initial time-to-closure was 1.6, 1.8, or 2.0 s. The conditions on catch trials differed across sessions to accommodate for the difference in visual gain, which affected the speed with which subjects moved through the virtual environment and hence their ability to safely pass through gaps. If the conditions on catch trials were the same across sessions, then there was a greater risk that subjects would respond “yes” to 100% of gaps in Session A (when visual gain was 1.5×) or “no” to 100% of gaps in Session B (when visual gain was 1.0×).

The key aspects of the design are summarized in Figure 7. The figure contains four main quadrants: two sessions (A and B) arranged in columns crossed with two trial types (normal and catch) arranged in rows. Within each quadrant, the values along the top row represent initial distances and values along the left side represent initial TTCs. Conditions in which visual gain was set to 1.0× (i.e., normal trials in Session A and catch trials in Session B) are shaded black, and conditions in which visual gain was set to 1.5× are shaded white. The subset of normal trials with initial conditions that match the initial conditions on catch trials within the same session are enclosed by the two rectangles with solid lines. Likewise, the subset of normal trial with initial conditions that match the initial conditions on catch trials in the other session are enclosed by the two rectangles with dotted lines. Readers may find it useful to refer back to Figure 7 as they read the results section below.

Figure 7.

Schematic of design of Experiment 1. The four main quadrants represent normal and catch trials in Sessions A and B. Within each quadrant, values along the top row correspond to initial distances and values along the side correspond to initial TTCs. Conditions in which visual gain was set to 1.0× (i.e., normal trials in Session A and catch trials in Session B) are shaded black, and conditions in which visual gain was set to 1.5× are shaded white. The subset of normal trials with initial conditions that match the initial conditions on catch trials in the same session are enclosed by the rectangles with solid lines. Likewise, the subset of normal trial with initial conditions that match the initial conditions on catch trials in the other session are enclosed by the rectangles with dotted lines.

Prior to starting the experiment, participants completed a short practice block designed to familiarize them with moving in the virtual environment. The task that participants performed in the practice block was a virtual fly ball catching task. Each trial began with subjects standing at a home location and pressing a button on a remote mouse. After a brief period, a fly ball was projected into the air to one of several landing locations up to 4 m away. The task was to move into position and reach out with the right hand to “catch” the virtual fly ball. The conditions were relatively easy such that participants could reach the landing location in time to catch the ball without having to run. After the practice session, subjects completed a short (9 trial) demo block. The conditions in the demo block were similar to those used in the actual experiment, and provided subjects with the opportunity to familiarize themselves with the timing of the task before starting the actual experiment.

Data analysis

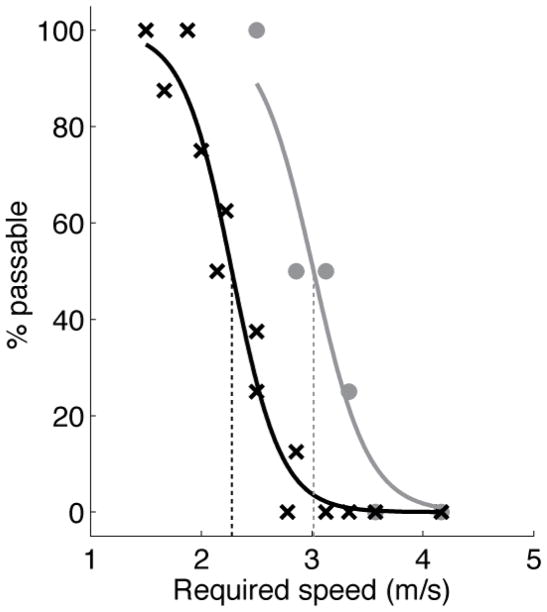
Separate analyses were conducted for data from Sessions A and B, and for normal and catch trials within both sessions. Analyses focused on two dependent measures: (1) the overall percentage of yes responses collapsed across initial distance and TTC, and (2) the critical required speed. The latter was calculated in the following way. For each condition, the minimum walking speed required to safely pass through the gap before it closed was calculated by dividing the initial distance by the time-to-closure. For the 15 combinations of initial distance and initial TTC used on normal trials, minimum required speed ranged from 1.5 m/s (i.e., 3 m and 2.0 s) to 4.17 m/s (i.e., 5 m and 1.2 s). The percentage of yes responses was then plotted as a function of minimum required speed for each condition, and the data were fit using a sigmoid function. This step is illustrated in Figure 8 using data from a representative subject. The black ×’s and gray circles represent data from normal trials and catch trials (respectively) in Session A. The black and gray curves are the best-fitting curves. The minimum required speed at which the best-fitting curve crossed 50% (see dotted lines in Figure 8) was the critical required speed. Thus, subjects tended to respond “yes” for conditions in which minimum required speed was less than their critical required speed, and “no” for conditions in which minimum required speed exceeded critical required speed. In the analyses reported below, it was assumed that changes in critical required speed reflect changes in perceived v_min that result from the manipulation of visual gain. For example, if subjects are more likely to perceive gaps as passable on catch trials in Session A, as predicted by the non-visual hypothesis and as illustrated in Figure 8, critical required speed would increase. Data from one subject were excluded because the overall percentage of yes responses was more than three standard deviations below the mean, and because there were too few yes responses to compute the critical required speed.

Figure 8.

Percentage of passable judgments as a function of required speed for a representative subject in Experiment 1. Black ×’s and gray circles represent data from normal trials and catch trials (respectively) in Session A of Experiment 1. Black and gray curves are the best-fitting curves for normal and catch trials. The dotted lines indicate the critical required speed for both types of trials.

Results

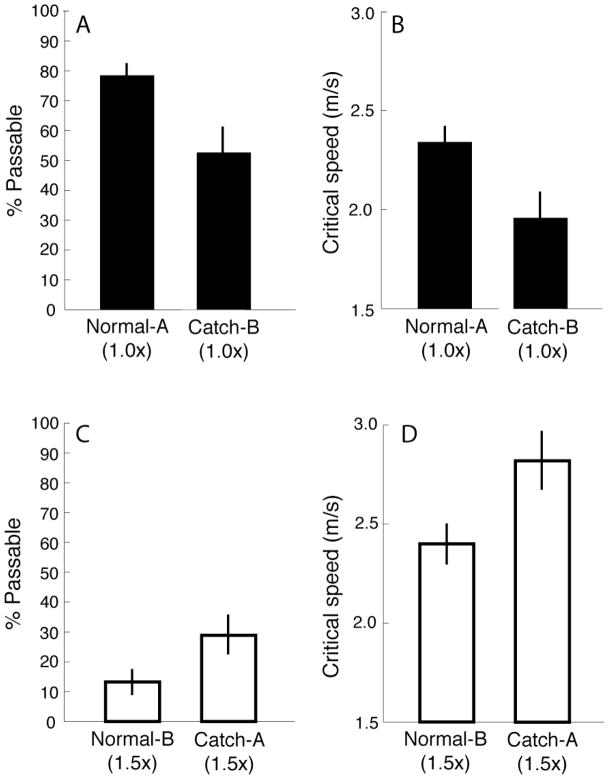
The first set of analyses compares judgments on catch trials with judgments on the subset of normal trials in the same session with matching initial conditions. When the percentage of yes responses and the critical required speed were computed for normal trials, we included only those trials with initial conditions that matched those on catch trials in the same session (indicated by the rectangular regions enclosed by a solid line in the upper quadrants of Figure 7). Thus, for Session A, we compared judgments on catch trials with judgments on normal trials with the following initial conditions: (1.2 s, 4 m), (1.4 s, 4 m), (1.6 s, 4 m), (1.2 s, 5 m), (1.4 s, 5 m), and (1.6 s, 5 m). Contrary to the predictions of the purely visual solution, subjects were more likely to judge gaps as passable on catch trials in Session A, when visual gain was unexpectedly increased to 1.5×, than they were on normal trials in the same session with matching initial conditions (t₈ = 3.56, p < .01, partial η² = .61; see Figure 9A). If the magnitude of optic flow that is attributed to self-motion is based entirely on visual self-motion information, then the manipulation of visual gain should not have affected passability judgments. The increase in % of yes responses implies that subjects relied, at least in part, on non-visual self-motion information. Figure 9B shows the same comparison using critical required speed as the dependent measure (see the data analysis section of the methods for an explanation of critical required speed). As expected based on the analysis of % yes judgments, mean critical required speed was significantly greater on catch trials (2.84 m/s) compared to normal trials (2.34 m/s) in Session A (t₈ = 3.97, p < .01, partial η² = .66). Judgments on normal trials and catch trials also differed in Session B. For this analysis, we compared catch trials in Session B with the subset of normal trials in Session B with initial conditions that matched those on catch trials (indicated by the rectangular region enclosed by a solid line in the upper right quadrant of Figure 7). When visual gain was unexpectedly decreased from 1.5× to 1.0×, subjects were less likely to judge gaps as passable (t₈ = 3.69, p < .01, partial η² = .63; Figure 9C) and critical speed decreased (t₈ = 5.48, p < .01, partial η² = .79; Figure 9D).

Figure 9.

Percentage of passable judgments (A) and critical value of required speed (B) on normal and catch trials in Session A of Experiment 1. C and D show the same analysis for Session B of Experiment 1.

Although the direction of the effect was consistent with the predictions of the non-visual solution, the magnitude of the effect was less than one would expect based on a purely non-visual solution. If subjects recovered γ̇_g by relying entirely on non-visual self-motion information, the critical value of required speed should have increased by 50% on catch trials in Session A and decreased by 33% on catch trials in Session B. The actual magnitudes of change were +21.4% (SD = 16.9%) and −18.1% (SD = 10.8%) in Sessions A and B, respectively. Therefore, we cannot conclude that the amount of optic flow attributed to self-motion is based entirely on non-visual information. The possibility exists that subjects relied on both visual and non-visual self-motion information. Experiment 2 is designed to further explore this hypothesis.

Alternative explanations for the effect of visual gain

We attribute the effect of visual gain to the influence of non-visual self-motion information on the recovery of γ̇_g. However, there are two alternative explanations that must also be considered. First, subjects may have relied entirely on visual self-motion information to recover γ̇_g, and were more likely to perceive gaps as passable on catch trials in Session A because the faster-than-normal rate of optic flow led them to perceive that their locomotor capabilities were suddenly enhanced. According to this account, the additional relative motion on catch trials in Session A was attributed to self-motion, consistent with the predictions of the purely visual hypothesis. Therefore, the perceived minimum speed (v_min) was unaffected by the manipulation of visual gain. Subjects were more likely to perceive gaps as passable on catch trials because the increase in visual gain led them to perceive that they were faster on catch trials. If this explanation is correct, subjects should also be more likely to perceive gaps as passable on normal trials in Session B, in which visual gain was 1.5×. This prediction was tested by comparing the percentage of yes responses and the critical required speed on normal trials in Sessions A and B, using the data from all 15 initial conditions. Interestingly, there were no significant differences between normal trials in Session A and normal trials in Session B for either the percentage of yes response (42.5% ± 3.5% vs. 44.8% ± 4.3%; t₈ = .79, p = .45, partial η² = .07) or the critical speeds (2.34 ± 0.08 m/s vs. 2.40 ± 0.10 m/s; t₈ = .87, p = .41, partial η² = .09).³ The fact that judgments were affected when visual gain was manipulated on catch trials but not when visual gain was manipulated between sessions cannot be explained by the first alternative explanation. This finding is discussed further below.

The second alternative explanation is that subjects were more likely to perceive gaps as passable on catch trials in Session A simply because they were closer to the gap at the moment that they made their responses. Due to the manipulation of visual gain, subjects were on average 0.51 m closer to the gap when they made their responses on catch trials compared to normal trials. This means that the increase in percentage of “yes” responses on catch trials in Session A could be explained without making reference to recovery of the object-motion component of optic flow. However, if subjects were more likely to perceive gaps as passable on catch trials in Session A because they were closer to the gap when they made their responses, then they should also be more likely to perceive gaps as passable on normal trials in Session B, in which visual gain was also 1.5×. As explained in the previous paragraph, subjects were no more likely to perceive gaps as passable on normal trials in Session B compared to normal trials in Session A. Therefore, the second alternative explanation for the effect of visual gain on catch trials can also be ruled out.

If subjects were more likely to perceive gaps as passable when visual gain was increased to 1.5× on catch trials, then why were they not also more likely to perceive gaps as passable when visual gain was 1.5× on normal trials in Session B? At first glance, this finding seems counterintuitive because subjects moved through the virtual environment 50% faster on normal trials in Session B, and therefore would have been able to pass through gaps that were impassable in Session A. As explained in the introduction, however, the results are actually consistent with the use of non-visual self-motion information to recover γ̇_g. Recall that the relation between non-visual self-motion information and the amount of optic flow due to self-motion varies with changes in the body (e.g., changes in load) and the environment (e.g., changes in surface properties). Therefore, it must be possible to recalibrate the relation between non-visual self-motion information and the amount of optic flow attributed to self-motion. If such recalibration took place in Session B when visual gain was set to 1.5×, the component of γ̇ that was attributed to self-motion would have been 50% greater. The remaining component, which is the component attributed to motion of the gap, would have been the same as that in Session A (compare Figures 5E and 5B). Therefore, if subjects recalibrated to the faster-than-normal optic flow, perceived v_min would have been unaffected by the manipulation of visual gain, which is exactly what was observed. This accounts for the counterintuitive finding that subjects were no more likely to perceive gaps as passable on normal trials in Session B, in which visual gain was 1.5×, than on normal trials in Session A, in which visual gain was 1.0×.

If the aforementioned null effect was, in fact, due to recalibration of non-visual self-motion information, then there should also be negative aftereffects on catch trials in Session B. This prediction was tested by comparing judgments on catch trials in Session B with judgments on the subset of normal trials in Session A with matching initial conditions [i.e., (1.6 s, 3 m), (1.8 s, 3 m), (2.0 s, 3 m), (1.6 s, 4 m), (1.8 s, 4 m), (2.0 s, 4 m)]. Because subjects were calibrated to the higher visual gain in Session B, a greater amount of relative motion should be attributed to self-motion (compare Figures 5F and 5B). Therefore, although the visual environment, including both the range of initial conditions and the visual gain, was identical in these two sets of conditions, subjects should be less likely to perceive gaps as passable on catch trials in Session B. The results, which are shown in Figure 10A–B, were consistent with this prediction (t₈ = 3.53, p < .01, partial η² = .61 for the % yes responses, and t₈ = 4.34, p < .01, partial η² = .70 for critical speed; see Figure 10A–B). Likewise, the opposite result was found when judgments on catch trials in Session A were compared with judgments on normal trials in Session B (t₈ = 3.44, p < .01, partial η² = .60 for % yes responses, and t₈ = 4.31, p < .01, partial η² = .70; see Figures 9C–D). Taken together, these negative aftereffects coupled with the null effect in the comparison of normal trials across sessions provides compelling evidence that perceiving passability involves recovery of γ̇_g and detection of the information in Equation 5.

Figure 10.

Percentage of passable judgments (A) and critical value of required speed (B) on normal trials in Session A versus catch trials in Session B. C and D shown the same analysis for normal trials in Session B versus catch trials in Session A.

Discussion

The primary aim of Experiment 1 was to measure the visual and non-visual contributions to the recovery of γ̇_g, which is required to detect the information about v_min captured by Equation 5. This was achieved by manipulating visual gain, which affected the speed with which subjects moved through the virtual environment, on a small percentage of randomly interleaved catch trials. Because the manipulation affected the moving cylinders and the stationary background in the same way, subjects should be equally likely to perceive the gap as passable on normal trials and catch trials if the recovery of γ̇_g is based entirely on visual self-motion information. On the other hand, if non-visual information is involved, then subjects should be more (or less) likely to perceive gaps as passable on catch trials in which visual gain increased (or decreased). A statistically significant effect in the direction predicted by the non-visual solution was observed. As indicated above, however, the magnitude of the effect was weaker than one would expect if the recovery of γ̇_g was based entirely on non-visual information.

One interpretation of this result is that the amount of optic flow attributed to self-motion was based on a combination of visual and non-visual information. However, the design of Experiment 1 does not allow us to rule out an alternative explanation that does not involve a role for visual self-motion information. Recall that subjects walked along a 3 m, tree-lined path before reaching the point at which the cylinders began to converge. The manipulation of visual gain affected the visual motion, not only after the cylinders began moving, but also during the approach phase. The possibility exists that subjects partially recalibrated to the altered visual gain during the 3 m approach phase; that is, walking for 3 m while viewing faster-than-normal optic flow (on catch trials in Session A) was sufficient for subjects to learn to attribute more optic flow to their own self-motion. If recalibration was only partial due to the short distance of the approach phase, then subjects would be more likely to perceive gaps as passable, but not by an amount that would be expected if recalibration was complete. This could also explain why the change in critical required speed on catch trials in Experiment 1 increased by less than 50%. Experiment 2 was designed to investigate this possibility.

Experiment 2

The following changes were made in Experiment 2 to rule out the possibility that subjects partially recalibrated within the 3 m approach phase in Experiment 1. First, there was only one session, and visual gain was set to 1.0× on normal trials and 1.5× on catch trials as in Session A of Experiment 1. Second, when visual gain increased to 1.5× on catch trials, the manipulation affected subjects’ movement relative to the stationary background and the cylinders before they began moving, but not relative to the cylinders after they began moving. That is, once the cylinders began moving, subjects’ movement relative to the cylinders was the same on normal trials and catch trials. Third, the appearance of the virtual environment was modified to eliminate visual information about self-motion once the cylinders began moving. This was achieved by changing the textured ground plane to a solid green ground plane, and by removing all posts that were within the field of view after subjects reached the point at which cylinder movement was triggered (see Figure 11). The only objects that were visible while the cylinders were moving were the cylinders themselves. That is, visual information about self-motion was available during the approach phase, but not while the cylinders were moving. This allowed us to isolate the effect of the visual gain manipulation during the approach phase on the calibration of non-visual information. If subjects recalibrate, even partially, to the change in visual gain during the 3 m approach phase, then they should attribute more of the relative motion between themselves and the obstacles to self-motion on catch trials. Because the motion of the cylinders was the same on normal trials and catch trials, subjects should be less likely to perceive the gap as passable on catch trials if partial recalibration occurs (see Figure 12). Therefore, if walking for 3 m with faster-than-normal visual gain is sufficient to recalibrate non-visual information, the % of yes responses and critical required speed should decrease on catch trials in Experiment 2.

Figure 11.

Layout (A) and grayscale version of screenshot (B) of virtual environment used in Experiment 2. The gray area in (A) indicates the subject’s field of view at the moment that the cylinders begin moving.

Figure 12.

Predictions for normal (A) and catch (B) trials in Experiment 2.

Method

Participants

Fifteen students participated in the experiment. They were recruited from psychology courses and received extra credit for participating. All participants reported that they had normal or corrected-to-normal vision and no visual or motor impairments.

Equipment, virtual environment, and procedure

The equipment, virtual environment, procedure, task, and design were similar to those used in Experiment 1. Subjects began each trial by standing at the home location and pressing a button on a remote mouse. A pair of stationary yellow obstacles appeared in the scene, at which time subjects could begin walking. On normal trials, the distance from subjects’ location at the onset of cylinder motion to the location of the cylinders when the gap was closed was 3, 4, or 5 m, and the amount of time it took for the gap to close was 1.4, 1.6, 1.8, or 2.0 s (see Figure 13). There were eight repetitions per condition for a total of 96 normal trials. On catch trials, five different combinations of initial distance and time-to-closure were used: 4.0 m and 1.4 s, 4.0 m and 1.6s, 4.0 m and 1.8 s, 5.0 m and 1.6 s, and 5.0 s and 1.8 s. There were four repetitions per condition for a total of 20 catch trials, yielding a total of 116 trials per session. The experiment was broken down into two blocks of equal length, and subjects completed a warm-up session prior to starting the experiment as in Experiment 1.

Figure 13.

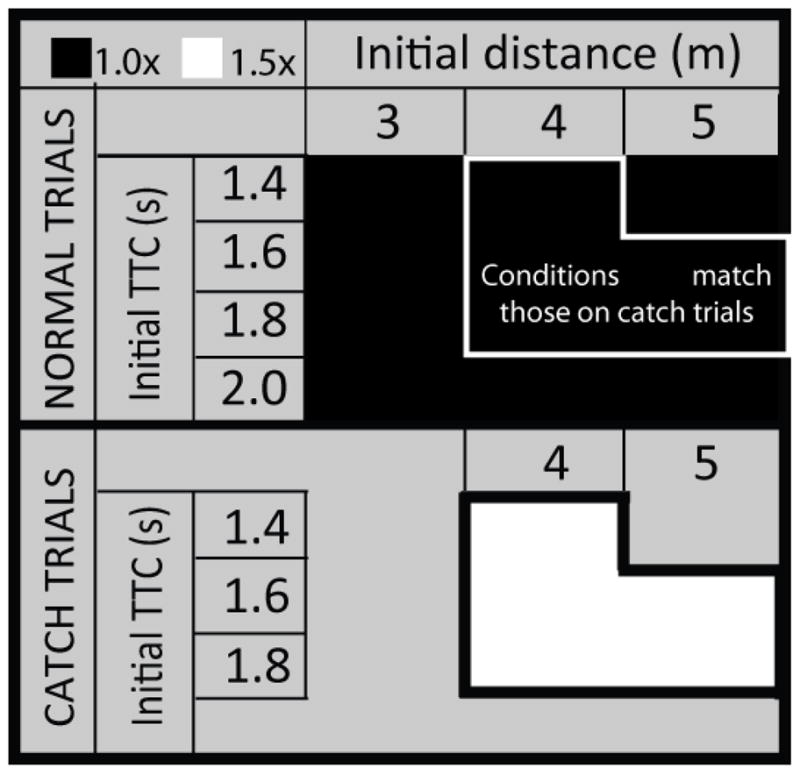
Schematic of design used in Experiment 2. The upper region corresponds to normal trials and the lower region corresponds to catch trials. Within each main regiong, different cells correspond to different conditions. Conditions in which visual gain was set to 1.0× (i.e., normal trials in Session A and catch trials in Session B) are shaded black, and conditions in which visual gain was set to 1.5× are shaded white. The subset of normal trials with initial conditions that match the initial conditions on catch trials are enclosed by a solid white line.

Results and Discussion

The percentage of yes responses was marginally significantly higher (t₁₄ = 2.06, p = .059, partial η² = .23) on catch trials (M = 26.7%; SE = 4.6) compared to normal trials (M = 21.7%; SE = 4.4). Similarly, the critical value of required speed was significantly higher (t₁₀ = 3.63, p < .01, partial η² = .57) on catch trials (M = 2.49; SE = 0.07) compared to normal trials (M = 2.33; SE = 0.08).⁴ In Experiment 1, the manipulation of visual gain affected passability judgments, but the magnitude of the effect was smaller than one would expect if subjects relied entirely on non-visual information to decompose optic flow. If this was due to the fact that non-visual information was recalibrated during the 3 m approach phase, the % of yes responses and critical required speed should have decreased on catch trials in Experiment 2. The fact that there was a small increase rather than a decrease for both dependent measures allows us to rule out the possibility that walking for 3 m while being exposed to faster-than-normal optic flow was sufficient for subjects to learn to attribute more optic flow to their own self-motion. This leaves us with the one remaining account of the Experiment 1 data, according to which both visual and non-visual self-motion information contribute to the recovery of the object-motion component of optic flow.

Why were subjects slightly more likely to perceive gaps as passable on catch trials in Experiment 2? One possibility is that when visual gain increased to 1.5×, subjects perceived that their locomotor capabilities suddenly improved – that is, that they could suddenly move faster through the virtual environment, and therefore safely pass through gaps that were previously perceived as impassable. It is important to point out, however, that the magnitude of this effect was quite small, and that only four of the 15 subjects showed an increase in the % of yes responses greater than 5%.

To summarize, the results of Experiment 2 rule out the possibility that subjects rapidly recalibrated during the 3 m approach phase of catch trials. The remaining explanation of the results of Experiment 1 is that subjects relied on a combination of visual and non-visual information.

General Discussion

Implications for affordance perception

The ability to perceive possibilities for action (i.e., affordances) is an essential part of selecting safe and efficient actions during locomotion through complex, dynamic environments. Although most research on affordance perception focuses on affordances that depend on one’s body dimensions (i.e., body-scaled affordances), selecting appropriate actions also requires perceiving affordances that depend on movement capabilities (i.e., action-scaled affordances). Most of the small number of studies on action-scaled affordances are aimed at measuring the accuracy with which such affordances can be perceived (e.g., Pepping & Li, 2000). As such, little progress has been made toward understanding the informational basis for the perception of action-scaled affordances, which is central to the broader theoretical question about whether affordances are directly perceived.

In this study, we introduced a new optical invariant that specifies the minimum walking speed needed to safely pass through a shrinking gap. Because the information specifies v_min in intrinsic units equal to the number of eyeheights that must be traveled in the amount of time remaining before the gap closes, such information can be calibrated to allow for the direct perception of the passability of shrinking gaps. Detecting information about v_min during self-motion requires recovering the component of the change in angular declination of the base on the gap that is due to the motion of the obstacles (γ̇_g). In the second part of this paper, we presented two experiments designed to investigate the contributions of visual and non-visual self-motion information to the recovery of γ̇_g. The main finding was that γ̇_g is recovered using a combination of visual and non-visual self-motion information.

One might wonder whether any conclusions can be drawn about the relative contributions of visual and non-visual self-motion information. In Experiment 1, the magnitude of the effect was roughly half of what one would expect if subjects relied entirely on non-visual information. It is tempting to conclude that visual and non-visual information contribute equally. However, their relative contributions may not be fixed. Factors such as the amount of visual structure in the scene, whether the person is accelerating or moving at a constant speed, and the inertial properties of the body may affect the relative contribution of visual and non-visual self-motion information.

The necessity of recalibration

Because the relation between non-visual self-motion information and the amount of optic flow attributed to self-motion is not fixed, it must be possible to recalibrate non-visual self-motion information as properties of the body and the environment change. The results of Experiment 1 demonstrate that experience walking with faster-than-normal optic flow is sufficient to drive recalibration of non-visual self-motion information. When visual gain was set to 1.5× on the majority of trials as it was in Session B, subjects learned that more of the relative motion between themselves and the gap should be attributed to their self-motion. In this sense, visual self-motion information also plays an important indirect role in the recovery of object motion during self-motion by calibrating non-visual information. Such findings add to the growing body of literature that demonstrates the critical role of calibration in the control of locomotion (Bruggeman, Zosh, & Warren, 2007; Durgin, Pelah, et al., 2005; Rieser, Pick, Ashmead, & Garing, 1995).

Broader implications for the visual control of locomotion

The focus of the present study was on situations in which two obstacles at equal depths converge to a common point along the locomotor axis, which we referred to as the shrinking gap problem. However, the usefulness of information about v_min is by no means restricted to perceiving the passability of a shrinking gap. The solution introduced in this study provides the basis for a general theory of affordance perception and the guidance of locomotion for a variety of tasks involving moving objects. In this section, we illustrate this point by showing how the solution could be applied to two different tasks.

First, let us relax the assumption that there are two obstacles at equal depths converging onto a single point on the locomotor path. When the environment contains multiple independently moving obstacles, the information captured by Equation 5 specifies for each obstacle the range of locomotor speeds at which one must move to avoid a collision with that obstacle. The set of locomotor speeds that do not result in collisions with any obstacles represent the possible trajectories that one could follow to safely pass through the field of moving obstacles. Such information could be used to decide whether to pass in front of or behind each obstacle, as well as how to control locomotor speed to avoid a collision.

Second, when the task is to intercept a moving target, the information captured by Equation 5 specifies the locomotor speed needed to guide interception. Although a systematic investigation of the role of information about v_min in the control of interception is beyond the scope of the present study, it is worth noting that aspects of human behavior in previous studies of locomotor interception are consistent with the predictions of our theory. If people rely on information about v_min to guide locomotion through a shrinking gap, then manipulations of visual and non-visual self-motion information should affect the control of locomotion in the same way that they affected affordance perception in the present study. Subjects in Fajen and Warren (2004) walked through a virtual environment (a room with a textured floor, ceiling, and walls) to intercept a moving target. Their behavior was consistent with a constant bearing angle strategy (Chardenon, Montagne, Laurent, & Bootsma, 2004; Fajen & Warren, 2004, 2007; Lenoir, Musch, Thiery, & Savelsbergh, 2002), according to which one moves so as to keep the target at a fixed direction relative to an exocentric reference frame. This is equivalent to walking along a straight path heading in front of the target while keeping the angle between the direction of locomotion and the target fixed. In one condition of Experiment 4, the virtual room moved in the same direction and at the same speed as the target. Compared to the control condition in which the virtual room was stationary, subjects maintained a smaller target-heading angle, as if they perceived that the target was moving slower than it actually was. Such behavior is not predicted by the constant bearing angle model, but is consistent with an influence of visual self-motion information on the recovery of the object-motion component of optic flow. When the background moves in the same direction as the target, the component of optic flow that remains after factoring out the component due to (visually-specified) self-motion is less than it is when the background is stationary. Therefore, one would expect subjects to follow a trajectory that maintains a smaller target-heading angle, which is exactly what was observed.

Toward a seamless account of affordance perception and the guidance of locomotion

Navigating through complex environments requires people to perceive and select appropriate affordances and to guide their movements to realize those affordances. Warren (1988) referred to the former as the affordance problem and the latter as the control problem. Most studies of the visual control of locomotion deal with either the affordance problem or the control problem but not both, as if these problems require different solutions (Fajen, 2005b, 2007; Stoffregen, 2000). Indeed, the fit between the environment and the person’s body dimensions and movement capabilities is emphasized in studies of affordance perception, but largely ignored in studies of continuous control (Bastin, Fajen, & Montagne, 2010; Fajen, 2005a, 2005c; e.g., Lee, 1976; Lenoir, et al., 2002; McBeath, Shaffer, & Kaiser, 1995; McLeod, Reed, & Dienes, 2006; Wann & Swapp, 2000; Yilmaz & Warren, 1995; but see Bastin, et al., 2010; Fajen, 2005a, 2005c). Of course, the ability to take one’s body dimensions and movement capabilities into account is just as important for continuous control as it is for action selection. In this sense, solutions to the affordance problem may provide insight into both action selection and continuous control. In this study, we have introduced a source of visual information that could be used to both perceive affordances and guide locomotion to realize affordances. As such, this study provides a significant step toward a seamless account of how people select actions and continually guide movement in a way that takes into account both their body dimensions and movement capabilities.