A SAS Macro for a Clustered Logrank Test

Abstract

The clustered logrank test is a nonparametric method of significance testing for correlated survival data. Examples of its application include cluster randomized trials where groups of patients rather than individuals are randomized to either a treatment or control intervention. We describe a SAS macro that implements the 2-sample clustered logrank test for data where the entire cluster is randomized to the same treatment group. We discuss the theory and applications behind this test as well as details of the SAS code.

1. Introduction

The logrank test is a nonparametric method of comparing survival curves that makes few assumptions about the distribution of the data. The clustered logrank test is an extension of the usual logrank test that adjusts for clustered data. This method may be applied to data from clinical trials where randomization occurs at the cluster level. Examples of clusters include households, workplaces, clinics, and geographic regions. Usual survival methods assume independent observations and should not be used to analyze clustered dat a. Ignoring the within-cluster correlation leads to an increase in Type I error under cluster randomization.

There are only a few SAS methods available for analyzing clustered survival data. One method is the PHREG procedure. This procedure has a covariance sandwich estimator option to adjust the variance for clustered data. A more recent method is to encode NLMixed with the full likelihood for the shared frailty model. In this paper we chose to translate Fortran code from Jung and Jeong [1] into SAS code to perform the clustered logrank test. This program is intended for studies where the entire cluster receives the same treatment.

In section 2.1 we will briefly review the theory behind the usual logrank test before describing its extension to clustered data (section 2.2). In section 2.3 we discuss the details of the program and its execution. In section 3 we will provide an example of the macro applied to a cluster randomized trial of an educational intervention for osteoporosis management. The Clustered Logrank Test Macro (©2009 Margaret Stedman) and example data are freely distributed under the terms of the GNU General Public License and available to download from our website: http://www.drugepi.info/links/downloads.php.

2. Methods

2.1. Logrank Test for Independent Data

For a general description of the usual Logrank test see [2, 3]. In brief, it is a nonparametric statistical test for comparing survival data. For example, consider a clinical trial in which patients are randomly assigned to either one of two treatment groups: a treated (g = 1) and control group (g = 2). Each group contains n_g independent random observations. Let (T_gi; g = 1, 2, i = 1…n_g) be their survival times and (C_gi; g = 1, 2, i = 1…n_g) be their censoring times. We assume that survival and censoring times are independent and that patients within each group share a common survival distribution (S_g(t)), hazard (λ_g(t)), and cumulative hazard (Λ_g(t)) functions. We observe the minimum follow-up time $T_{\mathit{\text{gi}}}^o$ between T_gi and C_gi and indicate if censoring occurred by D_gi where D_gi = I {T_gi ≤ C_gi}. So that our data consist of$(T_{\mathit{\text{gi}}}^o,D_{\mathit{\text{gi}}};g=1,2,i=1\dots n_g)$.

Under the null hypothesis we assume equal cumulative hazard functions (Λ_g) for both groups:

$$H_0:{\mathrm{\Lambda }}_1={\mathrm{\Lambda }}_2$$ (1)

To test the null hypothesis we compute the usual logrank statistic for independent data:

$$\mathit{\text{LR}}=\sqrt{n}{\displaystyle {\int }_{t=0}^{\infty }W(t)}\{d{\widehat{\mathrm{\Lambda }}}_1(t)-d{\widehat{\mathrm{\Lambda }}}_2(t)\}$$ (2)

where W(t) is a weight function at time t, which is non-preferential to early or late occurring events and n = n₁ + n₂, [2, 3]

$$W(t)=\frac{Y_1(t)Y_2(t)}{\mathit{\text{nY}}(t)}$$ (3)

$Y(t)=Y_1(t)+Y_2(t)\text{ and }{Y}_g(t)={\displaystyle {\sum }_{i=1}^{n_{\mathit{\text{gi}}}}I(T_{\mathit{\text{gi}}}^o\ge t)}$ are the number of patients at risk overall and within group g at time t respectively. The cumulative hazard is estimated by the Nelson-Aalen estimator: a cumulative ratio of the number of deaths to the number of observations at risk.

$${\widehat{\mathrm{\Lambda }}}_g(t)={\displaystyle {\int }_0^{\infty }}\frac{{\mathit{\text{dD}}}_g(t)}{Y_g(t)}$$ (4)

where $D_g(t)={\displaystyle {\sum }_{i=1}^{n_{\mathit{\text{gi}}}}{D}_{\mathit{\text{gi}}}(t)\text{ and }{D}_{\mathit{\text{gi}}}(t)=I(}{D}_{\mathit{\text{gi}}}=1,T_{\mathit{\text{gi}}}^o\le t)$ are the number of deaths within group g and the status of each patient at time t. The variance of the logrank statistic is:

$$\begin{array}{cc}\hfill \mathit{\text{var}}(\mathit{\text{LR}})& =\mathit{\text{nE}}{\displaystyle {\int }_{t=0}^{\infty }{\displaystyle \sum _{g=1}^2}\frac{W^2(t)}{Y_g(t)}\{1-\mathrm{\Delta }\mathrm{\Lambda }(t)\}d\mathrm{\Lambda }(t)}\hfill \\ \hfill \text{where}\mathrm{\Delta }\mathrm{\Lambda }(t)& =\mathrm{\Lambda }(t)-\underset{t\prime \to t}{\text{lim}}\mathrm{\Lambda }(t\prime )\hfill \end{array}$$ (5)

Under the null hypothesis Λ₁ = Λ₂= Λ and Z is assumed to follow a standard normal distribution:

$$Z=\frac{\mathit{\text{LR}}}{\sqrt{\mathit{\text{var}}(\mathit{\text{LR}})}}~N(0,1)\text{ under }{H}_0$$ (6)

We reject the null hypothesis when Z exceeds the critical value from the N(0, 1) distribution for a given level of Type I error.

2.2. Logrank test for clustered data

For clustered data we assume that observations are additionally defined by their cluster k. So that Y_gk corresponds to the number of patients at risk in group g and cluster k. Similarly, δ_gk is the number of deaths in group g and cluster k. Time is indexed differently than in the previous formulas. For example, Y_g(t_gki) is the number at risk in group g at the observed time (of either censoring or death) for observation i in group g and cluster k. Indexes with primes refer to the same range of values as those without primes, but indexes with primes are not necessarily fixed to their nonprime counterpart. For example, Y_g(t_g′k′i′), refers to the number of patients at risk in group g at some time t where g′ can vary indepent of g to any value within the range of g (either 1 or 2).

Jung and Jeong [1] proved that by partitioning the clustered logrank statistic (CLR) by group and cluster we can estimate the variance from the within cluster mean squared error (MSE_gk). Since the clusters and treatment groups are independent the MSE_gk can be summed across clusters to find the total variance for the CLR.

$$\mathit{\text{CLR}}={\displaystyle \sum _{g=1}^2}{\displaystyle \sum _{k=1}^{K_g}}{\mathit{\text{LR}}}_{\mathit{\text{gk}}}$$ (7)

$$\mathit{\text{var}}(\mathit{\text{CLR}})={\displaystyle \sum _{g=1}^2}{\displaystyle \sum _{k=1}^{k_g}}{\mathit{\text{MSE}}}_{\mathit{\text{gk}}}$$ (8)

$${\mathit{\text{MSE}}}_{\mathit{\text{gk}}}=E{({\mathit{\text{LR}}}_{\mathit{\text{gk}}})}^2$$ (9)

Note that CLR is equivalent to the logrank test (LR) for independent data. Despite its complex formula, the LR_gk is merely a partition of the logrank statistic for group g, cluster k:

$${\mathit{\text{LR}}}_{\mathit{\text{gk}}}=n{\displaystyle \sum _{i=1}^{n_{\mathit{\text{gk}}}}}\frac{{\delta }_{\mathit{\text{gki}}}W(t_{\mathit{\text{gki}}})}{Y_g(t_{\mathit{\text{gki}}})}-{\displaystyle \sum _{g\prime =1}^2}{\displaystyle \sum _{k\prime =1}^{k_{g\prime }}}{\displaystyle \sum _{i\prime =1}^{n_{g\prime k\prime }}}\frac{{\delta }_{g\prime k\prime i\prime }{Y}_{\mathit{\text{gk}}}(t_{g\prime k\prime i\prime })W(t_{g\prime k\prime i\prime })}{Y_g(t_{g\prime k\prime i\prime })Y(t_{g\prime k\prime i\prime })}$$ (10)

where W is a weight function specific to the log rank test:

$$W(t_{\mathit{\text{gki}}})=\frac{Y_1(t_{\mathit{\text{gki}}})Y_2(t_{\mathit{\text{gki}}})}{Y(t_{\mathit{\text{gki}}})}$$ (11)

Jung and Jeong [1] prove that CLR converges to a N(0; 1) under H₀. This is convenient for hypothesis testing purposes because the Wald test resolves to a standard normal distribution:

$$Z=\frac{\mathit{\text{CLR}}}{\sqrt{\mathit{\text{var}}(\mathit{\text{CLR}})}}~N(0,1)$$ (12)

Again, we reject the null hypothesis when Z exceeds the critical value for a given level of Type I error.

2.3. SAS Macro

The SAS program performs a 2-sample clustered logrank test. It is written in SAS version 9.1 and may not operate correctly in earlier versions. Users should confirm that the IML package has been installed prior to use. The full code for the clustered logrank test is posted to our web site: http://www.drugepi.info/links/downloads.php.

The macro is flexible and can accommodate variable cluster sizes and unbalanced designs. No assumptions are made with respect to the number of clusters per treatment group or number of observations per cluster. The SAS program requires five macro variables to be defined by the user. All five variables must have entries from the user in order for the macro to run. See Appendix A for a full description of the macro variables.

At the beginning of the program the number of clusters and total observations are counted and reported back to the user (step 1). The counts are given macro variable names to be used later in the program. In step 2, the data are sorted in descending order by time. In step 3 the number of observations at risk (Y) and the number of deaths (d) at each time point are computed. Variables are created to store the total number of observations at risk (YY) and the total number of deaths (DD) and group specific counts (denoted by g1 and g2). The weight (wt) for the logrank test is also computed at each time point. The data are collapsed down to one observation per time point. The group specific estimates for the Nelson-Aalen statistic (see formula 4) and its variance (see formula 5) are computed assuming independent observations. For a full description of the method see section 2.1

The clustered variance requires multiple steps to compile. The dataset with one observation per time point is joined with the original data in a one-to-many merge by time interval (step 4). Essentially this step re-weights the time specific data to the number of observations in the dataset. The remaining computations are applied to this dataset with SAS IML (step 5). To simplify the explanation of the code, it has been broken down into the following steps. Each step has been denoted by a comment statement in the program.

• 5.1
  Calculate part 1 of LR_gk for each cluster:

  $${\displaystyle \sum _{i=1}^{I_{\mathit{\text{gk}}}}}\frac{{\delta }_{\mathit{\text{gki}}}W(t_{\mathit{\text{gki}}})}{Y_g(t_{\mathit{\text{gki}}})}$$
• 5.2
  Compute part 2 of LR_gk

  • 5.2.1
    Events matrix: δ_g′k′i′
  • 5.2.2
    At risk matrix: Y_gk(t_g′k′i′)
  • 5.2.3
    Weight matrix:

    $$\frac{W(t_{g\prime k\prime i\prime })}{Y_g(t_{g\prime k\prime i\prime })Y(t_{g\prime k\prime i\prime })}$$
  • 5.2.4
    Multiply parts 2.1, 2.2, and 2.3 together.
• 5.3Subtract part 1 from part 2 to estimate the within cluster statistic LR_gk
• 5.4Square LR_gk and sum across clusters to find the clustered variance
• 5.5Display results

The input dataset should be structured so that each record contains a unique observation allowing for multiple records per cluster. The SAS program does not require an equal number of observations per cluster or equal number of clusters per treatment group. If there is only one observation per cluster, the program resolves to the standard unclustered logrank test. The input dataset should include (but is not limited to) at least the following variables: cluster identifier, treatment group, time to event, and censoring indicator. The program assumes that the treatment groups are ordered as control first and treated second. The censoring variable should be coded so that 1=event, 0=censored. The input dataset should be a permanent SAS dataset saved to the subdirectory specified by the user at the top of the program.

Output from the macro displays the number of clusters and observations per treatment group. The variance, assuming independent data, is presented alongside the clustered variance. A ratio of the two results gives an estimate of the variance inflation factor due to clustering. The logrank statistic listed in the output is the same for both the clustered and unclustered data. The Z statistic is computed by dividing the logrank statistic by the clustered logrank standard deviation. The p-value for the Z statistic assumes a two sided test.

3. Example study

We applied the clustered logrank test to results from a randomized controlled trial of an education program for physicians to improve osteoporosis management. Physicians were randomized to a one-on-one educational session versus no education. Those randomized to the intervention were provided information on how best to prevent osteoporosis in high-risk patients. Patients of the enrolled physicians were followed for a maximum of 296 days to determine when they received either a bone mineral density test or osteoporosis medication. The outcome was time until receipt of appropriate medical care. The average follow-up time was 263.5 days with 85% censoring. Since the treatment was randomized at the physician level, the individual patient outcomes were considered clustered within the physician. A total of 435 physicians were enrolled in the study. The number of patients per physician varied between 1 and 148. [4]

To demonstrate use of the macro, we simulated data to replicate the structure of the osteoporosis trial. To download the SAS dataset please visit our website: http://www.drugepi.info/links/downloads.php.

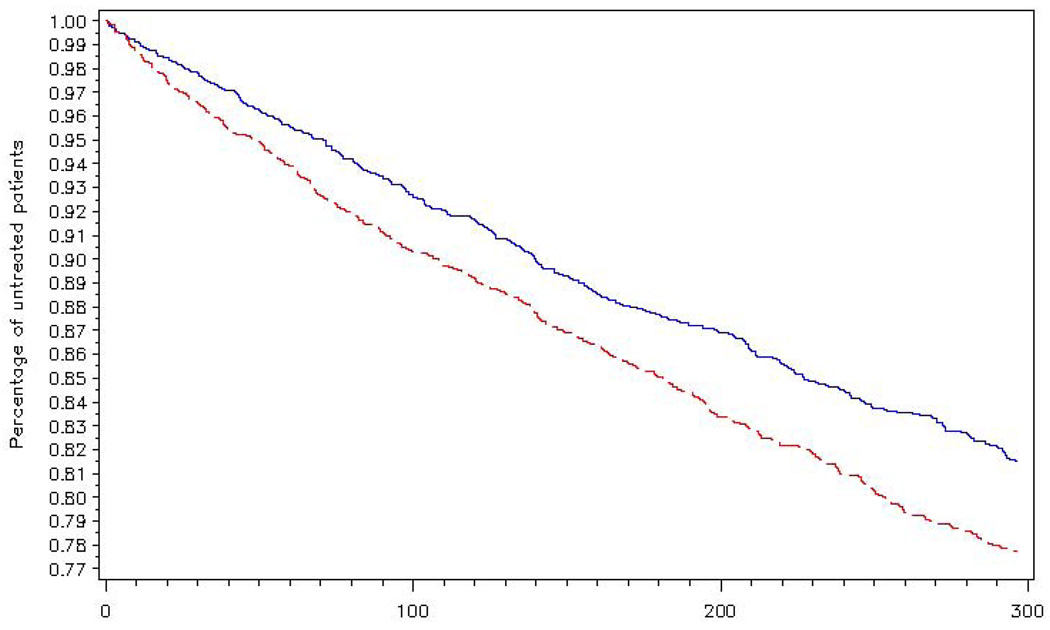
A codebook for the variables is listed in Appendix B. To create the simulated data we specified a shared frailty model with a Weibull baseline hazard and a lognormal physician effect. To simplify the example we simulated 458 physician clusters (229 per treatment group) with 8 observations per cluster. A treatment effect was specified to simulate a hazard ratio of approximately 1.12. All data were censored at 296 days. Figure 1 displays survival curves of time until receipt of medical care for patients of the intervention (red dashed line) and control physicians (blue solid line).

Figure 1.

Time until receipt of medical care for high-risk patients. Red dashed line represents the patients of physicians in the intervention group. Blue solid line represents patients of physicians in the comparison group.

To call the logrank macro using the simulated example data specify the input variables as follows:

$$\%\text{clusterlr}(\text{datain}=\text{simdata},\text{time}=\text{time},\text{cluster}=\text{drid},\text{group}=\text{treat},\text{censor}=\text{censor});$$

The clustered logrank test requires approximately 6 seconds of real time to complete and the results from the output are summarized in the Appendix C. The first half of the output (not shown) confirms the number of clusters and the number of observations per treatment group. Next, there is a table displaying the unclustered variance, the clustered variance, the clustered logrank test statistic, and the p-value. The clustered variance (378.89) is inflated to almost twice the size of the unclustered variance (186.71). The p-value for the clustered logrank test indicates that there is a significant difference between patients of the doctors who received the educational program compared to patients of doctors who did not receive the educational program (Clustered logrank=2.03, p=.042). If we had ignored the clustering we would have found a more strongly significant result (Usual logrank test=8.3709, p=0.0038).

4. Discussion

We have created a SAS macro program for the clustered logrank test originally developed by Jung and Jeong. [1] The Clustered Logrank Test Macro (©2009 Margaret Stedman) is freely available under the terms of the GNU General Public License. The program can be used to analyze survival data from any SAS dataset. The program may be applied to variable cluster sizes and unbalanced designs. Currently there is no other software freely available to run a clustered logrank test.

Other methods exist to analyze clustered survival data, such as the PHREG procedure with the covariance sandwich estimator option and the NLMixed procedure for the accelerated failure time frailty model. Both of these methods make assumptions about the distribution of the data or the structure of the covariance matrix. [5, 6] The clustered logrank test is a completely non-parametric method which makes no assumptions about the distribution of the data. It is unlikely that the clustered logrank test will be as powerful as optimal parametric methods that leverage distributional assumptions. The test is asymptotically equivalent to Cox Proportional Hazards with robust standard errors for a large enough sample of clusters [1, 7].

There are several areas for expansion of the macro. The current program is designed for analyzing survival data where the entire cluster is randomized to the same treatment group. Alternative designs, where randomization occurs within cluster, should be analyzed by a different method.[8] Although it is possible to compare multiple groups with the logrank test the clustered logrank test macro is currently limited to two sample tests. Jung and Jeong [1] have extended the method to include more than two groups so it is possible, though not simple, to extend the code to accommodate multiple groups. The logrank test is only one of a family of rank tests. Other rank tests include the Gehan-Wilcoxon and the Prentice-Wilcoxon rank tests. These tests apply different weights to the data. The weight statement could be easily redefined in the SQL step of the macro to extend the code to accommodate these other rank tests.

Appendix

A. Logrank Macro Variable Definitions.

Variable Name	Definition
datain	Name of the input dataset containing the data to be tested.
group	The treatment group or independent variable.
cluster	Identifies each unique cluster.
time	Time to event
censor	Indicator of censoring. 1=event, 0=censored

Appendix

B. Simulated Data (simdata.sas7bdat) Variable Definitions.

Variable Name	Definition
treat	The assigned treatment group: education or no education.
patid	The unique identifier for each patient.
drid	The randomized physician identifier.
time	Time until receipt of appropriate medical care.
censor	Indicator for the patient having received appropriate medical care.

Appendix

Table 1. C. Summary of Results from Example Data to Demonstrate the Clustered Logrank Test Macro.

Summary of results from example data.

Group 0 (Control group)
Number of clusters	229
Number of observations	1832
Group 1 (Treated group)
Number of clusters	229
Number of observations	1832
Independent variance	186.7077
Clustered variance	378.8884
Logrank statistic	39.53367
Clustered logrank test	2.031007
Clustered logrank p-value	0.042254