We made an error in the numerical example simulating the unconfined compression of a cylindrical cartilage sample, given in §5.2. In articular cartilage, the collagen fibres are close to lying on the transverse plane in the superficial zone and close to aligned with the axial direction in the deep zone. These two opposite situations correspond to model (A) and model (B), respectively, as described in §3.4 and figure 1. In both cases, the limit for the concentration parameter b approaching zero yields isotropy, which is attained in the middle zone. In our example, we imposed b to vary linearly with the coordinate running from the bone–cartilage interface to the articular surface: from 5 to 0 (model (B)) in the deep zone, and from 0 to 5 (model (A)) in the superficial zone. Also, in order to reproduce the experiment of Park et al. [1], we ‘cut’ a 0.5 mm layer of the deep zone, so that the concentration parameter b was varying from 2.85 to 0 in the deep zone.
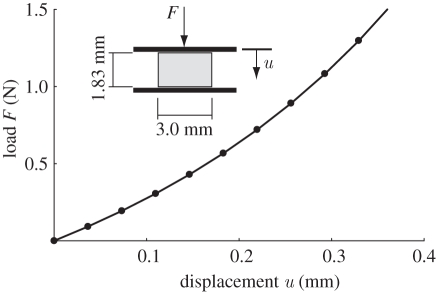
Because of an error in a sign in our code, the fibre distribution in the cylindrical sample of §5.2 is upside-down, i.e. model (A) was used in place of model (B), and vice versa. As a result of this error, things went such that a 0.5 mm layer of superficial (rather than deep) zone was ‘cut’. This implies that the contour plot shown in figure 4 is only roughly but not exactly upside-down, and the force response in figure 3 is not accurate because the zonal subdivision (deep-middle-superficial) is not as desired. Furthermore, the comparison of the radial displacement of the lateral boundary in figure 4 with the experiments of Fortin et al. [2] was not appropriate, as the radial displacements in their tests were relative to a cartilage sample attached to a layer of subchondral bone, which constrains radial displacement at the bone–cartilage interface.
Figure 3.
(corrected)
Figure 4.
(corrected)
While these errors do not affect the validity of the model nor the robustness of the numerical implementation, we felt it was important to correct them.
In this corrigendum, we addressed both issues, and simulated:
— the unconfined compression of the same sample as in our paper, with the correction in the sign in our code that inverted the use of models (A) and (B), in order to obtain the correct force–displacement diagram previously shown in figure 3; the corrected results remain qualitatively in good agreement with the experiments of Park et al. [1] (figure 3 corrected; note also that now the load F is correctly expressed in N), and
— the unconfined compression of a sample attached to a layer of subchondral bone (and therefore ‘prepared’ without cutting the deepest layer of the deep zone); the corrected results predict a more realistic radial displacement of the lateral boundary of the sample, particularly in the superficial zone, where the fibres (parallel to the articular surface) keep the tissue from developing large strains; the comparison with the experimental results shown in fig. 3 of the paper by Fortin et al. [2] is more accurate, with displacement being largest in the deep zone, and then getting smaller going towards the superficial zone (figure 4 corrected).
Finally, note that the article cited as ‘Federico in press’ has now been published in final form [3].
References
- 1.Park S., Hung C. T., Ateshian G. A. 2004. Mechanical response of bovine articular cartilage under dynamic unconfined compression loading at physiological stress levels. Osteoarthr. Cartilage 12, 65–73 10.1016/j.joca.2003.08.005 (doi:10.1016/j.joca.2003.08.005) [DOI] [PubMed] [Google Scholar]
- 2.Fortin M., Buschmann M. D., Bertrand M. J., Foster F. S., Ophir J. 2003. Dynamic measurement of internal solid displacement in articular cartilage using ultrasound backscatter. J. Biomech. 36, 443–447 10.1016/S0021-9290(02)00413-x (doi:10.1016/S0021-9290(02)00413-x) [DOI] [PubMed] [Google Scholar]
- 3.Federico S. 2010. Volumetric-distortional decomposition of deformation and elasticity tensor. Math. Mech. Solids 15, 672–690 10.1177/1081286509105591 (doi:10.1177/1081286509105591) [DOI] [Google Scholar]