Modeling DNA-Bending in the Nucleosome: Role of AA Periodicity

Abstract

This paper uses atomistic molecular mechanics within the framework of the Jumna model to study the bending properties of DNA segments, with emphasis on understanding the role of the 10 bp periodicity associated with AA repeats that has been found to dominate in nucleosomal DNA. The calculations impose a bending potential on 18 bp segments that is consistent with nucleosome structures (i.e., radius of curvature of 4.1 nm), and then determine the energies of the minimum energy structures for different values of the rotational register (a measure of the direction of bending of the DNA) subject to forces derived from the Amber force field (parm99bsc0). The results show that sequences that contain the 10 bp repeats but are otherwise random have a narrow distribution of rotational register values that minimize the energy such that it is possible to combine several minimized structures to give the 147 bp nearly planar loop structure of the nucleosome. The rotational register values that lead to minimum bending energy with 10 bp AA repeats have a narrower minor groove which points towards the histone interior at the positions of the AA repeats, which is a result that matches the experiments. The calculations also show that these sequences have a relatively flat potential energy landscape for bending to a 4.1 nm radius of curvature. Random sequences that do not have the 10 bp AA repeats have less stable bent structures, and a flat rotational register distribution, such that low energy nearly planar loops are less likely.

Introduction

Nucleosomes are fundamental subunits of chromatin in which a 147 base-pair (bp) segment of DNA wraps 1.67 turns around a histone protein complex to produce a roughly cylindrical structure that is about 11 nm in diameter. Understanding the precise wrapping of DNA in nucleosomes is a long-sought goal in cell biology as it is thought that nucleosome structure relates to gene regulation.¹ Recent experimental studies suggest that it is the mechanical properties of a given DNA sequence (its three dimensional shape and mechanical stiffness) that dictate its nucleosome positioning propensity (i.e., which determine the probability that a given 147 base-pair sequence in genomic DNA will bind to the histone proteins to become a nucleosome).^2-4 In particular, the nucleosome affinity of DNA sequences is found to be higher in sequences that have specific dinucleotides (AA, TT, TA) repeated every 10 bp⁵ than with other sequences.⁶ In addition, certain sequences, such as poly (dA:dT)⁷ are known to particularly disfavor nucleosome formation.⁸ The sequence-dependent mechanical properties of DNA are likely also important in other protein-DNA interactions, such as the binding of transcription factors in chromatin.⁹ A recent study ^10,11 has suggested that sequence dependent deformation of DNA may also facilitate specific histones-DNA interactions in nucleosomes.

The mechanical properties of DNA have been of interest to modelers for decades,^12-16 but past work has not provided the level of understanding needed to describe all the base-pair specific properties involved in nucleosome binding. In addition, there is a growing understanding that simple mechanical models of DNA, such as the worm-like chain (WLC) model are not able to describe high curvature properties of DNA, such as are important in nucleosome structures. In particular, AFM results from Phillips, Widom and colleagues,¹⁷ and other groups,^18,19 suggest that the energy of highly bent DNA conformations (5 nm radius of curvature) are substantially lower in energy than are predicted by WLC and other classical elasticity models. New models of DNA that describe sequence-specific mechanical properties have recently been developed, however these are limited to short-range (pair-wise) interaction effects,^20,21 or involve information-based algorithms.²² A recent study using the information-based DNABEND model was successfully used to describe the 10 bp periodicity requirement for nucleosome occupancy,²³ however DNABEND only includes dinucleotide interactions, and thus it cannot describe longer-range effects such as are likely relevant to the poly (dA:dT) behavior.

Fully atomistic molecular mechanics force fields, such as recent updates of Amber, are thought to contain accurate sequence dependent properties,^24-26 however the complexity of structures of interest to the nucleosome problem are such that only a few “benchmark” studies are possible with unconstrained structures^27,28. Thus there is an important need for models and modeling that are designed to describe the mechanical properties associated with nucleosome DNA structures containing 10s of bp for a wide variety of sequences. In this paper we show that the Jumna (JUnction Minimization of Nucleic Acids) model²⁹ is able to describe key sequence-dependent properties of DNA that are found in nucleosomes. Jumna is an atomistic model of DNA which breaks each strand down into a series of 3′-monophosphate nucleotides, and then the nucleotides are described in terms of translation and rotation, leading to a factor of 10 fewer variables than with standard atomistic (unconstrained) models. Jumna has been used in the past to study the bending properties of A-tract oligomers,³⁰ and has recently been applied to nucleosome properties³¹. In our application, we show that Jumna captures important aspects of base-pair specific nucleosome occupancies, with the only nucleosome-related constraint on DNA structure being the radius of curvature needed to wrap around the histone complex. We also study thermal average effects using an approximate Monte-Carlo approach, in internal coordinates and we make comparisons of the Jumna results with minimally constrained all-atom Cartesian coordinate molecular dynamics results for a model of nucleosomic DNA which includes explicit solvent and ions. Details of the MC and MD simulations are given in Supporting Information.

Description of Model

The calculations consider 18 bp duplex DNA's with nucleobases that are either (1) chosen randomly, or (2) chosen randomly, but with AA inserted every 10 base-pairs. The histone octamer is not included in the calculation, so any effects associated with protein/DNA interactions, such as neutralization of the inner face of the DNA, is not considered. The Jumna 14 model is taken from Lavery's work²⁹, using the Amber parm99bsc0^32,33 force field.^30,34 Constrained minimization is applied by using ten nucleotide periodic helical symmetry in order to avoid end effects. This is done by adding symmetry related sets of four base-pairs at each end of a chosen 10 bp sequence. Such calculations mimic periodic boundary conditions for the 10 bp primary sequence while only requiring 8 additional bp in the calculation. We tested this choice of 8 additional bp by doing calculations for longer sequences, and found that the results were unchanged compared to the 18bp length results.

For sequences that have AA repeats, the AA is inserted at positions 5,6 and 15,16. For each duplex, molecular mechanics calculations are performed to determine the minimum energy structure subject to a constrained radius of curvature of 4.1 nm. This bending is introduced using a superhelical coordinate system³⁰ (Figure 1), wherein the DNA is constrained to follow a superhelical pathway. Different directions of bending are defined by a variable called the rotational register that is sampled by rotating the DNA around its axis. Solvent effects are represented by a sigmoidal distance dependent dielectric function with sigmoidal slope of 0.356, a plateau value of 78 and damping the net phosphate charges to -0.5e. Variation of the results with respect to small changes in the sigmoidal slope and net phosphate charges was examined, and no qualitative differences were observed. We have also performed comparisons with molecular dynamics calculations that include explicit solvent and ions (described later) and the results show that the implicit solvation results are qualitatively correct.

Figure 1.

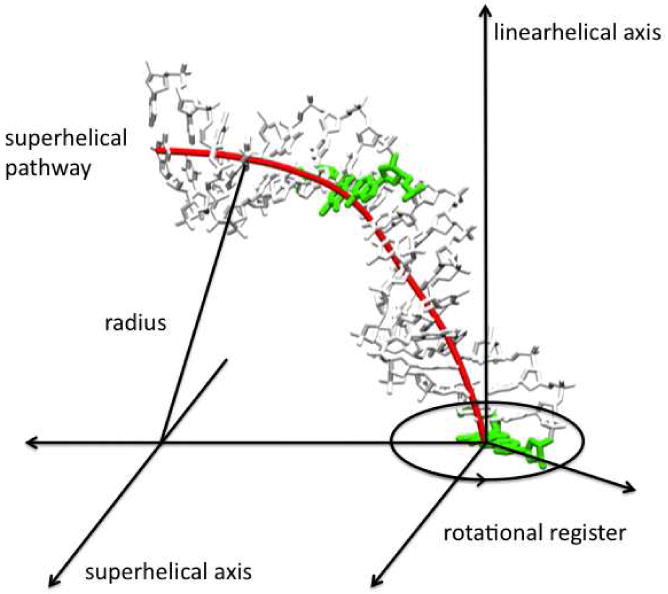
Definition of superhelical coordinate system and rotational register variable.

Energy minimization is done by using an adiabatic mapping procedure where the rotational register is restrained to values with a step interval of 10 degrees starting from zero degrees. Figure 2 (a) shows a few overlapped DNA structures obtained using the adiabatic mapping simulation. Here each step of the adiabatic mapping is started from the previous nearest neighbor conformation. We also did adiabatic mapping in which the rotational registers were sampled in the opposite direction, and the minimum energy structure from these two samplings was used to define a global minimum. No significant difference in the results from these two calculations was found.

Figure 2.

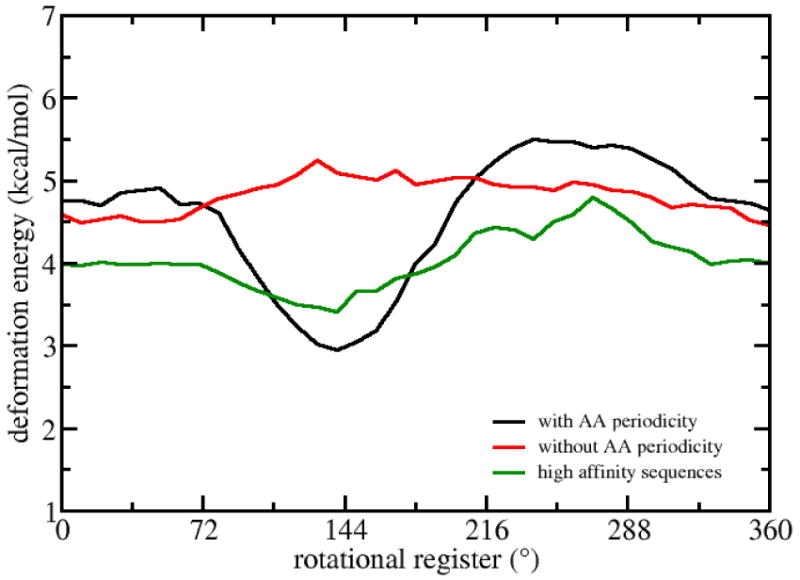
Average deformation energies as a function of rotational register, with results for random sequences (red), sequences with AA periodicity (black) and high affinity sequences (green). The standard deviations associated with the three sequence groups are, on average, 1.9, 1.7, 1.3 kcal/mol, respectively.

Results and discussion

Average deformation energy vs. rotational register

We have calculated the deformation energy of a 10 base pair repeating unit for a curvature that corresponds to the 4.1 nm radius of a nucleosome as a function of rotational register. Figure 2 presents average profiles for 110 random sequences, for 110 sequences with an AA repeats located at base pair positions 5,6 and 15,16 and for 40 sequences of known high nucleosome affinity as determined by the SELEX procedure in Ref 36. Although the 40 sequences are not genomic sequences, they have affinities similar to high affinity features of the mouse genome.³⁵

The figure shows that the energy profile of sequences with the AA repeats has a well-defined minimum in the rotational register range between 120° and 180°. This means that the DNA conformation demonstrates strong anisotropy to the direction of bending as defined by the rotational register. The narrow region is favored by as much as 1.5 kcal/mol compare to the other register values. In contrast, random sequences have a weak dependence of the average deformation energy on rotational register, with an energy of about 4.5 kcal/mol that is about 1.5 kcal/mol above the 3.0 kcal/mol minimum in the periodic AA result. The difference between the maximum and minimum average deformation energy is about 0.7 kcal/mol per 10 base pair segment for the random sequences. Of course any particular 18bp random sequence can show greater rotation register dependent deformation than the corresponding structure with AA repeats (see below). Meanwhile, the high affinity sequences display a profile that is consistent with one with AA repeats, though with a weaker preference for angles in the 120° to 180° range, with about 1 kcal/mol lower energy than with the random sequences.

The preferred rotational register region corresponds to the minor groove facing inward toward the center of the curvature at positions 5,6 where the AA base pairs are located as is shown in Figs 3 for an individual sequence. This shows that including AA every ten base-pairs in the DNA sequence makes bending more favorable and leads to a preferential direction of bending of the minor groove that is consistent with observations on nucleosomes. This behavior contrasts with what is obtained with coarse-grained harmonic and isotropic representations of DNA structures (such as the WLC model) which do not contain rotational register effects.

Figure 3.

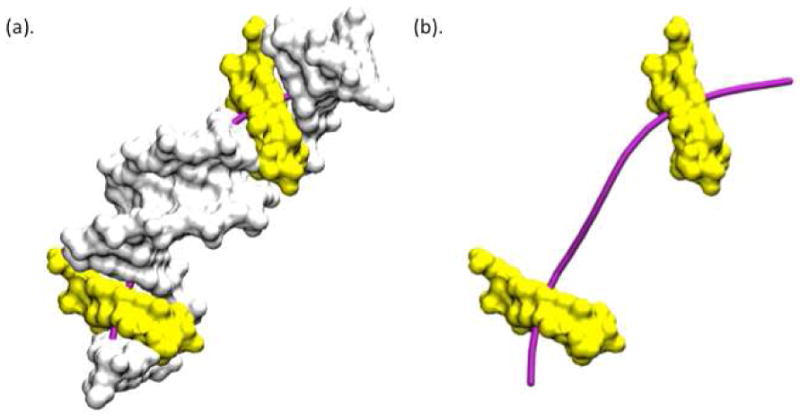
Optimum DNA structure for 4.1 nm radius of curvature for the sequence GGTGAAGCTGGGTGAAGC, based on the Jumna model and the Amber force field. 5,6 and 15,16 positions are shown by yellow color. Helical axes is shown by purple color.

A study³⁶ that measured the average relative free energy difference for binding of a large pool of chemically synthetic random DNAs to histone octamers and binding of a selected set of sequences that contain nucleosome positioning signals to histone octamers indicated that this energy difference is approximately 3 kcal/mol. This result, which nominally refers to 147 bp, is considerably smaller than the 1.5 kcal/mol result that we have obtained for 10 base pair sequences and the 1.0 kcal/mol from high affinity sequences. While it is now thought that the 1.5 kcal/mol refers only to about half of the base pairs that binds to the central histone tetramer of the nucleosome,³⁵ the difference in energy is still substantial (nominally 0.4 vs 1.5/1.0 kcal/mol/10 bp). However we note that the minimized rotational register values would all have to be the same in order for the 147 bp result to simply scale relative to the 10 bp result in Fig. 2. In addition, we note that the 147 bp result refers to a 300K free energy difference, while the result here is a minimum energy (0K result). Solvation effects beyond the implicit solvation model contained in Jumna can also contribute to the difference. Further discussion of temperature and solvent effects will be presented below. Also note that the actual nucleosome is superhelical, corresponding to a 5 degree change in the twist angle per 10 bp.³⁷ This change in twist is small relative to the width of the dip in Fig. 2, so it is not likely to influence this analysis. We also note that slide deformations are now thought to dominate the superhelical structure,³⁸ so the twisting might be less than is estimated here.

Rotational register distributions

Figure 4 shows distributions of rotational register values for both the periodic and completely random duplexes, based on calculations for 110 duplexes of each type. We see that the rotational register distributions are distinctly different, with the periodic duplexes leading to rotational registers that are localized to the 120° to 190° range. On the other hand, the completely random sequences produce a broad distribution of rotational register values with fluctuations that are comparable in width to the periodic results, but with almost no well defined structure. The systematic dip in the rotational register distribution for the periodic duplexes appears key to the stability of the 147 bp loops in nucleosomes.

Figure 4.

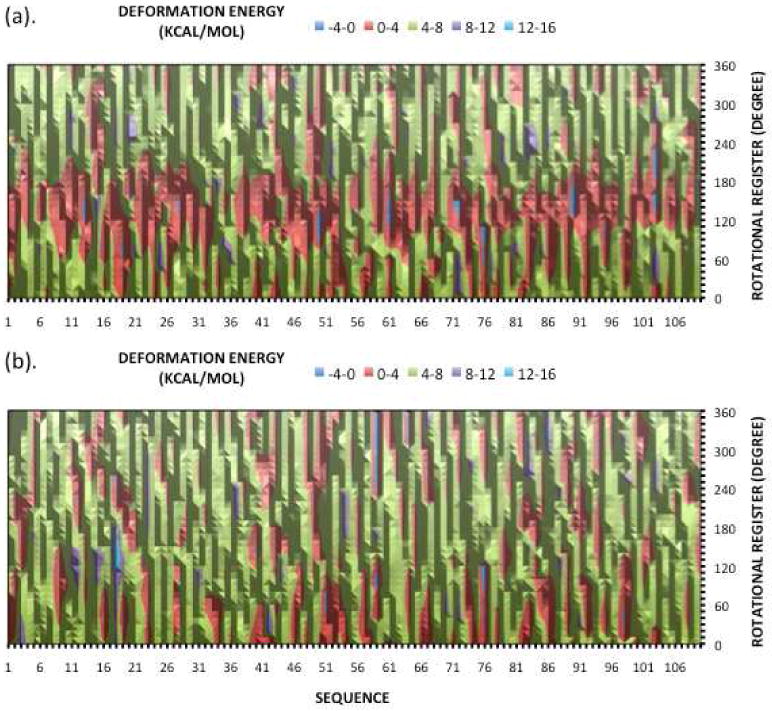
Distribution of deformation energies vs rotational register values, comparing results for 110 random sequences with no periodicity (bottom) with 110 random sequences with AA periodicity (top). (Units of contours are kcal/mol)

Analysis of minimum energy structures

Figure 3 shows the 18 bp duplex structure for the periodic sequence GGTGAAGCTGGGTGAAGC that has been minimized as a function of the rotational register (at 140 degrees in Fig. 3). This shows that the minor groove points inward toward the histone at positions 5 and 6 (yellow in Fig. 3), which is a known result from nucleosome structural studies.⁶ An analysis of the bent minimized structures with and without AA repeats for all sequences has been performed using 3DNA³⁹ and the average geometrical parameters at position 5 and 6 are summarized in Table 1. This reveals that the helical coordinate roll has large negative values at positions 5,6, corresponding to a narrowing of the minor groove. The local bending of the helix can also be characterized using a bending dial⁴⁰, in Fig. 5, which relates the magnitude and orientation of bending to the independent roll and tilt parameters. This shows that the periodic sequences tend to bend toward the minor groove at the fifth and sixth positions, in which more data points are located in the southern hemisphere (Figs. 5). Indeed, the sequences with AA repeats have approximately a 1-3 Å narrower minor groove width (which was measured based on the interstrand phosphate distance suggested by El Hassan⁴¹) next to position 5, 6 than the sequences without AA (See below). Similar energetic coupling between DNA bending and base-pair opening was observed previously by Ramstein and Lavery⁴². Experimental evidence of such conformations has been confirmed by measuring hydrogen exchange kinetics⁴³.

Table 1.

Average base-pair step parameters and local base-pair parameters for all sequences. Note that roll, propeller and opening are in degrees and the values in parenthesis are standard errors.

	Position	Random sequence	High affinity sequence	Sequence with AA
Roll	5	-1.0 (7.7)	-1.2 (11.0)	-4.8 (5.4)
	6	-0.5 (6.7)	-3.6 (8.6)	-9.3 (8.4)
Propeller	5	-5.8 (4.2)	-12.2 (4.1)	-13.0 (3.0)
	6	-6.2 (4.0)	-12.2 (6.2)	-11.9 (3.0)
Opening	5	-2.1 (1.6)	-3.8 (1.6)	-4.1 (1.3)
	6	-2.0 (1.2)	-4.8 (3.7)	-4.8 (1.6)

Figure 5.

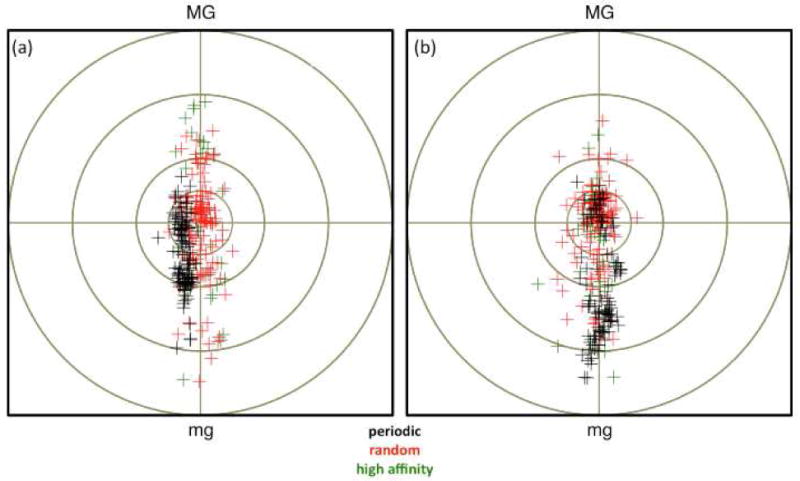
Bending dial at position 5 (panel a) and 6 (panel b) for random sequences with no periodicity (red), sequences with AA periodicity (black) and high affinity sequences (green). MG and mg are major and minor groove directions, respectively.

These trends are well illustrated in the distribution of each structural parameter (Fig. 5 and 6). Most importantly, large negative roll, propeller, opening values and small minor groove widths at positions 5 and 6 are accessible in random sequences, but they occur less frequently than in the sequences with AA repeats. Similar to the conclusions concerning the rotational register, the sequence dependence of these conformations should be critical to the formation of a stable nucleosome. It is interesting to noting that similar propeller and opening values occur in the high affinity sequences but the negative roll values are less pronounced, which shows that roll is more sensitive to other nucleosome positioning information.

Figure 6.

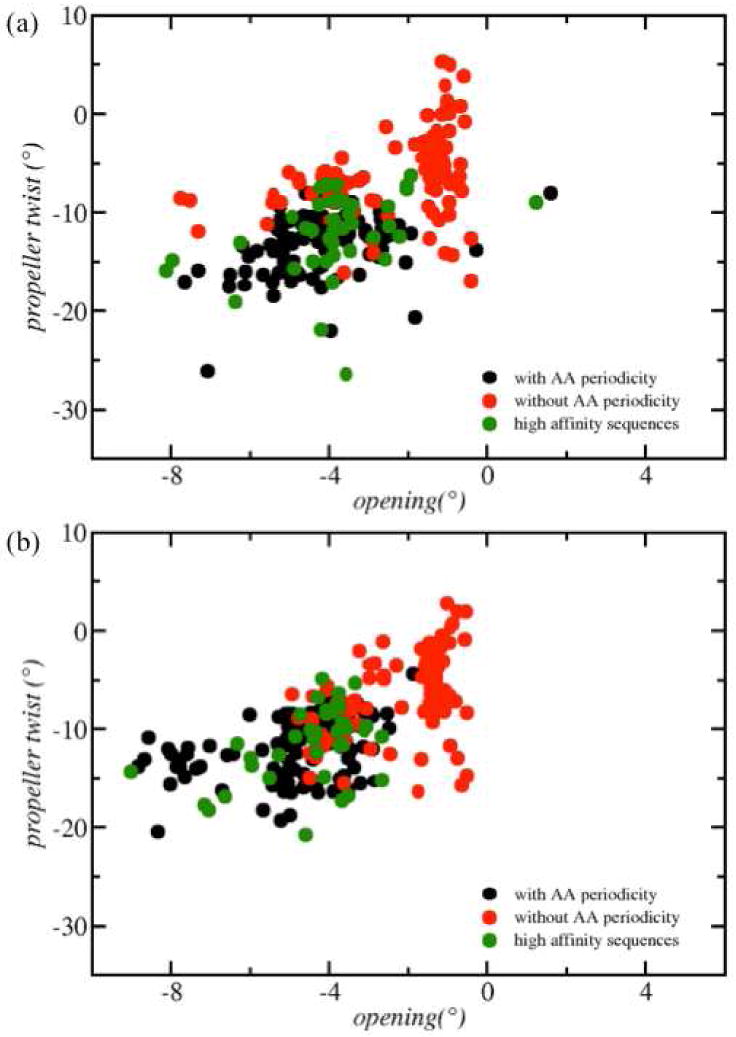
Distribution of propeller/opening values at position 5 (panel a) and 6 (panel b).

The structural features that we observe in the bent minimized structures are similar to features that are observed in nucleosome crystal structures. To show this we calculated base-pair step and local base-pair structural parameters associated with crystal structures taken from the Protein Data Bank (pdb codes 1kx5, 3afa and 3lel).^44-46 The results of calculations for first 50 bp from the crystal structure with pdb code 3lel are presented in Figure 7. These structures have periodic minor groove narrowing although this periodicity is not exact. For example in Figure 7 it can be seen that the minor groove is narrower at positions 6,18,26,36,46 (i.e., the period can be 9-12 bp). We also observe that positions of the DNA sequence where the minor groove is narrower usually have a few A or T bases that have negative roll, propeller and opening.

Figure 7.

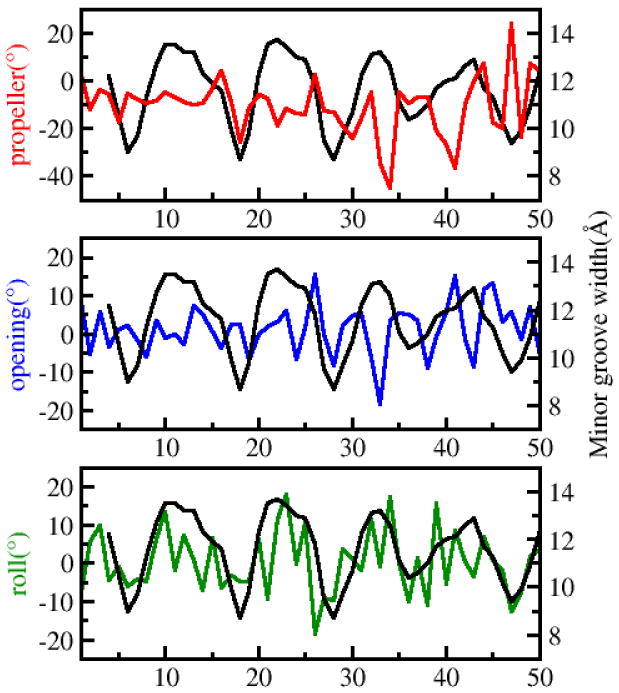
Minor groove and base-pair parameters for first 50 base-pairs from crystal structure with pdb code 3lel vs base pair number. Black curve is the minor groove width (in Angstroms), red curve shows the propeller coordinate (in degrees), blue curve is opening(in degrees), and green curve is roll (in degrees).

Minor groove width; Monte Carlo and molecular dynamics studies

The distribution of minor groove widths in all the sequences studied is presented in Fig. 8. This shows that for the structures with AA repeats the groove width is narrow only for positions close to the AA, while for the random structures, narrow widths are less likely (but do occur) and are randomly distributed.

Figure 8.

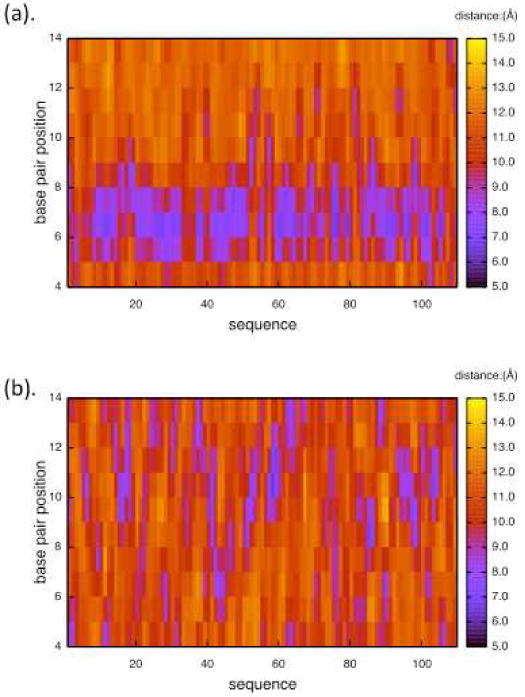
Distribution of minor groove widths for random sequences with no periodicity (bottom) and sequences with AA periodicity (top).

The average minor groove widths obtained in the current study are in general 1-2 Šnarrower than those found in nucleosome crystal structures. This could result from the molecular mechanics calculation in implicit solvent at 0K. To explain the differences, we carried out additional internal coordinate Monte-Carlo (MC) simulations using the same implicit solvent model in Jumna and we also performed fully atomistic molecular dynamics (MD) simulations using explicit solvent and ions at room temperature. In the explicit solvent simulations, we add harmonic restraints (25kcal/mol/ Ų) to the end base pairs to force the desired curvature.

The minimized structures are intrinsically stable at 0K. MC sampling in the internal coordinates of DNA^47-49 allows us to generate a structural ensemble around the minimized structure at room temperature, although the approach we used here is an approximate one that does not include for explicit backbone closure or the proper Jacobian corrections that arise from the use of curvilinear coordinates.⁴⁸ We chose one sequence to illustrate the temperature effect; however calculations not presented show that the results are generally applicable for all the sequences studied here. Average minor groove widths and associated fluctuations from the MC simulation for the sequence GCGGAACCCGGCGGAACC are plotted in Figure 9 (a). We see that the average groove widths are not significantly different from those in the 0K structure. This indicates that thermal fluctuations cannot solely explain the structural discrepancy between experiment and the Jumna calculation.

Figure 9.

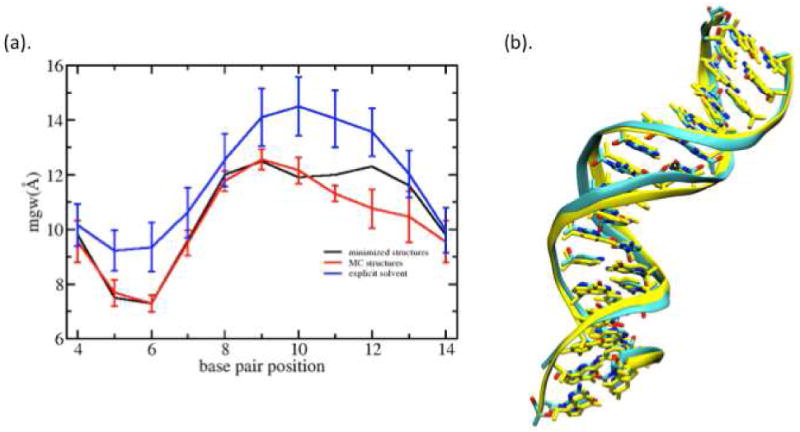
Sequence GCGGAACCCGGCGGAACC: (a) Minor groove widths from minimized structure, Monte-Carlo simulation and explicit solvent molecular dynamics simulation. (b) Comparison of minimized structure (CPK color) and 10ns MD trajectory average structure (yellow)

Another possible reason for the small minor groove width is the solvent model used in Jumna. The hydration of DNA cannot be treated explicitly in Jumna, so an implicit model was developed that might be unphysical for highly bent structures. To study this, the minor groove widths of a curved 18bp sequence were calculated using explicit all-atom solvent/ion simulations. These calculations were done using the same Amber force field, using the Jumna structure as input to the CHARMM program, and using a 1 ns equilibration period before the 10 ns production calculation. Further details are given in Supporting Information. The calculations show that the minor groove width is larger by 0.5-2 Å depending on the location along the sequence (Figure 9(a)). Thus the shift in minor groove width is systematic, with no direct connection to the location of the AA in the structure. These larger groove widths agree with experimental width values.

Note in Fig. 9(b) that the starting conformation (Jumna minimized structure) overlaps reasonably well with the trajectory average structure from the 10ns explicit solvent simulation including the base pair geometry. The same behavior was observed for 7 other sequences that we tested. These findings suggest that the solvent model in Jumna tends to produce too narrow a minor groove width but does not otherwise perturb the DNA structure. Thus except for the groove width, the qualitative structural features from Jumna are consistent with those from the more expensive and accurate MD method. This suggests that the preference for sequences with 10bp AA repeats to form stable nucleosomes and its physical interpretation in terms of the structural properties of AA steps should remain valid.

Conclusions

The results show that 10 bp AA repeats lead to DNA bending properties that are distinct from random DNA base-pair sequences, and which are consistent with observed nucleosome binding propensities. The minimum energy rotational register values span a smaller range for the periodic structures such that many minimized 10 bp segments can be pieced together to make the 147 bp nearly planar loop structure of the nucleosome. In addition, we find that periodic sequences have lower average deformation energies than random sequences, with the minor groove pointing towards the histone interior at the 5,6 position of each 10 bp segment. These results suggest that for DNA sequences with the 10 bp repeats, there is a natural driving force for nucleosome formation that arises from the intrinsic shape of the bending potential energy surface together with the narrow range of rotational register values that minimizes energies. In addition, the most important deformations of the AA base pairs in the 5,6 position involve negative values of the roll, propeller and opening coordinates that are distinct from what is found for random sequences.

In general, the Jumna model is able to provide useful insight to the sequence dependent bending properties of DNA but it has important limitations that need to be tested. We have performed some of these tests here by introducing Monte Carlo capabilities within Jumna, and by comparing with selected results from a fully atomistic model that included explicit ions and solvent. More detailed studies are needed to fully model nucleosome occupancies, including the dependence of mechanical properties on length of the DNA. It will also be important to perform a careful analysis of the thermodynamics of bending for AA repeats, and to including for explicit DNA-protein and DNA-DNA interactions.