Two-dimensional near-ultraviolet spectroscopy of aromatic residues in amyloid fibrils: a first principles study

Abstract

We report a first principles study of two dimensional electronic spectroscopy of aromatic side chain transitions in the 32-residue β-amyloid (Aβ_9–40) fibrils in the near ultraviolet (250–300 nm). An efficient exciton Hamiltonian with electrostatic fluctuations (EHEF) algorithm is used to compute the electronic excitations in the presence of environmental fluctuations. The through-space inter- and intra-molecular interactions are calculated with high level quantum mechanics (QM) approaches, and interfaced with molecular mechanics (MM) simulations. Distinct two dimensional near ultraviolet (2DNUV) spectroscopic signatures are identified for different aromatic transitions, and the couplings between them. 2DNUV signals associated with the transition couplings are shown to be very sensitive to the change of residue-residue interactions induced by residue mutations. Our simulations suggest that 2DNUV spectra could provide a useful local probe for the structure and kinetics of fibrils.

1. Introduction

Many important biological functions of proteins depend crucially on their fluctuating structures.^1,2 Optical spectroscopy is a widely used tool for identifying structural details and monitoring the transformations of biological complexes.^3–5 Traditional one-dimensional (1D) Ultraviolet (UV) techniques such as Linear absorption (LA) and circular dichroism (CD) are routinely used for probing proteins. Proteins are made of amino acid side chains connected by the peptide backbone. The nπ* and ππ* transitions of the peptide backbone in the far-ultraviolet (FUV) (190–250 nm) are used for estimating protein secondary structure content.^6,7 Other important transitions correspond to the aromatic side chains, which absorb in the near-ultraviolet (NUV) (> 250 nm) regime. These are easier to characterize since aromatic amino acids are relatively rare: Only three amino acids contain aromatic side chains: phenylalanine (Phe), tyrosine (Tyr), and tryptophan (Trp). FUV spectroscopy gives a global picture of secondary structure, while NUV spectroscopy provides a more detailed local probe.⁸

Multidimensional spectroscopy uses sequences of laser pulses to excite the vibrational or electronic degrees of freedom and watch for correlated events which take place during two (or more) controlled time intervals. The resulting correlation plots provide a multidimensional view of the relevant molecular motions, structures, and dynamical events.^9–13 The development of intense, coherent, high repetition rate ultrafast sources in the UV^3,14–17 should allow to extend multidimensional spectroscopy into the NUV.^18,19 Two dimensional UV (2DUV) spectroscopy has a great potential for protein structure refinement,²⁰ and 2DNUV could offer an additional powerful high resolution local observation window.

Accurate microscopic simulation algorithms are essential for designing and exploring the possible applications of 2DUV techniques. The UV spectra are strongly affected by environmental fluctuations of the backbone, side chains and the solvent. Direct Ab initio simulations of UV signals for large proteins with hundreds of chromophores are too expensive. The efficient map method widely used in two dimensional IR (2DIR) simulations^9,21,22 is not applicable to 2DUV. Since vibrational chromophores are highly localized, the IR transition can be modeled as point dipoles, and the electrostatic fluctuations may be simulated by sampling the electric fields at a few points. UV simulations are much more challenging. The transition charge densities are delocalized and proper description of the electrostatic interactions involves the computation of extended charge space distributions. Motions of proteins and the surrounding water lead to fluctuations of the electrostatic environment, which affect the intra- and inter-molecular interactions, excitation energies and the local Hamiltonian. A proper description environmental fluctuations which is crucial for the prediction of spectra requires thousands of MD snapshots.⁹ Since repeated first principles calculations are prohibitively expensive, it is necessary to adopt a QM/MM approach.

We have developed the EHEF (exciton Hamiltonian with electrostatic fluctuations) algorithm for first principles simulations of 2DUV spectra of proteins. In this algorithm, proteins are divided into fragments of amino acids and peptide bond units. Electronic excitations of isolated aromatic chromophores are treated at a high Ab initio level, the complete active space self-consistent field (CASSCF).²³ The surrounding protein amino acids and the solvent are treated by density function theory (DFT).²⁴ The inter- and intra-molecular interactions are calculated using a grid technique and effective charges fitted from the electrostatic potential. EHEF also provides a convenient interface for quantum mechanics (QM) and molecular mechanics (MM) calculations. The utilization of atomic frames in EHEF makes it possible to compute Coulomb interactions in all molecular dynamic (MD) snapshots, taking into account of environmental fluctuations at the QM level, yet avoiding repeated QM calculations.

Here we employ this protocol previously applied in the FUV region⁷ to simulate the 2DNUV spectra of the 32-residue β-amyloid (Aβ_9–40) fibril. Misfolded proteins which form amyloid fibrils are associated with more than 20 neurodegenerative diseases,^25,26 and their kinetic pathways and toxicity are under active study.^27,28 In the case of Alzheimer’s disease, fibrils are composed of β-amyloid (Aβ) peptides ranging from 39 to 42 residues, rich in β-sheet secondary structure. Our simulations demonstrate that 2DNUV techniques should provide a novel tool for visualizing molecular interactions, identifying the local structures, and monitoring transformations in proteins.

2. The simulation protocol

2.1 The exciton Hamiltonian

The NUV transitions will be modeled using the Frenkel exciton Hamiltonian,^29–32 which is constructed as described in ref. 7:

$$\hat{H}={\displaystyle \sum _{\mathit{\text{me}}}}{\epsilon }_{\mathit{\text{me}}}{\hat{B}}_{\mathit{\text{me}}}^{†}{\hat{B}}_{\mathit{\text{me}}}+{\displaystyle \sum _{\mathit{\text{me}},\mathit{\text{nf}}}^{m\ne n}}{J}_{\mathit{\text{me}},\mathit{\text{nf}}}{\hat{B}}_{\mathit{\text{me}}}^{†}{\hat{B}}_{\mathit{\text{nf}}}$$ (1)

where me is the e electronic transition on the m-th aromatic chromophore. ${\widehat{B}}_{\mathit{\text{me}}}^{†}$ is the creation Pauli operator which promotes the chromophore m into the excited state e, and B̂_me is the corresponding annihilation operator.

The excited state energy ε_me can be calculated as the summation of the excited energy of the isolated chromophore and its interactions with local electrostatic fields:

$${\epsilon }_{\mathit{\text{me}}}={\epsilon }_{\mathit{\text{me}},0}+{\displaystyle \sum _k^{k\ne m}}\frac{1}{4\pi \epsilon }\times {\displaystyle \int }{\displaystyle \int }\mathrm{d}{\mathbf{r}}_m\mathrm{d}{\mathbf{r}}_k\frac{[{\rho }_m^{\mathit{\text{ee}}}({\mathbf{r}}_m)-{\rho }_m^{\mathit{\text{gg}}}({\mathbf{r}}_m)]{\rho }_k^{\mathit{\text{gg}}}({\mathbf{r}}_k)}{|{\mathbf{r}}_m-{\mathbf{r}}_k|}$$ (2)

in which the first term ε_me,0 is the excited state energy of the isolated chromophore, and the second term describes the inter- and intra-molecular electrostatic corrections. Here k runs over all the atomic or molecular sites surrounding the excited chromophore, r_m and r_k are the positions coordinates, and ${\rho }_m^{\mathit{\text{gg}}}\text{and}{\rho }_k^{\mathit{\text{gg}}}({\rho }_m^{\mathit{\text{ee}}})$ represent the ground (excited) state charge density. ε is the dielectric constant. We have used the vacuum dielectric constant (ε = 1). The variation of the dielectric constant on the molecular length scale was not taken into account in our simulations. This will be studied in the future.

The resonant coupling between singly-excited states me and nf is given by $\langle 0|{\widehat{B}}_{\mathit{\text{me}}}\widehat{H}{\widehat{B}}_{\mathit{\text{nf}}}^{†}|0\rangle =J_{\mathit{\text{me}},\mathit{\text{nf}}}\text{where}|0\rangle$ is the ground state.

$$J_{\mathit{\text{me}},\mathit{\text{nf}}}=\frac{1}{4\pi \epsilon }{\displaystyle \int }{\displaystyle \int }\mathrm{d}{\mathbf{r}}_m\mathrm{d}{\mathbf{r}}_n\frac{{\rho }_{\mathit{\text{me}}}^{\mathit{\text{eg}}}({\mathbf{r}}_m){\rho }_{\mathit{\text{nf}}}^{\mathit{\text{gf}}}({\mathbf{r}}_n)}{|{\mathbf{r}}_m-{\mathbf{r}}_n|}$$ (3)

here ${\rho }_{\mathit{\text{me}}}^{\mathit{\text{eg}}}({\mathbf{r}}_n)\text{and}{\rho }_{\mathit{\text{nf}}}^{\mathit{\text{gf}}}({\mathbf{r}}_n)$ are the transition charge densities.

ε_me and J_me,nf are calculated using our EHEF algorithm at a high Ab initio level, as described below. The electronic excitation Hamiltonian is then constructed with the computed parameters using the matrix method as implemented in the DichroCalc program.^33,34

2.2 Electronic excitations of isolated aromatic chromophores

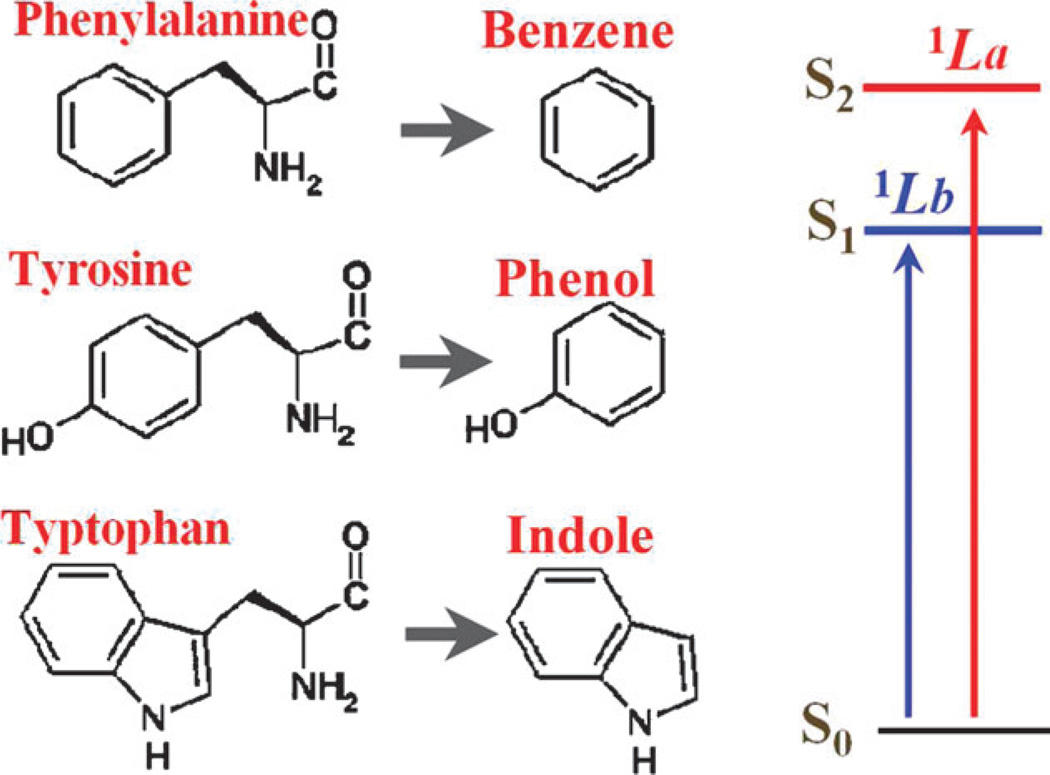
The NUV chromophores in the three natural aromatic amino acids, Phe, Tyr, and Trp, are benzene, phenol, and indole, respectively, as shown in Fig. 1. Each of these chromophores has four valence electronic excitations in the > 250 nm region, namely ¹L_b, ¹L_a, ¹B_a, ¹B_b in Platt’s notation.³⁵ The lower states ¹L_b and ¹L_a are responsible for the main NUV peaks. The CASSCF method²³ has been successfully employed for electronic excitations of aromatic chromophores.³⁶ we have calculated the electronic sates of isolated benzene, phenol and indole at the self-consistent reaction field (CASSCF/SCRF) and multi-configurational second-order perturbation theory (CASPT2)³⁷ level using the MOLCAS³⁸ package. These result in the excited state energies ε_me,0 listed in Table 1, as well as the corresponding electronic densities $({\rho }_m^{\mathit{\text{ee}}}\text{and}{\rho }_m^{\mathit{\text{gg}}})$ and transition densities ${\rho }_m^{\mathit{\text{ge}}}$. g is the ground state and e runs over the ¹L_b, ¹L_a, ¹B_a, ¹B_b states.

Fig. 1.

The three aromatic amino acids in proteins, phenylalanine (Phe), tyrosine (Tyr), and tryptophan (Trp), contain the chromophores benzene, phenol, and indole, respectively. The ¹L_b and ¹L_a excitations dominate the NUV signals in the wavelength region above 250 nm.

Table 1.

Computed excited state energies ε_me,0 for the isolated benzene, phenol and indole

εme,0/cm−1	1Lb	1La	1Ba	1Bb
Benzene	38 005	47 953	52 324	52 531
Phenol	36 492	46 205	50 930	51 968
Indole	35 396	38 053	51 030	48 955

2.3 The EHEF (exciton Hamiltonian with electrostatic fluctuations) algorithm

As pointed out by Kurapkat et al., interactions of chromophores with local electrostatic fields coming from the rest of the protein and the surrounding solvent shift the excited state energies.³⁹ The CASSCF calculations of isolated benzene, phenol, and indole must therefore be corrected to include these effects. A chromophore interacts with surroundings through long range Coulombic interactions, which results in the inter- and intra-molecular electrostatic corrections in eqn (2).

The proteins are divided into fragments of amino acids and peptide bond units. Their ground states are obtained from the first principles calculations. The peptide units of the protein backbone are modeled by CASSCF/SCRF and CASPT2 calculations of an isolated N-methylacetamide (NMA) molecule. The gas-phase electronic structures and charge densities of amino acids and water molecules were obtained with the hybrid DFT B3LYP/6-311 + + G** method implemented in the GAUSSIAN03 package.⁴⁰

The direct implementation of eqn (2) and (3) is too expensive for the present applications. Since the chromophores interact with many surrounding atoms or molecules, evaluating the factor $[{\rho }_m^{\mathit{\text{ee}}}({\mathbf{r}}_m)-{\rho }_m^{\mathit{\text{gg}}}({\mathbf{r}}_m)]{\rho }_k^{\mathit{\text{gg}}}({\mathbf{r}}_k)\text{or}{\rho }_{\mathit{\text{me}}}^{\mathit{\text{eg}}}({\mathbf{r}}_m){\rho }_{\mathit{\text{nf}}}^{\mathit{\text{gf}}}({\mathbf{r}}_n)$ will require a huge number of integrations of four basis wavefunctions over space. This is one of the most serious bottlenecks in standard quantum chemistry calculations. Some empirical methods have been developed in order to reduce computational cost: (1) the dipole approximation,^41,42 which describes the environmental influences as the interaction between electric dipole of the chromophore and the electric field induced by surroundings. This has a limited accuracy. (2) the map method,^9,21,22 which uses empirically fitted parameters to calculate the excited state energy as a function of electric fields at some selected positions or some special geometric variables. It has a limited predictive power because of the fitting procedure.⁷

An alternative approach, free from empirical parameters, is to calculate charge densities by coarse-graining the electronic wavefunction in space. Krueger et al.⁴³ had developed the transition density cube (TDC) method, in which 3-D space is divided into many small volume elements. Intra- and inter-molecular interactions were calculated directly from the Coulomb interactions between charges of the cubes in each molecule. The excited state energy and resonant coupling are then given by

$${\epsilon }_{\mathit{\text{me}}}={\epsilon }_{\mathit{\text{me}},0}+{\displaystyle \sum _{m_{\mu }}}{\displaystyle \sum _{k_{\nu }}^{k\ne m}}\frac{1}{4\pi \epsilon }\frac{(Q_{m_{\mu }}^{\mathit{\text{ee}}}-Q_{m_{\mu }}^{\mathit{\text{gg}}})Q_{k_{\nu }}^{\mathit{\text{gg}}}}{|{\mathbf{r}}_{m_{\mu }}-{\mathbf{r}}_{k_{\nu }}|}$$ (4)

and

$$J_{\mathit{\text{me}},\mathit{\text{nf}}}={\displaystyle \sum _{m_{\mu }}}{\displaystyle \sum _{n_{\nu }}^{n\ne m}}\frac{1}{4\pi \epsilon }\frac{Q_{m_{\mu }}^{\mathit{\text{eg}}}{Q}_{n_{\nu }}^{\mathit{\text{gf}}}}{|{\mathbf{r}}_{m_{\mu }}-{\mathbf{r}}_{n_{\nu }}|}$$ (5)

where the indices μ(ν) run over the cubes with permanent or transition charge Q_mμ (Q_kν or Q_nν) at position r_mμ (r_kν or r_nν). This grid method is accurate, but very expensive, since it requires a large number of cubes to maintain the precision (normally ≈ 500 000 cubes for a system with ≈ 50 atoms). Madjet et al.⁴² have developed a more efficient way for taking the charge distribution into account. In their TrEsp (transition charge from electrostatic potential) code, electrostatic potentials on sample points are computed at the quantum chemistry level. Partial charges are then assigned to atomic positions by fitting to potentials. TrEsp has been successfully employed in the study of photosynthetic complexes. However, charges distributed only at the atomic positions cannot represent the electronic cloud when the molecular orbitals are delocalized.

EHEF⁷ offers a good balance of accuracy and cost by combining the advantages of the TDC and TrEsp methods. The algorithm consists of five steps:

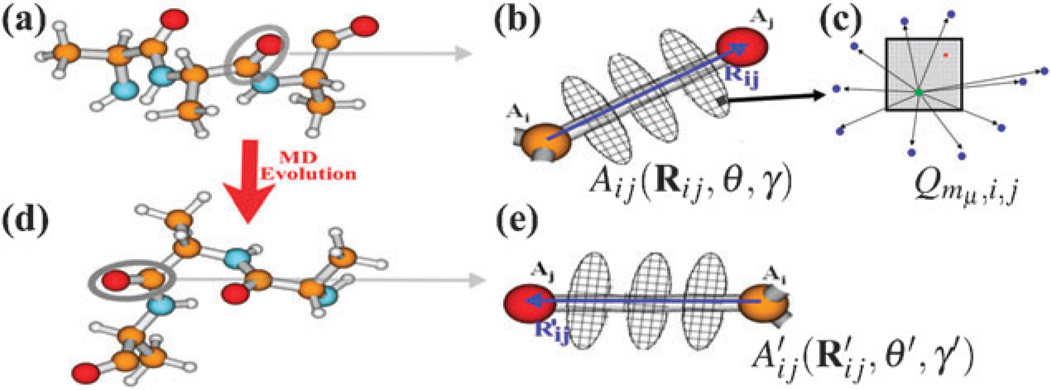
1. We define an atomic frame A_ij(R_ij,θ,γ) for each pair of atoms A_i and A_j in the molecule, as shown in Fig. 2(a) and (b). Here R_ij = r_Ai − r_Aj is the atom-atom vector, and the angle θ and dihedral angle γ are relative to the whole molecule.

2. For each atomic frame, we construct a set of (~ ten) planar disks perpendicular to R_ij, whose centers lie on R_ij, located in the range ±1.5|R_ij|. Each disk is divided into a limited number of (typically 20 to 50) grids, as shown in Fig. 2(b). The grids are stored with internal coordinates relative to the atomic frame.

3. Each grid in the atomic frame is divided into a large number of (typically 1000) small sub-grids, as shown in Fig. 2(c). Using standard quantum chemistry methods, we compute the electronic charge by integrating charge density (both permanent and transition densities) over space.⁷ q_mμ,i,j represents the transition charges of sub-grid μ in the A_ij atomic frame of the mth molecule, as shown in Fig. 2.

4. Random sample points are taken around each gird of the atomic frame in Fig. 2(c), and electrostatic potentials induced by the charges of small sub-grids are calculated. With the TrEsp technique,^7,42 the sample electrostatic potentials are used to fit out a fictitious charge Q_mμ,i,j for the grid μ in the A_ij atomic frame of the mth molecule.

5. The grid charges are finally used to compute the Coulomb interactions and electric dipoles. Eqn (4) and (5) are used to calculate the corrections of excitation energies and resonant couplings, respectively.

Fig. 2.

(a) Protein fragment with standard geometry. (b) The atomic frame A_ij(R_ij,θ,γ). (c) The grid in the atomic frame is divided into a large number of small sub-grids. A fictitious point charge Q_mμ,i,j is generated by fitting the sample electrostatic potentials induced by charges of sub-grids. (d) The fragment in a new MD snapshot. (e) Update the atomic frame to $A_{\mathit{\text{ij}}}^{\prime }(\mathbf{R}{\prime }_{\mathit{\text{ij}}},\theta \prime ,\gamma \prime )$.

Most localized charges are included as atomic partial charges. Delocalized charges vary slowly in space, and only require a sparse grid (typically ≈ 10 000 cubes for a system of 50 atoms), which is much smaller than that in the TDC method. The fictitious grid charges are fitted from the electrostatic potentials generated by a large number of sub-grids (normally ≈ 10⁷ cubes for a system with ≈ 50 atoms), which retains the same accuracy as the TDC method. Since the grid spacing is much smaller than interatomic distances, the computed excited state energies are as accurate as the full integration of eqn (2).

The utilization of the atomic frame in EHEF provides a convenient interface for QM and MM calculations. Proteins are not rigid and the interatomic distances and angles vary during the MD evolutions. We had introduced the following key approximation: we assume that the charge distributions in the atomic frame for each pair of atoms do not vary significantly during MM simulations, and can be held fixed. First principles (QM) calculations are carried out only on a limited number of standard geometries. As long as the chemical structure does not vary strongly, the charge grids computed for atomic frames of the standard geometries can be used for all MD snapshots. As shown in Fig. 2(d) and (e), the atomic frame A_ij(R_ij,θ,γ) of a standard geometry is updated to $A_{\mathit{\text{ij}}}^{\prime }(\mathbf{R}{\prime }_{\mathit{\text{ij}}},\theta \prime ,\gamma \prime )$ for a new MD snapshot. Since the charge grids of the standard geometry are stored with internal coordinates relative to the atomic frame, the update of the atomic frame automatically generates a new set of charge grids, which accurately reflect the electronic properties of the new MD snapshot. Using the charge distribution, we have calculated the interactions in eqn (4), and updated the excitation energies for each MD snapshot. Environmental fluctuations are taken into account at the QM level, with very few QM calculations.

2.4 2D signals

The Frenkel Hamiltonian matrix was diagonalized using the SPECTRON code.⁴⁴ 2D photon echo signals were calculated using the protocol described in ref. 20 and 45. We assume four short Gaussian laser pulses with central frequency 37 000 cm⁻¹ (270 nm) and full width at half-maximum (FWHM) 3754 cm⁻¹ (corresponds to a Fourier limited pulse of 2.8 fs), which span the absorption band in the NUV region. We have used these broadband pulses in order to reveal most detailed information. Narrower pulses will miss some of the features. These could be recovered using two color measurements. The four pulses in chronological order have wavevectors k₁, k₂, k₃, and k₄, with k₄ = −k₁ + k₂ + k₃. The absorption change of the k₄ beam is recorded as a function of the three consecutive delay times: t₁, t₂, and t₃. We have used the nonlinear exciton equations (NEE) approach. The scattering matrix of exciton quasi-particles is constructed as described in ref. 44. Calculations were performed for both the ordinary non chiral (xxxx) and chirality-induced (xxxy) polarization configurations. In the later, the k₁ pulse is polarized along the y axis and the other three pulses are x polarized. 2D signals are calculated by two-dimensional Fourier transform t₁ → Ω₁ and t₃ → Ω₃ with t₂ set to zero.

2D spectra will be plotted using non-linear scale which reveals both the strong and weak signals,

$$\text{arcsinh}(c\mathbf{S})=\text{ln}(c\mathbf{S}+\sqrt{1+c^2{\mathbf{S}}^2}),$$ (6)

The signal S is multiplied by a scale factor c to make it close to 1, so that weak amplitudes are amplified: for cS < 1 the scale is linear, arcsinh(cS) ≈ cS, and for larger cS it becomes logarithmic, arcsinh(cS) ≈ (S|S|⁻¹)ln(2|cS|).

2.5 Computation flow chart

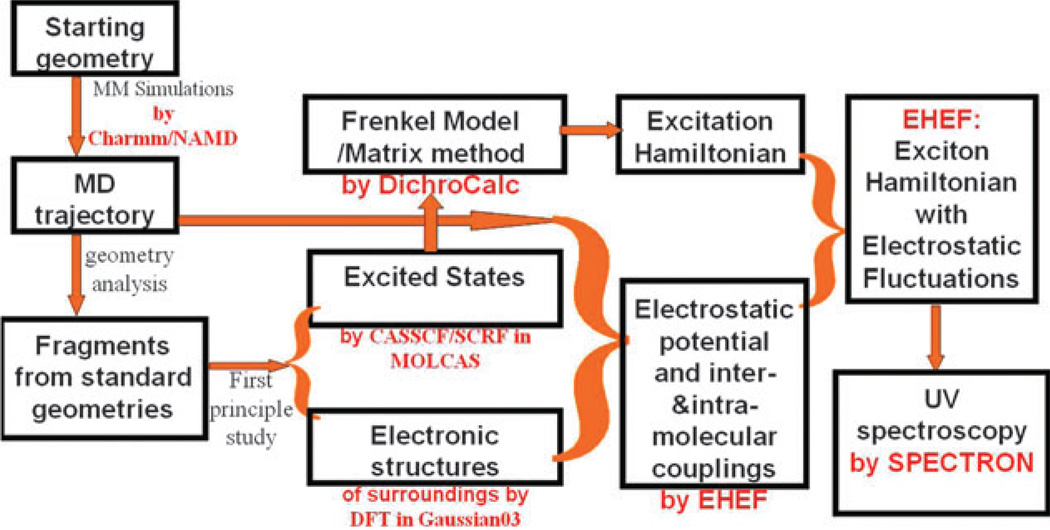
The computation flow chart is summarized in Fig. 3. Initial protein geometries are taken from experiments or the protein data bank. MM simulations of proteins in water are carried out with the CHARMM22 force field⁴⁶ using the software package NAMD.⁴⁷ Geometric variations along the MD trajectory were examined, and a set of standard geometries are selected. QM calculations are performed on the fragments (amino acids, peptide bond units, and water) at standard geometries, to yield the necessary information about ground and excited states. The EHEF algorithm is used to calculate the electrostatic potential, inter- and intra-molecular interactions. Based on the Frenkel model, the matrix method in DichroCalc program^33,34 uses the parameters from EHEF to construct effective exciton Hamiltonian with electrostatic fluctuations. UV spectra are finally simulated using the SPECTRON code.⁴⁴

Fig. 3.

Computation flow chart of 2DNUV simulations.

3. 2DNUV Spectra of β-amyloid (Aβ_9–40) fibrils

3.1 β-Amyloid (Aβ_9–40) fibrils

Tycko and co-workers had used NMR constraints to construct a detailed molecular model of the 32-residue β-amyloid (Aβ_9–40),⁴⁸ which is characterized by cross-β structural motifs. Fig. 4(a) shows the structure of a single Aβ_9–40 peptide, an asymmetric “U” structure composed of two β-strands as N-terminal (red) and C-terminal (blue), and a turn (green) which links the strands. Aβ_9–40 has three aromatic side chains: Tyr10, Phe19, Phe20, all on the N-terminal. Mutations of the native Aβ_9–40 peptide were obtained with the VMD tools.⁴⁹

Fig. 4.

(a) Aβ_1–40 sequence and the structure of a single Aβ_9–40 peptide, with N-terminal strand (red), C-terminal strand (blue), and turn region (green). It has three aromatic side chains, Tyr10, Phe19, Phe20, all located on the N-terminal. (b) Model structure of amyloid fibril made of twelve Aβ_9–40 molecules. Red and blue indicate two parallel β-sheets. (c) The model periodic fibril structure made of nine peptides used in the UV spectroscopy simulations.

MM simulations were carried out on the STAG(+2) structure composed of twelve native or mutated Aβ_9–40 monomers, as shown in Fig. 4(b). The two types of β-strands form separate, parallel β-sheets in amyloid fibrils. We ran a 1 fs time-step 200 ps simulation of the amyloid fibrils in vacuum to obtain an initial periodic structure. Cubic periodic boundary conditions were used. Long-range electrostatic interactions were computed using the particle-mesh Ewald (PME)⁵⁰ approach and a real space 12 Å cutoff for nonbonded interactions. Langevin dynamics with a 1 ps damping coefficient were used to achieve a constant temperature. The amyloid fibrils were then inserted in a TIP3P water box⁵¹ containing 9236 water molecules, which were not allowed to penetrate inside the fibrils. 36 chloride ions were added to neutralize the box. Using a NosÉ-Hoover Langevin piston⁵² with a decay period of 200 fs and a 100 fs damping time. The system was equilibrated at 1 atm constant pressure for 500 ps. After equilibration, we performed 5 ns NVT simulations at the room temperature.

Ensembles of MD geometric snapshots were harvested for the Ab initio studies. The aromatic side chains are located at the N-terminal (red in Fig. 4(b)), which is on the outer interface of the fibrils. We therefore focused on the upper stack of the fibrils, and neglected the influences from the bottom peptides. Since fibrils are composed of a large number of periodically arrayed peptides, we have only harvested the central Aβ_9–40 peptide of the upper stack from the MD ensembles. This peptide was repeated to build a set of fibrils with nine periodically arrayed peptides, as shown in Fig. 4(c). 1D (2D) UV simulations used 1000 (500) MD snapshots of this nine-peptide amyloid fibril. Altogether our simulations included 27 aromatic chromophores (nine peptides, each containing one Tyr and two Phe).

3.2 1D and 2DNUV spectra of the native fibril

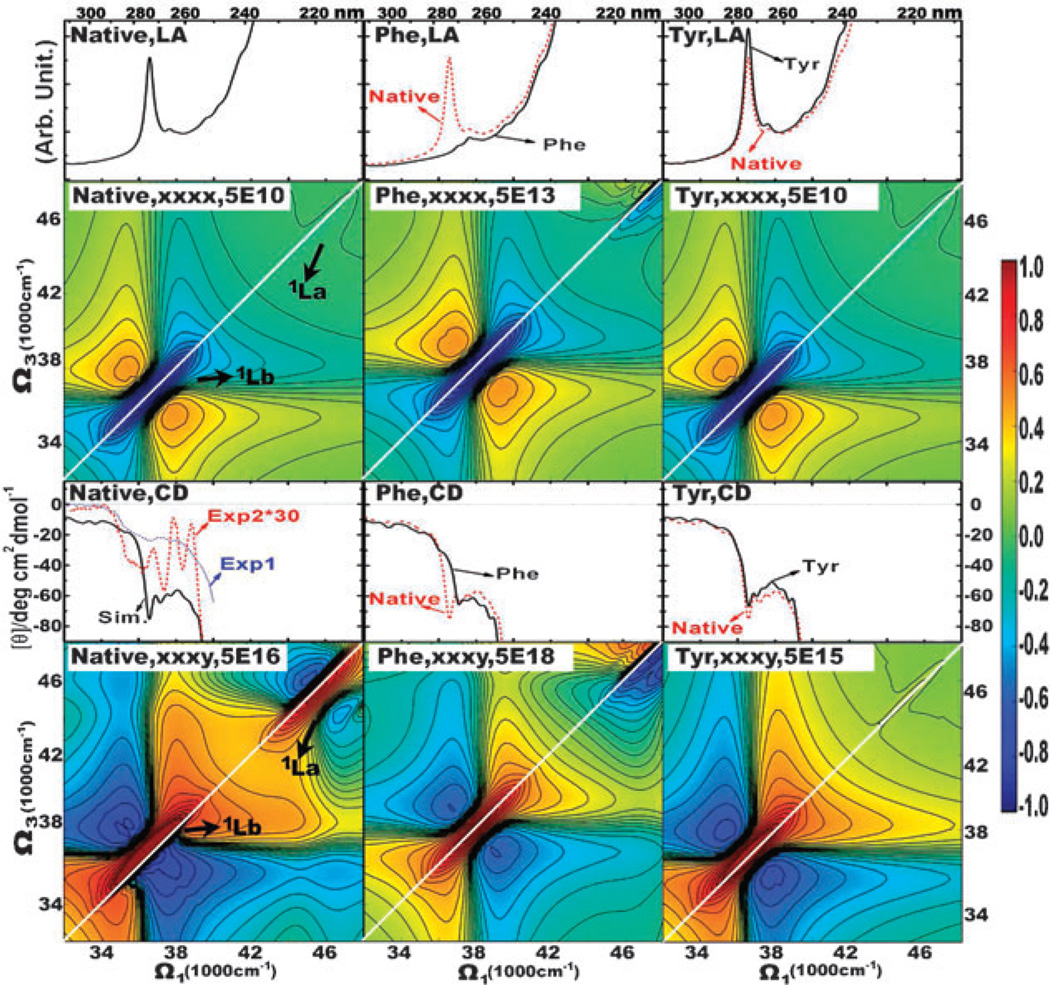
The simulated 1D spectra (LA and CD) of the native Aβ_9–40 fibril are displayed in Fig. 5. The NUV LA spectrum is dominated by a strong absorption peak at around 36 500 cm⁻¹ (274 nm), which is ascribed to the ¹L_b transition of the Tyr10 side chains. The simulated NUV CD spectrum is in good agreement with experiment. The absolute magnitude of simulated CD is close to that of the latest experimental CD spectrum (exp1).⁵³ The negative feature observed in exp1 from 35 000 cm⁻¹ (286 nm) to 40 000 cm⁻¹ (250 nm) is reproduced by the simulations. The CD peaks observed in exp2⁵⁴ are sharper than those in exp1 and in our simulated CD. Nevertheless, the primary negative CD valleys in exp2 at 36 800 cm⁻¹ (272 nm), 37 900 cm⁻¹ (264 nm), and 38 800 cm⁻¹ (258 nm) are well reproduced by the simulated ones at 36 900 cm⁻¹ (271 nm), 38 100 cm⁻¹ (262 nm), and 38 800 cm⁻¹ (258 nm), with less than 2 nm shifts.

Fig. 5.

Left column: spectra of the native Aβ_9–40 fibril. From top to bottom: LA, non-chiral (xxxx) 2DNUV signal, CD, chiral (xxxy) 2DNUV signal. 1D and 2D signals are averaged over 1000 and 500 MD snapshots, respectively. Blue dotted and red dashed lines in the CD of the fibrils are experimental spectra exp1⁵³ and exp2 (multiplied by 30),⁵⁴ respectively. 2DNUV signals are displayed with a nonlinear scale (eqn (6)), the scale factor c is given on the top, red signals are positive and blue signals are negative, and a white diagonal line is drawn to reveal the symmetry of signals. 2DNUV scale bar is plotted at the right edge. Middle and right columns: same as the left column but only for the Phe and Tyr residues, respectively.

The simulated 2DNUV spectra are displayed in the left column of Fig. 5. The non-chiral xxxx spectrum is symmetric with respect to the white diagonal line. Since the laser pulses are centered at 37 000 cm⁻¹, the xxxx signals are dominated by the ¹L_b transitions, which are displayed as a negative (blue) diagonal peak centered at 37 000 cm⁻¹ accompanied by two positive (red) side-bands. A relatively weak negative (blue) ¹L_a diagonal peak appears at around 46 500 cm⁻¹.

The chirality-induced xxxy signal shows a non-symmetric pattern shifted away from the diagonal line. The ¹L_b and ¹L_a transitions give the positive (red) diagonal peak with two negative (blue) side-bands centered at 37 000 cm⁻¹ and 46 500 cm⁻¹, respectively. The negative side-band of ¹L_b in the lower (upper) triangle region consists of one (two) negative peaks. That ¹L_b side-band in the lower triangle region is very strong and it pushes the positive diagonal peak away from the diagonal line. For the ¹L_a signals, the strong side-band in the upper triangle region shifts the diagonal peak away from the diagonal line. The two crosspeaks at Ω₁ = 37000 cm⁻¹, Ω₃ = 46 500 cm⁻¹ and Ω₁ = 46 500 cm⁻¹, Ω₃ = 37000 cm⁻¹, are spectroscopic signatures of couplings between the ¹L_b and ¹L_a transitions.

Using our simulations, we can separate the contributions of different aromatic chromophores to the 2DNUV signals and thereby examine the signatures of couplings between chromophores. We have constructed an exciton Hamiltonian which contains transitions only from the Phe side chains (Phe19 and Phe20 in the Aβ_9–40 peptide), or the Tyr side chains (Tyr10 in the Aβ_9–40 peptide). The simulated LA, 2DNUV xxxx, CD and 2DNUV xxxy spectra of the Phe (Tyr) transitions are displayed in the middle (right) column in Fig. 5. These spectra are different from those predicted by the full Hamiltonian (left column). Compared to the full LA and CD (1D) spectra, the Phe LA and CD spectra miss the strong signals at around 36 500 cm⁻¹ (274 nm) and keep the signals from 37 000 cm⁻¹ (270 nm) to 40 000 cm⁻¹ (250 nm). Correspondingly, the Tyr LA and CD (1D) spectra show weaker signals from 37 000 cm⁻¹ (270 nm) to 40 000 cm⁻¹ (250 nm). The 2DNUV spectra also show prominent features associated with different transitions. Upon the neglect of Tyr transitions, the dominant ¹L_b signal in the Phe 2DNUV xxxx and xxxy spectra blue-shifts for 1500 cm⁻¹. We have used the scale factor c in eqn (6) to normalize the strongest 2D signals to be 1. The scale factor is listed on the top of each 2DNUV spectrum. The scale factors show that the Phe 2DNUV ¹L_b xxxx and xxxy diagonal peaks are about 1000 and 100 times weaker than the full-transitions-induced ones, respectively. On the other hand, the Tyr ¹L_b xxxy signals become 10 times stronger. These suggest that the couplings between Phe and Tyr transitions suppress the Tyr transitions in the fibrils. Both the Phe and Tyr 2DNUV xxxy spectra are symmetric around the white diagonal line. The asymmetric pattern in the full spectrum thus reflects the strong couplings between Phe and Tyr transitions.

3.3 1D and 2DNUV spectra of mutated fibrils

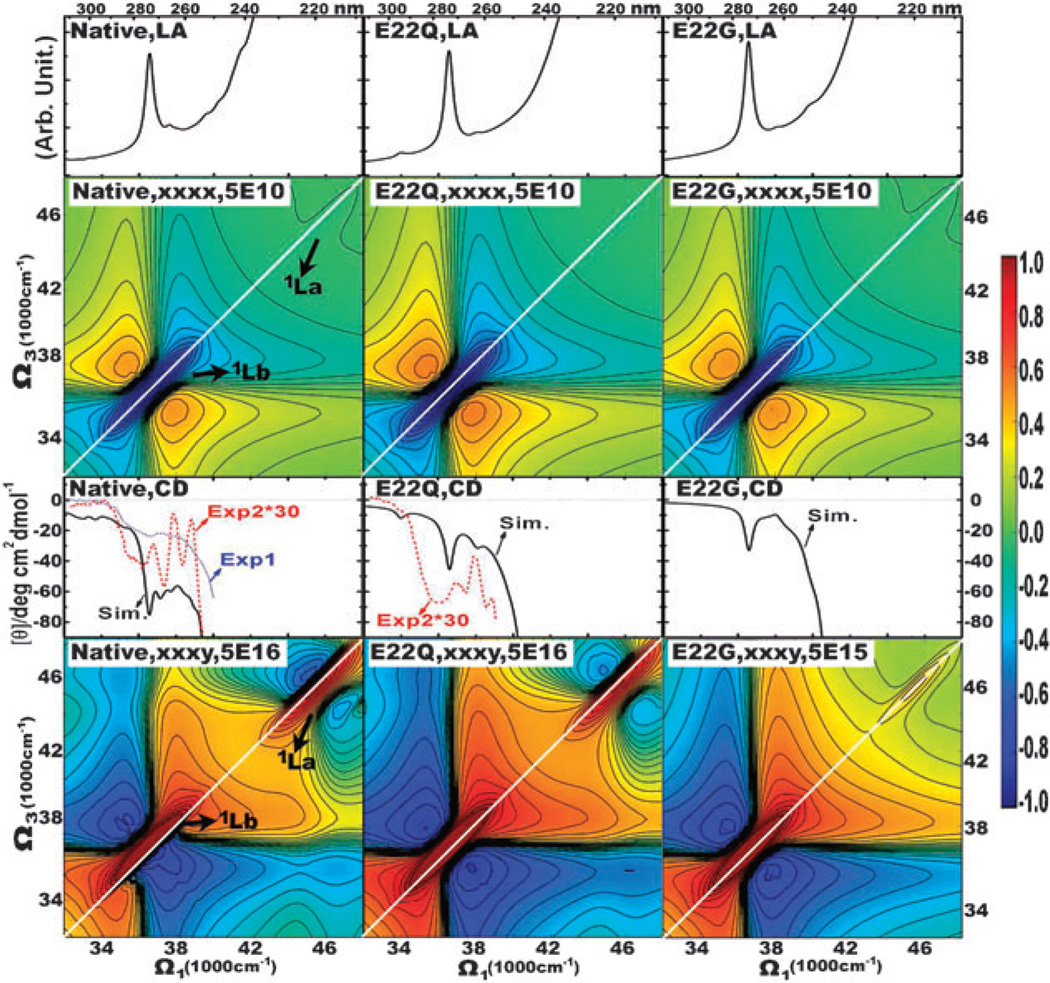
The mutated E22G β-amyloid fibril has been extensively studied by Sian et al.⁵⁴ The mutated E22Q Aβ_9–40 fibrils was obtained by changing the native Glutamic (E) at residue 22 (E22) to Glutamine (Q) in all peptides. It was found to change conformation and fibrillize more rapidly and produce shorter and stubbier fibrils than the native form. In the middle column of Fig. 6, we display the simulated spectra. Good agreement is seen with the experimental CD (exp2)⁵⁴ of the E22Q fibril. The simulated CD spectrum shows two negative valleys at 37 200 cm⁻¹ (269 nm) and 38 400 cm⁻¹ (260 nm) corresponding to those at 37 000 cm⁻¹ (270 nm) and 38 000 cm⁻¹ (263 nm) in exp2. The native and E22Q fibrils have virtually identical LA spectra. But the chirality-induced CD spectra show clear differences. With the mutations from the native fibril to E22Q, the negative CD signals around 240–280 nm become much weaker, and some fine spectral features disappear.

Fig. 6.

Same as Fig. 5 but for the mutated E22Q (middle column) and E22G (right column). The spectra of the native fibril are repeated in the left column for comparison.

These 1DUV spectra are highly congested, and differences due to local mutations are not clearly resolved. 2D photon echo signals depend on both singly and doubly excited electronic states, and thus contain richer spectral features associated with the geometric and electronic structures. In Fig. 6 we compare the 2DNUV spectra of the native and mutated E22Q fibrils. The non-chiral xxxx spectra are similar for the native and E22Q fibrils. The chirality-induced xxxy signals, in contrast, show a sensitivity to the fibril mutations. This is illustrated by the simulated spectra of the native and E22Q fibril shown in the bottom row. In the E22Q fibril, the ¹L_b xxxy signal at around 37 000 cm⁻¹ is symmetric, with one peak locating at both side-bands of the dominant diagonal peak. While in the native fibril, the spectrum is non-symmetric, and the numbers of negative peaks in both side-bands of the dominant diagonal peak are different. As discussed above, the non-symmetric spectral pattern in the native fibril is resulted from the couplings between chromophores. Therefore, we believe that the E22Q mutation has affected the residue-residue interactions in the native fibril. Correspondingly, we observed weaker crosspeaks for couplings of ¹L_b and ¹L_a in E22Q than the native fibril, which also implies the change of residue-residue interactions due to mutations.

We have further studied the mutated E22G (the native E22 to G (Glycine)) Aβ_9–40 fibril. The spectra are displayed in the right column of Fig. 6. The LA spectrum is very similar to the E22Q fibril. Their CD spectrum are also similar, but E22G has less fine spectral features. 2DNUV xxxx and xxxy spectra of E22G have essentially the same spectra as E22Q, except the crosspeaks for couplings of ¹L_b and ¹L_a disappear in E22G, and both of the ¹L_b and ¹L_a induced diagonal peaks are strictly symmetric. This is because the residue-residue interactions in the E22G fibril is much weaker than those in the native and E22Q fibrils. Thus, the ¹L_b transitions are less affected by couplings between chromophores and transitions. It is also the reason that the E22G mutation increases the intensity of the ¹L_b xxxy signal by about 10 times than the native and E22Q fibrils.

4. Conclusions

EHEF is a first principles simulation protocol for the 2DNUV spectra of proteins. It combines electronic structure computations of isolated protein fragments and solvent molecules, and gives accurate descriptions for aromatic transitions at the first principle level. It also provides an effective interface for QM and MM simulations, that avoids expensive repeated QM calculations and generates the fluctuating Hamiltonian at the QM level for all the MD snapshots. Simulations were carried out for the β-amyloid (Aβ_9–40) fibrils associated with the Alzheimer’s disease. The simulated 1DNUV spectra of fibrils in water in the presence of electrostatic fluctuations show good agreements with experiment. 2DNUV spectra are shown to provide a sensitive probe of molecular interactions and local structural details in fibrils. The spectroscopic signatures of ¹L_b and ¹L_a transitions, and their couplings are identified. Analysis of contributions of different aromatic chromophores to 2DNUV signals demonstrates strong signatures of interactions between chromophores. The 2DNUV chiral xxxy signals associated with couplings between transitions can reflect the change of residue-residue interactions, so that are sensitive to mutations of residues in the Aβ_9–40 peptide.