Population pharmacokinetics of pregabalin in healthy subjects and patients with post-herpetic neuralgia or diabetic peripheral neuropathy

Abstract

AIM

Pregabalin, a chemical analogue of the mammalian neurotransmitter γ-aminobutyric acid, has been approved in many countries for partial-onset seizures, generalized anxiety disorder and various other pain disorders, including neuropathic pain associated with post-herpetic neuralgia and diabetic peripheral neuropathy and fibromyalgia. The aim of this study was to develop a population pharmacokinetic model and quantify the influence of covariates on the parameters.

METHODS

This pregabalin population pharmacokinetic analysis was conducted on data from 14 clinical trials involving healthy subjects, subjects with impaired renal function and patients with post-herpetic neuralgia or diabetic peripheral neuropathy (n = 616). The data analysis was performed using nonlinear mixed effects modelling methodology as implemented by NONMEM.

RESULTS

A one-compartment model with first-order absorption and elimination adequately described pregabalin pharmacokinetics. The model indicated that pregabalin apparent clearance (CL/F) was proportional to estimated creatinine clearance (CL_cr). The pregabalin systemic exposure in patients with lower renal function who received pregabalin 150 mg twice daily was almost equal to that of patients with normal renal function administered pregabalin 300 mg twice daily. The systemic exposure stratified by lower or normal renal function was similar between patients with post-herpetic neuralgia and diabetic peripheral neuropathy.

CONCLUSION

The developed model identified CL_cr and ideal body weight as clinically influential covariates on CL/F and volume of distribution, respectively. This study indicates that renal function accounts for variability in the apparent clearance of pregabalin which is consistent with what is known about the elimination of this drug.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

• Pregabalin has been approved in many countries for partial-onset seizures, generalized anxiety disorder and a wide variety of pain disorders.

• Although pharmacokinetic studies have demonstrated that pregabalin apparent clearance is correlated with estimated creatinine clearance, quantitatively accurate estimation of this relationship is warranted for establishing clinical usage of this drug.

WHAT THIS STUDY ADDS

• A population pharmacokinetic model was developed from 14 pregabalin clinical trials using the first-order conditional estimation method, where a one-compartment model with first-order absorption and elimination adequately described pregabalin pharmacokinetics.

• Based on the developed model, pregabalin systemic exposure in patients with lower renal function (30 ≤ estimated creatinine clearance [CL_cr] <60 ml min⁻¹) is expected to be similar to exposure in patients with normal renal function (CL_cr≥60) administered twice the dose.

• This study indicated that the systemic exposure of pregabalin could be adjusted with reference to the estimated proportional relationship between pregabalin apparent clearance and CL_cr regardless of the disease.

Introduction

Pregabalin (Lyrica®) is a chemical analogue of the mammalian neurotransmitter γ-aminobutyric acid (GABA), which binds with high affinity to an auxiliary subunit of voltage-gated calcium channels, α₂δ site, in central nervous system tissues [1]. Potent binding at this site may lead to anticonvulsant, anxiolytic and analgesic effects by reducing the release of several neurotransmitters, including glutamate, noradrenaline and substance P [2–5]. Pregabalin has been approved in many countries as adjunctive therapy for adult patients with partial-onset seizures, and as monotherapy for generalized anxiety disorder and a variety of pain disorders, including neuropathic pain associated with post-herpetic neuralgia and diabetic peripheral neuropathy, and fibromyalgia.

Pregabalin is absorbed with oral bioavailability ≥90% and eliminated from the systemic circulation primarily by renal excretion as unchanged drug [6]. Indeed, a pharmacokinetic (PK) study in subjects with various degrees of renal function suggested that pregabalin clearance was clearly correlated with estimated creatinine clearance (CL_cr) [7]. In addition, Bockbrader et al. [8, 9] performed population PK analyses of pregabalin for patients with refractory partial seizures and chronic pain using nonlinear mixed effects models, where they showed that pregabalin apparent clearance (CL/F) was clearly proportional to CL_cr. Based on these findings, the systemic exposure of pregabalin is significantly influenced by renal function, and it is considered important to provide a quantitatively accurate estimation of the relationship between pregabalin clearance and CL_cr for establishing clinical usage of this drug.

The aim of this study was to investigate the population pharmacokinetics of pregabalin using data from 14 clinical trials and characterize the factors that contribute to variability in pregabalin pharmacokinetics.

Methods

Clinical studies and assay methods

Data used for the analysis were obtained from 14 clinical studies. Five of the nine phase 1 studies were conducted to investigate safety and pharmacokinetics following single and/or multiple oral administrations of pregabalin in healthy adult volunteers (Table 1). Two studies, HV03 and HV09, were designed to assess the effect of food on pregabalin pharmacokinetics and relative bioavailability of pregabalin, and the other two studies, HV05 and HV07, were conducted in subjects with various degrees of renal function and in elderly subjects, respectively. In all phase 1 studies, blood samples for plasma pregabalin concentrations were collected sequentially with a sufficient number of samples per subject to calculate individual parameters of noncompartment PK analysis. The dose range varied from a single dose of 1 mg to 300 mg twice daily (600 mg daily) or three times a day (900 mg daily).

Table 1.

Summary of clinical studies including number of subjects (observations) and mean (range) age, body weight and estimated creatinine clearance

Study/Country	Study design	Analysis population (observation)	Age (years)	Total body weight (kg)	CLcr (ml min−1)
Healthy volunteers*
HV01/US	R, DB, PC, XO, PK	29 (338)	40.1 (29, 49)	77.4 (60, 91)	104 (79.0, 152)
HV02/US	R, DB, PC, PG, PK	45 (1409)	35.4 (19, 50)	75.5 (61, 94)	108 (60.0, 155)
HV03/US	R, OP, XO, PK	11 (401)	54.2 (38, 65)	72.2 (56, 92)	100 (63.9, 147)
HV04/US	R, DB, PC, PK	12 (393)	31.8 (19, 48)	75.0 (61, 85)	120 (96.9, 147)
HV05/US	OP, PG, PK	26 (327)	56.4 (38, 75)	80.8 (45, 106)	57.0 (10.0, 122)
HV06/JP	R, SB, PC, PG, PK	30 (422)	22.9 (20, 28)	62.6 (52, 83)	113 (75.0, 163)
HV07/JP	R, SB, PC, PK	6 (67)	71.8 (67, 78)	60.1 (46, 68)	60.2 (54.0, 71.1)
HV08/JP	R, DB, PC, PG, PK	16 (483)	24.7 (20, 42)	63.3 (52, 79)	113 (91.2, 148)
HV09/US	R, OP, XO, PK	20 (810)	35.8 (21, 54)	68.3 (55, 86)	105 (68.9, 142)
Subtotal	–	195 (4650)	38.1 (19, 78)	72.1 (46, 106)	100 (10.0, 163)
Patients with post-herpetic neuralgia
PT01/US	MC, R, DB, PC, PG	92 (92)	74.3 (48, 87)	78.3 (48, 142)	63.6 (35.2, 227)
PT02/EU, AU	MC, R, DB, PC, PG	84 (84)	72.8 (33, 91)	72.9 (47, 110)	70.6 (34.9, 123)
PT03/US,CA	MC, R, DB, PC, PG	65 (101)	73.0 (45, 101)	74.6 (53, 102)	70.9 (23.7, 188)
PT04/JP	MC, R, DB, PC, PG	26 (50)	73.1 (42, 87)	54.3 (40, 70)	66.2 (32.8,120)
Subtotal	–	267 (327)	73.4 (33, 101)	73.4 (40. 142)	67.8 (23.7, 227)
Patients with diabetic peripheral neuropathy
PT05/JP	MC, R, DB, PC, PG	154 (298)	60.9 (35, 85)	65.6 (31, 113)	99.3 (32.2, 230)
All
Total	–	616 (5275)	59.1 (19, 101)	71.0 (31, 142)	86.0 (10.0, 230)

^*HV05 and HV07 were conducted on subjects with various degrees of renal function and on elderly subjects, respectively. US, United States; CL_cr, estimated creatinine clearance; R, randomized; DB, double-blind; PC, placebo-controlled; XO, crossover; PK, pharmacokinetics; OP, open-label; PG, parallel-group; JP, Japan; SB, single-blind; MC, multicentre; EU, European countries; AU, Australia; CA; Canada.

Regarding clinical efficacy studies, four studies, PT01, PT02, PT03 and PT04, and one study, PT05, were randomized studies in patients with post-herpetic neuralgia and diabetic peripheral neuropathy, respectively. In these studies, blood samples for plasma pregabalin concentrations were collected sparsely in outpatient settings, where one or two blood samples per patient were used for the population PK analysis. The doses used in these studies were 75–300 mg twice daily or 25–200 mg three times daily (up to 600 mg daily). All studies were approved by institutional review boards, and informed consent was obtained from all subjects.

Plasma samples were analysed for pregabalin using validated high-performance liquid chromatography (HPLC) methods with ultraviolet (UV) detection as published previously [10] or a validated liquid chromatography/tandem mass spectrometry (LC-MS/MS) method. In the HPLC-UV method of the first study (HV01), plasma pregabalin concentrations were measured with a lower limit of quantification (LLQ) of 0.005 µg ml⁻¹ (MW = 159.23). The precision and accuracy ranged from 1.7% to 3.5% and −1.3% to 4.0%, respectively. In the subsequent studies, the HPLC methods had similar ranges of precision and accuracy, while the LLQ varied across studies from 0.005 to 0.05 µg ml⁻¹. In studies HV08, HV09, PT04 and PT05, the LC-MS/MS method was used for measuring plasma pregabalin concentration with a LLQ of 0.025 µg ml⁻¹. Following extraction with methanol including the same internal standard as the HPLC-UV method, the supernatant was injected onto an API 365 LC-MS/MS system (Column, Aquasil C₁₈; mobile phase, an aqueous acetonitrile/methanol solution). The precision and accuracy ranged from 4.5% to 5.5% and −4.4% to −1.3%, respectively.

Data analyses

The data analysis was performed using nonlinear mixed effects modelling methodology as implemented by NONMEM Version 5 Level 1.1 and the key results were confirmed by NONMEM Version 7 Level 1.2 (ICON Development Solutions, Ellicott City, MD, USA). The software on a Pfizer analysis platform was used for this analysis and tested internally. NONMEM was used to estimate the population parameters, mean and interindividual variability and to identify potential covariates that explain interindividual variability in the parameters. The first-order conditional estimation method with η-ε interaction was used for all model runs [11].

Since the observed plasma pregabalin concentrations were rapidly absorbed and decreased in a monophasic manner after administration (data not shown) and the pharmacokinetics of pregabalin are known to be linear [10], pregabalin pharmacokinetics following single and multiple administrations were described using a one-compartment model with first-order absorption and elimination (NONMEM subroutine ADVAN2). Specifically, the expected level of the plasma pregabalin concentration, C_ij, for the ith individual at time t_ij following oral administration was modelled via the one-compartment model with nonlinear mixed effect modelling of fixed and random effect parameters. Equation [1] shows the plasma pregabalin concentration at t_ij following oral administration at time zero.

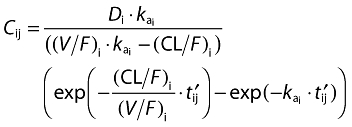(1)

Where

Here, t_lag is a common absorption lag-time and D_i represents dose. The parameters, k_a, CL/F and V/F, are fixed effect parameters or population mean parameters for absorption rate constant, apparent clearance and apparent volume of distribution, respectively. The vector of random effect parameters (η_kai, η_(CL/F)i, η_(V/F)i) linked with the individual-specific parameters (k_ai (CL/F)_i (V/F)_i) were assumed to follow normal distribution with mean zero and a variance-covariance matrix Ω with independent correlation structure.

The residual variability (intra-individual variability) was incorporated using an additive and proportional combined-error model. Specifically, the observed level of the plasma pregabalin concentration for the ith individual at time t_ij, Y_ij, is specified by Y_ij=C_ij+C_ij·ε_ij1+ε_ij2, where the independent error term ε_ij1 (ε_ij2) was assumed to follow a normal distribution with mean zero and variance σ₁² (σ₂²).

Inclusion of covariates was performed as described herein. Based on prior information about pregabalin pharmacokinetics, CL_cr and food status were tested in the base model development. The food status of each subject was recorded in the database based on self-reported data. The subject who received pregabalin with food within 2 h and with food but exact meal time unknown were assigned to fed, otherwise they were assigned to fasted. For the final model development steps, covariates were screened and added to the base model guided by a forward selection algorithm (significance level of α = 0.01, d.f. = 1) to obtain a full model. The covariates screened for disposition parameters were total body weight, height, age, subject type (healthy or patient), ethnicity (Japanese or non-Japanese), gender, body mass index (BMI), ideal body weight (IBW) [12] and lean body weight (LBW) [13]. Covariate values collected from the earliest visit were carried forward for subsequent visits until a new covariate value was collected.

CL_cr was calculated based on the Cockcroft & Gault (CG) equation [14] given as follows:

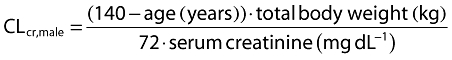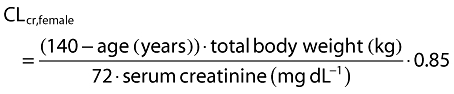The following equations were used for BMI, IBW and LBW calculations, respectively.

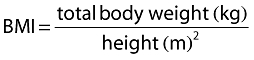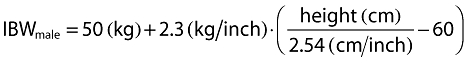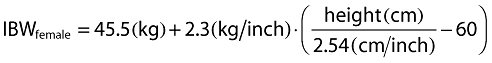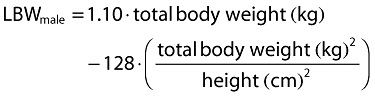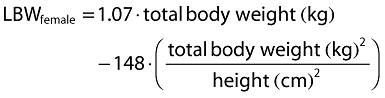After the full model was developed, formal statistical tests using a backward elimination algorithm were performed to select the final model. The formal statistical tests were performed based on likelihood ratio tests, which correspond to statistical significance of the difference in the NONMEM objective function values (ΔOFV). The significance level of the likelihood ratio tests was specified by α = 0.001 by convention in population PK analyses. The covariate parameter with the greatest P value (least significance), but greater than α, was excluded from the model for the next backward elimination step. The final model was obtained from the last stage of the backward elimination algorithm in which all of the remaining covariate parameters were significant when excluded one at a time. Since it has been reported that the likelihood ratio as the sole criterion is associated with risk of including false covariates [15], visual inspections were also performed using plots of the covariates to be tested and plots of trends of ηs before and after inclusion of covariates.

The final model was validated by diagnostic plots, nonparametric bootstrapping and visual predictive check. For the base and final models, observed concentrations (DV) vs. population- or individual-predicted concentrations (PRED or IPRED) were plotted for model diagnostics. In addition, conditional weighted residuals (CWRES) [16] were plotted against the predicted concentrations and time after last dose. Nonparametric bootstrapping with 300 resampling datasets was performed to check the validity of confidence intervals (CIs) for parameter estimates based on normal approximation under the final model. Regarding visual predictive check, 500 new datasets were simulated from the final model and used to construct 95% prediction intervals (the 2.5, 50 and 97.5 percentile points) for pregabalin concentrations.

Results

Demographic data

Data used for this PK analysis were obtained from 14 clinical studies (n = 616), as shown in Table 1. Of these, nine studies were conducted to investigate pharmacokinetics and safety in healthy subjects and subjects with impaired renal function, and five studies were conducted to investigate efficacy and safety in patients with post-herpetic neuralgia or diabetic peripheral neuropathy. The population PK analysis used a total of 5275 plasma pregabalin concentrations, of which 4650 (88.2%) observations were from healthy subjects and 625 (11.8%) were from patients with post-herpetic neuralgia or diabetic peripheral neuropathy. The median (range) of the sampling times after the last dose was 6.0 (0–168) h in healthy subjects and 2.3 (0–31) h at steady-state in patients. Regarding sparse sample collection for plasma pregabalin concentrations, there were 36 observations around the absorption phase (up to 0.75 h), 358 observations in the vicinity of C_max (0.75–3.00 h) and 231 observations around the elimination phase (>3.0 h). Pregabalin dose ranged between 1 and 300 mg across the studies.

The mean (range) age, body weight and CL_cr for all subjects (n = 616) were 59.1 (19–101) years, 71.0 (31–142) kg, and 86.0 (10.0–230) ml min⁻¹, respectively. The CL_cr was estimated using the CG equation [14] unless otherwise specified. The equation includes body weight as well as serum creatinine and age. The mean age in the patient studies, PT01 to PT05, tended to be higher than those in the healthy volunteer studies. The mean body weight values appeared similar across all studies, whereas the mean CL_cr values in the patient studies were lower than those in the healthy volunteer studies with the exception of two studies, HV05 and HV07, which were conducted to investigate the pharmacokinetics of pregabalin in subjects with impaired renal function and elderly subjects, respectively. Two subjects in the analysis data had missing values for height, which were replaced with the mean height value of 167 cm.

Patient demographics for all subjects (n = 616) are summarized in Table 2. The data consisted of 195 (32%) healthy volunteers including subjects with impaired renal function and 421 (68%) patients. Of the patients, 267 (63%) patients were diagnosed with post-herpetic neuralgia and 154 (37%) with diabetic peripheral neuropathy. The population included 229 (37%) female and 387 (63%) male subjects. Ethnicity consisted of White (n = 326, 53%), Black (n = 6, 0.97%), Asian (n = 256, 42%) and other (n = 28, 4.6%).

Table 2.

Subject demographics for the entire analysis dataset

Demographics variable	n	(%)
Gender
Male	387	(62.8)
Female	229	(37.2)
Patient type
Healthy volunteer	195	(31.7)
Post-herpetic neuralgia	267	(43.3)
Diabetic peripheral neuropathy	154	(25.0)
Ethnicity
White	326	(52.9)
Black	6	(0.974)
Asian*	256*	(41.6)
Other	28	(4.55)
Total	616

^*Asian included 252 Japanese subjects.

Base model development

Based on previous research [8, 9], a one-compartment model with first-order absorption and elimination was selected as the pregabalin PK structural model. Plasma pregabalin concentrations after single and multiple oral administrations showed that pregabalin was rapidly absorbed and eliminated from the systemic circulation in a monophasic manner, which suggested adequacy of the one-compartment model. As is known, CL_cr was correlated with pregabalin clearance and a high-fat meal reduced the rate of pregabalin absorption [7–9], effects of CL_cr on CL/F and food on absorption parameters, k_a and t_lag, were highly significant in a likelihood ratio test with P value <0.001, d.f. = 3. In a linear model to correlate CL/F with CL_cr, the intercept term accounted for only about 3% of mean CL/F and was not significantly different from zero with 95% CI of (–0.00628, 0.240), which suggests that the extra renal clearance of pregabalin can be ignored. The break point of CL_cr was estimated and significantly decreased the OFV. Figure 1 shows the relationships between individual observed CL/F and CL_cr or between individual predicted CL/F and CL_cr before and after adding the effect of CL_cr. These results indicated that pregabalin CL/F was proportional to CL_cr.

Figure 1.

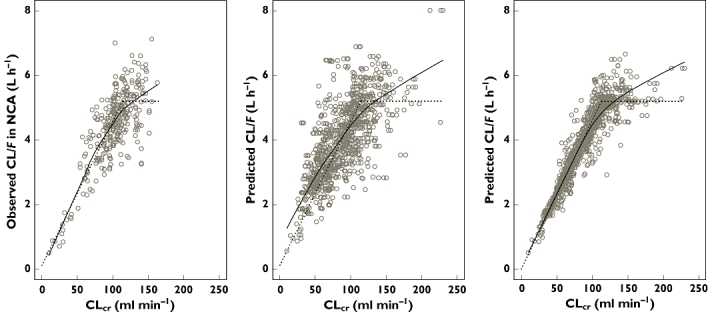
Scatter plots of pregabalin apparent clearance (CL/F) and estimated creatinine clearance (CL_cr). Circles in the left panel represent individual observed CL/F from noncompartment analysis (NCA; observed CL/F in NCA) vs. CL_cr (Note: the number of observed CL/F values were limited owing to the fact that NCA results were available only in healthy subjects and subjects with impaired renal function). Circles in the centre panel represent individual CL/F from post hoc Bayesian estimates in the initial base model without CL_cr effect on CL/F vs. CL_cr. Circles in the right panel represent the individual CL/F estimated from the final base model vs. CL_cr. Each solid line indicates a nonparametric regression with robust local linear fits. Each dotted line indicates the relationship between population mean CL/F vs. CL_cr in the final base model. Note: Several CL_cr values at different visits in the same subject (CL/F) are included in each plot

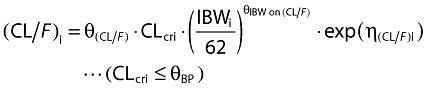
The diagnostic plots of the base model indicated that the model provided adequate description of the dataset (data not shown). The final form of the equation for the base model for individual i is given below:

where the parameter, θ, represents fixed effects, and η represents the random effects that follow a normal distribution with mean zero and variance Ω.

The estimation results of the population parameters are summarized in Table 3. The estimates (SE%) of CL/F[θ_CL/F multiplied by mean CL_cr in Table 1 (i.e. 0.0460 × 86)] and V/F were 3.96 l h⁻¹ (0.0772%) and 38.0 l (1.44%), respectively, which were considered valid in light of previously reported values [7–10].

Table 3.

Parameter estimates (SE%) for the base and final models

	Base model	Final model
Pharmacokinetic parameter	Estimate (SE%)	Estimate (SE%)	(95%CI*)	Nonparametric bootstrap, median (95%CI)
Objective function value	–4422.631	–4647.795	–	–
Drop from the base model	–	–225.164	–	–
CL/F (l h−1)
θCL/F	0.0460 (0.0772)	0.0462 (2.11)	(0.0443, 0.0481)	0.0461 (0.0448, 0.0476)
θBP	113 (1.71)	107 (5.22)	(96.0, 118)	107 (99.4, 122)
θIBW on CL/F	–	0.354 (24.5)	(0.184, 0.524)	0.350 (0.177, 0.505)
V/F (l)
θV/F	38.0 (1.44)	35.6 (2.03)	(34.2, 37.0)	35.6 (34.1, 37.2)
θIBW on V/F	–	0.819 (10.2)	(0.655, 0.983)	0.823 (0.636, 0.985)
θBMI on V/F	–	0.525 (10.7)	(0.415, 0.6350	0.534 (0.422, 0.633)
θAge on V/F	–	–0.125 (19.9)	(–0.174, −0.0762)	–0.131 (–0.177, −0.0750)
θGender on V/F	–	0.906 (2.26)	(0.866, 0.946)	0.903 (0.862, 0.952)
ka (h−1)
θka	8.99 (9.43)	7.99 (8.75)	(6.62, 9.36)	7.97 (6.77, 9.46)
θFood on ka	–0.927 (1.02)	–0.930 (0.978)	(–0.948, −0.912)	–0.930 (–0.947, −0.907)
tlag (h)
θtlag	0.243 (0.675)	0.243 (0.761)	(0.239, 0.247)	0.243 (0.238, 0.245)
θFood on tlag	0.813 (8.25)	0.811 (8.43)	(0.677, 0.945)	0.823 (0.656, 0.918)
Interindividual variability†
CV% (CL/F)	15.8 (7.93)	14.8 (8.25)	(12.2, 17.1)	14.6 (12.4, 17.4)
CV% (V/F)	17.1 (5.74)	8.54 (9.19)	(6.83, 9.96)	8.37 (6.76, 9.71)
CV% (ka)	98.1 (7.07)	93.2 (6.56)	(80.3, 105)	93.5 (82.8, 105)
Residual variability†
CV% (healthy)	22.0 (4.06)	22.0 (4.05)	(20.2, 23.7)	21.8 (20.2, 23.8)
SD (µg ml−1) (healthy)	0.0241 (20.4)	0.0239 (20.8)	(0.0103, 0.0322)	0.0235 (0.0125, 0.0343)
CV% (patient)	29.2 (7.68)	28.5 (8.81)	(23.1, 33.0)	28.2 (23.0, 32.3)
SD (µg ml−1) (patient)	0.218 (45.6)	0.236 (53.5)	(NC, 0.415)	0.240 (0.0902, 0.491)

^*The 95% CIs were calculated from estimate ± 1.96× SE from variance-covariance matrix provided by NONMEM.

^†Each CV% or SD was calculated based on first-order Tailor approximation; square root of ω² or σ². Each SE% was calculated based on first-order Tailor approximation of square root of ω² or σ²; SE[ω] = SE[ω²]/(2ω) or SE[σ] = SE[σ²]/(2σ). CI, confidence interval; CL/F, pregabalin apparent clearance; V/F, apparent volume of distribution; IBW, ideal body weight; NC, not calculated due to negative value of σ².

Final model development

The covariate selection was composed of two steps. As the first step, covariates were screened and added to the base model guided by a forward selection algorithm (significance level of α = 0.01, d.f. = 1) to obtain a full model. Of the covariates tested, effects of IBW on CL/F and effects of IBW, BMI, age and gender on V/F were selected as statistically significant covariates. Based on graphical inspection (Figure 2), age and IBW and gender and IBW looked slightly correlated, whereas the other covariates showed little correlation, which suggested that it was possible to include the covariates in the full model and proceed to the next step. As the second step, formal statistical tests using a backward elimination algorithm were performed to select the final model (significance level of α = 0.001, d.f. = 1). As a result, all the covariates in the full model remained in the model. The final form of the equation for individual i is given below.

Figure 2.

Scatter plots of individual random effects on pregabalin apparent clearance (CL/F) and volume of distribution (V/F) in the base model and covariates. ETA.CL, random effect on CL/F; ETA.V, random effect on V/F; AGE, age; WT, total body weight; BMI, body mass index; IBW, ideal body weight; CL_cr, estimated creatinine clearance; SEX (male = 0, female = 1); ETHN, ethnicity (non-Japanese = 0, Japanese = 1); TYPE (healthy = 0, patient = 1)

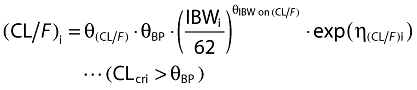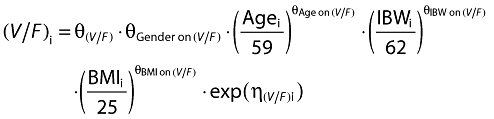The estimation results for the final model are summarized in Table 3. The ratio of maximum to minimum eigen values of the correlation matrix was 51.0, indicating that the final model estimates were stable and not influenced by ill-conditioning [17, 18].

Final model validation

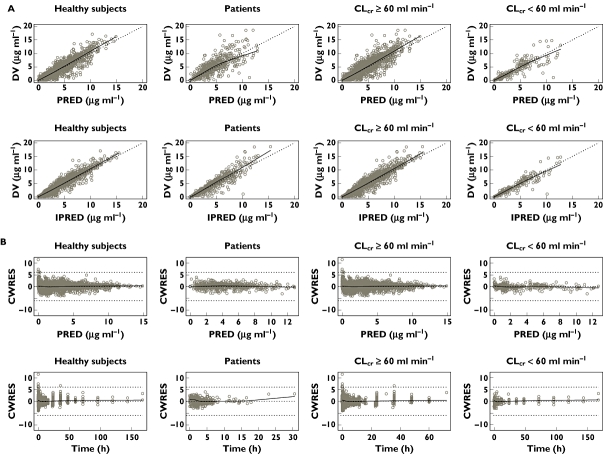
The final model was validated by diagnostic plots, nonparametric bootstrapping and a visual predictive check. Regarding diagnostic plots, Figure 3 shows scatter plots of mean PRED or IPRED vs. DV stratified by subject type (healthy subjects or patients) and renal function (CL_cr <60 or ≥60 ml min⁻¹). The plots indicate central tendency to the identity line (Y = X) and no major bias is observed. Plots of CWRES vs. PRED and time after the last dose (Time) are also presented in Figure 3. These plots do not show any systematic trend with regard to PRED or Time.

Figure 3.

(A) Scatter plots of observed pregabalin concentrations (DV) vs. population predicted mean concentrations (PRED) and DV vs. individual predicted concentrations (IPRED) for the final model stratified by subject type (healthy subjects or patients) and renal function (estimated creatinine clearance [CL_cr] <60 or CL_cr≥60 ml min⁻¹). Each dotted line represents concordance line (Y = X). Each solid line indicates a nonparametric regression with robust local linear fits. (B) Scatter plots of residuals normalized by the SD of the data (conditional weighted residuals [CWRES]) vs. PRED and CWRES vs. time after the last dose (Time) for the final model stratified by subject type (healthy subjects or patients) and renal function (CL_cr <60 or CL_cr≥60 ml min⁻¹). Dotted lines represent CWRES = 0, −6 and +6, respectively. Each line indicates a nonparametric regression with robust local linear fits

The final model developed during this analysis was also internally validated by nonparametric bootstrapping. The median values and 95% prediction intervals (2.5 and 97.5 percentile points) for each parameter estimate from 300 bootstrap datasets were comparable with each parameter estimate and the 95% CIs calculated with variance-covariance matrix for the parameter estimates provided by NONMEM (Table 3). Overall, the fixed and random effect parameters of the final model were distributed normally and estimated with good precision.

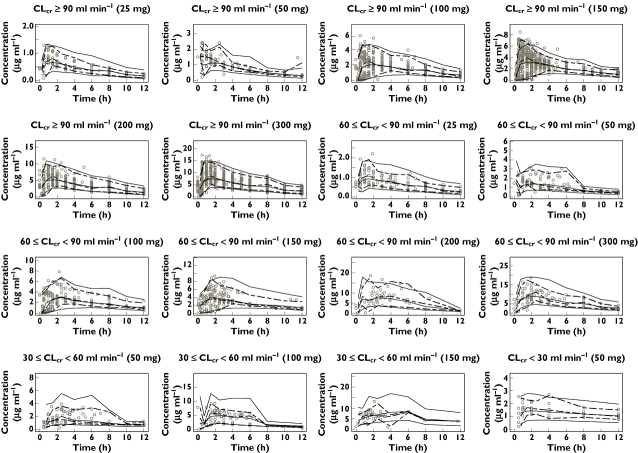
A visual predictive check was performed by providing plots of pregabalin concentration vs. time after the most recent administration stratified by pregabalin doses and renal functions (CL_cr≥90 ml min⁻¹, 60 ml min⁻¹≤ CL_cr <90 ml min⁻¹, 30 ml min⁻¹≤ CL_cr <60 ml min⁻¹, CL_cr <30 ml min⁻¹). Figure 4 illustrates the major findings. Although the 95% prediction intervals were somewhat wider than the observed intervals, the median values were comparable, and as a whole, the final model simulated the actual pregabalin PK profile across doses and levels of renal function.

Figure 4.

Visual predictive check plots representing pregabalin concentration vs. time after the most recent administration (up to 12 h) stratified by pregabalin doses (25, 50, 100, 150, 200 and 300 mg) and renal function (estimated creatinine clearance [CL_cr]≥90 ml min⁻¹, 60 ml min⁻¹≤ CL_cr <90 ml min⁻¹, 30 ml min⁻¹≤ CL_cr <60 ml min⁻¹, CL_cr <30 ml min⁻¹). Each panel shows observed pregabalin concentrations (circles), the observed 2.5, 50 and 97.5 percentile points (dotted lines) and the predicted (n = 500) 2.5, 50 and 97.5 percentile points (solid lines). Some plots in the lower renal functions are skipped owing to limited data

Assessment of dose adjustment by CL_cr

In one study (study PT05), patients with diabetic peripheral neuropathy were allocated to pregabalin 150 mg twice daily, 300 mg twice daily or placebo twice daily, where the dose was adjusted to 150 mg twice daily if patients allocated to 300 mg twice daily had lower renal function defined as 30 ≤ CL_cr <60 ml min⁻¹. Using information from this study, we confirmed whether the dose adjustment of pregabalin had been adequately performed by renal function (CL_cr). The individual AUC(τ,ss) was calculated using the post hoc Bayesian estimation of CL/F of the final model. As shown in Table 4, the mean AUC(τ,ss) (SD) of patients with normal renal function defined as CL_cr≥60 ml min⁻¹ who received pregabalin 150 mg and 300 mg twice daily were estimated as 37.5 (9.16) and 75.5 (17.1) µg ml⁻¹ h, respectively, whereas that of patients with the lower renal function allocated to or adjusted to 150 mg twice daily was estimated as 80.3 (16.5) µg ml⁻¹ h. The pregabalin exposure in patients with the lower renal function who received pregabalin 150 mg twice daily was almost equal to that in patients with the normal renal function administered pregabalin 300 mg twice daily, which suggests that pregabalin exposure was adequately controlled by the CL_cr-based dose adjustment.

Table 4.

Mean pregabalin AUC predicted from post hoc Bayesian estimates of individual apparent clearance in patients with diabetic peripheral neuropathy stratified by estimated creatinine clearance (CL_cr) and dose

CLcr	Dose (number of subjects)	CL/F (ml min−1)*	AUC(τ,ss) (µg ml−1 h)*
CLcr ≥ 60 ml min−1	300 mg twice daily (31)	69.2 (13.8)	75.5 (17.1)
CLcr ≥ 60 ml min−1	150 mg twice daily (109)	70.0 (14.6)	37.5 (9.16)
30 ≤ CLcr < 60 ml min−1	150 mg twice daily (14)	32.3 (6.34)	80.3 (16.5)

^*Arithmetic mean (SD).

Discussion

Previous research showed that pregabalin CL/F was clearly correlated with CL_cr[7–9]. In this study, we provided a population PK analysis of pregabalin for a large dataset from 14 pregabalin clinical trials involving healthy subjects, subjects with impaired renal function and patients with post-herpetic neuralgia or diabetic peripheral neuropathy. The analysis provided an accurate and reliable estimation of the relationship between pregabalin CL/F and CL_cr.

In the final model, effects of CL_cr and IBW were selected as statistically significant covariates on CL/F. However, the degree of change by IBW was relatively small when compared with that by CL_cr. When CL_cr changed from 60 ml min⁻¹ to 30 ml min⁻¹, CL/F proportionally and significantly decreased by 50%. On the contrary, even when IBW became extremely low (i.e. half of the mean 62 kg) CL/F deceased by 22%, a small change when compared with that of CL_cr.

Of the statistically significant covariates on V/F, only IBW was considered a clinically significant factor. When IBW changed to half or twice the mean, V/F changed by −43% and 76%, respectively. Regarding the other covariates, the degree of change was small. The reduction of V/F by age was of minor clinical importance because it decreased only 6.5% from the mean age (59 years) to the maximal observed age (101 years). The V/F decreased to 84% when BMI changed from 25 to 18 kg m⁻². Regarding gender effect on V/F, the 95% CIs for the ratio of females to males ranged from 86.6% to 94.6%, which fell within the clinically less significant range (80–125%). As a result, all the statistically significant covariates on V/F except for IBW were not considered clinically important.

Of the statistically selected covariates on V/F, the effect of IBW was considered clinically important. This suggested that it was valuable to explore simpler alternative models for V/F. In one model, we added only one covariate (IBW) to V/F. The fixed and random effects (IIV) for V/F and the fixed effect on IBW (power parameter) were estimated to be 36.0 l, 11.2% and 0.991, respectively, whereas all the other parameter estimates were not affected by removing age, BMI and gender from V/F. In another model, we applied the allometric equation to V/F; this was an allometric-based model for total body weight with the power parameter fixed to 1.0, which was developed with a mechanism-based concept [19]. In the allometric-based model, the fixed and random effects (IIV) for V/F were estimated to be 38.2 l and 16.9%, respectively, without influencing estimation of the other parameters. Based on the changes of the OFV and IIV on V/F, the former case, the IBW model for V/F was considered appropriate as an alternative simpler model for V/F. Since the fixed effects of IBW (power parameter) were almost 1.0, the IBW model for V/F would become an allometric model replacing total body weight with IBW.

In this analysis, the CG equation [14] was used for calculating CL_cr. The equation includes total body weight as well as serum creatinine and age. Since the CL/F of the final model was composed of both IBW, which is body weight relative to ideal weight for height, and the CL_cr whose equation includes body weight, it seemed that body weight–related variables were repeatedly selected as the covariate on CL/F. In addition, some of CL_cr values estimated from the CG equation were extremely high (e.g. over 200 ml min⁻¹). This suggested that alternative calculation methods for CL_cr should be tested. In the base-modelling step, instead of using CL_cr from the CG equation (CL_cr,CG), the other calculation methods for CL_cr[20, 21] were tested. The estimation methods were CL_cr calculated from IBW (CL_cr,IBW), obesity-adjusted IBW (CL_{cr,adjusted-IBW}) and body surface area (CL_cr,BSA). The extremely high CL_cr values were not improved by the other methods, though they slightly decreased using CL_cr,IBW[mean (range) = 88.9 (7.44, 196) ml min⁻¹]. Correlation coefficients between CL_cr,IBW, CL_{cr,adjusted-IBW} or CL_cr,BSA and individual CL/F estimated from an initial base model without inclusion of CL_cr were 0.671, 0.683 and 0.314, respectively, suggesting no strong correlation when compared with 0.667 from CL_cr,CG. In addition, after adding CL_cr,IBW, CL_{cr,adjusted-IBW} or CL_cr,BSA to the initial model, the OFV decreased by −520.603, −556.332 and −223.149, respectively, suggesting that they did not improve the model more than CL_cr,CG (–565.025). As a result, the CL_cr,CG was appropriate and comparable or superior to the other calculation methods in this population. Therefore, regarding covariate selection of IBW as well as CL_cr,CG on CL/F, it was likely that most of the variability of CL/F was explained by CL_cr,CG, but the remaining variability originating from renal function might be compensated by IBW in this analysis.

In the base model step, the break point was incorporated and estimated to be 113 ml min⁻¹. On the other hand, CL_cr values greater than 200 ml min⁻¹ (Figure 1) might suggest capping CL_cr values to something like 150 ml min⁻¹ in the model evaluation. The null hypothesis (H₀ : θ_BP = 150 ml min⁻¹) was tested and rejected in a likelihood ratio test with P value <0.001, d.f. = 1. As shown in Figure 1, CL/F appeared linearly correlated with CL_cr up to around 100 ml min⁻¹ and then constant, suggesting adequacy of the estimated break point (113 ml min⁻¹ in the base model). Together with the hypothesis test and visual inspection, it appears that estimation of the break point was reasonable in this analysis population.

Although effects of ethnicity (Japanese vs. non-Japanese), subject status (patients vs. healthy volunteers) and gender (females vs. males) on CL/F were not statistically significant and were not included in the final model, it was considered important to confirm their degree of impact on pregabalin systemic exposure. When adding each covariate to the final model, the ratios (95% CIs) of Japanese to non-Japanese, females to males and patients to healthy volunteers for CL/F were 104% (99.5, 109), 93.1% (86.5, 99.7) and 92.5% (85.2, 99.9), respectively, fell within the clinically less significant range (80–125%).

With regard to disease, differences in systemic exposure in patients with post-herpetic neuralgia or diabetic peripheral neuropathy were assessed using individual post hoc Bayesian estimation of CL/F of the final model. Based on the individual CL/F, pregabalin AUC(τ,ss) at 150 mg twice daily was predicted and summarized by the disease. The mean (SD) of AUC(τ,ss) for patients with post-herpetic neuralgia (n = 267) and diabetic peripheral neuropathy (n = 154) were 54.9 (19.1) and 41.3 (15.4) µg ml⁻¹ h, respectively, which suggested that systemic exposure in patients with post-herpetic neuralgia was slightly higher than in those with diabetic peripheral neuropathy. However, when considering renal function with definition CL_cr≥60 ml min⁻¹ as normal and 30 ≤ CL_cr <60 ml min⁻¹ as lower, the mean (SD) AUC(τ,ss) for patients with post-herpetic neuralgia and diabetic peripheral neuropathy with normal renal function were 42.4 (8.88) and 37.1 (8.69) µg ml⁻¹ h, respectively, while those with lower renal function were 70.8 (16.6) and 75.3 (15.5) µg ml⁻¹ h, respectively. This showed that AUC(τ,ss) estimated from the final model was similar between the patients with post-herpetic neuralgia and diabetic peripheral neuropathy. These results suggest that pregabalin systemic exposure was explained adequately by CL_cr regardless of the disease.

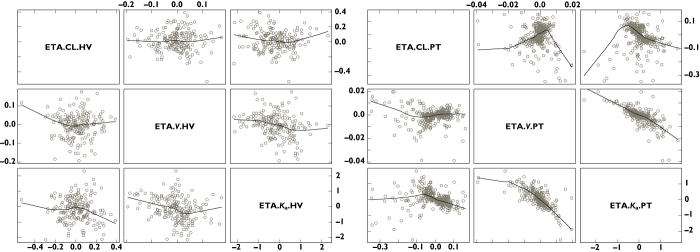
The η- and ε-shrinkage was reported to provide value of model diagnostics based on empirical Bayesian estimation [22]. In the final model, the η-shrinkage in healthy subjects for CL/F, V/F and k_a was 12.1%, 26.2% and 18.8%, respectively, whereas those in patients were 49.9%, 93.2% and 51.2%, respectively. The ε-shrinkage in healthy subjects and patients were 4.33% and 13.9%, respectively. As expected, η-shrinkage in patients were higher owing to few observations per patient. Figure 5 represents η plots in healthy subjects and patients separately. It shows the correlation between η_V/F and η_ka in patients and a lack of correlation in healthy subjects. The correlation in patients was considered to be due to the high η-shrinkage for V/F. It was reported that when shrinkage was present, model diagnostics should not be based on empirical Bayesian estimation but rather on simulation-based diagnostics or CWRES [22]. In this analysis, diagnostics based on visual predictive check and CWRES showed adequacy of the model and the model-building procedures were mainly based on NONMEM objective function values, thereby suggesting that the estimation of population parameters given in the final model is unlikely to be affected by these high shrinkage values found in patients.

Figure 5.

Scatter plots of the empirical Bayesian estimates in the final model in healthy subjects (left panel; ETA.CL.HV =η_CL/F, ETA.V.HV =η_V/F and ETA.k_a.HV =η_ka) and patients (right panel; ETA.CL.PT =η_CL/F, ETA.V.PT =η_V/F and ETA.k_a.PT =η_ka). Each line indicates a nonparametric regression with robust local linear fit

We provided information about CL_cr-based dose adjustment and systemic exposure by disease using the empirical Bayesian estimation. Since the high η-shrinkage value (49.9%) for CL/F in patients existed, it was considered necessary to confirm the result using another approach. The empirical Bayesian estimates (η_CL/F) in healthy volunteers were well estimated with normal distribution and low shrinkage value (12.1%). Therefore, under the assumption that interindividual variability in patients would be similar to that in healthy subjects, the η_CL/F in patients was resampled using nonparametric bootstrapping (n = 300) from that in healthy volunteers, and then the average systemic exposure in patients stratified by renal function or disease was calculated. In study PT05, pregabalin AUC(τ,ss) in 150 mg twice daily and 300 mg twice daily treatment groups (CL_cr≥60 ml min⁻¹) was predicted to be 36.8 (10.2) and 72.3 (18.9) µg ml⁻¹ h, respectively, while AUC(τ,ss) in 150 mg twice daily treatment group (CL_cr <60 ml min⁻¹) was predicted as 80.4 (21.6) µg ml⁻¹ h. Those results were similar to the original result (Table 4). In addition, differences in systemic exposure by disease were assessed using the bootstrapping data. The mean (SD) of AUC(τ,ss) at 150 mg twice daily in patients with post-herpetic neuralgia and diabetic peripheral neuropathy with CL_cr≥60 ml min⁻¹ was estimated as 41.9 (10.2) and 36.1 (9.35) µg ml⁻¹ h, respectively, while those patients with 30 ≤ CL_cr <60 ml min⁻¹ were 69.5 (16.0) and 76.9 (21.6) µg ml⁻¹ h, respectively. These data showed that the results of the CL_cr-based dose adjustment and exposure estimation by the disease were robust for the η-shrinkage.

In conclusion, this study strengthens evidence from previous reports [7–9] that pregabalin CL/F was proportional to CL_cr with precise estimates of the parameters and effects of covariates. The pregabalin systemic exposure in patients with lower renal function (30 ≤ CL_cr <60 ml min⁻¹) who received one-half the dose reached the expected level in patients with normal renal function (CL_cr≥60) who received the full dose, suggesting pregabalin dose was adequately adjusted by CL_cr. This study indicates that renal function accounts for variability in the apparent clearance of pregabalin which is consistent with what is known about the elimination of this drug.

Competing Interests

The studies described herein were funded by Pfizer Japan Inc. and Pfizer Inc. Satoshi Shoji, Misaki Suzuki, and Yoshiro Tomono are employees of Pfizer Japan Inc. Howard Bockbrader is an employee of Pfizer Inc. Although Dr Matsui and Pfizer Japan Inc. have a collaborative research contract, Dr Matsui was not funded by Pfizer Japan Inc. or Pfizer Inc to conduct this research or develop this manuscript.